Keywords

1 Introduction

In optimization, we set the objectives when looking for the best possible configuration of a set of variables. We can deal with these problems by discretizing the variables or taking the real values. Thus, each optimization problem is specified by defining the possible solutions (or states) and a general objective. The classical optimization paradigm is understood as to how the solution identifies by enumeration or differential calculus, the existence of an assumed (unique) solution, or the convergence of classical optimization methods for the solution of the corresponding first-order conditions.

Probabilistic distribution methods such as Montecarlo offer flexible forms of approximation, with some advantages regarding cost. In this sense, metaheuristics are high-level algorithms that are capable of determining a sufficiently satisfactory (almost optimal) solution for an approximate optimization problem, while other approaches use similarity.

We propose a heuristic algorithm that works in conjunction with clustering techniques based on [1]. The Montecarlo K-Means (MCKM) method was improved and evaluated with the optimization benchmark functions [4], which are high-Dimensional problems in a large search space. In all the benchmark cases analyzed, we came up with the improved heuristic Montecarlo Density K-Means (MCDKM), obtaining promising results comparable with those in the literature.

For this paper, our proposal goes a step further in solving different types of combinatorial optimization problems where search processes are involved. We have selected the Knapsack Problem (KP), which seeks to maximize the profits provided by a selection of elements to enter a Knapsack. The objective function would be defined as the total profit of the selected objects. KP is a classic combinatorial optimization problem with various applications in different industries, such as resource allocation, tasks, resource management/scheduling, or energy allocation management. KP is also part of a historical list of NP-Complete problems elaborated by Richard Karp [5].

Martello [8], on the background of this classic NP-Hard problem, offers an extensive review of the many effective heuristics to solve the KP. For example, a population-based approach such as incremental learning algorithm based on a greedy strategy in [7]. In addition, other different heuristic techniques, such as [3, 6, 9] are proposed to provide an acceptable solution to this problem.

Regarding the contribution of our heuristic method MCDKM, it has been validated that it can find feasible solutions. In the methodology, we will see how the partitions in n-dimensions of the search space may reduce the ordering times of the axes. The results section compares the solution quality found when varying the Dimensional arrays that organize the data, ranging from bi-dimensional to more than 50-dimension arrangement.

The paper organizes as follows. Section 2 describes the MCDKM heuristic method. Section 3 introduces the Knapsack problem into the MCDKM method, Sect. 4 details the implementation and the results, and finally, Sect. 5 presents the conclusions and future work.

2 Description of the MCDKM Heuristic Method

MCKM heuristic method [1] was initially developed to solve a particular combinatorial optimization problem. Our proposal goes a step further by adding a previous step. This is, we prepare the problem by parameterizing it and organizing the search in an n-dimensional space. Furthermore, we also perform a density analysis of the generated map. Bringing the problem into our parameters will contribute to the solution’s efficiency since, first, the search space can be significantly reduced. Second, the ordering times of the axes are improved, even when sorting them in a more significant number of dimensions. All this finally translates into a general improvement that contributes to increasing the quality of the solution and a good ratio between the size of the problem and the analyzed sample.

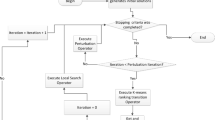
The procedure is shown in detail in Fig. 1. First, with Montecarlo, we generated a uniform sample that formed a map that is distributed through the whole search space. Then, the sample is reduced through the density analysis (for which we use the DBScan [2] algorithm), sweeping data to discard the sample that is not worth analyzing while keeping the remaining areas to perform another clustering process. Such clustering is made with k-means, which is now able to correctly partition the sample to group the feasible solutions into clusters for its selection.

Fig. 1.
figure 1

Flowchart showing the redesigned MCKM heuristic algorithm, highlighting its stages and showing benchmarks as a solution example.

Full size image

The now more robust MCDKM heuristic method was able to find the best solution values, which turned out to be very similar and comparable to the optimum solution of the benchmark functions. The success rate was between 97% and 99%, as seen in the results from [4].

3 The Knapsack Problem into the MCDKM Method

We are bringing the Knapsack Problem KP01 into our heuristic method to find a comparable efficient solution. This combinatorial optimization problem is sometimes exemplified as: the objective is for a supposed person to choose the elements that will allow him to maximize the benefit without exceeding the allowed capacity of a Knapsack. The problem can be stated as a problem of vectors \(X = (x_{1}, x_{2}, x_{3}, ... x_{n})\), which have components of zeros and ones, shown in Eq. 1, and have at most the restriction of the objective function Z(x), as seen in Eq. 2. Mathematically, we have the following:

$$\begin{aligned} W\left( x\right) =\ \sum _{i=1}^{n}x_{i}w_{i}\le \ W \end{aligned}$$
(1)
$$\begin{aligned} Z\ \left( x\right) =\ \sum _{i=1}^{n}x_{i}p_{i} \end{aligned}$$
(2)

where W denotes the maximum capacity of the backpack, x would be the elements whose index numbering can vary from 1 to n. Concerning \({w_{i}}\) and \({p_{i}}\) they represent the weight and value of the i element, meaning that the sum of the weights must not exceed the knapsack capacity, which is W. Now, Z(x) is the objective function (maximize or minimize). In addition, a vector x in Eq. 2 that meets the constraint W is feasible if we have a maximum result in Z(x).

Table 1. Dataset EX01: Knapsack capacity (W) = 6,404,180 and profit (P) = 13,549,094 elements n(i)=24
Full size table

Analyzing these statements is one of the essential steps in the methodology to adapt the parameters. First, we find the relationship between the variables to sort the data into a Montecarlo map.

Since this KP modality is a decision problem, our strategy considers the elements as belonging to different dimensions. This is, we divide the search space into multiple dimensions distributing the elements among them, and subsequently ordering according to all the possible combinations between them and identifying them with an ID.

We selected two available open-source datasets, EX01 from Kreher and Stinson which was checked with a branch and bound (B&B) algorithm. EX02 is a dataset available in the ORLibrary. EX03 dataset was based on EX01.

Table 1 shows a Dimensional array we designed for EX01. As seen, for a 2-D search space, 12 elements will be placed in each dimension, and the ordering is made out of all the possible combinations between these 12 elements. In the case of a 24-D search space, each element belongs to a dimension. Ordering the elements should be more efficient, which could be taken as an advantage in terms of resource use.

Table 2. Detail of the possible combinations (C) in the 1st-dim. of an 8-dim array.
Full size table
Fig. 2.
figure 2

Establishing a Montecarlo index for each combination in every dimension. Every sample fulfills the restriction in an 8-Dimensional search space.

Full size image
Table 3. Solution found by the heuristic method for a 8-Dimensional search space.
Full size table

The Montecarlo map generates by crossing data between the combinations of the elements, which must not exceed the restriction (Eq. 1) or the value is rejected. The uniform map is formed with the samples that meet the weight constraint. The binary code serves as a coordinate representation of such combinations since there are only two possible states. Each digit position represents whether an element will be packed or not, so we know what elements are within each coordinate. Afterward, ordering the axes is carried out in ascending order of best profit. In Table 2 we show how ordering a dimension takes place.

In Fig. 2, we illustrate how we define the map by establishing a Montecarlo index and referring to the position of each combination of elements in each dimension, which returns an integer when generating random samples.

After creating the Montecarlo map, we seek to reduce the search space. Now, the density clustering algorithm can be applied directly to this map, but it has to be adjusted to work efficiently.

We make such adjustment by cutting the map along the objective function axis. Cutting the map helps improve the clustering, and we can avoid analyzing the complete map. Sweeping of the data must occur, and then the stopping criterion is activated when more than 1 cluster is found. We aim for the largest number of clusters since it interprets as many feasible areas. Now, the rest of the sample can be discarded, narrowing the search space.

The results are detailed in Table 3, where the list of combinations found by the heuristic results in a MaxProfit (P) = 13,405,311 fulfilling the restriction since the sum of the weight (W) = 6,383,556.

Table 4. Shows the results for the EX01, EX02 and EX03.
Full size table

4 Implementation and Empirical Results

The headers of Table 4 detail the best solutions found for each data-set of the Knapsack Problem, such as the capacity (W), the number of elements (n), the fitness used, and the Optimal Profit (P), obtained with a branch and bound (B&B) algorithm. The rest of the Table represents the best results obtained by the MCDKM heuristic out of 30 executions for each space partition.

As expected, as the number of dimensions increased, the Axis sort time decreased when it required fewer elements, thus decreasing the total time until finding a solution. Therefore, it can be considered an advantage against other types of search algorithms capable of finding the optimal but entailing a high computational cost (like B&B). Also, as seen in Table 4, we emphasize the ratio between the number of samples and the size problem. As a result, the total samples needed to find an efficient solution was less than 1% in all cases.

Regarding EX03, we increased the complexity to compare us with other algorithms. In this case, we used branch and bound. We verified that, as the complexity of the problem increases, the execution time might also increase, influencing the prediction quality. Nevertheless, the solution maintained a prediction quality above 95% in less than 1 s (when partitioned into 80 dimensions). In contrast, the execution time was considerably longer even though the branch and bound algorithm obtained the optimal solution.

Therefore, heuristic search methods, especially ours that perform stochastic optimization, provide a good way to solve large combinatorial problems and offer a high-quality solution.

5 Conclusions and Future Work

The Knapsack Problem was entirely adapted and brought into our parameters. As a result, we found an efficient solution and achieved better results in the execution time when we increased the no. of partitions of the search space. Furthermore, we significantly reduced the number of samples needed to reach the best solutions compared to the full sample (which is the problem size) in all cases. Space ordering and sorting is an essential step in the methodology.

As we present in this paper, the MCDKM heuristic search algorithm proved some of its advantages, such as its applicability in combinatorial optimization problems. The MCDKM method has the potential to solve any KP01 using an n-Dimensional search space approach obtaining an efficient, high-quality solution with a success rate above 90% average. Solving the KP01, grants MCDKM the capability to deal with a range of other combinatorial optimization problems, such as resource allocation, production scheduling, distribution processes, etc.

Our heuristic model is constantly improving and considering more factors, for example, the relationship among multiple items. In addition, our model is expected to solve multi-objective and multi-Dimensional optimization problems. We believe that parallelization of the method would provide a fast convergence with the improvement in the execution times.