Keywords

1 Introduction

The k-nearest neighbors algorithm (k-NN) identifies, for a given query, the k most similar samples from a reference set. It has been applied in a broad range of applications in information retrieval and data mining, for example, in pattern classification [10], regression [33] and outlier detection [29]. k-NN is computationally intensive since every query involves the comparison to all the elements in the reference set. The computational complexity of a single nearest neighbors query with Euclidean distance is \(\mathcal {O}(nd)\), where n refers to the number of examples and d to the dimensionality of the dataset [21]. When the size of the reference set is large or a large number of queries need to be solved, the execution time may become unacceptably high. In low-dimensional spaces, the complexity of exact neighbors queries can be reduced using various indexing structures, as studied in [21], for example. However, in high-dimensional spaces, index searches typically become more exhaustive, where a k-NN query for a given point needs to search through a large fraction of the points in the reference set [38]. Thus, index search largely becomes ineffective in higher dimensional spaces and may even degrade performance relative to a brute-force search because the index search incurs some degree of overhead. To address the challenge of nearest neighbors searches in high-dimensional spaces, we propose a massively parallel algorithm that combines the computational capabilities of a central processing unit (CPU) with that of a graphical processing unit (GPU) to enable efficient brute-force search in high-dimensional data.

The rest of this paper is organized as follows. Section 2 presents the related work and techniques used for nearest neighbors search. In Sect. 3, we describe the proposed algorithm in detail, explain the implementation, and highlight our contributions. Section 4 shows how the algorithm scales in comparison to other widely used implementations. In Sect. 5, we summarize our findings and describe possible future research directions.

2 Related Work

Various techniques have been proposed for nearest neighbors search (mostly in metric spaces) encompassing (1) hierarchical methods, (2) pivot-based methods and (3) compression-based methods. Hierarchical methods typically use some form of tree structure to partition the search space. Notable examples include the k -d tree and its variants and the R-tree and its variants. The k-d tree uses binary space partitioning to statically organize k-dimensional points [4]. R-trees, on the other hand, divide space into minimum bounding rectangles, such that regions can intersect and form a hierarchy [16]. Pivot-based approaches store pre-computed distances to a set of so-called pivot points. Using the pre-computed distances and the triangle inequality, it is possible to exclude points from further consideration. The most prominent examples of pivot-based approaches are AESA [36] and LAESA [26]. AESA uses the full pairwise distance matrix of the reference set, and LAESA uses the pairwise distances to a set of chosen pivot points. Compression-based methods use some form of quantization and lower-bounding to achieve exact nearest neighbors search in more compact spaces. An example of a compression method is the VA-file [37] and its variants, which uses scalar quantization to organize the search space into a grid of cells enabling filtering of points that cannot be near the query. Algorithms that combine different aspects exist as well; for example, trees that use pivot points [35], or trees that use compression ideas [5].

A problem inherent with all of the mentioned techniques is that they rapidly decline in performance once the dimensionality of the dataset increases. In fact, under some assumptions regarding the data distribution, even an optimal index structure will, as dimensionality increases, always degenerate to visiting the entire data set [38]. For example, Kibriya and Eibe [21] empirically show that the classical tree variants generally become worse than brute-force search for datasets with more than 16 dimensions. More recently proposed methods also suffer from the curse-of-dimensionality as shown, for example, in [15] or [22].

An approach to tackle the curse-of-dimensionality is to rely on a brute-force search of the data and use parallelization to speed up the search. A benefit of such an approach is that it can be used for non-metric spaces, as it does not rely on any assumptions about the distance function being used. Paralellization methods include shared-nothing architectures such as MapReduce [13] (e.g. [23]), distributed-memory architectures such as MPI [9] (e.g. [2]), shared-memory architectures such as OpenMP [11] (e.g. [39]) and massively-parallel architectures such as GPGPU [24]. The brute-force GPGPU methods mainly differ in the selection of the k smallest elements from every row in the distance matrix, a problem we describe as k-selection. Tang et al. [34] identify three major variants to solve the k-selection problem. A naïve approach is to sort the list and then select the k first values in the sorted list (e.g. [3]). However, this method does unnecessary work when the sorted distances are not repeatedly used. A more efficient approach is to partially sort the distances only up to the first k values (e.g. [31]). Another option is to use selection algorithms instead of sorting (e.g. [1]), which recursively divide the distances into groups.

3 Algorithm

The primary motivation for our approach is to explore the combination of CPU-based shared-memory parallelism and the GPGPU paradigm to address the curse-of-dimensionality in nearest neighbors search. We propose a generic interface to solve high-dimensional k-NN queries and split the problem into distance computation and k-selection. Using the Julia programming language [7], multiple dispatch allows us to generically implement distance computation and k-selection approaches based on abstract types, which get just-in-time compiled for the concrete, user-provided subtypes. Distance computation is performed on the GPU, which we refer to as the device, and k-selection is asynchronously performed on the CPU, which we refer to as the host. The parallelization of the distance computation on the device and the k-selection on the host is made possible through batching strategies. Batching is necessary for two reasons: (1) device memory is typically highly restricted, and not all points in the reference and query sets might fit in device memory, and (2) we can asynchronously compute the k-selection of batch n while we calculate the distances for batch \(n + 1\); thus, we can overlap computations and achieve better resource utilization. Our approach enables nearest neighbors search for datasets that do not fit in memory, and work is efficiently distributed between CPU and GPU. For simplicity, we assume that the dataset initially resides in host memory, but the algorithm itself does not make assumptions about the input data location.

3.1 Distance Computation

Most of the literature on similarity search and nearest neighbors search is concerned with metric spaces. A metric \(\delta \) is required to be non-negative \(\delta (x,y) \ge 0\), identical \(\delta (x,y) = 0 \Leftrightarrow x = y\), symmetric \(\delta (x,y) = \delta (y,x)\) and triangular \(\delta (x,y) + \delta (y,z) \ge \delta (x,z)\). However, with the increasing complexity of data entities across various domains, many distances are used that are not metrics [32]. Relaxing the last three axioms, for example, leads to the notion of a premetric, i.e. a distance function satisfying only the non-negative and identical axioms. Because a brute-force approach does not rely on assumptions about the used distance function, we can use any metric or non-metric distance function. Furthermore, our high-level interface allows researchers to implement such distance functions without any knowledge of the underlying GPU platform. For the purpose of evalution, we use the popular Euclidean metric given by

$$\begin{aligned} d(r_i, q_j) = \sqrt{||r_i - q_j||^2}. \end{aligned}$$
(1)

The square of the distance metric can be written as

$$\begin{aligned} \begin{aligned} d^2(r_i, q_j)&= ||r_i - q_j||^2 \\&= (r_i - q_j)^{\top } (r_i - q_j) \\&= r_i^{\top } r_i + q_j^{\top } q_j - 2 r_i^{\top } q_j \\&= ||r_i||^2 + ||q_j||^2 - 2 r_i^{\top } q_j. \end{aligned} \end{aligned}$$
(2)

for all \(i \in \{1, 2, \ldots , N\}\) and \(j \in \{1, 2, \ldots , M\}\) where N is the number of reference points and M is the number of query points. If we now assume that the points in both sets are of dimensionality D and define the reference set as a matrix \(R^{N \times D}\) and the query set as a matrix \(Q^{M \times D}\), we can formulate the pairwise Euclidean distance matrix as

$$\begin{aligned} D = \sqrt{- 2 R^{\top } Q \underset{r}{+} ||R||^2 \underset{c}{+} ||Q||^2}. \end{aligned}$$
(3)

where \(||\cdot ||^2\) is the row-wise squared vector norm, \(+_r\) is the row-wise addition, \(+_c\) is the column-wise addition and \(\sqrt{\cdot }\) is the element-wise square root. For the computationally expensive dense matrix multiplication, it is common to use optimized libraries such as cuBLASFootnote 1, clBLASFootnote 2 or MAGMAFootnote 3. Because our implementation is based on the Julia programming language, we can implement such a distance kernel generically based on the notion of an abstract matrix type. Depending on the user-provided matrix, for example, a CUDA-specific subtype, the computation is dispatched on that subtype and just-in-time compiled, which might, for example, invoke a cuBLAS call for the matrix multiplication. Thus, our implementation can support different devices without code specific to the device platforms through multiple dispatch, and the JuliaGPU project [6].

3.2 k-Selection

As mentioned previously, the GPU-based methods mainly differ in the k-selection process. In our case, we choose to remove the k-selection process from the GPU entirely and instead perform the computation asynchronously on the CPU. The motivation for using the GPU for distance computations and the CPU for sorting is based on the observation that dense matrix operations are much faster on the GPU than on the CPU [18, 20, 40] and that it is much more difficult to significantly outperform CPU-based sorting on the GPU [14, 30]. As with distance computations, our approach is generic enough to use arbitrary k-selection procedures, but for the purpose of evaluation, we use the popular partial quicksort algorithm. Quicksort works by selecting a pivot element from the array and partitioning the other elements into two sub-arrays depending on whether they are smaller or larger than the pivot. The sub-arrays are then sorted recursively [17]. There is no need to recursively sort partitions that only contain elements that would fall after the k-th place in the final sorted array in the partial quicksort variant. Thus, if the pivot falls in position k or later, the recursion only takes place on the left partition [25].

3.3 Batching

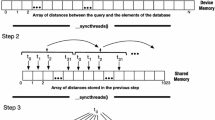
Recall that a k-nearest neighbors query identifies the k most similar samples from a reference set R. Of course, there can also be multiple queries, which we refer to as the query set Q. Because every point \(q \in Q\) is associated with a distance to every point \(r \in R\), a trivial batching approach would be to only batch the points in Q and load the entire reference set on the device. We call this approach Q-batch. Q-batch requires only a single k-selection step for each point in Q, because the distances from a single query point to all reference points are known after the distance computation for a batch is complete. The following figures show the distance computation (Fig. 1) and k-selection (Fig. 2) process using the Q-batch methodology. For simplicity, we ignore the memory transfer between host and device before each batch in the visualizations.

Fig. 1.
figure 1

Exemplary distance computation of three-dimensional points using Q-batch with a batch size of 2 where \(r(i, \cdot )\) is a point in the reference set, \(q(j, \cdot )\) is a point in the query set and d(j, i) refers to the distance from point \(q(j, \cdot )\) to \(r(i, \cdot )\).

Full size image
Fig. 2.
figure 2

Exemplary k-selection using Q-batch with a batch size of 2. Note that the selection process happens asynchronously on the host. The exemplary 1-nearest neighbors are marked with a red rectangle, thus the final nearest neighbors would be \(q(1) \rightarrow r(1), q(2) \rightarrow r(3)\) and \(q(3) \rightarrow r(2)\). (Color figure online)

Full size image

A problem with the Q-batch approach is that the full reference set must be on the device, which may not be feasible depending on the size of the reference set. A more generic approach is to batch the points in Q and R separately, given a batch size B, which yields a distance matrix that is at most of size \(B \times B\). We call this approach QR-batch and conceptually show in how it differs from Q batch in distance computation (Fig. 3) and k-selection (Fig. 4).

Fig. 3.
figure 3

Exemplary distance computation of three-dimensional points using QR-batch with a batch size of 2 where \(r(i, \cdot )\) is a point in the reference set, \(q(j, \cdot )\) is a point in the query set and d(j, i) refers to the distance from point \(q(j, \cdot )\) to \(r(i, \cdot )\).

Full size image
Fig. 4.
figure 4

Exemplary k-selection using QR-batch with a batch size of 2. Note that, in contrast to Q-batch, we have to split the k-selection process into two steps: first, we select the k possible candidates from the reference set, and then we perform k-selection on the possible candidates. Again, we mark the exemplary candidates and neighbors with a red rectangle showing that both methodologies yield the same result. (Color figure online)

Full size image

The implementation of the algorithms is open-source and available online; it can be found at https://github.com/davnn/ParallelNeighbors.jl.

4 Results

In this section, we compare our approach to popular libraries used for exact nearest neighbors search, namely Scikit-learn [28], NearestNeighbors.jl [8], PyTorch [27] and Faiss [19]. The first two libraries are CPU-based, and we use multithreaded parallelism for both libraries using all processors. Note that we only compare brute-force search and do not consider the tree-based implementations of the libraries because they do not scale to the tested dimensionalities. We use the GPU-based variants of the last two libraries. Both GPU-based variants do not natively support batching and transfer the entire data to the GPU before the computation. For the evaluation, we use a generic Euclidean distance kernel that follows the definition in Eq. 3 and only uses the high-level operations described in the equation. The definition of the distance kernel shows the generic capabilities of our approach, which enables researchers to develop custom distance functions without having to resort to GPU programming. Another point to mention is that we start all benchmarks with the data residing in host memory; thus, the benchmark times always include the transfer from host to device. The batch size for all evaluations is defined as \(\frac{n}{8}\) with a minimum batch size of 256 and a maximum batch size of 1024 for Q-batch and 2048 for QR-batch. We use uniform random points in the unit hypercube for all our evaluations, and the correctness of all algorithms is ensured by comparison to a reference implementation. Our experimental environment employs an AMD Ryzen 3900X CPU and a GeForce 1080 Ti GPU with CUDA Toolkit 11.3. An initial analysis regarding different numbers of neighbors k shows that all libraries scale alike with the number of neighbors; thus, we use \(k = 1\) for all further evaluations. We propose two benchmarks for the evaluation, (1) batch prediction and (2) online prediction. The first benchmark involves an equal amount of reference and query points \(n \in \{2^9, 2^{10}, \ldots , 2^{14}\}\) for varying dataset dimensionalities \(d \in \{2^9, 2^{10}, \ldots , 2^{14}\}\). In Fig. 5 we show the results for benchmark (1). The CPU-based approaches deteriorate significantly with an increasing number of reference and query points for all tested dimensionalities. For dimensionalities up to \(d = 2048\), the hybrid approaches incur an overhead compared to the GPU-based approaches, but starting with \(d = 4096\), the hybrid approaches outperform all other approaches despite using batch-wise data transfer. For the largest number of query and reference points and \(d = 16384\), using a hybrid approach results in a 30% to 40% decrease in processing time compared to the GPU libraries. Additionally, note that a one-time data transfer is more efficient than a batch-wise transfer from host to device; therefore, this benchmark favors the GPU-based libraries over our proposed approaches.

Fig. 5.
figure 5

Benchmark (1): Comparison of popular libraries to the proposed hybrid algorithms for \(k = 1\) neighbors. The number of query and reference points is visualized on the x-axis of each plot and the processing time in seconds is visualized on the y-axis.

Full size image

The second benchmark compares the GPU and hybrid approaches using a large number of reference points \(n \in \{2^{14}, 2^{15}, \ldots , 2^{18}\}\) with a single query point and fixed dimensionality \(d = 4096\). The dimensionality is chosen based on the observation that the compared algorithms show similar performance for that dimensionality in the first benchmark. The maximum number of reference points is the largest number of points fitting in GPU memory, enabling a comparison to libraries that do not support batch-wise data transfer. We additionally evaluate the difference between batch-wise and one-time data transfer for the hybrid approaches in this benchmark. The one-time data transfer evaluation can be interpreted as the lower bound of achievable processing time for batch-wise processing, only attainable if all data transfers can be scheduled asynchronously without impacting the rest of the computation. The result of benchmark (2) is depicted in Fig. 6. The hybrid approaches outperform the GPU-based variants when both use one-time data transfer; in this case, the processing time can be decreased by about 25% to 50%. Because there is only one query point in the second benchmark, Q-batch uses a batch size of one and shows almost no difference to one-time transfer. The performance difference between QR-batch with one-time and batch-wise data transfer hints at further optimization potential, which might be achievable through better memory allocation.

Fig. 6.
figure 6

Benchmark (2): Comparison of hybrid and GPU-based approaches for one query point with \(k = 1\) and \(d = 4096\). The number of reference points is visualized on the x-axis, and the processing time in seconds is visualized on the y-axis.

Full size image

Dashti et al. [12] show that the total speedup of massively-parallel nearest neighbors searches asymptotically approaches the speedup of the distance computation. If the time required for asynchronous memory transfer and CPU-based k-selection is smaller than the time required for GPU-based distance computation, a hybrid approach should outperform a purely CPU-based or GPU-based approach.

5 Conclusions

In this paper, we set out to tackle the curse-of-dimensionality in exact nearest neighbors searches. We propose a hybrid, massively-parallel nearest neighbors algorithm that uses batching to split the computational workload efficiently between CPU and GPU. We show that a highly-generic implementation of our method significantly outperforms popular exact nearest neighbors libraries for high-dimensional data. Most notably, the performance of our proposed hybrid approach scales linearly with the dimensionality of the data. Because datasets continually increase in size and dimensionality, we believe that high-performance nearest neighbors search strategies become more relevant in future research. While the low-dimensional similarity search community has attracted a large amount of research over the last 20 years, there are many open opportunities for future research in the high-dimensional case. Future researchers should investigate existing highly-optimized distance kernels and k-selection methods and combinations thereof in the CPU, GPU, hybrid, and distributed setting.