Abstract
Differential fault analysis (DFA) is a very powerful attack vector for implementations of symmetric cryptography. Most countermeasures are applied at the implementation level. At ASIACRYPT 2021, Baksi et al. proposed a design strategy that aims to provide inherent cipher level resistance against DFA by using S-boxes with linear structures. They argue that in their instantiation, the block cipher DEFAULT, a DFA adversary can learn at most 64 of the 128 key bits, so the remaining brute-force complexity of \(2^{64}\) is impractical.
In this paper, we show that a DFA adversary can combine information across rounds to recover the full key, invalidating their security claim. In particular, we observe that such ciphers exhibit large classes of equivalent keys that can be represented efficiently in normalized form using linear equations. We exploit this in combination with the specifics of DEFAULT’s strong key schedule to recover the key using less than 100 faulty computation and negligible time complexity. Moreover, we show that even an idealized version of DEFAULT with independent round keys is vulnerable to our information-combining attacks based on normalized keys.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Differential fault analysis (DFA) [6] is one of the earliest and most powerful attack vectors on symmetric cryptography if an adversary is capable of inducing physical faults. DFA is a significant threat for cryptographic implementations as it often requires just a few precise faults to recover the key, e.g., only two or three in the case of AES [11, 15]. This underlines the importance of research on countermeasures against this attack vector.
Most of the research in countermeasures focuses on defenses applied on the implementation level that do not require any changes in the protected primitive, mode of operation, or protocol. Among the earliest proposals are duplication-based countermeasures, where the encryption algorithm is computed twice, or encryption and decryption are computed and the results are compared. If the results do no match, no output is released; see Bar-El et al. [3] for an overview. A different line of research deals with infective countermeasures [10, 14, 17]. This class of defenses always generates an output, but aims to amplify the effect of a fault to the extent that the output becomes useless for an adversary. Other approaches aim to mitigate fault attacks on the mode of operation or on protocol level. The underlying idea of such countermeasures is to limit the observations an attacker can make per static secret to a small number, in the extreme case to one, to preclude the evaluation performed by DFA in the first place, or at least increase the burden in precision to induce the faults. Examples in this direction include fresh re-keying [13] as well as tamper- and leakage-resilient permutation-based cryptography [9]. Many modes for nonce-based authenticated encryption also provide a certain level of implicit protection [8]. Finally, some recent designs propose dedicated cryptographic primitives with features to facilitate protected implementations. Examples include the permutation FRIET [16] and the tweakable block cipher CRAFT [4], which permit efficient implementations with error detection. The most recent proposal in this category, DEFAULT, follows a more radical, fundamental approach by aiming to preclude DFA by design.
DEFAULT is a block cipher design following an interesting new design approach proposed by Baksi et al. [1] at ASIACRYPT 2021. The design approach aims to provide inherent cipher-level protection against DFA by using a fault protecting layer called DEFAULT-LAYER. This layer uses special S-boxes with linear structures. Because these linear structures imply that certain groups of keys are differentially equivalent, a DFA adversary cannot learn more than half of the key bits from attacking the S-box layer. The designers argue that an adversary can thus only recover 64 bits of DEFAULT’s 128-bit key using DFA, and the remaining key space of \(2^{64}\) candidates is too large to brute-force easily. For a larger security margin, the design approach can easily be scaled for a larger master key size. To provide resistance against cryptanalytic attacks, DEFAULT-LAYER is combined with a more conventional DEFAULT-CORE cipher design.
DEFAULT was originally proposed with a simple key schedule where each round key is identical to the master key [2]. The final published design [1] features a much stronger rotating key schedule. Here, consecutive round keys are derived using a 4-round function with full diffusion; after four round keys, the round keys start rotating. The purpose of this unusually strong construction is to thwart potential attacks that try to combine information learned from consecutive rounds.
 \(^\star \): but fault complexity differs)
\(^\star \): but fault complexity differs)
 : impractical (\(2^{64}\)).
: impractical (\(2^{64}\)).Our Contributions. In this paper, we show that an attacker can indeed combine information from multiple rounds, contradicting the claim. We propose attacks on DEFAULT-LAYER for both for the original simple key schedule and the final strong, rotating key schedule, summarized in Table 1. We even show how an idealized key schedule of completely independent round keys could be attacked. Our attacks follow the same classical attacker model as the design paper: we assume the attacker can induce single bitflip faults on the state between rounds and uses only DFA-style evaluation to learn key information. In summary:
-
We first target the original simple key schedule and show why and how an attacker can combine information from multiple DFAs with faults in different rounds. This allows us to learn more than half the key bits, contrary to the intuition underlying the original DEFAULT design that the attacker seems to learn the same information in each round. We demonstrate two possible approaches: combining information from encryption and decryption, or combining information from multiple consecutive rounds (IC-DFA in Table 1).
-
To tackle the strong key schedule with full diffusion between round keys, we consider an idealized version with fully independent round keys. We identify large classes of equivalent keys that produce the same permutation and then show how to recover a normalized version of the correct key, i.e., a representative of the key’s equivalence class. We derive a generic attack strategy using these normalized keys that is applicable to all DEFAULT-style ciphers with linear structures in their S-boxes (Generic NK-DFA in Table 1).
-
We show that we can exploit the specifics of the strong DEFAULT key schedule in combination with the normalized-key attack strategy to build an even more powerful attack and recover the DEFAULT key (IC-NK-DFA in Table 1).
-
Finally, we propose an optimization strategy to minimize the number of required faulty computations for the proposed attacks. We experimentally verified the attacks in simulations. Our source code is available online at https://extgit.iaik.tugraz.at/castle/tool/dfa_on_default.
Outline. In Sect. 2, we provide more background on DFA and relevant countermeasures. Additionally, we recall the specification of DEFAULT. In Sect. 3 we show attacks on the original DEFAULT design with a simple key schedule. In Sect. 4, we present the concept of equivalent keys. Based on this concept, we propose attacks on the updated DEFAULT design with 4 rotating keys in Sect. 5. In Sect. 6, we show optimized attacks that require fewer faulted computations. Finally, we discuss potential mitigations of the attack in Sect. 7.
2 Background
In this section, we recall the preliminaries on Differential fault analysis and other fault attacks, previously proposed countermeasures, and the design strategy of DEFAULT to prevent DFA by design.
2.1 Differential Fault Analysis
For cryptanalysis, the easiest way to see differential fault analysis is to see it as a short-cut differential [5] or truncated differential [12] attack. However, in contrast to cryptanalysis, where only inputs of an algorithm are manipulated, DFA makes use of the ability to insert (bitwise or truncated) differences anywhere during the computation of a cipher.
An easy example is the following differential fault attack on AES. Assume that we have an attacker that can insert a fault during the computation of a single S-box during the penultimate round of AES. For the attack, it does not matter which S-box is faulted; it just matters that only a single one is faulted. Then, at the output of AES, we see that 4 bytes have a difference. We can guess 4 bytes of the last round key associated with these differences and partially decrypt backwards to 4 S-box outputs of the penultimate round. If we observe a difference in more than one S-box, we know that this partial key guess is definitely wrong.
A similar attack can also be carried out on bit-level. Consider an S-box \(\mathcal {S}\) followed by a key addition in the last round of any cipher. An attacker who is able to trigger precise bitflip faults can fault a bit right before the S-box, thus inducing an input difference \(\varDelta _\text {in} = u \oplus u'\) between the original value u in the correct computation and the faulty \(u'\) in the faulted computation. For example, if they flip the least significant bit, \(\varDelta _\text {in} = \texttt {1}\). This will cause two different output values after the S-box with an output difference \(\varDelta _\text {out} = v \oplus v' = \mathcal S(u) \oplus \mathcal S(u')\). The resulting ciphertext bits will be \(c = v \oplus k\) and \(c' = v' \oplus k\). As the differential behaviour of \(\mathcal {S}\) depends on the values of u and thus of v, the attacker can now try for each key candidate k whether \(\mathcal {S}^{-1}(c \oplus k) \oplus \mathcal {S}^{-1}(c' \oplus k) = \varDelta _\text {in}\) and reject all key candidates that do not satisfy this. The number of remaining key candidates is given by the corresponding entry for \((\varDelta _\text {in}, \varDelta _\text {out})\) in the differential distribution table (DDT) of the S-box \(\mathcal S\) [5]. Thus, small entries in the DDT – which are otherwise desired for strong S-boxes against differential cryptanalysis – permit the attacker to learn more information about the key bits k.
Differential fault attacks can not only be performed by observing differences of outputs. They can also be mounted by inserting differences at inputs aiming to cancel them with faults. Whether or not this cancellation is possible reveals information on the propagation of the inserted differences, which in turn reveals information about the actual values in the computation, which reveals information about the key. These attacks are known as fault-based collision attacks [7].
2.2 Design and Specification of DEFAULT
DEFAULT [1] is a 128-bit block cipher designed to inherently resist DFA by limiting the amount of information a DFA attacker can learn about the key. The designers of DEFAULT specify two building blocks: DEFAULT-LAYER to provide security against DFA and DEFAULT-CORE to provide security against classical cryptanalysis. They propose a construction, where DEFAULT-CORE is sandwiched between two applications of DEFAULT-LAYER. So, the encryption function E can be expressed by
DEFAULT-LAYER uses a 128-bit state and applies a round function \(\mathcal R\) with successive key addition 28 times. DEFAULT-CORE uses the same round function with a different S-box 24 times. Each round consists of the same steps (Fig. 1):
SubCells. For DEFAULT-LAYER, the S-box \(\mathcal S\) from Table 2a is applied to every 4-bit nibble of the state. While DEFAULT-CORE uses the S-box \(\mathcal S_\text {core}\) from Table 2b. The differential properties of the S-box \(\mathcal S\) are what makes differential fault analysis difficult. As evident from Table 2c, the S-box contains 4 so-called linear structures: \(\texttt {0} \rightarrow \texttt {0}\), \(\texttt {6} \rightarrow \texttt {a}\), \(\texttt {9} \rightarrow \texttt {f}\), and \(\texttt {f} \rightarrow \texttt {5}\). A linear structure \(\alpha \rightarrow \beta \) is a differential transition that happens with 100% probability. In other words, \(\mathcal S(u) = v\) implies \(\mathcal S(u \oplus \alpha ) = v \oplus \beta \). While this is an undesirable property when considering classical adversaries, it does make differential fault analysis harder. In the usual DFA setup, we obtain \(c = k \oplus \mathcal S(u)\) and \(c' = k \oplus \mathcal S(u\oplus \varDelta _\text {in})\), where \(\varDelta _\text {in}\) is known but u is unknown. We solve these equations for the key k and the unknown internal value u. However, if (k, u) is a solution each non-trivial linear structure \(\alpha \rightarrow \beta \) leads to an additional solution \((k\oplus \beta , u\oplus \alpha )\). Therefore, when applying this setup to DEFAULT-LAYER, the key space can only be reduced to \(2^{64}\) candidates as 4 candidates per key nibble will always remain.
PermBits. A bit permutation is applied to the 128-bit state as depicted in Fig. 1. The design uses the same bit permutation as GIFT-128. Note that the position of a bit within a nibble is invariant for this bit permutation, i.e., if bit i is mapped to bit j we have \(i \equiv j \mod 4\). Additionally, when examining two rounds of DEFAULT, there are groups of 8 S-boxes that do not interact with other groups. Each color in Fig. 1 corresponds to one such group.
AddRoundConstants. A 6-bit constant is xored onto the state at indices 23, 19, 15, 11, 7 and 3. Additionally, the bit at index 127 is flipped.
AddRoundKey. The 128-bit state is xored with the 128-bit round key which is calculated according to the key schedule. In the first preprint version of DEFAULT a simple key schedule where all round keys equal the master key was proposed [2]. This simple key schedule is vulnerable to the information combining attacks we present in Sect. 3. To prevent these attacks, the DEFAULT designers propose a very strong key schedule in their final design. In their theoretical analysis, they first consider an idealized long-key cipher with independent round keys \(K_0, K_1, \ldots , K_{27}\), corresponding to a \(28 \times 128\)-bit key K. For that idealized key schedule, no information combining attacks are possible since each round uses a completely independent key. For the practical instantiation, they suggest to generate 4 distinct round keys \(K_0, \ldots , K_3\) where \(K_0 = K\) and \(K_{i} = \mathcal {R}(\mathcal {R}(\mathcal {R}(\mathcal {R}(K_{i-1}))))\) for \(i \in \{1, 2, 3\}\), where \(\mathcal {R}\) is the unkeyed round function. The rounds are then keyed iteratively with \(K_0, K_1, K_2, K_3, K_0, K_1, \ldots \). The designers argue that this definition is a reasonable approximation of the idealized version since 4 rounds provide full diffusion, and according to their analysis, combining information throughout 4 rounds is very difficult [1, Section 6.1]. The approach can be parametrized more generally with a variable number of x keys \(K_0, \ldots , K_{x-1}\) generated using a variable number of rounds \(\mathcal {R}^y\) for a more conservative choice at a higher performance cost. For a full specification, we refer to the design paper [1].
Note that the design does not specify a key addition before the first application of the round function. To simplify the following descriptions, we assume the initial unkeyed round is not present as it can be trivially removed.
Claims About DEFAULT. In summary, DEFAULT-LAYER is designed to limit the information available to a DFA adversary for each round and to prevent combining information across rounds. The linear structures in the S-boxes ensure that for each round at least \(2^{64}\) key candidates remain, while the strong key schedule is designed to prevent combining information across rounds.
3 Information-Combining DFA on Simple Key Schedule
In this section, we consider a simplified version of DEFAULT with a simple key schedule, where each round key equals the master key K. Such a simple key schedule was proposed in the first preprint version of DEFAULT [2]. We argue that for this design variant, the security claim is only valid for attackers targeting only the first or last round key of the cipher. We demonstrate how an attacker can efficiently combine key information learned from multiple different rounds of the cipher, for example from encryption and decryption rounds or from multiple consecutive rounds. This observation relies crucially on the structure of the bits of key information that can be derived by attacking a single S-box.
3.1 Limited Information Learned via DFA
As DEFAULT’s designers show, we can only learn a limited amount of information when inducing bit flips before the S-box. In particular, when faulting encryption, we can restrict the key at the output of the S-box to a space of \(\{\beta , \beta \oplus \texttt {5}, \beta \oplus \texttt {a}, \beta \oplus \texttt {f}\}\) for some \(\beta \). This allows to effectively reduce the key space for the corresponding key bits from 4 bits to 2 bits, but not further, since we cannot distinguish the four values in each set based on the differential behaviour.
However, we can also target an implementation of the decryption algorithm. When faulting decryption, we can restrict the key at the output of the inverse S-box to \(\{\alpha , \alpha \oplus \texttt {6}, \alpha \oplus \texttt {a}, \alpha \oplus \texttt {f}\}\) for some \(\alpha \). Note that this set is spanned by different basis vectors: \(\{\texttt {6}, \texttt {9}\}\) for decryption compared to \(\{\texttt {5}, \texttt {a}\}\) for encryption. Nevertheless, combining the knowledge from these two sets is not trivial as, during decryption, we learn information about the nibbles of the base key, while during encryption, we learn information about the nibbles of the inversely permuted key due to the bit permutation layer of the final round.
To efficiently represent the information we learn, we observe that we can express these sets of possible values in terms of linear equations. When faulting the final S-boxes during encryption, we learn the values of \(k_0 \oplus k_2\) and \(k_1 \oplus k_3\), where \((k_0, k_1, k_2, k_3)\) is any nibble of the inversely permuted key. For example, when we observe the transition \(\texttt {2}\rightarrow \texttt {7}\) in an S-box, we can restrict the output to the set of \(\{\texttt {0}, \texttt {2}, \texttt {5}, \texttt {7}, \texttt {8}, \texttt {a}, \texttt {d}, \texttt {f}\}\). This is equivalent to learning \(v_0 \oplus v_2 = 0\), where \((v_0, v_1, v_2, v_3)\) are the output bits of the S-box. Similarly, if we observe the transition \(\texttt {2}\rightarrow \texttt {d}\), we learn \(v_0\oplus v_2 = 1\). With the knowledge of the ciphertext, we can then use this knowledge to learn something about the key. In Table 3, we summarize which expression over the key bits can be learned based on the input difference of the S-box or inverse S-box.
As evident from Table 3, when faulting decryption, we can learn the values of \(k_1 \oplus k_2\) and \(k_0 \oplus k_3\), where \((k_0, k_1, k_2, k_3)\) is any nibble of the base key. We can complement this information by faulting encryption, which allows us to learn \(k'_0\oplus k_2\) and \(k'_1\oplus k'_3\), where \((k'_0, k'_1, k'_2, k'_3)\) is any nibble of inversely permuted key. When structured using linear equations, we can transform the equations about the inversely permuted key into equations about the base key by multiplying with the permutation matrix. Because the position of a bit within a nibble is invariant for the bit permutation, we can learn 3 linearly independent equations for each nibble of the key.
3.2 Basic Encrypt-Decrypt Attack on Simple Key Schedule
These observations allow us to reduce the key space to 32 bits by inducing 96 single-bit-flip faults. During encryption, we induce a difference of \(\texttt {2}\) and \(\texttt {8}\) for each S-box to learn \(k_0\oplus k_2\) and \(k_0\oplus k_1\oplus k_2\oplus k_3\) for each nibble of the inversely permuted key. Additionally, we induce a difference of \(\texttt {2}\) before each S-box during the final round of decryption to learn \(k_0\oplus k_3\). Then, we combine the information from these faults as explained above to obtain 96 linearly independent equations about the key. Iterating over the remaining \(2^{32}\) key candidates can be performed efficiently by computing the kernel of the matrix. We show in Sect. 6.1 that a similar reduction in key space can be achieved by using only 16 faults.
3.3 Basic Multi-round Attack on Simple Key Schedule
An even more powerful attack can be derived by performing the key-recovery over multiple rounds. The main advantage of targeting multiple rounds is the higher nonlinearity. This allows us to reduce the key space much more. For example, when attacking 3 rounds, we can reduce the key space to a set of \(2^{16}\) keys. This also has the advantage that only a single direction needs to be faulted, i.e., either encryption or decryption. For this attack, we are targeting encryption. Thus, we learn information about the inversely permuted key, which is equivalent to learning information about the base key.
To implement this attack, we first reduce the key space to 64 bits by performing the basic differential fault attack on the final round. In the next step, we expand our analysis to two rounds and analyze each group of \(4+4\) S-boxes, i.e., each color in Fig. 1, separately. Due to the S-box grouping, these 8 S-boxes do not interact with any other S-boxes in the first 2 rounds. An example of fault propagation is illustrated in Fig. 2b. We place a single fault before each of the 4 considered S-boxes in the penultimate round leading to 5 active S-boxes. For each fault, we have to guess 4 key nibbles in the final round. As the previous step restricts each nibble to 4 candidates, we need to try \(2^8\) key candidates. For the key addition right after the faulted S-box, we can pick any of the 4 candidates identified in the previous attack step as all of them lead to the same subset of the \(2^8\) key candidates of the final round. We analyze this property in more detail in Sect. 4. For each of these key guesses, we verify whether the difference before the penultimate round matches the induced fault. We repeat this attack for each of the 8 groups of \(4+4\) S-boxes each, thus faulting all 32 S-boxes once. This reduces the key space to 16 potential keys per S-box group or \(2^{32}\) keys in total.
Finally, we can reduce the overall key space to \(2^{16}\) keys by attacking 3 rounds. As with 2 rounds, we only need to consider a subset of S-boxes at a time. Because we are dealing with 3 rounds of diffusion, a single fault influences all even- or all odd-numbered S-boxes in the final round. We place our faults in such a way that the keys we guess for the final round overlap with the keys needed for the additional two rounds. Thus, we fault each S-box \(S_i\) with \(i \in \{0, 2, 8, 10, 21, 23, 29, 31\}\) twice: once by flipping the bit at index 1 and once by flipping the bit at index 2. For example, when faulting the S-box \(S_0\), the fault propagates as shown in Fig. 2c. As before, we only iterate over the keys which are left from the previous step. Because each fault affects 4 S-box groups from the previous step, we need to try \(2^{16}\) key candidates per fault. The 16 faults we perform for this step of the attack allow us to reliably reduce the key space for each half to 256 keys or \(2^{16}\) keys in total.
Overall, we perform 64 + 32 + 16 = 112 faults during this attack. The computational complexity is negligible as we store the key sets efficiently using Cartesian products: our straightforward simulated implementation finishes in a few seconds. We show in Sect. 6.2 that a similar reduction in key space can be achieved by using only 16 faults.
Combining Information Across Rounds. Why do faults propagating through multiple rounds divulge more information than only faulting a single round? Note that even after reducing the key space to 16 bits as in the above attack, we are unable to constrain any single nibble of the key to a space of fewer than 4 keys. However, we are able to heavily restrict the space of possible keys when considering larger parts of the key at once.
When considering the example of two rounds of S-boxes applied to a single bit flip as depicted in Fig. 3, we can observe exactly that effect. Based on faulting a single round, we have already reduced the space for each key nibble to 4 candidates. Now, we will use the correct ciphertext C and the faulted ciphertext \(C'\) to further reduce the key space. Concretely, we will show that if we pick one value for \(k_0\), we can restrict the space of \((k_1, k_2, k_3)\). Thus, when repeating this process, we can restrict the overall space of \((k_0, k_1, k_2, k_3)\). With the knowledge of \(k_0\), we can calculate \(v_0, v_0', u_0,\) and \(u_0'\). Therefore, we know the most significant bit of \(t_0, t_0', s_0,\) and \(s_0'\). When examining the faulted S-box, we can easily derive the output difference by examining the ciphertext. Due to the DDT, we know only 8 input/output pairs \((r, r', s, s')\) are compatible with that differential transition. When combining this with the knowledge of \(k_0\) and the most significant bit of \(t_0\), we can halve the space of \((r, r', s, s')\) and thus \((t, t')\) to 4 potential pairs. In turn, this halves the space of potential values for \((u_1, u_2, u_3)\) which translates into halving the space of \((k_1, k_2, k_3)\).
For the case where a different key is xored after the application of the S-box in the penultimate round, a very similar reasoning applies. All 4 candidates will lead to the same restricted set for \((t_0, t_0')\) and, thus, the same restricted set for \((k_1, k_2, k_3)\). This is because any difference between the chosen key and the actual key can be compensated by a difference in the unknown input to the S-box.
4 Exploiting Equivalence Classes of Keys
Most block cipher designs use relatively simple key schedules, such as the simple key schedule with \(K_i = K\), linear key schedules where \(K_i = L(K)\) for some bit permutation or linear function \(L(\cdot )\), or key update functions with similarly weak diffusion properties as a single cipher round. In such designs, it is usually easy to combine partial key information from one round with partial information from the next round and thus derive the full key, as we demonstrated in Sect. 3.
Therefore, the final DEFAULT design uses a stronger key schedule, as discussed in Sect. 2.2. To reasonably approximate a long-key cipher with independent round keys, it uses 4 round keys \(K_0, K_1, K_2,\) and \(K_3\) in a rotating fashion.
In this section, we observe that the idealized long-key cipher permits classes of equivalent keys that generate the same permutation. We characterize these classes based on the linear structures of the S-box and normalize them, i.e., define a unique representative for each class. Finally, we propose a generic attack strategy for ciphers with linear structures based on this observation. This strategy will be the basis for the concrete, optimized attacks we present in Sect. 5.
4.1 Equivalent Keys in the DEFAULT Framework
In ciphers with linear structures in its S-boxes and independent round keys, there exist large classes of keys that lead to exactly identical behavior. As a small example, consider a toy cipher consisting of one DEFAULT-LAYER S-box with a key addition before and after: \(v = \mathcal S (u\oplus k_0) \oplus k_1\), with \((k_0, k_1) \in \mathcal K\times \mathcal K = \mathbb F_2^4\times \mathbb F_2^4\) (Fig. 4). In that case, we have \((k_0, k_1) \equiv (k_0\oplus \texttt {6}, k_1\oplus \texttt {a}) \equiv (k_0\oplus \texttt {9}, k_1\oplus \texttt {f}) \equiv (k_0\oplus \texttt {f}, k_1\oplus \texttt {5})\). This works because a difference of, for example, \(\texttt {6}\) at the input of the S-box always leads to a difference of \(\texttt {a}\) at the output which is cancelled by the other key. These classes of equivalent keys allow us to define normalized keys \((\bar{k}_0, \bar{k}_1) \in \mathbb F_2^4 \times \mathcal N\), where \(\mathcal N = \{0,1,2,3\}\), thus heavily constraining the choices for \(k_1\). Crucially, every possible original key maps to one such normalized key. The same logic applies if there is a linear layer before the second key addition; the only difference being that the linear layer changes the output differences of the linear structures.
These linear structures form a linear subspace that we call the linear space of the round function. We use \(\mathcal L\) to denote the linear space of all \(n-1\) round functions. In the case of DEFAULT-LAYER, there are 32 S-boxes with \(2^2\) linear structures each. Thus, one round has a linear space of size \(2^{64}\) and \(\left| \mathcal L\right| = 2^{64 (n-1)}\).
As the effect of a key is invariant under addition of elements from the linear space, we can partition the key space into equivalence classes. We assign each key k to the set of keys that can be obtained by xoring k with \(l\in \mathcal L\). In other words, we consider the quotient space of the space of independent round keys modulo the linear space, \(\mathcal K^n \mathbin / \mathcal L\). Note that if we consider \(n-1\) rounds of a cipher with n independent keys, the effective key space is reduced by all \(n-1\) linear spaces of the individual rounds. Thus, in the case of DEFAULT-LAYER with 4 independent keys, there are \(|\mathcal L| = 2^{192}\) linear structures, so we can reduce the space of \(|\mathcal K^4| = 2^{4 \times 128} = 2^{512}\) keys to the space of \(|\mathcal K^4\mathbin /\mathcal L| = 2^{128 + 3 \times 64} = 2^{320}\) equivalence classes.
4.2 Normalized Keys
As working with linear spaces of equivalent keys can be quite tedious, we define one representative per equivalence class. We refer to this set of class representatives as the normalized keys \(\mathcal N^{(n)}\), where n is the number of round keys. This choice is arbitrary but does influence the computational complexity of the following attacks. Concretely, we want to reduce the potential choices for the parts of the key we have to guess at first. If we examine this at a per-S-box level, we can observe that for each of the equivalent keys, we can select a single one and compensate with the help of the key of the following round (see Fig. 4). We can repeat this process for the first \(n-1\) round keys and thus restrict these keys significantly. Thus, we only need to leave the final round key unconstrained. Therefore, we are able to restrict the space for the first \(n - 1\) round keys to a much smaller set \(\mathcal N\). As the last key is unconstrained we have
where \(\bar{K} = (\bar{K}_0, \bar{K}_1, \ldots , \bar{K}_{n-1})\) denotes such a normalized key.
In the case of DEFAULT-LAYER with 4 independent keys, this leads to a set of representatives where the nibbles of the first 3 rounds are constrained to the space \(\{\texttt {0},\texttt {1},\texttt {2},\texttt {3}\}\) while the final key is unconstrained. For example, the sequence of round keys shown in Fig. 5a is equivalent to the one shown in Fig. 5b. The algorithm used to normalize a given sequence of round keys schedule is outlined in Fig. 6. Note that the mapping from \(\mathcal K^n\), the set of sequences of round keys of length n, to the set of normalized keys \(\mathcal N^{(n)}\) is linear. Thus, it can be represented using a \(128n \times 128n\) matrix \(\mathbf{A}_{\mathcal K\rightarrow \mathcal N,n}\) of rank \(64n + 64\).
4.3 Generic Attack Strategy for Ciphers with Linear Structures
We can use the observation about equivalence classes to recover \(n-1\) equivalent round keys by performing DFA on \(n-1\) rounds with linear structures and examining the ciphertext. The model which we use for this generic attack is a cipher with a long key consisting of n independent rounds keys for \(n-1\) rounds, as illustrated in Fig. 7. Additionally, we assume that the input to these \(n-1\) rounds is unknown, as is the case for DEFAULT-LAYER. Note that one of the n keys remains unknown as we do not know the input and no more S-boxes remain to be faulted. In the case of DEFAULT, we can fault the S-boxes of DEFAULT-CORE to recover this final key \(\bar{K}_{n-1}\) using classical DFA. We would need 64 additional faults to recover \(\bar{K}_{n-1}\) using the most basic technique.
Instead of recovering the original key \(K = (K_0,\ldots ,K_{n-1})\), we recover the first \(n-1\) round keys of the normalized key \(\bar{K} = (\bar{K}_0, \ldots , \bar{K}_{n-1})\). We describe the attack strategy in terms of decryption. However, the attack on encryption is analogous with the only difference being that we need a different set of normalized keys and different indexing. We perform this attack by placing single bit flips before each S-box of the final round of decryption to recover \(\bar{K}_0\) uniquely. Once we have recovered the final round key, we can repeat the process to recover \(\bar{K}_1\) to \(\bar{K}_{n-2}\) uniquely. Thus, only a single round key, \(\bar{K}_{n-1}\), remains unknown.
Consider the toy cipher in Fig. 8 which encrypts an unknown internal value t by using \(c=k_0\oplus (\mathcal S(k_1\oplus \mathcal S(k_2\oplus (k_3\oplus t))))\) with \((k_0,k_1,k_2,k_3)=(\texttt {2}, \texttt {b}, \texttt {a}, \texttt {c})\). By inducing two faults after the xor of \(k_1\), we can reduce the space of \(\bar{k}_0\) to \(\{\texttt {2}, \texttt {7}, \texttt {8}, \texttt {d}\}\). This set corresponds to the linear space at the output of \(\mathcal S\) as it equals \(\texttt {2} \oplus \{\texttt {0}, \texttt {5}, \texttt {a}, \texttt {f}\}\). Therefore, we pick \(\bar{k}_0 = \texttt {2}\). Now we fault after the \(\textsc {xor}\) of \(k_2\) to reduce the space of \(\bar{k}_1\) to \(\{\texttt {1}, \texttt {4}, \texttt {b}, \texttt {e}\}\). Again, this corresponds to the linear space and we can pick \(\bar{k}_1 = 1\). Now we observe a difference between the normalized key and the actual key: \(\bar{k}_1 \oplus k_1 = \texttt {a}\). However, due to the linear structure \(\texttt {6}\rightarrow \texttt {a}\), we can compensate this by a difference of \(\texttt {6}\) in \(k_2\). Thus, when faulting after the xor of \(k_3\), we can reduce the space of \(\bar{k}_2\) to \(\{\texttt {3}, \texttt {6}, \texttt {9}, \texttt {c}\}\). Note that this includes \(k_2\oplus \texttt {6} = \texttt {c}\). We pick \(\bar{k}_2 = \texttt {3}\). Now the difference \(\bar{k}_2 \oplus (k_2 \oplus \texttt {6}) = \texttt {f}\) can be compensated by the linear structure \(\texttt {9}\rightarrow \texttt {f}\). Thus, if we knew the value of t, we would calculate \(\bar{k}_3 = 5\). Alternatively, we can fault the components that are used to calculate t to get more information about \(k_3\). For example, if another application of \(\mathcal S\) was performed before t, we would be able to reduce \(\bar{k}_3\) to a space of \(\{\texttt {0}, \texttt {5}, \texttt {a}, \texttt {f}\}\). In practice, it is not necessary to carry out all these calculations; instead, it is sufficient to restrict the guessed keys as described in Sect. 4.2.
When applying this attack to DEFAULT, we can recover 27 of the 28 normalized keys used by the idealized DEFAULT-LAYER. Once we have these keys, we can continue our attack by faulting DEFAULT-CORE which uses strong S-boxes that contain no non-trivial linear structures. This allows us to recover \(\bar{K}_{27}\), and subsequently, the actual key that was used for the cipher. This attack breaks DEFAULT in the fault model specified by the authors. As this attack needs a large amount of faults, we will show more efficient attacks in the next section. Alternatively, we can apply this strategy to \(n < 28\) independent round keys in which case we would be able to recover the normalized \((\bar{K}_0, \ldots , \bar{K}_{n-2})\) uniquely and \(\bar{K}_{n-1}\) up to a space of 64 bits by faulting the preceding round of DEFAULT-LAYER.
5 Information-Combining DFA on Rotating Key Schedule
So far, we have shown generic attacks that apply to idealized ciphers with independent round keys and exploit only the linear structures of the round function. In this section, we exploit the specifics of the rotating key schedule in DEFAULT to build attacks that require much fewer faults.
5.1 Basic Encrypt-Decrypt Attack on Rotating Key Schedule
We can combine the ideas of Sect. 3.2 and Sect. 4. By using equivalence classes, we can recover the normalized key up to 64 bits by faulting decryption. Then, we can combine this with another 32 bits of information gained by faulting encryption.
In this attack, we target the normalized key consisting of 4 round keys: \(\bar{K} = (\bar{K}_0, \bar{K}_1, \bar{K}_2, \bar{K}_3)\). First, we recover \(\bar{K}_0\), \(\bar{K}_1,\) and \(\bar{K}_2\) by placing faults before the S-boxes preceding the key addition. Due to the restrictions of the normalized key schedule, we can recover them uniquely by using 192 faults. Then, we place 64 faults before the S-boxes preceding the addition of \(K_3\) to recover \(\bar{K}_3\) up to a space of \(2^{64}\) candidates. As in the attack on DEFAULT-LAYER with a simple key schedule, we can represent this set of candidates as a system of linear equations. Next, we perform 32 faults just before the S-boxes in the final round of encryption to gain 32 additional equations about \(\bar{K}_3\). Thus, we can reduce the space for \(\bar{K}\) to a set of \(2^{32}\) normalized key candidates.
With the normalized key schedule reduced to a space that can be brute-forced, we still need a way to validate each key candidate. In this case, a plaintext-ciphertext pair is not sufficient as a normalized key does not uniquely identify the key used in DEFAULT-CORE. Therefore, we inject a single fault just after DEFAULT-CORE. By using the correct and faulty ciphertexts we obtain, we can validate each of the \(2^{32}\) key guesses to identify the correct normalized key. Once the normalized key is recovered, we can invert DEFAULT-LAYER to recover the intermediate value right after DEFAULT-CORE. Now, we can target DEFAULT-CORE using classical DFA on the strong S-boxes. The downside of this approach is the brute-force complexity of searching the \(2^{32}\) normalized key candidates.
5.2 Basic Multi-round Attack on Rotating Key Schedule
So far, we combined Sect. 4 and Sect. 3.2. Similarly, we can also combine the idea of equivalence classes from Sect. 4 with the multi-round attack of Sect. 3.3. This has the advantage of allowing us to uniquely identify the normalized key, thus eliminating the brute-force complexity. However, this attack is more challenging as the identical round keys are so far apart due to the strong key schedule.
The main idea of this attack is to first recover the first \(n=6\) keys under the assumption that they are chosen independently. Then, we want to equate \(K_0=K_4\) and \(K_1=K_5\). However, when using the attack strategy from Sect. 4.3 we only recover a set of normalized keys \((\bar{K}_0, \ldots , \bar{K}_5)\) up to 64 bits. We cannot add the equality relations \(\bar{K}_0 = \bar{K}_4\) and \(\bar{K}_1 = \bar{K}_5\) as this set of normalized keys is only a subset of the much larger set of possible non-normalized keys. Therefore, we need to transform the set of normalized keys to the set of non-normalized keys before applying the equations. After adding the equations, we can transform back to the set of normalized candidates for \((\bar{K}_0, \bar{K}_1, \bar{K}_2, \bar{K}_3\)).
This leads to an attack that is performed in 4 steps. We store these spaces of key candidates using systems of linear equations which allows us to perform this attack with negligible runtime complexity. These spaces are depicted in Fig. 9. In step (1), we assume the first \(n = 6\) round keys \(K_0, \ldots , K_5\) are independently chosen. We can restrict these six keys to a space of \(2^{64}\) normalized candidates by faulting decryption according to the strategy from Sect. 4.3. In step (2), we remove the condition that the round keys need to be normalized and obtain a set of \(2^{384}\) keys. In step (3), we restrict the set of non-normalized keys to only those where the conditions of the rotating key schedule are met, i.e., \(K_0 = K_4\) and \(K_1 = K_5\). Finally, in step (4), we add the restriction that the first 4 keys form a normalized sequence of round keys and receive a single result.
In the following description, we use k to denote the column vector corresponding to the bits of \((K_0, K_1, \ldots , K_5)\). Similarly, we use \(\bar{k}\) to denote the column vector corresponding to the bits of the normalized key \((\bar{K}_0, \bar{K}_1, \ldots , \bar{K}_5)\).
(1) Creating an equation system for the normalized key \(\boldsymbol{\bar{K}}\): We start our attack by assuming the first \(n=6\) keys \(K = (K_0,\ldots ,K_5)\in \mathcal K^6\) are chosen independently and applying the strategy of Sect. 4.3 on the first 6 keys. For now, we ignore the fact that \(K_0 = K_4\) and \(K_1 = K_5\). Thus, we obtain the normalized keys \(\bar{K}_0,\ldots ,\bar{K}_4\) uniquely using DFA. We need to fault each S-box in these 5 rounds twice to achieve this reduction. For example, we can inject a difference of \(\texttt {1}\) and \(\texttt {2}\) before each S-box. Furthermore, we can limit \(\bar{K}_5\) to a space of \(2^{64}\) candidates by faulting the S-boxes before \(K_5\) is added. Again, we need to fault each S-box twice, thus, arriving at a total of 384 faults.
Converting the information about \(\bar{K}_0\) to \(\bar{K}_4\) into linear equations is trivial as we uniquely know their value. For \(K_5\), we know only know 2 bits of information per nibble, which we can represent using two linear equations from Table 3 each. Therefore, we get the following equation, where A is a \(128n \times 128n\) matrix of rank \(128n - 64\) and \(\bar{k}\), b are column vectors:
(2) Converting the equation system to all possible keys \(\boldsymbol{K}\): The space of \(2^{64}\) candidates for the normalized key \(\bar{K}\) corresponds to a much larger space of candidates for the unrestricted key \(K = (K_0, K_1, \ldots , K_5)\). To describe this larger space using linear equations, we note that \(A_{\mathcal K\rightarrow \mathcal N,n} \cdot k = \bar{k}\) and substitute accordingly, where the matrix product is of rank 64n:
(3) Adding additional constraints due to the rotating key schedule: Because we know \(K_0 = K_4\) and \(K_1 = K_5\), we can add 256 additional equations. This restricts the space of solutions to \(2^{192}\) candidates which corresponds to one equivalence class for 4 independent round keys.
(4) Adding constraints to normalize the keys: Finally, we require that the first four round keys are normalized: \((K_0, K_1, K_2, K_3) \in \mathcal N^{(4)}\). In matrix notation, this is equivalent to \(A_{\mathcal K\rightarrow \mathcal N,4} \cdot k_{0\ldots 3} = k_{0\ldots 3}\). Note that we use a matrix that is related to but distinct from the normalization matrix used earlier. Therefore, we add the following linear equations:
where I is the identity matrix. Then, we get a full-rank system, which we can solve uniquely.
Thus, we are able to recover an equivalent key for DEFAULT-LAYER. As in Sect. 4.3, we still need to recover the key for DEFAULT-CORE which we can achieve by using classical DFA.
We note that this attack is not limited to a rotating key schedule with only 4 distinct round keys: it is applicable to any number of independent round keys, as long as we have two round keys which are used more than once. For example, this attack can also be used to recover the key in case the simple key schedule is used by faulting 3 keys. In general, attacking DEFAULT-LAYER with x rotating keys requires us to recover 64 bits of information about \(x+2\) keys each.
6 Reducing the Number of Faults
While the attacks discussed so far achieve their goals, they are not optimized for efficiency and require quite a number of faulted computations with different fault positions. We can improve the attacks by placing the faults earlier, further from the known plaintext or ciphertext. For this purpose, we need a differential model of the cipher that predicts how these faults propagate.
Differential Model. To store the set of possible differences for a state of the cipher, we use a dictionary that maps from one 128-bit difference to its associated probability. We then examine how this set of possible differences changes round by round. For each round, we examine all possible differences individually and see how they propagate through the round function. To achieve this, we look at each S-box and note the set of possible output difference by examining the differential distribution table. Then, the set of possible differences after the S-box is the Cartesian product of all the individual differences. We do not explicitly keep track of the probability as all transitions for a given input difference are equally likely, as is evident from the differential distribution table. For each of these differences, we apply the bit permutation and add them to the set of differences after the round. To calculate the probability, we divide the probability of observing the difference before the round by the number of potential differences. If an entry already exists, we increase the probability by the calculated amount.
Using the Model to Find Suitable Fault Targets. We can use this model to calculate the expected amount of information learned from a sequence of faults which allows us to search for suitable fault targets. We first calculate the set of 128-bit differences before the final S-boxes and their probabilities. We then convert this set into the set of possible differences for each nibble with associated probabilities. Now, we examine all 32 nibbles independently. For each nibble and each fault, we have a list of possible differences. We examine the Cartesian product of these lists over all faults. Each element in the product is one possible outcome. We calculate its probability as the product of the individual probabilities. For each fault, we look up the information we learn according to Table 3 and enter that into a matrix. The rank of the matrix tells us the overall amount of information we learn. By repeating that process for every element in the Cartesian product and each nibble, we can calculate the expected amount of information learned from that sequence of faults.
In general, we find that placing the faults such that they are processed by 4 S-boxes with successive key-additions, leads to enough diffusion such that most S-boxes in the final round are active while still allowing us to determine the input difference of the final S-box by examining the output difference. Therefore, we apply this model to all possible pairs of fault indices for encryption and decryption to find suitable targets. We find that when each fault is repeated 3 times, flipping the bits at index 2 and 22 during encryption and 33 and 39 during decryption provides the best results.
6.1 Optimized Encrypt-Decrypt Attack on Simple Key Schedule
According to the results of Sect. 6, we place our faults such that they are processed by 4 S-boxes. We then combine faulting the bits at index 2 and 22 during encryption with faulting the bits at index 33 and 37 during decryption. To decrease the size of the remaining key space, we repeat each fault 4 times, thus performing 16 faults in total. Using these faults, we gather enough information to reduce the size of the key space to between \(2^{33}\) and \(2^{39}\) in 95% of all cases. Figure 10a shows the distribution of the size of the key space after this attack.
6.2 Optimized Multi-round Attack on Simple Key Schedule
To reduce the number of required faults, we can use tricks similar to those in Sect. 6.1. Additionally, we can reuse faults instead of gathering new ones for each round. The following attack applies when faulting the decryption; for encryption, an analogous attack is possible.
We start the attack by inducing 16 separate faults at the S-boxes \(S_i\) with \(i \in \{0, 2, 8, 10, 21, 23, 29, 31\}\) such that each fault is processed by 4 key-dependent rounds of the cipher. Now, we can analyze these faulted encryptions based on the differential model similar to before and calculate the set of possible differences before each S-box in each round. We start by analyzing the final round: for each S-box, we try all 16 keys and verify whether the key is compatible with the set of possible differences. This reduces the key space per 4-bit key to a set of about 4 candidates: we can reduce the overall key space to a size of \(2^{64}\) in 50% of all cases and to at most \(2^{66}\) in about 90% of all cases.
Next, we analyze all faults across 2 rounds: for each fault and each potentially active S-box in the penultimate round, we try all keys and filter based on the possible differences calculated earlier. Usually, we need to iterate over \(2^8\) keys. This step reduces the size of the overall key space to \(2^{32}\) in about 75% of all cases and to at most \(2^{34}\) in about 99% of all cases.
Finally, we analyze the faults across 3 rounds: we can again filter based on all potentially active S-boxes in our targeted round. As in Sect. 3.3, however, we do not filter based on those S-boxes where we would need to guess the keys for more than 16 S-boxes. Thus, we usually need to iterate over \(2^{16}\) keys for each potentially active S-box and fault. After this step, we are left with at most \(2^{20}\) keys in about 90% of all cases. Figure 10b shows the distribution of the size of the key space after this attack.
6.3 Optimized Multi-round Attack on Rotating Key Schedule
For the optimized version of our most powerful attack, we use a dynamic number of faulted encryptions and fix the success probability at \(100\%\). As we need to learn 64 bits of information about 6 round keys each, we target 6 different rounds during our fault attack. We place the faults such that the are processed by 4 rounds of decryption before the currently targeted key is xored. We target the indices \(\{1, 5, 9, 13, \ldots , 25, 29\}\), i.e., we induce a difference of 2 for the 8 rightmost S-boxes. By applying the model of the differential behavior of the cipher to each fault, we calculate the set of possible differences at the input of the S-box that is applied before the targeted key is xored. Then, we can filter each nibble of the targeted key based on this expected difference. As in the basic attack, we restrict these 6 keys to form a normalized sequence of keys, i.e., the nibbles of the first 5 keys are restricted to \(\{\texttt {0},\texttt {1},\texttt {2},\texttt {3}\}\). We repeat faulting these 8 S-boxes until we learn 64 bits of additional information about the key. Once we have gathered all the required key information, we continue the attack as in Sect. 5.2.
When performing this attack, we find that we need \(83.6\pm 14.8\) faults on average to recover an equivalent key for DEFAULT-LAYER. As before, we can continue by performing classical DFA on DEFAULT-CORE. The histogram of needed faults is depicted in Fig. 11. We believe the fault complexity of this attack can be reduced even further by removing the requirement that each normalized round key needs to be recovered uniquely.
7 Discussion
We now discuss several potential mitigations for our attack and argue why each of them is not sufficient to preclude information-combining normalized-key DFA attacks.
Inverting one DEFAULT-LAYER. The attacks combining information from encryption and decryption work because we combine information from a DFA on the DEFAULT-LAYER, \(E_{\texttt {DEFAULT-LAYER}}\), with information from a DFA on the inverse DEFAULT-LAYER, \(E^{-1}_{\texttt {DEFAULT-LAYER}}\). Therefore, a possible mitigation for these attacks is to change one DEFAULT-LAYER to its inverse, so that a DFA during encryption and decryption is always mounted on the same function:
However, even then, it is possible to combine information of differential-based fault attacks of \(E_{\texttt {DEFAULT-LAYER}}\) and \(E^{-1}_{\texttt {DEFAULT-LAYER}}\) by combining a DFA with a collision fault attack [7].
Note that this attack is also a threat in the following scenario proposed by the designers [1, Sect. 4.1]: they suggest that the cipher could also only be protected by one DEFAULT-LAYER if the attacker model is limited to a single direction (either encryption or decryption), e.g., \(E_{\texttt {DEFAULT-LAYER}}\circ E_{\texttt {CORE}}\) for an adversary who targets only encryption. As discussed, this enables differential-based fault attacks on the core cipher using fault-based collision attacks.
Involutive S-box. Another way to achieve a similar result is to replace the S-box used in DEFAULT-LAYER with an involutive S-box. This would prevent the attacks combining information from encryption and decryption. Note that for this countermeasure to work, care must be taken when choosing the linear layer, as a different linear layer could lead to more linearly independent equations about the key. This does not protect against the multi-round or the generic attack.
Strong Linear Layer. A potential mitigation for the information combining attacks on DEFAULT with a simple key schedule is to use a strong linear layer. This would greatly increase the computational complexity of the multi-round attack from Sect. 3.3. However, the attacks based on normalized keys including the attack from Sect. 5.2 would still apply. Additionally, a strong linear layer would make attacks combining information from encryption and decryption easier.
Independent Round Keys. In their design paper, the authors note that using 28 independent round keys for DEFAULT-LAYER would make information combining attacks useless [1, Section 6.1]. While this is true for combining information across rounds, the ideas of equivalent keys from Sect. 4 still apply. In particular, the generic attack from Sect. 4.3 defeats this construction.
8 Conclusion
Due to the practical impact of DFA style attacks, strategies for protecting ciphers are highly relevant and different strategies have been explored in the past years. The authors of DEFAULT propose an interesting design strategy to inherently limit the amount of information an attacker can learn.
In this paper we showed that while indeed only a limited amount of information can be gained each round, we can combine information across rounds. While it intuitively appears that a simple key schedule prevents information-combining attacks, as the same key is used each round, we show that this is possible. For this reason, the designers proposed a strong key schedule with full diffusion, to ensure that it is infeasible to combine information from neighboring rounds. This indeed helps to prevent straight-forward information-combining DFA attacks.
Unfortunately, we can use the properties of the round function to characterize large classes of equivalent keys by identifying a set of normalized keys. These normalized keys permit us to combine information across many rounds, thus breaking DEFAULT with the proposed strong key schedule and even an idealized key schedule with independent round keys. The key observation is that starting from the ciphertext, in each round, the adversary can either learn additional information about the round key or arbitrarily pick one of the remaining candidates and move on to the next round. By optimizing the placement of faults, we can reduce the fault complexity to less than 100 faulted computations to recover an equivalent key for DEFAULT-LAYER with no additional brute-force cost.
Our analysis shows how challenging it is to prevent these implementation attacks. While cipher-level protection would be a great solution as it does not offload the responsibility to implementers, it seems substantial ideas beyond linear structures are necessary. This raises the question of how the DEFAULT design strategy can be adapted to achieve inherent protection against DFA.
References
Baksi, A., Bhasin, S., Breier, J., Khairallah, M., Peyrin, T., Sarkar, S., Sim, S.M.: DEFAULT: Cipher level resistance against differential fault attack. In: Tibouchi, M., Wang, H. (eds.) ASIACRYPT 2021. LNCS, vol. 13091, pp. 124–156. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92075-3_5
Baksi, A., et al.: DEFAULT: Cipher level resistance against differential fault attack. IACR Cryptology ePrint Archive, Report 2021/712 (2021), https://eprint.iacr.org/2021/712/20210528:092448
Bar-El, H., Choukri, H., Naccache, D., Tunstall, M., Whelan, C.: The sorcerer’s apprentice guide to fault attacks. Proc. IEEE 94(2), 370–382 (2006). https://doi.org/10.1109/JPROC.2005.862424
Beierle, C., Leander, G., Moradi, A., Rasoolzadeh, S.: CRAFT: lightweight tweakable block cipher with efficient protection against DFA attacks. IACR Trans. Symmet. Cryptol. 2019(1), 5–45 (2019). https://doi.org/10.13154/tosc.v2019.i1.5-45
Biham, E., Shamir, A.: Differential cryptanalysis of DES-like cryptosystems. In: Menezes, A., Vanstone, S.A. (eds.) CRYPTO 1990. LNCS, vol. 537, pp. 2–21. Springer, Berlin (1990). https://doi.org/10.1007/3-540-38424-3_1
Biham, E., Shamir, A.: Differential fault analysis of secret key cryptosystems. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 513–525. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052259
Blömer, J., Krummel, V.: Fault based collision attacks on AES. In: Breveglieri, L., Koren, I., Naccache, D., Seifert, J.P. (eds.) FDTC 2006. LNCS, vol. 4236, pp. 106–120. Springer, Berlin (2006). https://doi.org/10.1007/11889700_11
Dobraunig, C., Eichlseder, M., Korak, T., Lomné, V., Mendel, F.: Statistical fault attacks on nonce-based authenticated encryption schemes. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 369–395. Springer, Berlin (2016). https://doi.org/10.1007/978-3-662-53887-6_14
Dobraunig, C., Mennink, B., Primas, R.: Leakage and tamper resilient permutation-based cryptography. IACR Cryptology ePrint Archive, Report 2020/200 (2020). https://ia.cr/2020/200
Gierlichs, B., Schmidt, J.M., Tunstall, M.: Infective computation and dummy rounds: fault protection for block ciphers without check-before-output. In: Hevia, A., Neven, G. (eds.) LATINCRYPT 2012. LNCS, vol. 7533, pp. 305–321. Springer, Berlin (2012). https://doi.org/10.1007/978-3-642-33481-8_17
Giraud, C., Thillard, A.: Piret and quisquater’s DFA on AES revisited. IACR Cryptology ePrint Archive, Report 2010/440 (2010). https://ia.cr/2010/440
Knudsen, L.R.: Truncated and higher order differentials. In: Preneel, B. (ed.) FSE 1994. LNCS, vol. 1008, pp. 196–211. Springer, Berlin (1994). https://doi.org/10.1007/3-540-60590-8_16
Medwed, M., Standaert, F.X., Großschädl, J., Regazzoni, F.: Fresh re-keying: Security against side-channel and fault attacks for low-cost devices. In: Bernstein, D.J., Lange, T. (eds.) AFRICACRYPT 2010. LNCS, vol. 6055, pp. 279–296. Springer, Berlin (2010). https://doi.org/10.1007/978-3-642-12678-9_17
Patranabis, S., Chakraborty, A., Mukhopadhyay, D.: Fault tolerant infective countermeasure for AES. In: Chakraborty, R.S., Schwabe, P., Solworth, J.A. (eds.) SPACE 2015. LNCS, vol. 9354, pp. 190–209. Springer, Berlin (2015). https://doi.org/10.1007/978-3-319-24126-5_12
Piret, G., Quisquater, J.J.: A differential fault attack technique against SPN structures, with application to the AES and KHAZAD. In: Walter, C.D., Koç, Ç.K., Paar, C. (eds.) CHES 2003. LNCS, vol. 2779, pp. 77–88. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45238-6_7
Simon, T., Batina, L., Daemen, J., Grosso, V., Massolino, P.M.C., Papagiannopoulos, K., Regazzoni, F., Samwel, N.: Friet: An authenticated encryption scheme with built-in fault detection. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12105, pp. 581–611. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45721-1_21
Tupsamudre, H., Bisht, S., Mukhopadhyay, D.: Destroying fault invariant with randomization - A countermeasure for AES against differential fault attacks. In: Batina, L., Robshaw, M. (eds.) CHES 2014. LNCS, vol. 8731, pp. 93–111. Springer, Berlin (2014). https://doi.org/10.1007/978-3-662-44709-3_6
Acknowledgments
We thank the DEFAULT designers for their comments. Additional funding was provided by a generous gift from Google. Any findings expressed in this paper are those of the authors and do not necessarily reflect the views of the funding parties.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Nageler, M., Dobraunig, C., Eichlseder, M. (2022). Information-Combining Differential Fault Attacks on DEFAULT. In: Dunkelman, O., Dziembowski, S. (eds) Advances in Cryptology – EUROCRYPT 2022. EUROCRYPT 2022. Lecture Notes in Computer Science, vol 13277. Springer, Cham. https://doi.org/10.1007/978-3-031-07082-2_7
Download citation
DOI: https://doi.org/10.1007/978-3-031-07082-2_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-07081-5
Online ISBN: 978-3-031-07082-2
eBook Packages: Computer ScienceComputer Science (R0)



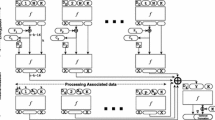



 ) and fault propagation example (
) and fault propagation example (
 ) in the multi-round information-combining DFA on
) in the multi-round information-combining DFA on 








