Supervised Multi-view Latent Space Learning by Jointly Preserving Similarities Across Views and Samples

Abstract

In multi-view learning, leveraging features from various views in an optimal manner to improve the performance on predictive tasks is a challenging objective. For this purpose, a broad range of approaches have been proposed. However, existing works focus either on capturing (1) the common and complementary information across views, or (2) the underlying between-view relationships by exploiting view pair similarities. Besides, for the latter, we find that the obtained similarities cannot representatively reflect the differences among views. Towards addressing these issues, we propose a novel approach called MELTS (Multi-viEw LatenT space learning with Similarity preservation) for multi-view classification. MELTS first utilizes distance correlation to explore hidden between-view relationships. Furthermore, by assuming that different views share certain common information and each view carries its unique information, the method leverages both (1) the similarity information of different view pairs and (2) the label information of distinct sample pairs, to learn a latent representation among multiple views. The experimental results on both synthetic and real-world datasets demonstrate that MELTS considerably improves classification accuracy compared to other alternative methods.

1 Introduction

In the real world, an object can often be described by multiple different features. For example, in the vision domain, a video can be described by language, visual and audio features. These data are called multi-view data and are often collected from different data sources or measured by different methods. Multi-view classification widely exist in real-world applications, such as image classification [9] and disease diagnosis [11].

Multi-view data have two important principles: consensus and complementary principles [4]. Since different views share information, the consensus principle suggests that distinct views should be in agreement. Existing methods focus primarily on extracting common information shared by all views (e.g. [3]). The main idea is to map the original views into a latent subspace and maximize the consensus among the learned representations from distinct views. This group of methods reduce feature redundancy, however, they fail to capture the complementary information contained in individual views.

On the other hand, the complementary principle assumes that each view contains some unique information. The recent methods [4, 8] tend to learn representations that contain both the consistency information shared by all views and the complementary information of each individual view, simultaneously. To further make effective use of complementary information, a diversity constraint is added to enforce the learned representations from different views to be independent of one other [7]. Promoting sufficient diversity across different views essentially ignores the true underlying relationship among the views.

To explore the relationship among views, recently, [10] presented a method that utilizes Jensen Shannon divergence (JS-divergence) to calculate the similarities between view pairs. However, we observe that the view-pair similarities cannot be captured correctly when the number of samples and some between-sample distances are large, due to the manner in which JS-divergence is formulated.

Fig. 1.

An illustration of the constituent components of the MELTS framework.

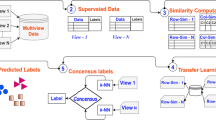
To address the aforementioned issues, we propose a novel approach MELTS (Multi-viEw LatenT space learning with Similarity preservation) aimed at preserving similarities between view pairs as well as between sample pairs in the learned representations. Figure 1 illustrates the framework of the approach. MELTS learns a latent subspace that is composed of a shared component across all views and a specific component for each view. To capture the relationship among views, we propose to utilize distance correlation [6] to calculate the similarity between each view pair in the original data. We assume that if two views are less similar, then their specific components will contain more discriminative information. Otherwise, their specific components will be similar to each other. Such a latent representation true learning approach would tend to preserve the latent relationships between views. In addition, by taking label information into account, MELTS minimizes the distances between any sample pairs in the subspace if they are from the same class, which further enhances the separability of the learned features. After learning the representations, a linear classifier is applied for classification.

The contributions of this work are summarized as follows:

• We identified the cause of the problem of using JS-divergence to calculate the relationship between view pairs and proposed to utilize distance correlation as a remedy.

• We proposed a method MELTS that simultaneously leverages both (1) the similarity information for different view pairs and (2) the label consistency of sample pairs to learn a latent representation among multiple views.

2 Proposed Approach

Let the matrix $\mathbf{X} _{i}=\left[ \mathbf{x} _{1}^{i},\cdots ,\mathbf{x} _{n}^{i}\right] \in \mathbb {R}^{d_{i}\times n}$ represent a set of data samples in the i-th view, where $d_{i}$ denotes the feature dimension of the i-th $\left( i = 1,\cdots ,k \right)$ view and k denotes the number of views. Further, let $\mathbf{Y} \in \mathbb {R}^{ n \times c}$ be the label matrix, where c is the number of classes and each row is a label vector in which the b-th entry is 1 and the rest are $-1$ if its corresponding sample falls in the b-th class. The goal is to classify each sample by learning the latent representations among k different views of the training samples. Since an individual sample is described by multiple views, we assume that the latent representations contain a shared component $\mathbf{Z} \in \mathbb {R}^{n\times d_{s}}$ among all views and a specific component $\mathbf{Z} _{i} \in \mathbb {R}^{n\times d}$ within each single view, where $d_{s}$ and d are the dimensions of the shared and specific components, respectively.

2.1 View Pair Correlation Preserving

Before describing our model, we first introduce the view pair correlation preserving term, which intends to capture the discriminative information among multiple views by exploring correlation between view pairs. We hypothesize that if a view-pair correlation under the original representation is strong, then the view-specific components of two views should be similar. For example, if two views’ original representations $\mathbf{X} _{i}$ and $\mathbf{X} _{j}$ are correlated, we expect that $\mathbf{Z} _{i}$ and $\mathbf{Z} _{j}$ are similar, which means $\mathbf{Z} _{i}$ and $\mathbf{Z} _{j}$ are close to each other in the projected space. By utilizing this term, the latent relationships between the views can be preserved. However, each view may contain different feature dimension, which brings a challenge to measure the between-view correlation. To address this issue, one recent work [10] applies JS-divergence to measure the similarity between view pairs. Specifically, they first calculate the distance between any two samples in each view. After computing the distance probability between all sample pairs in each view, they use JS-divergence to calculate the similarity between view pairs. When view pairs are more similar, JS-divergence is closer to zero.

Computing the difference of distance probability distributions in two views allows to measure the similarity between views with different feature dimensions. However, we found that when (1) the number of samples is large (or even when some values of sample pairs’ distances are large) and (2) the difference of distance probability between two views is small; the view pair similarity calculated by JS-divergence tends to be small, which fails to capture the relationship among the views. The main reason is that larger values of the number of samples and sample pairs’ distances make the distance probabilities smaller and cause negligible difference between the distance probability distributions of two views, which leads to the JS-divergence being close to zero.

In our model, we adopt the idea of distance correlation [6], which originally was designed to describe the dependence between two random variables. Distance correlation utilizes distance covariance to capture the relationship between views and avoids to calculate the distance probability, which can overcome the problem of using JS-divergence. Let $l_{a,b}^{i}$ represent the Euclidean distance between the samples a and b in the i-th view, and let $\mathbf{L} ^{i}$ be the distance matrix containing all pairwise distances. After double centering of each distance, the distance correlation between views i and j is: $dCorr(\mathbf{X} _{i},\mathbf{X} _{j})= \frac{dCov(\mathbf{X} _{i},\mathbf{X} _{j})}{\sqrt{dVar(\mathbf{X} _{i})dVar(\mathbf{X} _{j})}},$ where $dCov(\mathbf{X} _{i},\mathbf{X} _{j})=\sqrt{\frac{1}{n^{2}}\sum _{a=1}^{n}\sum _{b=1}^{n}t_{a,b}^{i}t_{a,b}^{j}}$ and $dVar(\mathbf{X} _{i})=dCov(\mathbf{X} _{i},\mathbf{X} _{i})$. The view pair correlation preserving is achieved by minimizing the following term:$\frac{1}{k(k-1)}\sum _{i<j} \Vert \mathbf{Z} _{i}$ $- \mathbf{Z} _{j} \Vert _{F}^{2}C_{i,j}$, where $C_{i,j} = dCorr(\mathbf{X} _{i},\mathbf{X} _{j})$ acts as a weight based on the correlation between the views i and j. When the correlation value is large, the term intends to pull the specific components of the two views closer in the projected space. Otherwise, it tries to pull them further apart.

2.2 Label Pair Consistency Preserving

To further leverage the label information, we introduce a term that enforces the samples from the same class to be closer to one another in the latent space, which enhance the separability of the learned representations. Specifically, by concatenating the latent representations of all views results in $\mathbf{H} =\left[ \mathbf{Z} \ \mathbf{Z} _{1}\ \cdots \ \mathbf{Z} _{k} \right] \in \mathbb {R}^{ n \times \left( d_{s}+kd \right) }$, we obtain the samples that contain all views’ information in the projected space. For samples q and l, the learned features are $\mathbf{H} ^{q} \in \mathbb {R}^{ \left( d_{s}+kd \right) }$ and $\mathbf{H} ^{l} \in \mathbb {R}^{ \left( d_{s}+kd \right) }$, respectively. The consistency weights are defined as follows: if q and l are from the same class, $s_{q,l} =1$; otherwise, $s_{q,l} =0$; where $q,l=1,...,n$. Therefore, the sample label pair consistency term is: $\frac{1}{n^{2}}\sum _{q=1}^{n}\sum _{l=1}^{n}\left\| \mathbf{H} ^{q} - \mathbf{H} ^{l}\right\| _{2}^{2}s_{q,l}=\frac{2}{n^{2}}tr(\mathbf{H} ^{T} \mathbf{L} \mathbf{H} ),$ where $\mathbf{L} = \mathbf{D} - \mathbf{S}$ is the Laplacian of the similarity matrix $\mathbf{S}$, and $\mathbf{D}$ is the diagonal matrix with $d_{q,q} = \sum _{l=1}^{n}s_{q,l}$. By minimizing the sample label pair consistency term, when two samples are from the same class, the distance between their latent representations is reduced.

2.3 Complete Objective Function

Recall that multi-view data follows the consensus and complementary principles. Our goal is to learn a latent representation for each view that preserves (1) the information shared among all views and (2) specific information coming from each single view. Following [8], this can be achieved by minimizing the following term:$\sum _{i=1}^{k} \Vert \mathbf{X} _{i}^\mathrm {T}{} \mathbf{P} _{i}+\mathbf{1} {} \mathbf{b} _{i}^\mathrm {T}$ $-\left[ \mathbf{Z} \ \mathbf{Z} _{i} \right] \Vert _{F}^{2} \;$, where $\mathbf{P} _{i} \in \mathbb {R}^{d_{i}\times \left( d_{s}+d \right) }$ is the transformation matrix of the i-th view used to map the original representation $\mathbf{X} _{i}$ into the latent space; $\mathbf{b} _{i} \in \mathbb {R}^{\left( d_{s}+d \right) }$ is a bias term and $\mathbf{1} \in \mathbb {R}^{n}$ is an all-ones vector. The learned feature vector for the i-th view $[\mathbf{Z} \ \mathbf{Z} _{i}] \in \mathbb {R}^{n\times \left( d_{s}+d \right) }$ consists of the shared component $\mathbf{Z}$ across all views and the specific component $\mathbf{Z} _{i}$ of the i-th view. After learning the view specific and shared components, a linear classifier is designed for classification. Following [8], the corresponding loss function is formulated as: $\left\| \mathbf{H} {} \mathbf{W} +\mathbf{1} {} \mathbf{b} ^\mathrm {T}-\mathbf{Y} \right\| _{F}^{2},$ where $\mathbf{W} \in \mathbb {R}^{\left( d_{s}+kd \right) \times c}$ is a transformation matrix that maps the projected features $\mathbf{H}$ into the label space and $\mathbf{b} \in \mathbb {R}^{c}$ is a bias term. By minimizing the loss function, the difference between the predicted outputs $\mathbf{H} {} \mathbf{W} +\mathbf{1} {} \mathbf{b} ^\mathrm {T}$ and the ground-truth $\mathbf{Y}$ tends to reduce.Therefore, the complete objective function is defined as:

$$\begin{aligned} \min \limits _\mathbf{W ,\mathbf{P} _{i},\mathbf{Z} ,\mathbf{Z} _{i},\mathbf{b} ,\mathbf{b} _{i}}&\sum _{i=1}^{k}\left\| \mathbf{X} _{i}^\mathrm {T}{} \mathbf{P} _{i}+\mathbf{1} {} \mathbf{b} _{i}^\mathrm {T}-\left[ \mathbf{Z} \ \mathbf{Z} _{i} \right] \right\| _{F}^{2} + \frac{\alpha }{k(k-1)}\sum _{i<j}\left\| \mathbf{Z} _{i} - \mathbf{Z} _{j}\right\| _{F}^{2}C_{i,j} \nonumber \\&+ \frac{\beta }{n^{2}}\sum _{q=1}^{n}\sum _{l=1}^{n}\left\| \mathbf{H} ^{q} - \mathbf{H} ^{l}\right\| _{2}^{2}s_{q,l} + \gamma \left\| \mathbf{H} {} \mathbf{W} +\mathbf{1} {} \mathbf{b} ^\mathrm {T}-\mathbf{Y} \right\| _{F}^{2}+ \theta \left\| \mathbf{W} \right\| _{F}^{2} \;, \end{aligned}$$

(1)

where $\left\| \mathbf{W} \right\| _{F}^{2}$ is a regularization term included to help prevent overfitting. Note that the first three terms aim to learn the latent representation among multiple views by utilizing the label information of the sample pairs and the similarity information of the view pairs. The last two terms constitute a regularized loss between the predicted outputs and the ground-truth.

2.4 Optimization Procedure

For the objective function from Eq. (1), we solve the problem by using an alternating optimization strategy and update $\mathbf{W}$, $\{\mathbf {P}_{i}\}_{i=1}^{k}$, $\mathbf{Z}$, $\{\mathbf {Z}_{i}\}_{i=1}^{k}$, $\mathbf{b}$, $\{\mathbf {b}_{i}\}_{i=1}^{k}$, iteratively to optimize these variables.

First, we fix $\mathbf{W}$, $\mathbf{Z}$, $\{\mathbf {Z}_{i}\}_{i=1}^{k}$, $\mathbf{b}$ and update $\{\mathbf {P}_{i}\}_{i=1}^{k}$, $\{\mathbf {b}_{i}\}_{i=1}^{k}$: by setting the derivative of Eq. (1) w.r.t. $\mathbf{P} _{i}$, $\mathbf{b} _{i}$ to zero, we get $\mathbf {P}_{i}=-(\mathbf {X}_{i}\mathbf {X}_{i}^\mathrm {T})^{-1}\mathbf {X}_{i}(\mathbf {1}\mathbf {b}_{i}^\mathrm {T}-[\mathbf {Z}\ \mathbf {Z}_{i}])$ and $\mathbf {b}_{i}=\frac{1}{n}[\mathbf {Z}\ \mathbf {Z}_{i}]^\mathrm {T}\mathbf {1}-\frac{1}{n}\mathbf {P}_{i}^\mathrm {T}\mathbf {X}_{i}\mathbf {1}$.

Next, we fix $\{\mathbf {P}_{i}\}_{i=1}^{k}$, $\{\mathbf {b}_{i}\}_{i=1}^{k}$, $\mathbf {Z}$, $\{\mathbf {Z}_{i}\}_{i=1}^{k}$ and update $\mathbf{W}$, $\mathbf{b}$: by setting the derivative of the Eq. (1) w.r.t. $\mathbf{W}$, $\mathbf{b}$ to zero, yields $\mathbf{W} =-(\mathbf{H} ^\mathrm {T}{} \mathbf{H} +\frac{\theta }{\gamma } \mathbf{I} )^{-1}{} \mathbf{H} ^{T}(\mathbf{1} {} \mathbf{b} ^\mathrm {T} -\mathbf{Y} )$ and $\mathbf{b} =\frac{1}{n}{} \mathbf{Y} ^\mathrm {T}{} \mathbf{1} -\frac{1}{n}{} \mathbf{W} ^\mathrm {T}{} \mathbf{H} ^\mathrm {T}{} \mathbf{1}$.

Lastly, we fix $\{\mathbf {P}_{i}\}_{i=1}^{k}$, $\{\mathbf {b}_{i}\}_{i=1}^{k}$, $\mathbf{W}$, $\mathbf{b}$ and update $\mathbf{Z}$, $\{\mathbf {Z}_{i}\}_{i=1}^{k}$: Note that we update $\mathbf {Z}_{i}$ in a view-by-view manner. When updating $\mathbf{Z} _{i}$, $\mathbf{Z}$ and $\{\mathbf {Z}_{j}\}_{j\ne i}$ are fixed. Now, considering that $\mathbf{H} =\left[ \mathbf{Z} \ \mathbf{Z} _{1}\ \cdots \ \mathbf{Z} _{k} \right]$, $\frac{\beta }{n^{2}}\sum _{q=1}^{n}\sum _{l=1}^{n}\left\| \mathbf{H} ^{q} - \mathbf{H} ^{l}\right\| _{2}^{2}s_{q,l}$ can be rewritten as $\frac{2 \beta }{n^{2}}(tr(\mathbf{Z} ^\mathrm {T}{} \mathbf{L} {} \mathbf{Z} )+ \cdots +tr(\mathbf{Z} _{k}^\mathrm {T}{} \mathbf{L} {} \mathbf{Z} _{k}))$. By setting $\mathbf{B} =\mathbf{1b} ^\mathrm {T}-\mathbf{Y}$ and $\mathbf{E} _{1}= \mathbf{Zw} +\sum _{j\ne i}^{k}{} \mathbf{Z} _{j}{} \mathbf{w} _{j}+\mathbf{B}$, $\gamma \left\| \mathbf{HW} +\mathbf{1b} ^\mathrm {T}-\mathbf{Y} \right\| _{F}^{2}$ can be rewritten as $\gamma \left\| \mathbf{Z} _{i}{} \mathbf{w} _{i} + \mathbf{E} _{1}\right\| _{F}^{2}$, where $\mathbf{w} _{i} \in \mathbb {R}^{d \times c}$.

By setting $\mathbf{A} _{i}=\mathbf{X} _{i}^\mathrm {T}{} \mathbf{P} _{i}+\mathbf{1b} _{i}^\mathrm {T}$ and denoting $\mathbf{P} _{i}=[\mathbf{P} _{i1}\ \mathbf{P} _{i2}]$, $\mathbf{P} _{i1}\in \mathbb {R}^{d_{i}\times d_{s}}$, $\mathbf{P} _{i2}\in \mathbb {R}^{d_{i}\times d}$, $\mathbf{b} _{i}=[\mathbf{b} _{i1}\ \mathbf{b} _{i2}]$, $\mathbf{b} _{i1}\in \mathbb {R}^{d_{s}}$, and $\mathbf{b} _{i2}\in \mathbb {R}^{d}$, we get $\mathbf{A} _{i}=[\mathbf{A} _{i1}\ \mathbf{A} _{i2}]=[\mathbf{X} _{i}^\mathrm {T}{} \mathbf{P} _{i1}+\mathbf{1b} _{i1}^\mathrm {T}\ \mathbf{X} _{i}^\mathrm {T}{} \mathbf{P} _{i2}+\mathbf{1b} _{i2}^\mathrm {T}]$. Taking the derivative of Eq. (1) and setting it to zero yields $\frac{2\beta }{n^{2}}{} \mathbf{L} {} \mathbf{Z} _{i} + \mathbf{Z} _{i}\left( \mathbf{I} +\frac{\alpha }{k(k-1)}(\sum _{j\ne i}C_{i,j})\mathbf{I} +\gamma \mathbf{w} _{i}{} \mathbf{w} _{i}^{T} \right) = \mathbf{A} _{i2}+\frac{\alpha }{k(k-1)}\sum _{j\ne i}$ $C_{i,j}{} \mathbf{Z} _{j}-\gamma \mathbf{E} _{1}{} \mathbf{w} _{i}^{T}$, where $\mathbf{I} \in \mathbb {R}^{d \times d}$ is an identity matrix. The closed-form solution of the given term can be computed using the algorithm from [1].

When updating $\mathbf{Z}$, $\{\mathbf {Z}_{i}\}_{i=1}^{k}$ are fixed. By setting $\mathbf{E} _{2}= \sum _{i=1}^{k}{} \mathbf{Z} _{i}{} \mathbf{w} _{i}+\mathbf{B}$ and the derivative of Eq. (1) w.r.t. $\mathbf{Z}$ to zero, we obtain $\frac{2\beta }{n^{2}}{} \mathbf{L} {} \mathbf{Z} + \mathbf{Z} \left( k*\mathbf{I} +\gamma \mathbf{ww} ^\mathrm {T} \right) = \sum _{i=1}^{k}{} \mathbf{A} _{i1}-\gamma \mathbf{E} _{2}{} \mathbf{w} ^\mathrm {T}$, where $\mathbf{I} \in \mathbb {R}^{ds \times ds}$ is an identity matrix. The optimization problem of the given term can also be solved using the algorithm from [1].

3 Experiments

3.1 Experiment Setting

Three publicly available and widely used datasets, including image, text, or even multi-source data, were used in the experiments. MSRC-V1 [12] is a scene image dataset. For a given image, the task is to predict the image’s category. The dataset consists of six views, 7 classes and a total of 210 samples. TweetFit [2] consists of recordings from individual users’ sensors and the data were collected from multiple social media. For a given user, the task is to predict the user’s body mass index (BMI). We selected users with data available for all data sources, which consists of 8 classes, 205 samples and three views. BBCSport¹ is a sport news text dataset. For a given text, the task is to predict the text’s category. The dataset consists of 116 samples, 5 classes and four views.

We compared the classification accuracy of MELTS with the following methods. SVM applied to the concatenation of multiple views. MVDA [5] determines a discriminant common space by learning linear transforms of each view. MVCS [8] learns a latent subspace from multiple views by simultaneously considering the correlated information across the views and the unique information within each single view. WeReg [9] adaptively assigns weights to distinct views to account for view importance.

In all experiments, standard fivefold cross-validation was utilized and the average accuracies along with their standard deviations on each dataset were reported. For each of the 5 trials, we randomly choose $75\%$ of the data for training, and the rest for validation.

The parameters were fine-tuned based on validation performance. PCA was used on the original data to initialize the shared component $\mathbf{Z}$ and each specific component $\mathbf{Z} _{i}$. Let $d_{i}^{*}$ denote the feature dimension of the i-th view representation obtained by PCA and $d^{*}$ denote the minimum of $\{ d_{1}^{*}, \cdots ,d_{k}^{*} \}$. As for the hyperparameters of MELTS, $\alpha$, $\beta$, $\gamma$, $\theta$ were selected from $\{10^{-3}, 10^{-2}, \cdots , 10^{2}, 10^{3} \}$ based on optimal performance, while ds and d were selected from $\{1,\frac{1}{4}d^{*},\frac{1}{2}d^{*},\frac{3}{4}d^{*},$ $d^{*}\}$. The tradeoff parameter C, i.e. the inverse regularization strength, for SVM was selected from $\{10^{-3}, 10^{-2}, \cdots , 10^{2}, 10^{3} \}$. For MVDA, a 1-Nearest Neighbor classifier was applied to the low-dimensional representations for classification. Since MELTS is built on the basis of MVCS, it was compared to MVCS under the same ds and d to show the influence of the added terms. In the case of WeReg, for fair comparison, a sample’s label is predicted based on the maximum label probability instead of using the kNN-based prediction approach from [9].

3.2 Results on Synthetic Data and Real-World Datasets

We initially assess the performance of the proposed method on the synthetic data. We generated a dataset with three views containing 300 samples, each having 200 features. The samples were generated from six normal distributions with different parameters, thus defining six separate classes of samples. 50 out of the 200 features were generated to be similar to increase feature redundancy. To better understand the effect of view similarity, we generate similar parameter values for the first two views and generate the third view by using distinct parameter values. The pairwise between-view similarities based on distance correlation are following: $dCorr(\mathbf{X} _{1},\mathbf{X} _{2}) = 0.99$, $dCorr(\mathbf{X} _{1},\mathbf{X} _{3}) = dCorr(\mathbf{X} _{2},\mathbf{X} _{3}) = 0.59$. It can be inferred that view 1 is more similar to view 2, than to view 3.

Table 1 shows the classification accuracies obtained by all models on the synthetic data. First, SVM and WeReg perform poorly since these three methods directly concatenate the features of all views and ignore the feature redundancy across multi-view representations. Compared with SVM and WeReg, MELTS attains an improvement of $39\%$ and $35\%$, respectively. Second, MELTS achieves $34\%$ higher accuracy than MVDA since the method ignores the hidden specific information of each single view. Furthermore, MELTS produces $2\%$ higher accuracy than MVCS, which suggests that leveraging the sample pairs’ label information and the view pairs’ similarities can help learn more relevant and discriminative features.

The experimental results on the three real-world datasets are also reported in Table 1. Compared with MVCS, MELTS achieves considerable improvements on the three datasets. For example, MELTS achieves $7\%$ higher accuracy than MVCS on MSRC-V1 and $14\%$ on TweetFit. WeReg obtains lower performance than MELTS on the three datasets, as it ignores the latent relationships among the different views. The results obtained by MVDA are much lower than those of MELTS on all datasets. Moreover, on most datasets, MELTS obtains the smallest standard deviation, which demostrates the stability of our method.

Table 1. Average accuracy obtained by MELTS and the alternative methods.

4 Conclusion

In this paper, we proposed MELTS, a novel multi-view learning approach. MELTS learns a latent subspace, containing the common information across all views and the individual information carried by each view. MELTS effectively models the between-view relationships and utilizes the label information to enhance the discriminability in the learned latent subspace. The results indicate that MELTS achieves better classification performance than other methods.