Keywords

1 Introduction

Nowadays the ZMP concept is often used as an aid in controlling a biped robot to walk stably, provided that it must remain in the interior of the base of support of biped robot [1]. During robot walking, a common method of controlling ZMP is to maintain the actual ZMP following a pre-calculated reference ZMP trajectory [2]. However, one limitation when following a pre-calculated ZMP trajectory is that the robot is not able to recover from an unexpectedly large push. In fact, men prove quickly recover from a push, by doing a fast step along with the speed obtained after the push. Several techniques have been applied to push recover to humanoid robot, which often take a quick step in the direction of the applied force [3]. All these techniques have similarities as all humanoid robots are subject to the same laws of physics. For example, the Sarcos biped [4], and other humanoids [5, 6] uses a capture region to ensure biped push recovery. Although, the method of using capture region allows many humanoid robots to control steady walking. However, to mimic human behaviors, this method has not responded. Authors in [7] suggested a new LIPM model used the resultant momentum simulation within the COM based on flywheel regarding to rotating angular bounds replacing unique weigh. Recently, authors in [8, 9] applied that LIPM model to calculate the decisive regions that recognize strategies appropriate (related to hip, foot position, etc.) could be applied to recover biped balance regarding to push action accident.

As analyzed above, solutions recover in case push accident during biped walking with a controller are very complex, with push in the direction of the robot’s movement. To compensate for this lack, we use a flywheel located on the upper body of the biped robot and control it to generate angular momentum against the sudden horizontal force applied to the biped robot, so that the biped still performs a steady walk with the desired ZMP trajectory. Section 2 of this paper presents our solution, Sect. 3 present simulation results and experimental results when applying the proposed solution for small-sized two-legged robot HUBOT 4.1. Section 4 presents the conclusions.

2 Solution for Recovery the Horizontal Push of a Bipedal Robot During Walking

The walking pattern generator for a pre-designed ZMP orbital walking bipedal robot, based on a NARX model combined with an artificial neural network model (ANN) optimally identified by improved differential evolutionary (IDE) optimization algorithm. Called xZMP_ref(k), yZMP_ref(k) the desired ZMP point coordinates, the mathematical model of the NARX-ANN is detailed in [10]. The mathematical model of the biped (trajectories for both feet and hip, inverse kinematics, forward kinematics and the ZMP coordination (xZMP_real, yZMP_real)) is detailed in [11]. In order for the biped robot to walk in the desired ZMP trajectory, we identify the proposed model so that formula (1) has a minimum value.

$$ E_{N} (\theta ) = \sum\limits_{k = 1}^{N} {\left( {\left( {x_{{{\text{zmp}}\_{\text{ref}}}} (k) - x_{{{\text{zmp}}\_{\text{real}}}} (k)} \right)^{2} + \left( {y_{{{\text{zmp}}\_{\text{ref}}}} (k) - y_{{{\text{zmp}}\_{\text{real}}}} (k)} \right)^{2} } \right)} $$
(1)

where θ are the weights of the neural network model. Pseudo-code IDE algorithm training NARX-ANN model is detailed in [10].

Fig. 1.
figure 1

Model of a bipedal robot with a horizontal flywheel (frontal plane)

Full size image

In the frontal plane, a biped robot with a flywheel is equivalent to a flywheel inverted pendulum, as shown in Fig. 1. Let \(\theta = \left( {\theta_{p} ,\theta_{w} } \right)^{T} \in \,\Re^{2}\) be the configuration vector of the system and M be the inertial matrix with the elements: \(m_{11} = m_{p} \left( {{{l_{p} } \mathord{\left/ {\vphantom {{l_{p} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)^{2} + m_{w} l_{p}^{2} + I_{p} + I_{w}\) and \(m_{12} = m_{21} = m_{22} = I_{w}\). Where, mp is the mass of the body of the pendulum, mw is the mass of the flywheel, lP is the length of the body of the pendulum, IP is the moment of inertia of the pendulum body about the axis of rotation passing through the center of mass of the pendulum body, Iw is the moment of inertia of the flywheel about an axis of rotation passing through its center of mass. Under these assumptions the equations of motion can be taken from any standard text, for example (Spong and Vidyasagar [12]), as

$$ m_{11} \ddot{\theta }_{p} + m_{12} \ddot{\theta }_{w} = \phi \left( {\theta_{p} } \right) + F_{y} $$
(2)
$$ m_{21} \ddot{\theta }_{p} + m_{22} \ddot{\theta }_{w} = \tau $$
(3)

where, \(\phi \left( {\theta_{p} } \right) = m_{0} \sin \theta_{p}\), \(m_{0} = \left( {m_{p} l_{p} + m_{w} {{l_{p} } \mathord{\left/ {\vphantom {{l_{p} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)g_{0}\) and g0 is called the gravitation, and the kinetic energy of the system considers only rotational kinetic energy and a force acting horizontally on the pendulum body Fy and a torque acting on the flywheel \(\tau = K_{m} u\), where Km is the torque coefficient of the motor and u is the control signal.

The stabilized gait controller is designed and implemented as an open-loop controller. The input of this controller is the rotation angle of the joints in the legs of the robot, which is recognized based on the adaptive evolutionary neural network model. Recovery push controller is implemented online as follows: read the tilt angle of the bipedal robot relative to the vertical in the horizontal plane (θp) through the IMU sensor located in the upper body; If a sudden horizontal force is applied to the biped, the horizontal thrust recovery controller will trigger the flywheel to rotate in the direction of the applied force to generate torque to counteract the horizontal push. The PID controller is implemented based on the error e(t) of the set signal θp_ref and the measured value of the system θp_real (t) and tries to minimize the error e(t) over time by adjusting the control variable u(t).

3 Results and Analysis

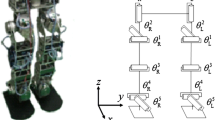
The small-size biped robot (HUBOT-4.1) have total weight is 1.5 kg and height is 40 cm. The flywheel is designed as an independent block, consists of an IMU sensor (MPU-6050) and a brushless and gearless DC motor (24H4004H160) and a propeller with a radius equal to 8 cm. Based on Sect. 2, we choose the parameters of the nonlinear regression model and the neural network model as follows: the neurons in hidden layer is q = 8, the total number of samples in one step is N = 202, the positive effect function of the neurons in the hidden layer is sig-mode, the positive effect function of the neurons in the output is linear. For identification we use the IDE algorithm as suggested with: mutation value F = Random [0.4; 1.0] and crossover probability CR = Random [0.7; 1.0]. Figure 2 shows rotation angle of 10 joints of at the two legs of HUBOT-4.1 after performing parameter identification of the NARX + ANN model using the IDE algorithm. The ten rotation joint-angular trajectories illustrated in Fig. 2, are used to perform gait simulations and evaluate the stability of HUBOT-4.1 locomotion as Fig. 3. From Figs. 2 and 3, they are clear to confirm that the technical solution has been achieved as desired.

Fig. 2.
figure 2

Rotating angular trajectories

Full size image
Fig. 3.
figure 3

Simulated gait result

Full size image

The parameters of the flywheel inverted pendulum model are as follows: lp = 0.25 m, mw = 0.2 kg, mp = 0.7 kg, Iw = 3.6e−4 kg · m2, Ip = 3.645e−3 kg · m2, g0 = 9.81 m/s2, Km = 5.5e−3 N · m/W1/2. The initial conditions for the system are: \(\theta_{p0,y} = {\pi \mathord{\left/ {\vphantom {\pi {20}}} \right. \kern-\nulldelimiterspace} {20}}\), \(\dot{\theta }_{p0,y} = 0\), \(\dot{\theta }_{w0,y} = 0\). A PID controller (have Kp = 1200, Ti = 0.5, Td = 0.75), is used to stabilize the horizontal flywheel inverted pendulum around vertical equilibrium \(\theta_{p\_ref,y} = 0\). Figure 4 illustrates the trajectory (θp, \(\dot{\theta }_{p}\), \(\dot{\theta }_{w}\), \(\tau\)), where noise is taken into account. From Fig. 4, it can be seen that the optimal PID controller handles noise well and the pendulum converges back to vertical equilibrium. Figure 5 examines the case of a flywheel inverted pendulum being acted upon by a sudden horizontal force. At the time t = 10 s, there is a force Fy acting suddenly in the horizontal direction (both directions are different), the PID controller still handles the unexpected force well and the pendulum converges back to equilibrium by vertical.

Fig. 4.
figure 4

State trajectories of θp, \(\dot{\theta }_{p}\), \(\dot{\theta }_{w}\), \(\tau\)

Full size image
Fig. 5.
figure 5

State trajectories of θp, \(\dot{\theta }_{p}\), \(\dot{\theta }_{w}\), \(\tau\)

Full size image

Figure 6 illustrates the case where forces act in both different directions. The experimental results confirm that the proposal controller has been successfully applied to biped HUBOT 4.1.

Fig. 6.
figure 6

Results of HUBOT-4.1 in robust and stable walking with sudden horizontal force

Full size image

4 Conclusions

This paper proposes an innovative solution to recovery horizontal push to a walking biped robot by using a flywheel. A dynamic model for a biped robot aimed at restoring horizontal thrust is innovatively suggested. This model combined with the PID control on θp was implemented in MATLAB/Simulink to demonstrate that the biped robot converges back to a straight equilibrium when there is a sudden force acting in the horizontal direction. A walking pattern model for biped robot to walk in desired ZMP trajectory based on the nonlinear NARX model in conjunction with the ANN model optimized by improved differential evolutionary IDE algorithm. Simulation and experimental results show that the proposed solution is effective.