Keywords

1 Introduction

The theoretical scheme of coalition games is superimposed in this article on the problem of transport development of Russian Asia, which has a long history but has not been solved so far. Leaving aside the reasons for this situation, analyzed in detail in the literature of the issue (see, for example), attention is further concentrated on the problem of integrating logical-heuristic and economic-mathematical models of strategic decision-making concerning the distribution of limited investment resources of the state-investor between executors (contractors) of competing railway projects (hereinafter - CRP) and the systems of such projects. The task is to find such an allocation which would ensure the maximum possible stability of one or another system of construction contractors. In other words, we will talk about finding the option which has the greatest allocative efficiency of the coalition structure of project contractors by the stability criterion.

Research Object Description.

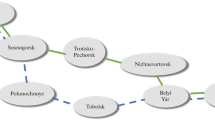
Specifically, the following CRP, which form a skeletal system of transport support strategy of Russia in Siberia and the Far East in the long term (see Fig. 1), will be discussed.

This strategy is ambivalent: on the one hand, it is focused on the sustainable socio-economic development of the country’s eastern macro-region, which has so far been only focally developed in economic terms and sparsely populated in social terms. On the other hand, the strategy aims to ensure national security, reflecting the possibility of an adequate response to any attempts by some aggressive neighbors to restrain Russia’s development by military means.

  1. 1.

    Transpolar Railway (TR) of CRP, which is a continuation to Uelen of the Stalin’s project of the early fifties in the last century, partially implemented from Salekhard to Igarka (see Fig. 1), and now reanimated as a continuation of the Northern Latitudinal Railway (NLR) project [1].

  2. 2.

    The Mainland-Sakhalin Railway (MS), as well as the TR, started to be built in Stalin’s times and is now considered not only as a means of stable land connection of the island with the Far East economy and society, but also as a possibility of connection with the Japanese railway network through the La Perouse Strait with all the economic and political positive effects for Russia [2].

  3. 3.

    The North Siberian Railway (SevSib) connects (see Fig. 1) the Trans-Siberian Railway (via the meridional branch Tomsk - Bely Yar) with the Sverdlovsk Railway (via the branch Nizhnevartovsk - Strezhevoy). Sevsib can be considered as a double of Transsib, as the railroad completing the formation of the second latitudinal transport interregional corridor from the Okhotsk Sea to the Baltic Sea [3].

  4. 4.

    The Lensko-Kamchatsky Railway (LKR) crosses Eastern Siberia from Ust-Kut at the western end of BAM to Magadan, then along the coast of the Sea of Okhotsk goes to Kamchatka and to the ice-free port of Petropavlovsk-Kamchatsky. The idea of laying the main line belongs to E. Norman and has been actively discussed for the last 10 years (see, [4,5,6]). Now the interest in LKR has aggravated [7], because the route of the main line passes near or even through the Penzhinskaya Bay itself, where the construction of a tidal hydroelectric power plant of unique capacity is possible. Its electric power may be used for obtaining hydrogen, strategic resource of 21st century [8].

  5. 5.

    CRP (hereinafter referred to as PO) from Polunochnoye station (Sverdlovsk railroad) to Obskaya-2 station (Northern railroad); the project is part of the transport support of the program (mega-project) “The Industrial Urals - The Polar Urals”. Both the program itself and the PO railroad are multi-vector enterprises, the results of which are multidimensional and of strategic importance for Russia as a whole. The documentation on the PO project was ready back in 2009, but for various reasons (see, for example, [9, 10]), the financing of the project was closed. Nevertheless, we include it in the list of five large-scale projects under analysis, because without its implementation, neither a full-fledged transport access to the Arctic, nor further effective use of the unique resource potential of the Urals, in our opinion, is possible.

Fig. 1.
figure 1

System of large-scale railway projects in Siberia and the Far East in the long term

Full size image

2 Methods

2.1 Toolkit and Results of the Computational Experiment

Even from the brief description of the CRP system analyzed below with the help of coalition game theory schemes, it can be seen that behind each project there are powerful “interested parties” - subjects of the Federation, state corporations, and private investors. Game theory distinguishes between coalitions of interest and coalitions of action. Under the assumption of “interested parties” and construction contractors in our case are united and form competing action coalitions. The sustainability of the multitrillion-dollar program implementation financed by the state for the transport development of Siberia and the Far East depends on the composition of such coalitions and their configuration.

In the applied aspect, the problem is reduced to the problem of finding the distribution of public funds between the coalitions of action, as defined above. To solve the problem, we use the Shepley algorithm in the format described in [10] with one exception. In [10], as well as in other primary sources known to us, it is not explained where the values of the characteristic functions of the coalitions come from. It turns out that this most important indicator, indicating what the guaranteed gain of a particular coalition is equal to, appears as if “out of the picture,” which reduces the applied value of sharing according to the Shepley price.

To eliminate this drawback, we define the values of the characteristic functions using the software product ORDEX [11, 12]. The program implements an approach that allows, using a logical-heuristic model, to determine the relative numerical estimates of the importance of CRP from the above list of 1–5, using the expert ordering of the group of experts, produced by the non-growth of their quality in terms of the importance of the project to achieve the goal of transport development of Siberia and the Far East.

3 Results

The use of this approach and product in assessing the relative importance of the projects in the list 1–5 provided the following result (see Table 1).

Table 1. Coefficients of relative significance
Full size table

Let us put the data of Table 1 into the format of Shepley algorithm [10] but for five participants.

\({\text{TR }} = {\upnu }({0},{37}){\text{ MS }} = {\upnu }({25}){\text{ SevSib }} = {\upnu }({18}){\text{ LKR }} = {\upnu }({0},{12}){\text{ PO}} = {\upnu }\left( {{0}{\text{.08}}} \right)\)

\(\begin{array}{*{20}l} {\nu \, (\emptyset ) \, = \, 0} \hfill \\ {\nu \, \left( 1 \right) \, = \, 0} \hfill \\ {\nu \, \left( 2 \right) \, = \, 0} \hfill \\ {\nu \, \left( 3 \right) \, = \, 0} \hfill \\ \begin{gathered} \nu \, \left( 4 \right) \, = \, 0 \hfill \\ \nu \, \left( 5 \right) \, = \, 0 \hfill \\ \end{gathered} \hfill \\ \end{array}\)

\(\begin{gathered} \begin{array}{*{20}l} {\nu \, \left( {12} \right) \, = \, 0.365304 \, + \, 0.253207 \, = \, 0.62} \hfill \\ {\nu \, \left( {13} \right) \, = \, 0.365304 \, + \, 0.175509 \, = \, 0.54} \hfill \\ {\nu \, \left( {14} \right) \, = \, 0.365304 \, + \, 0.121655 \, = \, 0.49} \hfill \\ {\nu \, \left( {15} \right) \, = \, 0.365304 \, + \, 0.084325 \, = \, 0.45} \hfill \\ {\nu \, \left( {23} \right) \, = \, 0.253207 \, + \, 0.175509 \, = \, 0.43} \hfill \\ {\nu \, \left( {24} \right) \, = \, 0.253207 \, + \, 0.121655 \, = \, 0.37} \hfill \\ {\nu \, \left( {25} \right) \, = \, 0.253207 \, + \, 0.084325 \, = \, 0.34} \hfill \\ {\nu \, \left( {34} \right) \, = \, 0.175509 \, + \, 0.121655 \, = \, 0.30} \hfill \\ {\nu \, \left( {35} \right) \, = \, 0.175509 \, + \, 0.084325 \, = \, 0.26} \hfill \\ \end{array} \hfill \\ \nu \, \left( {45} \right) \, = \, 0.121655 \, + \, 0.084325 \, = \, 0.21 \hfill \\ \end{gathered}\)

\(\begin{array}{*{20}l} {\nu \, \left( {123} \right) \, = \, 0.365304 \, + \, 0.253207 \, + \, 0.175509 \, = \, 0.79} \hfill \\ {\nu \, \left( {124} \right) \, = \, 0.365304 \, + \, 0.253207 \, + \, 0.121655 \, = \, 0.74} \hfill \\ {\nu \, \left( {125} \right) \, = \, 0.365304 \, + \, 0.253207 \, + \, 0.084325 \, = \, 0.70} \hfill \\ {\nu \, \left( {134} \right) \, = \, 0.365304 \, + \, 0.175509 \, + \, 0.121655 \, = \, 0.66} \hfill \\ {\nu \, \left( {135} \right) \, = \, 0.365304 \, + \, 0.175509 \, + \, 0.084325 \, = \, 0.63} \hfill \\ {\nu \, \left( {145} \right) \, = \, 0.365304 \, + \, 0.121655 \, + \, 0.084325 \, = \, 0.57} \hfill \\ {\nu \, \left( {234} \right) \, = \, 0.253207 \, + \, 0.175509 \, + \, 0.121655 \, = \, 0.55} \hfill \\ {\nu \, \left( {235} \right) \, = \, 0.253207 \, + \, 0.175509 \, + \, 0.084325 \, = \, 0.51} \hfill \\ {\nu \, \left( {245} \right) \, = \, 0.253207 \, + \, 0.121655 \, + \, 0.084325 \, = \, 0.46} \hfill \\ {\nu \, \left( {345} \right) \, = \, 0.175509 \, + \, 0.121655 \, + \, 0.084325 \, = \, 0.38} \hfill \\ {\nu \, \left( {1234} \right) \, = \, 0.365304 \, + \, 0.253207 \, + \, 0.121655 \, + \, 0.121655 \, = \, 0.92} \hfill \\ {\nu \, \left( {1235} \right) \, = \, 0.365304 \, + \, 0.253207 \, + \, 0.175509 \, + \, 0.084325 \, = \, 0.88} \hfill \\ {\nu \, \left( {1345} \right) \, = \, 0.365304 \, + \, 0.175509 \, + \, 0.121655 \, + \, 0.084325 \, = \, 0.75} \hfill \\ \begin{gathered} \nu \, \left( {1245} \right) \, = \, 0.365304 \, + \, 0.253207 \, + \, 0.121655 \, + \, 0.084325 \, = \, 0.82 \hfill \\ \nu \, \left( {2345} \right) \, = \, 0.253207 \, + \, 0.175509 \, + \, 0.121655 \, + \, 0.084325 \, = \, 0.63 \hfill \\ \end{gathered} \hfill \\ \end{array}\)

\(\nu \, (1, \, 2, \, 3, \, 4, \, 5) \, = \, \nu \, ({\text{N}}) \, = \, 1\)

For player 1 (project TR) the following possibilities are available:

figure a

Similar calculations are performed for all other project players using the formula

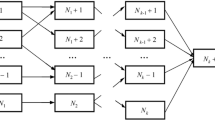
$$ {\upgamma }_{n} \left( S \right) = \frac{{S!\left( {n - s - 1} \right)!}}{n!} $$
(1)

where n is the set of players-projects, s is the number of players in the coalition S. The choice of such weighting multipliers is due to the following circumstances: a coalition of n players can be formed in n! different ways; there are s! different ways of organization for s players in the coalition S before player i joins it; players not in the extended coalition, whose number is n-s-1, can be organized in (n-s-1)! different ways. Hence, if we assume that all n! ways of forming coalitions consisting of n players are equally probable, then γn(S) is nothing but the probability of player i joining the coalition S. In the game, each player is given four possibilities [11].

The weights corresponding to each of these four possibilities are as follows:

$$ \gamma_{4} \left( S \right) \, = \frac{{s!\left( {n - s - 1} \right)!}}{n!} = \frac{{4!\left( {4 - 5 - 1} \right)!}}{5!} = \, 0.20 $$
$$ \gamma_{3} \left( S \right) \, = \frac{{s!\left( {n - s - 1} \right)!}}{n!} = \frac{{3!\left( {3 - 5 - 1} \right)!}}{5!} = \, 0.05 $$
$$ \gamma_{2} \left( {\text{S}} \right) \, = \, 0.03 $$
$$ \gamma_{1} \left( {\text{S}} \right) \, = \, 0.05 $$

Let us determine the Shepley price. Assume that each player has a payoff equal to the average of his contributions to all the coalitions he could have joined. The i-th player’s gain is equal to the weighted average of v (S ∪ {i}) - v (S), where S - is any subset of players that does not contain a player i, and S ∪ {i} the same subset including the players. The weighted average according to [11] is equal to the payment of

$$ {\text{P}}^{i} = \mathop \sum \limits_{S \subset N}^{{}} {\upgamma }_{n} \left( S \right)\left[ {v\left( {SY\left\{ i \right\}} \right) - v\left( S \right)} \right] $$
(2)

Consequently, the winnings for the players will be:

for player 1

\( \begin{aligned} {\text{P}}^{1} = & ({\mathbf{0}}.{\mathbf{20}} \cdot 0.37) + ({\mathbf{0}}.{\mathbf{05}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{05}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{05}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{05}} \cdot 0.37) \\ & + ({\mathbf{0}}.{\mathbf{3}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{3}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{3}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{3}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{3}} \cdot 0.37 + {\mathbf{0}}.{\mathbf{3}} \cdot 0.37) \\ & + ({\mathbf{0}}.{\mathbf{05}} \cdot 0.62 + {\mathbf{0}}.{\mathbf{05}} \cdot 0.54 + {\mathbf{0}}.{\mathbf{05}} \cdot 0.49 + {\mathbf{0}}.{\mathbf{05}} \cdot 0.45) = 0.32; \\ \end{aligned} \)

for player 2

\({\text{P}}^{2} = \, 0.24;\)

for player 3

\({\text{P}}^{3} = \, 0.18;\)

for player 4 it will be:

\({\text{P}}^{4} = \, 0.14;\)

for player 5

\({\text{P}}^{5} = \, 0.11.\)

Total

\({\text{P }} = \, 0.32 \, + \, 0.24 \, + \, 0.18 \, + \, 0.14 \, + \, 0.11 \, = \, 1\)

So, in this game, the vector of division corresponding to Shepley price is shown in Table 2.

Table 2. The vector of division corresponding to Shepley
Full size table

4 Acknowledgements and Discussion

In terms of content, the result means that any amount of government funds allocated to contractors to implement the five projects examined should be divided among them in the proportion shown in Table 2.

If we compare the result of Table 2 with the sharing of funds among the contractors in proportion to the coefficients in Table 1, we see that the sharing in Table 2, which takes into account the “strength” of the coalitions, is “fair” to the LKR and PO contractors. In fact, this is the result that ensures the stability of the contracting system when the analysis of the characteristic function of the game describes all possible coalitions, namely, specifies the maximum total gain that each coalition can guarantee itself [10].