Keywords

1 Introduction

In the last decade, deep learning and machine learning models have become widespread in many practical applications. This has been beneficial as these models provide intelligent, automated processing of tasks that up to now were hard for machines. However, at the same time, concerns related to the ethics and safety of these models have arisen as well. One is the problem of interpretability, i.e., explaining how these models function. This is an old problem, which has been studied (possibly under different names, such as explainable AI) since decades ago in statistics and machine learning (e.g. [2, 11, 14, 21]). A second problem is explaining why the model made a decision or how to change it [28]. This problem is more recent and has become more pressing due to concerns over the opaqueness of current AI systems. That said, related problems have been studied in data mining or knowledge discovery from databases [1, 9, 23, 30], in particular in applications such as customer relationship management (CRM).

Much of the recent works focus on a specific version of the second problem that focuses on changing a classifier’s decision in a prescribed way [28]. This problem is called counterfactual explanation [28]. Formally, a counterfactual explanation seeks a minimal change to a given input’s features that will change the classifier’s prediction in the desired way. These explanations are very helpful in understanding the behavior of a model for a given instance, as they can answer questions like what input feature the model focuses on to make a certain prediction. Mathematically, the problem of counterfactual explanations can be formulated as an optimization problem. The objective is to minimize the change in input features subject to classified as user-defined class. This similar formulation has been used in deep nets for adversarial examples and model inversion [10, 13, 16, 17, 22, 25, 26, 31]. There are also formulations that are specific for linear models [6, 24, 27]. Most algorithms to solve the optimization assume differentiability of the classifier with respect to its input instance so that gradient-based optimization can be applied. However, none of these algorithms apply to decision trees, which define nondifferentiable classifiers.

Decision trees have long been widely used in applications and are regularly highly ranked in user surveys such as KDnuggets.com or data mining and machine learning reviews such as [29]. This is particularly owing to their ease of interpretability compared to more accurate classifiers such as neural nets or decision forests. However, the prediction accuracy of decision trees learned using the recently introduced Tree Alternating Optimization (TAO) algorithm [3, 7, 38] is much higher than using traditional algorithms such as CART or C5.0. This applies both to the traditional, axis-aligned trees, but also to the far more accurate oblique trees (having hyperplane splits) and sparse oblique trees (having hyperplane splits with few nonzero weights), as well as to trees of more complex forms [34, 37], and to forests using bagging, boosting or other ensembling mechanisms, but where each tree is trained with TAO [8, 12, 33, 35, 36]. Finally, the stronger predictive power of sparse oblique decision trees together with their interpretability and fast inference makes them useful for other uses, such as in understanding deep neural networks [18, 19] or compressing deep neural networks [20].

For these reasons, solving counterfactual explanations for decision trees is important in practice. Our recent work from [4, 5] shows that the counterfactual problem can be solved exactly and efficiently in a decision tree. We showed that the counterfactual problem in decision trees is equivalent to solving the counterfactual problem in each leaf region and picking the best among them (see Sect. 2). This exact formulation for solving the counterfactual problem in decision trees allows us to extend the problem, which can answer some very interesting questions. For instance, what is the closest class to change from the original class, what is the closest boundary if changing the only feature, which feature has the lowest cost to change the class to a target class, and more. We describe these extended problems in detail in Sect. 3. These problems are very difficult and probably very expensive to answer in other models like a neural network. However, we show that in decision trees using the [4, 5] framework, we can solve these extended problems exactly and efficiently.

Next, we first briefly describe our formulation of the counterfactual problem and how to solve it exactly (Sect. 2); this follows closely the main results of [4, 5]. Then we describe each extended problem in detail (Sect. 3). Finally, in Sect. 4 we discuss these extended problems along with real-life use cases.

2 Solving Counterfactual Exactly in Decision Trees

2.1 Leaf Region: Definition

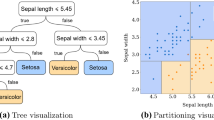
Assume we are given a classification tree that can map an input instance \(\mathbf {x}\in \mathbb {R}^D\), with D real features (attributes), to a class in \(\{1,\dots ,K\}\). Assume the tree is rooted, directed and binary (where each decision node has two children) with decision nodes and leaves indexed in the sets \(\mathcal {D}\) and \(\mathcal {L}\), respectively, and \(\mathcal {N}= \mathcal {D}\cup \mathcal {L}\). We index the root as \(1 \in \mathcal {D}\). For example, in Fig. 1 we have \(\mathcal {N}= \{1,\dots ,15\}\), \(\mathcal {L}= \{5,8,9,11,\dots ,15\}\) and \(\mathcal {D}= \mathcal {N}\setminus \mathcal {L}\). In oblique decision trees each decision node \(i \in \mathcal {D}\) has a real-valued decision function \(f_i(\mathbf {x})\) defined by a hyperplane (linear combination of all the features) \(f_i(\mathbf {x}) = \mathbf {w}^T_i \mathbf {x}+ b_i\), with fixed weight vector \(\mathbf {w}_i \in \mathbb {R}^D\) and bias \(b_i \in \mathbb {R}\). For axis-aligned trees, \(\mathbf {w}_i\) is an indicator vector (having one element equal to 1 and the rest equal to 0). The decision function \(f_i(\mathbf {x})\) send down an input instance \(\mathbf {x}\in \mathbb {R}^D\) to i’s right child if \(f_i(\mathbf {x}) \ge 0\) and down i’s left child otherwise. Each leaf \(i \in \mathcal {L}\) is labeled with one class label \(y_i \in \{1,\dots ,K\}\). For an input instance \(\mathbf {x}\)  the tree predicts its label by sending down \(\mathbf {x}\)  via the decision nodes, to exactly one leaf and outputting its label. The parameters \(\{\mathbf {w}_i,b_i\}_{i \in \mathcal {D}}\) and \(\{y_i\}_{i \in \mathcal {L}}\) are estimated by TAO [3, 7] (or another algorithm) when learning the tree from a labeled training set.

The tree partitions the input space into \(\left|\mathcal {L}\right|\) regions, one per leaf, as shown in Fig. 1 (bottom panel). Each region is an axis-aligned box in case of axis-aligned trees and a polytope for oblique trees. This region is defined by the intersection of the hyperplanes found in the path from the root to the leaf. Specifically, define a linear constraint \(z_i (\mathbf {w}^T_i \mathbf {x}+ b_i) \ge 0\) for decision node i where \(z_i = +1\) if going down its right child and \(z_i = -1\) if going down its left child. Then we define the constraint vector for leaf \(i \in \mathcal {L}\) as \(\mathbf {h}_i(\mathbf {x}) = ( z_j (\mathbf {w}^T_j \mathbf {x}+ b_j) )_{j \in \mathcal {P}_i \setminus \{i\}}\), where \(\mathcal {P}_i = \{1,\dots ,i\}\) is the path of nodes from the root (node 1) to leaf i. We call \(\mathcal {F}_i = \{\mathbf {x}\in \mathbb {R}^D\mathpunct {:}\ \mathbf {h}_i(\mathbf {x}) \ge 0\}\) the corresponding feasible set, i.e., the region in input space of leaf i. For example, in Fig. 1 (top) the path from the root to leaf 14 is \(\mathcal {P}_{14} = \{1,3,6,10,14\}\) and its region is given by:

$$\begin{aligned} \mathbf {h}_{14}(\mathbf {x}) = \begin{pmatrix} \,\,\,\,f_1(\mathbf {x}) \\ -f_3(\mathbf {x}) \\ -f_6(\mathbf {x}) \\ -f_{10}(\mathbf {x}) \end{pmatrix} = \begin{pmatrix} \,\,\,\,\mathbf {w}^T_1 \mathbf {x}+ b_1 \\ -\mathbf {w}^T_3 \mathbf {x}- b_3 \\ -\mathbf {w}^T_6 \mathbf {x}- b_6 \\ -\mathbf {w}^T_{10} \mathbf {x}- b_{10} \end{pmatrix} \ge \mathbf {0}. \end{aligned}$$

2.2 Counterfactual Problem in Decision Trees

In this section we briefly describe the counterfactual problem in a decision tree. Assume we are given a source input instance \(\overline{\mathbf {x}} \in \mathbb {R}^D\) which is classified by the tree as class \(\overline{y}\), i.e., \(T(\overline{\mathbf {x}}) = \overline{y}\), and we want to find the closest instance \(\mathbf {x}^*\) that would be classified as another class \(y \ne \overline{y}\) (the target class). We define the counterfactual explanation for \(\overline{\mathbf {x}}\) as the (or a) minimizer \(\mathbf {x}^*\) of the following problem:

$$\begin{aligned} \min _{\mathbf {x}\in \mathbb {R}^D}{ E(\mathbf {x};\overline{\mathbf {x}}) } \quad \text {s.t.} \quad T(\mathbf {x}) = y,\ \mathbf {c}(\mathbf {x}) = \mathbf {0},\ \mathbf {d}(\mathbf {x}) \ge \mathbf {0} \end{aligned}$$
(1)

where \(E(\mathbf {x};\overline{\mathbf {x}})\) is a cost of changing attributes of \(\overline{\mathbf {x}}\), and \(\mathbf {c}(\mathbf {x})\) and \(\mathbf {d}(\mathbf {x})\) are equality and inequality constraints (in vector form). The fundamental idea is that problem (1) seeks an instance \(\mathbf {x}\) that is as close as possible to \(\overline{\mathbf {x}}\) while being classified as class y by the tree and satisfying the constraints \(\mathbf {c}(\mathbf {x})\) and \(\mathbf {d}(\mathbf {x})\).

The constraint \(T(\mathbf {x}) = y\) makes the problem severely nonconvex, nonlinear and nondifferentiable because of the tree function \(T(\mathbf {x})\). However as described in [4, 5] this problem can be solved exactly and efficiently. In [4] we show that problem (1) is equivalent to:

$$\begin{aligned} \min _{i \in \mathcal {L}}{ \min _{\mathbf {x}\in \mathbb {R}^D}{ E(\mathbf {x};\overline{\mathbf {x}}) } } \quad \text {s.t.} \quad y_i = y,\ \mathbf {h}_i(\mathbf {x}) \ge \mathbf {0},\ \mathbf {c}(\mathbf {x}) = \mathbf {0},\ \mathbf {d}(\mathbf {x}) \ge \mathbf {0}. \end{aligned}$$
(2)

In English, what this means is that solving problem (1) over the entire space can be done by solving it within each leaf’s region (defined by \( \mathbf {h}_i\), Sect. 2.1) and then picking the leaf with the best solution. This is shown in Fig. 1 (bottom panel). That is, the problem has the form of a mixed-integer optimization where the integer part is done by enumeration (over the leaves (\(\mathcal {L}\))) and the continuous part (within each leaf) by other means to be described later.

Hence, the problem we still need to solve is the problem over a single leaf \(i \in \mathcal {L}\) (having the desired label \(y_i = y\)), and henceforth we focus on this. We write it as:

$$\begin{aligned} \min _{\mathbf {x}\in \mathbb {R}^D}{ E(\mathbf {x};\overline{\mathbf {x}}) } \quad \text {s.t.} \quad \mathbf {h}_i(\mathbf {x}) \ge \mathbf {0},\ \mathbf {c}(\mathbf {x}) = \mathbf {0},\ \mathbf {d}(\mathbf {x}) \ge \mathbf {0}. \end{aligned}$$
(3)

here, \(\mathbf {h}_i(\mathbf {x})\) is the set of hyperplanes that represents decision rule of the nodes in the path from root to leaf i (Sect. 2.1). If the function \(E(\mathbf {x};\cdot )\) is convex over \(\mathbf {x}\) and the constraints \(\mathbf {c}(\mathbf {x})\) and \(\mathbf {d}(\mathbf {x})\) are linear, then this problem is convex (since for oblique trees \(\mathbf {h}_i(\mathbf {x})\) is linear). In particular, if E is quadratic then the problem is convex quadratic program (QP), which can be solved very efficiently with existing solvers. See [4, 5] for more details.

Fig. 1.
figure 1

Top: an oblique classification tree with \(K = 3\) classes (colored white, light gray and gray) from [4]. A decision node i sends an input instance \(\mathbf {x}\) to its right child if \(f_i(\mathbf {x}) \ge 0\) and to its left child otherwise. The decision function \(f_i(\mathbf {x}) = \mathbf {w}^T_i \mathbf {x}+ b_i\), where \(\mathbf {w}\) and b are weights and the bias respectively. Bottom the space of the input instances \(\mathbf {x}\in \mathbb {R}^2\), assumed two-dimensional, partitioned according to each leaf’s region in polytopes (the region boundaries are labeled with the corresponding decision node function). The source instance \(\overline{\mathbf {x}}\) is in the white class and the counterfactual one (using the \(\ell _2\) distance) subject to being in the gray class is \(\mathbf {x}^*\).

Full size image

2.3 Separable Problems: A Special Case for Axis-Aligned Trees

Our earlier work [4, 5] provides following result, which vastly simplifies the problem for axis-aligned trees.

Theorem 1

In problem (1), assume that each constraint depends on a single element of \(\mathbf {x}\) (not necessarily the same) and that the objective function is separable, i.e., \(E(\mathbf {x};\overline{\mathbf {x}}) = \sum ^D_{d=1}{ E_d(x_d;\overline{x}_d) }\). Then the problem separates over the variables \(x_1,\dots ,x_D\).

This means that, within each leaf, we can solve for each \(x_d\) independently, by minimizing \(E_d(x_d;\overline{x}_d)\) subject to the constraints on \(x_d\). Further, the solution is given by the following result.

Theorem 2

Consider the scalar constrained optimization problem, where the bounds can take the values \(l_d = -\infty \) and \(u_d = \infty \):

$$\begin{aligned} \min _{x_d \in \mathbb {R}}{ E_d(x_d;\overline{x}_d) } \quad \text {s.t.} \quad l_d \le x_d \le u_d. \end{aligned}$$
(4)

Assume \(E_d\) is convex on \(x_d\) and satisfies \(E_d(\overline{x}_d;\overline{x}_d) = 0\) and \(E_d(x_d;\overline{x}_d) \ge 0\) \(\forall x_d \in \mathbb {R}\). Then \(x^*_d\), defined as the median of \(\overline{x}_d\), \(l_d\) and \(u_d\), is a global minimizer of the problem:

$$\begin{aligned} x^*_d = \text {median}(\overline{x}_d,l_d,u_d) = {\left\{ \begin{array}{ll} l_d, &{} \overline{x}_d < l_d \\ u_d, &{} \overline{x}_d > u_d \\ \overline{x}_d, &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$
(5)

We can apply these theorems to axis-aligned trees (assuming each of the extra constraints \(\mathbf {c}(\mathbf {x})\) and \(\mathbf {d}(\mathbf {x})\) depends individually on a single feature), because each of the constraints \(\mathbf {h}_i(\mathbf {x}) \ge \mathbf {0}\) in the path from the root to leaf i involve a single feature of \(\mathbf {x}\). Within each leaf \(i \in \mathcal {L}\) we can represent the constraints (which represents the path from the root to i) as bounding box \(\mathbf {l}_i \le \mathbf {x}\le \mathbf {u}_i\), and solve elementwise by applying the median formula described above. After solving the counterfactual problem in each leaf, we return the result of the best leaf. This makes solving the counterfactual explanation problem exceedingly fast for axis-aligned trees.

2.4 Categorical Variables

Although many popular benchmarks in machine learning use only continuous variables, in practice, most of the datasets contain categorical variables. This is true especially in legal, financial, or medical applications, for instance, use cases in Sect. 4.

In this work we handle categorical variables as described in [4, 5]. That is we encode the categorical variables as one-hot. This means, if an original categorical variable can take C different categories, we encode it using C dummy binary variables jointly constrained so that exactly one of them is 1 (for the corresponding category): \(x_1,\dots ,x_C \in \{0,1\}\) s.t. \(\mathbf {1}^T \mathbf {x}= 1\).

Since we only need to read the values of dummy variables during training, we treat them as if they were continuous and without the above constraints. However, when solving the counterfactual problem, we modify those variables, so we need to respect the above constraints. This makes the problem a mixed-integer optimization, where some variables are continuous and others binary (the dummy variables). While these problems are NP-hard in general, in many practical cases, we can expect to solve them exactly and quickly using modern mixed-integer optimization solvers, such as CPLEX or Gurobi [15].

3 Exploring Different Types of Counterfactual Explanation Questions

The counterfactual problem (2) accommodates a variety of useful, practical questions about the source instance (\(\overline{\mathbf {x}}\)). We list each below and explain how that can be solved exactly.

  1. 1.

    Finding the closest boundary. The minimum-distance change to \(\overline{\mathbf {x}}\) that changes its original class k. Solve the problem (3) in every leaf except the ones with label k, and pick the solution with the lowest cost.

  2. 2.

    Critical attribute for change to the target class y. Which attribute has the lowest cost to change the class of \(\overline{\mathbf {x}}\) to a target class y, if changing only one attribute? For given a attribute d, we add all other attributes to the equality constraint (\(\mathbf {c}(\mathbf {x}) = \mathbf {0}\)) and solve the counterfactual problem (2). We repeat this process for each attribute in \(\overline{\mathbf {x}}\) and pick the attribute for which the counterfactual (\(\mathbf {x}^*\)) has the lowest cost.

  3. 3.

    Critical attribute for changing the class. Which attribute has the lowest cost to change the class of \(\overline{\mathbf {x}}\) to any other class if changing only one attribute? For each attribute, we solve the finding the closest boundary problem, where other attributes are in the equality constraint; and pick the attribute for which the counterfactual (\(\mathbf {x}^*\)) have the lowest cost.

  4. 4.

    Robust counterfactuals. Here, we want to find the counterfactuals that are well inside a leaf region rather than on the boundary, so they are more robust to flipping their class due to small changes. This problem can easily be solved by shrinking the leaf region size in problem 3. That is in problem 3, the constraint “\(\mathbf {h}_i(\mathbf {x}) \ge \mathbf {0}\)” becomes “\(\mathbf {h}_i(\mathbf {x}) \ge \epsilon \)”, where \(\epsilon > 0\).

We can also use the counterfactual problem (2) to explore more practical problems that are related to the regression trees.Consider a regression tree T, where \(T(\overline{\mathbf {x}})\) and \(T(\mathbf {x}^*)\) represent the predicted value of the source instance (\(\overline{\mathbf {x}}\)) and the counterfactual (\(\mathbf {x}^*\)). Similar, to above we list each problem below and explain how that problem can be solved exactly.

  1. 1.

    \(T(\mathbf {x}^*) > T(\overline{\mathbf {x}})\): find the minimum change in \(\overline{\mathbf {x}}\) that increase its predicted value. For this we only consider the leaves whose label is larger than the \(T(\overline{\mathbf {x}})\), and solve problem (3) in each of them and pick the \(\mathbf {x}^*\) with the lowest cost.

  2. 2.

    \(T(\mathbf {x}^*) \ge T(\overline{\mathbf {x}})+\beta \) find the minimum change in \(\overline{\mathbf {x}}\) that increase its predicted value atleast by \(\beta \). Same as above, the only difference is the leaves we consider have the label greater than \(T(\overline{\mathbf {x}})+\beta \).

  3. 3.

    \( \alpha \ge T(\mathbf {x}^*) \ge \beta \) find the minimum change in \(\overline{\mathbf {x}}\) that change its predicted value between \(\alpha \) and \(\beta \). It is again same as the previous two, but this time we only consider the leaves with label between \(\alpha \) and \(\beta \).

All these extended problems can be applied to any type of decision tree with hard thresholds, but here we only focus on oblique trees.

4 Experiments

Since we show all extension problems (Sect. 3) can be solved exactly by converting them into the problem (2), we do not need to assess the optimality and validity of the generated counterfactual examples experimentally. Instead, we apply each problem to a real-life dataset [32] and explain their usage with three use case studies.

  • Our first use case deals with the students’ grades in secondary education of two Portuguese schools. For each student, we have social, demographic, and school-related attributes and their final grades. In this study, we focus on the students who have failing grades, and we suggest the changes that can improve students’ grades by applying our extension problems.

  • Next, we focus on the loan applicants as credit risk from the German credit dataset. We focus on the applicants that are a bad credit risk. Our goal here is not only to generate counterfactuals that can classify these candidates as good credit risk but also to suggest more changes to have a stronger credit profile. We do this by generating counterfactuals that are more robust to small changes.

  • Our last use case study focuses on the median value of owner-occupied homes in multiple suburbs of Boston. We treat this as a regression problem whose goal is to predict the value of the home. Then we apply our formulations to explore what factors affect the value of a home at different price points.

In all the case studies, our model is an oblique decision tree that we train using a recently proposed algorithm called tree alternating optimization (TAO) [3, 7]. To generate counterfactuals we use \(\ell _2\) distance as our cost function (E). Also, these datasets contain categorical variables, so to generate counterfactuals, we use Gurobi [15] to solve the mixed-integer optimization problem.

Next, we describe each dataset in brief and then discuss each use case study in detail.

4.1 Dataset Information

All our datasets are from UCI [32], and they are described in the same order as the user case study. Since none of the datasets contains a separate test set, we randomly divide the instances into training (80%) and test (20%) sets.

  • Student Portuguese Grades. Each instance have three grades, but we use only the final grades, and remove the other two from the attributes. The final grades are in the range of 1 to 20. So, we divide these grades into five categories. These categories are as follows:

    • If the grades are greater or equal to 16, then excellent.

    • If grades are either 15 or 14, then good.

    • If grades are either 14 or 13, then satisfactory.

    • If grades are in range between 12 and 10, then sufficient.

    • If grades are 9 or lower, then fail.

    The prediction task is to determine the final grades of a student. There are 649 instances, and each has 30 attributes (after removing the two grades). Out of 30 attributes, 11 are integer, and the rest are categorical. We convert each categorical attribute into a one-hot encoding attribute. Thus each instance of the dataset has 64 attributes.

  • German Credit. The prediction task is to determine whether an applicant is considered a good or a bad credit risk for 1 000 loan applicants. There are 20 attributes, out of which 7 are integer, and the rest are categorical. Similarly to the above dataset, we convert each categorical attribute to a one-hot encoding attribute. Thus each instance of the dataset has 61 attributes.

  • Boston Housing Dataset. We use this dataset for regression. The task is to predict the median price of owner-occupied homes. There are 506 instances, and each instance describes a Boston suburb or town. For each instance, there is 13 attribute all continuous except one which is binary.

4.2 Use Case Study 1

Our oblique tree for this classification task achieves 56.92% test error and 33.14% train error. The tree has a depth of 9 and 34 leaves.

First consider a student whose attributes are described in the second column of Table 1. The current final grades of the student is fail. If create a counterfactual with target class as excellent, the following attributes change (third column in Table 1):

  • reduce previous class failures from 2 to 1.

  • mother’s job should be changed from services to teacher.

  • father’s job should be changed from services to teacher.

  • change higher education plan from no to yes.

However, it is hard to jump from failing grades to excellent grades in real life. Also, it requires changing many attributes, which might not be feasible like mother’s job and father’s job. Instead, the student can try making small changes, which are enough for passing the class. For this, we try to find the closest other class boundary problem here since any other class will lead to passing the class. The closest class we find is sufficient and requires the following change (fourth column in Table 1).

  • reduce previous class failures from 2 to 1.

This is also expected the closest class to change is sufficient as this lowest thing to be considered as passing the class. Moreover, it does not suggest big changes like changing parent’s jobs, but only change previous class failures which easier to achieve.

Next, we consider another student (fifth column in Table 1). This student also failed the class. If we upgrade the grades directly to satisfactory allowing only attribute to change, then the attributes that will change the class with the lowest cost will be (sixth column in Table 1):

  • reduce free time from high(4) to very low(1).

This also makes sense as reducing free time after school can be devoted to studies. That said, it is still a large change. So, we search for the closest different class allowing only one attribute to change (last column in Table 1). The closet class would be sufficient, and the attribute with the lowest cost is:

  • reduce going out frequency from medium(3) to low(2).

This makes sense as, again, time spent on going out can be used for studies. Also, the numeric cost to change to lower grade (sufficient) is 3 times lower than the upper grade (satisfactory).

Table 1. Example illustrating the construction of counterfactual instances with our extended formulations for an oblique decision tree on the Student Portuguese grades dataset. Column 2-4: For source \(\overline{\mathbf {x}}_1\), \(\mathbf {x}^{*}_{11}\) and \(\mathbf {x}^{*}_{12}\) represents counterfactual with the given target class and the closest class respectively. Column 5-7: For source \(\overline{\mathbf {x}}_2\), both counterfactuals are generated by changing only one attribute that has the lowest cost. \(\mathbf {x}^{*}_{21}\) and \(\mathbf {x}^{*}_{22}\) represent counterfactual with the given target class and the closest class, respectively. “=” means the attribute value is the same as in the source instance.
Full size table

4.3 Use Case Study 2

The predictive task in the study is to predict how much a loan applicant is of credit risk. Our oblique tree achieves a test error of 18.5% and a train error of 17.5% for this dataset. The depth of the tree is 8.

The goal here is to generate diverse counterfactuals, where each subsequent counterfactual is more robust than the previous one. When generating a counterfactual, the algorithm generates a counterfactual in each target leaf that is closest to the input instance. If all the attributes are continuous, then this generated counterfactual will always exist on the boundary of the leaf, as shown in the Fig. 1. However, if we shrunk these leaves ’ regions, we can force the algorithm to generate counterfactuals inside the leaf region (generating robust counterfactuals). As described in Sect. 3, for a leaf i this can be done by adding a small positive constant (\(\epsilon > 0\)) in Eq. (3).

$$\begin{aligned} \min _{\mathbf {x}\in \mathbb {R}^D}{ E(\mathbf {x};\overline{\mathbf {x}}) } \quad \text {s.t.} \quad \mathbf {h}_i(\mathbf {x}) \ge \epsilon ,\ \mathbf {c}(\mathbf {x}) = \mathbf {0},\ \mathbf {d}(\mathbf {x}) \ge \mathbf {0}. \end{aligned}$$
(6)

Consider an example described in the Table 2. This instance is classified as bad creditor. Next, we generate a counterfactual for it. The generated counterfactual will able to change its label from bad to good creditor. However, it is either on the boundary of the target leaf region or very close to it (due to categorical variables). This means the changes suggested by the counterfactual (\(\mathbf {x}^*_1\)) will only suggest changes that are the bare minimum for a good creditor. However, if we force the algorithm to generate counterfactuals deep in the leaf region, it will suggest the changes that make the counterfactual much better creditor.

This is also evident from the Table 2. As we increase the value of \(\epsilon \), the number of features changed also increases. Thus, creating a user profile (\(\mathbf {x}_4^*\)) that is a better creditor than the first counterfactual (\(\mathbf {x}_1^*\)). This can also be seen as the distance between the original instances and the counterfactual increases as the leaf regions get smaller (increasing value of \(\epsilon \)).

These kinds of problems can be very useful, as shown in the above case. Here, we give a solution for now and give a strategy to become much better creditor.

In theory, the distance between the source instance and counter should increase with the value of \(\epsilon \) continuously, but in the presented case, it happens in intervals. The reason is due to the presence of integer and categorical attributes because the solution can only change when an attribute changes by an integer or category.

Table 2. Counterfactual solution trajectory as a function of \(\epsilon \) for Credit dataset. \(\ell _2\) distance is also mentioned between source instance (\(\overline{\mathbf {x}}\)) and the counterfactual \(\mathbf {x}^*\).
Full size table
Table 3. Example illustrating the construction of counterfactual instances for regression with our extended formulations for an oblique decision tree on the Boston housing dataset. We show the dataset attributes, source instance \(\overline{\mathbf {x}}\), and 3 counterfactual instances (with different Median home value) with various conditions. We have rounded each attribute value to 2 decimal places.“=” means the attribute value is the same as the source after rounding.
Full size table

4.4 Use Case Study 3

This user study deals with predicting the median home value of different suburbs and towns in Boston. We train a regression tree for this task. Our tree achieves a test mean squared error of 14.57 and train mean squared error of 13.19. The depth of the tree is 6, and the number of leaves is 21.

We consider an instance that has attributes described in the second column of Table 3. We apply our extension problems here to determine how for the given instance (\(\overline{\mathbf {x}}\)), the attributes need to change to accommodate the new median home value. We investigate three scenarios:

  • \(T(\mathbf {x}^*) > T(\overline{\mathbf {x}})\) meaning have higher median home value. Almost all of the attributes change (third column of the Table 3), the ones that change the most are as follows. The crime rate, nitric oxides concentration, distances to Boston employment centres, and pupil-teacher ratio decreases which make sense. Because having low crime rate means safer neighborhood and low nitric oxides concentration means the air quality is better. Also, having low pupil-teacher ratio means more teacher per student, which is beneficial for the families with children in school, and then distances to Boston employment centers is important for the people who need employment maybe for other family members. On the other side, the average rooms per dwelling increases, which is reasonable as it means bigger homes and thus higher prices.

  • \(T(\mathbf {x}^*) > T(\overline{\mathbf {x}}) +5 \) meaning the median home value should be greater than 19.72. As shown in the fourth column of the Table 3 the crime rate and nitric oxides concentration further decrease. The pupil-teacher ratio also decreases but compare to the previous scenario it is higher by a small reason. It may be the increased value of average rooms per dwelling and tract bounds river compensate for it.

  • \( 30 \ge T(\mathbf {x}^*) \ge 25\) meaning the median home value should be between 25 and 30. As shown in the fifth column of the Table 3 again the crime rate and nitric oxides concentration plays an important role in the value. The biggest change is the average rooms per dwelling which almost doubled. This is expected as described earlier.

This case study shows for this particular instances the crime rate, nitric oxides concentration and average rooms per dwelling plays an important role in deciding the median home value of the home. Also, average rooms per dwelling compensates for some attributes like pupil-teacher ratio.

5 Conclusion

Classification and regression trees are very important in applications such as education, business, law and medicine, where counterfactual explanations are of particular relevance. These can be formulated as a constrained optimization problem and solved exactly and efficiently for both continuous and categorical features, possibly in an interactive way. The formulation can be applied to answer a variety of practical questions and we have illustrated this in several case studies. Python code implementing the algorithm is available at the authors’ web page.