Keywords

1 Introduction

The need for solving systems of linear algebraic equations (SLAEs) with multiple right-hand sides (RHS) occurs in a variety of applications, including the structural analysis problems [7], uncertainty quantification [8], Brownian dynamics simulations [15], quantum chromodynamics [5], turbulent flow simulations [9], and others. The use of methods performing multiple solutions at once allows to significantly improve the performance of the calculations compared to the multiple solutions with single RHS due to increasing the arithmetic intensity of the corresponding methods [17]. However, the required functionality is not implemented in most of the popular open-source libraries typically used for solving large sparse SLAEs.

The newly developed XAMG library [13, 14] is among the few examples of the codes capable for solving systems with multiple RHSs. The library provides a set of Krylov subspace and algebraic multigrid iterative methods widely used to solve the systems corresponding to the elliptic differential equations. The XAMG library focuses on solution of series of systems of equations, thus reusing the hypre library to construct the multigrid matrix hierarchy and providing an optimized implementation for the “solve”-part of the methods only. The brief description of the XAMG library and several usage examples are presented in [13]. The current paper supplements [13], highlights some aspects of the XAMG library design and provides the thorough performance evaluation results.

The rest of the paper is organized as follows. The capabilities of the XAMG library are summarized in the first section. The second section presents some basic design features of the library developed. The third section describes some specific optimizations, implemented in the code. The fourth section presents the detailed performance evaluation results. Finally, Conclusions section summarizes the paper.

2 Capabilities of the XAMG Library

The XAMG library is a header-style template-based C++ code based on C++11 standard specification. The library implements a set of iterative methods typically used to solve large sparse systems of linear algebraic equations, corresponding to the elliptic differential equations. These include the Krylov subspace (both classical and modified formulations [6, 12, 16]), algebraic multigrid, Jacobi, Gauss-Seidel, and Chebyshev polynomial methods. The library provides hierarchical three-level parallelization with the hybrid MPI+POSIX shared memory parallel programming model (MPI+ShM).

The library design combining dynamic polymorphism and static template-based polymorphism opens up several opportunities compared to the popular open-source libraries like hypre or PETSc. Among the examples is the possibility to easily combine multiple solvers operating in different precision. The combination of this kind was used in [11] to construct the mixed-precision iterative refinement algorithm. The algorithm combines two solvers, the inner one operating with single precision, and the outer one operating with basic (double) precision. The proposed combination allows to perform most of the calculations with single precision while preserving the overall solution tolerance in double precision providing calculation speedup by a factor of 1.5–1.7.

The combination of compile-time polymorphism of matrix objects with the object-oriented style of inheritance also makes it possible to implement a sophisticated approach to data compression for different matrix elements. The matrix construction algorithms are able to detect the minimal necessary precision of integer index types for each matrix block at runtime and choose the suitable pre-compiled object template with optimal index data types. This results in a significant reduction of memory transfers.

Declaring the number of RHSs as a template parameter allows for a simple automated vectorization of main vector-vector and matrix-vector subroutines with basic C++ idioms and directives. The flexibility of the library design also introduces the capability to extend the set of matrix storage formats utilized in the library. Different storage formats can also be combined in a single matrix hierarchy. The ability to add accelerators support is also a code design feature.

3 Basic Design Features

3.1 Program Code Elements of XAMG Library

The current section provides a brief outline of the XAMG program code design principles by describing the main classes and subroutines implemented in the XAMG library. These include the vector and matrix data structures, “blas”- and “blas2”-like sparse linear algebra subroutines, solver classes, and solver parameter classes.

Vector Class. XAMG::vector::vector class is a simple representation of the vector type. The main integer or floating-point data type is not used in class specialization and is hidden inside via a simple type erasure technique. The vector may, in fact, represent NV vectors. The real number of vectors in this structure is not a compile-time specialization but a runtime one.

Matrix Classes. XAMG::matrix::matrix is an aggregation class. It holds a complex hierarchical structure of the decomposed matrix. As a result of the decomposition, the set of matrix subblocks appears, containing the actual matrix data. The matrix subblocks are implemented as classes inherited from an abstract XAMG::matrix::backend interface. These inherited classes represent the data structures specific to a concrete sparse matrix data storage format. The XAMG library contains implementation for two basic data storage formats, CSR and dense, and they are implemented as the XAMG::matrix::csr_matrix and XAMG::matrix::dense_matrix classes. Other matrix storage formats can be added as well. The XAMG::matrix::matrix class holds only references to the abstract XAMG::matrix::backend interface, so other matrix storage formats can be easily added. The matrix subblocks can then be stored in different matrix formats, even within a single matrix scope.

The inherited matrix classes are instantiated with a floating-point type and index types as template parameters at compile time. The runtime polymorphism of basic matrix data types is required for a more flexible design allowing ad hoc reduced-precision floating-point calculations and compression of indices features implementation. The special creator function is implemented for this purpose. It chooses a correct template-specialized constructor of a matrix object using a bit-encoded type fingerprint combined at runtime depending on the concrete matrix properties and decomposition. This creator function provides a runtime choice between all possible combinations of template types in matrix specializations, and it is implemented as an automatically generated if-else tree, which can be re-generated at compile time.

Basic Subroutines. Functions and procedures grouped in XAMG::blas and XAMG::blas2 namespaces are designed to cover all necessary vector and matrix-vector arithmetic operations used in the main workflow of the XAMG solvers code. Most of the subroutines are specialized by a template parameter of the data type (typically, the floating-point type). Additionally, the number of RHSs, NV, is specified as an integer template parameter. This fact makes it possible for a C++ compiler to vectorize loops in the “blas” and “blas2” subroutines. The subroutines are designed to implement a loop iterating over RHS as the most nested loop. Therefore, since this loop appears to be a constant-range loop after the template instantiation, the compiler’s vectorization possibilities are quite straightforward.

The matrix-vector subroutines in XAMG::blas2 namespace are specialized by both the concrete (non-abstract) matrix class and the NV parameter. The abstract matrix class has a subset of virtual functions which work as a direct connection to the XAMG::blas2 subroutines. This design decision makes it possible to call the XAMG::blas2 subroutines polymorphically in runtime for any concrete matrix object via an abstract interface. This adds a necessary generalization level to a solver program code.

A special proxy-class blas2_driver is used to implement the “blas2” calls from an abstract matrix interface. This class adds a connection between the NV compile-time parameter, representing the number of RHSs and the concrete matrix type. This artificial connection is required because the matrix itself is not supposed to be specialized with the number of RHSs at a compile-time. The proxy-class blas2_driver object belongs to each matrix subblock and is created once the first “blas2” operation is started. The necessity to hold and to create these proxy-objects in runtime is a trade-off of this design.

Solver Classes. The XAMG solvers are inherited from an abstract basic_solver_interface class. The two main virtual functions are present: setup() and solve(). The solve() function encapsulates the specific solver algorithm. The setup() is typically an empty function, besides the algebraic multigrid solver implementation: for this solver the actions of constructing the multigrid hierarchy are placed into this function. The current multigrid solver implementation in XAMG uses the subroutines from the hypre library to accomplish the multigrid hierarchy construction.

Solver Parameters. A two-level parameter dictionary organizes and holds all the solver parameters. For each solver role, which can be one of the: “solver”, “preconditioner”, “pre_smoother”, “post_smoother” and “coarse_grid_solver”, the key-value directory of parameters is held. The available parameters are defined by a solver method. The key for a parameter is a string; the value type is defined individually for each parameter as a floating-point, integer, or string type. For any parameter which is not set explicitly, the appropriate default value is set by the library. The XAMG::global_param_list class represents the top-level dictionary, the XAMG::param_list is a key-value holder for each solver parameters’ set. XAMG::global_param_list::set_default() functions must be always called after the parameters’ set up to handle the default settings correctly and to perform some parameters consistency checks.

MPI+ShM Parallel Programming Model. The hierarchical three-level hybrid parallel programming model is used in vector and matrix data types representation and in basic subroutines design. The hybrid programming model implements the specific data decomposition which reflects the typical hardware structure of modern HPC systems. The hierarchy levels include cluster node level, NUMA node level within a cluster node scope, and CPU core level. Decomposition ensures better data locality on each structural level. Moreover, the POSIX shared memory is used as a storage media for all intra-node decomposition levels, which makes it possible to eliminate the message-passing parallel programming paradigm usage (MPI) on these levels and switch to shared-memory parallel programming paradigm in the subroutines design. This MPI+ShM parallel programming model helps to reach better scalability outlook compared to other sparse linear algebra libraries.

4 Code Optimizations

The XAMG library contains several specific optimizations that improve the performance of the calculations compared to other libraries. These include reduced-precision floating-point calculations, compression of indices in the matrix subblocks, vector status flags indicating if the whole vector is identical to zero, and others. These optimizations are discussed in detail in the current section.

4.1 Reduced-Precision Floating-Point Calculations

The use of mixed-precision calculations for preconditioning operations is a well-known way to improve the overall performance of linear solvers [3]. The reduced-precision preconditioner calculations do not affect the overall solution tolerance, but may increase the number of iterations till convergence. In most practical cases, however, the use of single-precision floating-point numbers allows to obtain the guess values without any penalty in the overall number of iterations till convergence, and, thus, can be considered as an option to speed up the calculations.

4.2 Compression of Indices

The multilevel data segmentation implemented in the XAMG library [13], leads to a multiblock representation of the matrices. Typically each block, except the diagonal one, contains only several rows and columns, and the indices range can be represented by 2-byte or even 1-byte integer numbers only. The theoretical estimates allow to predict the range of the potential speedup due to reducing the amount of memory to store the matrix by 10–20%. The corresponding speedup is expected in the calculations.

4.3 Vector Status Flags

An optimization proposed in [10] assumes the introduction of an additional boolean flag indicating if the whole vector is equal to zero or not. Simple check if the vector is zero in matrix-vector operations eliminates some trivial algorithmic steps and speeds up the calculations. The current implementation in the XAMG library extends that idea and the corresponding checks for zero vectors are used in all vector and matrix-vector operations.

4.4 Per Level Hierarchy Construction

The hypre library provides various coarsening and interpolation algorithms as well as lots of methods tuning parameters. Most of these algorithms and parameters can be set the same for all levels of multigrid matrix hierarchy. In practice, however, mixed combinations of coarsening and interpolation algorithms can provide a faster convergence rate or lower multigrid hierarchy matrices complexity. The optional per level matrix hierarchy construction implemented in the XAMG library allows to build the matrices level by level, and set specific algorithm parameters for every hierarchy level.

4.5 Vectorization of Basic Operations

Vectorization of the computations is an important factor in achieving the maximal performance for modern CPUs. The efficient use of long registers can provide fold calculations speedup for compute-bound applications. However, for memory-bound applications, the real performance gain is much lower. Moreover, the sparse linear algebra applications typically suffer serious difficulties in the efficient implementation of operations with sparse matrices, including SpMV, due to the use of specific data storage formats with indirect elements indexing.

The generalized sparse matrix-vector multiplication is a much better candidate for taking the benefits of CPU vector instructions. Due to the element-wise indexing of the RHS elements (m RHSs with n unknowns line up in a long vector of \(m \cdot n\) elements with the element-by-element ordering, i.e. m elements with index 0, m elements with index 1, etc.), this type of operations can at least be vectorized over RHSs. The main computational kernels in the XAMG library, including the vector and matrix-vector operations, are instrumented with pragmas to maximize the vectorization effect. The list of pragmas used includes the compiler-specific data alignment and data dependency hints.

5 Performance Evaluation

The detailed evaluation procedure presented below shows the step-by-step investigation of the efficiency of the XAMG library and the impact of implemented optimization features on the overall code performance. The evaluation starts with a single-node performance analysis. This session includes (i) the comparison of execution times for identical numerical method configurations in the XAMG and hypre, (ii) the performance gain for multiple RHS calculations, and (iii) the comparison of the double-precision, mixed-precision and single-precision calculations. The multi-node runs investigate (i) the XAMG library scalability compared to hypre, (ii) analysis of changes in the strong scalability for various numbers of RHSs, and (iii) the effect of data compression optimizations on the calculation time reduction.

5.1 Test Application

The examples/ directory of the XAMG source code [14] contains a couple of usage examples in the form of some small and ready to use C++ and C example programs. A written in C example program can be used as a reference to the C language API of the XAMG library. Additionally, a comprehensive integration test application is provided, making it possible to easily test all the library features and make some productivity evaluations. This test code is located in the examples/test/ directory of the library source tree. This integration test application is used to produce all evaluation results presented below. This integration test code also features:

  • an internal matrix generator for two specific Poisson equation problems;

  • an interface to the graph reordering library used to construct an optimal data decomposition;

  • a command-line parser and YAML configuration file reader;

  • some additional performance monitoring tools and profilers integration;

  • a run-time debugger integration;

  • a YAML output generator for a test result.

The bunch of test configurations, which are present in the examples/test/yaml/ directory, can be used for testing purposes the way like this:

figure a

The input YAML file, which name is given in the “-​load” option here, stores all method configurations in a key-value form. A short overview of allowed solver parameters can be found in [2]. The “-​result” key is optional and sets up the file name for the test application report output. For information on other command-line options of the integration test application, one may consult the “-​help” option output.

5.2 Testing Methodology

The performance evaluation is performed for two groups of SLAEs. The first one corresponds to a set of model SLAEs obtained as a result of spatial discretization of the 3D Poisson equation

$$\varDelta u = f$$

with the 7-point stencil in a cubic domain with the regular grid; the grid size varies from \(50^3\) till \(300^3\). The second group of test matrices corresponds to SLAEs performed in direct numerical simulation of turbulent flow in a channel with a wall-mounted cube [9]. This group includes two matrices of 2.3 mln. and 9.7 mln. unknowns with constant RHSs. The corresponding matrix generators are available with the integration test application, published in the XAMG source code repository.

The single-node runs performed in the test sessions, are calculated with native matrix ordering. The multi-node runs use graph partitioning (the PT-Scotch graph partitioning library [4] to construct optimal data decomposition) to reduce the amount and volume of inter-node communications.

Various numerical method configurations are evaluated during the tests; the specific set of the methods is indicated in the corresponding subsection. In order to avoid possible variations in the convergence rate affecting the number of iterations till convergence, all the results presented below indicate the calculation times per one iteration of the corresponding numerical method.

Comparison with the hypre library is performed for the most recent version 2.20.0 available to date. The library is built with Intel MKL [1] and OpenMP parallelization support.

The two compute systems, Lomonosov-2 and HPC4, are used for the performance evaluation to demonstrate the potential of the developed XAMG library. The first one consists of compute nodes with a single Intel Xeon Gold 6126 processor and InfiniBand FDR interconnect; Intel compilers 2019 with Intel MPI Library 2019 Update 9 are used to compile the code. The HPC4 system consists of compute nodes with two Intel Xeon E5-2680v3 processors and InfiniBand QDR interconnect, and GNU compilers 8.3.1 with OpenMPI 4.0.1 are used in the tests. In all the cases all available physical CPU cores per node (12 or 24 cores correspondingly) are utilized during the calculations.

5.3 Single-Node Performance Evaluation Results

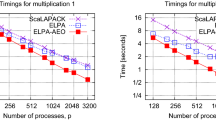
Single RHS Results Comparison with hypre. The performance evaluation starts with the comparison of single-node calculation times for the XAMG and hypre libraries when solving SLAE with a single RHS. The set of test cases includes three numerical method configurations and a full set of first group test matrices. The numerical method configurations considered include the BiCGStab method used as the main solver and the classical algebraic multigrid method with V-cycle as the preconditioner. The method configurations differ in the choice of pre- and post-smoothers. The three configurations explore three popular ones, i.e. the Jacobi method, the hybrid symmetric Gauss-Seidel method, and the Chebyshev iterative method. The full method configurations can be found in the corresponding YAML configuration files stored in the project repository in examples/test/yaml/single_node directory.

The obtained comparison results for pure MPI execution mode demonstrate that the XAMG library in all the cases outperforms hypre library (Fig. 1). The observed performance gain is about 1.2–1.4 except for the smallest test matrix, \(50^3\). In that case, the XAMG library demonstrates much higher performance gain, on average by a factor of 2.2 for Lomonosov-2 and by a factor of 6.5–7.5 for HPC4. Such a significant difference can in part be related to the implementation of the direct method used as a coarse grid SLAE solver. Because the solver setup phase is expected to be calculated only once for multiple SLAE solutions, XAMG multiplies the inverse matrix by the RHS instead of solving small SLAEs with the dense matrix.

Fig. 1.
figure 1

Comparison of single iteration calculation times with the XAMG and hypre libraries, and relative calculations speedup for the single node of Lomonosov-2 (left) and HPC4 (right) supercomputers. Pure MPI execution mode; from top to bottom: Gauss-Seidel smoother, Chebyshev smoother, Jacobi smoother.

Full size image

Multiple RHSs Results. The next test series focuses on the investigation of the performance gain due to the simultaneous solution of the system with multiple RHSs. The theoretical estimates, based on memory traffic reduction, predict the potential speedup by a factor of 2–2.5 [9]. The tests, performed with the SLAE from the first group with the matrix \(150^3\), demonstrate the behavior of the single iteration calculation time per one RHS as a function of the number of RHSs. The tests are performed for the Gauss-Seidel smoother configuration.

The obtained calculation results show a clear tendency to reduce the execution times when increasing the number of RHSs up to 32 (Fig. 2). The point of 32 RHSs becomes the global minimum for both compute systems, and the further increase of the number of RHSs leads to a slow performance gain degradation. The speedup per RHS, defined as

$$ P_m = \frac{m T_1}{T_m},$$

where m is the number of RHSs and \(T_i\) is the calculation time with i RHS vectors, demonstrate the performance gain by a factor of 2.2–2.5. These values are in good agreement with theoretical estimates. The further increase in the number of RHSs leads to slow performance degradation. The role of further matrix traffic reduction becomes insignificant compared to increasing role of the matrix and vector cache sweeping effect when performing the SpMV multiplication.

Fig. 2.
figure 2

Single iteration calculation times per RHS for the single node of Lomonosov-2 (left) and HPC4 (right) supercomputers. Cube test matrix \(150^3\), Gauss-Seidel smoother configuration, pure MPI execution mode.

Full size image

Reduced-Precision Floating-Point Calculations. The third test series focuses on the investigation of the potential of reduced-precision floating-point calculations. The test series includes a comparison of double-precision calculations, double-precision calculations with multigrid preconditioner performed with single-precision, and single-precision calculations. All the scenarios can be easily realized with the XAMG library due to template-based library design. The test session uses Chebyshev smoother configuration and the first group test matrix \(200^3\). The use of reduced-precision for multigrid solver can be specified in the YAML configuration file by adding the parameter “mg_reduced_precision: 1” in the “preconditioner_params” section.

The single iteration calculation times presented in Fig. 3 are in agreement with the ones, presented above for the other method configuration and matrix size: the monotone decrease of the calculation time per RHS can be achieved up to 16–32 RHSs. The double-precision calculations, as expected, provide the highest calculation times among the configurations considered. The mixed-precision calculations provide speedup up to 5–10% (Fig. 4). Finally, the single-precision calculations demonstrate the speedup by a factor of 1.6–2. While the performance gain for the mixed-precision calculations remains almost constant, the single to double-precision calculation speedup shows a stable increase. The observed speedup exceeds 2 and this effect is related to the lower cache load when using single-precision floating-point numbers.

Fig. 3.
figure 3

Single iteration calculation times per RHS for the single node of Lomonosov-2 (left) and HPC4 (right) supercomputers with various floating-point number tolerance. Cube test matrix \(200^3\), Chebyshev smoother configuration, pure MPI execution mode.

Full size image
Fig. 4.
figure 4

Relative calculation speedup due to the use of reduced-precision floating-point data types. Results for the single node of Lomonosov-2 (left) and HPC4 (right) supercomputers. Cube test matrix \(200^3\), Chebyshev smoother configuration, pure MPI execution mode.

Full size image

5.4 Multi-node Performance Evaluation Results

The multi-node performance is investigated for several test matrices and two numerical method configurations. The tests performed include the comparison of the XAMG library performance with hypre for the SLAEs with a single RHS as well as scalability results for the XAMG library with a different number of RHSs.

Single RHS Calculation Results. The first set of experiments is performed on the HPC4 compute system with two test SLAEs corresponding to cubic computational domain with \(150^3\) and \(250^3\) unknowns. The same method configuration with Gauss-Seidel smoother, as in the previous experiments, is used. The test series performed includes five different runs: the hypre library calculations in pure MPI and hybrid MPI+OpenMP execution modes, the XAMG library calculations with pure MPI and MPI+ShM execution modes, and the XAMG library calculations in hybrid MPI+ShM mode with data compression optimizations (compression of indices and reduced-precision floating-point calculations for multigrid hierarchy). The hybrid MPI+OpenMP and MPI+ShM modes are executed in the “\(2\,\times \,12\)” configuration with a single communicating MPI process per each processor.

The obtained performance evaluation results are presented in Fig. 5. The data is presented in terms of the relative speedup, which is defined as a ratio of the single-node calculation time for the hypre library, executed in a pure MPI mode, to the calculation time with the specific number of compute nodes and execution mode:

$$ S^i_p = \frac{T_1^{hypre, MPI}}{T_p^i}. $$

Results, presented in Fig. 5, show a clear advantage of hybrid programming models, and much better scalability for both the XAMG and hypre libraries compared to the pure MPI results. The XAMG library with MPI+ShM programming model significantly outperforms the hypre library. Additionally, the use of data compression allows to obtain an extra 10% calculations speedup.

The second set of experiments is performed on the Lomonosov-2 supercomputer. Here, the test matrices of the second group are used with the optimized iterative method configuration (this method configuration was used in [9] when modeling turbulent flows). The method also uses the preconditioned BiCGStab method with algebraic multigrid preconditioner and Gauss-Seidel smoother, but the parameters of the multigrid method are tuned to minimize the coarse level matrices fill in while preserving the same iterations convergence rate. The corresponding YAML configuration file is also available with XAMG source code in examples/test/yaml/multi_node/ directory.

Results, presented in Fig. 6, reproduce the same behavior for the XAMG library as above: the use of the compression techniques allow to speedup the calculations. The impact of the hybrid model (executed in the “\(1\times 12\)” configuration), however, is lower than for the HPC4 system due to twice lower the number of MPI processes per node, UMA architecture (each compute node contains a single processor only), and faster interconnect installed. Surprisingly, the hypre calculation times with pure MPI mode become lower than the hybrid mode ones for the considered range of compute nodes: the 1.5 times speedup is observed. Nonetheless, the XAMG library in hybrid execution mode outperforms the hypre library results by a factor of 1.5–1.7.

Fig. 5.
figure 5

Relative calculation speedup for the XAMG and hypre libraries in various execution modes. HPC4 supercomputer, cube test matrices with \(150^3\) (left) and \(250^3\) (right) unknowns.

Full size image
Fig. 6.
figure 6

Relative calculation speedup for the XAMG and hypre libraries in various execution modes. Lomonosov-2 supercomputer, second group test matrices with 2.3 mln. (left) and 9.7 mln. (right) unknowns.

Full size image

6 Conclusions

The details of the XAMG library for solving systems of linear algebraic equations with multiple right-hand sides are presented in the paper. The XAMG library provides the implementation of a set of iterative methods typically used to solve systems of linear algebraic equations derived from elliptic differential equations. The paper highlights some fundamental library design aspects, including the basic data structures and a couple of specific optimizations implemented in the code.

The detailed performance evaluation is presented for two different compute systems with UMA and NUMA architecture. The XAMG library is compared with hypre for single-node and multi-node runs. The obtained results show for the single-node runs the speedup against hypre by a factor of 1.2–1.3, and it increases to 2 for parallel runs performed. The potential of the XAMG library for solving SLAEs with multiple RHSs is demonstrated by a series of calculations, demonstrating the performance gain due to solving system with multiple RHSs compared to multiple solutions of SLAEs with a single RHS. The corresponding results demonstrate the speedup by a factor of 2.2–2.5.