Abstract
Scheduling theory is a major field in operations research and discrete applied mathematics. This paper focuses on several recent developments in scheduling theory and a broad range of new applications – from multiagent scheduling to robots in communication networks. The survey presents a personal view on current trends, critical issues, strengths and limitations of this advantageous field.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction and Brief History
Scheduling theory is a field in operations research and discrete applied mathematics which is concerned with the optimal allocation of scarce resources (for instance, machines, processors, robots, operators, etc.) to activities over time, with the objective of optimizing one or several performance measures. The systematic study and efficient computer-aided solution of scheduling problems started about 70 years ago, being initiated by seminal papers by Johnson (1954) [1], Bellman (1956) [2], and Smith (1956) [3].
Since then a great diversity of scheduling models and solution techniques have been developed. Vast applications are found in industry, communications, transport, planning of military operations, healthcare, etc. Today, scheduling theory is a rapidly evolving area fruitfully contributing to computer science, artificial intelligence, industrial engineering and data science. The interested reader can find many nice examples of scheduling problems and elegant algorithms in surveys, textbooks, and monographs by Tanaev et al. [4], Lee et al. [5], Chen et al. [6], Pinedo [7], Blazewicz et al. [8], Levner [9], and Lenstra and Shmoys [10].
This paper describes the current state and prospects for the development of theoretical and practical research in the field of scheduling theory. The article is organized as follows. The second section discusses recent theoretical and algorithmic advances, including models and algorithms for multiagent scheduling, issues of integrating scheduling theory and queueing theory, etc. Section 3 is devoted to the description of scheduling models in artificial intelligence and scheduling of flying unmanned aerial vehicles and broadband wireless communication networks based on them. The final Sect. 4 briefly describes the directions for further research.
2 Recent Theoretical and Algorithmic Advances
2.1 Multiagent Schedulings
Research on multi-agent scheduling started about 20 years ago with papers by Baker and Smith [11] and Agnetis et al. [12] in which two-agent scheduling was introduced. In multiagent scheduling problems, activities (jobs) are allocated to resources (machines) similarly as in conventional single-agent single-objective scheduling problem but the major difference is that each job is controlled by an (usually human) agent who has his/her own criteria which may be competing and which is to be optimized by each agent.
Extensive surveys of recent multiagent scheduling models and algorithms are given in Agnetis et al. [13, 14], and Cheng et al. [15].
The multiagent scheduling, and, in particular, corresponding coordination mechanisms, are studied in a novel area in game theory known as job scheduling games, in which multiple users (agents) wish to utilize multiple machines, the incentive of each user being to optimize his/her own objective function [16].
2.2 Integrating Scheduling Theory and Queueing Theory
For many years queueing theory and scheduling theory have been developed independently and, as a consequence, have different performance measures, problem formulations and techniques. However, in recent years, the scheduling community has noticed that the long-term stochastic reasoning as studied in queueing theory can be usefully combined, both theoretically and practically, with short-term algorithmic reasoning studied in scheduling theory, and this fact can be used in applications when solving practical artificial intelligence and big data processing problems.
Interesting that as early as in 1956, Richard Bellman has noticed in [2]: “If we fix the [job] order and fasten our attention upon the distribution of idle times, the distribution of waiting times, and similar questions, we enter the domain of queuing theory (see Kendall, 1951 [49]). In this connection, we would like to point out that the explicit formulas of Johnson may be of some utility in determining limiting distributions”.
The queueing system consists of a single or several lines of waiting jobs (customers) and the available number of servers. Factors that are to be studied include: the line length(s), number of lines and the queue servicing discipline. Queue servicing discipline is the priority rule, similar to that in the scheduling theory, for determining the order of service to customers in waiting lines. Similar to what happens in the scheduling theory, the most common used are the following greedy priority rules: “first come, first served” (FCFS, FIFO); highest-profit or “best” customer first; largest orders first, longest wait-time first, and many others (see, for instance [8, 17,18,19].
An important aspect of the queueing system is the line structure. Analogous structures are investigated in the scheduling theory. However, different jobs in the queueing systems have different probabilistic characteristics and requirements for processing on different resources, and these characteristics often do not become known until the jobs arrive.
Some basic questions studied in queueing theory are beyond the scope of scheduling theory, like, e.g., “What is the average waiting time for customers in a line and in the system?”
In [20], Terekhov et al. took initial steps toward integrating queueing and scheduling for dynamic scheduling problems. The dynamic scheduling problems are characterized by a varying stream of jobs arriving stochastically over time. Each job requires a combination of resources, sequentially and/or in parallel, using different processing times. The existence of any particular job and its corresponding characteristics are not known until its arrival. However, the authors in [20] assumed, - as in queueing theory but not as in scheduling settings, that stochastic characteristics of the distribution of job arrivals are known. Jobs may require a complex routing through the available resources, which may be heterogeneous but with known and deterministic capacities. To solve a dynamic scheduling problem, the jobs must be assigned to appropriate resources and start times, respecting the resource and temporal constraints. As jobs arrive, there must be an online process to make decisions: it is not possible to solve the entire problem of-line.
Solving dynamic scheduling problems is challenging both due to the combinatorics of the interaction of jobs, resources, and time, and due to the stochastics: to make a decision, one can use only the information that is known with certainty at a decision point and the stochastic properties of scenarios that may occur in the future.
The authors of [20] showed that the well-known queueing theory notion of stability can be used to analyze periodic scheduling algorithms, and that, for each of the problems studied, periodic scheduling algorithms can be maximally stable, that is, no queueing policy or scheduling algorithm can allow the system to operate at a higher load or achieve a higher throughput. For one dynamic scheduling problem, the long-term stochastic reasoning of queueing can be combined with short-term combinatorial reasoning and produces a hybrid scheduling algorithm that achieves better performance than either queueing or scheduling approaches can provide if used alone.
These authors empirically demonstrated that for a comparatively simple dynamic flowshop, the use of combinatorial scheduling has a small impact on schedule quality. In contrast, for more complicated flexible queueing networks, a novel algorithm that combines long-term guidance from queueing theory with short-term decision making outperforms all other tested approaches.
Integrating Scheduling Theory and Queueing Theory has many yet unsolved challenges.
2.3 An Improved Near-Optimal Algorithm for the Traveling Salesman Problem
One of the fundamental problems in scheduling theory and discrete optimization is the traveling salesman problem (TSP), included in Karp’s initial list of 21 NP-complete problems [21]. In TSP we are given a set of n nodes (cities) V along with their pairwise symmetric distances, \(V \times V \rightarrow R \ge 0\). The goal is to find a Hamiltonian cycle of minimum cost. In the metric TSP problem, which we shall study in this section, the distances satisfy the triangle inequality.
First, we recall the classical Christofides–Serdyukov (CS) algorithm, also known in literature as the Christofides algorithm. Nicos Christofides and Anatoly Serdyukov have discovered it independently more than four decades ago, in [22] and [23], respectively (see also [24]). This algorithm finds approximate solutions to the metric TSP and guarantees that its solution is always within a factor of 3/2 of the optimal solution value. Such type algorithms are called near-optimal or with performance guarantees. Let \(G = (V, w)\) be an instance of the travelling salesman problem. That is, G is a complete graph on the set V of vertices, and the function w assigns a nonnegative real weight to every edge of G. The CS algorithm works as follows: Given an instance of the metric TSP, choose a minimum spanning tree and then add the minimum cost matching on the odd degree vertices of the tree. In spite of its simplicity, this algorithm is the best known to date polynomial time approximation algorithm with the performance guarantee for the metric traveling salesman problem. It is worth mentioning that there known the ‘complementary’ inapproximability results, for instance, it is NP-hard to approximate TSP within a factor of 123/122 [25].
For many years, nobody could improve the Christofides-Serdukov algorithmic result. And only quite recently, Karlin, Klein, and Gharan [26] introduced a novel approximation algorithm with a slightly better approximation ratio \(r = (3/2 - 10^{36})\).
Theorem 1
For some absolute constant \({>}{10^{36}}\), there is a randomized algorithm that outputs a tour with expected cost at most \(3/2 - \varepsilon \) times the cost of the optimum solution.
The method [26] closely follows the Christofides-Serdyukov’s algorithm, but uses a special randomly chosen tree rather than the minimum spanning tree. The authors note that their algorithm makes use of the Held-Karp relaxation [27]. They also remark that although their approximation factor is only slightly better than Christofides-Serdyukov’s, in their numerical experiments they did not discover any example where the approximation ratio of the algorithm exceeded 4/3 in expectation. This recent approach is an exciting and promising direction for further study and improvement of the classical Christofides-Serdyukov algorithm.
2.4 Almost-Optimal (Fully Polynomial Time Approximation) Scheduling Algorithms
An algorithm A for solving an optimization problem P (in particular, a scheduling problem) is called an almost optimal algorithm (or a fully polynomial-time approximation scheme FPTAS) if given an input I for P and an \(\varepsilon > 0\), the algorithm A finds in time polynomial in the size of I and in \(1/ \varepsilon \), a solution s for I that satisfies: \(| OPT(I) - f(s) | \le \varepsilon OPT(I)\), where OPT(I) is the optimal value of a solution for I.
A polynomial time approximation scheme PTAS is an algorithm which takes an instance of an optimization problem and a parameter \(\varepsilon > 0\) and, in polynomial time in the problem size, produces a solution that is within a factor \(1 + \varepsilon \) of being optimal for a minimization problem (or \(1 - \varepsilon \) for maximization problems). There exists dozens of different types of PTAS and FPTAS for many classes of scheduling problems (see Sahni [28], Babat [29], Gens and Levner [30], Lawler [31], Kovalyov et al. [32], Kovalyov and Kubiak [33], Woeginger [34], Hoesel.and Wagelmans [35], and references therein).
In this section, we give a brief description of several not-trivial FPTAS that have appeared in recent years. Liu and Wu [36] considered a scheduling problem in a flexible supply chain where jobs can be either processed in house, or outsourced to a third-party supplier with the goal of minimizing the sum of holding and delivery costs subject to an upper bound on the outsourcing cost. The problem with identical job processing times has been proved to be binary \(\mathcal {N}\mathcal {P}\)-hard; a fully polynomial time approximation scheme that runs in \(O(n^8(1/\varepsilon ^2))\) time has been known. This paper derives a faster FPTAS. Kacem and Levner [37] revisited he problem of scheduling a set of proportional deteriorating non-resumable jobs on a single machine subject to maintenance. The maintenance has to be started prior to a given deadline. The jobs as well as the maintenance are to be scheduled so that to minimize the total completion time. For this problem a new dynamic programming algorithm and a faster fully polynomial time approximation scheme are proposed improving a recent result by Luo and Chen [JIMO (2012), 8:2, 271–283]. Yin et al. [38] considered the problem of scheduling n independent and simultaneously available jobs without preemption on a single machine, where the machine has a fixed maintenance activity. The objective is to find the optimal job sequence to minimize the total amount of late work, where the late work of a job is the amount of processing of the job that is performed after its due date. The authors first discussed the approximability of the problem, then developed two pseudo-polynomial dynamic programming algorithms and constructed a fully polynomial-time approximation scheme for the problem. Finally, the authors performed extensive numerical studies to evaluate the performance of the proposed algorithms in practice. Zhao and Hsu [39] considered a single-machine scheduling problem in which the processing time of a job is a linear increasing function of its starting time. The objective is to minimize the weighted number of tardy jobs. A pseudo-polynomial dynamic programming algorithm and a new fully polynomial-time approximation scheme were proposed.
Halman et al. [40] presented a new framework for obtaining fully polynomial time approximation schemes for stochastic univariate dynamic programs with either convex or monotone single-period cost functions. This framework is workable for the stochastic scheduling problems and is developed through the establishment of two sets of computational rules, namely, the calculus of K-approximation functions and the calculus of K-approximation sets. Using this general framework, the novel FPTASs for several NP-hard scheduling problems were obtained.
More details on the properties of the FPTAS algorithms can be found in the tutorial [41].
3 Novel Models and Applications
3.1 Scheduling and Artificial Intelligence. Robots are Everywhere
In recent decades, there is a growing interest on scheduling problems for autonomous robots and robotic systems. There are numerous applications of artificial intelligence (AI) and smart robots in different industries, on the earth and in space (see, e.g., Pinedo [7], Blazewicz et al. [8], Levner et al. [9], Agnetis et al. [14]) and in communications and transport (Vishnevsky et al. [42, 43]). Modern flexible manufacturing systems are integrated with computer-controlled hoists, robots and other automatic devices. Robots have expanded production capabilities in manufacturing world making the technological processes faster, more efficient and precise than ever before. As larger and more complex robotic systems are implemented, more sophisticated scheduling models, methods and algorithms are required for performing and optimizing these processes.
More details on AI and robotic scheduling problems and algorithms are presented in [7,8,9, 42, 43].
3.2 Scheduling of Flying Unmanned Stations in Airborne Communication Networks
The unmanned aerial vehicle communication networks (UAV-CN) contain a set of unmanned aerial vehicles (UAVs) that constitute together a network which may be used for very many applications. The UAVs autonomously fly in 3-dimensional space in ad-hoc mode and carry out the communications and collaboration missions. The specificity of such communication networks is a high-speed of UAVs constituting the network nodes, which has a crucial impact on efficient routing. Another factor affecting the quality of communication service is the power issue that is limited and should be optimized during the design of the UAV-CNs.
In the last decade, unmanned aerial communication systems have emerged in different areas, such as military and police operations, search and evacuation emergency missions, detection of ecological disasters, border surveillance, traffic monitoring, etc. In these systems, unmanned aerial vehicles communicate with each other based on a flying network to provide services to customers such as live streaming, high-speed access point, etc. (see Vishnevsky et al. [42, 43]). The performance of UAV-CNs can be advantageous in emergency, for example, rescuing and searching people in areas where the conventional communication network is unavailable. In [44], the authors propose a method for detecting the coordinates of subscribers with the Wi-Fi signals generated from victims’ phones using a flying network for emergencies based on UAV swarms.
According to the IEEE classification (see [45, 46]), the wireless communication networks can be divided into two large domains: Infrastructure-based networks (IBN) and infrastructure-less networks (ILN), also called ad hoc networks.
Infrastructure-based network (IBN) has two subgroups, stationary and mobile. The stationary subgroup consists of stationary (static) base stations (BS) while the mobile subgroup consists of mobile nodes (MN) and master stations (MS) which are known as access points (AP).
The communication among MN is done with the help of access points which use different frequencies to establish the communication.
The infrastructure-less (ad hoc) networks are grouped, in turn, into wireless sensor network (WSN), wireless mesh networks (WMN), and mobile ad hoc networks (MANET). Next, the mobile ad hoc networks are classified into two sub groups: vehicular ad-hoc networks VANET and unmanned aerial vehicle communication networks UAV-CN.
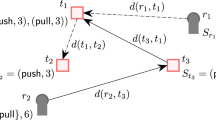
As a typical fragment in novel applications, consider a perspective of exploiting classic scheduling models and methods for efficient scheduling of a flying UAV-CNs with the minimum number of UAVs.
We suggest to use the extension of the Kats-Levner model [47, 48] for defining the minimum number of vehicles to meet a fixed schedule. In a new setting, we have the following problem. We study a cyclic process in which a set of several sensors perform m operations of data collection. A number of flying unmanned stations (drones) are used to transfer information of sensors from one sensor to another. The durations of data collecting and data transfers are known. The problem that has the key performance measure, the number of drones to be used. The aim is to find the minimum number of drones needed to meet a given cyclic schedule, for a fixed cycle length.
If the transfer times in the considered UAV (drone) scheduling problem satisfy the triangle inequality then the minimal number of UAVs needed to meet a given cyclic schedule of a fixed period length, is equal to the optimum solution of the \(m \times m\) assignment problem. The complexity of the algorithm is \(O(m^3)\), independently of the range within which the cycle length value may vary. The problem has several practical modifications (see, for instance, [47, 48]).
4 Concluding Remark: A Look to the Future
There exist a number of related attractive fields which are not covered in this survey, for instance, knowledge-based scheduling, real time scheduling, scheduling in cloud computing, and scheduling with communication delays. They will be overviewed in our future work.
Notes
- 1.
This Section Is Dedicated to the Memory of Dr. Anatoly Ivanovich Serdyukov (1951–2001).
References
Johnson, S.M.: Optimal two- and three-stage production schedules with setup times included. Naval Res. Logist. Q. 1, 61–68 (1954)
Bellman, R.: Mathematical aspects of scheduling theory. J. Soc. Ind. Appl. Math. 4, 168–205 (1956)
Smith, W.E.: Various optimizers for single-stage production. Naval Res. Logist. Q. 3(1–2), 59–66 (1956)
Tanaev, V.S., Gordon, V.S., Shafransky, Y.M.: Scheduling Theory. Single-Stage Systems. Kluwer, Dordrecht (1994)
Lee, C.Y., Lei, L., Pinedo, M.: Current trends in deterministic scheduling. Ann. Oper. Res. 70, 1–41 (1997). https://doi.org/10.1023/A:1018909801944
Chen, B., Potts, C.N., Woeginger, G.J.: A review of machine scheduling: complexity, algorithms and approximability. In: Du, D.-Z., Pardalos, P.M. (eds.) Handbook of Combinatorial Optimization, pp. 21–169. Kluwer Academic Publishers, Dordrecht (1998)
Pinedo, M.: Scheduling: Theory. Algorithms and Systems. Prentice Hall, Englewood Cliffs (2016)
Blazewicz, J., Ecker, K.H., Pesch, E., Schmidt, G., Weglarz, J.: Handbook on Scheduling. Springer, Berlin (2007). https://doi.org/10.1007/978-3-540-32220-7
Levner, E. (ed.): Multiprocessor Scheduling Theory and Applications. I-TECH Education and Publishing, Vienna (2007)
Lenstra, J.K., Shmoys, D.B. (eds.): Elements of Scheduling. Centrum Wiskunde & Informatica, Amsterdam (2020)
Baker, K., Smith, J.C.: A multiple criterion model for machine scheduling. J. Sched. 6, 7–16 (2003). https://doi.org/10.1023/A:1022231419049
Agnetis, A., Mirchandani, P., Pacciarelli, D., Pacifici, A.: Scheduling problems with two competing agents. Oper. Res. 52, 229–242 (2004)
Agnetis, A., Pacciarelli, D., Pacifici, A.: Combinatorial models for multi-agent scheduling problems. Ch. 2 in [9], pp. 21–47 (2007)
Agnetis, A., Billaut, J.-C., Gawiejnowicz, S., Pacciarelli, D., Soukhal, A.: Multiagent Scheduling. Models and Algorithms. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-41880-8
Cheng, C.T., Ng, J.J.Y.: Multi-agent scheduling on a single machine with max-form criteria. Eur. J. Oper. Res. 188, 603–609 (2008)
Cohen, J., Dürr, C., Kim, T.N.: Non-clairvoyant scheduling games. Theory Comput. Syst. 49, 3–23 (2011). https://doi.org/10.1007/s00224-011-9316-9
Vishnevsky, V., Semenova, O.: Polling systems and their application to telecommunication networks. Mathematics 9(2), 117 (2021). https://doi.org/10.3390/math9020117
Dudin, A.N., Klimenok, V.I., Vishnevsky, V.M.: The Theory of Queuing Systems with Correlated Flows. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-32072-0
Klimenok, V., Dudin, A., Vishnevsky, V.: Priority multi-server queueing system with heterogeneous customers. Mathematics 8(9), 1501 (2020). https://doi.org/10.3390/math8091501
Terekhov, D., Tran, T.T., Down, D.G., Beck, J.C.: Integrating Queueing theory and scheduling for dynamic scheduling problems. J. Artif. Intell. Res. 50(2014), 535–572 (2014)
Karp, R.M.: Reducibility among combinatorial problems. In: Miller, R.E., Thatcher, J.W., Bohlinger, J.D. (eds.) Complexity of Computer Computations. The IBM Research Symposia Series, pp. 85–103. Springer, Boston (1972). https://doi.org/10.1007/978-1-4684-2001-2_9
Christofides, N.: Worst-case analysis of a new heuristic for the travelling salesman problem (PDF), Report 388. Graduate School of Industrial Administration, CMU (1976)
Serdyukov, A.I.: On some extremal walks in graphs. Upravlyaemye Sistemy 17, 76–79 (1978). (in Russian)
van Bevern, R., Slugina, V.A.: A historical note on the 3/2-approximation algorithm for the metric traveling salesman problem (2020). arXiv:2004.02437v2 [cs.DS]
Karpinski, M., Lampis, M., Schmied, R.: New inapproximability bounds for TSP. J. Comput. Syst. Sci. 81(8), 1665–1677 (2015)
Karlin, A.R., Klein, N., Gharan, S.O.: A (slightly) improved approximation algorithm for metric TSP (2020). arXiv:2007.01409
Held, M., Karp, R.M.: The traveling salesman problem and minimum spanning trees. Oper. Res. 18, 1138–1162 (1970). https://doi.org/10.1007/BF01584070
Sahni, S.: Approximate algorithms for the 0/1 knapsack problem. J. ACM 22, 115–124 (1975)
Babat, L.G.: Linear functions on the N-dimensional unit cube. Dokl. Akad. Nauk SSSR 222, 761–762 (1975). (in Russian)
Gens, G.V., Levner, E.V.: Fast approximation algorithms for job sequencing with deadlines. Discrete Appl. Math. 3, 313–318 (1981)
Lawler, E.L.: A fully polynomial approximation scheme for the total tardiness problem. Oper. Res. Lett. 1, 207–208 (1982)
Kovalyov, M.Y., Potts, C.N., Van Wassenhove, L.N.: A fully polynomial approximation scheme for scheduling a single machine to minimize total weighted late work. Math. Oper. Res. 19, 86–93 (1994)
Kovalyov, M.Y., Kubiak, W.: A fully polynomial time approximation scheme for minimizing Makespan of deteriorating jobs. J. Heuristics 3, 287–297 (1998). https://doi.org/10.1023/A:1009626427432
Woeginger, G.J.: When does a dynamic programming formulation guarantee the existence of an FPTAS? INFORMS J. Comput. 12, 57–75 (2000)
van Hoesel, C.P.M., Wagelmans, A.P.M.: Fully polynomial approximation schemes for single-item capacitated economic lot-sizing problems. Math. Oper. Res. 26, 339–357 (2001)
Liu, S.C., Wu, C.C.: A faster FPTAS for a supply chain scheduling problem to minimize holding costs with outsourcing. Asia-Pac. J. Oper. Res. 33, 05 (2016)
Kacem, I., Levner, E.: An improved approximation scheme for scheduling a maintenance and proportional deteriorating jobs. J. Ind. Manage. Optim. 12(3), 811–817 (2016)
Yin, Y.Q., Xu, J.Y., Cheng, T.C.E., Wu, C.C., Wang, D.-J.: Approximation schemes for single-machine scheduling with a fixed maintenance activity to minimize the total amount of late work. Naval Res. Logist. 63(2), 172–183 (2016)
Zhao, C.L., Hsu, C.-J.: Fully polynomial-time approximation scheme for single machine scheduling with proportional-linear deteriorating jobs. Eng. Optim. 51(11), 1938–1943 (2019)
Halman, N., Klabjan, D., Li, C.-L., Orlin, J., Simchi-Levi, D.: Fully polynomial time approximation schemes for stochastic dynamic programs. SIAM J. Discrete Math. 28(4), 1725–1796 (2014)
Schuurman, P., Woeginger, G.J.: Approximation schemes, a tutorial. Unpublished book (2002). http://www.math.nsc.ru/LBRT/k5/DEP/P.Schuurman,%20G.Woeginger.pdf
Vishnevsky, V.M., Mikhailov, E.A., Tumchenok, D.A., Shirvanyan, A.M.: Mathematical model of the operation of a tethered unmanned platform under wind loading. Math. Models Comput. Simul. 12(4), 492–502 (2020). https://doi.org/10.1134/S2070048220040201
Vishnevsky, V., Meshcheryakov, R.: Experience of developing a multifunctional tethered high-altitude unmanned platform of long-term operation. In: Ronzhin, A., Rigoll, G., Meshcheryakov, R. (eds.) ICR 2019. LNCS (LNAI), vol. 11659, pp. 236–244. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26118-4_23
Dinh, T.D., Vishnevsky, V., Larionov, A., Vybornova, A., Kirichek, R.: Structures and deployments of a flying network using tethered multicopters for emergencies. In: Vishnevskiy, V.M., Samouylov, K.E., Kozyrev, D.V. (eds.) DCCN 2020. LNCS, vol. 12563, pp. 28–38. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-66471-8_3
Nawaz, H., Ali, H.M., Laghari, A.A.: UAV communication networks issues: a review. Arch. Comput. Methods Eng. 28(3), 1349–1369 (2020). https://doi.org/10.1007/s11831-020-09418-0
Khan, M.A., Qureshi, I.M., Safi, A., Khan, I.U.: Flying ad-hoc networks (FANETs): a review of communication architectures, and routing protocols. In: 1st International Conference on Latest Trends in Electrical Engineering and Computing Technologies (2017). https://www.researchgate.net/publication/311707613
Kats, V., Levner, E.: Minimizing the number of robots to meet a given cyclic schedule. Ann. Oper. Res. 69, 209–226 (1997). https://doi.org/10.1023/A:1018980928352
Kats, V., Levner, E.: Minimizing the number of vehicles in periodic scheduling: the non-Eucledean case. Eur. J. Oper. Res. 107, 371–377 (1998)
Kendall, D.G.: Some problems in the theory of queues. J. Roy. Statist. Soc. Ser. B 13, 151–185 (1951)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Levner, E., Vishnevsky, V. (2021). Recent Advances in Scheduling Theory and Applications in Robotics and Communications. In: Vishnevskiy, V.M., Samouylov, K.E., Kozyrev, D.V. (eds) Distributed Computer and Communication Networks: Control, Computation, Communications. DCCN 2021. Lecture Notes in Computer Science(), vol 13144. Springer, Cham. https://doi.org/10.1007/978-3-030-92507-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-92507-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92506-2
Online ISBN: 978-3-030-92507-9
eBook Packages: Computer ScienceComputer Science (R0)