Keywords

1 Introduction

Network slicing in 5G can be defined as a network configuration that allows multiple networks (virtualized and independent) to be created on top of a common physical infrastructure. This configuration has become an essential component of the overall 5G architectural landscape [17]. Each “slice” or portion of the network can be allocated based on the specific needs of the application, use case or customer.

Network slicing involves dividing the physical architecture of 5G into multiple virtual networks or layers. Each network layer includes control plane functions, user traffic plane functions, and a radio access network. Each layer has its own characteristics and is aimed at solving a particular business problem. 3GPP defines three standard network layers [1]:

  • super-broadband access (eMBB, Enhanced Mobile Broadband) – users of the global Internet, CCTV cameras;

  • ultra-reliability and low latency (URLLC, Ultra Reliable Low Latency Communication) – driverless transport, augmented and virtual reality;

  • low enegry and low latency (IoT, Internet of Things) – millions of devices transmitting small amounts of data from time to time.

Figure 1 shows an example of a network slicing by traffic (service) types. In this paper, it is proposed to consider a resource queueing system operating in a random environment as a mathematical model of such a technology, assuming that service requests occur when the random environment is in the appropriate state. We analyze the system in the limiting condition of extremely frequently changing states of the environment, thus, this will insignificantly affect the main probabilistic and numerical characteristics. We assume that requests for the services form a Poisson process with constant intensity, depending on the type of service (i.e. the state of the random environment). The request service duration and the amount of the provided resource also depend on the type of service and do not change for requests that are in service when the random environment changes its state. We present a detailed description of the model in the Sect. 2.

Fig. 1.
figure 1

Example of network slicing

Full size image

There are many papers where queues in a random environment were studied. For example, [13] considers queueing system M/M/C, where the arrivals and service rates are modulated by a random environment for which the underlying process C(t) is an irreducible continuous-time Markov chain. B. D’Auria [6] investigated an \(M/M\infty \) queue whose parameters depend on an external random environment that is specified by a semi-Markovian process. Boxma and Kurkova [2] studied an M/M/1 queue with the special feature that the speed of the server alternates between two constant values. There are a lot more papers [3, 4, 7,8,9,10, 12], where authors consider queueing systems operating in a random environment.

Resource queueing systems have been analyzed extensively in recent years. For example, in [15], a model of a multi-server queueing system with losses caused by lack of resources necessary to service claims was considered. In [18], it was investigated a heterogeneous wireless network model in terms of a queueing system with limited resources and signals that trigger the resource reallocation process. In [19] Tikhonenko studied a queueing system with processor sharing and limited resources.

In [16], it was considered an \(M/GI/\infty \) queueing system in a random environment. The dynamic screening method and asymptotic analysis were applied as well as we do in this paper. In [5], a mathematical model of an insurance company in the form of the infinite-server queueing system operating in a random environment was studied using the asymptotic analysis method. Paper [11] considers a non-Markovian infinite-server multi-resource queuing system. The result was found under the asymptotic condition of the growing intensity of the arrival process. All these papers consider an infinite-server queue in a random environment or with requirements for resources. Unlike them, we consider the \(M/GI/\infty \) queueing model with both a random environment and requirements for resources in this paper.

The paper is organized as follows. In Sect. 2, the mathematical model is described and the goal of the study is formulated. In Sect. 3, the dynamic screening method is explained, moreover, balance equations are obtained and written using characteristic functions. The asymptotic analysis and final equations are derived in Sect. 4. Section 5 presents a numerical example and conclusions on the accuracy of the obtained approximation.

2 Mathematical Model

Consider a queueing system with an unlimited number of servers and an unlimited capacity of some resource that operates in a random environment (Fig. 2), such the functioning of the system depends on the environment state. The random environment is specified by a continuous-time Markov chain with a finite number of states \(k\in \{1,\dots ,K\}\) and generator \(\mathbf {Q}=\{q_{k\nu }\},\,k,\nu =1,\dots ,K\). When the process is in state k, the rate of the Poisson arrival process is equal to \(\lambda _k\) and the service time has distribution with CDF \(B_k(x)\). We compose the arrivals rates into diagonal matrix \(\mathbf {\Lambda }=\text {diag}\{\lambda _k\},\,k=1,\dots ,K\). In addition, each arrival occupies a resource of a random size \(v_k>0\) with the CDF \(G_k(y)={\text {P}}\{v_k<y\}\) which depends on the environment state.

When the environment state changes, the resource amounts and the service rates change only for new customers, as for customers already under service, these values stay the same. When a customer completes servicing, it leaves the system and releases the resource that it occupied during the capture. Capture is understood as the moment when the customer arrives, at which the resource is allocated.

A stochastic process \(\left\{ k(t),i(t),v(t)\right\} \) describes the system’s state at time t as follows:

  • the environment state at time t is denoted by \(k(t)\in \{1,\dots ,K\}\),

  • the number of customers in the system at time t is denoted by \(i(t)\in \{0,1,2,\dots \}\),

  • the total amount of occupied resource at time t is denoted by \(v(t) \ge 0\).

Our goal is to find the steady-state probability distribution of the total amount of the occupied resources v(t).

Fig. 2.
figure 2

Structure of the model

Full size image

3 Dynamic Screening Method

We consider an infinite-server queue with non-exponential service times. This is the reason why we can not apply some classical methods directly here (for example, the method of supplementary variables). Otherwise, we should deal with the number of variables and equations that are unlimited and changing. To avoid the problem, we apply the dynamic screening method [14] whose modification for the resource queue is described below.

3.1 Method Description

Let at moment \(t_0\) the system is empty. We fix a moment \(T>{{t}_{0}}\) in the future. Let us draw two time axes (Fig. 3). The moments of customers arrivals are marked on the axis 0. We mark on axis 1 only those arrivals that before the moment T have not finished their service. We name the arrivals on axis 1 as “screened”, and the entire point process on axis 1 is named as the “screened process”.

Let us define function \({{S}_{k}}(t)\) that determines the dynamic screening probability on axis 1 as follows:

$${{S}_{k}}(t)=1-{{B}_{k}}(T-t).$$

The customer arrived at the system at the moment \(t<T\) does not finish service before moment T and occupies a certain amount of the resource with probability \({{S}_{k}}(t)\). On the other hand, the customer leaves the system and releases the resource occupied at the arriving with the probability \(1-{{S}_{k}}(t)\), hence it is not considered in the “screened” process. The values of \({{S}_{k}}(t)\) belong to the segment [0, 1]. In Fig. 3, colored areas depict different states of the random environment.

Fig. 3.
figure 3

Example of the customers arrivals screening

Full size image

Let us denote the number of screened arrivals, which occurred during time \([{{t}_{0}},t)\) by n(t), and the total amount of resource occupied by the screened customers by w(t).

Basing on the results obtained in [14] and [11], it is not hard to show that

$$\begin{aligned} \begin{array}{c} \mathrm {P}\{k(T)=k,i(T)=m,v(T)<x\} \\ =\,\mathrm {P}\{k(T)=k,n(T)=m,w(T)<x\},\quad k\in \{1,\ldots ,K\} \end{array} \end{aligned}$$
(1)

for any non-negative values of m and x. So, we can first study the stochastic process \(\{k(t),n(t),w(t)\}\) instead of process \(\{k(t),i(t),v(t)\}\). After that, we can substitute \(t=T\) into the final expressions and obtain the goal due to the moment T is chosen arbitrarily.

3.2 Balance Equations

We denote the probabilities

$$P_k(n,w,t)=\mathrm {P}\{k(t)=k,n(t)=n,w(t)<w\}.$$

For \(P_k(n,w,t)\), we write the following system according to the total probability law and dynamic screening method

$$\begin{aligned} \begin{array}{c} {{P}_{k}}\left( n,w,t+\varDelta t \right) ={{P}_{k}}\left( n,w,t \right) \left( 1-{{\lambda }_{k}}\varDelta t \right) \left( 1+{{q}_{kk}}\varDelta t \right) \\ +\,{{\lambda }_{k}}\varDelta t{{S}_{k}}\left( t \right) \int \limits _{0}^{w}{{{P}_{k}}\left( n-1,w-y,t \right) d{{G}_{k}}\left( y \right) }\\ +\,{{\lambda }_{k}}\varDelta t\left( 1-{{S}_{k}}\left( t \right) \right) {{P}_{k}}\left( n,w,t \right) +\sum \limits _{{\begin{matrix} v=1 \\ v\ne k \end{matrix}}}^{K}{{{q}_{\nu k}}\varDelta t{{P}_{\nu }}\left( n,w,t \right) }+o(\varDelta t). \end{array} \end{aligned}$$

We obtain the system of Kolmogorov integro-differential equations

$$\begin{aligned} \begin{aligned} \frac{\partial {{P}_{k}}\left( n,w,t \right) }{\partial t}=&\,{{\lambda }_{k}}{{S}_{k}}\left( t \right) \left[ \int \limits _{0}^{w}{{{P}_{k}}\left( n-1,w-y,t \right) d{{G}_{k}}\left( y \right) }-{{P}_{k}}\left( n,w,t \right) \right] \\&\qquad \qquad \;\;\; +\,\sum \limits _{\nu =1}^{K}{{{q}_{\nu k}}{{P}_{\nu }}\left( n,w,t \right) }, \end{aligned} \end{aligned}$$
(2)

with the initial condition

$$\begin{aligned} {{P}_{k}}(n,dw,{{t}_{0}})= {\left\{ \begin{array}{ll} {{r}_{k}}\delta _0(dw), &{} \text {if }n=0,\\ 0, &{} \text {else,}\\ \end{array}\right. } \end{aligned}$$
(3)

where \({{r}_{k}}\) is the element of row vector \(\mathbf {r}\), which satisfies the system of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {rQ}=\mathbf {0},\\ \mathbf {re}=1, \\ \end{array}\right. } \end{aligned}$$

and \(\mathbf {e}\) is a column vector that consists of ones.

3.3 Characteristic Functions

Let us define the partial characteristic functions as

$$\begin{aligned} {{h}_{k}}(u,v,t)=\sum \limits _{n=0}^{\infty }{{{e}^{jun}}\int \limits _{0}^{\infty }{{{e}^{jvw}}{{p}_{k}}(n,dw,t)}}, \end{aligned}$$

where \(j=\sqrt{-1}\), and we rewrite the system (2)–(3) for functions \(h_k(u,v,t)\)

$$\begin{aligned} \begin{aligned}&\frac{\partial {{h}_{k}}\left( u,v,t \right) }{\partial t}={{\lambda }_{k}}{{S}_{k}}\left( t \right) \left( e^{ju}G_k^*(v)-1\right) h_k(u,v,t)\\&\qquad \quad +\,\sum \limits _{\nu =1}^{K}{{{q}_{\nu k}}{{h}_{\nu }}\left( u,v,t \right) },\quad k\in \{1,\ldots ,K\}, \end{aligned} \end{aligned}$$

with the initial condition

$$\begin{aligned} h_k(u,dv,t_0)={{r}_{k}}\delta _0(dv) \end{aligned}$$

where

$$\begin{aligned} G_{k}^{*}(v)=\int \limits _{0}^{\infty }{{{e}^{jvy}}}d{{G}_{k}}(y). \end{aligned}$$

Then, we rewrite the obtained system as matrix equation

$$\begin{aligned} \frac{\partial \mathbf {h}\left( u,v,t \right) }{\partial t}=\mathbf {h}\left( u,v,t \right) \left[ \mathbf {\Lambda }\mathbf {S}(t)\left( e^{ju}\mathbf {G}(v)-\mathbf {I}\right) +\mathbf {Q}\right] , \end{aligned}$$
(4)

with the initial condition

$$\begin{aligned} \mathbf {h}\left( u,dv,t_0 \right) =\mathbf {r}\delta _0(dv) \end{aligned}$$
(5)

where

$$\begin{aligned}&\;\;\, \mathbf {h}\left( u,v,t\right) =\left[ h_1\left( u,v,t\right) ,\ldots ,h_K\left( u,v,t\right) \right] ,\\&\mathbf {S}\left( t\right) =\text {diag}\{S_k(t)\},\quad \mathbf {G}\left( v\right) =\text {diag}\{G_k^*(v)\} \end{aligned}$$

and \(\mathbf {I}\) is identity matrix.

4 Asymptotic Analysis Method

Problem (4)–(5) seems as it can not be solved analytically in a direct way, so, we apply the method of asymptotic analysis to solve it.

4.1 Method Description

Asymptotic analysis method for queueing systems consists of analysis of the equations defining any characteristics of the system and allows to obtain probability distribution and numerical characteristics in the analytical form under some asymptotic condition. We will use the asymptotic analysis method under the condition of growing arrivals rate and extremely frequent changes in the environment state to solve the Eq. (4)–(5). We set

$$\begin{aligned} \widetilde{\mathbf {\Lambda }}=N\mathbf {\Lambda },\ \ \widetilde{\mathbf {Q}}=N\mathbf {Q},\ \ N\rightarrow \infty . \end{aligned}$$

Then (4) can be rewrite as

$$\begin{aligned} \frac{1}{N}\frac{\partial \mathbf {h}\left( u,v,t\right) }{\partial t}=\mathbf {h}\left( u,v,t\right) \left[ \mathbf {\Lambda }\mathbf {S}\left( t\right) \left( e^{ju}\mathbf {G}\left( v\right) -\mathbf {I}\right) +\mathbf {Q}\right] . \end{aligned}$$
(6)

4.2 First Order Asymptotic

In (6), (5), we substitute

$$\begin{aligned} \frac{1}{N}=\varepsilon ,\ \ u=\varepsilon x,\ \ v=\varepsilon y,\ \ \mathbf {h}\left( u,v,t\right) =\mathbf {f}_\mathbf {1}\left( x,y,t,\varepsilon \right) , \end{aligned}$$
(7)

and then it can be rewritten as

$$\begin{aligned} \varepsilon \frac{\partial \mathbf {f}_\mathbf {1}\left( x,y,t,\varepsilon \right) }{\partial t}=\mathbf {f}_\mathbf {1}\left( x,y,t,\varepsilon \right) \left[ \mathbf {\Lambda }\mathbf {S}\left( t\right) \left( e^{j\varepsilon x}\mathbf {G}\left( \varepsilon y\right) -\mathbf {I}\right) +\mathbf {Q}\right] . \end{aligned}$$
(8)

In (8) we set \(\varepsilon \rightarrow 0 \) and denote

$$\lim _{\varepsilon \rightarrow 0}\mathbf {f_1}(x,y,t,\varepsilon )=\mathbf {f_1}(x,y,t),$$

this yields

$$\mathbf {f_1}(x,y,t)\mathbf {Q}=\mathbf {0},$$

it then follows that \(\mathbf {f_1}(x,y,t)\) can be represented as a product

$$\begin{aligned} {{\mathbf {f}}_{1}}(x,y,t)=\mathbf {r}{{\varPhi }_{1}}(x,y,t), \end{aligned}$$
(9)

where \({\varPhi }_{1}(x,y,t)\) is a scalar function that satisfies the initial condition \({\varPhi }_{1}(x,y,t_0)=1\).

We multiply (8) by \(\mathbf {e}\), divide by \(\varepsilon \), set \(\varepsilon \rightarrow 0\) and substitute (9):

$$\begin{aligned} \frac{\partial \varPhi _1\left( x,y,t\right) }{\partial t}=\varPhi _1\left( x,y,t\right) \mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \left( jx\mathbf {I}+jy{\mathbf {A}}_{1}\right) \mathbf {e}, \end{aligned}$$
(10)

where

$$\begin{aligned} {\mathbf {A}}_{1} =\text {diag}\{a_k\},\quad a_k=\int \limits _0^\infty ydG_k(y). \end{aligned}$$

The solution of Eq. (10) is given as

$$\begin{aligned} \varPhi _1\left( x,y,t\right) =\exp {\left\{ jx\int \limits _{t_0 }^{t }{\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( \tau \right) \mathbf {e}d\tau }+jy\int \limits _{t_0 }^{t }{\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( \tau \right) {\mathbf {A}}_{1}\mathbf {e}d\tau }\right\} }. \end{aligned}$$
(11)

Denoting

$$\begin{aligned} m_1\left( t\right) {\mathop {=}\limits ^{\varDelta }}\int _{t_0}^{t}{\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( \tau \right) \mathbf {e}d\tau },\ \ m_2\left( t\right) {\mathop {=}\limits ^{\varDelta }}\int _{t_0}^{t}{\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( \tau \right) {\mathbf {A}}_{1}\mathbf {e}d\tau }, \end{aligned}$$

and making substitution inverse to (9) and (7), we obtain the first order approximation

$$\begin{aligned}&\mathbf {h}^{(1)}\left( u,v,t\right) =\mathbf {f}_\mathbf {1}\left( x,y,t,\varepsilon \right) \approx \mathbf {f}_\mathbf {1}\left( x,y,t\right) =\mathbf {r}\varPhi _1\left( x,y,t\right) \\&\qquad \qquad \; =\mathbf {r}\exp {\left\{ juNm_1\left( t\right) +jvNm_2\left( t\right) \right\} }. \end{aligned}$$

4.3 Second Order Asymptotic

In (4), we make a substitution

$$\begin{aligned} \mathbf {h}\left( u,v,t\right) =\mathbf {h}_{2}\left( u,v,t\right) \exp {\left\{ juNm_1\left( t\right) +jvNm_2\left( t\right) \right\} }, \end{aligned}$$
(12)

we obtain

$$\begin{aligned} \begin{aligned}&\qquad \qquad \quad \;\, \frac{1}{N}\frac{\partial \mathbf {h}_{2}\left( u,v,t\right) }{\partial t}=\mathbf {h}_{2}\left( u,v,t\right) \\&\times \,\left[ \mathbf {\Lambda }\mathbf {S}\left( t\right) \left( e^{ju}\mathbf {G}\left( v\right) -\mathbf {I}\right) +\mathbf {Q}-\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {e}\left( ju\mathbf {I}+jv\mathbf {A}_{1}\right) \right] . \end{aligned} \end{aligned}$$
(13)

We substitute

$$\begin{aligned} \frac{1}{N}=\varepsilon ^2,\ \ u=\varepsilon x,\ \ v=\varepsilon y,\ \ \mathbf {h}_{2}\left( u,v,t\right) =\mathbf {f}_{2}\left( x,y,t,\varepsilon \right) \end{aligned}$$
(14)

into (13), and we obtain

$$\begin{aligned} \begin{aligned}&\qquad \qquad \quad \;\;\; \varepsilon ^2\frac{\partial \mathbf {f}_{2}\left( x,y,t,\varepsilon \right) }{\partial t}=\mathbf {f}_{2}\left( x,y,t,\varepsilon \right) \\&\times \,\left[ \mathbf {\Lambda }\mathbf {S}\left( t\right) \left( e^{j\varepsilon x}\mathbf {G}\left( \varepsilon y\right) -\mathbf {I}\right) +\mathbf {Q}-\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {e}\left( j\varepsilon x\mathbf {I}+j\varepsilon y\mathbf {A}_{1}\right) \right] . \end{aligned} \end{aligned}$$
(15)

As \(\varepsilon \rightarrow 0\), denoting

$$\begin{aligned} \underset{\varepsilon \rightarrow \infty }{\mathop {\lim }}\,{{\mathbf {f}}_{2}}(x,y,t,\varepsilon )={{\mathbf {f}}_{2}}(x,y,t), \end{aligned}$$

we obtain

$$\begin{aligned} {{\mathbf {f}}_{2}}(x,y,t)\mathbf {Q}=\mathbf {0}. \end{aligned}$$

This yields

$$\begin{aligned} \mathbf {f}_{2}\left( x,y,t\right) =\mathbf {r}\varPhi _2\left( x,y,t\right) , \end{aligned}$$
(16)

where \(\varPhi _2\left( x,y,t\right) \) is a scalar function that satisfies the initial condition \({\varPhi }_{2}(x,y,t_0)=1\). We represent \(\mathbf {f}_{2}\left( x,y,t\right) \) as the expansion

$$\begin{aligned} \mathbf {f}_{2}\left( x,y,t,\varepsilon \right) =\varPhi _2\left( x,y,t\right) \left[ \mathbf {r}+\mathbf {g}\left( t\right) \left( j\varepsilon x\mathbf {I}+j\varepsilon y\mathbf {A}_{1}\right) \right] +O\left( \varepsilon ^2\right) , \end{aligned}$$
(17)

where \(\mathbf {g}\left( t\right) \) is a row vector.

We substitute the first degree Maclaurin expansion of \(e^{z}\) into Eq. (15)

$$\begin{aligned} \varepsilon ^2\frac{\partial \mathbf {f}_\mathbf {2}\left( x,y,t,\varepsilon \right) }{\partial t}=\mathbf {f}_\mathbf {2}\left( x,y,t,\varepsilon \right) \left[ \mathbf {\Lambda }\mathbf {S}\left( t\right) \left( \mathbf {I}-\mathbf {er}\right) \left( j\varepsilon x\mathbf {I}+j\varepsilon y\mathbf {A}_{1}\right) +\mathbf {Q}\right] . \end{aligned}$$

Then we substitute (17) into the obtained equation

$$\begin{aligned} \begin{aligned}&\qquad \, \varPhi _2\left( x,y,t\right) \left[ \mathbf {r}+\mathbf {g}\left( t\right) \left( j\varepsilon x\mathbf {I}+j\varepsilon y\mathbf {A}_1\right) \right] \\&\times \,\left[ \mathbf {\Lambda }\mathbf {S}\left( t\right) \left( \mathbf {I}-\mathbf {er}\right) \left( j\varepsilon x\mathbf {I}+j\varepsilon y\mathbf {A}_1\right) +\mathbf {Q}\right] =O\left( \varepsilon ^2\right) . \end{aligned} \end{aligned}$$

We divide both sides by \(\varepsilon \) and set \(\varepsilon \rightarrow 0\)

$$\begin{aligned} \varPhi _2\left( x,y,t\right) \left[ \mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \left( \mathbf {I}-\mathbf {er}\right) +\mathbf {g}\left( t\right) \mathbf {Q}\right] \left[ jx\mathbf {I}+jy\mathbf {A}_1\right] =0. \end{aligned}$$

This yields

$$\begin{aligned} \mathbf {g}\left( t\right) \mathbf {Q}=\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \left( \mathbf {er}-\mathbf {I}\right) . \end{aligned}$$
(18)

Hence, vector \(\mathbf {g}\left( t\right) \) is defined by the inhomogeneous linear system. The solution \(\mathbf {g}\left( t\right) \) of the system (18) we can write as

$$\begin{aligned} \mathbf {g}\left( t\right) =c\left( t\right) \mathbf {r}+\mathbf {d}\left( t\right) , \end{aligned}$$

where c(t) is an arbitrary scalar function and the row vector \(\mathbf {d}\left( t\right) \) is any specific solution to system (18) satisfying a certain condition, for example:

$$\begin{aligned} \mathbf {d}\left( t\right) \mathbf {e}=0. \end{aligned}$$

The solution has the form

$$\begin{aligned} \mathbf {d}\left( t\right) =\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {G}, \end{aligned}$$

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {G}\mathbf {Q}=\mathbf {er}-\mathbf {I}, \\ \mathbf {Ge}=\mathbf {0}. \\ \end{array}\right. } \end{aligned}$$

Finally, the solution of (18) has the form

$$\begin{aligned} \mathbf {g}\left( t\right) =c\left( t\right) \mathbf {r}+\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {G}. \end{aligned}$$

Let us now derive the explicit expression for the function \(\varPhi _2\left( x,y,t\right) \). To do this, we approximate the exponential function in (15) with the second degree Maclaurin expansion and make substitution (17). This yields the equation

$$\begin{aligned} \begin{aligned}&\qquad \;\;\, \varepsilon ^2\frac{\partial \varPhi _2\left( x,y,t\right) }{\partial t}\mathbf {r}=\varPhi _2\left( x,y,t\right) \left[ \mathbf {r}+\mathbf {g}\left( t\right) \left( j\varepsilon x\mathbf {I}+j\varepsilon y\mathbf {A}_1\right) \right] \\&\times \,\left[ j\varepsilon y\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {A}_1+\frac{\left( j\varepsilon y\right) ^2}{2}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {A}_2+j\varepsilon x\mathbf {\Lambda }\mathbf {S}\left( t\right) +j\varepsilon xj\varepsilon y\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {A}_1\right. \\&\qquad \;\;\, +\,\left. \frac{\left( j\varepsilon x\right) ^2}{2}\mathbf {\Lambda }\mathbf {S}\left( t\right) +\mathbf {Q}-j\varepsilon x\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {eI}-j\varepsilon y\mathbf {r}\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {eA}_1\right] , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \mathbf {A}_2=\text {diag}\{\alpha _k\},\quad \alpha _k = \int \limits _0^\infty y^2 dG_k(y). \end{aligned}$$

We then multiply both parts of the obtained equation by vector \(\mathbf {e}\). Due to (18), we can write

$$\begin{aligned} \begin{aligned}&\frac{\partial \varPhi _2\left( x,y,t\right) }{\partial t}=\varPhi _2\left( x,y,t\right) \left[ \frac{\left( jx\right) ^2}{2}\left[ \mathbf {r}+2\mathbf {g}\left( t\right) \left( \mathbf {I}-\mathbf {er}\right) \right] \mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {e}\right. \\&\qquad \qquad +\,\frac{\left( jy\right) ^2}{2}\left[ \mathbf {r}\mathbf {A}_2+2\mathbf {g}\left( t\right) \left( \mathbf {I}-\mathbf {er}\right) \mathbf {A}_1\mathbf {A}_1\right] \mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {e}\\&\qquad \qquad \;\;\;\; +\,\left. jxjy\left[ \mathbf {r}+2\mathbf {g}\left( t\right) \left( \mathbf {I}-\mathbf {er}\right) \right] \ \mathbf {A}_1\mathbf {\Lambda }\mathbf {S}\left( t\right) \mathbf {e}\right] . \end{aligned} \end{aligned}$$

Denoting

$$\begin{aligned} \begin{aligned}&\qquad K_{11}\left( t\right) {\mathop {=}\limits ^{\varDelta }}\int _{t_0}^{t}{\left[ \mathbf {r}+2\mathbf {g}\left( \tau \right) \left( \mathbf {I}-\mathbf {er}\right) \right] \mathbf {\Lambda }\mathbf {S}\left( \tau \right) \mathbf {e}d\tau },\\&K_{22}\left( t\right) {\mathop {=}\limits ^{\varDelta }}\int _{t_0}^{t}{\left[ \mathbf {r}\mathbf {A}_2+2\mathbf {g}\left( \tau \right) \left( \mathbf {I}-\mathbf {er}\right) \mathbf {A}_1\mathbf {A}_1\right] \mathbf {\Lambda }\mathbf {S}\left( \tau \right) \mathbf {e}d\tau },\\&\quad \;\, K_{12}\left( t\right) {\mathop {=}\limits ^{\varDelta }}\int _{t_0}^{t}{\left[ \mathbf {r}+2\mathbf {g}\left( \tau \right) \left( \mathbf {I}-\mathbf {er}\right) \right] \ \mathbf {A}_1\mathbf {\Lambda }\mathbf {S}\left( \tau \right) \mathbf {e}d\tau }, \end{aligned} \end{aligned}$$

we obtain the solution

$$\begin{aligned} \varPhi _2\left( x,y,t\right) =\exp {\left\{ \frac{\left( jx\right) ^2}{2}K_{11}\left( t\right) +\frac{\left( jy\right) ^2}{2}K_{22}\left( t\right) +jxjyK_{12}\left( t\right) \right\} }. \end{aligned}$$

Making substitution inverse to (16), (14) and (12), we obtain the second order approximation

$$\begin{aligned} \begin{aligned}&\mathbf {h}^{(2)}\left( u,v,t\right) \approx \mathbf {r}\exp \left\{ juNm_1\left( t\right) +jvNm_2\left( t\right) +\frac{\left( ju\right) ^2}{2}NK_{11}\left( t\right) \right. \\&\qquad \qquad \qquad \;\; +\,\left. \frac{\left( jv\right) ^2}{2}NK_{22}\left( t\right) +jujvNK_{12}\left( t\right) \right\} . \end{aligned} \end{aligned}$$

4.4 Main Result

Multiplying by vector \(\mathbf {e}\), we obtain the approximation of the characteristic function of stochastic process \(\{n(t),w(t)\}\)

$$\begin{aligned} h^{(2)}\left( u,v,t\right) =\mathbf {h}^{(2)}\left( u,v,t\right) \mathbf {e}, \end{aligned}$$

and going to steady-state regime, we put \(t=T\) and \(t_0\rightarrow -\infty \), using (1), we obtain the approximation for the characteristic function of process \(\{i(t),v(t)\}\)

$$\begin{aligned} h\left( u,v\right) \approx \exp {\left\{ juNm_1+jvNm_2+\frac{\left( ju\right) ^2}{2}NK_{11}+\frac{\left( jv\right) ^2}{2}NK_{22}+jujvNK_{12}\right\} }, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{c} m_1= \mathbf {r}\mathbf {\Lambda }\mathbf {Be},\quad m_2= \mathbf {r}\mathbf {\Lambda }{\mathbf {A}}_{1}\mathbf {Be},\\ K_{11}= \mathbf {r}\mathbf {\Lambda }\mathbf {B}\mathbf {e}+2\mathbf {r}\mathbf {\Lambda }\mathbf {B}\mathbf {G}\mathbf {\Lambda }\mathbf {e}-2\mathbf {r}\mathbf {\Lambda }(\mathbf {M}\circ \mathbf {G})\mathbf {\Lambda }\mathbf {e},\\ K_{22}= \mathbf {r}\mathbf {A}_2\mathbf {\Lambda }\mathbf {B}\mathbf {e}+2\mathbf {r}\mathbf {A}_1\mathbf {\Lambda }\mathbf {B}\mathbf {G}\mathbf {A}_1\mathbf {\Lambda }\mathbf {e}-2\mathbf {r}\mathbf {A}_1\mathbf {\Lambda }(\mathbf {M}\circ \mathbf {G})\mathbf {A}_1\mathbf {\Lambda }\mathbf {e},\\ K_{12}= \mathbf {r}\mathbf {A}_1\mathbf {\Lambda }\mathbf {B}\mathbf {e}+2\mathbf {r}\mathbf {A}_1\mathbf {\Lambda }\mathbf {B}\mathbf {G}\mathbf {\Lambda }\mathbf {e}-2\mathbf {r}\mathbf {A}_1\mathbf {\Lambda }(\mathbf {M}\circ \mathbf {G})\mathbf {\Lambda }\mathbf {e},\\ \mathbf {B}=\text {diag}\left\{ \int \limits _{0}^{\infty }\left( 1-B_k\left( \tau \right) \right) d\tau \right\} ,\\ \mathbf {M}=\left[ \int \limits _{0}^{\infty }\left( 1-B_k\left( \tau \right) \right) \left( 1-B_{k^{'}}\left( \tau \right) \right) d\tau \right] ,\quad k,k^{'}\in \{1,\ldots ,K\}. \end{array} \end{aligned}$$

Here notation \(\mathbf {X}\circ \mathbf {Y}\) means Hadamard (element-wise) product of matrices \(\mathbf {X}\) and \(\mathbf {Y}\).

Finally, the steady-state probability distribution of two-dimensional stochastic process \(\{i(t),v(t)\}\) can be approximated by the Gaussian distribution with means vector

$$\mathbf {m}=N\left[ m_1\quad m_2\right] $$

and covariance matrix

$$ \mathbf {K}=N\left[ \begin{array}{cc} K_{11} &{} K_{12} \\ K_{12} &{} K_{22} \end{array} \right] . $$

In particular, the stationary characteristic function of the distribution of the total amount of occupied resource v(t) can be approximated as follows:

$$\begin{aligned} h\left( v\right) \approx \exp {\left\{ jvNm_2+\frac{\left( jv\right) ^2}{2}NK_{22}\right\} }. \end{aligned}$$
(19)

So, this distribution can be approximated by the Gaussian one with mean \(Nm_2\) and variance \(NK_{22}\).

5 Numerical Example

Consider the following example. Let the random environment have three states \(\{1,2,3\}\) and be defined by the generator

$$ \widetilde{\mathbf {Q}}=N\cdot \left[ \begin{array}{ccc} -3 &{} 1 &{} 2 \\ 1 &{} -2 &{} 1 \\ 2 &{} 2 &{} -4 \end{array} \right] . $$

Let we have Poission arrivals with intensities

$$ \widetilde{\mathbf {\Lambda }}=N\cdot \text {diag}\{0.1;1;10\}. $$

Let service times have gamma distribution with the following shape and rate parameters:

$$\alpha _1=1.9,\ \beta _1=2; \quad \alpha _2=0.5,\ \beta _2 = 1; \quad \alpha _3=0.4,\ \beta _2 =3,$$

and resource requirements, also, have gamma distribution with parameters

$$\bar{\alpha }_1=\bar{\beta }_1=0.5; \quad \bar{\alpha }_2=\bar{\beta }_2 = 1.5; \quad \bar{\alpha }_3=\bar{\beta }_3 = 2.$$

Here indices mean the state of the random environment when the customer arrives.

Let us estimate the accuracy of obtained approximation (19) and find a lower bound of parameter N for the applicability of the proposed approximation. To do this, we carried out series of simulation experiments (in each of them \(10^{7}\) arrivals were generated) for increasing values of N and compared the asymptotic distributions with the empiric ones by using the Kolmogorov distance \(\varDelta = \sup \limits _x |F(x)-\tilde{F}(x)|\) as an accuracy measure. Here F(x) is the cumulative distribution function (CDF) built on the basis of simulation results, and \(\tilde{F}(x)\) is the CDF based on Gaussian approximation (19).

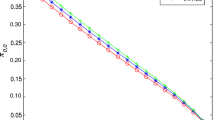
Table 1 presents the Kolmogorov distances between the asymptotic and empirical distribution functions of the total amount of resources occupied in the system. We see that the approximation accuracy increases with growing of parameter N, which is also illustrated by Fig. 4.

Table 1. Kolmogorov distances for the distribution of the total amount of occupied resource between ones basing on the approximation and the simulation results for various values of parameter N
Full size table
Fig. 4.
figure 4

Comparison of the approximation and simulation results for the distribution function of the total amount of occupied resource

Full size image

If we suppose that the error \(\varDelta \le 0.05\) is acceptable, we may conclude that the Gaussian approximation can be applicable for the cases \(N>15\).

6 Conclusion

In the paper, we have studied a resource queueing system \(M/GI/\infty \) operating in a random environment. We have considered the case when the service time and the occupied resource do not change for the customers already under service when the random environment state changes. We have applied the dynamic screening method and the asymptotic analysis method to find the approximation of the probability of the total amount of occupied resource. It has been obtained that this distribution can be approximated by Gaussian distribution under the condition of growing arrival rate and extremely frequent changes of the states of the random environment. The parameters of the corresponding Gaussian distribution have been obtained.