A Multi-Reservoir Echo State Network with Multiple-Size Input Time Slices for Nonlinear Time-Series Prediction

Abstract

A novel multi-reservoir echo state network incorporating the scheme of extracting features from multiple-size input time slices is proposed in this paper. The proposed model, Multi-size Input Time Slices Echo State Network (MITSESN), uses multiple reservoirs, each of which extracts features from each of the multiple input time slices of different sizes. We compare the prediction performances of MITSESN with those of the standard echo state network and the grouped echo state network on three benchmark nonlinear time-series datasets to show the effectiveness of our proposed model. Moreover, we analyze the richness of reservoir dynamics of all the tested models and find that our proposed model can generate temporal features with less linear redundancies under the same parameter settings, which provides an explanation about why our proposed model can outperform the other models to be compared on the nonlinear time-series prediction tasks.

1 Introduction

Nonlinear Time-series Prediction (NTP) [19] is one of the classical machine learning tasks. The goal of this task is to make predicted values close to the corresponding actual values. Recurrent Neural Networks (RNNs) [12] are a subset of Neural Networks (NNs) and have been widely used in nonlinear time-series prediction tasks. Many related works have reported that RNNs-based methods outperform other NNs-based methods on some prediction tasks [9, 13]. However, the classical RNN model and its extended models such as Long Short-Term Memory (LSTM) [5] and Gated Recurrent Unit (GRU) [1] often suffer from expensive computational costs along with gradient explosion/vanishing problems in the training process.

Reservoir Computing (RC) [6, 17] is an alternative computational framework which provides a remarkably efficient approach for training RNNs. The most important characteristic of this framework is that a predetermined non-linear system is used to map input data into a high-dimensional feature space. Based on this characteristic, a well-trained RNN can be built with relatively low computational costs.

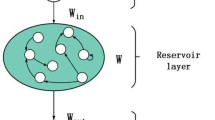
As one of the important implementations of RC, Echo State Network (ESN), was first proposed in Ref. [6] and has been widely used to handle NTP tasks [8, 14]. The standard architecture of ESN, including an input layer, a reservoir layer, and an output layer, is shown in Fig. 1(a). We can see that an input weight matrix, $\mathbf {W}_{in}$, represents the connection weights between the input layer and the reservoir layer. Moreover, a reservoir weight matrix denoted by $\mathbf {W}_{res}$ represents the connection weights between neurons inside the reservoir layer. The readout weight matrix, $\mathbf {W}_{out}$, represents the connection weights between the reservoir layer and the output layer. A feedback matrix from the output layer to the reservoir layer is denoted by $\mathbf {W}_{back}$. Typically, the element values of three matrices, $\mathbf {W}_{in}$, $\mathbf {W}_{res}$, and $\mathbf {W}_{back}$, are randomly drawn from certain uniform distributions and are kept fixed. Only $\mathbf {W}_{out}$ (dash lines) need to be trained by the linear regression.

Fig. 1.

(a) A standard ESN, (b) A standard GroupedESN.

Based on the above introduced ESN, we can quickly obtain a well-trained RNN. However, this simple architecture leads to a huge limitation in enhancing its representation ability and further makes the corresponding prediction performances on the NTP task hard to be improved. An effective remedy proposed in Ref. [4] is to feed the input time series into N independent randomly generated reservoirs for producing N different reservoir states, and then combine them to enrich the features used for training the output weight matrix. The authors of Ref. [4] called this architecture “GroupedESN" and reported that the prediction performances obtained by their proposed model is much better than those obtained by the standard ESN on some tasks. We show a schematic diagram of GroupedESN in Fig. 1(b).

The purpose of multi-reservoir ESN, including GroupedESN, inherited from the standard ESN is to extract features from each “data point" in a time series. In most of related works [4, 15], we found that they only used each sampling point in a time series as the “data point" and extracted the corresponding temporal feature from them in each reservoir. In fact, the scheme of extracting features from inseparable sampling points can capture the most fine-grained temporal dependency from the input series. However, this monotonous scheme unavoidably ignores some useful temporal information in the “time slices" composed of a period of continuous sampling points [20]. Figure 2 shows an example of transforming the original sampling points of a time series into several time slices of size two.

Fig. 2.

An example of transforming original sampling points of a time series into time slices of size two.

In this paper, we propose a novel multi-reservoir ESN model, Multi-size Input Time Slice Echo State Network (MITSESN), which can extract various temporal features corresponding to input time slices of different sizes. We compare the proposed model with the standard ESN and the GroupedESN on the three NTP benchmark datasets and demonstrate the effectiveness of our proposed MITSESN. We provide an empirical analysis of richness in the reservoir-state dynamics to explain why our proposed model performs better than the other tested models on the NTP tasks.

The rest of this paper is organized as follows: We describe the details of the proposed model in Sect. 2. We report the experimental results, including results on three NTP benchmark datasets and corresponding analyses of richness in Sect. 3. We conclude this work in Sect. 4.

2 The Proposed Model: MITSESN

A schematic diagram of our proposed MITSESN is shown in Fig. 3. This is a case where an original input time series with length four is fed into the proposed MITSESN with three independent reservoirs. The original input time series is transformed into three time slices of different sizes. Then, each time slice is fed into the corresponding reservoir and the generated reservoir states are concatenated together. Finally, the concatenated state matrix is decoded to the desired values. Based on the above introduction, we can observe that our proposed MITSESN can be divided into three parts: the series-to-slice transformer, the multi-reservoir encoder, and the decoder. We introduce the details of these parts as below.

Fig. 3.

An example of the proposed MITSESN with three independent reservoirs.

2.1 Series-to-Slice Transformer

We define the input vector and the target vector at time t as $\mathbf {u}(t)\in \mathbb {R}^{N_{U}}$ and $\mathbf {y}(t)\in \mathbb {R}^{N_{Y}}$, respectively. The length of input series and that of target series are denoted by $N_{T}$.

To formulate the transformation from the original input time-series points into input time slices of different sizes, we define the maximal size of the input slice used in the MITSESN as M. In our model, the maximal size of the input slice is equivalent to the number of different sizes. We denote the size of input slice by m, where $1\le m\le M$. In order to keep the length of the transformed input time slice the same as those of the original input time series, we add zero paddings of length $(m-1)$ into the beginning of the original input series, which can be formulated as follows:

$$\begin{aligned} \mathbf {U}^{m}_{zp} = \underbrace{[\mathbf {0},\ldots ,\mathbf {0}}_{m-1},\mathbf {u}(1),\mathbf {u}(2),\ldots ,\mathbf {u}(N_{T})], \end{aligned}$$

(1)

where $\mathbf {U}^{m}_{zp}\in \mathbb {R}^{N_{U}\times (N_{T}+m-1)}$ is the zero-padded input matrix. Based on the above settings, we can obtain the transformed input matrix corresponding to input time slices of size m as follows:

$$\begin{aligned} \mathbf {U}^{m} = \left[ \mathbf {u}^{m}(1), \mathbf {u}^{m}(2),\ldots , \mathbf {u}^{m}(N_{T}) \right] , \end{aligned}$$

(2)

where $\mathbf {U}^{m}\in \mathbb {R}^{mN_{U}\times N_{T}}$ and $\mathbf {u}^{m}(t)$ is composed of the vertical concatenation of vectors from the t-th column to the $(t+m-1)$-th column in $\mathbf {U}^{m}_{zp}$. We show an example of $\mathbf {U}^{m}$ when $m=3$ as follows:

$$\begin{aligned} \begin{aligned} \mathbf {U}^{3}&= \left[ \mathbf {u}^{3}\left( 1 \right) , \mathbf {u}^{3}\left( 2 \right) , \ldots , \mathbf {u}^{3}\left( N_{T} \right) \right] \\&=\begin{bmatrix} \mathbf {0}&{}\mathbf {0} &{}\ldots &{}\mathbf {u}\left( N_{T}-2 \right) \\ \mathbf {0}&{}\mathbf {u}\left( 1 \right) &{}\ldots &{}\mathbf {u}\left( N_{T}-1 \right) \\ \mathbf {u}\left( 1 \right) &{}\mathbf {u}\left( 2 \right) &{}\ldots &{}\mathbf {u}\left( N_{T} \right) \end{bmatrix} \end{aligned}. \end{aligned}$$

(3)

2.2 Multi-reservoir Encoder

We adopt the basic architecture of GroupedESN in Fig. 1(b) to build the multi-reservoir encoder. However, the feeding strategy of the multi-reservoir encoder is different from that of GroupedESN. We assume that input time slices of size m are fed into the m-th reservoir. Therefore, there are totally M reservoirs in the multi-reservoir encoder. For the m-th reservoir, we define the input weight matrix and the reservoir weight matrix as $\mathbf {W}^{m}_{in}\in \mathbb {R}^{N^{m}_{R}\times mN_{U}}$ and $\mathbf {W}^{m}_{res}\in \mathbb {R}^{N^{m}_{R}\times N^{m}_{R}}$, respectively, where $N^{m}_{R}$ represents the size of the m-th reservoir. The state of the m-th reservoir at time t, $\mathbf {x}^{m}(t)$, is calculated as follows:

$$\begin{aligned} \mathbf {x}^{m}(t) = \left( 1-\alpha \right) \mathbf {x}^{m}\left( t-1 \right) + \alpha \tanh \left( \mathbf {W}^{m}_{in}\mathbf {u}^{m}(t)+\mathbf {W}^{m}_{res}\mathbf {x}^{m}(t-1) \right) , \end{aligned}$$

(4)

where the element values of $\mathbf {W}^{m}_{in}$ are randomly drawn from the uniform distribution of the range $\left[ -\theta , \theta \right]$. The parameter $\theta$ is the input scaling. The element values of $\mathbf {W}^{m}_{res}$ are randomly chosen from the uniform distribution of the range $\left[ -1, 1 \right]$. To ensure the “Echo State Property" (ESP) [6], $\mathbf {W}^{m}_{res}$ should satisfy the condition described as follows:

$$\begin{aligned} \rho \left( \left( 1-\alpha \right) \mathbf {E}+\alpha \mathbf {W}_{res}^{m}\right) <1, \end{aligned}$$

(5)

where $\rho \left( \cdot \right)$ denotes the spectral radius of a matrix argument, the parameter $\alpha$ represents the leaking rate which is set in the range $\left( 0,1 \right]$, and $\mathbf {E} \in \mathbb {R}^{N^{m}_{R}\times N^{m}_{R}}$ is the identity matrix. Moreover, we use the parameter $\eta$ to denote the sparsity of $\mathbf {W}^{m}_{res}$.

We denote the reservoir-state matrix composed of $N_{T}$ state vectors corresponding to the m-th reservoir as $\mathbf {X}^{m} \in \mathbb {R}^{N^{m}_{R} \times N_{T}}$. By concatenating M reservoir-state matrices in the vertical direction, we obtain a concatenated state matrix, $\mathbf {X}\in \mathbb {R}^{ \sum _{m=1}^{M} N^{m}_{R}\times N_{T} }$, which can be written as follows:

$$\begin{aligned} \mathbf {X} = \left[ \mathbf {X}^{1}; \mathbf {X}^{2};\ldots ; \mathbf {X}^{M} \right] . \end{aligned}$$

(6)

2.3 Decoder

We use the linear regression for converting the concatenated state matrix into the output matrix, which can be formulated as follows:

$$\begin{aligned} \mathbf {\hat{Y}}=\mathbf {W}_{out}\mathbf {X}, \end{aligned}$$

(7)

where $\mathbf {\hat{Y}}\in \mathbb {R}^{N_{Y}\times N_{T}}$ is the output matrix. The readout matrix $\mathbf {W}_{out}$ is given by the closed-form solution as follows:

$$\begin{aligned} \mathbf {W}_{out} = \mathbf {Y}\mathbf {X}^\mathrm {T}\left( \mathbf {X}\mathbf {X}^\mathrm {T}+\lambda \mathbf {I} \right) ^{-1}, \end{aligned}$$

(8)

where $\mathbf {Y}\in \mathbb {R}^{N_{Y}\times N_{T}}$ represents the target matrix, $\mathbf {I}\in \mathbb {R}^{\sum _{m=1}^{M} N^{m}_{R}\times \sum _{m=1}^{M} N^{m}_{R}}$ is an identity matrix, and the parameter $\lambda$ symbolizes the Tikhonov regularization factor [18].

3 Numerical Simulations

In this section, we report the details and results of simulations. Specifically, three benchmark nonlinear time-series datasets and the corresponding task settings are described in Sec. 3.1, the evaluation metrics are listed in Sec. 3.2, the tested models and parameter settings are described in Sec. 3.3, the corresponding simulation results are presented in Sec. 3.4. The analyses of richness for all the tested models are given in Sec. 3.5.

3.1 Datasets Descriptions and Task Settings

We leverage three nonlinear time-series datasets, including the Lorenz system, MGS-17, and KU Leuven datasets, to evaluate the prediction performances of our proposed model. Glimpses of the above datasets are shown in Fig. 4. The partitions of the training set, the validation set, the testing set, and the initial transient set are listed in Table 1. We introduce the details of these datasets and task settings as below.

Lorenz System. The equation of Lorenz system [10] is formulated as follows:

$$\begin{aligned} \begin{aligned}&\frac{\mathrm {d} x}{\mathrm {d} t}=\sigma (y-x), \\&\frac{\mathrm {d} y}{\mathrm {d} t}=x(\delta -z)-y, \\&\frac{\mathrm {d} z}{\mathrm {d} t}=x y-\beta z. \end{aligned} \end{aligned}$$

(9)

When $\delta = 28$, $\sigma =10$, and $\beta =8/3$, the system exhibits a chaotic behavior. In our evaluation, we used the chaotic Lorenz system and set the initial condition at $\left( x\left( 0 \right) , y\left( 0 \right) ,z\left( 0 \right) \right) = \left( 12,2,9 \right)$. We adopted the sampling interval $\varDelta t = 0.02$ and rescaled by the scaling factor 0.1, which is the same as those reported in [7]. We set a six-step-ahead prediction task on x values, which can be represented as $\mathbf {u}(t) = x(t)$ and $\mathbf {y}(t) = x(t+6)$.

MGS-17. The equation of Mackey-Glass system [11] is formulated as follows:

$$\begin{aligned} z(t+1)=z(t)+\delta \cdot \left( a \frac{z(t-\varphi / \delta )}{1+z(t-\varphi / \delta )^{n}}-b z(t)\right) , \end{aligned}$$

(10)

where a, b, n, and $\delta$ are fixed at 0.2, $-0.1$, 10, and 0.1, respectively. The Mackey-Glass system exhibits a chaotic behavior when $\varphi >16.8$. We kept the value of $\varphi$ equal to 17 (MGS-17). The task on MGS-17 is to predict the 84-step-ahead value of z [7], which can be represented as $\mathbf {u}(t) = z(t)$ and $\mathbf {y}(t) = z(t+84)$.

KU Leuven. KU Leuven dataset was first proposed in a time-series prediction competition held at KU Leuven, Belgium [16]. We set an one-step-ahead prediction task on this dataset for the evaluation.

Fig. 4.

Examples of three nonlinear time-series datasets.

Table 1. The partitions of Lorenz system, MGS-17, and KU Leuven datasets.

3.2 Evaluation Metrics

We use two evaluation metrics in this work, including Normalized Root Mean Square Error (NRMSE) and Symmetric Mean Absolute Percentage Error (SMAPE), to evaluate the prediction performances. These two evaluation metrics are formulated as follows:

$$\begin{aligned} {\text {NRMSE}}=\frac{\sqrt{\frac{1}{N_{T}} \sum _{t=1}^{N_{T}}\left( \mathbf { \hat{y} }(t)- \mathbf {y}(t)\right) ^{2}}}{\sqrt{\frac{1}{N_{T}}\sum _{t = 1}^{N_{T}}\left( \mathbf {y}\left( t \right) -\bar{\mathbf {y}} \right) ^2}}, \end{aligned}$$

(11)

$$\begin{aligned} \mathrm {SMAPE}=\frac{1}{N_{T}} \sum _{t=1}^{N_{T}} \frac{\left| \hat{\mathbf {y}}(t)-\mathbf {y}(t)\right| }{\left( \left| \hat{\mathbf {y}}(t)\right| +\left| \mathbf {y}(t)\right| \right) / 2}, \end{aligned}$$

(12)

where $\bar{\mathbf {y}}$ denotes the mean of data values of $\mathbf {y}(t)$ from $t=1$ to $N_{T}$.

3.3 Tested Models and Parameter Settings

In our simulation, we compared the prediction performances of our proposed model with those of ESN and GroupedESN. We denote the overall reservoir size $N_{R} = \sum _{m=1}^{M} N^{m}_{R}$ for all the models. Two architectures with $M=2$ and $M=3$ for GroupedESN and MITSESN were considered. We represent the architecture with M reservoirs as $N^{1}_{R}-N^{2}_{R}-\cdots -N^{M}_{R}$.

To make a fair comparison, we set $N_{R}$ the same for each model. For simplicity, the size of each reservoir in the GroupedESN and the proposed MITSESN was kept the same. The parameter settings for all the tested models are listed in Table 2. The spectral radius, the sparsity of reservoir weights, and the Tikhonov regularization were set at 0.95, 90%, and 1E-06, respectively. The input scaling, the leaking rate and the overall reservoir size were searched in the ranges of [0.01, 0.1, 1], $\left[ 0.1,0.2,\ldots ,1 \right]$, and $\left[ 150,300,\ldots ,900 \right]$, respectively. For each setting, we averaged the results over 20 realizations.

Table 2. The parameter settings for all the tested models

3.4 Simulation Results

We report the averaged prediction performances on the three datasets in Tables 3, 4 and 5. It is obvious that our proposed MITSESN with three reservoirs obtains the smallest NRMSE and SMAPE among all the tested models with the same overall reservoir size. By comparing the prediction performances of the GroupedESN with those of our proposed MITSESN, we can clearly find that the strategy of extracting temporal features from multi-size input time slices can significantly improve the prediction performances. Moreover, with the increase of the size of input time slices, the performance is obviously improved. Especially, our simulation results on MGS-17 show that only adding more reservoirs is not a universally effective method to improve prediction performances for the GroupedESN. Lastly, we observe that the best prediction performances of all the tested models are obtained under the maximal values in the searching range of input scaling and reservoir size, which indicates that all the models benefit from high richness [3]. We investigate how this important characteristic changes under different $N_{R}$ for all the tested models in the following section.

Table 3. Average performances of the six-step-ahead prediction task on the Lorenz system.

Table 4. Average performances of the 84-step-ahead prediction task on the MGS-17.

3.5 Analysis of Richness

The richness is a desirable characteristic in the reservoir state as suggested by Ref. [2]. Typically the higher richness indicates the less redundancy held in the reservoir state. We leverage the Uncoupled Dynamics (UD) proposed in [3] to measure the richness of $\mathbf {X}$ for all the tested models. The UD of $\mathbf {X}$ is calculated as follows:

$$\begin{aligned} \underset{d}{\arg \min }\left\{ \sum _{k=1}^{d} R_{k} \mid \sum _{k=1}^{d} R_{k} \ge \mathcal {A}\right\} , \end{aligned}$$

(13)

where $\mathcal {A}$ is in the range of $\left( 0,1 \right]$ and represents the desired ratio of explained variability in the concatenated state matrix. We kept $\mathcal {A}=0.9$ in the following evaluation. $R_{k}$ denotes the normalized relevance of the i-th principal component, which can be formulated as follows:

$$\begin{aligned} R_{i}=\frac{\sigma _{i}}{\sum _{j=1}^{N_{R}} \sigma _{j}}, \end{aligned}$$

(14)

where $\sigma _{i}$ denotes the i-th singular value in the decreasing order. The higher the value of UD in Eq. (13) is, the less linear redundancy held in the concatenated state matrix $\mathbf {X}$ is. For the evaluation settings, we used a univariable time series of length 5000 and we randomly chose each value from the uniform distribution of the range $[-0.8,0.8]$. We fixed the leaking rate $\alpha =1$ and input scaling $\theta =1$ in all the models.

Table 5. Average performances of the one-step-ahead prediction task on the KU Leuven dataset.

The average UDs of all the tested models when varying $N_{R}$ from 150 to 900 are shown in Fig. 5. It is obvious that the MITSESN (M=3) outperforms the other models when varying $N_{R}$ from 300 to 900. With the increase of $N_{R}$ (from $N_{R}=450$), differences between UDs of our proposed MITSESN with those of ESN and GroupedESNs $(M=2$ and 3) gradually become larger and larger, which indicates that our proposed MITSESN can generate less linear redundancy in the concatenated state matrix than the ESN and the GroupedESN under the case of the larger $N_{R}$. Moreover, we find that the larger size of input time slices is, the less linear redundancy in the concatenated state matrix of MITSESN is. The above analyses explain the reasons why our proposed MITSESN outperforms the ESN and the GroupedESNs, and the MITSESN ($M=3$) has the best performances on the three prediction tasks.

Fig. 5.

UDs of all the tested models varying $N_{R}$ from 150 to 900.

4 Conclusion

In this paper, we proposed a novel multi-reservoir echo state network, MITSESN, for nonlinear time-series prediction tasks. Our proposed MITSESN can extract various temporal features from multi-size input time slices. The prediction performances on three benchmark nonlinear time-series datasets empirically demonstrate the effectiveness of our proposed model. We provided an empirical analysis from the prospective of reservoir-state richness to show the superiority of MITSESN.

As future works, we will continue to evaluate the performances of the proposed model on the other temporal tasks such as time series classification tasks.