Weighted P-Rank: a Weighted Article Ranking Algorithm Based on a Heterogeneous Scholarly Network

Abstract

The evaluation and ranking of scientific article have always been a very challenging task because of the dynamic change of citation networks. Over the past decades, plenty of studies have been conducted on this topic. However, most of the current methods do not consider the link weightings between different networks, which might lead to biased article ranking results. To tackle this issue, we develop a weighted P-Rank algorithm based on a heterogeneous scholarly network for article ranking evaluation. In this study, the corresponding link weightings in heterogeneous scholarly network can be updated by calculating citation relevance, authors’ contribution, and journals’ impact. To further boost the performance, we also employ the time information of each article as a personalized PageRank vector to balance the bias to earlier publications in the dynamic citation network. The experiments are conducted on three public datasets (arXiv, Cora, and MAG). The experimental results demonstrated that weighted P-Rank algorithm significantly outperforms other ranking algorithms on arXiv and MAG datasets, while it achieves competitive performance on Cora dataset. Under different network configuration conditions, it can be found that the best ranking result can be obtained by jointly utilizing all kinds of weighted information.

This study was funded by National Natural Science Foundation of Peoples Republic of China(61672130, 61972064). The Fundamental Rearch Funds for the Central Universities(DUT19RC(3)01) and LiaoNing Revitalization Talents Program(XLYC1806006). The Fundamental Research Funds for the Central Universities, No. DUT20RC(5)010.

1 Introduction

Academic impact assessment and ranking have always been a hot issue, which plays an important role in the process of the dissemination and development of academic research [1,2,3]. However, it is difficult to assess the real quality of academic articles due to the dynamic change of citation networks [4]. Furthermore, the evaluation result will be heavily influenced by utilizing different bibliometrics indicators or ranking methods [5]. As a traditional ranking method, PageRank [6] algorithm has already been widely and effectively used in various ranking tasks. Liu et al. [7], for instance, employed the PageRank algorithm to evaluate the academic influence of scientists in the co-authorship network. In [8], Bollen et al. utilized a weighted version of the PageRank to improve the calculation methodology of JIF. It is worth remarking that the vast majority of ranking algorithms such as PageRank and its variants deem the article (node) creation as a static citation network. In the real citation network, however, articles are published and cited in time sequence. Such approaches do not consider the dynamic nature of the network and are always biased to old publications. Therefore, the recent articles tend to be underestimated due to the lack of enough citations. To address this issue, Sayyadi and Getoor proposed a timeaware method, FutureRank [4], which calculates the future PageRank score of each article by jointly employing citation network, authorship network, and time information. In comparison to the other methods without time weight, FutureRank is practical and ranks academic articles more accurately. Furthermore, Walker et al. proposed a ranking model called CiteRank [9], which utilizes a simple network traffic model and calculates the future citations of each article by considering the publication time of articles. However, a main problem of the network traffic model is that it does not reveal the mechanism of how the article scores change. Moreover, although PageRank algorithm is advanced at exploring the global structure of the citation network, it neglects certain local factors that may influence the ranking results.

This paper aims to develop a weighted P-Rank algorithm based on a heterogeneous scholarly network and explore how the changes of the link weightings between different subnetworks influence the ranking result. To further boost the performance of weighted P-Rank algorithm, we utilize the time information of each article as a personalized PageRank vector to balance the bias to earlier publications in the dynamic citation network. The key contributions of this work can be summarized as follows:

• A weighted article ranking method based on P-Rank algorithm and heterogeneous graph is developed.

• The weighted P-Rank algorithm considers the influence of citation revelance, authors’ contribution, journals’ impact, and time information to the article ranking method comprehensively.

• We evaluate the performance of weighted P-Rank method under different conditions by manipulating the corresponding parameters that can be used to structure graph configurations and time settings.

• By introducing the corresponding link weightings in each heterogeneous graph, the performance of the weighted P-Rank algorithm significantly outperforms the original P-Rank algorithm on three public datasets.

2 Article Ranking Model

In this section, we introduce the proposed article ranking algorithm in detail. Specificially, we first define and describe a heterogeneous scholarly network that is composed of author layer, paper layer and journal layer, and how the different elements in the three layers are linked and interacted. Furthermore, a link weighting method based on P-Rank algorithm is developed to compute the article score in the heterogeneous scholarly network.

2.1 Heterogeneous Scholarly Network

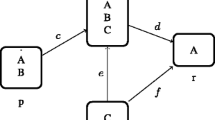
A complete heterogeneous scholarly network consists of three subnetworks (i.e., author network, paper citation network, and journal network). There exist three types of edges in the network i.e., undirected edge between the authors and the papers, directed citation edge between the original paper and its citing papers, and undirected edge between the papers and the published journals. As stated in [10], the heterogeneous scholarly graph of papers, authors, and journals can be expressed as the following form:

$$\begin{aligned} G(V,E) = ({V_P} \cup {V_A} \cup {V_J},{E_P} \cup {E_{PA}} \cup {E_{PJ}}) \end{aligned}$$

(1)

where $V_P$, $V_A$, and $V_J$ are the paper nodes, author nodes, and journal nodes in the three layers respectively. $E_P$ denotes the citation link in the paper layer, $E_{PA}$ denotes the link between paper and author, and $E_{PJ}$ denotes the link between paper and journal.

Fig. 1.

Visualization of a heterogeneous scholarly network

As shown in Fig. 1a, the paper-author network and paper-journal network are two undirected graphs which can be represented as ${G_{PA}} = ({V_P} \cup {V_A},{E_{PA}})$ and ${G_{PJ}} = ({V_P} \cup {V_J},{E_{PJ}})$, respectively. In Fig. 1b, by contrast, the paper citation network is a directed graph ${G_{P}} = ({V_P},{E_{P}})$, the arrows point in the direction of paper citation: ${P_4} \rightarrow {P_5}$ means ${P_4}$ cites ${P_5}$. In this work, we assign link weights to the corresponding subnetworks such that the three unweighted graphs can be updated as ${G_{P}} = ({V_P},{E_{P}},{W_{P}})$, ${G_{PA}} = ({V_P} \cup {V_A},{E_{PA}}, {W_{PA}})$, and ${G_{PJ}} = ({V_P} \cup {V_J},{E_{PJ}}, {W_{PJ}})$, in which ${W_{P}}$, ${W_{PA}}$, and ${W_{PJ}}$ refer to the link weight in the three graphs, respectively. With link weightings (${W_{P}}$, ${W_{PA}}$, and ${W_{PJ}}$) defined in the corresponding ${G_{P}}$, ${G_{PA}}$, and ${G_{PJ}}$, the unweighted heterogeneous scholarly graph G(V, E) becomes

$$\begin{aligned} G(V,E,W) = ({V_P} \cup {V_A} \cup {V_J},{E_P} \cup {E_{PA}} \cup {E_{PJ}},{W_P} \cup {W_{PA}} \cup {W_{PJ}}) \end{aligned}$$

(2)

2.2 Link Weighting in Paper Citation Graph (${G_{P}}$)

In this study, we develop a link weighting to assign weight in the paper citation graph (${G_{P}}$) based on the citation relevance between two papers, which can be utilized to improve the reasonability of the article ranking. To be specific, the citation relevance (link weighting) between two different papers is mainly influenced by two factors, namely, text similarity (semantic-based) and citation network structure (structure-based). Supposing that the citation relevance between two papers is higher if the two papers are more likely to be similar in semantic and share mutual links and common nodes in the citation network.

In our work, the “slide” weighted overlap approach improved by ADW [11] is employed, which can be used to compute the semantic similarity between the abstracts $T_i$ and $T_j$ from papers i and j. Let S be the intersection of overlapping senses with non-zero probability in both signatures and $r_i^j$ be the rank of sense ${s_i} \in S$ in signature j, where rank 1 represents the highest rank. The slide overlap $\mathrm{Similarit}\mathrm{y}_{1}(P_{i},P_{j})$ can be computed using:

$$\begin{aligned} \mathrm{Similarity}_{1}({P_i},{P_j}) = \mathrm{tanh}\left( \frac{\alpha \cdot \sum \nolimits _{i = 1}^{\left| S \right| } e^{{({r_i^1} + {r_i^2})}^{- 1}}}{\beta \cdot \sum \nolimits _{i = 1}^{\left| S \right| } e^{{(2i)^{- 1}}}} \right) \end{aligned}$$

(3)

where $\tanh ( \cdot )$ is hyperbolic tangent function, and $\sum \nolimits _{i = 1}^{\left| S \right| } (2i)^{ - 1}$ is the maximum value to bound the similarity distributed over the interval [0,1]. Note that the maximum value would occur when each sense has the same rank in both signatures. Moreover, we normalize parameters $\alpha$ and $\beta$ such that $\alpha +\beta = 1$.

In this work, we employ cosine similarity to measure the citation relevance of two papers in terms of network structure. The cosine similarity between two paper nodes in the citation network can be calculated by:

$$\begin{aligned} \mathrm{Similarity}_{2}({P_i},{P_j}) = \cos ({P_i},{P_j}) = \frac{{\left| {{N_{{P_i}}} \cap {N_{{P_j}}}} \right| }}{{\sqrt{\left| {{N_{{P_i}}}} \right| \times \left| {{N_{{P_j}}}} \right| } }} \end{aligned}$$

(4)

where $N_{{P_i}}$ denotes the neighborhood of node $P_i$, and $\left| {{N_{{P_i}}} \cap {N_{{P_j}}}} \right|$ denotes the number of nodes that link to both $P_i$ and $P_j$.

Based on the $\mathrm{Similarity_1}$ (semantic-based) and $\mathrm{Similarity_2}$ (structure-based), the link weight between two paper nodes in the paper citation graph (${G_{P}}$) can be represented as follows:

$$\begin{aligned} {W_{i,j}} = {\lambda _1} \cdot {\mathrm{Similarit}}{{\mathrm{y}}_1}({P_{{i}}},{P_{{j}}}) + {\lambda _2} \cdot \mathrm{Similarity}_{2}({P_i},{P_j}) \end{aligned}$$

(5)

where $W_{i,j}$ is the weight from paper i to paper j in ${G_{P}}$, $\mathrm{Similarity}_1$ and $\mathrm{Similarity}_2$ are the semantic-based and structure-based similarities between two papers respectively. Parameters $\lambda _1$ and $\lambda _2$ are two corresponding coefficients, which can be defined as the following form:

$$\begin{aligned} {\lambda _{\mathrm{1}}} = {e^{\mu [{\mathrm{Similarity}}_{1}({P_i},{P_j}) - {\varepsilon _1}]}} \end{aligned}$$

(6)

$$\begin{aligned} {\lambda _{\mathrm{2}}} = {e^{\mu [{\mathrm{Similarity}}_{2}({P_i},{P_j}) - {\varepsilon _2}]}} \end{aligned}$$

(7)

with $\mu$ being a parameter shaping the exponential function, and $\varepsilon _1$ and $\varepsilon _2$ being the media values of $\mathrm{Similarity_1}$ and $\mathrm{Similarity_2}$ respectively. Here let $\mu =6$ so that those similarity values that exceed the threshold can be constrained by the exponential curve. Parameters $\lambda _1$ and $\lambda _2$ are normalized as ${\lambda _1} + {\lambda _2} = 1$.

For a ${G_{P}}$ with n papers, the adjacency matrix of the citation network can be denoted as an $n \times n$ matrix, where the link weight between two paper nodes can be calculated by:

$$\begin{aligned} {M_{i,j}} = \left\{ \begin{array}{ll} W_{i,j}&{}\quad \mathrm{if\;paper}\;i\;\mathrm{cites\;paper}\;j \\ 0&{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

(8)

Let $\overline{M}$ be the fractionalized citation matrix where ${\overline{M} _{i,j}} = \frac{{{M_{i,j}}}}{{\sum \nolimits _{i = 1}^n {{M_{i,j}}} }}$. Let e be the n-dimensional vector whose elements are all 1 and v be an n-dimensional vector which can be viewed as a personalized vector [12]. Next let $x{(v)_{{\mathrm{paper}}}}$ denote the PageRank vector corresponding to the vector $x{(v)_{{\mathrm{paper}}}}$, and x(v) can be calculated from $x = \overline{\overline{M}} x$ where $\overline{\overline{M}} = d\overline{M} + (1 - d)v{e^T}$. Thus, PageRank vector x can be computed using:

$$\begin{aligned} x{(v)_{{\mathrm{paper}}}} = (1 - d){(I - d\overline{M} )^{ - 1}}v \end{aligned}$$

(9)

where d (set at 0.85) is a damping factor. Let $Q = (1 - d){(I - d\overline{M} )^{ - 1}}$, then $x = Qv$. For any given v, PageRank vector x(v) can be obtained from Qv.

2.3 Link Weighting in Paper-Author Graph (${G_{PA}}$)

In the paper-author graph (${G_{PA}}$), let $P{\mathrm{= }}\left\{ {{p_1},{p_2},...,{p_n}} \right\}$ denote the set of n papers and $A{\mathrm{= }}\left\{ {{a_1},{a_2},...,{a_m}} \right\}$ denote the set of m authors, then ${G_{PA}}$ can be represented as an $n \times m$ adjacency matrix, where the link weight ${A_{author\;i,j}}$ from author j to paper i is:

$$\begin{aligned} A_{\mathrm{author}}\;(i,j) = \left\{ \begin{array}{ll} 1&{}\quad \mathrm{if}\;\mathrm{author}\;j\;\mathrm{writes}\;\mathrm{paper}\;i\\ 0&{}\quad \mathrm{otherwise} \end{array}\right. \end{aligned}$$

(10)

In this study, the link weights in ${G_{PA}}$ can be deemed as the level of authors’ contributions to their articles. Modified Raw Weight ($W_{R,j}$) [13] is adopted to assess the authors’ contributions according to the relative rankings of authors in co-authored publications. For the author of rank j the Modified Raw Weight is:

$$\begin{aligned} {W_{R,j}} = \frac{{n - \frac{j}{{\mathrm{2}}} + 1}}{{\sum \nolimits _{j = 1}^{n} {{n_j}} }} = \frac{{2n - j + 2}}{{n \cdot (n + 1)}} \cdot \frac{2}{3} \end{aligned}$$

(11)

where $W_{R,j}$ is the Modified Raw Weight of author j, j is the position of author j in the author list, n is the total number of authors in the paper, and ${\sum \nolimits _{j = 1}^{n} {{n_j}} }$ is the sum of author positions. Hence, the unweighted ${G_{PA}}$ can be updated by:

$$\begin{aligned} A_{\mathrm{author}}\;(i,j)= \left\{ \begin{array}{ll} W_{R,j}&{}\quad \mathrm{if}\;\mathrm{author}\;j\;\mathrm{writes}\;\mathrm{paper}\;i\\ 0&{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

(12)

2.4 Link Weighting in Paper-Journal Graph (${G_{PJ}}$)

In the initial P-Rank algorithm, the paper-journal graph (${G_{PJ}}$) can be represented as an $n \times q$ adjacency matrix, where n and q are the number of papers and journals, respectively:

$$\begin{aligned} A_{\mathrm{journal}}\;(i,j) = \left\{ \begin{array}{ll} 1&{}\quad \mathrm{if}\;\mathrm{paper}\;i\;\mathrm{is}\;\mathrm{published}\;\mathrm{on}\;\mathrm{journal}\;j\\ 0&{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

(13)

Here we develop a weighted ${G_{PJ}}$ in which the corresponding link weight can be updated by the journal impact factors [14, 15]. Similar to ${G_{PA}}$, the link weights in ${G_{PJ}}$ can be regarded as the level of journals’ impact to the published articles. Here, the “mapminmax” function defined in MATLAB R2018b version is used to normalize the JIF list, the range distributed over the interval [0.1,1]. The formula 13 can thus be rewritten as below:

$$\begin{aligned} A_{\mathrm{journal}}\;(i,j) = \left\{ \begin{array}{ll} \mathrm{Normalize[JIF}_{j}\mathrm{]}&{}\quad \mathrm{if}\;\mathrm{paper}\;i\;\mathrm{is}\;\mathrm{published}\;\mathrm{on}\;j\\ 0&{}\qquad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

(14)

2.5 Weighted P-Rank Algorithm

The weighted P-Rank score of papers can be expressed as $x{(v)_{\mathrm{paper}}}$ in Eq. 9, where the personalized vector is

$$\begin{aligned} v = {({\varphi _1}({(\frac{{x{{(v)}_{{\mathrm{author}}}}}}{{{n_{{\mathrm{p\_author}}}}}})^T} \times A_{{\mathrm{author}}}^T) + {\varphi _2}({(\frac{{x{{(v)}_{{\mathrm{journal}}}}}}{{{n_{{\mathrm{p\_journal}}}}}})^T} \times A_{{\mathrm{journal}}}^T))^T} \end{aligned}$$

(15)

where $\;{n_{\mathrm{{p_ - }author}}}$ represents a vector with the number of publications for each author, and $\;{n_{\mathrm{{p_ - }journal}}}$ represents a vector with the number of publications for each journal. The mutual dependence (intra-class and inter-class walks) of papers, authors, and journals is coupled by the parameters $\varphi _{\mathrm{1}}$ and $\varphi _{\mathrm{2}}$, which are set at 0.5 as default. The weighted P-Rank scores of author and journal can be expressed as:

$$\begin{aligned} x{(v)_{{\mathrm{author}}}} = A_{{\mathrm{author}}}^T \times x{(v)_{{\mathrm{paper}}}} \end{aligned}$$

(16)

$$\begin{aligned} x{(v)_{{\mathrm{journal}}}} = A_{{\mathrm{journal}}}^T \times x{(v)_{{\mathrm{paper}}}} \end{aligned}$$

(17)

In this study, we adopt a time weight $T{_i}$ to eliminate the bias to earlier publications, which can be regarded as a personalized PageRank vector. Here according to the time-aware method proposed in FutureRank [4], the function $T{_i}$ is defined as:

$$\begin{aligned} T{_i} = {e^{ - \rho \times ({T_{\mathrm{current}}} - {T_{\mathrm{publish}}})}} \end{aligned}$$

(18)

where $T_{\mathrm{publish}}$ denotes the publication time of paper i, and ${T_{\mathrm{current}}} - {T_{\mathrm{publish}}}$ denotes the number of years since the paper i was published. $\rho$ is a constant value set to be 0.62 based on FutureRank [4]. The sum of $T{_i}$ for all the articles is normalized to 1.

Taken together, the weighted P-Rank score of a paper can be calculated by:

$$\begin{aligned} x{(v)_{\mathrm{paper}}} = \gamma \cdot Pagerank(\overline{M} ,v) + \delta \cdot T + (1 - \gamma - \delta ) \cdot \frac{1}{{n_p}} \end{aligned}$$

(19)

with parameters $\gamma$ and $\delta$ being constants of the algorithm. $(1 - \gamma - \delta ) \cdot \frac{1}{{n_p}}$ represents the probability of random jump, where ${{n_p}}$ is the number of paper samples.

In the proposed algorithm, the initial score of each paper is set to be $\frac{1}{{n_p}}$. For articles which do not cite any other papers, we suppose that they hold links to all the other papers. Hence, the sum of $x{(v)_{\mathrm{paper}}}$ for all the papers will keep to be 1 in each iteration. The steps above are recursively conducted until convergence (threshold is set at 0.0001). The pseudocode of the weighted P-Rank algorithm is given in Algorithm 1.

3 Experiments

3.1 Datasets and Experimental Settings

Three public datasets are used in this study, i.e. arXiv (hep-th), Cora, and MAG. The summary statistics of three datasets are listed in Table 1. It is worth remarking that the ${A_{\mathrm{journal}}}$ values of all conference articles were sampled from the average JIF of all journals calculated in the corresponding dataset.

Table 1. The datasets utilized in experiments

All experiments are conducted on a computer with 3.30 GHz Intel i9-7900X processor and 64 GB RAM under Linux 4.15.0 operating system. The program codes of data preprocessing and graphs modeling are written by Python 3.6.9, which is available on https://github.com/pjzj/Weighted-P-Rank.

3.2 Evaluation Metrics

Spearman’s Rank Correlation

In this paper, Spearman’s rank correlation coefficient is used to assess the performance of proposed algorithm under different conditions. For a dataset $\mathbf{{X}} = [{\mathbf{{x}}_1},{\mathbf{{x}}_2},...,{\mathbf{{x}}_N}] \in {\mathbb {R}^{D \times N}}$ with N samples, N original data are converted into grade data, and the correlation coefficient $\rho$ can be calculated by:

$$\begin{aligned} \rho = \frac{{\sum \limits _{i = 1}^n {({R_1}({P_i}) - {{\overline{R} }_1})({R_2}({P_i}) - {{\overline{R} }_2})} }}{{\sqrt{\sum \limits _{i = 1}^n {{{({R_1}({P_i}) - {{\overline{R} }_1})}^2}} \sum \limits _{i = 1}^n {{{({R_2}({P_i}) - {{\overline{R} }_2})}^2}} } }} \end{aligned}$$

(20)

where ${R_1}({P_i})$ denotes the position of paper $P_i$ in the first rank list, ${R_2}({P_i})$ denotes the position of paper $P_i$ in the second rank list, and ${{\overline{R} }_1}$ and ${{\overline{R} }_2}$ denote the average rank positions of all papers in the two rank lists respectively.

Robustness

Here according to the corresponding historical time point on three datasets, the whole time on each dataset can be divided into two periods. The time period before the historical time point can be denoted as ${T_{1}}$, while the whole period can be denoted as ${T_{2}}$. The robustness of algorithm can thus be measured by calculating the correlation of ranking scores in ${T_{1}}$ and ${T_{2}}$.

3.3 Experimental Results

Graph Configurations

Two parameters can be set in graph configurations: $\varphi _{\mathrm{1}}$ and $\varphi _{\mathrm{2}}$. By using various combinations of graphs, we compare and assess four different cases of P-Rank algorithm with previous works. The cases and the associated parameters are listed below:

• ${G_{P}}$ ($\varphi _{\mathrm{1}}=0$, $\varphi _{\mathrm{2}}=0$): which is the traditional PageRank algorithm for rank calculation.

• ${G_{P}}$ + ${G_{PA}}$ (${\varphi _1} = 1$, ${\varphi _2} = 0$): A new graph (${G_{PA}}$) is introduced into the heterogeneous network which only utilizes citation and authorship.

• ${G_{P}}$ + ${G_{PJ}}$ (${\varphi _1} = 0$, ${\varphi _2} = 1$): A new graph (${G_{PJ}}$) is introduced into the heterogeneous network which only utilizes citation and journal information.

• ${G_{P}}$ + ${G_{PA}}$ + ${G_{PJ}}$ (${\varphi _1} = 0.5$, ${\varphi _2} = 0.5$): Two new graphs (${G_{PA}}$ and $G_{PJ}$) are introduced into the heterogeneous network which uses citation, authorship, and journal information simultaneously.

Time Settings

Based on whether to use time information, there exist two kinds of settings:

• No-Time ($\delta =0$): which does not utilize article time information to enhance the effect of the recent published articles.

• Time-Weighted (see Eq. 19): which can be used to balance the bias to earlier published articles in the citation network.

Table 2. Spearman’s ranking correlation of different graph configurations on three datasets.

With these assumptions, we are now ready to verify Spearman’s ranking correlation of different cases on three datasets, as shown in Tables 2, 3, 4 and 5. From an analysis of Table 2, it can be found that the best performance (arXiv: 0.5449; Cora: 0.3352; MAG: 0.4994) of proposed algorithm is all achieved from the weighted graph configurations as follows: ${G_{P}}$ + ${G_{PA}}$ + ${G_{PJ}}$. In addition, we note that under the four graph configuration conditions (${G_{P}}$; ${G_{P}}$ + ${G_{PA}}$; ${G_{P}}$ + ${G_{PJ}}$; ${G_{P}}$ + ${G_{PA}}$ + ${G_{PJ}}$), an important observation from the experimental results is that weighted graphs significantly outperform unweighted graphs.

Table 3. Spearman’s ranking correlation of two time settings on arXiv dataset.

Table 4. Spearman’s ranking correlation of two time settings on Cora dataset.

Table 5. Spearman’s ranking correlation of two time settings on MAG dataset.

Fig. 2.

Spearman’s ranking correlation and robustness of six algorithms on three datasets.

Fig. 3.

ROC curves obtained by 6 ranking algorithms (Weighted P-Rank, P-Rank, PageRank, FutureRank, HITS, and CiteRank) on three different datasets.

By comparing and analyzing the data from Tables 3, 4 and 5, under the conditions of two time settings (No-Time and Time-Weighted), it can be seen that the performance of Time-Weighted configurations always outperform the results of corresponding No-Time configurations, and the best performance (arXiv: 0.7115; Cora: 0.3962; MAG: 0.5933) is obtained by jointly utilizing all kinds of configurations as follows: ${G_{P}}$ + ${G_{PA}}$ + ${G_{PJ}}$+Time-Weighted.

For better comparison, we also measure the performance of the weighted P-Rank and five famous algorithms (PageRank, FutureRank, HITS, CiteRank, and P-Rank) on three datasets by using Spearman’s rank correlation and robustness. We see from Fig. 2 that weighted P-Rank achieved superior rank correlation (arXiv: 0.707; Cora: 0.388; MAG: 0.599) and robustness performance (arXiv: 0.918; Cora: 0.484; MAG: 0.732), in particular compared to the initial P-Rank algorithm.

It can be seen from Fig. 3 that weighted P-Rank algorithm (as plotted by red curve) significantly outperforms other ranking algorithms on arXiv and MAG datasets, while it achieves competitive performance on Cora dataset. The AUC vales obtained by weighted P-Rank on arXiv, Cora, and MAG datasets are 0.6733, 0.5586, and 0.6593 respectively. By a sharp contrast, the AUC values achieved by initial P-Rank algorithm are unsatisfactory, especially on arXiv dataset (only 0.3461). This result indicates that link weighting plays an important role in heterogeneous graphs, which will be very helpful to improve the performance of the article ranking algorithm.

4 Conclusion

This paper developed a weighted P-Rank algorithm based on a heterogeneous scholarly network for article ranking evaluation. The study is dedicated to assigning weight to the corresponding links in ${G_{P}}$, ${G_{PA}}$, and ${G_{PJ}}$ by calculating citation relevance (${G_{P}}$), authors’ contribution (${G_{PA}}$), and journals’ contribution (${G_{PJ}}$). Under conditions of two weighting combinations (Unweighted and Weighted) and four graph configurations (${G_{P}}$, ${G_{P}}$ + ${G_{PA}}$, ${G_{P}}$ + ${G_{PJ}}$, and ${G_{P}}$ + ${G_{PA}}$ + ${G_{PJ}}$), the performance of weighted P-Rank algorithm is further evaluated and analyzed. The experimental results showed that the weighted P-Rank method achieved promising performance on three different datasets, and the best ranking result can be achieved by jointly employing all kinds of weighting information. Additionally, we note that the article ranking result can be further improved by utilizing time-weighting information.

In the future, a series of meaningful studies can be conducted subsequently, combining network topology and link weighting. For instance, we would test the effect of link weighting on more ranking methods and verify how the parameters influence the performance of the algorithms.