Keywords

1 Introduction

It is known that, at the free edge of an orthotropic plate planar and flexural vibrations can occur independently of each other [1,2,3,4,5,6]. When the plate is bent these vibrations become coupled and giving raise to two new types of vibrations localized at the free edge: predominantly tangential and predominantly bending vibrations. The transformation of the one type of vibration into the other occurs at the free end of a thin cylindrical elastic panel. For these vibrations a complex distribution of frequencies of natural vibrations occurs depending on the geometrical and mechanical parameters of finite and infinite cylindrical panels [4,5,6,7,8,9,10,11]. With the increase of the number of free edges of a cylindrical panel the distribution becomes increasingly complex [5,6,7,8,9,10,11]. Recently free vibrations of a thin elastic orthotropic cylindrical panel with free edges were investigated [20]. Using generalized Kantorovich-Vlasov method the corresponding dispersion equations are derived to find the natural frequencies of possible types of vibrations. In general, the form of dispersion equations depends on the boundary conditions. Therefore, the frequency distributions will be different for different boundary conditions. It would be interesting to investigate the change in distribution of natural frequencies with the change in boundary conditions by considering cantilever plates (orthotropic rectangular plates with one rigid clamped edge and the other three edges free) and cantilever cylindrical panels (orthotropic cylindrical panels with one rigid clamped end and the other three edges free). The investigation of the edge resonance of cantilever plates and cantilever cylindrical panels is of practical importance since such elements are important components of modern structures and constructions. Therefore, the question of free vibrations of these elements is of vital importance and it demands special attention. Meanwhile, it is one of the most difficult problems in the theory of vibrations of plates and shells [5]. In practice these difficulties are resolved by using a combination of analytical and asymptotic theories, as well as by numerical methods.

In the present work, for the first time, free vibrations of cantilever plate and cantilever cylindrical panel are investigated. It is shown that due to difference in boundary conditions the dispersion equations of the considered problem is different from the one derived in [20]. It is proved that the problem prevents separation of variables for the given boundary conditions. It can be proved that such problems for cylindrical shells of orthotropic materials with simple boundary conditions are self-conjugate and nonnegative definite. Therefore, the generalized Kantorovich-Vlasov method can be applied to them [12,13,14,15,16]. As the basic functions the following eigenfunctions of the problem are used:

$$ w^{VIII} = \theta^{8} w,\,\;\left. w \right|_{\beta = 0,s} = \left. {w^{\prime}} \right|_{\beta = 0,s} = \,\left. {w^{\prime\prime}} \right|_{\beta = 0,s} = \left. {w^{\prime\prime\prime}} \right|_{\beta = 0,s} = 0,\,\,\,0 \le \beta \le s, $$
(1)

The problem (1) is a self-conjugate and has a positive simple discrete spectrum with a limit point at the infinity. The eigenfunctions corresponding to the eigenvalues \(\theta {}_{m}^{8} ,m = \overline{1,\infty }\), of the problem (1) have the form:

$$ w_{m} (\theta _{m} \beta ) = \frac{{\Delta _{1} }}{\Delta }x_{1} (\theta _{m} \beta ) + \frac{{\Delta _{2} }}{\Delta }x_{2} (\theta _{m} \beta ) + \frac{{\Delta _{3} }}{\Delta }x_{3} (\theta _{m} \beta ) + x_{4} (\theta _{m} \beta ),0 \le \beta \le s,m = \overline{{1, + \infty }} , $$
(2)
$$ \begin{aligned} x_{1} (\theta_{m} \beta ) & = ch\theta_{m} \beta \, - ch\frac{{\theta_{m} \beta }}{\sqrt 2 }\,\cos \frac{{\theta_{m} \beta }}{\sqrt 2 } - sh\frac{{\theta_{m} \beta }}{\sqrt 2 }\sin \frac{{\theta_{m} \beta }}{\sqrt 2 }, \\ x_{2} (\theta_{m} \beta ) & = sh\theta_{m} \beta \, - \sqrt 2 \,ch\frac{{\theta_{m} \beta }}{\sqrt 2 }\,\sin \frac{{\theta_{m} \beta }}{\sqrt 2 }, \\ & x_{3} (\theta_{m} \beta ) = \sin \theta_{m} \beta \, - \sqrt 2 sh\frac{{\theta_{m} \beta }}{\sqrt 2 }\,\cos \frac{{\theta_{m} \beta }}{\sqrt 2 }, \\ x_{4} (\theta_{m} \beta ) & = \cos \theta_{m} \beta \, - ch\frac{{\theta_{m} \beta }}{\sqrt 2 }\,\cos \frac{{\theta_{m} \beta }}{\sqrt 2 } + sh\frac{{\theta_{m} \beta }}{\sqrt 2 }\sin \frac{{\theta_{m} \beta }}{\sqrt 2 }, \\ \end{aligned} $$
(3)
$$ \Delta = \left| \begin{gathered} x_{1} (\theta_{m} s)\,\,x_{2} (\theta_{m} s)\,x_{3} (\theta_{m} s) \hfill \\ x^{\prime}_{1} (\theta_{m} s)\,\,x^{\prime}_{2} (\theta_{m} s)\,x^{\prime}_{3} (\theta_{m} s) \hfill \\ x^{\prime\prime}_{1} (\theta_{m} s)\,\,x^{\prime\prime}_{2} (\theta_{m} s)\,x^{\prime\prime}_{3} (\theta_{m} s) \hfill \\ \end{gathered} \right|\,,\,\;\;\Delta_{1} = - \left| \begin{gathered} x_{4} (\theta_{m} s)\,\,x_{2} (\theta_{m} s)\,x_{3} (\theta_{m} s) \hfill \\ x^{\prime}_{4} (\theta_{m} s)\,\,x^{\prime}_{2} (\theta_{m} s)\,x^{\prime}_{3} (\theta_{m} s) \hfill \\ x^{\prime\prime}_{4} (\theta_{m} s)\,\,x^{\prime\prime}_{2} (\theta_{m} s)\,x^{\prime\prime}_{3} (\theta_{m} s) \hfill \\ \end{gathered} \right|\,,\, $$
$$ \Delta_{2} = - \left| \begin{gathered} x_{1} (\theta_{m} s)\,\,x_{4} (\theta_{m} s)\,x_{3} (\theta_{m} s) \hfill \\ x^{\prime}_{1} (\theta_{m} s)\,\,x^{\prime}_{4} (\theta_{m} s)\,x^{\prime}_{3} (\theta_{m} s) \hfill \\ x^{\prime\prime}_{1} (\theta_{m} s)\,\,x^{\prime\prime}_{4} (\theta_{m} s)\,x^{\prime\prime}_{3} (\theta_{m} s) \hfill \\ \end{gathered} \right|\,,\,\;\;\Delta_{3} = - \left| \begin{gathered} x_{1} (\theta_{m} s)\,\,x_{2} (\theta_{m} s)\,x_{4} (\theta_{m} s) \hfill \\ x^{\prime}_{1} (\theta_{m} s)\,\,x^{\prime}_{2} (\theta_{m} s)\,x^{\prime}_{4} (\theta_{m} s) \hfill \\ x^{\prime\prime}_{1} (\theta_{m} s)\,\,x^{\prime\prime}_{2} (\theta_{m} s)\,x^{\prime\prime}_{4} (\theta_{m} s) \hfill \\ \end{gathered} \right|\,,\, $$

This eigenfunctions with their first and second derivatives define an orthogonal basis in a Hilbert space \(L{}_{2}[0,s]\,\) [16]. Here \(\theta_{m} \,,m = \overline{1, + \infty }\), are the positive zeros of the determinant of Vronsky for functions (3) at the point \(\beta = s.\) Let us define

$$ \begin{aligned} \,\beta^{\prime}_{m} & = \int\limits_{0}^{s} {\left( {w^{\prime}_{m} (\theta_{m} \beta )} \right)^{2} d\beta } /\int\limits_{0}^{s} {\left( {w_{m} (\theta_{m} \beta )} \right)^{2} } d\beta, \\ & \beta^{\prime\prime}_{m} = \int\limits_{0}^{s} {\left( {w^{\prime\prime}_{m} (\theta_{m} \beta )} \right)^{2} d\beta } /\int\limits_{0}^{s} {\left( {w^{\prime}_{m} (\theta_{m} \beta )} \right)^{2} } d\beta \,. \\ \end{aligned} $$
(4)

Notice that, the derivatives in formulas (3) and (4) are taken with respect to \(\theta_{m} \beta\) and \(\beta^{\prime}_{m} \to 1\), \(\beta^{\prime\prime}_{m} \to 1\,\) at \(m \to + \infty\).

2 The Statement of the Problem and the Basic Equations

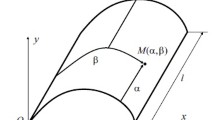
It is assumed that the generatrices of the cylindrical panel are orthogonal to the ends of the panel. The curvilinear coordinates \((\alpha ,\beta )\) are defined on the median surface of the shell where \(\alpha (0 \le \alpha \le l)\) and \(\beta (0 \le \beta \le s)\) are the lengths of the generatrix and the directing circumference, respectively; l – is the length of the panel; and s – is the length of the directing circumference.

As the initial equations describing vibrations of the panel, we will use the equations corresponding to the classical theory of orthotropic cylindrical shells written in the selected curvilinear coordinates \(\alpha\) and \(\beta\) (Fig. 1):

$$ \begin{aligned} & - B_{11} \frac{{\partial^{2} u_{1} }}{{\partial \alpha^{2} }} - B_{66} \frac{{\partial^{2} u_{1} }}{{\partial \beta^{2} }} - (B_{12} + B_{66} )\frac{{\partial^{2} u_{2} }}{\partial \alpha \partial \beta } + \frac{{B_{12} }}{R}\frac{{\partial u_{3} }}{\partial \alpha } = \lambda u_{1} \,, \\ & - (B_{12} + B_{66} )\frac{{\partial^{2} u_{1} }}{\partial \alpha \partial \beta } - B_{66} \frac{{\partial^{2} u_{2} }}{{\partial \alpha^{2} }} - B_{22} \frac{{\partial^{2} u_{2} }}{{\partial \beta^{2} }} + \frac{{B_{22} }}{R}\frac{{\partial u_{3} }}{\partial \beta } - \frac{{\mu^{4} }}{{R^{2} }}\left( {4B_{66} \frac{{\partial^{2} u_{2} }}{{\partial \alpha^{2} }} } \right. \\ & \left. { + B_{22} \frac{{\partial^{2} u_{2} }}{{\partial \beta^{2} }}} \right) - \frac{{\mu^{4} }}{R}\left( {B_{22} \frac{{\partial^{3} u_{3} }}{{\partial \beta^{3} }} + (B_{12} + 4B_{66} )\frac{{\partial^{3} u_{3} }}{{\partial \beta \partial \alpha^{2} }}} \right) = \lambda u_{2} , \\ \end{aligned} $$
(5)
$$ \begin{aligned} & \mu^{4} \left( {B_{11} \frac{{\partial^{4} u_{3} }}{{\partial \alpha^{4} }} + 2(B_{12} + 2B_{66} )\frac{{\partial^{4} u_{3} }}{{\partial \alpha^{2} \partial \beta^{2} }} + B_{22} \frac{{\partial^{4} u_{3} }}{{\partial \beta^{4} }}} \right)\\ & + \frac{{\mu^{4} }}{R}\left( {B_{22} \frac{{\partial^{3} u_{2} }}{{\partial \beta^{3} }} + } \right.\left. {(B_{12} + 4B_{66} )\frac{{\partial^{3} u_{2} }}{{\partial \beta \partial \alpha^{2} }}} \right) - \frac{{B_{12} }}{R}\frac{{\partial \,u_{1} }}{\partial \alpha } - \frac{{B_{22} }}{R}\frac{{\partial \,u_{2} }}{\partial \beta } + \frac{{B_{22} }}{{R^{2} }}u_{3} = \lambda u_{3} \\ \end{aligned} $$
Fig. 1.
figure 1

Middle surface of a cylindrical panel

Full size image

Here, \(u_{1} ,u_{2}\) and \(u_{3}\) are projections of the displacement vector on the directions \(\alpha\) and \(\beta\), and on the normal to the median surface of the shell, respectively; \(R\) is the radius of the directing circumference of the median surface; \(\mu^{4} = h^{2} /12\) (\(h\) is the thickness of the shell); \(\lambda = \omega^{2} \rho\), where \(\omega\) is the angular frequency, \(\rho\) is the density of the material; \(B_{ij}\) are the elasticity coefficients. The boundary conditions has the form [17]:

$$ \begin{gathered} \left. {\frac{{\partial u_{1} }}{\partial \alpha } + \frac{{B_{12} }}{{B_{11} }}\left( {\frac{{\partial u_{2} }}{\partial \beta } - \frac{{u_{3} }}{R}} \right)} \right|_{\alpha = 0} = 0,\,\;\;\left. {\frac{{\partial u_{2} }}{\partial \alpha } + \frac{{\partial u_{1} }}{\partial \beta } + \frac{{4\mu^{4} }}{R}\left( {\frac{{\partial^{2} u_{3} }}{\partial \alpha \partial \beta } + \frac{1}{R}\frac{{\partial u_{2} }}{\partial \alpha }} \right)} \right|_{\alpha = 0} = 0, \hfill \\ \left. {\frac{{\partial^{2} u_{3} }}{{\partial \alpha^{2} }} + \frac{{B_{12} }}{{B_{11} }}\left( {\frac{{\partial^{2} u_{3} }}{{\partial \beta^{2} }} + \frac{1}{R}\frac{{\partial u_{2} }}{\partial \beta }} \right)} \right|_{\alpha = 0} \, = 0,\;\;\left. {\frac{{\partial^{3} u_{3} }}{{\partial \alpha^{3} }} + \frac{{B_{12} + 4B_{66} }}{{B_{11} }}\left( {\frac{{\partial^{3} u_{3} }}{{\partial \alpha \partial \beta^{2} }} + \frac{1}{R}\frac{{\partial^{2} u_{2} }}{\partial \alpha \partial \beta }} \right)} \right|_{\alpha = 0} = 0. \hfill \\ \end{gathered} $$
(6)
$$ \left. {u_{1} } \right|_{\alpha = l} = \left. {u_{2} } \right|_{\alpha = l} = \left. {u_{3} } \right|_{\alpha = l} = \left. {\frac{{\partial u_{3} }}{\partial \alpha }} \right|_{\alpha = l} = 0 $$
(7)
$$ \begin{gathered} \frac{{B_{12} }}{{B_{22} }}\left. {\frac{{\partial u_{1} }}{\partial \alpha } + \frac{{\partial u_{2} }}{\partial \beta } - \frac{{u_{3} }}{R}} \right|_{\beta = 0,s} = 0,\,\,\,\,\,\,\, \hfill \\ \left. {\frac{{B_{12} }}{{B_{22} }}\frac{{\partial^{2} u_{3} }}{{\partial \alpha^{2} }} + \frac{{\partial^{2} u_{3} }}{{\partial \beta^{2} }} + \frac{1}{R}\frac{{\partial u_{2} }}{\partial \beta }} \right|_{\beta = 0,s} \,\, = 0, \hfill \\ \left. {\frac{{\partial^{3} u_{3} }}{{\partial \beta^{3} }} + \frac{{B_{12} + 4B_{66} }}{{B_{22} }}\frac{{\partial^{3} u_{3} }}{{\partial \beta \partial \alpha^{2} }} + \frac{1}{R}\frac{{\partial^{2} u_{2} }}{{\partial \beta^{2} }} + \frac{{4B_{66} }}{{B_{22} }}\frac{1}{R}\frac{{\partial^{3} u_{2} }}{{\partial \alpha^{2} }}} \right|_{\beta = 0,s} = 0,\,\,\,\, \hfill \\ \left. {\frac{{\partial u_{2} }}{\partial \alpha } + \frac{{\partial u_{1} }}{\partial \beta }} \right|_{\alpha = 0,s} = 0.\, \hfill \\ \end{gathered} $$
(8)

Relations (6) and (8) are the conditions of free edges for \(\alpha = 0\) and \(\beta = 0,\,s\), respectively, while conditions (7) indicate that the edge \(\alpha = l\) is rigid-clamped.

3 The Derivation and Analysis of the Characteristic Equations

Let’s formally replace the spectral parameter \(\lambda\) by \(\lambda_{1} ,\,\lambda_{2}\) and \(\,\lambda_{3}\) in the first, second, and third equations of the system (5), respectively. The solution of system (5) is searched in the form

$$ (u_{1} ,\,\,u_{2} ,u_{3} ) = \,\{ u_{m} w_{m} (\theta_{m} \beta ),\,\,v_{m} w^{\prime}_{m} (\theta_{m} \beta ),w_{m} (\theta_{m} \beta )\} \exp (\theta_{m} \chi \alpha ),\,\,\,\,\,m = \overline{1, + \infty } . $$
(9)

Here,\(w_{m} (\theta_{m} \beta ),m = \overline{1,\infty }\), are determined from (2) and \(u_{m} ,\,v_{m}\) and \(\chi\) are unknown constants. In this case, the conditions (8) are obeyed automatically. Let us insert Eq. (9) into Eq. (5). The obtained equations are multiplied by the vector functions \(\left( {w_{m} (\theta_{m} \beta ),w^{\prime}_{m} (\theta_{m} \beta ),w_{m} (\theta_{m} \beta )} \right)\) in a scalar way and then integrated in the limits from 0 to \(s\). From the first two equations we have

$$ (c_{m} + \varepsilon_{m}^{2} a^{2} g_{m} d_{m} )u_{m} = \varepsilon_{m} \chi \left\{ {a_{m} - a^{2} \frac{{B_{22} (B_{12} + B_{66} )}}{{B_{11} B_{66} }}\beta^{\prime}_{m} l_{m} + \varepsilon_{m}^{2} a^{2} \frac{{B_{22} B_{12} }}{{B_{11} B_{66} }}d_{m} } \right\}, $$
(10)
$$ (c_{m} + \varepsilon_{m}^{2} a^{2} g_{m} d_{m} )v_{cm} = \varepsilon_{m} \left\{ {\,b_{m} - a^{2} g_{m} l_{m} } \right\}, $$
(11)

From the third equation, by taking into account the relations (10) and (11), the characteristic equation is obtained

$$ \begin{gathered} R_{mm} c_{m} + \varepsilon_{m}^{2} \left\{ {\,c_{m} + b_{m} \beta^{\prime}_{m} - \frac{{B_{12} }}{{B_{22} }}\chi^{2} a_{m} + a^{2} [R_{mm} g_{m} d_{m} - 2\,l_{m} b_{m} \beta^{\prime}_{m} } \right.] \hfill \\ + \varepsilon_{m}^{2} \left. {a^{2} d_{m} (b_{m} + \frac{{B_{12} }}{{B_{11} }}\chi^{2} ) + a^{4} g_{m} l_{m}^{2} \beta^{\prime}_{m} } \right\} = 0,\,\,m = \overline{1,\infty } \,\,. \hfill \\ \end{gathered} $$
(12)
$$ \begin{aligned} a_{m} & = \frac{{B_{12} }}{{B_{11} }}\chi^{2} + \frac{{B_{22} }}{{B_{11} }}\beta^{\prime}_{m} + \frac{{B_{12} }}{{B_{11} }}\eta_{2m}^{2} + (\beta^{\prime}_{m} - \beta^{\prime\prime}_{m} )\frac{{B_{12} B_{22} }}{{B_{11} B_{66} }}\,;\, \\ b_{m} & = B_{1} \chi^{2} - \frac{{B_{22} }}{{B_{11} }}\left( {\beta^{\prime}_{m} - \eta_{1m}^{2} } \right)\,;\,\, \\ c_{m} & = \chi^{4} - B_{2} \chi^{2} + \left( {\frac{{B_{66} }}{{B_{11} }}\eta_{1m}^{2} + \eta_{2m}^{2} } \right)\chi^{2} + (\beta^{\prime}_{m} - \eta_{1m}^{2} )\left( {\frac{{B_{22} }}{{B_{11} }}\beta^{\prime\prime}_{m} - \frac{{B_{66} }}{{B_{11} }}\eta_{2m}^{2} } \right);\, \\ \end{aligned} $$
(13)
$$ \begin{aligned} B_{1} & = \frac{{B_{11} B_{22} - B_{12}^{2} - B_{12} B_{66} }}{{B_{11} B_{66} }};\, \\ B_{2} & = \,\frac{{B_{11} B_{22} \beta^{\prime\prime}_{m} - B_{12}^{2} \beta^{\prime}_{m} - 2B_{12} B_{66} \beta^{\prime}_{m} }}{{B_{11} B_{66} }},\, \\ d_{m} & = \frac{{4B_{66} }}{{B_{11} }}\chi^{2} - \beta^{\prime\prime}_{m} ; \\ \end{aligned} $$
$$ \begin{aligned} \,g_{m} & = \frac{{B_{22} }}{{B_{66} }}\chi^{2} - \frac{{B_{22} }}{{B_{11} }}\beta^{\prime}_{m} + \frac{{B_{22} }}{{B_{11} }}\eta_{1m}^{2} ,\,\, \\ l_{m} & = \frac{{B_{12} + 4B_{66} }}{{B_{22} }}\chi^{2} - \beta^{\prime\prime}_{m} ,\,\,\,\,\eta_{im}^{2} = \,\frac{{\lambda_{i} }}{{B_{66} \theta_{m}^{2} }},\,\,i = \overline{1,3} \,, \\ \end{aligned} $$
$$ \begin{aligned} R_{mm} & = a^{2} \left( {\frac{{B_{11} }}{{B_{22} }}\chi^{4} - \frac{{2(B_{12} + 2B_{66} )}}{{B_{22} }}\beta^{\prime}_{m} \chi^{2} + \beta^{\prime}_{m} \beta^{\prime\prime}_{m} } \right) - \frac{{B_{66} }}{{B_{22} }}\eta_{3m}^{2} ,\,\,\, \\ a^{2} & = \frac{{h^{2} }}{12}\theta_{m}^{2} \,,\varepsilon_{m} = \frac{1}{{R\theta_{m} }}\,. \\ \end{aligned} $$

Let \(\chi_{j} ,\,\,j = \overline{1,4}\), be pairwise different roots of Eq. (12) with non-positive real parts and \(\chi_{4 + j} = - \chi_{j} ,\,j = \overline{1,4} \,\). Let \((u_{1}^{(j)} ,u_{2}^{(j)} ,u_{3}^{(j)} ),\,\,j = \overline{1,8}\), be nontrivial solutions of type (9) of the system (5) at \(\chi = \chi_{j} ,\,j = \overline{1,8}\), respectively. The solution of the problem (5–8) is searched in the form

$$ u_{i} = \sum\nolimits_{j = 1}^{8} {u_{i}^{(j)} w_{j} } ,\,\,i = \overline{1,3} . $$
(14)

Let us insert Eq. (14) into the boundary conditions (6) and (7). Each of the obtained equation is multiplied by \(w(\theta_{m} \beta )\), except of the second one, which is multiplied by \(w^{\prime}(\theta_{m} \beta )\), and then integrated in the limits from \(0\) to \(s\). As a result, we obtain the system of equations.

$$ \begin{aligned} & \sum\limits_{j = 1}^{8} {\frac{{M_{ij}^{(m)} w_{j} }}{{c_{m}^{(j)} + \varepsilon_{m}^{2} a^{2} g_{m}^{(j)} d_{m}^{(j)} }}} = 0\,,\,\,\,\,\,i = \overline{1,4} \, \\ & \sum\limits_{j = 1}^{8} {\frac{{M_{ij}^{(m)} \exp (\theta_{m} \chi_{j} \alpha )w_{j} }}{{c_{m}^{(j)} + \varepsilon_{m}^{2} a^{2} g_{m}^{(j)} d_{m}^{(j)} }}} = 0\,,\,\,\,\,\,i = \overline{5,8} \,\;,\;\;\;\;m = \overline{1,\infty } \\ \end{aligned} $$
(15)
$$ \begin{gathered} M_{{1j}}^{{(m)}} = \chi _{j}^{2} a_{m}^{{(j)}} - \frac{{B_{{12}} }}{{B_{{11}} }}b_{m}^{{(j)}} \beta _{m}^{\prime } - \frac{{B_{{12}} }}{{B_{{11}} }}c_{m}^{{(j)}} + \varepsilon _{m}^{2} a^{2} \frac{{B_{{12}} B_{{22}} }}{{B_{{11}}^{2} }}d_{m}^{{(j)}} (\beta _{m}^{\prime } - \eta _{{1m}}^{2} ) \hfill \\ \quad - a^{2} \frac{{B_{{22}} }}{{B_{{11}} }}l_{m}^{{(j)}} \beta _{m}^{\prime } \left( {\chi _{j}^{2} + \frac{{B_{{12}} }}{{B_{{11}} }}\beta _{m}^{\prime } - \frac{{B_{{12}} }}{{B_{{11}} }}\eta _{{1m}}^{2} } \right), \hfill \\ M_{{2j}}^{{(m)}} = \beta _{m}^{\prime } \chi _{j} \left\{ {a_{m}^{{(j)}} + b_{m}^{{(j)}} + a^{2} \left[ {4c_{m}^{{(j)}} - l_{m}^{{(j)}} \left( {\frac{{B_{{22}} }}{{B_{{66}} }}\chi _{j}^{2} + \frac{{B_{{12}} B_{{22}} }}{{B_{{11}} B_{{66}} }}\beta _{m}^{\prime } + \frac{{B_{{22}} }}{{B_{{11}} }}\eta _{{1m}}^{2} } \right)} \right]} \right. \hfill \\ \quad + a^{2} \varepsilon _{m}^{2} \left( {4b_{m}^{{(j)}} + \frac{{B_{{12}} B_{{22}} }}{{B_{{11}} B_{{66}} }}d_{m}^{{(j)}} - 4a^{2} g_{m}^{{(j)}} \frac{{B_{{12}} }}{{B_{{22}} }}\chi _{j}^{2} } \right)\Bigg\}, \hfill \\ M_{{3j}}^{{(m)}} = \left( {\chi _{j}^{2} - \frac{{B_{{12}} }}{{B_{{11}} }}\beta _{m}^{\prime } } \right)c_{m}^{{(j)}} + \varepsilon _{m}^{2} \left[ {a^{2} g_{m}^{{(j)}} \left( {\frac{{4B_{{66}} }}{{B_{{22}} }}\chi _{j}^{4} - \frac{{B_{{11}} B_{{22}} \beta _{m}^{{\prime \prime }} - B_{{12}}^{2} \beta _{m}^{\prime } }}{{B_{{11}} B_{{22}} }}\chi _{j}^{2} } \right) - \frac{{B_{{12}} }}{{B_{{11}} }}b_{m}^{{(j)}} \beta _{m}^{\prime } } \right], \hfill \\ M_{{4j}}^{{(m)}} = \chi _{j}\Bigg\{ \left( {\chi _{j}^{2} - \frac{{B_{{12}} + 4B_{{66}} }}{{B_{{11}} }}\beta _{m}^{\prime } } \right)c_{m}^{{(j)}} + \varepsilon _{m}^{2} \left[ {a^{2} g_{m}^{{(j)}} } \right. \hfill \\ \quad \times \left( {\frac{{4B_{{66}} }}{{B_{{22}} }}\chi _{j}^{4} - \frac{{B_{{11}} B_{{22}} \beta _{m}^{{\prime \prime }} - B_{{12}}^{2} \beta _{m}^{\prime } - 4B_{{12}} B_{{66}} \beta _{m}^{\prime } }}{{B_{{11}} B_{{22}} }}\chi _{j}^{2} } \right)\left. {\left. { - \frac{{B_{{12}} + 4B_{{66}} }}{{B_{{11}} }}b_{m}^{{(j)}} \beta _{m}^{\prime } } \right]{\mkern 1mu} } \right\}, \hfill \\ M_{{5j}}^{{(m)}} = \left( {b_{m}^{{(j)}} + a^{2} g_{m}^{{(j)}} l_{m}^{{(j)}} } \right)\beta _{m}^{\prime } , \hfill \\ M_{{6j}}^{{(m)}} = \beta _{m}^{\prime } \chi _{j} \left\{ {a_{m}^{{(j)}} - a^{2} \frac{{B_{{22}} (B_{{12}} + B_{{66}} )}}{{B_{{11}} B_{{66}} }}\beta _{m}^{\prime } l_{m}^{{(j)}} + \varepsilon _{m}^{2} a^{2} \frac{{B_{{22}} B_{{12}} }}{{B_{{11}} B_{{66}} }}d_{m}^{{(j)}} } \right\}, \hfill \\ M_{{7j}}^{{(m)}} = c_{m}^{{(j)}} + \varepsilon _{m}^{2} a^{2} g_{m}^{{(j)}} d_{m}^{{(j)}} ,M_{{8j}}^{{(m)}} = \chi _{j} \left( {c_{m}^{{(j)}} + \varepsilon _{m}^{2} a^{2} g_{m}^{{(j)}} d_{m}^{{(j)}} } \right),j = \overline{{1,8}} . \hfill \\ \end{gathered} $$
(16)

The superscript \(j\) in parentheses means that the corresponding function is taken at \(\chi = \chi_{j}\). In order to the system (15) has a nontrivial solution, it is necessary and sufficient that

$$ \Delta = \exp \left( { - \sum\limits_{j = 1}^{4} {z_{j} } } \right)Det\left\| {T_{ij}^{(m)} } \right\|_{i,j = 1}^{2} = 0,\,\,\,\,\,m = \overline{1,\infty } \,, $$
(17)
$$ \begin{aligned} T_{11} & = \left\| {M_{ij}^{(m)} } \right\|_{i,j = 1}^{4} \,,\,\,\,\,T_{12} = \left\| {\left( { - 1} \right)^{i - 1} M_{ij}^{(m)} \exp (z_{j} )} \right\|_{i,j = 1}^{4} \,,z_{j} = \theta_{m} \chi_{j} l, \\ T_{21} & = \left\| {M_{ij}^{(m)} \exp (z_{j} )} \right\|_{i = 5,j = 1}^{8,4} \,,\,\,\,\,\,\,\,T_{22} = \left\| {\left( { - 1} \right)^{i - 1} M_{ij}^{(m)} } \right\|_{i = 5,j = 1}^{8,4} \,. \\ \end{aligned} $$
(18)

It is shown numerically that the left side of this equality becomes small when any two roots of Eq. (12) become close to each other. This highly complicates calculations and can lead to false solutions. It turns out that from the left side of Eq. (17) a multiplier that tends to zero can be separated when the roots approach each other. Let us introduce the following notations:

$$ \begin{aligned} [z_{i} z_{j} ] & = \theta_{m} l(\exp (z_{i} ) - \exp (z_{j} ))/(z_{i} - z_{j} ),\,\,\,[z_{i} z_{j} z_{k} ] = \theta_{m} l\left( {[z_{i} z_{j} ] - [z_{i} z_{k} ]} \right)/(z_{j} - z_{k} ), \\ \,[z_{1} z_{2} z_{3} z_{4} ] & = \theta_{m} l\left( {[z_{1} z_{2} z_{3} ] - [z_{1} z_{2} z_{4} ]} \right)/(z_{3} - z_{4} ), \\ \end{aligned} $$
$$ \begin{aligned} \sigma_{1} & = \sigma_{1} (\chi_{1} ,\chi_{2} ,\chi_{3} ,\chi_{4} ) = \chi_{1} + \chi_{2} + \chi_{3} + \chi_{4} , \\ \sigma_{2} & = \sigma_{2} (\chi_{1} ,\chi_{2} ,\chi_{3} ,\chi_{4} ) = \chi_{1} \chi_{2} + \chi_{1} \chi_{3} + \chi_{1} \chi_{4} + \chi_{2} \chi_{3} + \chi_{2} \chi_{4} + \chi_{3} \chi_{4} , \\ \sigma_{3} & = \sigma_{3} (\chi_{1} ,\chi_{2} ,\chi_{3} ,\chi_{4} ) = \chi_{1} \chi_{2} \chi_{3} + \chi_{1} \chi_{2} \chi_{4} + \chi_{1} \chi_{3} \chi_{4} + \chi_{2} \chi_{3} \chi_{4} , \\ \sigma_{4} & = \sigma_{4} (\chi_{1} ,\chi_{2} ,\chi_{3} ,\chi_{4} ) = \chi_{1} \chi_{2} \chi_{3} \chi_{4} , \\ \overline{\sigma }_{k} & = \sigma_{k} (\chi_{1} ,\chi_{2} ,\chi_{3} ,0),\,\,\,\overline{\overline{\sigma }}_{k} = \sigma_{k} (\chi_{1} ,\chi_{2} ,0,0),\,\,k = \overline{1,4} . \\ \end{aligned} $$
(19)

In this case, \(\overline{\sigma }_{4} = \overline{\overline{\sigma }}_{4} = \overline{\overline{\sigma }}_{3} = 0.\) Let \(f_{n} ,\,\,n = \overline{1,6}\), be a symmetric polynomial of \(nth\) order in variables \(\chi_{1} ,\chi_{2} ,\chi_{3} ,\chi_{4}\). It is known that it can be uniquely expressed in terms of elementary symmetric polynomials. By introducing the notations.

$$ f_{n} = f_{n} (\sigma_{1} ,\sigma_{2} ,\sigma_{3} ,\sigma_{4} );\;\overline{f}_{n} = f_{n} (\overline{\sigma }_{1} ,\overline{\sigma }_{2} ,\overline{\sigma }_{3} ,0);\;\overline{\overline{f}}_{n} = f_{n} (\overline{\overline{\sigma }}_{1} ,\overline{\overline{\sigma }}_{2} ,0,0),\;n = \overline{1,6} ; $$
(20)
$$ \begin{aligned} f_{1} & = \sigma_{1} ,\,\,f_{2} = \sigma_{1}^{2} - \sigma_{2} ;\,\,f_{3} = \sigma_{1}^{3} - 2\sigma_{1} \sigma_{2} + \sigma_{3} ;\,\,\,f_{4} = \sigma_{1}^{4} - 3\sigma_{1}^{2} \sigma_{2} + \sigma_{2}^{2} + 2\sigma_{1} \sigma_{3} - \sigma_{4} \,;\, \\ \overline{f}_{5} & = \overline{\sigma }_{1}^{5} - 4\overline{\sigma }_{1}^{3} \overline{\sigma }_{2} + 3\overline{\sigma }_{1} \overline{\sigma }_{2}^{2} + 3\overline{\sigma }_{1}^{2} \overline{\sigma }_{3} - 2\overline{\sigma }_{2} \overline{\sigma }_{3} \,;\,\,\,\,\overline{\overline{f}}_{6} = \overline{\overline{\sigma }}_{1}^{6} - 5\overline{\overline{\sigma }}_{1}^{4} \overline{\overline{\sigma }}_{2} + 6\overline{\overline{\sigma }}_{1}^{2} \overline{\overline{\sigma }}_{2}^{2} - \overline{\overline{\sigma }}_{2}^{3} \,, \\ \end{aligned} $$
(21)

and performing elementary operations with columns of determinant (17), we obtain

$$ Det\left\| {T_{ij}^{(m)} } \right\|_{i,j = 1}^{2} = K^{2} \,Det\left\| {m_{ij} } \right\|_{i,j = 1}^{8} \,\,,\,m = \overline{1,\infty } \,\,\,, $$
(22)
$$ K = (\chi_{1} - \chi_{2} )(\chi_{1} - \chi_{3} )(\chi_{1} - \chi_{4} )(\chi_{2} - \chi_{3} )(\chi_{2} - \chi_{4} )(\chi_{3} - \chi_{4} )\,\,. $$
(23)

The expressions for \(m_{ij}\) are given in Appendix 1. The Eq. (17) are equivalent to the equations

$$ Det\left\| {m_{ij} } \right\|_{i,j = 1}^{8} = 0\,,\,m = \overline{1,\infty } \,\,. $$
(24)

By taking into account the possible relations between \(\lambda_{1} ,\lambda_{2}\) and \(\lambda_{3}\) we conclude that Eq. (24) determine frequencies of the corresponding types of vibrations. For \(\lambda_{1} = \lambda_{2} = \lambda_{3} = \lambda ,\) the Eq. (12) are the characteristic equations of the system (5), and the Eq. (24) are the dispersion equations of the problem (5–8).

In Sect. 6, the asymptotics of the dispersion Eq. (24) for \(\varepsilon_{m} = 1/\theta_{m} R \to 0\) (transition to a cantilever rectangular plate or to vibrations localized at the free edges of the cantilever cylindrical panel) and for \(\theta_{m} l \to \infty\) (transition to a semi-infinite cantilever cylindrical panel or to vibrations localized at the free edges of the cantilever cylindrical panel) are investigated. For checking the reliability of the asymptotic relations found in Sect. 6, the free planar and bending vibrations of a cantilever rectangular plate are investigated in the next two sections.

4 Planar Vibrations of an Orthotropic Cantilever Rectangular Plate

Let an orthotropic rectangular plate is defined in a triorthogonal system of rectilinear coordinates \((\alpha ,\beta ,\gamma )\) with the origin on the free face plane such that the coordinate plane \(\alpha \beta\) coincides with the midsurface of the plate and the principal axes of symmetry of the material are aligned with the coordinate lines (Fig. 2). Let \(s\,\,and\,\,l\) be the width and the length of the plate, respectively. The problem of the existence of free planar vibrations of a cantilever rectangular plate is investigated. As the initial equations consider the equations of low-amplitude planar vibrations of the classical theory of orthotropic plates [17]

$$ \begin{aligned} & - B_{11} \frac{{\partial^{2} u_{1} }}{{\partial \alpha^{2} }} - B_{66} \frac{{\partial^{2} u_{1} }}{{\partial \beta^{2} }} - (B_{12} + B_{66} )\frac{{\partial^{2} u_{2} }}{\partial \alpha \partial \beta } = \lambda u_{1} ; \\ & - (B_{12} + B_{66} )\frac{{\partial^{2} u_{1} }}{\partial \alpha \partial \beta } - B_{66} \frac{{\partial^{2} u_{2} }}{{\partial \alpha^{2} }} - B_{22} \frac{{\partial^{2} u_{2} }}{{\partial \beta^{2} }} = \lambda u_{2} \,, \\ \end{aligned} $$
(25)
Fig. 2.
figure 2

Rectangular plate with rigid clamped edge

Full size image

Here \(\alpha \,\,(0 \le \alpha \le l)\) and \(\beta \,\,(0 < \beta < s)\) are the orthogonal rectilinear coordinates of a point on the middle surface; \(u_{1}\) and \(u_{2}\) are the displacements in \(\alpha\) and \(\beta\) directions, respectively; \(B_{ik} ,\,\,i,k = 1,2,6\), are the coefficients of elasticity; \(\lambda = \omega^{2} \rho\), where \(\omega\) is the natural frequency; and \(\rho\) is the density of the material. The boundary conditions have the form [17]

$$ \left. {\frac{{\partial u_{1} }}{\partial \alpha } + \frac{{B_{12} }}{{B_{11} }}\frac{{\partial u_{2} }}{\partial \beta }} \right|_{\alpha = 0} = \,\left. {\frac{{\partial u_{2} }}{\partial \alpha } + \frac{{\partial u_{1} }}{\partial \beta }} \right|_{\alpha = 0} = 0\,, $$
(26)
$$ \left. {u_{1} } \right|_{\alpha = l} = \left. {u_{2} } \right|_{\alpha = l} = 0,\,\, $$
(27)
$$ \frac{{B_{12} }}{{B_{11} }}\left. {\frac{{\partial \,u_{1} }}{\partial \alpha } + \frac{{\partial \,u_{2} }}{\partial \beta }} \right|_{\beta = 0,s} = \,\left. {\frac{{\partial \,u_{2} }}{\partial \alpha } + \frac{{\partial \,u_{1} }}{\partial \beta }} \right|_{\beta = 0,s} = 0\,. $$
(28)

Here conditions (26) and (28) mean that the edges \(\alpha = 0\) and \(\,\beta = 0,s\) are free, while conditions (27) indicate that the edge \(\alpha = l\) is rigid-clamped. The problem (25–28) does not allow separation of variables. The differential operator corresponding to this problem is self-conjugate and nonnegative definite. Therefore, the generalized Kantorovich-Vlasov method of the reduction to ordinary differential equations can be used to find vibration eigenfrequencies and eigenmodes [12,13,14,15,16]. The solution of the system (25) is searched in the form

$$ (u_{1} ,\,\,u_{2} ) = \,\{ u_{m} w_{m} (\theta_{m} \beta ),\,\,v_{m} w^{\prime}_{m} (\theta_{m} \beta )\} \exp (\theta_{m} y\alpha ),\,\,\,\,\,m = \overline{1, + \infty } \,. $$
(29)

In this case, the conditions (28) are satisfied automatically. Let us insert (29) into Eq. (25). Then, the obtained equations are multiplied by vector functions \(\left( {w_{m} (\theta_{m} \beta ),w^{\prime}_{m} (\theta_{m} \beta )} \right)\) in a scalar way and integrated in the limits from 0 to \(s\). As a result, the system of equations is obtained

$$ \begin{gathered} (y^{2} - \frac{{B_{66} }}{{B_{11} }}(\beta^{\prime}_{m} - \eta_{m}^{2} ))u_{m} - \frac{{B_{12} + B_{66} }}{{B_{11} }}y\beta^{\prime}_{m} \,v_{m} = 0, \hfill \\ \frac{{B_{12} + B_{66} }}{{B_{66} }}yu_{m} + (y^{2} - \frac{{B_{22} }}{{B_{66} }}\beta^{\prime\prime}_{m} + \eta_{m}^{2} )v_{m} = 0, \hfill \\ \end{gathered} $$
(30)

where \(\eta_{m}^{2} = \lambda /\left( {\theta_{m}^{2} B_{66} } \right),\;\theta_{m}\), and \(\beta^{\prime}_{m} ,\;\beta^{\prime\prime}_{m}\), are determined in Eqs. (2) and (4), respectively. By equating the determinant of system (30) to zero, the following characteristic equation of the system of Eq. (25) is found:

$$ c_{m} = y^{4} - B_{2} y^{2} + \frac{{B_{11} + B_{66} }}{{B_{11} }}\eta_{m}^{2} y^{2} + (\beta^{\prime}_{m} - \eta {}_{m}^{2} )\left( {\frac{{B_{22} }}{{B_{11} }}\beta^{\prime\prime}_{m} - \frac{{B_{66} }}{{B_{11} }}\eta {}_{m}^{2} } \right) = 0\,,\,\,m = \overline{1, + \infty } \,\,. $$
(31)

Let \(y_{1}\) and \(y_{2}\) be various roots of Eq. (31) with non-positive real parts and \(y_{2 + j} = - y_{j} \,,\,j = 1,2\). As the solution of system (30) for \(y = y_{j} \,,j = \overline{1,4}\), we take

$$ u_{m}^{(j)} = \frac{{B_{12} + B_{66} }}{{B_{11} }}\beta^{\prime}\,y_{j} ,\,\,\,\,v_{m}^{(j)} = y_{j}^{2} - \frac{{B_{66} }}{{B_{11} }}(\beta^{\prime}_{m} - \eta_{m}^{2} )\,,\,\,\,\,j = \overline{1,4} \,\,. $$
(32)

The solution of the problem (25–28) can be presented in the form

$$ u_{1} = \sum\nolimits_{j = 1}^{4} {u_{m}^{(j)} w_{m} (\theta_{m} \beta )\exp (\theta_{m} y_{j} \alpha )w_{j} } ,\,\,\,u_{2} = \sum\nolimits_{j = 1}^{4} {v_{m}^{(j)} w^{\prime}_{m} (\theta_{m} \beta )\exp (\theta_{m} y_{j} \alpha )w_{j} } .\,\, $$
(33)

Let us insert Eq. (33) into the boundary conditions (26) and (27). Each of the obtained equation is multiplied by \(w(\theta_{m} \beta )\), except of the second one, which is multiplied by \(w^{\prime}(\theta_{m} \beta )\), and then integrated in the limits from \(0\) to \(s\). As a result, the system of equations is obtained

$$ \left\{ \begin{gathered} \sum\limits_{j = 1}^{4} {R_{1j}^{(m)} } w_{j} = 0,\,\,\,\,\,\,\,\,\sum\limits_{j = 1}^{4} {R_{5j}^{(m)} \exp (z_{j} )\,} w_{j} = 0, \hfill \\ \sum\limits_{j = 1}^{4} {R_{2j}^{(m)} } w_{j} = 0,\,\,\,\,\,\,\,\sum\limits_{j = 1}^{4} {R_{6j}^{(m)} \exp (z_{j} )\,} w_{j} = 0.\, \hfill \\ \end{gathered} \right.\;\;\;m = \overline{1, + \infty } \,\,. $$
(34)
$$ \begin{aligned} R_{1j}^{(m)} & = y_{j}^{2} + \frac{{B_{12} }}{{B_{11} }}(\beta^{\prime}_{m} - \eta_{m}^{2} ),\,\,\,\,\,R_{2j}^{(m)} = y_{j} \left( {y_{j}^{2} + \frac{{B_{12} }}{{B_{11} }}\beta^{\prime}_{m} + \frac{{B_{66} }}{{B_{11} }}\eta_{m}^{2} } \right),\,\,\, \\ R_{5j}^{(m)} & = y_{j}^{2} - \frac{{B_{66} }}{{B_{11} }}(\beta^{\prime}_{m} - \eta_{m}^{2} ),\,\,\,R_{6j}^{(m)} = y_{j} \frac{{B_{12} + B_{66} }}{{B_{11} }}\beta^{\prime}_{m} \,,\,\,z_{j} = \theta_{m} y_{j} l\,,j = \overline{1,4} \,. \\ \end{aligned} $$
(35)

By equating the determinant \(\Delta_{e}\) of the system (34) to zero and performing elementary operations with columns of the determinant the following dispersion equation is obtained

$$ \Delta_{e} = \exp ( - z_{1} - z_{2} )\,(y_{2} - y_{1} )^{2} \,Det\left\| {l_{ij} } \right\|_{i,j}^{4} = 0\,\,\,.\, $$
(36)
$$ \begin{aligned} \,\,l_{11} & = R_{11}^{(m)} ,\,\,\,l_{12} = y_{1} + y_{2} ,\,\,\,\,l_{13} = l_{11} \exp (z_{1} )\,,\,\,\,l_{14} = l_{12} \exp (z_{2} ) + l_{11} [z_{1} z_{2} ];\, \\ l_{21} & = R_{21}^{(m)} ,\,\,l_{22} = y_{1} y_{2} + \left( {B_{11} B_{22} \beta^{\prime\prime}_{m} - B_{12}^{2} \beta^{\prime}_{m} - B_{12} B_{66} \beta^{\prime}_{m} } \right)/(B_{11} B_{66} ) - \eta_{m}^{2} ,\, \\ \,\,l_{23} & = - l_{21} \exp (z_{1} ),\,\,l_{24} = - l_{22} \exp (z_{2} ) - l_{21} [z_{1} z_{2} ];\,\,\,\, \\ \,\,n_{31} & = R_{31} = y_{j}^{2} - \frac{{B_{66} }}{{B_{11} }}(\beta^{\prime}_{m} - \eta_{m}^{2} ),\,\,\,n_{32} = y_{1} + y_{2} , \\ l_{31} & = n_{31} \exp (z_{1} ),\,\,\,l_{32} = n_{32} \exp (z_{2} ) + n_{31} [z_{1} z_{2} ];\,l_{33} = n_{31} ,\,\,\,l_{34} = n_{32} ,\, \\ n_{41} \, & = \frac{{B_{12} + B_{66} }}{{B_{11} }}y_{1} \beta^{\prime}_{m} \,,\,\,\,n_{42} = \frac{{B_{12} + B_{66} }}{{B_{11} }}\beta^{\prime}_{m} ; \\ l_{41} & = n_{41} \exp (z_{1} ),\,\,\,l_{42} = n_{42} \exp (z_{2} ) + n_{41} [z_{1} z_{2} ];\,l_{43} = - n_{41} ,\,\,\,l_{44} = - n_{42} ,\, \\ z_{j} & = \theta_{m} y_{j} l\,,\,\,\,[z_{1} z_{2} ] = \theta_{m} l\,(\exp (z_{2} ) - \exp (z_{1} ))/(z_{2} - z_{1} ). \\ \end{aligned} $$
(37)

The Eq. (36) is equivalent to the equation

$$ \begin{aligned} Det\left| {l_{ij} } \right|_{i,j = 1}^{4} = & \left( {(B_{12} + B_{66} )/B_{11} } \right)^{2} K_{2m} (\eta_{m}^{2} )Q(\eta_{m}^{2} )(1 + \beta^{\prime}_{m} \exp (2(z_{1} + z_{2} ))) \\ & \quad - 4(\,l_{21} \,l_{11} n_{32} n_{42} + l_{12} \,l_{22} n_{31} n_{41} )\exp (z_{1} + z_{2} ) \\ & \quad + (l_{11} l_{22} + l_{21} l_{12} )(n_{32} n_{41} + n_{31} n_{42} )(\exp (2z_{1} ) + \exp (2z_{2} )) \\ & \quad + 2(l_{11} l_{21} (n_{31} n_{42} + n_{32} n_{41} ) + n_{31} n_{41} \left( {l_{11} l_{22} + l_{21} l_{12} } \right))(\exp (z_{2} ) \\ & \quad - \exp (z_{1} ))[z_{1} z_{2} ] + 4\,l_{11} l_{21} n_{41} n_{31} [z_{1} z_{2} ]^{2} = 0\,. \\ \end{aligned} $$
(38)
$$ \begin{aligned} K_{2m} \left( {\eta_{m}^{(2)} } \right) & = (\beta^{\prime}_{m} - \eta_{m}^{2} )\left( {\frac{{B_{11} B_{22} \beta^{\prime\prime}_{m} - B_{12}^{2} \beta^{\prime}_{m} }}{{B_{11} B_{66} }} - \eta_{m}^{2} } \right) - \eta_{m}^{2} y_{1} y_{2} \,,\,\,\,\,\,\,\,\,\, \\ Q(\eta_{m}^{2} ) & = y_{1} y_{2} + \frac{{B_{66} }}{{B_{11} }}(\beta^{\prime}_{m} - \eta_{m}^{2} )\,. \\ \end{aligned} $$

If \(y_{1}\) and \(y_{2}\) are the roots of Eq. (31) with negative real parts, then, at \(\theta_{m} l \to \infty\), the roots of Eq. (38) are approximated by the roots of the equation

$$ K_{2m} \left( {\eta_{m}^{(2)} } \right) = (\beta^{\prime}_{m} - \eta_{m}^{2} )\left( {\frac{{B_{11} B_{22} \beta^{\prime\prime}_{m} - B_{12}^{2} \beta^{\prime}_{m} }}{{B_{11} B_{66} }} - \eta_{m}^{2} } \right) - \eta_{m}^{2} y_{1} y_{2} = 0\,\,. $$
(39)

The Eq. (39) is an analogue of the Rayleigh equation for a long enough orthotropic rectangular plate with a free side (compare with [8,9,10,11]). Thus, the eigenfrequencies of the problem (25–28) can be found from (38).

To find the corresponding eigenmodes, the coefficients \(w_{j} \,,\,j = \overline{1,4}\) have to be determined from the system of Eq. (34) and inserted into (33). We can take

$$ \begin{aligned} w_{1} & = \frac{{R_{1}^{(m)} \exp (z_{1} + 2z_{2} ) + R_{52}^{(m)} R_{2}^{(m)} \exp (z_{1} ) - 2R_{12}^{(m)} R_{22}^{(m)} R_{51}^{(m)} \exp (z_{2} )}}{{R_{51}^{(m)} R_{1}^{(m)} - R_{51}^{(m)} R_{2}^{(m)} \exp (2z_{1} ) + 2R_{11}^{(m)} R_{21}^{(m)} R_{52}^{(m)} \exp (z_{1} + z_{2} )}}, \\ w_{2} & = \frac{{R_{51}^{(m)} R_{2}^{(m)} - R_{51}^{(m)} R_{1}^{(m)} \exp (2z_{1} + z_{2} ) - 2R_{11}^{(m)} R_{21}^{(m)} R_{52}^{(m)} \exp (z_{1} )}}{{R_{51}^{(m)} R_{1}^{(m)} - R_{51}^{(m)} R_{2}^{(m)} \exp (2z_{1} ) + 2R_{11}^{(m)} R_{21}^{(m)} R_{52}^{(m)} \exp (z_{1} + z_{2} )}}, \\ w_{3} & = - \frac{{R_{52}^{(m)} R_{1}^{(m)} \exp (z_{1} ) + R_{52}^{(m)} R_{2}^{(m)} \exp (z_{1} + 2z_{2} ) - 2R_{12}^{(m)} R_{22}^{(m)} R_{51}^{(m)} \exp (2z_{1} + z_{2} )}}{{R_{51}^{(m)} R_{1}^{(m)} - R_{51}^{(m)} R_{2}^{(m)} \exp (2z_{1} ) + 2R_{11}^{(m)} R_{21}^{(m)} R_{52}^{(m)} \exp (z_{1} + z_{2} )}}, \\ w_{4} & = \exp (z_{2} ),\,\,\,R_{1}^{(m)} = R_{11}^{(m)} R_{22}^{(m)} - R_{12}^{(m)} R_{21}^{(m)} ,\,\,R_{2}^{(m)} = R_{11}^{(m)} R_{22}^{(m)} + R_{12}^{(m)} R_{21}^{(m)} . \\ \end{aligned} $$
(40)

as solutions to the system of Eq. (34) at a given dimensionless eigenfrequency characteristic \(\eta_{m}\).

5 Bending Vibrations of an Orthotropic Cantilever Rectangular Plate

Consider an orthotropic rectangular plate with thickness \(h,\,\,\) width \(\,s\), and length \(\,\,l\) (Fig. 2). Consider now the problem of the existence of free bending vibrations of a cantilever rectangular plate. Let us start with the equation of low-amplitude bending vibrations of the classical theory of orthotropic plates [17]

$$ \mu^{4} \left( {B_{11} \frac{{\partial^{4} u_{3} }}{{\partial \alpha^{4} }} + 2(B_{12} + 2B_{66} )\frac{{\partial^{4} u_{3} }}{{\partial \alpha^{2} \partial \beta^{2} }} + B_{22} \frac{{\partial^{4} u_{3} }}{{\partial \beta^{4} }}} \right) = \lambda u_{3} \,\,, $$
(41)

where \(\alpha \,\,(0 \le \alpha \le l)\) and \(\beta \,\,(0 \le \beta \le s)\) are the orthogonal rectilinear coordinates of a point of the median plane of the plate; \(u_{3}\) is the normal component of the displacement vector of a point of the median plane; \(B_{ik} ,\,\,i,k = 1,2,6\) are the elasticity coefficients; \(\mu^{4} = h^{2} /12\); \(\lambda = \omega^{2} \rho\), where \(\omega\) is the natural frequency; \(\rho\) is the density of the material.

The boundary conditions are given as follows:

$$ \left. {\frac{{\partial^{2} u_{3} }}{{\partial \alpha^{2} }} + \frac{{B_{12} }}{{B_{11} }}\frac{{\partial^{2} u_{3} }}{{\partial \beta^{2} }}} \right|_{\alpha = 0} = \,\left. {\frac{{\partial^{3} u_{3} }}{{\partial \alpha^{3} }} + \frac{{B_{12} + 4B_{66} }}{{B_{11} }}\frac{{\partial^{3} u_{3} }}{{\partial \alpha \partial \beta^{2} }}} \right|_{\alpha = 0} = 0, $$
(42)
$$ \,\,\left. {u_{3} } \right|_{\alpha = l} = \left. {\frac{{\partial u_{3} }}{\partial \alpha }} \right|_{\alpha = l} = 0\,, $$
(43)
$$ \frac{{B_{12} }}{{B_{22} }}\left. {\frac{{\partial^{2} u_{3} }}{{\partial \alpha^{2} }} + \frac{{\partial^{2} u_{3} }}{{\partial \beta^{2} }}} \right|_{\beta = 0,s} = \,\left. {\frac{{\partial^{3} u_{3} }}{{\partial \beta^{3} }} + \frac{{B_{12} + 4B_{66} }}{{B_{22} }}\frac{{\partial^{3} u_{3} }}{{\partial \beta \partial \alpha^{2} }}} \right|_{\beta = 0,s} = 0\,, $$
(44)

Here the conditions (42) and (44) mean that the edges \(\alpha = 0\) and \(\,\beta = 0,s\) are free; while the conditions (43) indicate that the edge \(\alpha = l\) is rigid-clamped. The problem (41–44) does not allow separation of variables. The differential operator corresponding to this problem is self-conjugate and nonnegative definite. Therefore, the generalized Kantorovich-Vlasov method of the reduction to ordinary differential equations can be used to find the vibration eigenfrequencies and eigenmodes [12,13,14,15,16]. The solution of the system (41) is searched in the form

$$ u_{3} = \,w_{m} (\theta_{m} \beta )\exp (\theta_{m} y\alpha ),\,\,\,\,\,m = \overline{1, + \infty } \,\,, $$
(45)

where \(w_{m} (\theta_{m} \beta )\,\,\) is defined in (2). The conditions (44) are satisfied automatically. Substitute (45) into Eq. (41). After multiplying the resulting equation by \(w_{m} (\theta_{m} \beta )\) and integrating it in the limits from \(0\) to \(s\) the characteristic equation is obtained

$$ R_{mm} = a^{2} \left( {\frac{{B_{11} }}{{B_{22} }}y^{4} - \frac{{2(B_{12} + 2B_{66} )}}{{B_{22} }}\beta^{\prime}_{m} y^{2} + \beta^{\prime}_{m} \beta^{\prime\prime}_{m} } \right) - \frac{{B_{66} }}{{B_{22} }}\eta_{m}^{2} = 0\,,\,\,\,m = \overline{1, + \infty } \,\,, $$
(46)
$$ \,\,\eta_{m}^{2} = \frac{\lambda }{{\theta_{m}^{2} B_{66} }},\,\,\,a^{2} = \theta_{m}^{2} h^{2} /12\,\,\,, $$
(47)

where \(\theta_{m}\) and \(\beta^{\prime}_{m} ,\beta^{\prime\prime}_{m}\) are defined in Eqs. (2) and (4), respectively. Let \(y_{3}\) and \(y_{4}\) be various roots of Eq. (46) with non-positive real parts, \(y_{2 + j} = - y_{j} \,\,,\,j = 3,4\). The solution of the problem (41–44) is searched in the form

$$ u_{3} = \sum\nolimits_{j = 3}^{6} {w_{m} (\theta_{m} \beta )\exp (\theta_{m} y_{j} \alpha )\,\,w_{j} } \,\,. $$
(48)

By inserting Eq. (48) into the boundary conditions (42) and (43), and after multiplying the resulting equations by \(w_{m} (\theta_{m} \beta )\), and integrating them in the limits from \(0\) to \(s\), the system of equations is obtained

$$ \left\{ \begin{gathered} \sum\limits_{j = 3}^{6} {R_{3j}^{(m)} } W_{j} = 0,\,\,\,\,\,\,\,\,\,\sum\limits_{j = 3}^{6} {R_{4j}^{(m)} \,} W_{j} = 0,\, \hfill \\ \sum\limits_{j = 3}^{6} {R_{7j}^{(m)} } W_{j} = 0,\,\,\,\,\,\,\,\,\,\sum\limits_{j = 3}^{6} \, R_{8j}^{(m)} W_{j} = 0\,\,. \hfill \\ \end{gathered} \right. $$
(49)
$$ \begin{aligned} R_{3j}^{(m)} & = y_{j}^{2} - \frac{{B_{12} }}{{B_{11} }}\beta^{\prime}_{m} ,\,\,\,R_{4j}^{(m)} = y_{j}^{3} - \frac{{B_{12} + 4B_{66} }}{{B_{11} }}\beta^{\prime}_{m} y_{j} ,\, \\ R_{7j}^{(m)} \, & = \exp (z_{j} )\,,\,\,\,\,R_{8j}^{(m)} = y_{j} \exp (z_{j} )\,\,;\,\,z_{j} = \theta_{m} y_{j} l\,,j = \overline{3,6} \,\,. \\ \end{aligned} $$
(50)

By equating the determinant of system (49) \(\Delta_{b}\) to zero and performing elementary operations on the columns of the determinant, the dispersion equation is obtained

$$ \Delta_{b} = \exp ( - z_{3} - z_{4} )\,(y_{4} - y_{3} )^{2} \,Det\left\| {b_{ij} } \right\|_{i,j}^{4} = 0\,\,, $$
(51)
$$ \begin{aligned} b_{11} & = R_{33}^{(m)} ,\,\,\,b_{12} = y_{3} + y_{4} ,\,\,\,b_{13} = b_{11} \exp (z_{3} )\,,\,\,\, \\ b_{14} & = b_{12} \exp (z_{4} ) + b_{11} [z_{3} z_{4} ]; \\ b_{21} & = R_{43}^{(m)} ,\,\,\,b_{22} = y_{3} y_{4} + \beta^{\prime}_{m} \,B_{12} /B_{11} ,\,\, \\ b_{23} & = - b_{21} \exp (z_{3} ),\,\, \\ b_{24} & = - b_{22} \exp (z_{4} ) - b_{21} [z_{3} z_{4} ]\, \\ b_{31} & = \exp (z_{3} ),\,\,\,b_{32} = [z_{3} z_{4} ],\,\, \\ b_{33} & = 1,\,\,b_{34} = 0;\,\,\,\,b_{41} = y_{3} \exp (z_{3} ),\,\,\, \\ b_{42} & = \exp (z_{4} ) + y_{3} [z_{3} z_{4} ],\, \\ b_{43} & = - y_{3} ,\,\, \\ b_{44} & = - 1;\,\,\,[z_{3} z_{4} ] = \theta_{m} l\,(\exp (z_{4} ) - \exp (z_{3} ))/(z_{4} - z_{3} );\,\,\,z_{j} = \theta_{m} y_{j} l\,,j = 3,4\,. \\ \end{aligned} $$
(52)

The Eq. (51) is equivalent to the equation

$$ \begin{aligned} Det\left| {b_{ij} } \right|_{i,j = 1}^{4} = & - K_{1m} (\eta_{m} )\,\,(1 + \exp (\,\,\,2\,\,(z_{3} + z_{4} ))) - 4y_{3} \,b_{12} \,b_{22} \,\exp \,(z_{3} + z_{4} ) \\ & \quad + (b_{11} b_{22} + b_{21} b_{12} )(\exp (2z_{3} ) + \exp (2z_{4} )) \\ & \quad + 2[b_{11} b_{21} + y_{3} \left( {b_{11} b_{22} + b_{21} b_{12} } \right)(\exp (z_{4} ) - \exp (z_{3} ))[z_{3} z_{4} ] \\ &\quad + 4y_{3} b_{11} b_{21} [z_{3} z_{4} ]^{2} = 0,\,\,m = \overline{1,\infty } \,. \\ \end{aligned} $$
(53)
$$ K_{1m} \left( {\eta_{m}^{2} } \right) = y_{3}^{2} y_{4}^{2} + 4\frac{{B_{66} }}{{B_{11} }}\beta^{\prime}_{m} y_{3} y_{4} - \left( {\frac{{B_{12} }}{{B_{11} }}} \right)\beta_{m}^{\prime 2} . $$
(54)

If \(y_{3}\) and \(y_{4}\) are the roots of Eq. (46) with negative real parts, then, at \(\theta_{m} l \to \infty\), the roots of Eq. (53) are approximated by the roots of the equation

$$ K_{1m} \left( {\eta_{m}^{2} } \right) = y_{3}^{2} y_{4}^{2} + 4\frac{{B_{66} }}{{B_{11} }}\beta^{\prime}_{m} y_{3} y_{4} - \left( {\frac{{B_{12} }}{{B_{11} }}} \right)^{2} \left( {\beta^{\prime}_{m} } \right)^{2} = 0\,,\,m = \overline{1,\infty } \,\,. $$
(55)

The Eq. (55) is an analogue of the Konenkov equation for a long enough orthotropic rectangular plate with a free side (compare with [8,9,10,11, 19, 20]). Thus, eigenfrequencies of the problem (41–44) can be found from (53).

To find the corresponding eigenmodes, the coefficients \(w_{j} \,,\,j = \overline{3,6}\) have to be determined from the system of Eq. (49) and inserted into Eq. (48). As solutions to the system of Eq. (49) at a given dimensionless eigenfrequency characteristic \(\eta_{m}\), it can be taken

$$ \begin{aligned} W_{3} & = \frac{{R_{3}^{(m)} \exp (z_{3} + z_{4} ) - R_{4}^{(m)} \exp (z_{3} ) + 2R_{34}^{(m)} R_{44}^{(m)} \exp (z_{4} )}}{{R_{3}^{(m)} - R_{4}^{(m)} \exp (2z_{3} ) + 2R_{33}^{(m)} R_{43}^{(m)} \exp (z_{3} + z_{4} )}}\,\,, \\ W_{4} & = \frac{{R_{3}^{(m)} \exp (2z_{3} + z_{4} ) - R_{4}^{(m)} \exp (z_{4} ) + 2R_{33}^{(m)} R_{43}^{(m)} \exp (z_{3} )}}{{R_{3}^{(m)} - R_{4}^{(m)} \exp (2z_{3} ) + 2R_{33}^{(m)} R_{43}^{(m)} \exp (z_{3} + z_{4} )}}\,\,, \\ W_{5} & = \frac{{\exp (z_{3} )[R_{3}^{(m)} + R_{4}^{(m)} \exp (z_{4} ) - 2R_{34}^{(m)} R_{44}^{(m)} \exp (z_{3} )]}}{{R_{3}^{(m)} - R_{4}^{(m)} \exp (2z_{3} ) + 2R_{33}^{(m)} R_{43}^{(m)} \exp (z_{3} + z_{4} )}}\,\,, \\ W_{6} & = - \exp (z_{4} );\,\,R_{3}^{(m)} = R_{33}^{(m)} R_{44}^{(m)} - R_{34}^{(m)} R_{43}^{(m)} ,\,\,R_{4}^{(m)} = R_{33}^{(m)} R_{44}^{(m)} + R_{34}^{(m)} R_{43}^{(m)} \,\,. \\ \end{aligned} $$
(56)

6 Asymptotics of Dispersion Eq. (24)

6.1 Asymptotics of Dispersion Eq. (24) at \(\varepsilon_{m} \to 0\)

Using the previous formulas, we assume that \(\eta_{1m} = \eta_{2m} = \eta_{3m} = \eta_{m}\). Then, as \(\varepsilon_{m} \to 0\,\,\), Eq. (12) transform into

$$ c_{m} = y^{4} - B_{2} y^{2} + \frac{{B_{11} + B_{66} }}{{B_{11} }}\eta_{m}^{2} y^{2} + (\beta^{\prime}_{m} - \eta {}_{m}^{2} )\left( {\frac{{B_{22} }}{{B_{11} }}\beta^{\prime\prime}_{m} - \frac{{B_{66} }}{{B_{11} }}\eta {}_{m}^{2} } \right) = 0\,,\,m = \overline{1, + \infty } \,\,, $$
(57)
$$ R_{mm} = a^{2} \left( {\frac{{B_{11} }}{{B_{22} }}y^{4} - \frac{{2(B_{12} + 2B_{66} )}}{{B_{22} }}\beta^{\prime}_{m} y^{2} + \beta^{\prime}_{m} \beta^{\prime\prime}_{m} } \right) - \frac{{B_{66} }}{{B_{22} }}\eta_{m}^{2} = 0\,,\,m = \overline{1, + \infty } \,\,. $$
(58)

Here the limiting process \(\varepsilon_{m} \to 0\) is understood in the sense that by fixing the radius \(R\) and \(b\)– the distance between the boundary generatrices of the cylindrical panel, a transition to a cylindrical panel of radius \(R^{\prime} = nR\) and to the limit \(\varepsilon^{\prime}_{m} = 1/(n\theta_{m} R) = \varepsilon_{m} /n \to 0\) at \(n \to \infty\) is performed.

The Eqs. (57) and (58) are characteristic equations for the equations of planar and bending vibrations of orthotropic cantilever plates, respectively. The roots of the Eqs. (57) and (58) with non-positivec real parts, as in Sects. 4 and 5, are denoted by \(y_{1} ,y_{2}\) and \(y_{3} ,y_{4}\), respectively. In the same way as in [19], it is proved that for

$$ \varepsilon_{m} < < 1;\,\,\,\,\,y_{i} \ne y_{j} ,\,\,\,i \ne j, $$
(59)

the roots \(\chi^{2}\) of Eq. (12) can be presented as

$$ \chi_{i}^{2} = y_{i}^{2} + \alpha_{i}^{(m)} \varepsilon_{m}^{2} + \beta_{i}^{(m)} \varepsilon_{m}^{4} + ...,\,\,\,\,i = \overline{1,4} \,,\,\,\,m = \overline{1, + \infty } \,\,\,\,. $$
(60)

Under the condition (59), considering the relations (16), (22) and (60) and the fact that

$$ M_{3j}^{(m)} = M_{4j}^{(m)} = M_{7j}^{(m)} = M_{8j}^{(m)} = O(\varepsilon_{m}^{2} ),\,\,j = 1,\,2\,\,,\, $$
(61)

Equation (24) can be reduced to the form

$$ \left. {Det\left\| {m_{ij} } \right\|} \right|_{i,j = 1}^{8} = N^{2} (\eta_{m}^{2} )K_{3m}^{2} (\eta_{m}^{2} )Det\left| {l_{ij} } \right|_{i,j = 1}^{4} Det\left| {b_{ij} } \right|_{i,j = 1}^{4} + O(\varepsilon_{m}^{2} ) = 0,\,\,m = \overline{1, + \infty } \,, $$
(62)

where \(Det\left| {l_{ij} } \right|_{i,j = 1}^{4}\) and \(Det\left| {b_{ij} } \right|_{i,j = 1}^{4}\) are determined by (38) and (53), respectively, and

$$ \begin{gathered} N(\eta _{m}^{2} ) = (y_{3} + y_{1} )(y_{3} + y_{2} )(y_{4} + y_{1} )(y_{4} + y_{2} ), \hfill \\ K_{{3m}} (\eta _{m}^{2} ) = (\beta _{m}^{\prime } - \eta _{m}^{2} )\left( {\frac{{B_{{22}} }}{{B_{{11}} }}\beta _{m}^{{\prime \prime }} - \frac{{B_{{66}} }}{{B_{{11}} }}\eta _{m}^{2} } \right)\left( {\frac{{B_{{12}} }}{{B_{{12}} + B_{{66}} }} - a^{2} \frac{{\left( {B_{{12}} + 4B_{{66}} } \right)}}{{B_{{66}} }}\beta _{m}^{\prime } } \right)^{2} \hfill \\ \quad + \left( {B_{2} - \frac{{B_{{11}} + B_{{66}} }}{{B_{{11}} }}\eta _{m}^{2} } \right) \times \left( {\frac{{B_{{12}} }}{{B_{{12}} + B_{{66}} }} - a^{2} \frac{{\left( {B_{{12}} + 4B_{{66}} } \right)}}{{B_{{66}} }}\beta _{m}^{\prime } } \right) \hfill \\ \quad \times \left( {\frac{{B_{{22}} \beta _{m}^{\prime } + B_{{12}} \eta _{m}^{2} }}{{B_{{12}} + B_{{66}} }} + (\beta _{m}^{\prime } - \beta _{m}^{{\prime \prime }} )\frac{{B_{{12}} B_{{22}} }}{{B_{{66}} (B_{{12}} + B_{{66}} )}} + a^{2} \frac{{B_{{22}} }}{{B_{{66}} }}\beta _{m}^{\prime } \beta _{m}^{{\prime \prime }} } \right) \hfill \\ \quad + \left( {\frac{{B_{{22}} \beta _{m}^{\prime } + B_{{12}} \eta _{m}^{2} }}{{B_{{12}} + B_{{66}} }} + (\beta _{m}^{\prime } - \beta _{m}^{{\prime \prime }} )\frac{{B_{{12}} B_{{22}} }}{{B_{{66}} (B_{{12}} + B_{{66}} )}} + a^{2} \frac{{B_{{22}} }}{{B_{{66}} }}\beta _{m}^{\prime } \beta _{m}^{{\prime \prime }} } \right)^{2} . \hfill \\ \end{gathered} $$
(63)

From Eq. (62), it follows that in the limit \(\varepsilon_{m} \to 0\), Eq. (24) decompose into the totality of equations

$$ \begin{gathered} Det\left| {l_{{ij}} } \right|_{{i,j = 1}}^{4} = 0,m = \overline{{1, + \infty }} ;Det\left| {b_{{ij}} } \right|_{{i,j = 1}}^{4} = 0,m = \overline{{1, + \infty }} ;K_{{3M}} (\eta _{m}^{2} ) = 0, \hfill \\ m = \overline{{1, + \infty }} . \hfill \\ \end{gathered} $$
(64)

Here the first two equations are the dispersion equations of the planar and bending vibrations, respectively, as in the similar problems for an orthotropic cantilever rectangular plate.

The roots of the third equation correspond to planar vibrations of a cylindrical panel. The third equation appears as the result of using the equation of the corresponding classical theory of orthotropic cylindrical shells.

If \(y_{1} ,y_{2}\) and \(y_{3} ,y_{4}\) are the roots of the Eqs. (57) and (58), respectively, with negative real parts, then, at \(\theta_{m} l \to \infty\), Eqs. (24) and (62) will be transformed into the equations

$$ \begin{aligned} Det\left\| {m_{ij} } \right\|_{i,j = 1}^{8} & = \left( {\left( {B_{12} + B_{66} } \right)/B_{11} } \right)^{2} N^{2} (\eta_{m}^{2} )Q(\eta_{m}^{2} )K_{1m} (\eta_{m}^{2} )K_{2m} (\eta_{m}^{2} )K_{3m}^{2} (\eta_{m}^{2} )\\ & \quad + O(\varepsilon_{m}^{2} ) + \sum\nolimits_{j = 1}^{4} {O(\exp (z_{j} ))} = 0,\,\,m = \overline{1, + \infty \,} \,. \\ \end{aligned} $$
(65)

From Eq. (65), it follows that, for \(\varepsilon_{m} \to 0\) and \(\theta_{m} l \to \infty\), the roots of dispersion Eq. (24) are approximated by roots of the equations.

$$ K_{1m} (\eta_{m}^{2} ) = 0,\,m = \overline{1, + \infty \,;} \,\,\,K_{2m} (\eta_{m}^{2} ) = 0,\,m = \overline{1, + \infty \,;} \,\,\,K_{3m} (\eta_{m}^{2} ) = 0,\,m = \overline{1, + \infty } \,\,. $$
(66)

The first two equations of (66) are the dispersion equations of the bending and planar vibrations of long enough orthotropic cantilever rectangular plate with free sides (see Eqs. (55) and (39)). Hence, for small \(\varepsilon_{m}\) and large \(\theta_{m} l\), the approximate values of the roots of Eq. (24) correspond to the roots of Eqs. (64) and (66) (compare Tables 1 and 2).

6.2 Asymptotics of Dispersion Eq. (24) at \(\theta_{m} l \to \infty\)

In the previous formulas it was assumed that the roots \(\chi_{1} ,\chi_{2} ,\chi_{3}\), and \(\chi_{4}\) (the roots of Eq. (12)) have negative real parts. Then Eq. (24) can be reduced to the form

$$ Det\left\| {m_{ij} } \right\|_{i,j = 1}^{8} = Det\left\| {m_{ij} } \right\|_{i,j = 1}^{4} .Det\left\| {m_{ij} } \right\|_{i = 5,j = 1}^{8,4} + \sum\nolimits_{j = 1}^{4} {O(\exp (\theta_{m} \chi_{j} l))} = 0\,,\,m = \overline{1, + \infty } \,\,. $$
(67)

Hence, it follows that for \(\theta_{m} l \to \infty\) the roots of Eq. (24) are approximated by roots of the equations

$$ Det\left\| {m_{ij} } \right\|_{i,j = 1}^{4} = 0\,,\,m = \overline{1, + \infty \,;} \,\,\,Det\left\| {m_{ij} } \right\|_{i = 5,j = 1}^{8,4} = 0,\,\,m = \overline{1, + \infty } \,\,. $$
(68)

The first totality of Eq. (68) determines all possible localized free vibrations at the free end faces of an orthotropic semi-infinite cylindrical panel, or determines all possible localized free vibrations at the free faces of an orthotropic cantilever cylindrical panel.

The second totality of Eq. (68) determines all possible localized free vibrations at the free end faces of an orthotropic semi-infinite cantilever cylindrical panel.

Notice, that if \(\varepsilon_{m} \to 0\), the equations of (68) have the following asymptotic forms

$$ \begin{aligned} Det\left\| {m_{ij} } \right\|_{i,j = 1}^{4} & = \left( {\left( {B_{12} + B_{66} } \right)/B_{11} } \right)^{2} N(\eta_{m}^{2} )K_{1m} (\eta_{m}^{2} )K_{2m} (\eta_{m}^{2} )K_{3m} (\eta_{m}^{2} )\\ & \quad + O(\varepsilon_{m}^{2} )\,,\,\,m = \overline{1, + \infty } \,, \\ Det\left\| {m_{ij} } \right\|_{i = 5,j = 1}^{8,4} & = N(\eta_{m}^{2} )K_{3m} (\eta_{m}^{2} )Q(\eta_{m}^{2} ) + O(\varepsilon_{m}^{2} )\,,\,\,\,m = \overline{1, + \infty } \,\,\,. \\ \end{aligned} $$
(69)

Thus, by taking into account (68) and (69), we conclude that the dispersion Eq. (24) for \(\theta_{m} l \to \infty \,\) and \(\varepsilon_{m} \to 0\) take the form (65).

7 Numerical Results

In the Table 1 the values of some \(\eta_{m}\) roots of the first two equations of (64) and (66) are given for an orthotropic cantilever rectangular boron plastic plate with parameters [18]

$$ \begin{aligned} \rho & = 2 \cdot 10^{3} \,kg/M^{3} ;\,\,E_{1} = 2.646.\,10^{11} N/M^{2} \,;\, \\ {\rm E}_{2} & = 1.323 \cdot 10^{10} ;\,\,\,\,G = 9.604 \cdot 10^{9} \,;\nu_{1} = 0.2\,;\,\nu_{2} = 0.01\,. \\ \end{aligned} $$
(70)

In the Table 2 some dimensionless characteristics of the eigenvalues \(\eta_{m}\) for predominantly bending, predominantly planar and nonsymmetrical vibrations of an orthotropic cantilever cylindrical boron plastic panel with the same mechanical characteristics and the geometrical parameters: \(R = 40\,;\,s = 4.00167;\,\,l = 5,\,\,l = 15\,.\) are given.

Table 1. Characteristics of Eigenfrequencies of a cantilever rectangular Boron Plate with \(s = 4,\,\,l = 5,\,l = 15.\)
Full size table
Table 2. Characteristics of Eigenfrequencies for Predominantly Bending, Predominantly Planar and Nonsymmetrical Vibrations of an Cantilever Cylindrical Boron Plastic Panel with \(s = 4.00167,\,\,l = 5,\,\,l = 15.\)
Full size table

In the Table 2 after the characteristics of eigenfrequencies the type of vibration is indicated: \(b\)- predominantly bending, \(e\)- predominantly planar. For \(1 \le m \le 16\), the third equation of (64) has no roots. The elasticity modules \({\rm E}_{1}\) and \({\rm E}_{2}\) correspond to the directions of generatrix and directrix, respectively.

In the Table 2, the case with \(\eta_{1} = \eta_{2} = \eta_{3} = \eta\) corresponds to the problem (5–8). The case with \(\eta_{1} = \eta_{2} = 0\) and \(\eta_{3} = \eta\) corresponds to the problem (5–8), where are no tangential components of the inertia force, i.e., we have the predominantly bending type of vibrations. The case with \(\eta_{1} = \eta_{2} = \eta ,\,\,\eta_{3} = 0\) corresponds to the predominantly planar type of vibrations.

The following equalities hold for isotropic materials:

$$ \,\frac{{B_{12} }}{{B_{11} }} = \frac{{B_{12} }}{{B_{22} }} = \upsilon \,,\,\,\frac{{B_{66} }}{{B_{11} }} = \frac{{B_{66} }}{{B_{22} }} = \frac{1 - \upsilon }{2}\,\,. $$
(71)

Hence, in the dispersion equations and the characteristics calculations it can be set

$$ B_{11} = B_{22} = 1,\,\;B_{12} = \upsilon ,\,\;B_{66} = (1 - \upsilon )/2\,. $$

8 Conclusion

Numerical calculations show that the first eigenfrequencies localized at the free end of the cantilever cylindrical panel where the normal component of inertia force is not zero are the frequencies of the predominantly bending type. Along with the first frequencies of quasitransverse vibrations, there are frequencies of undamped quasitangential vibrations. With the increase of \(m\), these vibrations become of Rayleigh type. The analysis of the numerical data indicates that for \(\varepsilon_{m} \to 0\) free vibrations of cantilever cylindrical panel decompose into quasitransverse and quasitangential vibrations, and their frequencies tend to the frequencies of a cantilever rectangular plate. Numerical results show that asymptotic formulas (62) and (65) of dispersion Eq. (24) and the mechanism presented here are good reference points for finding the eigenfrequencies of the problem (5–8). The first eigenfrequencies of vibrations of cantilever cylindrical panel depend on the chosen basic functions satisfying the same boundary conditions. For \(\theta_{m} \to \infty\), the frequencies of vibrations at free end faces of a finite cantilever cylindrical panel become practically independent of the basic functions and of the boundary conditions on generatrices [8, 9, 20].

Note that in the current work and in [20] the same basic functions are used for Kantorovich-Vlasov method and the characteristic equations of the classical equations of cylindrical shells and plates coincide. Meanwhile due to the different boundary conditions the dispersion equations of the problems are different and lead to different distributions of natural frequencies.