Exact Analytical Periodic Solutions in Special Cases and Numerical Analysis of a Half-Undamped 1-DOF Piecewise-Linear Vibratory System

Abstract

A lot of realistic systems are better described by piecewise-linear models than by continuous models, including systems with dry friction or impact as well as some controlled systems. Such models are usually strongly nonlinear and do not have general exact analytical solutions. This paper analyzes a harmonically excited 1-DOF piecewise-linear vibratory system that has a damped domain and an undamped domain. The purposes are to find some exact analytical solutions of the system and find the connection between the analytical solutions and the numerical ones. Though the system is linear and can be analytically analyzed in each domain, no general closed-form solution for its motion has been found because the switching times between the two domains are solutions of transcendental equations. To solve the problem, a special method is proposed: the initial conditions and the parameters are adjusted so that the homogeneous solution in the damped domain is cancelled, and the excitation is subharmonic in the undamped domain. As a result, the transcendental equations are simplified and exact analytical expressions for periodic motions are found for special cases of the parameters. The obtained motions are single-penetration multi-periodic, which is a typical behavior of the considered bilinear system as seen in the bifurcation diagram. Thus, the proposed method may be used to investigate dynamic behaviors of more complicated piecewise-linear systems.

1 Introduction

Piecewise ordinary differential equations (ODEs) are found useful to model real systems where non-smooth phenomena, e.g., dry friction and impact, may occur [1,2,3]. With the development of control methods [4,5,6], the controllers can also produce non-smoothness. The solutions of piecewise ODEs, which reflex the dynamics of the modelled systems, are the topic of a lot of studies, and they do show abundant of phenomena including periodic and chaotic vibrations [7,8,9,10]. Some solutions may coexist, leading to difficulties of global dynamics analysis. For instance, examining the same piecewise-linear system with asymmetric piecewise stiffness and damping, two coexisting periodic solutions are reported in [9] while it is shown later that there are more coexisting solutions including a chaotic solution [10], and there is still no guarantee that all solutions have been found. Furthermore, the non-smooth nature of the system may make common methods for smooth system become less effective. Thus, specialized numerical algorithms [7,8,9,10] and semi-analytical method [2] have been developed to study this type of systems.

Even in the case of piecewise-linear, i.e., the ODEs are linear in each domain, it is well-known that there is usually no analytical solution if harmonic excitation presents [2]. It is because the difficulties in determining the switching times between the domains require solutions using numerical methods. This approach is adopted by all the mentioned studies on the topic.

A curios question arises as to find piecewise-linear ODEs that have exact analytical periodic solutions, and if they exist, the next question would be to find the connection between the obtained results and the solutions of the non-analytical-solution cases. To answer the former question, this paper presents an original method: simplifying the equations for switching times by adjusting the system parameters.

This paper focuses on a harmonically excited 1-DOF system with a gap-activate gap-deactivate (GAGD) linear viscous-elastic support and a GAGD spring. Firstly, the model and its equations are presented. Secondly, analytical analysis is performed where possible. Then, the parameters are adjusted to get special cases that have exact analytical solutions. Lastly, numerical analysis is performed to investigate the global dynamics of the system.

2 The Model Problem

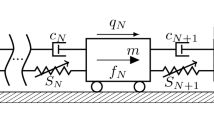
The system depicted in Fig. 1 has two different domains of motion caused by the GAGD supports [10]: the first is the damped domain in which the displacement of the body is positive (Fig. 1a); the second is the undamped domain in which the displacement of the body is negative, and no damping is active (Fig. 1b). The governing equations are

$$ \left\{ \begin{gathered} m\ddot{u} + d\dot{u} + k_1 u = F\cos (\Omega t){\text{ if }}u \ge 0 \hfill \\ m\ddot{u} + k_2 u = F\cos (\Omega t){\text{ if }}u < 0 \hfill \\ \end{gathered} \right. $$

(1)

The parameters m, d, k₁, k₂, and Ω are positive.

Fig. 1.

A half-undamped 1-DOF piecewise-linear vibratory system.

The dimensionless forms read

$$ \left\{ \begin{gathered} \ddot{x} + 2\gamma \dot{x} + \omega_1^2 x = \cos \tau {\text{ if }}x \ge 0 \hfill \\ \ddot{x} + \omega_2^2 x = \cos \tau {\text{ if }}x < 0 \hfill \\ \end{gathered} \right. $$

(2)

in which $\tau = \Omega t,x = \frac{m\Omega^2 }{F}u,\omega_1 = \frac{1}{\Omega }\sqrt {\frac{k_1 }{m}} ,\omega_2 = \frac{1}{\Omega }\sqrt {\frac{k_2 }{m}} ,\gamma = \frac{d}{2m\Omega }$, and the over dot now denotes $\frac{{\text{d}}}{{{\text{d}}\tau }}$ for the sake of simplicity. Consider the initial conditions

$$ \left\{ \begin{gathered} x(\tau_0 ) = 0 \hfill \\ \dot{x}(\tau_0 ) = v_0 > 0 \hfill \\ \end{gathered} \right. $$

(3)

in which 0 ≤ τ₀ < 2π. The body initially moves in the damped domain and until a time point τ₁ that

$$ \left\{ \begin{gathered} x(\tau_1 ) = 0 \hfill \\ \dot{x}(\tau_1 ) = v_1 < 0 \hfill \\ \end{gathered} \right., $$

(4)

the body moves into the undamped domain until a time point τ₂ that the displacement reaches zero and the velocity is positive, and so on. One can write the body’s motion from τ₀ and τ₂ as follows

$$ \left\{ \begin{gathered} x_I (\tau ) = x_{Ih} (\tau ) + x_{Ip} (\tau ) \, \tau_0 \le \tau \le \tau_1 \hfill \\ x_{II} (\tau ) = x_{IIh} (\tau ) + x_{IIp} (\tau ) \, \tau_1 \le \tau \le \tau_2 \hfill \\ \end{gathered} \right., $$

(5)

Where the subscription I is for the damped domain and II for the undamped domain.

3 Analytical Analysis

3.1 Damped Domain

The particular solution is

$$ x_{Ip} (\tau ) = A_I \cos \tau + B_I \sin \tau $$

(6)

with the coefficients

$$ A_I = \frac{\omega_1^2 - 1}{{(\omega_1^2 - 1)^2 + 4\gamma^2 }},\,\,\,\,\,B_I = \frac{2\gamma }{{(\omega_1^2 - 1)^2 + 4\gamma^2 }} $$

(7)

The homogeneous solution in the damped domain is

$$ \left\{ \begin{gathered} x_{Ih} (\tau ) = e^{ - \gamma (\tau - \tau_0 )} \left( {C_I \cos \left( {\sqrt {\omega_1^2 - \gamma^2 } (\tau - \tau_0 )} \right) + D_I \sin \left( {\sqrt {\omega_1^2 - \gamma^2 } (\tau - \tau_0 )} \right)} \right){\text{ if }}\gamma < \omega_1 \hfill \\ x_{Ih} (\tau ) = C_I e^{ - \gamma (\tau - \tau_0 )} + D_I (\tau - \tau_0 )e^{ - \gamma (\tau - \tau_0 )} {\text{ if }}\gamma = \omega_1 \hfill \\ x_{Ih} (\tau ) = C_I e^{ - (\gamma + \sqrt {\gamma^2 - \omega_1^2 } )(\tau - \tau_0 )} + D_I e^{ - (\gamma - \sqrt {\gamma^2 - \omega_1^2 } )(\tau - \tau_0 )} {\text{ if }}\gamma > \omega_1 \hfill \\ \end{gathered} \right. $$

(8)

The constants of integral C_I and D_I are obtained from the initial conditions (3): in underdamped case

$$ \left\{ \begin{gathered} C_I = - A_I \cos \tau_0 - B_I \sin \tau_0 \hfill \\ D_I = \frac{v_0 + A_I \sin \tau_0 - B_I \cos \tau_0 - \gamma (A_I \cos \tau_0 + B_I \sin \tau_0 )}{{\sqrt {\omega_1^2 - \gamma^2 } }} \hfill \\ \end{gathered} \right., $$

(9)

in critical damped case

$$ \left\{ \begin{gathered} C_I = - A_I \cos \tau_0 - B_I \sin \tau_0 \hfill \\ D_I = v_0 + A_I \sin \tau_0 - B_I \cos \tau_0 - \gamma (A_I \cos \tau_0 + B_I \sin \tau_0 ) \hfill \\ \end{gathered} \right., $$

(10)

and in overdamped case

$$ \left\{ \begin{gathered} C_I = \frac{{ - v_0 - A_I \sin \tau_0 + B_I \cos \tau_0 + (\gamma - \sqrt {\gamma^2 - \omega_1^2 } )(A_I \cos \tau_0 + B_I \sin \tau_0 )}}{{2\sqrt {\gamma^2 - \omega_1^2 } }} \hfill \\ D_I = \frac{{v_0 + A_I \sin \tau_0 - B_I \cos \tau_0 - (\gamma + \sqrt {\gamma^2 - \omega_1^2 } )(A_I \cos \tau_0 + B_I \sin \tau_0 )}}{{2\sqrt {\gamma^2 - \omega_1^2 } }} \hfill \\ \end{gathered} \right.. $$

(11)

3.2 Undamped Domain

In the non-resonant case ω₂ ≠ 1, the particular solution is

$$ x_{IIp} (\tau ) = A_{II} \cos \tau + B_{II} \sin \tau $$

(12)

with the coefficients.

$$ A_{II} = \frac{1}{\omega_2^2 - 1},\,\,B_{II} = 0 $$

(13)

In the resonant case ω₂ = 1, the particular solution is

$$ x_{IIp} (\tau ) = A_{II} \tau \cos \tau + B_{II} \tau \sin \tau $$

(14)

with the coefficients

$$ A_{II} = 0,\,\,B_{II} = \frac{1}{2} $$

(15)

The homogeneous solution in the undamped domain is

$$ x_{IIh} (\tau ) = C_{II} \cos \left( {\omega_2 (\tau - \tau_1 )} \right) + D_{II} \sin \left( {\omega_2 (\tau - \tau_1 )} \right). $$

(16)

The constants of integral are

$$ \left\{ \begin{gathered} C_{II} = - A_{II} \cos \tau_1 - B_{II} \sin \tau_1 \hfill \\ D_{II} = \frac{{v_1 + A_{II} \sin \tau_1 - B_{II} \cos \tau_1 }}{\omega_2 } \hfill \\ \end{gathered} \right.\,\,{\text{if}}\,\,\omega_{2} \, \ne \,{1}, $$

(17)

$$ \left\{ \begin{gathered} C_{II} = - A_{II} \tau_1 \cos \tau_1 - B_{II} \tau_1 \sin \tau_1 \hfill \\ D_{II} = \frac{{v_1 + A_{II} \tau_1 \sin \tau_1 - A_{II} \cos \tau_1 - B_{II} \tau_1 \cos \tau_1 - B_{II} \sin \tau_1 }}{\omega_2 } \hfill \\ \end{gathered} \right.\,\,{\text{if}}\,\,\omega_{2} = 1 $$

(18)

Since the body is back to the first domain at τ₂, and generally at τ_2k for any non-negative integer k, its motion in the time interval [τ_2k, τ_2k+2] can be obtained in a similar way. The equations in this section, however, do not give the analytical solution for the initial problem because the switching times τ_i (i = 1, 2, …) is not known yet. Generally, each of them is a solution of one of the transcendental equations

$$ A\cos x + B\sin x + C\cos (\omega x) + D\sin (\omega x) = 0, $$

(19)

$$ Ax\cos x + Bx\sin x + C\cos x + D\sin x = 0, $$

(20)

$$ A\cos x + B\sin x + e^{ - \beta x} (C\cos (\omega x) + D\sin (\omega x)) = 0, $$

(21)

$$ A\cos x + B\sin x + e^{ - \beta x} (C + xD) = 0, $$

(22)

$$ A\cos x + B\sin x + Ce^{ - \alpha x} + De^{ - \beta x} = 0, $$

(23)

where A, B, C and D are real constants, and α, β and ω are positive constants.

Such transcendental equations do not have general closed-form solutions. Thus, the switching times and the solutions of the ODEs do not have general analytical expressions.

4 Special Cases with Analytical Periodic Solutions

On the one hand, the transcendental equations to solve for switching times depend on five parameters: ω₁, ω₂, γ, τ₀ and v₀. On the other hand, if

$$ \left\{ \begin{gathered} \tau_2 - \tau_0 = 2n\pi \hfill \\ v_2 = v_0 \hfill \\ \end{gathered} \right. \, n = 1,2,... $$

(24)

a period-n motion will be found. The critical idea is to make the transcendental equations simpler. In the damped domain, simplification can be done by eliminating the homogeneous solution, which means

$$ C_I = D_I = 0, $$

(25)

The following initial conditions and terminal conditions must hold

$$ \left\{ \begin{gathered} x_I (\tau_0 ) = \frac{\omega_1^2 - 1}{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\cos \tau_0 + \frac{2\gamma }{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\sin \tau_0 = 0 \hfill \\ v_0 = \dot{x}_I (\tau_0 ) = - \frac{\omega_1^2 - 1}{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\sin \tau_0 + \frac{2\gamma }{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\cos \tau_0 > 0 \hfill \\ x_I (\tau_1 ) = \frac{\omega_1^2 - 1}{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\cos \tau_1 + \frac{2\gamma }{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\sin \tau_1 = 0 \hfill \\ v_1 = \dot{x}_I (\tau_1 ) = - \frac{\omega_1^2 - 1}{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\sin \tau_1 + \frac{2\gamma }{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\cos \tau_1 > 0 \hfill \\ \end{gathered} \right.{ 0} \le \tau_0 < 2\pi. $$

(26)

The solution for the first two lines of (26) are

$$ \tau_0 = {\text{atan}} 2(1 - \omega_1^2 ,2\gamma ),\,\,v_0 = \frac{1}{{\sqrt {(\omega_1^2 - 1)^2 + 4\gamma^2 } }} $$

(27)

The motion of the body in the damped domain is harmonic, so the displacement reaches zero after a half period; hence

$$ \tau_0 = \tau_1 + \pi ,\,\,v_1 = - v_0. $$

(28)

The motion of the body in the undamped domain (non-resonant) is deduced from Subsect. 3.2

$$ x_{II} (\tau ) = \frac{1}{\omega_2^2 - 1}\cos \tau - \frac{1}{\omega_2^2 - 1}\cos \tau_1 \cos \left( {\omega_2 (\tau - \tau_1 )} \right) + \frac{{ - v_0 + \frac{1}{\omega_2^2 - 1}\sin \tau_1 }}{\omega_2 }\sin \left( {\omega_2 (\tau - \tau_1 )} \right). $$

(29)

Equation (29) already satisfies initial conditions for the motion in the undamped domain. It is desired to also satisfy the terminal conditions according to (24):

$$ \left\{ \begin{gathered} x_{II} (\tau_1 + (2n - 1)\pi ) = 0 \hfill \\ \dot{x}_{II} (\tau_1 + (2n - 1)\pi ) = v_0 \hfill \\ \end{gathered} \right. \, n = 1,2,... $$

(30)

It is easily proved that if

$$ \omega_2 = \frac{1}{2n - 1} \,\,\,\, n = 2,\,\,3,\,\,...\,\,, $$

(31)

Equation (30) is satisfied. The case n = 1 is excluded since it leads to resonance and invalidates (29).

The motion of the body in the time interval from τ₀ to τ₂ is then expected to be

$$ \left\{ \begin{gathered} x(\tau ) = \frac{\omega_1^2 - 1}{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\cos \tau + \frac{2\gamma }{{(\omega_1^2 - 1)^2 + 4\gamma^2 }}\sin \tau \, \tau_0 = {\text{atan}} 2(1 - \omega_1^2 ,2\gamma ) \le \tau < \tau_0 + \pi \hfill \\ x(\tau ) = - \frac{(2n - 1)^2 }{{4n(n - 1)}}\cos \tau - \frac{(2n - 1)^2 }{{4n(n - 1)}}\cos \tau_0 \cos \left( {\frac{\tau - \tau_0 - \pi }{{2n - 1}}} \right) \hfill \\ \, - \left( {\frac{2n - 1}{{\sqrt {(\omega_1^2 - 1)^2 + 4\gamma^2 } }} - \frac{(2n - 1)^3 }{{4n(n - 1)}}\sin \tau_0 } \right)\sin \left( {\frac{\tau - \tau_0 - \pi }{{2n - 1}}} \right) \, \tau_0 + \pi \le \tau \le \tau_0 + 2n\pi \hfill \\ \end{gathered} \right. $$

(32)

It should be noted that (32) only becomes a valid solution of the original system if

$$ x(\tau ) \le 0 \,\,\, \tau_0 + \pi \le \tau < \tau_0 + 2n\pi $$

(33)

Inequality (33) is transcendental, so it is not easy to solve. However, its exact solution is not necessary here.

To conclude, the following system

$$ \left\{ \begin{gathered} \ddot{x} + 2\gamma \dot{x} + \omega_1^2 x = \cos \tau {\text{ if }}x \ge 0 \hfill \\ \ddot{x} + \frac{1}{(2n - 1)^2 }x = \cos \tau \, n = 2,3,...{\text{ if }}x < 0 \hfill \\ \end{gathered} \right. $$

(34)

has a period-n solution of the form (32) if (33) is satisfied.

A question arises, as to whether there exists a valid solution for any value of n. It has not been strictly proved, but it can be illustrated by considering an even more specific case of ω₁ = 1

$$ \left\{ {\begin{array}{*{20}l} {\ddot{x} + 2\gamma \dot{x} + x = \cos \tau \,{\text{if}}\,x \ge 0} \\ {\ddot{x} + \frac{1}{{(2n - 1)^{2} }}x = \cos \tau n = 2,3,...\,{\text{if}}\,x < 0.} \\ \end{array} } \right. $$

(35)

In this case, (32) becomes

$$ \left\{ \begin{gathered} x(\tau ) = \frac{1}{2\gamma }\sin \tau \, 0 \le \tau < \pi \hfill \\ x(\tau ) = - \frac{(2n - 1)^2 }{{4n(n - 1)}}\cos \tau - \frac{(2n - 1)^2 }{{4n(n - 1)}}\cos \left( {\frac{\tau - \pi }{{2n - 1}}} \right) - \frac{2n - 1}{{2\gamma }}\sin \left( {\frac{\tau - \pi }{{2n - 1}}} \right) \, \pi \le \tau \le 2n\pi \hfill \\ \end{gathered} \right. $$

(36)

In the second line of (36), only the last term can be varied by changing positive parameter γ. This term is negative in the open interval (π, 2nπ) and gets smaller as γ is reduced. In other words, one may probably reduce γ to a sufficiently small value so that (33) is satisfied.

For illustration, the parameters are chosen as follows:

$$ \gamma = 0.5,\,\,\omega_1 = 1,\,\,\omega_2 = 1/(2n - 1), $$

(37)

where n is the control parameter that is not restricted to be integer.

Some periodic solutions obtained with the exact analytical expressions are shown in Fig. 2.

Fig. 2.

Phase portraits and Poincaré points of periodic motions with analytical expressions.

5 Numerical Results and Discussion

Simulation where exact analytical expressions are not applicable is done by a specialized method for piecewise-linear systems based on matrix exponential [10]. The bifurcation diagram (Fig. 3) is obtained by integrating with initial conditions (x(0), $\dot{x}$(0)) = (0,1) and ignoring the first 6000 periods. It bridges the gaps between the exact analytical solutions. Chaos may occur between two consecutive integer values of n as the lower order solution bifurcates while the higher order does not exist yet.

Fig. 3.

Bifurcation diagram obtained by integrating with initial conditions (x(0), $\dot{x}$(0)) = (0,1).

It should be noted that the bifurcation diagram obtained by integrating with fixed initial conditions does not show coexisting solutions. Hence, interpolated cell-mapping method is used to plot the basins of attraction [11]. Figure 4 shows that at n = 6.5, there are two coexisting stable periodic motions with fractal basins of attraction. At n = 3, a chaotic motion coexists with a stable periodic motion that has exact analytic expressions (Fig. 5).

Though the exact analytical periodic solutions are only valid for very specific parameters and do not fully characterize the global dynamics, they describe a type of single-penetration multi-periodic motion that is typical for the bilinear system as seen in the bifurcation diagram. The exact analytical solutions can be used as a tool to validate numerical methods.

Fig. 4.

Global dynamics at n = 6.5.

Fig. 5.

Global dynamics at n = 3.

6 Conclusions and Outlook

A 1-DOF piecewise-linear system that has a damped domain and an undamped domain excited by a harmonic force is investigated. The analytical analysis has been performed for each domain; however, the piecewise motion does not have a general closed-form solution because the switching times between domains are solutions of transcendental equations.

The exact analytical periodic motions are found for special cases of parameters: the frequency of the homogenous solution of the undamped domain is a whole number n (higher than one) multiple of the frequency of the excitation, and parameters in the damped domain are suitable, e.g., natural frequency equal to excitation frequency and low damping. Each of the motion has a period of n times the period of excitation but only moves from undamped domain to damped domain one time during its period. Thus, the obtained motions are single-penetration multi-periodic.

The exact analytical solutions can be used to partly predict the dynamics of the system. It can also be used as an effective tool to validate numerical methods.

Future work will apply the presented method to investigate more complicated systems, e.g., multi-DOF systems.