Building Hierarchical Tree Representations Using Homological-Based Tools

Abstract

A new algorithm for computing the $\alpha$-tree hierarchical representation of a grey-scale digital image is presented here. The technique is based on an efficient simplified version of the Homological Spanning Forest (HSF) for encoding homological and homotopy-based information of binary digital images. We create one Adjacency Tree (AdjT) for each intensity contrast in a fully parallel manner. These trees, which define a Contrast Adjacency Forest (CAdjF), are in turn transversely interconnected by another couple of trees: the classical $\alpha$-tree, and a new one complementing it, called here the $\alpha ^*$-tree. They convey the information of the contours and the flat regions of the original color image, plus the relations between them. Using both the $\alpha$ and $\alpha ^*$-trees, this new topological representation prevents some classical drawbacks that appear when working with a single tree. An implementation in OCTAVE/MATLAB validates the correctness of our algorithm.

1 Introduction

Hierarchical image representations describe the content of an image from fine to coarse level through a tree structure, where the nodes represent the image regions at different levels and the edges model the hierarchical relationships among those regions. More concretely, $\alpha$-trees were first introduced to avoid relying on an ordering relation among image pixels (as in Max- and Min- trees). They are based on representing quasi-constant color regions of the original image, by relying on local dissimilarities. This hierarchical representation supports a wide family of image operators on graphs, and its practical usage has been extensively demonstrated.

In this paper we propose a new method to find a semantically correct partition of gray-level or color nD digital images from which several structures, such as Contrast Adjacency Forest, $\alpha$-tree and $\alpha ^{*}$-tree, are directly obtained. Our simplification allows to reduce the computation time by extending the degree of parallelism to every single pixel.

The paper has the following sections. Section 2 summarizes the main related work and Sect. 3 is devoted to recall the machinery and definitions of hierarchical representations. Next, the algorithm for constructing the trees using HSF structures is described in Sect. 4. Finally, conclusions are summarized in Sect. 5. In addition, this section introduces the applications and future research.

2 Related Work

Although there are in the literature a wide amount of methods for computing Max and Min trees and other hierarchical representations, results dealing with an efficient construction of $\alpha$-trees are certainly limited. In [3] the authors mainly focus on the computational issues of classical $\alpha$-tree’s construction algorithms, and propose various schemes for their efficient computation, using parallelism for modern multicore processor. In [9] a quasi-linear method based on a dedicated Union-Find procedure is proposed. The paper [4] fuses these two approaches. In general, many research papers have addressed computational efficiency of Union-Find procedures, including tuning parallel algorithms for specific computers. Another approach is that of using saliency maps to achieve an efficient construction of the $\alpha$-tree by relying on Khalimsky grids [2]. Recently, some authors have dealt with (memory) efficient $\alpha$-tree computation [5]. Nevertheless, all of them use a classical divide-and-conquer approach, by dividing the original image into strips. The issue is that this division necessarily implies more data dependencies between the strips in which the original image was divided (it makes harder the union-find stage). Thus, a pure parallel approach is not possible. In this respect, none of these methods use the ideal mathematical scenario for promoting parallelism in a natural way, that is, topology. The intrinsic nature of topological properties is essentially qualitative and local-to-global, having the additional advantage that its magnitudes are robust under deformations, translations and rotations. Nevertheless, the results in the literature in that sense are rare, and to our knowledge, no fully parallel computation for $\alpha$-trees and other hierarchical structures is currently available.

3 Background

Let us now introduce some basic concepts to be used in the following sections. We will use the notations introduced in [3]. Let I be a digital image and E its definition domain. An image segmentation is a partition P of E, that is a mapping $x \rightarrow P(x)$ from E into P(E) such that $\forall x \in E, x \in P(x)$ and $\forall x,y \in E$ either $P(x) = P(y)$ or $P(x) \cap P(y) =\emptyset$, with P(x) indicating a set of P containing $x \in E$.

Let us define $\pi (x \leadsto y)$ a path of length N between any two elements $x,y \in E$, composed by a chain of pairwise adjacent elements $\langle x=x_0,x_1,...,x_{N-1}=y \rangle$. We will consider here 4-adjacency between pixels, meaning that two pixels are adjacent if they share an edge. Let d(x, y) be a predefined dissimilarity measure between attributes of x and y. This measure can be defined, for instance, as the dissimilarity among pixel intensities, that is, contrast for grey level images.

Given these definitions, we could say that the hierarchical $\alpha$-tree representation is based on depicting an image through its $\alpha$-connected components [13] ($\alpha$-CCs), also $\alpha$-zones. For a given pixel x, its $\alpha$-zone is made up of all pixels reachable from x through a path in which within its intermediary steps, $d(x_i,x_{i+1})$ is less or equal to a given $\alpha$. Let us denote the $\alpha$-zone of a given pixel x as $\alpha -\mathcal {Z}(x)$. Let us observe that $\alpha$-zones define a partition or segmentation, i.e. $\bigcup _{x \in E} \alpha -\mathcal {Z}(x) = E$. It is possible to construct a tree of $\alpha$-zones, that is the $\alpha$-tree, by ordering them by inclusion relation. A zone covering the complete image is represented by the root of the tree.

4 Generation of the CAdjF, $\alpha$ and $\alpha ^*$-trees

We present an extension of our previous works (see [7, 8]) to generate the structure that allows an efficient construction of $\alpha$-trees, and other hierarchical structures that will be later introduced. The main notion presented in these previous works was the concept of Homological Spanning Forest (HSF). This concept is built by modeling the initial image as a special Abstract Cell Complex (ACC for short, see [6]). For the rest of the paper, let I be a 2D digital image having $m\times n$ pixels and q ordered levels of intensities.

Roughly speaking, an HSF of I is the set of two trees, denoted by $HST_{0,1}$ and $HST_{1,2}$, living at interpixel level within the self-dual cartesian square grid of I and appropriately connecting all the interpixel elements without redundancy. These interpixel elements (also called cells) are the own pixels (having dimension 0), the edges between pixels (excepting those of the border of I) of dimension 1 and the corners between pixels of dimension 2 (excepting those of the border of I). In particular, if we denote by $\widetilde{HSF}_{0,1}$ a spanning tree of all the image pixels, $HSF_{0,1}$ is a subdivision of $\widetilde{HSF}_{0,1}$ in the sense that it has as nodes all the $m\cdot n$ pixels of I (0-cells) and $(m\cdot n - 1)$ 1-cells connecting them. The $HSF_{1,2}$ is a tree whose nodes are all the $(m-1) \cdot (n-1)$ 2-cells of I and the rest of 1-cells (concretely, $(m-1)\cdot (n-1)$ too) that are not included in $HSF_{0,1}$. Exhaustively applying operations of cell-pairing (coupling a 0-cell with 1-cell or a 1-cell with 2-cell) within these trees, we detect cells (called critical) that remain unpaired in some HSF-trees. Although the critical cells obviously depend on an specific cell pairing, they can be used as combinatorial representatives of integer homology classes.

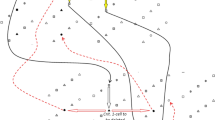
An example of this (non-unique) HSF representation is shown in Fig. 1. There is one critical 0-cell for each connected component (represented by purple triangles) and one critical 1-cell for each monochrome hole (represented by yellow arrows). However, HSF can be simplified to just one HST for binary images. In fact, this tree remains to be $\widetilde{HSF}_{0,1}$, and, then only 0-cells (which are image pixels with two possible colors) are contemplated for tree building. This tree can be divided into rooted sub-trees, with their root (called attractor) being detected when an edge “touches” two different colors. Such structure is shown in Fig. 2. This simplified representation implies a more efficient topological computation [10, 11] and, from now on, it will be the underlying topological encoding for all the digital image structures used in this paper.

Fig. 1.

A 3-color synthetic image and its HSF. Circles: 0-cells; triangles: 1-cells; solid squares: 2-cells. $(0-1)$-tree: blue and red segments linking 0 and 1-cells; and $(1-2)$-tree: blue and green segments linking 1 and 2-cells. Critical 0-cells (representative elements of CCs): purple triangles. Critical 1-cells (representative elements of monochrome 1-holes): yellow arrows. (Color figure online)

The method presented here is based on building the adjacency trees (AdjT) of a set of $q+2$ contrast images of dimension $(2m+1)\times (2n+1)$ ${ I_c,} \{ c=-1,0,1,\dots , q \}$, where c runs over the dissimilarity values among pixels (whose minimum and maximum values are 0 and q respectively) plus an additional trivial contrast image $I_{-1}$. For this purpose, we use the previous simplified HSF framework for B/W images. The AdjT offers a hierarchically and topologically consistent representation, modeling the nesting structure of spatial regions, where each node represents a connected component (CC) or region, and two nodes are adjacent if one of them is surrounded by the other (see [12]).

Fig. 2.

Simplified HSF and Jump distance matrix for the image in Fig. 1. The distance of each pixel is referred to its CC attractor (zero highlighted in bold).

We design and implement here a parallel algorithm for computing those AdjTs starting from a HSF representation of contrast binary images, so that they contain image information in terms of hierarchical representations (like the $\alpha$-tree and others). We consider here pixel intensity as dissimilarity measure, so that each $I_c$ is a binary image containing: background (BG) pixels as flat zones and foreground (FG) pixels as boundaries.

The computed set of AdjT, which conforms an adjacency forest, is called Contrast Adjacency Forest (CAdjF). The CAdjF includes another useful representation, called $\alpha ^*$-tree, which is defined through an opposite concept to that of the $\alpha$-zone. Whereas this last is made up of all pixels reachable from a pixel, in the sense that there exists a path whose adjacent pixels do not exceed a certain contrast c, an $\alpha ^*$-contour is composed of these pixel frontiers that impedes some path between two pixels, in the sense that this path cuts through two adjacent pixels that exceeds c. Two interesting cases become manifest for $I_c$ images:

• a) An $\alpha ^*$-contour can surround a BG region of an $I_c$, denoting a monochrome hole in its corresponding $\alpha$-zone of I.

• b) A set of $\alpha ^*$-contours can belong to a BG region. In this case, the longer this set is, the “weaker” its corresponding $\alpha$-zone is. In other words, it is more probable that the zone contains adjacent pixels with a high dissimilarity. This issue is efficiently computed using the proposed algorithms, allowing a fast identification of “bad” $\alpha$-zones for forthcoming applications (see Sect. 5).

We observe that the corresponding pixels of $I_c$ of the $\alpha$-zones plus those of the $\alpha ^*$-contours define a partition or segmentation of $I_c$. Then, ordering $\alpha$-zones and $\alpha ^*$-contours (more exactly their corresponding pixels) by inclusion relation, it is possible to construct the $\alpha$-tree, and the $\alpha ^*$-tree.

Apart from these trees, our construction allows to compute at the same time (without any additional timing complexity) additional information of regions and contours, like areas and perimeters (see [10]), which might be used for further processing (see Sect. 5). In addition, and what is more important, CAdjF is generated in a very efficient manner following our previous implementations discussed in [10, 11]. Two important achievements are thus retained:

• 1) The parallel algorithm is achieved here through the proper conversion of color images into a set of binary contrast images $I_c$, and;

• 2) No processing step is done in a sequential manner. This allows to maintain the theoretical time complexity of the whole process near the logarithm of the width plus height of the image.

Generation of B/W contrast images $I_c$ from the original color image I is done (for each intensity contrast c) as follows (see an example in Fig. 3). Every cell of I (of any dimension) is transformed into a 0-cell of $I_c$, using the rules:

• Every 0-cell of I is transformed into a BG pixel in $I_c$, meaning that the “interior” of a pixel is a flat zone.

• 1-cells of I represent its contours; thus, if the two neighboring 0-cells of I have an intensity dissimilarity bigger or equal than c, their corresponding $I_c$ pixels would be set to FG; BG otherwise.

• Finally, for each corresponding $I_c$ pixel of a 2-cell of I, only if its four 4-adjacent $I_c$ pixels were BG, it will be set to BG; FG otherwise. The BG of $I_c$ corresponds to 2-cells of $I_c$ having their 4-adjacent 0-cells identical, which means that the color area of I is flat.

Fig. 3.

Left: a fragment (9 pixels) of a color image. Numbers represent color intensities of the original image pixels (0-cells), crosses are 1-cells and solid squares 2-cells. Right: The corresponding B/W $I_c$ ($c=0$) of this color image, including the HSF, depicted as lines.

According to the proposed framework, the parallel process for constructing the CAdjF is divided into two main phases (Fig. 4).

• 1) Generation of contrast images. From the original image I, a set $I_c$ of contrast images are generated, according to the previous convention. For example, for grey level images, a set of 255+2 $I_c$ images can be generated fully in parallel, as there are no dependencies among these generations. If there were enough PEs, the timing order would be O(1).

• 2) $HSF_c$ computation. For any previous $I_c$-images, their corresponding $HSF_c$s are computed in parallel. The results are a set of jump matrices $J_c$. At the same time, additional information for FG CCs (e.g. contour perimeters) and BG CCs (e.g. areas of flat zones) are also calculated. Each element of these matrices contains a jump distance to the corresponding CC attractor. We refer the reader to [10] for a detailed matrix-based description of this second phase.

• 3) Once the HSFs of contrast images are built, their AdjTs are computed by simply following the pointers representing jump distances. In [10] a full example is described for a B/W image. In the present method, AdjTs are extracted in the same manner, once the representative attractor lists of each $J_c$ are completed. Besides, the set $J_c$ comprises the information of $\alpha$-tree as well as the $\alpha ^*$-tree. The pseudocode for this phase is described in Algorithm 1.

Fig. 4.

Phases involved in the parallel CAdjF generation. Complexity orders are shown below each stage.

To sum up, having enough PEs, the time order would be $O(log(n))+O(s_{max})$, being $s_{max}$ defined in [10]. A summary of the previous phases and the generation of the set $I_c$ follows. Figure 5, Left shows a $8\times 13$ synthetic image where each region is labelled with a letter and a number that represents its grey level. For completeness, we define a first contour image $I_{-1}$, which defines four contours for each pixel (trivial case, Fig. 5, Right). The only $I_c$ BG pixels come from I 0-cells. Jump distance matrix $J_{-1}$ simply consists of the corresponding distances (for FG pixels) to the unique FG attractor (most right upper red dot), and a null distance for the inner BG pixels. Note that there is also a set of BG pixels in the image borders, in order to get a correct AdjT representation. Thus, $I_{-1}$ AdjT is composed of exclusively one FG node and as many BG nodes as pixels I has.

Fig. 5.

Synthetic $8\times 13$ image I (which has been surrounded by one pixel width additional borders) and its HSF. Green empty circles of $I_c$ are BG pixels; red solid dots of $I_c$ are BG pixels; Edges follows the same color convention. (Color figure online)

Next $I_{c}$ images are shown in Fig. 6(a) for $c=0$, and (B) for $c=1$. In Fig. 6(a), there is a CC for each region of I, and a FG CC for each monochrome hole of I. In Fig. 6(b), those I regions that share a border and have a grey difference of 1 are fused. In general, the higher the considered contrast, the lower the number of contour perimeter that persist and the number of BG zones that remain. Thus, subfigures 6c and 6d show the $I_{c}$ images for $c=2$, and $c=3$. Finally, for the highest existent contrast value in I (in this case $c=4$), the $I_{c}$ image results in a different trivial case: only one BG CC and only one FG CC (image border is considered to be out of I, and subfigure 6e shows $I_{4}$).

Once the complete set of $J_{c}$ has been obtained, it is straightforward to obtain the $\alpha$ and $\alpha ^*$-trees, as the same linear addresses are used for all the $J_{c}$. We proceed in parallel for each attractor and each $J_{c}$ by simply looking at the same element in the previous $J_{c-1}$ The corresponding elements point to the same or to a different attractor. In the first case, no branch appears at the tree (e.g. region C2 for $\alpha =0, 1, 2$ in Fig. 7a); in the second one, a link must be drawn (e.g. region fusion of E4F3E5 for $\alpha =0$ to 1 in Fig. 7a). Similar examples for the $\alpha ^*$-trees are depicted in Fig. 7b; in this case, there are contours that persist for different $\alpha$ values. Finally, all of them collapse into the tree root (trivial $c=-1$).

Fig. 6.

HSFs for the previous synthetic image; Since no contrast is bigger than 4 in (e), the HSF only contains one BG CC and one FG CC.

Fig. 7.

Representation of the $\alpha$-tree and $\alpha ^*$-tree

Fig. 8.

(1) An image presenting chaining effect. (2) Perimeters for $I_0, I_1, I_2$. (3) Perimeters for $I_3$. (4) A chessboard image that does not present chaining effect.

5 Conclusions, Applications and Future Research

The Contrast Adjacency Forest is a hierarchical representation of a color digital image based on the intensity contrasts of its regions. The building of this Forest is done in a fully parallel manner with a theoretical computing time near the logarithm of the width plus the height of an image. This representation contains in turn another pair of trees ($\alpha$ and $\alpha ^*$-tree), which are suitable for additional applications, while maintaining such an efficient computation timing. Moreover, they prevent some classical drawbacks that appears when working only with the $\alpha$-tree. One of the mayor drawbacks of $\alpha$-tree is the so-called chaining effect (see [4] for a deep discussion). This occurs when there are a set of adjacent regions with incremental intensities. Thus, the first level of this tree would join a big area that actually contains very different intensities. A classical example is given in Fig. 8 (1), where all its pixels would belong promptly to the first $\alpha$-zone. However, this problem can be detected by looking at the perimeters returned by the $\alpha ^*$-tree. Figure 8 (2) and (3) show that other region contours must survive in $I_c$ for several levels of c. Conversely, for an image with a smaller intensity range (like the chessboard-like of Fig. 8 (4)), $\alpha ^*$-tree perimeters will disappear in the next $I_c$. Therefore, inspecting the progression of perimeters with respect to c would cut off artifacts of this chaining effect (in a negligible computing time), and without the need of computing the $\omega -tree$ (see [1]).

Implementation of the presented method is quite straightforward by using the algorithm presented in [10] (or its most enhanced version in [11]). Although an optimized code for the current proposal has not yet been written, the theoretical timing estimation for building the CAdjF appears to be almost the same as that of [11] (if sufficient processing elements were available), due to the few changes with respect to the previous work that are required.

With respect to applications, our hierarchical representation contains a richer topological information than a unique tree. Thus, further processing can produce additional results. A proposal to be considered in the short term is the introduction of stronger conditions for the $I_c$ pixels to be considered as FG, that is, for the activation of the region contours. Additionally, more elaborated topological filters can be defined by extending our hierarchical representation.