Abstract
There are many randomness notions. On the classical account, many of them are about whether a given infinite binary sequence is random for some given probability. If so, this probability turns out to be the same for all these notions, so comparing them amounts to finding out for which of them a given sequence is random. This changes completely when we consider randomness with respect to probability intervals, because here, a sequence is always random for at least one interval, so the question is not if, but rather for which intervals, a sequence is random. We show that for many randomness notions, every sequence has a smallest interval it is (almost) random for. We study such smallest intervals and use them to compare a number of randomness notions. We establish conditions under which such smallest intervals coincide, and provide examples where they do not.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The field of algorithmic randomness studies what it means for an infinite binary sequence, such as \(\omega =0100110100\dots \), to be random for an uncertainty model. Classically, this uncertainty model is often a single (precise) probability  . Some of the best studied precise randomness notions are Martin-Löf randomness, computable randomness, Schnorr randomness and Church randomness. They are increasingly weaker; for example, if a sequence \(\omega \) is Martin-Löf random for a probability p, then it is also computably random, Schnorr random and Church random for p. Meanwhile, these notions do not coincide; it is for example possible that a path \(\omega \) is Church random but not computably random for \(\nicefrac {1}{2}\). From a traditional perspective, this is how we can typically differentiate between various randomness notions [1, 2, 6, 10].
. Some of the best studied precise randomness notions are Martin-Löf randomness, computable randomness, Schnorr randomness and Church randomness. They are increasingly weaker; for example, if a sequence \(\omega \) is Martin-Löf random for a probability p, then it is also computably random, Schnorr random and Church random for p. Meanwhile, these notions do not coincide; it is for example possible that a path \(\omega \) is Church random but not computably random for \(\nicefrac {1}{2}\). From a traditional perspective, this is how we can typically differentiate between various randomness notions [1, 2, 6, 10].
As shown by De Cooman and De Bock [3,4,5], these traditional randomness notions can be generalised by allowing for imprecise-probabilistic uncertainty models, such as closed probability intervals  . These more general randomness notions, and their corresponding properties, allow for more detail to arise in their comparison. Indeed, every infinite binary sequence \(\omega \) is for example random for at least one closed probability interval. And for the imprecise generalisations of many of the aforementioned precise randomness notions, we will see that for every (or sometimes many) \(\omega \), there is some smallest probability interval, be it precise or imprecise, that \(\omega \) is (almost) random for—we will explain the modifier ‘almost’ further on. It is these smallest probability intervals we will use to compare a number of different randomness notions.
. These more general randomness notions, and their corresponding properties, allow for more detail to arise in their comparison. Indeed, every infinite binary sequence \(\omega \) is for example random for at least one closed probability interval. And for the imprecise generalisations of many of the aforementioned precise randomness notions, we will see that for every (or sometimes many) \(\omega \), there is some smallest probability interval, be it precise or imprecise, that \(\omega \) is (almost) random for—we will explain the modifier ‘almost’ further on. It is these smallest probability intervals we will use to compare a number of different randomness notions.
We will focus on the following three questions: (i) when is there a well-defined smallest probability interval for which an infinite binary sequence \(\omega \) is (almost) random; (ii) are there alternative expressions for these smallest intervals; and (iii) for a given sequence \(\omega \), how do these smallest intervals compare for different randomness notions? Thus, by looking from an imprecise perspective, we are able to do more than merely confirm the known differences between several randomness notions. Defining randomness for closed probability intervals also lets us explore to what extent existing randomness notions are different, in the sense that we can compare the smallest probability intervals for which an infinite binary sequence is random. Surprisingly, we will see that there is a large and interesting set of infinite sequences \(\omega \) for which the smallest interval that \(\omega \) is (almost) random for is the same for several randomness notions.
Our contribution is structured as follows. In Sect. 2, we introduce (im)precise uncertainty models for infinite binary sequences, and introduce a generic definition of randomness that allows us to formally define what it means for a sequence to have a smallest interval it is (almost) random for. In Sect. 3, we provide the mathematical background on supermartingales that we need in order to introduce a number—six in all—of different randomness notions in Sect. 4: (weak) Martin-Löf randomness, computable randomness, Schnorr randomness, and (weak) Church randomness. In the subsequent sections, we tackle our three main questions. We study the existence of the smallest intervals an infinite binary sequence \(\omega \) is (almost) random for in Sect. 5. In Sects. 6 and 7, we provide alternative expressions for such smallest intervals and compare them; we show that these smallest intervals coincide under certain conditions, and provide examples where they do not. To adhere to the page limit, the proofs of all novel results—that is, the ones without citation—are omitted. They are available in Appendix B of an extended on-line version [8].
2 Forecasting Systems and Randomness
Consider an infinite sequence of binary variables \(X_1,\dots ,X_n,\dots \), where every variable \(X_n\) takes values in the binary sample space  , generically denoted by \(x_n\). We are interested in the corresponding infinite outcome sequences \((x_1,\dots ,x_n,\dots )\), and, in particular, in their possible randomness. We denote such a sequence generically by \(\omega \) and call it a path. All such paths are collected in the set
, generically denoted by \(x_n\). We are interested in the corresponding infinite outcome sequences \((x_1,\dots ,x_n,\dots )\), and, in particular, in their possible randomness. We denote such a sequence generically by \(\omega \) and call it a path. All such paths are collected in the set  .Footnote 1 For any path \(\omega =(x_{1},\dots ,x_{n},\dots ) \in \varOmega \), we let
.Footnote 1 For any path \(\omega =(x_{1},\dots ,x_{n},\dots ) \in \varOmega \), we let  and
and  for all \(n \in \mathbb {N}\). For \(n=0\), the empty sequence
for all \(n \in \mathbb {N}\). For \(n=0\), the empty sequence  is called the initial situation and is denoted by \(\square \). For any \(n \in {\mathbb {N}_0}\), a finite outcome sequence \((x_1,\dots ,x_n)~\in ~\mathcal {X}^n\) is called a situation, also generically denoted by \(s\), and its length is then denoted by
is called the initial situation and is denoted by \(\square \). For any \(n \in {\mathbb {N}_0}\), a finite outcome sequence \((x_1,\dots ,x_n)~\in ~\mathcal {X}^n\) is called a situation, also generically denoted by \(s\), and its length is then denoted by  . All situations are collected in the set
. All situations are collected in the set  . For any \(s=(x_{1},\dots ,x_{n}) \in \mathbb {S}\) and \(x \in \mathcal {X}\), we use \(sx\) to denote the concatenation \((x_{1},\dots ,x_{n},x)\).
. For any \(s=(x_{1},\dots ,x_{n}) \in \mathbb {S}\) and \(x \in \mathcal {X}\), we use \(sx\) to denote the concatenation \((x_{1},\dots ,x_{n},x)\).
The randomness of a path \(\omega \in \varOmega \) is always defined with respect to an uncertainty model. Classically, this uncertainty model is a real number  , interpreted as the probability that \(X_n\) equals 1, for any \(n \in \mathbb {N}\). As explained in the Introduction, we can generalise this by considering a closed probability interval
, interpreted as the probability that \(X_n\) equals 1, for any \(n \in \mathbb {N}\). As explained in the Introduction, we can generalise this by considering a closed probability interval  instead. These uncertainty models will be called interval forecasts, and we collect all such closed intervals in the set \(\mathcal {I}\). Another generalisation of the classical case consists in allowing for non-stationary probabilities that depend on \(s\) or
instead. These uncertainty models will be called interval forecasts, and we collect all such closed intervals in the set \(\mathcal {I}\). Another generalisation of the classical case consists in allowing for non-stationary probabilities that depend on \(s\) or  . Each of these generalisations can themselves be seen as a special case of an even more general approach, which consists in providing every situation \(s\in \mathbb {S}\) with a (possibly different) interval forecast in \(\mathcal {I}\), denoted by \(\varphi (s)\). This interval forecast \(\varphi (s) \in \mathcal {I}\) then describes the uncertainty about the a priori unknown outcome of
. Each of these generalisations can themselves be seen as a special case of an even more general approach, which consists in providing every situation \(s\in \mathbb {S}\) with a (possibly different) interval forecast in \(\mathcal {I}\), denoted by \(\varphi (s)\). This interval forecast \(\varphi (s) \in \mathcal {I}\) then describes the uncertainty about the a priori unknown outcome of  , given that the situation \(s\) has been observed. We call such general uncertainty models forecasting systems.
, given that the situation \(s\) has been observed. We call such general uncertainty models forecasting systems.
Definition 1
A forecasting system is a map \(\varphi :\mathbb {S}\rightarrow \mathcal {I}\) that associates with every situation \(s\in \mathbb {S}\) an interval forecast \(\varphi (s) \in \mathcal {I}\). We denote the set of all forecasting systems by \(\varPhi \).
With any forecasting system \(\varphi \in \varPhi \), we associate two real processes \(\underline{\varphi }\) and \(\overline{\varphi }\), defined by  and
and  for all \(s\in \mathbb {S}\). A forecasting system \(\varphi \in \varPhi \) is called precise if \(\underline{\varphi }=\overline{\varphi }\). A forecasting system \(\varphi \in \varPhi \) is called stationary if there is an interval forecast \(I \in \mathcal {I}\) such that \(\varphi (s)=I\) for all \(s\in \mathbb {S}\); for ease of notation, we will then denote this forecasting system simply by I. The case of a single probability p corresponds to a stationary forecasting system with
for all \(s\in \mathbb {S}\). A forecasting system \(\varphi \in \varPhi \) is called precise if \(\underline{\varphi }=\overline{\varphi }\). A forecasting system \(\varphi \in \varPhi \) is called stationary if there is an interval forecast \(I \in \mathcal {I}\) such that \(\varphi (s)=I\) for all \(s\in \mathbb {S}\); for ease of notation, we will then denote this forecasting system simply by I. The case of a single probability p corresponds to a stationary forecasting system with  . A forecasting system \(\varphi \in \varPhi \) is called temporal if its interval forecasts \(\varphi (s)\) only depend on the situations \(s\in \mathbb {S}\) through their length
. A forecasting system \(\varphi \in \varPhi \) is called temporal if its interval forecasts \(\varphi (s)\) only depend on the situations \(s\in \mathbb {S}\) through their length  , meaning that \(\varphi (s)=\varphi (t)\) for any two situations \(s,t \in \mathbb {S}\) that have the same length
, meaning that \(\varphi (s)=\varphi (t)\) for any two situations \(s,t \in \mathbb {S}\) that have the same length  .
.
In some of our results, we will consider forecasting systems that are computable. To follow the argumentation and understand our results, the following intuitive description will suffice: a forecasting system \(\varphi \in \varPhi \) is computable if there is some finite algorithm that, for every \(s\in \mathbb {S}\) and any \(n \in {\mathbb {N}_0}\), can compute the real numbers \(\underline{\varphi }(s)\) and \(\overline{\varphi }(s)\) with a precision of \(2^{-n}\). For a formal definition of computability, which we use in our proofs, we refer the reader to Appendix A of the extended on-line version, which contains these proofs [8].
So what does it mean for a path \(\omega \in \varOmega \) to be random for a forecasting system \(\varphi \in \varPhi \)? Since there are many different definitions of randomness, and since we intend to compare them, we now introduce a general abstract definition and a number of potential properties of such randomness notions that will, as it turns out, allow us to do so.
Definition 2
A notion of randomness \(\text {R}\) associates with every forecasting system \(\varphi \in \varPhi \) a set of paths \(\varOmega _\text {R}(\varphi )\). A path \(\omega \in \varOmega \) is called \(\text {R}\)-random for \(\varphi \) if \(\omega \in \varOmega _\text {R}(\varphi )\).
All of the randomness notions that we will be considering further on, satisfy additional properties. The first one is a monotonicity property, which we can describe generically as follows. If a path \(\omega \in \varOmega \) is R-random for a forecasting system \(\varphi \in \varPhi \), it is also R-random for any forecasting system \(\varphi ' \in \varPhi \) that is less precise, meaning that \(\varphi (s) \subseteq \varphi '(s)\) for all \(s\in \mathbb {S}\). Consequently, this monotonicity property requires that the more precise a forecasting system is, the fewer R-random paths it ought to have.
Property 1
For any two forecasting systems \(\varphi ,\varphi ' \in \varPhi \) such that \(\varphi \subseteq \varphi '\), it holds that  .
.
Furthermore, it will also prove useful to consider the property that every path \(\omega \in \varOmega \) is R-random for the (maximally imprecise) vacuous forecasting system \(\varphi _v \in \varPhi \), defined by  for all \(s\in \mathbb {S}\).
for all \(s\in \mathbb {S}\).
Property 2
 .
.
Thus, if Properties 1 and 2 hold, every path \(\omega \in \varOmega \) will in particular be R-random for at least one interval forecast—the forecast  —and if a path \(\omega \in \varOmega \) is R-random for an interval forecast \(I \in \mathcal {I}\), then it will also be R-random for any interval forecast \(I' \in \mathcal {I}\) for which \(I \subseteq I'\). It is therefore natural to wonder whether every path \(\omega \in \varOmega \) has some smallest interval forecast \(I\) such that \(\omega \in \varOmega _\text {R}(I)\). In order to allow us to formulate an answer to this question, we consider the sets \(\mathcal {I}_\text {R}(\omega )\) that for a given path \(\omega \in \varOmega \) contain all interval forecasts \(I \in \mathcal {I}\) that \(\omega \) is R-random for. If there is such a smallest interval forecast, then it is necessarily given by
—and if a path \(\omega \in \varOmega \) is R-random for an interval forecast \(I \in \mathcal {I}\), then it will also be R-random for any interval forecast \(I' \in \mathcal {I}\) for which \(I \subseteq I'\). It is therefore natural to wonder whether every path \(\omega \in \varOmega \) has some smallest interval forecast \(I\) such that \(\omega \in \varOmega _\text {R}(I)\). In order to allow us to formulate an answer to this question, we consider the sets \(\mathcal {I}_\text {R}(\omega )\) that for a given path \(\omega \in \varOmega \) contain all interval forecasts \(I \in \mathcal {I}\) that \(\omega \) is R-random for. If there is such a smallest interval forecast, then it is necessarily given by

As we will see, for some randomness notions R, \(I_\text {R}(\omega )\) will indeed be the smallest interval forecast that \(\omega \) is random for. Consequently, for these notions, and for every \(\omega \in \varOmega \), the set \(\mathcal {I}_\text {R}(\omega )\) is completely characterised by the interval forecast \(I_\text {R}(\omega )\), in the sense that \(\omega \) will be R-random for an interval forecast \(I \in \mathcal {I}\) if and only if \(I_\text {R}(\omega )\subseteq I\).
In general, however, this need not be the case. For example, consider the situation depicted in Fig. 1. It could very well be that for some randomness notion
 : that satisfies Properties 1 and 2, there is a path \(\omega ^*\in \varOmega \) that is R-random for all interval forecasts of the form
: that satisfies Properties 1 and 2, there is a path \(\omega ^*\in \varOmega \) that is R-random for all interval forecasts of the form  and
and  , with \(p<\nicefrac {1}{3}\) and \(\nicefrac {2}{3}\le q\), but for no others. Then clearly,
, with \(p<\nicefrac {1}{3}\) and \(\nicefrac {2}{3}\le q\), but for no others. Then clearly,  , but \(\omega ^*\) is not R-random for \(I_\text {R}(\omega ^*)\).
, but \(\omega ^*\) is not R-random for \(I_\text {R}(\omega ^*)\).
In addition, it need not even be guaranteed that the intersection \(I_\text {R}(\omega )\) is non-empty. To guarantee that it will be, and as an imprecise counterpart of the law of large numbers, it suffices to consider the additional property that if a path \(\omega \in \varOmega \) is R-random for an interval forecast \(I \in \mathcal {I}\), then this I should imply the following bounds on the relative frequency of ones along \(\omega \).
Property 3
For all interval forecasts \(I \in \mathcal {I}\) and all paths \(\omega \in \varOmega _\text {R}(I)\), it holds that  .
.
Properties 1–3 hold for all randomness notions
 that we will consider, whence also, \(I_\text {R}(\omega )\ne \emptyset \). We repeat that for some of these notions, \(I_\text {R}(\omega )\) will be the smallest interval forecast that \(\omega \in \varOmega \) is R-random for. If not, we will sometimes still be able to show that \(I_\text {R}(\omega )\) is the smallest interval forecast that \(\omega \) is almost R-random for.
that we will consider, whence also, \(I_\text {R}(\omega )\ne \emptyset \). We repeat that for some of these notions, \(I_\text {R}(\omega )\) will be the smallest interval forecast that \(\omega \in \varOmega \) is R-random for. If not, we will sometimes still be able to show that \(I_\text {R}(\omega )\) is the smallest interval forecast that \(\omega \) is almost R-random for.
Definition 3
A path \(\omega \in \varOmega \) is called almost R-random for an interval forecast \(I \in \mathcal {I}\) if it is R-random for any interval forecast \(I' \in \mathcal {I}\) of the form

If a path \(\omega \in \varOmega \) is almost R-random for the interval forecast \(I_\text {R}(\omega )\), then \(I_\text {R}(\omega )\) almost completely characterises the set \(\mathcal {I}_\text {R}(\omega )\): the only case where we cannot immediately decide whether a path \(\omega \) is R-random for an interval forecast \(I \in \mathcal {I}\) or not, occurs when \(\min I= \min I_\text {R}(\omega )\) or \(\max I= \max I_\text {R}(\omega )\). Moreover, if Property 1 holds, then as our terminology suggests, \(\omega \in \varOmega \) is almost R-random for every interval forecast \(I \in \mathcal {I}\) it is random for.
In the remainder of this contribution, we intend to study the smallest interval forecasts a path is (almost) random for, for several notions of randomness. In the next section, we start by introducing the mathematical machinery needed to introduce some of these notions, and in particular, the martingale-theoretic approach to randomness, which makes extensive use of the concept of betting. Generally speaking, a path \(\omega \in \varOmega \) is then considered to be random for a forecasting system \(\varphi \in \varPhi \) if a subject can adopt no implementable betting strategy that is allowed by \(\varphi \) and makes him arbitrarily rich along \(\omega \). This approach will enable us to introduce the notions of Martin-Löf randomness, weak Martin-Löf randomness, computable randomness and Schnorr randomness, which differ only in what is meant by ‘implementable’ and in the way a subject should not be able to get arbitrarily rich [6].
3 A Martingale-Theoretic Approach—Betting Strategies
Consider the following betting game involving an infinite sequence of binary variables \(X_1,\dots ,X_n,\dots \) There are three players: Forecaster, Sceptic and Reality.
Forecaster starts by specifying a forecasting system \(\varphi \in \varPhi \). For every situation \(s\in \mathbb {S}\), the corresponding interval forecast \(\varphi (s)\) expresses for every gamble \(f:\mathcal {X}\rightarrow \mathbb {R}\) whether or not Forecaster allows Sceptic to select \(f\); the set of all gambles is denoted by \(\mathcal {L}(\mathcal {X})\). A gamble \(g \in \mathcal {L}(\mathcal {X})\) is offered by Forecaster to Sceptic if its expectation  is non-positive for every probability \(p \in I\), or equivalently, if \(\max _{p \in I}E_p(g) \le 0\).
is non-positive for every probability \(p \in I\), or equivalently, if \(\max _{p \in I}E_p(g) \le 0\).
After Forecaster has specified a forecasting system \(\varphi \in \varPhi \), Sceptic selects a betting strategy that specifies for every situation \(s\in \mathbb {S}\) an allowable gamble \(f_s\in \mathcal {L}(\mathcal {X})\) for the corresponding interval forecast \(\varphi (s) \in \mathcal {I}\), meaning that \(\max _{p \in \varphi (s)}E_p(f_s) \le 0\).
The betting game now unfolds as Reality reveals the successive elements \(\omega _{n}\in \mathcal {X}\) of a path \(\omega \in \varOmega \). In particular, at every time instant \(n \in {\mathbb {N}_0}\), the following actions have been and are completed: Reality has already revealed the situation \(\omega _{1:n}\), Sceptic engages in a gamble \(f_{\omega _{1:n}} \in \mathcal {L}(\mathcal {X})\) that is specified by his betting strategy, Reality reveals the next outcome \(\omega _{n+1}~\in ~\mathcal {X}\), and Sceptic receives a (possibly negative) reward \(f_{\omega _{1:n}}(\omega _{n+1})\). We furthermore assume that Sceptic starts with initial unit capital, so his running capital at every time instant \(n \in {\mathbb {N}_0}\) equals \(1+\sum _{k=0}^{n-1} f_{\omega _{1:k}}(\omega _{k+1})\). We also don’t allow Sceptic to borrow. This means that he is only allowed to adopt betting strategies that, regardless of the path that Reality reveals, will guarantee that his running capital never becomes negative.
In order to formalise Sceptic’s betting strategies, we will introduce the notion of test supermartingales. We start by considering a real process \(F:\mathbb {S}\rightarrow \mathbb {R}\); it is called positive if \(F(s) >0\) for all \(s\in \mathbb {S}\) and non-negative if \(F(s) \ge 0\) for all \(s\in \mathbb {S}\). A real process \(F\) is called temporal if \(F(s)\) only depends on the situation \(s\in \mathbb {S}\) through its length  , meaning that \(F(s)=F(t)\) for any two \(s,t\in \mathbb {S}\) such that
, meaning that \(F(s)=F(t)\) for any two \(s,t\in \mathbb {S}\) such that  . A real process \(S\) is called a selection process if \(S(s) \in \{0,1\}\) for all \(s\in \mathbb {S}\).
. A real process \(S\) is called a selection process if \(S(s) \in \{0,1\}\) for all \(s\in \mathbb {S}\).
With any real process \(F\), we can associate a gamble process \(\varDelta F:\mathbb {S}\rightarrow \mathcal {L}(\mathcal {X})\), defined by  for all \(s\in \mathbb {S}\) and \(x \in \mathcal {X}\), and we call it the process difference for \(F\). If \(F\) is positive, then we can also consider another gamble process \(D_F:\mathbb {S}\rightarrow \mathcal {L}(\mathcal {X})\), defined by
for all \(s\in \mathbb {S}\) and \(x \in \mathcal {X}\), and we call it the process difference for \(F\). If \(F\) is positive, then we can also consider another gamble process \(D_F:\mathbb {S}\rightarrow \mathcal {L}(\mathcal {X})\), defined by  for all \(s\in \mathbb {S}\) and \(x \in \mathcal {X}\), which we call the multiplier process for \(F\). And vice versa, with every non-negative real gamble process \(D:\mathbb {S}\rightarrow \mathcal {L}(\mathcal {X})\), we can associate a non-negative real process
for all \(s\in \mathbb {S}\) and \(x \in \mathcal {X}\), which we call the multiplier process for \(F\). And vice versa, with every non-negative real gamble process \(D:\mathbb {S}\rightarrow \mathcal {L}(\mathcal {X})\), we can associate a non-negative real process  defined by
defined by  for all \(s=(x_{1},\dots ,x_{n}) \in \mathbb {S}\), and we then say that
for all \(s=(x_{1},\dots ,x_{n}) \in \mathbb {S}\), and we then say that  is generated by \(D\).
is generated by \(D\).
When given a forecasting system \(\varphi \in \varPhi \), we call a real process \(M\) a supermartingale for \(\varphi \) if for every \(s\in \mathbb {S}\), \(\varDelta M(s)\) is an allowable gamble for the corresponding interval forecast \(\varphi (s)\), meaning that \(\max _{p \in \varphi (s)}E_p(\varDelta M(s)) \le 0\). Moreover, a supermartingale \(T\) is called a test supermartingale if it is non-negative and  . We collect all test supermartingales for \(\varphi \) in the set \(\overline{\mathbb {T}}(\varphi )\). It is easy to see that every test supermartingale \(T\) corresponds to an allowed betting strategy for Sceptic that starts with unit capital and avoids borrowing. Indeed, for every situation \(s=(x_{1},\dots ,x_{n}) \in \mathbb {S}\), \(T\) specifies an allowable gamble \(\varDelta T(s)\) for the interval forecast \(\varphi (s)\in \mathcal {I}\), and Sceptic’s running capital \(1+\sum _{k=0}^{n-1}\varDelta T(x_{1:k})(x_{k+1})\) equals \(T(s)\) and is therefore non-negative, and equals 1 in \(\square \).
. We collect all test supermartingales for \(\varphi \) in the set \(\overline{\mathbb {T}}(\varphi )\). It is easy to see that every test supermartingale \(T\) corresponds to an allowed betting strategy for Sceptic that starts with unit capital and avoids borrowing. Indeed, for every situation \(s=(x_{1},\dots ,x_{n}) \in \mathbb {S}\), \(T\) specifies an allowable gamble \(\varDelta T(s)\) for the interval forecast \(\varphi (s)\in \mathcal {I}\), and Sceptic’s running capital \(1+\sum _{k=0}^{n-1}\varDelta T(x_{1:k})(x_{k+1})\) equals \(T(s)\) and is therefore non-negative, and equals 1 in \(\square \).
We recall from Sect. 2 that martingale-theoretic randomness notions differ in the nature of the implementable betting strategies that are available to Sceptic. More formally, we will consider three different types of implementable test supermartingales: computable ones, lower semicomputable ones, and test supermartingales generated by lower semicomputable multiplier processes. A test supermartingale \(T\in \overline{\mathbb {T}}(\varphi )\) is called computable if there is some finite algorithm that, for every \(s\in \mathbb {S}\) and any \(n \in {\mathbb {N}_0}\), can compute the real number \(T(s)\) with a precision of \(2^{-n}\). A test supermartingale \(T\in \overline{\mathbb {T}}(\varphi )\) is called lower semicomputable if there is some finite algorithm that, for every \(s\in \mathbb {S}\), can compute an increasing sequence \((q_n)_{n\in {\mathbb {N}_0}}\) of rational numbers that approaches the real number \(T(s)\) from below—but without knowing, for any given n, how good the lower bound \(q_n\) is. Similarly, a real multiplier process \(D\) is called lower semicomputable if there is some finite algorithm that, for every \(s\in \mathbb {S}\) and \(x \in \mathcal {X}\), can compute an increasing sequence \((q_n)_{n\in {\mathbb {N}_0}}\) of rational numbers that approaches the real number \(D(s)(x)\) from below. For more details, we refer the reader to Appendix A of the extended on-line version [8].
4 Several Notions of (Imprecise) Randomness
At this point, we have introduced the necessary mathematical machinery to define our different randomness notions. We start by introducing four martingale-theoretic ones: Martin-Löf (ML) randomness, weak Martin-Löf (wML) randomness, computable (C) randomness and Schnorr (S) randomness. Generally speaking, for these notions, a path \(\omega \in \varOmega \) is random for a forecasting system \(\varphi \in \varPhi \) if Sceptic has no implementable allowed betting strategy that makes him arbitrarily rich along \(\omega \). We stress again that these randomness notions differ in how Sceptic’s betting strategies are implementable, and in how he should not be able to become arbitrarily rich along a path \(\omega \in \varOmega \). With these types of restrictions in mind, we introduce the following sets of implementable allowed betting strategies.

For a path \(\omega \) to be Martin-Löf, weak Martin-Löf or computably random, we require that Sceptic’s running capital should never be unbounded on \(\omega \) for any implementable allowed betting strategy; that is, no test supermartingale \(T\in \overline{\mathbb {T}}_\text {R}(\varphi )\) should be unbounded on \(\omega \), meaning that \(\limsup _{n \rightarrow \infty }T(\omega _{1:n})=\infty \).
Definition 4
([5]). For any  , a path \(\omega \in \varOmega \) is R-random for a forecasting system \(\varphi \in \varPhi \) if no test supermartingale \(T\in \overline{\mathbb {T}}_\text {R}(\varphi )\) is unbounded on \(\omega \).
, a path \(\omega \in \varOmega \) is R-random for a forecasting system \(\varphi \in \varPhi \) if no test supermartingale \(T\in \overline{\mathbb {T}}_\text {R}(\varphi )\) is unbounded on \(\omega \).
For Schnorr randomness, we require instead that Sceptic’s running capital should not be computably unbounded on \(\omega \) for any implementable allowed betting strategy. More formally, we require that no test supermartingale \(T\in \overline{\mathbb {T}}_\text {S}(\varphi )\) should be computably unbounded on \(\omega \). That \(T\) is computably unbounded on \(\omega \) means that \(\limsup _{n \rightarrow \infty }[T(\omega _{1:n})-\tau (n)] \ge 0\) for some real map \(\tau :{\mathbb {N}_0}\rightarrow \mathbb {R}_{\ge 0}\) that is
-
(i)
computable;
-
(ii)
non-decreasing, so \(\tau (n+1) \ge \tau (n)\) for all \(n \in {\mathbb {N}_0}\);
-
(iii)
unbounded, so \(\lim _{n \rightarrow \infty }\tau (n)=\infty \).Footnote 2
Since such a real growth function \(\tau \) is unbounded, it expresses a (computable) lower bound for the ‘rate’ at which \(T\) increases to infinity along \(\omega \). Clearly, if \(T\in \overline{\mathbb {T}}_\text {S}(\varphi )\) is computably unbounded on \(\omega \in \varOmega \), then it is also unbounded on \(\omega \).
Definition 5
([5]). A path \(\omega \in \varOmega \) is S-random for a forecasting system \(\varphi \in \varPhi \) if no test supermartingale \(T\in \overline{\mathbb {T}}_\text {S}(\varphi )\) is computably unbounded on \(\omega \).
De Cooman and De Bock have proved that these four martingale-theoretic randomness notions satisfy Properties 1 and 2 [5, Propositions 9,10,17,18]. To describe the relations between these martingale-theoretic imprecise-probabilistic randomness notions, we consider the sets \(\varOmega _\text {R}(\varphi )\), with  ; they satisfy the following inclusions [5, Section 6].
; they satisfy the following inclusions [5, Section 6].
Thus, if a path \(\omega \in \varOmega \) is Martin-Löf random for a forecasting system \(\varphi \in \varPhi \), then it is also weakly Martin-Löf, computably and Schnorr random for \(\varphi \). Consequently, for every forecasting system \(\varphi \in \varPhi \), there are at most as many paths that are Martin-Löf random as there are weakly Martin-Löf, computably or Schnorr random paths. We therefore call Martin-Löf randomness stronger than weak Martin-Löf, computable, or Schnorr randomness. And so, mutatis mutandis, for the other randomness notions.
We also consider two other imprecise-probabilistic randomness notions, which have a more frequentist flavour: Church randomness (CH) and weak Church randomness (wCH). Their definition makes use of yet another (but simpler) type of implementable real processes; a selection process \(S\) is called recursive if there is a finite algorithm that, for every \(s\in \mathbb {S}\), outputs the binary digit  .
.
Definition 6
([5]). A path \(\omega \in \varOmega \) is CH-random (wCH-random) for a forecasting system \(\varphi \in \varPhi \) if for every recursive (temporal) selection process \(S\) for which \(\lim _{n \rightarrow \infty }\sum _{k=0}^{n-1}S(\omega _{1:k})=\infty \), it holds that

For a stationary forecasting system \(I \in \mathcal {I}\), the conditions in these definitions simplify to the perhaps more intuitive requirement that
It is easy to see that these two randomness notions also satisfy Properties 1 and 2. Since the notion of weak Church randomness considers fewer selection processes than Church randomness does, it is clear that if a path \(\omega ~\in ~\varOmega \) is Church random for a forecasting system \(\varphi \in \varPhi \), then it is also weakly Church random for \(\varphi \). Hence, \(\varOmega _\text {CH}(\varphi )\subseteq \varOmega _\text {wCH}(\varphi )\). For computable forecasting systems, we can also relate these two ‘frequentist flavoured’ notions with the martingale-theoretic notions considered before [5, Sections 6 and 7]: for every computable forecasting system \(\varphi \in \varPhi \),

5 Smallest Interval Forecasts and Randomness
From now on, we will focus on stationary forecasting systems and investigate the differences and similarities between the six randomness notions we consider. We start by studying if there is a smallest interval forecast for which a path is (almost) random. To this end, we first compare the sets \(\mathcal {I}_\text {R}(\omega )\), with  . They satisfy similar relations as the sets \(\varOmega _\text {R}(\varphi )\)—but without a need for computability assumptions.
. They satisfy similar relations as the sets \(\varOmega _\text {R}(\varphi )\)—but without a need for computability assumptions.
Proposition 1
([5, Sect. 8]). For every path \(\omega \in \varOmega \), it holds that

Similarly to before, if a path \(\omega \in \varOmega \) is Martin-Löf random for an interval forecast \(I \in \mathcal {I}\), then it is also weakly Martin-Löf, computably, Schnorr and (weakly) Church random for I. Observe that for our weakest notion of randomness, Definition 6—with \(S=1\)—guarantees that all interval forecasts \(I \in \mathcal {I}_\text {wCH}(\omega )\) satisfy Property 3, and therefore, by Proposition 1, all six randomness notions that we are considering here satisfy Property 3. Since the sets \(\mathcal {I}_\text {R}(\omega )\) are also non-empty by Property 2, the interval forecasts \(I_\text {R}(\omega )\) are well-defined and non-empty for all  . Moreover, since the sets \(\mathcal {I}_\text {R}(\omega )\) satisfy the relations in Proposition 1, their intersections \(I_\text {R}(\omega )\) satisfy the following inverse relations.
. Moreover, since the sets \(\mathcal {I}_\text {R}(\omega )\) satisfy the relations in Proposition 1, their intersections \(I_\text {R}(\omega )\) satisfy the following inverse relations.
Corollary 1
For every path \(\omega \in \varOmega \), it holds that

For Church and weak Church randomness, it holds that every path  is in fact Church and weakly Church random, respectively, for the interval forecasts \(I_\text {CH}(\omega )\) and \(I_\text {wCH}(\omega )\).
is in fact Church and weakly Church random, respectively, for the interval forecasts \(I_\text {CH}(\omega )\) and \(I_\text {wCH}(\omega )\).
Proposition 2
Consider any  and any path \(\omega \in \varOmega \). Then \(I_\text {R}(\omega )\) is the smallest interval forecast that \(\omega \) is R-random for.
and any path \(\omega \in \varOmega \). Then \(I_\text {R}(\omega )\) is the smallest interval forecast that \(\omega \) is R-random for.
A similar result need not hold for the other four types of randomness we are considering here. As an illustrative example, consider the non-stationary but temporal precise forecasting system \(\varphi _{\sim \nicefrac {1}{2}}\) defined, for all \(s\in \mathbb {S}\), by

It has been proved that if a path \(\omega \in \varOmega \) is computably random for \(\varphi _{\sim \nicefrac {1}{2}}\), then \(\omega \) is Church random and almost computably random for the stationary precise model \(\nicefrac {1}{2}\), whilst not being computably random for \(\nicefrac {1}{2}\) [3].
While in general \(I_\text {R}(\omega )\) may not be the smallest interval forecast that a path \(\omega \in \varOmega \) is R-random for, De Cooman and De Bock have effectively proved that for  , every path \(\omega \in \varOmega \) is almost R-random for \(I_\text {R}(\omega )\), essentially because the corresponding sets \(\mathcal {I}_\text {R}(\omega )\) are then closed under finite intersections.
, every path \(\omega \in \varOmega \) is almost R-random for \(I_\text {R}(\omega )\), essentially because the corresponding sets \(\mathcal {I}_\text {R}(\omega )\) are then closed under finite intersections.
Proposition 3
([5, Sect. 8]). Consider any  and any path \(\omega \in \varOmega \). Then \(I_\text {R}(\omega )\) is the smallest interval forecast for which \(\omega \) is almost R-random.
and any path \(\omega \in \varOmega \). Then \(I_\text {R}(\omega )\) is the smallest interval forecast for which \(\omega \) is almost R-random.
It should be noted that there is no mention of Martin-Löf randomness in Propositions 2 and 3. Indeed, it is an open problem whether every path \(\omega \in \varOmega \) is (almost) ML-random for the interval forecast \(I_\text {ML}(\omega )\). We can however provide a partial answer by focusing on paths \(\omega \in \varOmega \) that are ML-random for a computable precise forecasting system \(\varphi \in \varPhi \).
Proposition 4
If a path \(\omega \in \varOmega \) is ML-random for a computable precise forecasting system \(\varphi \in \varPhi \), then \(I_\text {ML}(\omega )\) is the smallest interval forecast for which \(\omega \) is almost ML-random.
6 What Do Smallest Interval Forecasts Look Like?
Having established conditions under which \(I_\text {R}(\omega )\) is the smallest interval forecast \(\omega \) is (almost) random for, we now set out to find an alternative expression for this interval forecast. Forecasting systems will play a vital role in this part of the story; for every path \(\omega \in \varOmega \) and every forecasting system \(\varphi \in \varPhi \), we consider the interval forecast \(I_\varphi (\omega )\) defined by

When we restrict our attention to computable forecasting systems \(\varphi \in \varPhi \), and if we assume that a path \(\omega \in \varOmega \) is R-random for such a forecasting system \(\varphi \), with  , then the forecasting system \(\varphi \) imposes outer bounds on the interval forecast \(I_\text {R}(\omega )\) in the following sense.
, then the forecasting system \(\varphi \) imposes outer bounds on the interval forecast \(I_\text {R}(\omega )\) in the following sense.
Proposition 5
For any  and any path
and any path  that is R-random for a computable forecasting system \(\varphi \in \varPhi \): \(I_\text {R}(\omega )\subseteq I_\varphi (\omega )\).
that is R-random for a computable forecasting system \(\varphi \in \varPhi \): \(I_\text {R}(\omega )\subseteq I_\varphi (\omega )\).
If we only consider computable precise forecasting systems \(\varphi \in \varPhi \) and assume that a path \(\omega \in \varOmega \) is R-random for \(\varphi \), with  , then the forecasting system \(\varphi \) completely characterises the interval forecast \(I_\text {R}(\omega )\).
, then the forecasting system \(\varphi \) completely characterises the interval forecast \(I_\text {R}(\omega )\).
Theorem 1
For any  and any path \(\omega \in \varOmega \) that is R-random for a computable precise forecasting system \(\varphi \in \varPhi \): \(I_\text {R}(\omega )=I_\varphi (\omega )\).
and any path \(\omega \in \varOmega \) that is R-random for a computable precise forecasting system \(\varphi \in \varPhi \): \(I_\text {R}(\omega )=I_\varphi (\omega )\).
When the computable precise forecasting systems \(\varphi \in \varPhi \) are also temporal, this result applies to Schnorr and weak Church randomness as well.
Theorem 2
For any  and any path
and any path
 that is
that is
 -random for a computable precise temporal forecasting system \(\varphi \in \varPhi \): \(I_\text {R}(\omega )=I_\varphi (\omega )\).
-random for a computable precise temporal forecasting system \(\varphi \in \varPhi \): \(I_\text {R}(\omega )=I_\varphi (\omega )\).
7 When Do These Smallest Interval Forecasts Coincide?
Finally, we put an old question into a new perspective: to what extent are randomness notions different? We take an ‘imprecise’ perspective here, by comparing the smallest interval forecasts for which a path \(\omega \in \varOmega \) is (almost) R-random, with  . As we will see, it follows from our previous exposition that there are quite some paths for which these smallest interval forecasts coincide.
. As we will see, it follows from our previous exposition that there are quite some paths for which these smallest interval forecasts coincide.
Let us start by considering a path \(\omega \in \varOmega \) that is ML-random for some computable precise forecasting system \(\varphi \in \varPhi \); similar results hold when focusing on weaker notions of randomness. We know from Eq. (1) that \(\omega \) is then also wML-, C- and CH-random for \(\varphi \). By invoking Propositions 2, 3 and 4, we infer that \(I_\text {R}(\omega )\) is the smallest interval forecast that \(\omega \) is (almost) R-random for, for any  . Moreover, by Theorem 1, these smallest interval forecasts all equal \(I_\varphi (\omega )\) and therefore coincide, i.e., \(I_\text {ML}(\omega )=I_\text {wML}(\omega )=I_\text {C}(\omega )=I_\text {CH}(\omega )=I_\varphi (\omega )\).
. Moreover, by Theorem 1, these smallest interval forecasts all equal \(I_\varphi (\omega )\) and therefore coincide, i.e., \(I_\text {ML}(\omega )=I_\text {wML}(\omega )=I_\text {C}(\omega )=I_\text {CH}(\omega )=I_\varphi (\omega )\).
By only looking at temporal computable precise forecasting systems \(\varphi \in \varPhi \), we can even strengthen these conclusions. For example, using a similar argument as before—but using Theorem 2 instead of 1—we see that if \(\omega \) is ML-random for such a forecasting system \(\varphi \), then the smallest interval forecasts \(I_\text {R}(\omega )\) for which \(\omega \) is (almost) R-random coincide for all six randomness notions that we consider.
Looking at these results, the question arises whether there are paths \(\omega \in \varOmega \) for which the various interval forecasts \(I_\text {R}(\omega )\) do not coincide. It turns out that such paths do exist. We start by showing that the smallest interval forecasts \(I_\text {C}(\omega )\) and \(I_\text {S}(\omega )\) for which a path \(\omega \in \varOmega \) is respectively almost C- and almost S-random do not always coincide; this result is mainly a reinterpretation of a result in [5, 10].
Proposition 6
There is a path \(\omega \in \varOmega \) such that  .
.
We are also able to show that there is a path \(\omega \in \varOmega \) such that \(I_\text {C}(\omega )=\nicefrac {1}{2}\) is the smallest interval forecast it is almost C-random for, whereas \(\omega \) is not almost ML-random for \(\nicefrac {1}{2}\); for this result, we have drawn inspiration from [9].
Proposition 7
For every  , there is a path \(\omega \in \varOmega \) such that \(I_\text {C}(\omega )=\nicefrac {1}{2}\) and \(I \notin \mathcal {I}_\text {ML}(\omega )\) for any \(I \in \mathcal {I}\) such that
, there is a path \(\omega \in \varOmega \) such that \(I_\text {C}(\omega )=\nicefrac {1}{2}\) and \(I \notin \mathcal {I}_\text {ML}(\omega )\) for any \(I \in \mathcal {I}\) such that  .
.
Clearly, the path \(\omega \in \varOmega \) in Proposition 7 cannot be Martin-Löf random for a precise computable forecasting system \(\varphi \in \varPhi \), because otherwise, the interval forecasts \(I_\text {C}(\omega )\) and \(I_\text {ML}(\omega )\) would coincide by Eq. (1) and Theorem 1, and \(\omega \) would therefore be almost Martin-Löf random for \(\nicefrac {1}{2}\) by Proposition 4, contradicting the result. So the path \(\omega \) in this result is an example of a path for which we do not know whether there is a smallest interval forecast that \(\omega \) is almost Martin-Löf random for. However, if there is such a smallest interval forecast, then Proposition 7 shows it is definitely not equal to \(\nicefrac {1}{2}\); due to Corollary 1, it must then strictly include \(\nicefrac {1}{2}\).
8 Conclusions and Future Work
We’ve come to the conclusion that various (non-stationary) precise-probabilistic randomness notions in the literature are, in some respects, not that different; if a path is random for a computable precise (temporal) forecasting system, then the smallest interval forecast for which it is (almost) random coincides for several randomness notions. The computability condition on the precise forecasting system is important for this result, but we don’t think it is that big a restriction. After all, computable forecasting systems are those that can be computed by a finite algorithm up to any desired precision, and therefore, they are arguably the only ones that are of practical relevance.
An important concept that made several of our results possible was that of almost randomness, a notion that is closely related to randomness but is—slightly—easier to satisfy. In our future work, we would like to take a closer look at the difference between these two notions. In particular, the present discussion, together with our work in [7], makes us wonder to what extent the distinction between them is relevant in a more practical context.
We also plan to continue investigating the open question whether there is for every path some smallest interval forecast for which it is (almost) Martin-Löf random. Finally, there is still quite some work to do in finding out whether the randomness notions we consider here are all different from a stationary imprecise-probabilistic perspective, in the sense that there are paths for which the smallest interval forecasts for which they are (almost) random do not coincide.
Notes
- 1.
\(\mathbb {N}\) denotes the natural numbers and
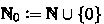 denotes the non-negative integers (A real \(x \in \mathbb {R}\) is called negative, positive, non-negative and non-positive, respectively, if \(x<0\), \(x>0\), \(x\ge 0\) and \(x \le 0\)).
denotes the non-negative integers (A real \(x \in \mathbb {R}\) is called negative, positive, non-negative and non-positive, respectively, if \(x<0\), \(x>0\), \(x\ge 0\) and \(x \le 0\)). - 2.
Since \(\tau \) is non-decreasing, it being unbounded is equivalent to \(\lim _{n \rightarrow \infty }\tau (n)=\infty \).
References
Ambos-Spies, K., Kucera, A.: Randomness in computability theory. Contemporary Math. 257, 1–14 (2000)
Bienvenu, L., Shafer, G., Shen, A.: On the history of martingales in the study of randomness. Electron. J. Hist. Probab. Stat. 5, 1–40 (2009)
De Cooman, G., De Bock, J.: Computable randomness is inherently imprecise. In: Proceedings of the Tenth International Symposium on Imprecise Probability: Theories and Applications. Proceedings of Machine Learning Research, vol. 62, pp. 133–144 (2017)
De Cooman, G., De Bock, J.: Randomness and imprecision: a discussion of recent results. In: Proceedings of the Twelfth International Symposium on Imprecise Probability: Theories and Applications. Proceedings of Machine Learning Research, vol. 147, pp. 110–121 (2021)
De Cooman, G., De Bock, J.: Randomness is inherently imprecise. Int. J. Approximate Reasoning (2021). https://www.sciencedirect.com/science/article/pii/S0888613X21000992
Downey, R.G., Hirschfeldt, D.R.: Algorithmic Randomness and Complexity. Springer, New York (2010). https://doi.org/10.1007/978-0-387-68441-3
Persiau, F., De Bock, J., De Cooman, G.: A remarkable equivalence between non-stationary precise and stationary imprecise uncertainty models in computable randomness. In: Proceedings of the Twelfth International Symposium on Imprecise Probability: Theories and Applications. Proceedings of Machine Learning Research, vol. 147, pp. 244–253 (2021)
Persiau, F., De Bock, J., De Cooman, G.: The smallest probability interval a sequence is random for: a study for six types of randomness (2021). https://arxiv.org/abs/2107.07808, extended online version
Schnorr, C.P.: A unified approach to the definition of random sequences. Math. Syst. Theory 5, 246–258 (1971)
Wang, Y.: Randomness and Complexity. PhD thesis, Ruprecht Karl University of Heidelberg (1996)
Acknowledgments
Floris Persiau’s research was supported by FWO (Research Foundation-Flanders), project number 11H5521N.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Persiau, F., De Bock, J., de Cooman, G. (2021). The Smallest Probability Interval a Sequence Is Random for: A Study for Six Types of Randomness. In: Vejnarová, J., Wilson, N. (eds) Symbolic and Quantitative Approaches to Reasoning with Uncertainty. ECSQARU 2021. Lecture Notes in Computer Science(), vol 12897. Springer, Cham. https://doi.org/10.1007/978-3-030-86772-0_32
Download citation
DOI: https://doi.org/10.1007/978-3-030-86772-0_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-86771-3
Online ISBN: 978-3-030-86772-0
eBook Packages: Computer ScienceComputer Science (R0)






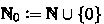 denotes the non-negative integers (A real
denotes the non-negative integers (A real