Bayesian Crowdsourcing with Constraints

Abstract

Crowdsourcing has emerged as a powerful paradigm for efficiently labeling large datasets and performing various learning tasks, by leveraging crowds of human annotators. When additional information is available about the data, constrained or semi-supervised crowdsourcing approaches that enhance the aggregation of labels from human annotators are well motivated. This work deals with constrained crowdsourced classification with instance-level constraints, that capture relationships between pairs of data. A Bayesian algorithm based on variational inference is developed, and its quantifiably improved performance, compared to unsupervised crowdsourcing, is analytically and empirically validated on several crowdsourcing datasets.

Work in this paper was supported by NSF grant 1901134.

1 Introduction

Crowdsourcing, as the name suggests, harnesses crowds of human annotators, using services such as Amazon’s Mechanical Turk [16], to perform various learning tasks such as labeling, image tagging and natural language annotations, among others [11]. Even though crowdsourcing can be efficient and relatively inexpensive, inference of true labels from the noisy responses provided by multiple annotators of unknown expertise can be challenging, especially in the typical unsupervised scenario, where no ground-truth data is available.

It is thus practical to look for side information that can be beneficial to the crowdsourcing task, either from experts or from physical constraints associated with the task. For example, queries with known answers may be injected in crowdsourcing tasks in Amazon’s Mechanical Turk, in order to assist with the evaluation of annotator reliability. Methods that leverage such information fall under the constrained or semi-supervised learning paradigm [5]. Seeking improved performance in the crowdsourcing task, we focus on constrained crowdsourcing, and investigate instance-level or pairwise constraints, such as must- and cannot-link constraints, which show up as side information in unsupervised tasks, such as clustering [3]. Compared to label constraints, instance-level ones provide ‘weaker information,’ as they describe relationships between pairs of data, instead of anchoring the label of a datum. Semi-supervised learning with few label constraints is typically employed when acquiring ground-truth labels is time consuming or expensive, e.g. annotation of biomedical images from a medical professional. Instance-level constraints on the other hand are used when domain knowledge is easier to encode between pairs of data, e.g. road lane identification from GPS data.

To accommodate such available information, the present work capitalizes on recent advances in Bayesian inference. Relative to deterministic methods, the Bayesian approach allows for seamless integration of prior information for the crowdsourcing task, such as annotator performance from previous tasks, and at the same time enables uncertainty quantification of the fused label estimates and parameters of interest. Our major contributions can be summarized as follows: (i) We develop a Bayesian algorithm for crowdsourcing with pairwise constraints; (ii) We derive novel error bounds for the unsupervised variational Bayes crowdsourcing algorithm, in Theorem 1. These error bounds are extended for the proposed constrained algorithm in Theorem 2; and (iii) Guided by the aforementioned theoretical analysis, we provide a constraint selection scheme. In addition to the error bounds, the performance of the proposed algorithm is evaluated with extensive numerical tests. Those corroborate that there are classification performance gains to be harnessed, even when using weaker side information, such as the aforementioned must- and cannot-link constraints.

Notation: Unless otherwise noted, lowercase bold fonts, $\boldsymbol{x}$, denote vectors, uppercase ones, $\mathbf {X}$, represent matrices, and calligraphic uppercase, $\mathcal {X}$, stand for sets. The (i, j)th entry of matrix $\mathbf {X}$ is denoted by $[\mathbf {X}]_{ij}$. ${{\,\mathrm{Pr}\,}}$ or p denotes probability, or the probability mass function; $\sim$ denotes “distributed as,” $|\mathcal {X}|$ is the cardinality of set $\mathcal {X}$, ${{\,\mathrm{\mathbb {E}}\,}}[\cdot ]$ denotes expectation, and $\mathbbm {1}(\mathcal {A})$ is the indicator function for the event $\mathcal {A}$, that takes value 1, when $\mathcal {A}$ occurs, and is 0 otherwise.

2 Problem Formulation and Preliminaries

Consider a dataset consisting of N data $\{x_n\}_{n=1}^{N}$, with each datum belonging to one of K classes with corresponding labels $\{y_n\}_{n=1}^{N}$; that is, $y_n = k$ if $x_n$ belongs to class k. Consider now M annotators that observe $\{x_n\}_{n=1}^{N}$, and provide estimates of labels. Let $\check{y}_n^{(m)}\in \{1,\ldots ,K\}$ be the label estimate of $x_n$ assigned by the m-th annotator. If an annotator has not provided a response for datum n we set $\check{y}_n^{(m)} = 0.$ Let $\check{\mathbf {Y}}$ be the $M\times N$ matrix of annotator responses with entries $[\check{\mathbf {Y}}]_{mn} = \check{y}_n^{(m)}$, and $\mathbf {y} := [y_1,\ldots ,y_N]^{\top }$ the $N\times 1$ vector of ground truth labels. The task of crowdsourced classification is: Given only the annotator responses in $\check{\mathbf {Y}}$, the goal is find the ground-truth label estimates $\{\hat{y}_n\}_{n=1}^N$.

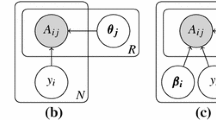
Per datum $x_n$, the true label $y_n$ is assumed drawn from a categorical distribution with parameters $\boldsymbol{\pi } := [\pi _1,\ldots ,\pi _K]^\top$, where $\pi _k := {{\,\mathrm{Pr}\,}}(y_n = k)$. Further, consider that each learner has a fixed probability of deciding that a datum belongs to class $k'$, when presented with a datum of class k; thus, annotator behavior is presumed invariant across the dataset. The performance of an annotator m is then characterized by the so-called confusion matrix $\mathbf {\Gamma }^{(m)}$, whose $(k,k')$-th entry is $[\mathbf {\Gamma }^{(m)}]_{k,k'} := \gamma _{k,k'}^{(m)} = {{\,\mathrm{Pr}\,}}\left( \check{y}_n^{(m)} = k' | y_n = k\right) .$ The $K\times K$ confusion matrix showcases the statistical behavior of an annotator, as each row provides the annotator’s probability of deciding the correct class, when presented with a datum from each class. Collect all annotator confusion matrices in $\mathbf {\Gamma }:=[\mathbf {\Gamma }^{(1)},\ldots ,\mathbf {\Gamma }^{(m)}].$ Responses of different annotators per datum n are presumed conditionally independent, given the ground-truth label $y_n$; that is, $p\left( \check{y}_{n}^{(1)} = k_1,\ldots ,\check{y}_{n}^{(M)}=k_M | y_n = k\right) = \prod _{m=1}^{M} p\left( \check{y}_{n}^{(m)} = k_m | y_n = k\right) .$ The latter is a standard assumption that is commonly employed in crowdsourcing works [7, 13, 37]. Finally, most annotators are assumed to be better than random.

2.1 Prior Works

Arguably the simplest approach to fusing crowdsourced labels is majority voting, where the estimated label of a datum is the one most annotators agree upon. This presumes that all annotators are equally “reliable,” which may be unrealistic. Aiming at high-performance label fusion, several approaches estimate annotator parameters, meaning the confusion matrices as well as class priors. A popular approach is joint maximum likelihood (ML) estimation of the unknown labels $\mathbf {y}$, and the aforementioned confusion matrices using the expectation-maximization (EM) algorithm [7]. As EM guarantees convergence to a locally optimal solution, alternative estimation methods have been recently advocated. Spectral methods invoke second- and third-order moments of annotator responses to infer the unknown annotator parameters [12, 13, 31, 37].

A Bayesian treatment of crowdsourced learning, termed Bayesian Classifier Combination was introduced in [15]. This approach used Gibbs sampling to estimate the parameters of interest, while [28] introduced a variational Bayes EM (VBEM) method for the same task. Other Bayesian approaches infer communities of annotators, enhancing the quality of aggregated labels [19, 35]. For sequential or networked data, [20, 23, 32, 33] advocated variational inference and EM-based alternatives. All aforementioned approaches utilize only $\check{\mathbf {Y}}$. When features $\{x_n\}_{n=1}^{N}$ are also available, parametric models [22], approaches based on Gaussian Processes [25, 26], or deep learning [1, 2, 24, 27] can be employed to classify the data, and simultaneously learn a classifier.

Current constrained or semi-supervised approaches to crowdsourcing extend the EM algorithm of Dawid and Skene [30], by including a few ground-truth labels. The model in [36] includes a graph between datapoints to enable label prediction for data that have not been annotated, while [17] puts forth a max-margin majority vote method when label constraints are available. When features $\{x_n \}_{n=1}^{N}$ are available, [14] relies on a parametric model to learn a binary classifier from crowd responses and expert labels.

The present work develops a Bayesian constrained approach to crowdsourced classification, by adapting the popular variational inference framework [4]. In addition, it provides novel performance analysis for both Bayesian unsupervised and semi-supervised approaches. The proposed method does not require features $\{x_n \}_{n=1}^{N}$, but relies only on annotator labels – a first attempt at incorporating instance-level constraints for the crowdsourced classification task.

3 Variational Inference for Crowdsourcing

Before presenting our constrained approach, this section will recap a Bayesian treatment of the crowdsourcing problem. First, variational Bayes is presented in Sect. 3.1, followed by an inference algorithm for crowdsourcing [28] in Sect. 3.2. A novel performance analysis for the VBEM algorithm is also presented in Sect. 3.2.

3.1 Variational Bayes

Consider a set of observed data collected in $\mathbf {X}$, and a set of latent variables and parameters in $\mathbf {Z}$ that depend on $\mathbf {X}$. Variational Bayes seeks $\mathbf {Z}$ that maximize the marginal of $\mathbf {X}$, by treating both latent variables and parameters as random [4]. EM in contrast treats $\mathbf {Z}$ as deterministic and provides point estimates. The log-marginal of $\mathbf {X}$ can be written as

$$\begin{aligned} \ln p(\mathbf {X})&= \int q(\mathbf {Z})\ln \frac{p(\mathbf {X},\mathbf {Z})}{q(\mathbf {Z})}d\mathbf {Z} - \int q(\mathbf {Z})\ln \frac{p(\mathbf {Z}|\mathbf {X})}{q(\mathbf {Z})}d\mathbf {Z} = L(q) + \mathrm{KL}(q||p) \end{aligned}$$

(1)

where $L(q): = \int q(\mathbf {Z})\ln \frac{p(\mathbf {X},\mathbf {Z})}{q(\mathbf {Z})}d\mathbf {Z}$, and $\mathrm{KL}(q||p) = -\int q(\mathbf {Z})\ln \frac{p(\mathbf {Z}|\mathbf {X})}{q(\mathbf {Z})}d\mathbf {Z}$ denotes the Kullback-Leibler divergence between pdfs q and p [6]. This expression is maximized for $q(\mathbf {Z}) = p(\mathbf {Z}|\mathbf {X})$, however when $p(\mathbf {Z}|\mathbf {X})$ is an intractable pdf, one may seek distributions q from a prescribed tractable family $\mathcal {Q}$, such that $\mathrm{KL}(q||p)$ is minimized. One such family is the family of factorized distributions, which also go by the name of mean field distributions. Under the mean field paradigm, the variational distribution $q(\mathbf {Z})$ is decomposed into a product of single variable factors, $q(\mathbf {Z}) = \prod _i q(\mathbf {Z}_i)$, with $q(\mathbf {Z}_i)$ denoting the variational distribution corresponding to the variable $\mathbf {Z}_i.$

It can be shown that the optimal updates for each factor are given by [4]

$$\begin{aligned} \ln q^*(\mathbf {Z}_i) = {{\,\mathrm{\mathbb {E}}\,}}_{-\mathbf {Z}_i}\left[ \ln p(\mathbf {X},\mathbf {Z}) \right] + c \end{aligned}$$

(2)

where c is an appropriate constant, and the ${-\mathbf {Z}_i}$ subscript denotes that the expectation is taken w.r.t. the terms in q that do not involve $\mathbf {Z}_i$, that is $\prod _{j\ne i}q(\mathbf {Z}_j)$. These optimal factors can be estimated iteratively, and such a procedure is guaranteed to converge at least to a local maximum of (1).

3.2 Variational EM for Crowdsourcing

Next, we will outline how variational inference can be used to derive an iterative algorithm for crowdsourced classification [28]. The Bayesian treatment of the crowdsourcing problem dictates the use of prior distributions on the parameters of interest, namely $\boldsymbol{\pi }$, and $\mathbf {\Gamma }$. The probabilities $\boldsymbol{\pi }$ are assigned a Dirichlet distribution prior with parameters $\boldsymbol{\alpha }_{0}:=[\alpha _{0,1},\ldots ,\alpha _{0,K}]^\top$, that is $\boldsymbol{\pi }\sim \mathrm{Dir}(\boldsymbol{\pi };\boldsymbol{\alpha }_{0})$, whereas for an annotator m, the columns $\{\boldsymbol{\gamma }_k^{(m)} \}_{k=1}^{K}$ of its confusion matrix are considered independent, and $\boldsymbol{\gamma }_k^{(m)}$ is assigned a Dirichlet distribution prior with parameters $\boldsymbol{\beta }_{0,k}^{(m)} := [\beta _{0,k,1}^{(m)},\ldots ,\beta _{0,k,K}^{(m)}]^\top$, respectively. These priors on the parameters of interest are especially useful when only few data have been annotated, and can also capture annotator behavior from previous crowdsourcing tasks. The joint distribution of $\mathbf {y},\check{\mathbf {Y}},\boldsymbol{\pi }$ and $\mathbf {\Gamma }$ is

$$\begin{aligned}&p(\mathbf {y},\boldsymbol{\pi },\check{\mathbf {Y}},\mathbf {\Gamma };\boldsymbol{\alpha }_{0},\mathbf {B}_0) = \prod _{n=1}^{N}\pi _{y_n}\prod _{m=1}^{M}\prod _{k'=1}^{K}(\gamma _{y_n,k'}^{(m)})^{\delta _{n,k'}^{(m)}}p(\boldsymbol{\pi };\boldsymbol{\alpha }_{0})p(\mathbf {\Gamma };\mathbf {B}_0) \end{aligned}$$

(3)

with $\mathbf {B}_0$ collecting all prior parameters $\boldsymbol{\beta }_{0,k}^{(m)}$ for $k=1,\ldots ,K$ and $m=1,\ldots ,M$, and $\delta _{n,k}^{(m)}:=\mathbbm {1}(\check{y}_n^{(m)} = k)$. The parametrization on $\boldsymbol{\alpha }_{0},\mathbf {B}_0$ will be henceforth implicit for brevity.

With the goal of estimating the unknown variables and parameters of interest, we will use the approach outlined in the previous subsection, to approximate $p(\mathbf {y},\boldsymbol{\pi },\mathbf {\Gamma }|\check{\mathbf {Y}})$ using a variational distribution $q(\mathbf {y},\boldsymbol{\pi },\mathbf {\Gamma })$. Under the mean-field class, this variational distribution factors across the unknown variables as $q(\mathbf {y},\boldsymbol{\pi },\mathbf {\Gamma }) = q(\mathbf {y})q(\boldsymbol{\pi })q(\mathbf {\Gamma }).$ Since the data are assumed i.i.d. [cf. Sect. 2], $q(\mathbf {y})$ is further decomposed into $q(\mathbf {y}) = \prod _{n=1}^{N}q(y_n).$ In addition, since annotators are assumed independent and the columns of their confusion matrices are also independent, we have $q(\mathbf {\Gamma }) = \prod _{m=1}^{M}\prod _{k=1}^{K}q(\boldsymbol{\gamma }_{k}^{(m)})$. The variational Bayes EM algorithm is an iterative algorithm, with each iteration consisting of two steps: the variational E-step, where the latent variables $\mathbf {y}$ are estimated; and the variational M-step, where the distribution of the parameters of interest $\boldsymbol{\pi },\mathbf {\Gamma }$ are estimated.

At iteration $t+1$, the variational distribution for the unknown label $y_n$ is given by

$$\begin{aligned} \ln q_{t+1}(y_n) = {{\,\mathrm{\mathbb {E}}\,}}_{-y_n}\left[ \ln p(\mathbf {y},\boldsymbol{\pi }, \check{\mathbf {Y}},\mathbf {\Gamma }) \right] + c. \end{aligned}$$

(4)

The subscript of q denotes the iteration index. The expectation in (4) is taken w.r.t. the terms in $q_{t}$ that do not involve $y_n$, that is $\prod _{n'\ne n}q_{t}(y_{n'})q_{t}(\boldsymbol{\pi })q_{t}(\mathbf {\Gamma })$. Upon expanding $p(\boldsymbol{y},\boldsymbol{\pi },\check{\mathbf {Y}},\mathbf {\Gamma })$, (4) becomes

$$\begin{aligned}&\ln q_{t+1}(y_n) = {{\,\mathrm{\mathbb {E}}\,}}_{\boldsymbol{\pi }}\left[ \ln \pi _{y_n}\right] + {{\,\mathrm{\mathbb {E}}\,}}_{\mathbf {\Gamma }}\left[ \sum _{m=1}^{M}\sum _{k'=1}^{K}\delta _{n,k'}^{(m)}\ln \gamma _{y_n,k'}^{(m)} \right] + c . \end{aligned}$$

(5)

Accordingly, the update for the class priors in $\boldsymbol{\pi }$ is

$$\begin{aligned} \ln q_{t+1}(\boldsymbol{\pi }) = {{\,\mathrm{\mathbb {E}}\,}}_{-\boldsymbol{\pi }}\left[ \ln p(\mathbf {y},\boldsymbol{\pi }, \check{\mathbf {Y}},\mathbf {\Gamma }) \right] + c \end{aligned}$$

(6)

where the expectation is taken w.r.t. $q_{t+1}(\mathbf {y})q_t(\mathbf {\Gamma })$. Based on (6), it can be shown [28] that

$$\begin{aligned} q_{t+1}(\boldsymbol{\pi }) \propto \text {Dir}(\boldsymbol{\pi } ; \boldsymbol{\alpha }_{t+1}) \end{aligned}$$

(7)

where $\boldsymbol{\alpha }_{t+1} := [\alpha _{t+1,1},\ldots ,\alpha _{t+1,K}]^\top$ with $\alpha _{t+1,k} = N_{t+1,k} + \alpha _{0,k}$, $N_{t+1,k} :=\sum _{n=1}^{N}q_{t+1}(y_n = k)$. As a direct consequence of this, the term involving $\boldsymbol{\pi }$ in (5) is given by ${{\,\mathrm{\mathbb {E}}\,}}_{\boldsymbol{\pi }}\left[ \ln \pi _{k}\right] = \psi \left( \alpha _{t,k}\right) - \psi \left( \bar{\alpha }_{t}\right) ,$ with $\psi$ denoting the digamma function, and $\bar{\alpha }_{t} := \sum _{k=1}^{K}\alpha _{t,k}$.

For the k-th column of $\mathbf {\Gamma }^{(m)}$ the update takes the form

$$\begin{aligned}&\ln q_{t+1}(\boldsymbol{\gamma }_{k}^{(m)}) = {{\,\mathrm{\mathbb {E}}\,}}_{-\boldsymbol{\gamma }_{k}^{(m)}}\left[ \ln p(\mathbf {y},\boldsymbol{\pi }, \check{\mathbf {Y}},\mathbf {\Gamma }) \right] + c \end{aligned}$$

(8)

Using steps similar to the update of $q(\boldsymbol{\pi })$, one can show that

$$\begin{aligned} q_{t+1}(\boldsymbol{\gamma }_{k}^{(m)}) \propto \text {Dir}(\boldsymbol{\gamma }_{k}^{(m)} ; \boldsymbol{\beta }_{t+1,k}^{(m)}) \end{aligned}$$

(9)

with $\boldsymbol{\beta }_{t+1,k}^{(m)} := [\beta _{t+1,k,1}^{(m)},\ldots ,\beta _{t+1,k,1}^{(m)}]$, $\beta _{t+1,k,k'}^{(m)} := N_{t+1,k,k'}^{(m)} + \beta _{0,k,k'}^{(m)}$ and $N_{t+1,k,k'}^{(m)}:= \sum _{n=1}^{N}q_{t+1}(y_n = k)\delta _{n,k'}^{(m)}$. Consequently at iteration $t+1$, and upon defining $\bar{\beta }_{t+1,k}^{(m)}:=\sum _{\ell }^{K}\beta _{t+1,k,\ell }^{(m)}$, we have ${{\,\mathrm{\mathbb {E}}\,}}_\mathbf {\Gamma }[\ln \gamma _{k,k'}^{(m)}] = \psi \left( \beta _{t+1,k,k'}^{(m)}\right) - \psi \left( \bar{\beta }_{t+1,k}^{(m)} \right) .$ Given initial values for ${{\,\mathrm{\mathbb {E}}\,}}_{\boldsymbol{\pi }}\left[ \ln \pi _{y_n}\right]$ and ${{\,\mathrm{\mathbb {E}}\,}}_{\mathbf {\Gamma }}\left[ \sum _{m=1}^{M}\ln \gamma _{y_n,\check{y}_n^{(m)}}^{(m)} \right]$ per variational E-step, first the variational distribution for each datum $q(y_n)$ is computed using (4). Using the recently computed $q(\mathbf {y})$ at the variational M-step, the variational distribution for class priors $q(\boldsymbol{\pi })$ is updated via (6) and the variational distributions for each column of the confusion matrices $q(\boldsymbol{\gamma }_{k}^{(m)})$ are updated via (8). The E- and M-steps are repeated until convergence. Finally, the fused labels $\hat{\mathbf {y}}$ are recovered at the last iteration T as

$$\begin{aligned} \hat{y}_n = \mathop {{{\,\mathrm{argmax}\,}}}\limits _{k} \, q_{T}(y_n = k). \end{aligned}$$

(10)

The overall computational complexity of this algorithm is $\mathcal {O}(NKMT)$. The updates of this VBEM algorithm are very similar to the corresponding updates of the EM algorithm for crowdsourcing [7].

Performance Analysis. Let $\boldsymbol{\pi }^*$ comprise the optimal class priors, $\mathbf {\Gamma }^*$ the optimal confusion matrices, and $\mu _m := {{\,\mathrm{Pr}\,}}(\check{y}_n^{(m)} \ne 0)$ the probability an annotator will provide a response. The following theorem establishes that when VBEM is properly initialized, the estimation errors for $\boldsymbol{\pi },\mathbf {\Gamma }$ and the labels $\mathbf {y}$ are bounded. Such proper initializations can be achieved, for instance, using the spectral approaches of [12, 31, 37].

Theorem 1

Suppose that $\gamma _{k,k'}^{*(m)}\ge \rho _\gamma$ for all $k,k',m$, $\pi _k^{*}\ge \rho _\pi$ for all k, and that VBEM is initialized so that $|{{\,\mathrm{\mathbb {E}}\,}}[\pi _k] - \pi _k^*|\le \varepsilon _{\pi ,0}$ for all k and $|{{\,\mathrm{\mathbb {E}}\,}}[\gamma _{k,k'}^{(m)}] - \gamma _{k,k'}^{*(m)}|\le \varepsilon _{\gamma ,0}$ for all $k,k',m$. It then holds w.p. at least $1-\nu$ that for iterations $t=1,\ldots ,T$, update (4) yields

$$\begin{aligned}&\max _{k} |q_t(y_n = k) - \mathbbm {1}(y_n = k)| \le \varepsilon _{q,t}:= K\exp (-U) \nonumber \\&U := D+ f_\pi (\varepsilon _{\pi ,t-1}) + Mf_\gamma (\varepsilon _{\gamma ,t-1})\nonumber , \end{aligned}$$

(11)

where D is a quantity related to properties of the dataset and the annotators, while $f_\pi ,f_\gamma$ are decreasing functions. Consequently for $k,k'=1,\ldots ,K$, $m=1,\ldots ,M$ updates (6) and (8) yield respectively

$$\begin{aligned}&|{{\,\mathrm{\mathbb {E}}\,}}[\pi _k] - \pi _k^*|\le \epsilon _{\pi ,k,t} := \frac{N(\varepsilon _{q,t} + g_\pi (\nu )) + \alpha _{0,k} + \rho _\pi \bar{\alpha }_0}{N + \bar{\alpha }_0} \\&|{{\,\mathrm{\mathbb {E}}\,}}[\gamma _{k,k'}^{(m)}] - \gamma _{k,k'}^{*(m)}|\le \epsilon _{\gamma ,k,k',t}^{(m)} := \frac{2N(g_\gamma (\nu ) + \varepsilon _{q,t}) + \beta _{0,k,k'}^{(m)} + \bar{\beta }_{0,k}^{(m)} }{N\mu _m\pi _k^* - N\frac{g_\gamma (\nu )}{\gamma _{k,k'}^{*(m)}} - N\varepsilon _{q,t} + \bar{\beta }_{k}^{(m)}} \end{aligned}$$

(12)

with $g_\pi (\nu )$ and $g_\gamma (\nu )$ being decreasing functions of $\nu$ and $\varepsilon _{\pi ,t}:=\max _{k}\epsilon _{\pi ,k,t}, \varepsilon _{\gamma ,t}:= \max _{k,k',m} \epsilon _{\gamma ,k,k',t}^{(m)}$ .

Detailed theorem proofs are deferred to Appendix A of the supplementary material [34]. Theorem 1 shows that lowering the upper bound on label errors $\varepsilon _{q}$, will reduce the estimation error upper bounds of $\{\gamma _{k,k'}^{(m)}\}$ and $\boldsymbol{\pi }$. This in turn can further reduce $\varepsilon _{q,t}$, as it is proportional to $\varepsilon _\pi$, and $\varepsilon _\gamma$. With a VBEM algorithm for crowdsourcing and its performance analysis at hand, the ensuing section will introduce our constrained variational Bayes algorithm that can incorporate additional information to enhance label aggregation.

4 Constrained Crowdsourcing

This section deals with a constrained (or semi-supervised) variational Bayes approach to crowdsourcing. Here, additional information to the crowdsourcing task is available in the form of pairwise constraints, that indicate relationships between pairs of data. Throughout this section, $N_C$ will denote the number of available constraints that are collected in the set $\mathcal {C}$.

First, we note that when label constraints are available, the aforementioned VBEM algorithm can readily handle them, in a manner similar to [30]. Let $\mathcal {C}$ denote the set of indices for data with label constraints $\{ y_n\}_{n\in \mathcal {C}}$ available. These constraints can then be incorporated by fixing the values of $\{q(y_n)\}_{n\in \mathcal {C}}$ to 1 for all iterations. The variational distributions for data $n\not \in \mathcal {C}$ are updated according to (5), while confusion matrices and prior probabilities according to (8) and (6), respectively.

Next, we consider the case of instance-level constraints, which are the main focus of this work. Such information may be easier to obtain than the label constraints of the previous subsection, as pairwise constraints encapsulate relationships between pairs of data and not “hard” label information. The pairwise constraints considered here take the form of must-link and cannot-link relationships, and are collected respectively in the sets $\mathcal {C}_\mathrm{ML}$ and $\mathcal {C}_\mathrm{CL}$, and $\mathcal {C} = \mathcal {C}_\mathrm{ML}\cup \mathcal {C}_\mathrm{CL}$, $N_\mathrm{ML} = |\mathcal {C}_\mathrm{ML}|, N_\mathrm{CL} = |\mathcal {C}_\mathrm{CL}|$. All constraints consist of tuples $(i,j)\in \{1,\ldots ,N\}\times \{1,\ldots ,N\}$. A must-link constraint $(i,j), i\ne j$ indicates that two data points, $\boldsymbol{x}_i$ and $\boldsymbol{x}_j$ must belong to the same class, i.e. $y_i = y_j$, whereas a cannot-link constraint $(i',j')$ indicates that two points $\boldsymbol{x}_{i'}$ and $\boldsymbol{x}_{j'}$ are not in the same class; $y_{i'} \ne y_{j'}$. Note that instance level constraints naturally describe a graph $\mathcal {G}$, whose N nodes correspond to the data $\{x_n\}_{n=1}^{N}$, and whose (weighted) edges are the available constraints. This realization is the cornerstone of the proposed algorithm, suggesting that instance-level constraints can be incorporated in the crowdsourcing task by means of a probabilistic graphical model.

Specifically, we will encode constraints in the marginal pmf of the unknown labels $p(\mathbf {y})$ using a Markov Random Field (MRF), which implies that for all $n=1,\ldots ,N$, the local Markov property holds, that is $p(y_n|\mathbf {y}_{-n}) = p(y_n | \mathbf {y}_{\mathcal {C}_n})$, where $\mathbf {y}_{-n}$ denotes a vector containing all labels except $y_n$, while $\mathbf {y}_{\mathcal {C}_n}$ a vector containing labels for $y_{n'}$, where $n'\in \mathcal {C}_n,$ and $\mathcal {C}_n$ is a set containing indices such that $n': (n,n')\in \mathcal {C}$. By the Hammersley-Clifford theorem [10], the marginal pmf of the unknown labels is given by

$$\begin{aligned} p(\mathbf {y}) = \frac{1}{Z}\exp \left( \sum _{n=1}^{N}\ln \pi _{y_n} + \eta \underset{n'\in \mathcal {C}_n}{\sum } V(y_n,y_{n'}) \right) \end{aligned}$$

(13)

where Z is the (typically intractable) normalization constant, and $\eta > 0$ is a tunable parameter that specifies how much weight we assign to the constraints. Here, we define the V function as $V(y_n,y_{n'}) = w_{n,n'}\mathbbm {1}(y_n = y_{n'})$, where

$$\begin{aligned} w_{n,n'} = \mathbbm {1}\left( (n,n')\in \mathcal {C}_\mathrm{ML}\right) - \mathbbm {1}\left( (n,n')\in \mathcal {C}_\mathrm{CL}\right) \end{aligned}$$

(14)

The weights $w_{n,n'}$ can also take other real values, indicating the confidence one has per constraint $(n,n')$, but here we will focus on ${-1,0,1}$ values. This $V(y_n,y_{n'})$ term promotes the same label for data with must-link constraints, whereas it penalizes similar labels for data with cannot-link constraints. Note that more sophisticated choices for V can also be used. Nevertheless, this particular choice leads to a simple algorithm with quantifiable performance, as will be seen in the ensuing sections. Since the number of constraints is typically small, for the majority of data the term $\sum V(y_n,y_{n'})$ will be 0. Thus, the $\ln \pi$ term in the exponent of (13) acts similarly to the prior probabilities of Sect. 3.2. Again, adopting a Dirichlet prior $\mathrm{Dir} (\boldsymbol{\pi };\boldsymbol{\alpha }_{0}),$ and $\boldsymbol{\gamma }_k^{(m)}\sim \mathrm{Dir}(\boldsymbol{\gamma }_k^{(m)}; \boldsymbol{\beta }_{0,k}^{(m)})$ for all m, k, and using mean-field VB as before, the variational update for the n-th label becomes

$$\begin{aligned}&\ln q_{t+1}(y_n = k) = {{\,\mathrm{\mathbb {E}}\,}}_{\boldsymbol{\pi }}\left[ \ln \pi _{k}\right] + c \\&+ {{\,\mathrm{\mathbb {E}}\,}}_{\mathbf {\Gamma }}\left[ \sum _{m=1}^{M}\sum _{k'=1}^{K}{\delta _{n,k'}^{(m)}}\ln \gamma _{k,k'}^{(m)} \right] + \eta \sum _{n'\in \mathcal {C}_{n}}w_{n,n'}q_{t}(y_{n'} = k) . \nonumber \end{aligned}$$

(15)

where we have used ${{\,\mathrm{\mathbb {E}}\,}}_{y_{n'}}[\mathbbm {1}(y_{n'} = k)] = q_{t}(y_{n'} = k).$ The variational update for label $y_n$ is similar to the one in (5), with the addition of the $\eta \sum _{n'\in \mathcal {C}_{n}}w_{n,n'}q_{t}(y_{n'} = k)$ term that captures the labels of the data that are related (through the instance constraints) to the n-th datum. Updating label distributions via (15), updates for $\boldsymbol{\pi }$ and $\mathbf {\Gamma }$ remain identical to those in VBEM [cf. Sect. 3.2]. The instance-level semi-supervised crowdsourcing algorithm is outlined in Algorithm 1. As with its plain vanilla counterpart of Sect. 3.2, Algorithm 1 maintains the asymptotic complexity of $\mathcal {O}(NMKT)$.

4.1 Performance Analysis

Let $\tilde{C}$ with cardinality $|\tilde{C}|=\tilde{N}_C$ be a set comprising indices of data that take part in at least one constraint, and let $\tilde{C}^{c}$ with $|\tilde{C}^{c}| = \bar{N}_C$ denote its complement. The next theorem quantifies the performance of Algorithm 1.

Theorem 2

Consider the same setup as in Theorem 1, instance level constraints collected in $\mathcal {C}$, and the initalization of Algorithm 1 satisfying $\max _{k} |q_{0}(y_n = k) - \mathbbm {1}(y_n = k)| \le \varepsilon _{q,0}$ for all k, n. Then the following hold w.p. at least $1-\nu$: For iterations $t=1,\ldots ,T$, update (15) yields for $n\in \tilde{\mathcal {C}}$

$$\begin{aligned}&\max _{k} |q_t(y_n = k) - \mathbbm {1}(y_n = k)| \le \tilde{\varepsilon }_{q,t}\\&\tilde{\varepsilon }_{q,t} := \max _{n} K\exp \left( -U - \eta W_n\right) = \max _{n} \varepsilon _{q,t}\exp (-\eta W_n)\nonumber \\&W_n:= N_\mathrm{ML,n}(1 - 2\varepsilon _{q,t-1}) - 2N_\mathrm{CL,n}\varepsilon _{q,t-1} + N_\mathrm{CL,n,min} \nonumber \end{aligned}$$

(16)

with $N_\mathrm{ML,n}, N_\mathrm{CL,n}$ denoting the number of must- and cannot-link constraints for datum n respectively, and $N_\mathrm{CL,n,min}:=\min _{k} N_\mathrm{CL,n,k}$, where $N_\mathrm{CL,n,k}$ is the number of cannot-link constraints of datum n, that belong to class k. For data without constraints, that is $n\in \tilde{\mathcal {C}}^{c}$

$$\begin{aligned}&\max _{k} |q_t(y_n = k) - \mathbbm {1}(y_n = k)| \le \varepsilon _{q,t} = K\exp (-U), \end{aligned}$$

with U as defined in Theorem 1. For $k,k'=1,\ldots ,K$, $m=1,\ldots ,M$ updates (6) and (8) yield respectively

$$\begin{aligned}&|{{\,\mathrm{\mathbb {E}}\,}}[\pi _k] - \pi _k^*|\le \epsilon _{\pi ,k,t} := \frac{\tilde{N}_C\tilde{\varepsilon }_{q,t} + \bar{N}_C\varepsilon _{q,t} + Ng_\pi (\nu ) + \alpha _{0,k} + \rho _\pi \bar{\alpha }_0}{N + \bar{\alpha }_0} \end{aligned}$$

(17)

$$\begin{aligned}&|{{\,\mathrm{\mathbb {E}}\,}}[\gamma _{k,k'}^{(m)}] - \gamma _{k,k'}^{*(m)}|\le \epsilon _{\gamma ,k,k',t}^{(m)} := \frac{2Ng_\gamma (\nu ) + 2\tilde{N}_C\tilde{\varepsilon }_{q,t} + 2\bar{N}_C\varepsilon _{q,t} + \beta _{0,k,k'}^{(m)} + \bar{\beta }_{0,k}^{(m)} }{N\mu _m\pi _k^* - N\frac{g_\gamma (\nu )}{\gamma _{k,k'}^{*(m)}} - \tilde{N}_C\tilde{\varepsilon }_{q,t} - \bar{N}_C\varepsilon _{q,t} + \bar{\beta }_{k}^{(m)}} \end{aligned}$$

(18)

and $\varepsilon _{\pi ,t}:=\max _{k}\epsilon _{\pi ,k,t}, \varepsilon _{\gamma ,t}:= \max _{k,k',m} \epsilon _{\gamma ,k,k',t}^{(m)}$.

Comparing Theorem 2 to Theorem 1, the error bounds for the labels involved in constraints introduced by Algorithm 1 will be smaller than the corresponding bounds by VBEM, as long as $\max _n W_n > 0$. This in turn reduces the error bounds for the parameters of interest, thus justifying the improved performance of Algorithm 1 when provided with good initialization. Such an initialization can be achieved by using spectral methods, or, by utilizing the output of the aforementioned unconstrained VBEM algorithm.

4.2 Choosing $\eta .$

Proper choice of $\eta$ is critical for the performance of the proposed algorithm, as it represents the weight assigned to the available constraints. Here, using the number of violated constraints $N_\mathrm{V} := \sum _{(n,n')\in \mathcal {C}_\mathrm{ML}} \mathbbm {1}(y_n \ne y_{n'}) + \sum _{(n,n')\in \mathcal {C}_\mathrm{CL}} \mathbbm {1}(y_n = y_{n'})$ as a proxy for performance, grid search can be used to select $\eta$ from a (ideally small) set of possible values $\mathcal {H}.$

4.3 Selecting Instance-Level Constraints

In some cases, acquiring pairwise constraints, can be costly and time consuming. This motivates judicious selection of data we would prefer to query constraints for. Here, we outline an approach for selecting constraints using only the annotator responses $\check{\mathbf {Y}}$. In addition to providing error bounds for VBEM under instance level constraints, Theorem 2 reveals how to select the $N_C$ constraints in $\mathcal {C}$. Equations (17) and (18) show that in order to minimize the error bounds of the priors and confusion matrices, the data with the largest label errors $|q(y_n = k) - \mathbbm {1}(y_n = k)|$ should be included in $\mathcal {C}.$ The smaller error bounds of (17) and (18) then result in smaller error bounds for the labels, thus improving the overall classification performance. Let $\tilde{\mathcal {C}}_u$ denote the set of data for which we wish to reduce the label error. In order to minimize the error $\tilde{\varepsilon }_q$ per element of $\tilde{\mathcal {C}}_u$, the term $W_n$ in the exponent of (16) should be maximized. To this end, data in $\tilde{\mathcal {C}}_u$ should be connected with instance-level constraints to data that exhibit small errors $\varepsilon _q$. Data connected to each $n\in \tilde{\mathcal {C}}_u$, are collected in the set $\tilde{\mathcal {C}}_c(n).$

Since the true label errors are not available, one has to resort to surrogates for them. One class of such surrogates, typically used in active learning [9], are the so-called uncertainty measures. These quantities estimate how uncertain the classifier (in this case the crowd) is about each datum. Intuitively, data for which the crowd is highly uncertain are more likely to be misclassified. In our setup, such uncertainty measures can be obtained using the results provided by VBEM, and specifically the label posteriors $\{q_T(y_n)\}_{n=1}^{N}$. As an alternative, approximate posteriors can be found without using the VBEM algorithm, by taking a histogram of annotator responses per datum. Using these posteriors, one can measure the uncertainty of the crowd for each datum. Here, we opted for the so-called best-versus-second-best uncertainty measure, which per datum n is given by

$$\begin{aligned} H(\hat{y}_n) = \max _{k}q_T(y_n = k) - \max _{k'\ne k}q_T(y_n = k'). \end{aligned}$$

(19)

This quantity shows how close the two largest posteriors for each datum are; larger values imply that the crowd is highly certain for a datum, whereas smaller ones indicate uncertainty.

Using the results of VBEM and the uncertainty measure in (19), $\left\lfloor {N_C/K}\right\rfloor$ are randomly selected without replacement, to be included in $\tilde{\mathcal {C}}_u$, with probabilities $\lambda _n \propto 1-H(\hat{y}_n)$. For each $n\in \tilde{\mathcal {C}}_u$, K data are randomly selected, with probabilities $\lambda _n^{\dagger } \propto H(\hat{y}_n)$, and are included in $\tilde{\mathcal {C}}_{c}(n)$. Using this procedure, data in $\tilde{\mathcal {C}}_{c}(n), n\in \tilde{\mathcal {C}}_u$ are likely the ones that the crowd is certain of. Finally, the links $\{(n,n'), n\in \tilde{\mathcal {C}}_u, n'\in \tilde{\mathcal {C}}_{c}(n)\}$ are queried and included in the constraint set $\mathcal {C}$. Note here that each uncertain data point is connected to K certain ones, to increase the likelihood that its label error will decrease.

Remark 3

The principles outlined in this subsection can be leveraged to develop active semi-supervised crowdsourcing algorithms. We defer such approaches to future work.

5 Numerical Tests

Performance of the proposed semi-supervised approach is evaluated here on several popular crowdsourcing datasets. Variational Bayes with instance-level constraints (abbreviated as VB - ILC) [cf. Sect. 4, Algorithm 1] is compared to majority voting (abbreviated as MV), the variational Bayes method of Sect. 3.2 that does not include side-information (abbreviated as VB), and the EM algorithm of [7] (abbreviated as DS) that also does not utilize any side information. Here, simple baselines are chosen to showcase the importance of including constraints in the crowdsourcing task. To further show the effect of pairwise constraints VB - ILC is compared to Variational Bayes using label constraints (abbreviated as VB - LC), as outlined at the beginning of Sect. 4.

Table 1. Dataset properties

Fig. 1.

Macro F-score for the RTE dataset, with the same number of constraints for VB-LC and VB - ILC

Fig. 2.

Macro F-score for the Sentence Polarity dataset, with the same number of constraints for VB-LC and VB - ILC

As figure of merit, the macro-averaged F-score [21] is adopted to indicate the per-class performance of an algorithm. The datasets considered here are the RTE [29], Sentence Polarity [25], Dog [8], and Web [38]; see Table 1 for their properties, where $\tilde{\delta }$ denotes the average number of responses per annotator. For the datasets presented here, results indicating the micro-averaged F-score, alongside dataset descriptions and results with 6 additional datasets are included in Appendix B of the supplementary material [34]. MATLAB [18] was used throughout, and all results represent the average over 20 Monte Carlo runs. In all experiments VB and DS are initialized using majority voting, while VB - LC and VB - ILC are initialized using the results of VB, since, as shown in Theorem 2 VB-ILC requires good initialization. For the RTE, Dog, and Sentence Polarity datasets, the prior parameters are set as $\boldsymbol{\alpha _0} = \boldsymbol{1}$, where $\boldsymbol{1}$ denotes the all-ones vector, and $\boldsymbol{\beta }_{0,k}^{(m)}$ is a vector with K at its k-th entry and ones everywhere else, for all k, m. For the Web dataset, all priors are set to uniform as this provides the best performance for the VB based algorithms. The values of $\eta$ for Algorithm 1 are chosen as described in Sect. 4.2 from the set $\mathcal {H}=\{0.01, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 100, 500\}.$ When instance-level constraints in $\mathcal {C}$ are provided to VB-ILC, constraints that can be logically derived from the ones in $\mathcal {C}$ are also included. For example, if $(i,j)\in \mathcal {C}_\mathrm{ML}$ and $(j,k)\in \mathcal {C}_\mathrm{ML}$, a new must-link constraint (i, k) will be added. Similarly, if $(i,j)\in \mathcal {C}_\mathrm{ML}$ and $(j,k)\in \mathcal {C}_\mathrm{CL}$, then a cannot-link constraint (i, k) will be added.

Fig. 3.

Macro F-score for the Dog dataset, with the same number of constraints for VB-LC and VB - ILC

Fig. 4.

Macro F-score for the Web dataset, with the same number of constraints for VB-LC and VB - ILC

Fig. 5.

Macro F-score for the RTE dataset, with random and uncertainty based constraint selection for VB-ILC

Fig. 6.

Macro F-score for the Sentence polarity dataset, with random and uncertainty based constraint selection for VB-ILC

Fig. 7.

Macro F-score for the Dog dataset, with random and uncertainty based constraint selection for VB-ILC

Fig. 8.

Macro F-score for the Web dataset, with random and uncertainty based constraint selection for VB-ILC

Figs. 1, 2, 3, 4 show classification performance when VB-LC and VB-ILC are provided with $N_C$ randomly selected constraints, that is $N_C$ label constraints for VB-LC and $N_C$ instance-level constraints for VB-ILC. VB - LC and VB - ILC exhibit improved performance as the number of constraints increases. As expected, VB - LC outperforms VB - ILC, when $K>2$, since label information is stronger than instance-level information. Interestingly, for $K=2$, VB-ILC exhibits comparable performance to VB-LC in the Sentence polarity dataset, and outperforms VB-LC in the RTE dataset. Nevertheless, VB-ILC outperforms its unsupervised counterparts as $N_C$ increases, corroborating that even relatively weak constraints are useful. The performance of the constraint selection scheme of Sect. 4.3 is evaluated in Figs. 5, 6, 7, 8. The uncertainty sampling based variant of VB - ILC is denoted as VB - ILC, BVSB. Uncertainty sampling for selecting label constraints is clearly beneficial, as it provides performance gains compared to randomly selecting constraints in all considered datasets. Figures 9, 10, 11, 12 show the effect of providing VB-ILC with constraints derived from $N_C$ label constraints. When provided with $N_C$ label constraints from K classes, and with $z_k$ denoting the proportion of constraints from class k, the resulting number of must-link constraints is $N_\mathrm{ML} = \sum _{k=1}^{K} {N_C z_k \atopwithdelims ()2}$, since for each class every two points must be connected. The number of cannot-link constraints is $N_\mathrm{CL} = \sum _{k=1}^{K}\sum _{k'=1}^{K-1} N_C^2 z_k z_{k'+1}$, as for each class every point must be connected to all points belonging to other classes. In this case, VB - ILC almost matches the performance of VB - LC. This indicates that when provided with an adequate number of instance-level constraints, VB - ILC performs as well as if label constraints had been provided.

Fig. 9.

Macro F-score for the RTE dataset, with label derived constraints for VB-ILC

Fig. 10.

Macro F-score for the Sentence Polarity dataset, with label derived constraints for VB-ILC

Fig. 11.

Macro F-score for the Dog dataset, with label derived constraints for VB-ILC

Fig. 12.

Macro F-score for the Web dataset, with label derived constraints for VB-ILC

6 Conclusions

This paper investigated constrained crowdsourcing with pairwise constraints, that encode relationships between data. The performance of the proposed algorithm was analytically and empirically evaluated on popular real crowdsourcing datasets. Future research will involve distributed and online implementations of the proposed algorithm, and other types of constraints alongside semi-supervised crowdsourcing with dependent annotators, and dependent data.