Keywords

1 Introduction

This paper presents a new heuristic to solve a lot-sizing and scheduling problem that arises in practical cases from the food industry. The problem we address is large and complex, which real-life applications often involve multiple production machines and specific constraints, which makes this problem complex to solve and motivates the planners to use optimization tools in order to reduce the costs incurred during their production process. However, modeling such complex systems leads to large mathematical formulations that are (in general) intractable with commercial solvers for Mixed Integer Programs (MIP). As a consequence, we aim to develop new approaches that enable us to obtain solutions to this problem in a quick and efficient fashion. Our work focuses on a multi-item capacitated lot-sizing problem including lost sales, safety stock, overtimes and sequence dependent setups on parallel machines. The discrete lot-sizing is a classical problem in the Operations Research literature since the work of Wagner and Whitin [13] and it has since been enriched with various additional considerations in order to model more accurately practical situations. Limited production capacity is among the most popular extensions of the original problem and has been the topic of multiple surveys, see e.g. [9] and [12]. The model we consider further generalizes this setting to include lost sales and shortage costs, as in [2] where the authors introduce new classes of valid inequalities. Parallel resources production is more and more common in the literature, with a distinction between identical [3] and non-identical [8] machines. We focus on the latter in this paper.

The integration of lot-sizing and scheduling constraints greatly increases the complexity of the problems, which often leads researchers to propose heuristic solutions. Notable ones include [7], who develop a MIP-based neighborhood search heuristics to address a lot-sizing and scheduling problem on parallel machines. [4] present an industrial problem in which setup times depend on the sequence of production and propose a solution procedure based on subtour elimination and patching. [6] reviews the main modeling techniques for this class of problems and compare the efficiency of several solution methods. Iterative heuristics has been studied in the literature for the capacitated lot-sizing and scheduling problem in [11]. In [5], the authors used a two-level method to deal with the lot-sizing and the scheduling phases separately. In the related field of Production Routing problem, [1] use a two-phase method to dissociate the production and the distribution part.

In this paper, we propose a three-phase iterative method for the production problem described above, that has been introduced in [10] and is referred to as CLSSD-PM for multi-item capacitated lot-sizing problem with lost sales, safety stock, overtimes, and sequence-dependent setups on parallel machines. Section 2 describes the notations and assumptions. In Sect. 3, we present an original three-phase iterative method, with a quick description of each phase. In Sect. 4, we succinctly present the preliminary results obtained on a set of instances generated from industrial data. Finally, we propose some ideas to improve the procedure as well as perspectives for future research in the Sect. 5.

2 Notations and Assumptions

The problem studied in this paper is directly related to the problem originally presented in [10]. For an extensive presentation, the reader can refer to this paper. In this problem, we consider N different items that can be produced over a discrete finite horizon of T periods and M non-identical parallel machines. We denote \(\mathcal {N}\), \(\mathcal {M}\) and \(\mathcal {T}\) the set of items, machines and periods, respectively. For all items \(i\in \mathcal {N}\), we consider a deterministic demand \(d^{i}_{t}\) in each period \(t\in \mathcal {T}\), which is either satisfied from on-hand inventory or lost. We denote \(\tau ^i_m\) the production time of one unit of item i on machine m. Sequence-dependent setup times are denoted \(\lambda ^{ij}_m\) for a given machine m and for each pair (i, j) of items. Note that we allow asymmetric setup times but assume they satisfy the triangle inequality. For each machine \(m\in \mathcal {M}\), we consider a time-dependent capacity \(C_{mt}\) corresponding to the total time available in period t. However, in some circumstances this capacity can be exceeded up to a larger value \(\overline{C}_{mt}\) which is the “true” available time capacity in period t. In that case, \(\overline{C}_{mt} - C_{mt}\) corresponds to the maximum overtime allowed. Finally, we also impose that every production of item i have to be greater than a minimum production quantity denoted \(q^i_{min}\). The objective is to minimize the costs incurred in the production problem. We denote \(p^i_{mt}\) the cost of producing one unit of item i in period t on machine m. In addition, we denote \(c_{mt}\) the per-unit of time usage cost of machine m during period t. For each unit of overtime, an additional cost \(\bar{c}_{mt}\) is applied. We define the safety stock as an “optimal" inventory level to reach in each period. Inventory-related cost are then defined with respect to its value, namely a deficit cost \(h^{i-}_{t}\) and an overstock cost \(h^{i+}_{t}\) for each unit below or above the safety stock level. Finally, for each unmet unit of demand for item i in period t, a shortage cost \(l^i_t\) is incurred.

Throughout the remainder of this paper, we use the following decision variables:

\(x^{i}_{mt} \in \mathbb {R}_+\):

Quantity of item i produced in period t on machine m

\(y^{i}_{mt} \in \{0,1\}\):

binary variables equal to 1 if item i is affected to machine m in period t

\(U_{mt} \in \mathbb {R}_+\):

Time usage of machine m in period t

\(O_{mt} \in \mathbb {R}_+\):

Time in overtime of machine m in period t

\(L^{i}_{t} \in \mathbb {R}_+\):

Quantity of lost sales for item i in period t

\(I_{t}^{i} \in \mathbb {R}_+\):

Inventory of item i on hand at the end of period t

\(I_{t}^{i+} \in \mathbb {R}_+\):

Overstock (based on safety stock value) of item i at the end of period t

\(I_{t}^{i-} \in \mathbb {R}_+\):

Safety stock deficit of item i at the end of period t

\(z^{i}_{t} \in \{0,1\}\):

Binary variable equals to 1 if the stock of item i is null at the end of period t

3 Three-Phase Iterative Approach

In this section we present a three-phase iterative method to solve the problem under study. The central idea is to decompose the original problem into three (smaller) subproblems we can solve sequentially, where the output of a phase serves as an input for the following one. Below is an overview of one iteration of the heuristic:

  • The first phase minimizes the costs induced by production and inventory management, considering virtual sequence-independent setup times per item. Capacity restrictions are also relaxed based on the information provided by the other phases.

  • The second phase proposes production sequences for the items affected to each machine and period.

  • The last phase decides the quantity to produce and pushes its output information into the first phase of the next iteration as an additional constraint.

The procedure loops through these different phases until a stopping criteria (either the time limit or a given number of iterations without improvement) is met.

First Phase: Assignment. We describe the first phase with a mathematical model based on an aggregate formulation. In this phase, we do not consider the sequence dependent setup times, which are approximated. For that purpose, we introduce \(ST^{i}_{mt}\) the setup time for item i for machine m at period t (set to 0 at the first iteration). The aggregate formulation is expressed with the following MIP:

$$\begin{aligned} \min&{\sum _{t\in \mathcal {T}}\sum _{m\in \mathcal {M}} (c_{mt}U_{mt} +\bar{c}_{mt} O_{mt})} \nonumber \\&\ {+\sum _{t\in \mathcal {T}}\sum _{i\in \mathcal {N}}\left( h^{i+}_{t}I^{i+}_{t}+h^{i-}_{t}I^{i-}_{t}+ l^{i}_{t}L^{i}_{t} +\sum _{m\in \mathcal {M}} p^i_{mt} x^i_{mt}\right) } \end{aligned}$$
(1)
$$\begin{aligned} \text {s.t.}&U_{mt} =\sum _{i\in \mathcal {N}}(\tau ^i_{m}x^{i}_{mt} + ST^{i}_{mt}y^{i}_{mt}) \quad&\forall m \in \mathcal {M},\forall t\in \mathcal {T} \end{aligned}$$
(2)
$$\begin{aligned} U_{mt}&\le C_{mt} + O_{mt}&\forall m \in \mathcal {M},\forall t\in \mathcal {T} \end{aligned}$$
(3)
$$\begin{aligned} I^i_t&= S^{i}_{t}+I^{i+}_{t}-I^{i-}_{t}&\forall i\in \mathcal {N},\forall t\in \mathcal {T} \end{aligned}$$
(4)
$$\begin{aligned} I^i_t&=I^{i}_{t-1}+\sum _{m\in \mathcal {M}} x^{i}_{mt}+L^{i}_{t}-d^i_t&\forall i\in \mathcal {N},\forall t\in \mathcal {T} \end{aligned}$$
(5)
$$\begin{aligned} I^{i}_{t}&\le D^i_{tT}(1-z^{i}_{t})&\forall i\in \mathcal {N},\forall t\in \mathcal {T} \end{aligned}$$
(6)
$$\begin{aligned} L^{i}_{t}&\le z^{i}_{t}d^{i}_{t}&\forall i\in \mathcal {N},\forall t\in \mathcal {T} \end{aligned}$$
(7)
$$\begin{aligned} x^{i}_{mt}&\le D^{i}_{t-1,T}y^{i}_{mt}&\forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T}\end{aligned}$$
(8)
$$\begin{aligned} x^{i}_{mt}&\ge q^{i}_{\min }y^{i}_{mt}&\forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T}\end{aligned}$$
(9)
$$\begin{aligned} L^{i}_{t}&,I^{i}_{t},I^{i+}_{t},I^{i-}_{t}\ge 0&\forall i\in \mathcal {N},\forall t\in \mathcal {T}\end{aligned}$$
(10)
$$\begin{aligned} U_{mt}&,O_{mt}\ge 0&\forall m\in \mathcal {M},\forall t\in \mathcal {T}\end{aligned}$$
(11)
$$\begin{aligned} y^{i}_{mt}&\in \{0,1\}&\forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T}\end{aligned}$$
(12)
$$\begin{aligned} z^{i}_{t}&\in \{0,1\}&\forall i\in \mathcal {N}, \forall t\in \mathcal {T}\end{aligned}$$
(13)
$$\begin{aligned} x^i_{mt}&\ge 0&\forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T} \end{aligned}$$
(14)

The objective (1) is to minimize the cost of production including line usage costs, lost sales and inventory stocks. Constraints (2) define the total working time of each machine which is equal to the production time and the approximated setup times. Constraints (3) define the time usage and overtime variables. Constraints (4) define the inventory stock from the safety stock, the overstock and the deficit. Constraints (5) are the inventory flow conservation equations through the planning time horizon. Constraints (6) and (7) ensure that lost sales for item i occur only when the corresponding stock is null. Constraints (8) use the cumulative demand over the remainder of the horizon as an upper bound on the quantity of each item produced on each machine in a given period. Constraints (9) force the production to be higher than its minimum value. Finally constraints (10) and (14) define the domain of specific variables.

An additional constraint is necessary to link the information from the following phases after the first iteration. We denote \(\widetilde{y}^{i}_{mt}\) and \(\widetilde{x}^{i}_{mt}\) as the value of the corresponding variables \(y^i_{mt}\) and \(x^i_{mt}\) decided in the previous iteration. In addition, we also define for each machine m and period t the residual capacity \(Cap^{res}_{mt}\) as the remaining available machine time after the previous iteration of the algorithm. Before the first iteration, we initialize these values as follows: \(\widetilde{y}^{i}_{mt}=0\), \(\widetilde{x}^{i}_{mt}=0\) and \(Cap^{res}_{mt} = \overline{C}_{mt}\). The following constraints (15) then indicate that for each item, the production time is bounded by the last solution but can be increased or decreased depending on items that are added to/removed from the assignment derived in the previous iteration and the residual capacity. Parameters \(\sigma ^{i}_{mt}\) then correspond to the proportion of the production time available that is allocated to item i.

$$\begin{aligned} \tau ^{i}_{m}x^{i}_{mt} + (1-\widetilde{y}^{i}_{mt})ST^i_{mt} y^i_{mt}&\le \tau ^{i}_{m}\widetilde{x}^{i}_{mt} + (\sum _{\begin{array}{c} j\ne i \\ \widetilde{x}^{j}_{mt}\ne 0 \end{array}} (1- y^{j}_{mt})(\tau ^{j}_{m}\widetilde{x}^{j}_{mt}+ ST^{j}_{mt}) \nonumber \\&\quad + \,Cap^{res}_{mt}- \sum _{\begin{array}{c} j\ne i\\ \widetilde{x}^{j}_{mt}= 0 \end{array}}(\tau ^{j}_{m}q^j_{\min }+ST^j_{mt}) y^j_{mt})\sigma ^{i}_{mt}\\&\quad \forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T}\nonumber \end{aligned}$$
(15)

Second Phase: Sequencing. From the first phase, we obtain the assignment of items to each pair machine-period (m, t). The goal of this phase is then to solve \(M \times T\) sequencing problems with a straightforward mathematical formulation adapted from the TSP problem. For conciseness we do not detail it in this paper.

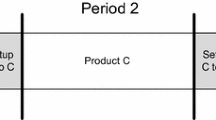
Third Phase: Production. The last phase solves the production problem. We denote \(\varLambda _{mt}\) the sum of setup times on machine m in period t obtained from the previous phase. If \(\varLambda _{mt} + \sum _{i \in \mathcal {N}}q^{i}_{\min }\widetilde{y}^{i}_{mt}>\overline{C}_{mt}\), i.e. the capacity is not sufficient to carry out the setup times and the minimum production for the current affectation, we set \(\varLambda _{mt}=0\) and \(\widetilde{y}^{i}_{mt}=0\) for all \(i \in \mathcal {N}\). Otherwise, the values \(\varLambda _{mt}\) and \(\tilde{y}^i_{mt}\) remain the same. Note that since the assignment decisions \(\tilde{y}^i_{mt}\) are fixed in the first phase, they are considered as parameter in this step and thus the only binary variables considered are \(z^{i}_{t}\) to ensure a First-Come First-Serve discipline, which make the problem easy to solve.

$$\begin{aligned} \min&{\sum _{t\in \mathcal {T}}\sum _{m\in \mathcal {M}} (c_{mt}U_{mt} + \bar{c}_{mt} O_{mt})}\nonumber \\&\ {+\sum _{t\in \mathcal {T}}\sum _{i\in \mathcal {N}}\left( h^{i+}_{t}I^{i+}_{t}+h^{i-}_{t}I^{i-}_{t}+ l^{i}_{t}L^{i}_{t} +\sum _{m\in \mathcal {M}} p^i_{mt} x^i_{mt}\right) } \end{aligned}$$
(16)
$$\begin{aligned} \text {s.t.}&U_{mt} =\sum _{i\in \mathcal {N}}\tau ^i_{m}x^{i}_{mt} + \varLambda _{mt} \quad&\forall m \in \mathcal {M},\forall t\in \mathcal {T}\end{aligned}$$
(17)
$$\begin{aligned}&U_{mt} \le C_{mt} + O_{mt}&\forall m \in \mathcal {M},\forall t\in \mathcal {T}\end{aligned}$$
(18)
$$\begin{aligned}&O_{mt} \le \overline{C}_{mt}-C_{mt}&\forall m\in \mathcal {M},\forall t\in \mathcal {T}\nonumber \\&\qquad {\text{ Constraints } \text{(4)-(7) }} \end{aligned}$$
(19)
$$\begin{aligned}&x^{i}_{mt} \le D^{i}_{t-1,T}\widetilde{y}^{i}_{mt}&\forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T}\end{aligned}$$
(20)
$$\begin{aligned}&x^{i}_{mt} \ge q^{i}_{\min }\widetilde{y}^{i}_{mt}&\forall i\in \mathcal {N}, \forall m\in \mathcal {M}, \forall t\in \mathcal {T}\\&\qquad {\text {Constraints (10), (11), (13), (14)}} \nonumber \end{aligned}$$
(21)

Update the Parameters of the First Phase. At the end of the third phase, there is a crucial update step on the input parameters of the first phase. The algorithm updates the individual setup times based on their marginal contribution to the production sequence computed in the second step. That is, for each item i in the sequence of production on machine m in period t, the setup time \(ST^{i}_{mt}\) corresponds to the additional time needed to insert this item is the sequence based on its direct predecessor and successor. On the other hand, we use the cheapest insertion time for all items that are not already included in the current sequence. This idea is described more in details in [1]. Current affectation decisions are stored in the variables \(\tilde{y}^i_{mt}\), while a priori production quantities \(\tilde{x}^i_{mt}\) are directly extracted from the production decisions \(x^i_{mt}\) in the third phase. The three-phase algorithm is presented in flowchart 1.

Fig. 1.
figure 1

Flowchart of the 3-phase approach

Full size image

4 Experimental Results

In this section, we present the experimental results obtained with our three-phase method. Our instances are designed from actual data from industrial cases. We derived 48 different instances combining the following parameters: \(N \in \{ 20, 30,40\}\), \(T\in \{15, 30\}\), \(M\in \{1,2\}\). Note that these preliminary tests are not representative of the industrial reality, where the number of different items can be significantly larger than this benchmark. We use IBM Ilog CPLEX v12.10.0 to solve each phase and set a time limit of 900 s as a stopping criterion. If UB corresponds to the best feasible solution found by the method tested, the gap is defined as follows:

$$\begin{aligned} \text {Gap} = 100\cdot \frac{UB-LB}{LB}, \end{aligned}$$
(22)

where LB is the best lower bound obtained after 4 h with CPLEX. Table 1 presents a Gap comparison between the 3-phase method and a straightforward MIP resolution in 900 s by CPLEX. We set \(\sigma ^{i}_{mt}=1/N\) in constraints (15). Although the results suggest that our method needs refinement before we consider applying it on larger instances, it shows some promises as a decision support tools for practitioners. In particular for larger instances, the 3-phase method seems to be more robust to obtain adequate solution. We observe that the computational time is mainly decided by the first and the second phase while the third one is solved quickly. For instances with \(N\ge 30\), the second phase take a significant amount of the total computational time (Fig. 1).

Table 1. Average gaps obtained with the 3-phase method
Full size table

5 Perspectives

We study a problem encountered in the food industry. Since the problem is too complex to obtain good solution using a straightforward MIP resolution, we base our approach on an iterative resolution from a decomposition into three smaller subproblems. Our first preliminary results suggest that some enhancement must be implemented to improve the method. To that end, we could consider the addition of diversification mechanisms in the first phase to speed up the convergence. Another direction under investigation rely on the clustering approach introduced in [10] to simplify the second phase and compute efficiently good production sequences. Another research direction is to use heuristics or MIP-heuristics in the first and second phases to speed up the resolution.