An Improved Chicken Swarm Optimization Algorithm with Fireworks Factor

Abstract

Considering the problem that the original chicken swarm optimization algorithm ethnic diversity and easy to fall into local optimum problems, an improved chicken swarm optimization algorithm based on fireworks (FW-ICSO) algorithm was proposed. In this algorithm, roulette was introduced to die out some chickens, produce new chicken’s methods is implemented in fireworks algorithm, and adding an inertia factor to balance search capability. Finally, FW-ICSO is tested with twenty benchmark function and compared with other similar algorithms to confirm their effectiveness in terms of the accuracy and convergence rate of the results.

1 Introduction

Swarm intelligence optimization algorithms are novel type of computational method by simulating the swarm behavior or predatory behavior of natural creatures. At present, researchers have proposed a variety of swarm intelligence optimization algorithms, such as particle swarm optimization (PSO) [1], Genetic algorithm (GA) [2], firefly algorithm (FA) [3].

The chicken swarm optimization (CSO) algorithm was originally presented by Meng et al. [4] at the Fifth International Conference on swarm intelligence (ICSI) in 2014. The algorithm simulates the regular pattern of foraging and the hierarchy order in the chicken swarm, the proposed algorithm has become the focus of a growing number of scholars, they are extensively used in applications. Such as, Dinghui Wu et al. [5] have used the Markov chain to analyze the convergence of clustering algorithm and verified the global convergence of CSO; Deb S et al. [6] summarized the research progress of chicken swarm olony optimization algorithm;Hafez A I et al. [7] proposed an innovative approach for feature selection based on chicken swarm optimization; Cui D [8] proposed projection pursuit model for evaluation of flood and drought disasters based on chicken swarm optimization algorithm; Osamy W et al. [9] proposed the Chicken Swarm Optimization based Clustering Algorithm to improve energy efficiency in Wireless Sensor Network.

Although the CSO algorithm has fast convergence rate and high optimum accuracy, there is easy to trap in the local optimum. Therefore, the optimization of the CSO algorithm becomes the focus of the researcher. Such as, Dinghui Wu et al. [10] proposed a method, which added the part of chicken learning cock, and introduced inertia weight and learning factor; Wang J et al. [11] proposed the improved Chicken Swarm Optimization algorithm to solve the interruptible load scheduling scheme; Bin Li et al. [12] proposed algorithm is a combination of the grey wolf optimizer (GWO) and the particle swarm optimization (PSO) algorithm with CSO; N. Bharanidharan et al. [13] proposed a method, which Improved chicken swarm optimization to classify dementia MRI images using a novel controlled randomness optimization algorithm.

In this paper, an improved chicken swarm optimization algorithm based on fireworks (FW-ICSO) algorithm was developed. Firstly, the roulette algorithm is used to select and eliminate individuals. Secondly, combines the advantage of the firework algorithm (FWA) [14] to generate new particles and improve the population diversity. Then, adding inertia factor to balance search capability. Finally, FW-ICSO is tested with a set of test functions and compared with other algorithms. The experimental data show that FW-ICSO has obvious advantages.

The rest of the paper is organized as follows: Sect. 2 introduces the idea of the chicken swarm optimization algorithm and update formula. The improvements of the FW-ICSO algorithm are introduced in Sect. 3. In Sect. 4, simulation results of FW-ICSO are presented. Finally, conclusions and expectation are stated in Sect. 5.

2 CSO Algorithm Introduction

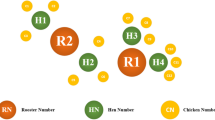
The CSO algorithm was proposed by observing chicken swarm behavior.The best quality food is taken as the target point, through the continued transport of position information among chickens of different grades in each subgroup, and comparison with their best position, the next direction of each chicken is determined and the food finally funds. The central idea of CSO is as follows:

• 1) The chicken swarm is divided into multiple subgroups, which are composed of roosters, hens, and chicks.

• 2) Each subgroup consists of only one rooster and several hens and chicks, roosters have the best fitness and act as the leader in a subgroup. The individuals with the worst fitness values will be defined as chicks and the rest are hens.

• 3) The hierarchy and mother-child relationships are updated every few times.

• 4) The roosters lead its subgroup foraging, hens always looking for food follow the roosters, each chick follows their mothers to search for food.

In the algorithm, the entire swarm population was set to $N$, then $N_{R} ,N_{M} ,N_{H} ,N_{C}$ were the number of roosters, mother hens, hens, and chicks. $x$ denotes the position of each chicken, then the position update of the rooster can be expressed as:

$$ x_{i,j} \left( {t + 1} \right) = x_{i,j} \left( t \right) \times \left[ {1 + Randn\left( {0,\sigma^{2} } \right)} \right] $$

(1)

$$ \sigma^{2} = \left\{ {\begin{array}{*{20}c} {{1,}\begin{array}{*{20}c} {} & {} \\ \end{array} {\rm{if }}\,\,f_{i} \le f_{k} } \\ {\exp (\frac{{f_{k} - f_{i} }}{{\left| {f_{i} } \right| + \varepsilon }}),\begin{array}{*{20}c} {} & {} \\ \end{array} {\rm{otherwise}}} \\ {k \in \left[ 1 \right.,\left. {N_{R} } \right],\begin{array}{*{20}c} {} & {} \\ \end{array} k \ne i} \\ \end{array} } \right. $$

(2)

In formula (1), $x_{i,j} (t)$ denote the position of the $i$ th rooster on the $j$ th dimension in the $t$ th iteration($j \in \left[ {1,d} \right]$, d is the dimension of the search space); $Randn\left( {0,\sigma^{2} } \right)$ is a Gaussian distribution with mean 0 and standard deviation $\sigma^{2}$. Formula (1) simulates the rooster’s position moves.

In formula (2), k is a rooster’s index, which is randomly selected from the roosters’ group ($k \ne i$), $\varepsilon$ is the smallest constant in the computer. Formula (2) simulates the competitive relationship between different roosters.

The position update of the hens (include mother hens) can be expressed as:

$$ \begin{array}{*{20}l} {x_{{i,j}} \left( {t + 1} \right) = x_{{i,j}} \left( t \right) + C_{1} \times {\text{Rand}} \times \left( {x_{{r_{1} ,j}} \left( t \right) - x_{{i,j}} \left( t \right)} \right) + C_{2} \times } \hfill \\ {{\text{Rand}} \times \left( {x_{{r_{2} ,j}} \left( t \right) - x_{{i,j}} \left( t \right)} \right)} \hfill \\ \end{array} $$

(3)

$$ C_{1} = \exp (\frac{{f_{i} - f_{{r_{1} }} }}{{abs\left( {f_{i} } \right) + \varepsilon }}) $$

(4)

$$ C_{2} = \exp (f_{{r_{2} }} - f_{i} ) $$

(5)

In the formula (3), $Rand$ represents a random number between [0,1]; $r_{1}$ is the rooster in the same subgroup, $r_{2}$ is chicken(rooster or hen), which randomly calculated in the entire swarm($r_{1} \ne r_{2}$), and the fitness of $r_{2}$ is better than the fitness of $i$.

The position update of the chicks can be expressed as:

$$ x_{i,j}^{t + 1} = x_{i,j}^{t} + FL\left( {x_{m,j}^{t} - x_{i,j}^{t} } \right) $$

(6)

In the formula (6), $m$ is the index of the mother hen of chicks $i$; $FL$ is the adjustment parameter of chick following its mother, $FL \in \left[ {0,2} \right]$.

The algorithm CSO is shown in Algorithm 1.

3 FW-ICSO Algorithm Introduction

Although convergence accuracy and rate of the traditional CSO algorithm is quite remarkable, the ethnic diversity is relatively single, and the chicks easily fall into local optimum, which leads to the depression of algorithm efficiency. Therefore, this paper proposed the FW-ICSO algorithm, additional the elimination mechanism, and use the FWA algorithm to generate new individuals, which is conducive to jumping out of the local optimum; additional the inertia factor, and balancing the searchability.

3.1 Elimination Mechanism

In this paper, using the roulette algorithm, after the G cycle, the poorly fitness part of chickens will be eliminated. Roulette algorithm: Link the probability of each individual being selected to its fitness, with better fitness comes a lower probability of being selected, and with worse fitness comes a greater probability of being selected.

Firstly, calculate the probability of each individual being selected:

$$ P\left( {x_{i} } \right) = \frac{{f\left( {x_{i} } \right)}}{{\mathop \sum \nolimits_{j = 1}^{N} f\left( {x_{j} } \right)}} $$

(7)

Secondly, calculate the cumulative probability:

$$ Q\left( {x_{i} } \right) = \mathop \sum \nolimits_{k = 1}^{i} P\left( {x_{k} } \right) $$

(8)

If the individual's fitness is poor, the corresponding selection probability will be greater. After the selection probability is converted to the cumulative probability, the corresponding line segment will be longer, and the probability of being selected will be greater.

Finally, generate a random number $judge$, $judge \in \left[ {rPercent,1} \right]$. If $Q(x_{i} ) > judge$, eliminate the individual.

3.2 Creates New Individuals

In order to create new individuals, this paper introduces the FWA [12] algorithm. Assuming that $n$ individuals are eliminated in part 3.1, then set the first $n$ individuals with better fitness as the center. Calculate the explosive strength, explosive amplitude and displacement, then create new individuals, and select individuals with good fitness to join the algorithm.

• (a) Explosive strength

  This parameter is used to determine the number of new individuals. Good fitness individuals will create more new individuals, and poor fitness individuals will create fewer new individuals.

In formula (9): $S_{i}$ represents the number of new individuals produced by the $i$ th individual; $m$ is the constant used to control the number of new individuals of the maximum explosive amplitude, $Y_{\max }$ is the worst fitness.

$$ S_{i} = m\frac{{Y_{\max } - f\left( {x_{i} } \right) + \varepsilon }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {Y_{\max } - f\left( {x_{i} } \right)} \right) + \varepsilon }} $$

(9)

• (b) Explosive amplitude

  The explosive amplitude is used to limit the range of individuals to create new individuals. Good fitness solutions can be very close to the global solution, so the smaller the explosive amplitude, on the contrary, the larger the explosive amplitude.

  $$ A_{i} = \hat{A}\frac{{f\left( {x_{i} } \right) - Y_{\min } + \varepsilon }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {f\left( {x_{i} } \right) - Y_{\min } } \right) + \varepsilon }} $$

  (10)

In formula (10): $A_{i}$ represents the explosive amplitude of the $i$ th individual creating new individuals; $\hat{A}$ is the constant of the maximum explosive amplitude; $Y_{\min }$ is the best fitness.

• (c) Displacement operation

  With the explosive strength and explosive amplitude, and according to the Displacement operation, S_i new individuals can be created.

  $$ \Delta x_{i}^{k} = x_{i}^{k} + rand\left( {0,A_{i} } \right) $$

  (11)

In formula (11): $x_{i}^{k}$ represents the location of the ith individual; $\Delta x_{i}^{k}$ represents the location of the new individual;$rand(0,A_{i} )$ is the random displacement distance.

3.3 Inertial Factor

In the test without adding inertial factor $\omega$, although the FW-ICSO algorithm can achieve better results than other algorithms, its stability is not strong, so the inertial factor ω is added to solve this problem.

The updated roosters' position formula is:

$$ x_{i,j} \left( {t + 1} \right) = \omega \times x_{i,j} \left( t \right) \times \left[ {1 + N\left( {0,\sigma^{2} } \right)} \right] $$

(12)

The updated hens' position formula is:

$$ \begin{array}{*{20}l} {x_{{i,j}} \left( {t + 1} \right) = \omega \times x_{{i,j}} \left( t \right) + C_{1} \times {\text{Rand}} \times \left( {x_{{r_{1} ,j}} \left( t \right) - x_{{i,j}} \left( t \right)} \right) + C_{2} \times } \hfill \\ {{\text{Rand}} \times \left( {x_{{r_{2} ,j}} \left( t \right) - x_{{i,j}} \left( t \right)} \right)} \hfill \\ \end{array} $$

(13)

The updated chicks' position formula is:

$$ x_{i,j}^{t + 1} = \omega \times x_{i,j}^{t} + F\left( {x_{m,j}^{t} - x_{i,j}^{t} } \right) $$

(14)

3.4 The Flow of the FW-CSO Algorithm

The algorithm FW-ICSO is shown in Algorithm 2.

4 Experimental Comparison and Analysis

4.1 Experimental Parameter Settings

Fifteen benchmark functions in Table 1 are applied to compare FW-ICSO, CSO, ISCSO[15], PSO, BOA [16]. Set the D = 50; The search bounds are [−100,100]; The total particle number of each algorithm to 100; The maximum number of iterations is 1000; The algorithms run 50 times independently for each function. The parameters for algorithms are listed in Table 2.

Table 1. Fifteen benchmark functions

Table 2. The main parameter settings of the five algorithms

4.2 Experiment Analysis

As can be seen from Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 and 30 the FW-ICSO has a considerable convergence speed. In Fig. 1, 15, and 17, the convergence speed of the FW-ICSO algorithm is much faster, the PSO and BOA has fallen into the local optimum. CSO and ISCSO converge at the same speed, but compared with FW-ICSO, the speed is much slower, and it falls into the local optimum. Therefore, FW-ICSO can avoid falling into the local optimal solution.

Fig. 1.

Comparison of algorithm convergence in F1 function

Fig. 2.

Comparative ANOVA tests of algorithms in F1 function

Fig. 3.

Comparison of algorithm convergence in F2 function

Fig. 4.

Comparative ANOVA tests of algorithms in F2 function

Fig. 5.

Comparison of algorithm convergence in F3 function

Fig. 6.

Comparative ANOVA tests of algorithms in F3 function

Fig. 7.

Comparison of algorithm convergence in F4 function

Fig. 8.

Comparative ANOVA tests of algorithms in F4 function

Fig. 9.

Comparison of algorithm convergence in F5 function

Fig. 10.

Comparative ANOVA tests of algorithms in F5 function

Fig. 11.

Comparison of algorithm convergence in F6 function

Fig. 12.

Comparative ANOVA tests of algorithms in F6 function

Fig. 13.

Comparison of algorithm convergence in F7 function

Fig. 14.

Comparative ANOVA tests of algorithms in F7 function

Fig. 15.

Comparison of algorithm convergence in F8 function

Fig. 16.

Comparative ANOVA tests of algorithms in F8 function

Fig. 17.

Comparison of algorithm convergence in F9 function

Fig. 18.

Comparative ANOVA tests of algorithms in F9 function

Fig. 19.

Comparison of algorithm convergence in F10 function

Fig. 20.

Comparative ANOVA tests of algorithms in F10 function

Fig. 21.

Comparison of algorithm convergence in F11 function

Fig. 22.

Comparative ANOVA tests of algorithms in F11 function

Fig. 23.

Comparison of algorithm convergence in F12 function

Fig. 24.

Comparative ANOVA tests of algorithms in F12 function

Fig. 25.

Comparison of algorithm convergence in F13 function

Fig. 26.

Comparative ANOVA tests of algorithms in F13 function

Fig. 27.

Comparison of algorithm convergence in F14 function

Fig. 28.

Comparative ANOVA tests of algorithms in F14 function

Fig. 29.

Comparison of algorithm convergence in F15 function

Fig. 30.

Comparative ANOVA tests of algorithms in F15 function

In Fig. 3, 7, 9, 11, and 23, FW-ICSO has a considerable speed of convergence. Although other algorithms perform well, they are still slower than FW-ICSO in terms of speed. Therefore, the convergence speed of the FW-ICSO algorithm is excellent. It can be seen from their variance graphs, the variance of FW-ICSO is small and stable. Therefore, FW-ICSO is not only fast, but also very stable.

It can be seen from Table 3 that the FW-ICSO is better than the data of other algorithms in the Worst, Best, Mean, and Std of each function except F4 and F14. In function F4, the standard deviation of FW-ICSO was worse than that of BOA, and the worst fitness of FW-ICSO was better than the best fitness of BOA. although the standard deviation is worse than BOA, it is also within the acceptable range. In function F14, the standard deviation of FW-ICSO was larger than the standard deviation of ISCSO, but the value is relatively close, and other values are better than ISCSO.

In terms of time consumption, since the algorithm time of CSO itself is longer than other algorithms, the speed of FW-ICSO algorithm is 0.1 to 0.2 s slower than that of CSO algorithm, but when the time loss is acceptable, the accuracy will be greatly improved.

Table 3. Accuracy comparison table

5 Conclusion and Future Work

In order to improve the CSO algorithm, this paper proposes the FW-ICSO algorithm to select individuals for elimination through the roulette algorithm, introduces the explosion strength, explosion amplitude, and displacement operations in the FWA algorithm, generates new individuals to join the algorithm, and introduces the searchability of the inertial balance algorithm. Finally, tested FW-ICSO with Fifteen benchmark functions, the results demonstrate that it is true, the convergence speed, accuracy, and robustness of the FW-ICSO algorithm are considerable.