Optimal Energy Management of Electric Vehicles Supplied by Battery and Supercapacitors: A Multi-Objective Approach

Abstract

Excluding passive topology, hybrid energy storage system (HESS) requires energy management strategy (EMS) which is traditionally developed by mono-objective approach. Meanwhile, energy management of HESS can be considered as multi-objective problems. Recently, multi-objective EMS has been studied; however, there is a lack of a proper benchmark for performance evaluation and/or EMS tuning. This chapter proposes a methodology for multi-objective global optimal EMS generating a Pareto front benchmark. The optimization process is organized in the form of a hierarchical structure, whereas the optimal solutions are obtained by using dynamic programming (DP) algorithm. Filtering strategy is used as an example of a rule-based strategy for performance evaluation using the generated benchmark. Numerical validations are carried out based on a real electric vehicle (EV) platform of our laboratory. The results confirm the advantages of the proposed approach for multi-objective benchmarking the real-time EMS performance by comparing to the generated Pareto front. Representative solutions in accordance with the typical weighting factor values are also reported to demonstrate the advanced EMS behaviors with different priorities given to the considered objectives. The proposed EMS can therefore be insightful to design and/or to tune the real-time strategies.

1 Introduction

Energy management strategy (EMS) is mandatory for hybrid energy storage system (HESS) of electric vehicles (EVs), except the passive topology [1,2,3]. Among various topologies of HESS, the semi-active configuration using battery and supercapacitor (SC) is studied due to its good trade-off between cost and performance [4]. The strategy plays the role of sharing the instantaneous power between the sources to achieve the goal of energy management. The EMS can be conventionally developed by using mono-objective approaches [5,6,7,8,9,10,11]. In a battery/SC system, the single objective is often to extend the battery lifetime while handling SC state of charge (SoC) and current kept into their operation boundaries [5, 7,8,9,10,11].

Recently, several efforts are dedicated to develop multi-objective EMS, e.g., [12,13,14]. Decomposition methodologies are used in [14] to deal with multi-objective problems by using mono-objective methods. This paper uses the approach to study the energy management of series HEVs using battery/SC HESS. Fuel consumption and electric cost are addressed in a scalar objective function with equal priorities. In [13], a global objective function is obtained by summation of three single costs without any weighting factor. The negotiations between the conflicting objectives are therefore not fully considered. Generally, these above works obtain unique solutions for multi-objective problems.

A contribution as a framework of multi-objective optimization for hybrid electric vehicles (HEVs) is presented in [12] which is a complete work on multi-objective EMS with Pareto optimality. This framework is rigorous but complicated with numerous mathematical developments. In addition, the author of [12] used dynamic programming (DP) to evaluate the performance of the Pareto-based real-time strategy. However, this is not a Pareto set of global optimal solutions but only a particular one. Recent work presented in [15] has proposed a multi-objective optimal EMS for battery/SC EVs by employing an alternative approach of using Pontryagin’s minimum principle (called alt-PMP) which has been introduced in [16]. That study obtains a quasi-analytical solution which is efficient in terms of computation resource and therefore faster than DP.

On the other hand, the benchmarking role of offline optimal strategies should be emphasized. Despite that real-time EMS can be developed based on optimization techniques such as model predictive control (MPC) [17, 18], stochastic DP [19], adaptive PMP [20, 21], and meta-heuristic methods [22], they are all sub-optimal strategies. Hence, there is a necessity for a benchmark to examine their effectiveness, in which the benchmark should be a global optimal solution of the energy management problem. To do so, the whole driving condition, which is the disturbance of the optimal control system, must be assumed to be known in advance. As a consequence, the optimal benchmark should be an offline strategy obtained by numerical simulation.

The aim of this chapter is to introduce a multi-objective offline optimal EMS for the battery/SC HESS to generate a Pareto front benchmark for performance evaluation and/or EMS tuning. The multi-objective optimization problems are treated by using a hierarchical structure proposed in [23]. This approach is to decompose the EMS into strategic and tactical levels that are in accordance with the multi-objective scalarization and the optimization problem-solving layers, in which weighted sum method is traditionally used for scalarization of multiple objective functions [24,25,26]. Using this method, each objective is associated with a weighting factor that reflects the priority given to it. The weighted objective functions are then combined in a summation to form a scalar single objective function to be solved using an appropriate optimization method. At the tactical layer, global optimal solutions for the benchmark are deduced by using DP. This is a backward computation dynamic optimization method which is well-known for the ability of deducing global optimal solution for a wide range of complex nonlinear systems [27, 28]. On the other hand, comparing to a DP-based optimal benchmark for evaluating the performance of real-time EMS is a common practice in energy management studies such as [29]. To give an example on the evaluation using the Pareto front benchmark, the well-known filtering strategy is used with a range of cutoff frequencies.

In the following, Sect. 2 states the multi-objective energy management problem for battery/SC EVs and addresses the general methodology of the chapter. In Sect. 3, the studied system is modeled and controlled with a well-known rule-based EMS which is the filtering strategy. Section 4 then presents multi-objective optimal EMS with the weighted sum scalarization method using DP. Numerical results obtained via simulation carried out based on a real EV reference model are given and discussed in Sect. 5. Conclusion and perspectives are then drawn in Sect. 6.

2 Problem Statement and General Methodology

In this section, firstly, the studied system is described with the engineering problem statement. Secondly, the necessity of multi-objective approach to deal with this problem is figured out. The role of a Pareto front benchmark is also discussed. Next, the general formulation of the energy management problems is given. Finally, the general methodology for multi-objective optimal EMS development is developed.

2.1 Studied System and Engineering Problem Statement

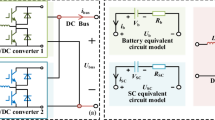
A semi-active configuration of HESS is studied as presented in Fig. 1. Battery directly maintains the DC voltage supplied to the traction subsystem. SCs are connected to the DC bus through a bidirectional DC/DC converter composed of a power inductor and a chopper. Since this work focuses on the energy management of the HESS, the traction subsystem can be simplified as a dynamic current source. This current source imposes the demanded traction current i _trac, which reflect the traction subsystem dynamics, to the HESS.

Fig. 1

Studied system: an EV supplied by a battery/SC HESS

2.2 Multi-Objective Approach with Pareto Front for Benchmarking

The above engineering problem statement figures out the necessity of considering SC losses in addition to the battery degradation. That means the energy management problem should be treated by using a multi-objective approach instead of the mono-objective one. A more general discussion is given here to address the advantages of the multi-objective approach over its counterpart. Since this work is to deduce an optimal benchmark, it is limited to addressing the advantages of the multi-objective benchmark approach.

To be general, the battery and the SCs can be considered as main and auxiliary sources associated with the objective functions J _main and J _aux, respectively. Here, J _main and J _aux are generally defined as the main and the auxiliary objectives of the energy management problem for illustration purpose. Their specific meanings will be assigned regarding the battery power and the SC losses in Sect. 4. Let us assume that there are three strategies denoted by 1, 2, and 3 to be evaluated and improved (Fig. 2). By using mono-objective approach (see Fig. 2a), that is, the comparison with only one criterion J _main, it is easy to select Strategy 3 as the best one. However, as seen in Fig. 2b, the picture can change with a multi-objective viewpoint when J _aux is considered. Even though Strategy 2 has slightly higher value of J _main, it takes much less cost J _aux than Strategy 3 does. It can be therefore considered as a better choice than Strategy 3. This illustration shows why a multi-objective approach can bring a global picture that covers necessary points of view for a correct performance evaluation.

Fig. 2

Illustration of multi-objective approach for performance evaluation of EMS: (a) mono-objective evaluation, (b) multi-objective evaluation, (c) Pareto front as an optimal benchmark

Next, the role of a multi-objective benchmark, which is a Pareto front, is illustrated in Fig. 2c. Pareto front is a set of non-dominated solutions of a multi-objective optimization problem. If these solutions are global optimal for given trade-offs, the Pareto front can serve as a multi-objective benchmark. Utopia point is the unrealistic ideal solution which optimizes all the conflicting objectives. Strategies can be evaluated by comparisons with the benchmark.

One may argue the disadvantage of the multi-objective approach that it is somehow subjective and requires expertise for compromises. However, that is the essences of real-world engineering, especially for the hybrid systems which are the combinations of different characteristics. Furthermore, once a multi-objective strategy is developed, it is easy to be reduced to mono-objective as a typical case. By contrast, if only the mono-objective one is developed, there can be a lack of a global viewpoint. Consequently, some better solutions may be missed to be taken into account.

A common question is often raised; that is, how to select “the best of the best” solution on the Pareto front which is a set of the non-dominated solutions? That selection can be done by two approaches as explained in [24]: (i) ideal method where the full Pareto front is carried out first and then the solution is chosen based on higher-level technical information and (ii) preference-based method where the trade-off is done first and then the optimization problem is solved to obtain only a single solution regarding the preferred choice. Both approaches are often heuristic that relies on the developer’s expertise. On the other hand, the aim of this study is to achieve a benchmark for evaluating the performance of the other EMS. For that purpose, the whole Pareto front should serve as the benchmark instead of a single point, and the chosen α granularity is enough to have a graphical representation at this stage.

2.3 General Formulation of Energy Management Problems

An energy management problem can be formulated by adopting the form of optimal control [27, 30] as follows:

Find the optimal control laws $\underline {u}^*(t)$ for the system:

$$\displaystyle \begin{aligned} \dfrac{d}{dt}\underline{x}(t) = \underline{f} \left[ \underline{x}(t),\underline{u}(t),\underline{w}(t),t \right]; {} \end{aligned} $$

(1)

in which $\underline {x}(t)$ is the state variables and $\underline {w}(t)$ the disturbances, which minimize the objective functions $\left [J_1 \cdots J_n \right ]$ given as:

$$\displaystyle \begin{aligned} \underline{J} = \left[J_1 \cdots J_n \right]^{T} {} \end{aligned} $$

(2)

with the constraints

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \underline{p}\left[ \underline{x}(t),\underline{u}(t),t \right] \leq 0 \\ \underline{q}\left[ \underline{x}(t),\underline{u}(t),t \right] = 0 ; \end{array} \right. {} \end{aligned} $$

(3)

where $\underline {p}$ and $\underline {q}$ are sets of functions expressing the inequality and equality constraints of the system, respectively. The objective functions (2) are expressed by:

(4)

where g and h denote arbitrary functions and t ₀ and t _f are the initial and the final time, respectively.

When the problem is properly formulated, one can use various types of methods to solve it depending upon the study purpose. They can be either rule-based or optimization-based as well as either real-time or offline methods [1].

2.4 General Methodology

Problem formulation is to translate the engineering problem stated in Sect. 2.1 to the mathematical formulation in the form aforementioned in Sect. 2.3. Besides, an optimal benchmark requires the global optimal solutions of the optimization problems. DP is known to be suitable for deducing such kind of solutions [27].

Moreover, dealing with multiple objective functions is the discipline of multi-objective optimization [24, 26]. There are two main groups of multi-objective optimization methods: vectorization and scalarization [24, 31]. The vectorization techniques are to iteratively generate populations of the feasible solutions in the searching space. The populations would converge to a set of non-dominated solutions which is the Pareto front. Alternatively, the scalarization methods are to form a single (scalar) objective function from the original multiple objectives by assigning them weighting factors. Optimization techniques are then applied to solve the problem of this scalar function regarding the variation of the weights that deduce the Pareto front. It is pointed out that the vectorization is not always suitable for optimal control, while the latter group has advantages [31]. It is because the vectorization techniques require to solve a lot of optimization subproblem for the populations of solution candidates that would be very time-consuming. The vectorization approach is more appropriate for optimal design/sizing of the energy storage systems, e.g., a well-investigated design is presented in [32]. Hence, the scalarization technique is employed in this study of multi-objective optimal control for energy management problem.

2.4.1 Structure of Optimal Multi-Objective Energy Management

An energy system can be dealt with in three levels: system model, control, and strategy (see Fig. 3a). As EMS is at the higher level than the local control, it has slower dynamics than the lower layer. It is therefore not necessary and not effective to consider the full dynamical model for EMS development and study [23]. Thus, model reduction should be done in order to effectively develop the EMS. At this step, a reduced model is carried out from the full dynamical system and the local control. The energy management problem is then formulated based on this reduced model.

Fig. 3

General methodology: (a) model reduction and strategy decomposition for EMS development, (b) structure of multi-objective global optimal EMS using DP

According to the formulated problem and the study objective, different structures of EMS could be used. In this study, the hierarchical structure of two management layers proposed in [23] is adapted. The strategy is decomposed into strategic and tactical layers. The philosophy is that the strategic layer gives the global directions and then the tactical one handles the system by following these guidelines. In [23], the structure is realized in the real-time EMS by a rule-based strategy at the higher layer; it restricts the searching space of the optimization-based strategy at the lower layer.

This study adapts the above hierarchical structure to deal with the multi-objective optimal energy management problem (see Fig. 3b comparing with the right part of Fig. 3a). The multi-objective scalarization plays the role of the strategic layer. It gives the scalarized objective function as a guideline for the lower layer. The tactic is realized by DP which globally minimize each given scalarized objective function. Since DP is a backward calculation technique, a backward model must be deduced from the reduced model. It is presented in details in Sect. 4.2. It is also worth to note that DP is a closed-loop optimal control method [27] and, thus, state feedback is mandatory. Meanwhile, multi-objective scalarization handles its duty in an open-loop scheme. The measure going from the tactical layer to the strategic one is therefore eliminated.

2.4.2 Pareto Front Benchmark Generation

The steps for generating the Pareto front benchmark are illustrated in Fig. 4. There are several techniques to scalarize the multiple objective functions, in which the most used is the weighted sum method [24, 25]. Weighting factors k _i are given to each objective function and then summed to create a single multi-objective function. Moreover, it is necessary to make the objective functions dimensionless due to the different units of the performance measurements. Normalization factors are therefore introduced. The choices of these factors depend upon the detailed applications. The weighted sum objective function J _ws is therefore expressed as follows:

$$\displaystyle \begin{aligned} J_{\mathrm{ws}} & = k_1\dfrac{J_1}{J_{1 \mathrm{\_nom}}} + (1-k_1) \\ & \quad \times \left( k_2\dfrac{J_2}{J_{2 \mathrm{\_nom}}} + \dots + \left( k_{n-1}\dfrac{J_{n-1}}{J_{n-1 \mathrm{\_nom}}} + (1-k_{n-1})\dfrac{J_{n}}{J_{n \mathrm{\_nom}}} \right) \right) {} \end{aligned} $$

(5)

where 0 ≤ k _i ≤ 1 and $J_{i \mathrm {\_nom}}$ is the normalization factor with $i \in \left \lbrace 1, \dotsc , n-1 \right \rbrace$.

Fig. 4

Illustration of multi-objective benchmark generation

Since the studied battery/SC HESS can be considered as the combination of a main source and an auxiliary source (see Sect. 2.2), the weighted sum objective function is depicted by:

$$\displaystyle \begin{aligned} J_{\mathrm{ws}} = \alpha \dfrac{J_{\mathrm{main}}}{J_{\mathrm{main\_nom}}} + (1-\alpha)\dfrac{J_{\mathrm{aux}}}{J_{\mathrm{aux\_nom}}}; {} \end{aligned} $$

(6)

in which α ∈{0, 1} is the weighting factor.

By the given weighting factors, the multi-objective problem is scalarized to a series of single objective problems. Thereafter, each single problem is solved by using DP to produce the optimal solution for the given weighting factor. The set of these optimal solutions is the Pareto front benchmark as illustrated in Fig. 4.

3 Modeling, Control, and Rule-Based Strategy

Before dealing with the strategy level, the system should be properly controlled. Moreover, in this study, the EMS is not independently developed, but by following a systematic procedure. It is based on the model organization and control scheme of the system using a unified formalism. Therefore, it is necessary to carry out the modeling and the control of the system.

3.1 Modeling and Control

For control and energy management, it is sufficient to use simple models of the battery and the SCs [21, 29] as follows:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} u_{\mathrm{bat}} = u_{\mathrm{bat\_OC}}(SoC_{\mathrm{bat}}) - r_{\mathrm{bat}}(SoC_{\mathrm{bat}})i_{\mathrm{bat}} \\ SoC_{\mathrm{bat}} = SoC_{\mathrm{bat}}(0) - \dfrac{1}{3600C_{\mathrm{bat}}}\int_0^t{i_{\mathrm{bat}}dt} \end{array} \right.; {} \end{aligned} $$

(7)

$$\displaystyle \begin{aligned} u_{\mathrm{SC}} = u_{\mathrm{SC}}(0) - \dfrac{1}{C_{\mathrm{SC}}}\int_0^t{i_{\mathrm{SC}}dt} - r_{\mathrm{SC}}i_{\mathrm{SC}}; {} \end{aligned} $$

(8)

where u _bat is the battery voltage, $u_{\mathrm {bat\_OC}}$ the battery open-circuit voltage which is a function of battery state of charge SoC _bat, r _bat the battery series resistance, i _bat the battery current, C _bat the battery capacity, u _SC the SC voltage, r _SC the SC series resistance, C _SC the SC capacitance, and i _SC the SC current.

The inductor of the converter is given by its linear dynamic model as:

$$\displaystyle \begin{aligned} u_{\mathrm{SC}} = L\dfrac{d}{dt}i_{\mathrm{SC}} + r_{\mathrm{L}}i_{\mathrm{SC}} + u_{\mathrm{ch}} ; {} \end{aligned} $$

(9)

in which L is the inductor inductance, r _L is the inductor series resistance, and u _ch is the chopper voltage.

The average linear model of the chopper is utilized:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} u_{\mathrm{ch}} = m_{\mathrm{ch}} u_{\mathrm{bat}} \\ i_{\mathrm{ch}} = m_{\mathrm{ch}} \eta_{\mathrm{ch}}^k i_{\mathrm{SC}} \end{array} \right. \text{ with } k = \left\{ \begin{aligned} &1 \text{ if } u_{\mathrm{bat}}i_{\mathrm{ch}} \geq 0 \\ -&1 \text{ if } u_{\mathrm{bat}}i_{\mathrm{ch}} < 0 \end{aligned} \right.; {} \end{aligned} $$

(10)

where i _ch is the chopper current, m _ch the duty cycles of pulse width modulation, and η _ch the chopper average efficiency.

The parallel connection model is the Kirchhoff’s current law:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} u_{\mathrm{bat}} = \text{common} \\ i_{\mathrm{trac}} = i_{\mathrm{bat}} + i_{\mathrm{ch}} \end{array} \right. {} \end{aligned} $$

(11)

where i _trac is the traction current.

The traction part is simplified as an equivalent dynamic current source which generates the traction current as a function of the traction power and the battery voltage:

$$\displaystyle \begin{aligned} i_{\mathrm{trac}} = \dfrac{P_{\mathrm{trac}}}{u_{\mathrm{bat}}}. {} \end{aligned} $$

(12)

Tuning path goes from the control variable m _ch to the objective variable i _bat. Then, the control path is carried out by inversion of the tuning path.

Based on the control path, the control scheme is deduced by step-by-step inversions of the element models. There are two main kinds which are direct and indirect inversions. The elements which do not store energy are directly inverted from their modeling equations. For example, from (11), the direct inversion of the parallel connection is given as:

$$\displaystyle \begin{aligned} i_{\mathrm{ch\_ref}} = i_{\mathrm{trac\_mea}} - i_{\mathrm{bat\_ref}}. {} \end{aligned} $$

(13)

By contrast, the elements containing dynamic models cannot be directly inverted because that leads to derivative terms which unrespect the physical causality conditions [33]. Hence, indirect inversions must be used for them. This kind of inversion is realized by closed-loop control. In this case, the SC current control is derived from (9) as follows:

$$\displaystyle \begin{aligned} u_{\mathrm{ch\_ref}} = u_{\mathrm{SC\_mea}} - \left(k_{\mathrm{P}} + k_{\mathrm{I}} \dfrac{1}{s}\right) (i_{\mathrm{SC\_ref}} - i_{\mathrm{SC\_mea}}) {} \end{aligned} $$

(14)

where k _P and k _I are the factors of the well-known proportional-integral (PI) controller.

3.2 Rule-Based Filtering Strategy

The filtering-based strategy is used as an example for performance evaluation with a low-pass filter (LPF) [5, 6]:

$$\displaystyle \begin{aligned} i_{\mathrm{bat\_ref}} = \dfrac{1}{\tau_{\mathrm{LPF}}s + 1}i_{\mathrm{trac\_ref}}; {} \end{aligned} $$

(15)

where τ _LPF is the time constant of the LPF. The cutoff frequency of the filter is calculated by:

$$\displaystyle \begin{aligned} f_{\mathrm{c}} = \dfrac{1}{2\pi\tau_{\mathrm{LPF}}}. {} \end{aligned} $$

(16)

The SC voltage is constrained in its upper and lower limitations [34]. Besides, in the intervals that there is no power request from the traction subsystem, the battery charges the SCs if the SC voltage is lower than $u_{\mathrm {SC\_max}}$.

4 Multi-Objective Optimal Energy Management System

4.1 Problem Formulation

4.1.1 System Dynamical Model

Formulating an optimal control problem is the step to determine the system dynamical model, the objective function, and the constraints which are generally addressed in (1), (2), and (3). The model can be obtained by combining the component models given in (7)–(12) as in [35]. By that, one can eventually get a nonlinear model of current and voltage relationships [21]. However, we can deduce a more general linear model considering the power and energy relationships of the HESS inherited from [15] as illustrated in Fig. 5.

Fig. 5

The studied battery/SC HESS power flows

By defining the positive direction of the source powers as discharging to supply the traction subsystem, the power coupling node is given by:

$$\displaystyle \begin{aligned} P_{\mathrm{bat}} + P_{\mathrm{SC}} = P_{\mathrm{trac}}. {} \end{aligned} $$

(17)

From the SC subsystem power P _SC, the SC subsystem losses can be calculated by:

$$\displaystyle \begin{aligned} P_{\mathrm{SC\_loss}} = P_{\mathrm{SC}}\left(k_{\mathrm{SC}}\eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}} - k_{\mathrm{SC}}\right) \text{ with } k_{\mathrm{SC}} = \left\{ \begin{aligned} &1 \text{ if } P_{\mathrm{SC}} \geq 0 \\ -&1 \text{ if } P_{\mathrm{SC}} < 0 \end{aligned} \right.; {} \end{aligned} $$

(18)

in which η _SC is the SC subsystem efficiency considering the DC/DC converter losses and the Joule’s losses caused by the SC series resistance r _SC.

On the other hand, the charging and discharging dynamics of the pure SC capacitance are modeled by:

$$\displaystyle \begin{aligned} \dfrac{d}{dt}E_{\mathrm{SC}} = -P_{\mathrm{SC0}} {} \end{aligned} $$

(19)

where the pure charging/discharging power P _SC0 is given by:

$$\displaystyle \begin{aligned} P_{\mathrm{SC0}} = P_{\mathrm{SC}}\eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}}. {} \end{aligned} $$

(20)

Hence, considering the battery power P _bat as the control variable and the SC energy E _SC as the state variable, the dynamical model used for EMS development can be deduced as the following:

$$\displaystyle \begin{aligned} \dfrac{d}{dt}E_{\mathrm{SC}} = \left(P_{\mathrm{bat}} - P_{\mathrm{trac}}\right) \eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}} {} \end{aligned} $$

(21)

where the traction power demand P _trac is the disturbance imposed to the system.

4.1.2 Objective Functions

This study is to minimize the two objectives which are battery degradation and SC losses given by:

$$\displaystyle \begin{aligned} \underline{J} = \begin{bmatrix} J_{\mathrm{bat}} & J_{\mathrm{SC}} \end{bmatrix}. {} \end{aligned} $$

(22)

These objectives are conflicted to each other because minimizing the battery degradation requires to use more SC power, i.e., more SC losses, to support the battery and vice versa. Dealing with such conflicted multiple objectives falls within the scope of multi-objective optimization methods.

In order to reduce the battery aging factors, from the control point of view, the battery power usage should be reduced. Moreover, in terms of optimal control, it is convenient to have the control variable taken into account in the objective function. Thus, the battery objective function can be given by:

$$\displaystyle \begin{aligned} J_{\mathrm{bat}} = \int_0^T P_{\mathrm{bat}}^2 dt {} \end{aligned} $$

(23)

where T is the final time of the driving cycle; the quadratic function is employed to reduce the battery power in both positive and negative regions.

The objective function to be minimized from the SC side is the SC subsystem losses $P_{\mathrm {SC\_loss}}$. From (18), applying the quadratic form, the SC objective function is addressed as:

$$\displaystyle \begin{aligned} J_{\mathrm{SC}} = \int_0^T \left(P_{\mathrm{bat}} - P_{\mathrm{trac}}\right)^2 \left(k_{\mathrm{SC}}\eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}} - k_{\mathrm{SC}}\right)^2 dt. {} \end{aligned} $$

(24)

As aforementioned in Sect. 2.4, the two objective functions should be normalized in order to properly apply the weighted sum method for scalarization of the objective function vector $\underline {J}$ as follows:

$$\displaystyle \begin{aligned} J_{\mathrm{ws}} = \alpha \dfrac{J_{\mathrm{bat}}}{J_{\mathrm{bat\_nom}}} + \left(1 - \alpha\right) \dfrac{J_{\mathrm{SC}}}{J_{\mathrm{SC\_nom}}} {} \end{aligned} $$

(25)

with 0 ≤ α ≤ 1 being the weighting factor. Here, we define the scalarization factors $J_{\mathrm {bat\_nom}}$ and $J_{\mathrm {SC\_nom}}$ as the mean of the optimal solutions of $P_{\mathrm {bat}}^2$ and $P_{\mathrm {SC\_loss}}^2$ pre-computed individually in the case of α = 0 and α = 1, respectively, as follows:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} J_{\mathrm{bat\_nom}} &= {\mathrm{mean}\left({P^*_{\mathrm{bat}}}^2\middle|{}_{\alpha = 0}\right)} \\ J_{\mathrm{SC\_nom}} &= {\mathrm{mean}\left({P^*_{\mathrm{SC\_loss}}}^2\middle|{}_{\alpha = 1}\right)} \end{aligned} \right. {} \end{aligned} $$

(26)

Applying (23), (24), and (26) to (25), the weighted sum objective function to be implemented for computation of the studied optimal control problem is given by:

$$\displaystyle \begin{aligned} J_{\mathrm{ws}} = \int_0^T \left[ \alpha \dfrac{P_{\mathrm{bat}}^2}{\mathrm{mean}\left({P^*_{\mathrm{bat}}}^2\middle|{}_{\alpha = 0}\right)} + \left(1 - \alpha\right) \dfrac{\left(P_{\mathrm{bat}} - P_{\mathrm{trac}}\right)^2 \left(k_{\mathrm{SC}}\eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}} - k_{\mathrm{SC}}\right)^2}{\mathrm{mean}\left({P^*_{\mathrm{SC\_loss}}}^2\middle|{}_{\alpha = 1}\right)} \right]dt. {}\end{aligned} $$

(27)

If the higher priority is given to the objective of extending battery lifetime, i.e., α is close to 0, the battery power will be controlled to be small that means lower aging stress. By contrast, if α is close to 1, P _bat will be managed to be close to P _trac so that the second term of the objective function J _ws can be minimized.

4.1.3 Constraints

Constraints of the control and state variables can be imposed to an optimal control problem. In practical applications, they are often the limitations of the variables, which are the battery power P _bat and the SC energy E _SC [15].

An upper boundary of P _bat can avoid the high peak power demand which can be harmful for the battery. On the other hand, we should limit the maximum charging power of the battery, which is a lower boundary because it is in the negative direction, due to the same reason. Hence, the control variable constraints of the studied problem are given by:

$$\displaystyle \begin{aligned} P_{\mathrm{bat\_min}} \leq P_{\mathrm{bat}} \leq P_{\mathrm{bat\_max}}. {} \end{aligned} $$

(28)

These boundaries can be calculated from the maximum continuous load current and the maximum charging current which are often given vis-à-vis the battery C-rate.

The second sort of constraints is for the state variable that is often among the most critical issues of optimal control. In a battery/SC HESS, the SC energy is indeed restricted due to the limited voltage and capacitance of the SCs as follows:

$$\displaystyle \begin{aligned} \dfrac{1}{2}C_{\mathrm{SC}}u_{\mathrm{SC\_nom}}^2 \leq E_{\mathrm{SC}} \leq \dfrac{1}{2}C_{\mathrm{SC}}\left(0.5u_{\mathrm{SC\_nom}}\right)^2. {} \end{aligned} $$

(29)

Moreover, it is interesting that a final-state constraint can be enforced to an optimal control problem. This sort of constraint is especially useful for energy management of HESS where the auxiliary source energy should be recovered at the end of the driving cycle. It firstly implies that the SCs only support the battery to compensate the power fluctuation, whereas the battery mostly provides the whole energy for range autonomy. Secondly and more important for the benchmark purpose, the final-state constraint may ensure a fair comparison to evaluate the effectiveness of the EMS in terms of battery power smoothing and energy consumption. In the studied HESS, this charge-sustaining condition is given by:

$$\displaystyle \begin{aligned} E_{\mathrm{SC}}(T) = E_{\mathrm{SC}}(0). {} \end{aligned} $$

(30)

Consequently, the multi-objective optimal HESS energy management problem can be formulated as the following:

$$\displaystyle \begin{aligned} &\begin{aligned} P_{\mathrm{bat}}^* &= \mathrm{arg\ min} \left\{ \int_0^T \left[ \alpha \dfrac{{P_{\mathrm{bat}}}^2}{\mathrm{mean}\left({P^*_{\mathrm{bat}}}^2\middle|{}_{\alpha = 0}\right)}\right.\right. \\ & \quad + \left.\left.\left(1 - \alpha\right) \dfrac{\left(P_{\mathrm{bat}} - P_{\mathrm{trac}}\right)^2 \left(k_{\mathrm{SC}}\eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}} - k_{\mathrm{SC}}\right)^2}{\mathrm{mean}\left({P^*_{\mathrm{SC}}}^2\middle|{}_{\alpha = 1}\right)} \right]dt \right\} \end{aligned} \\ &\begin{aligned} \text{s.t.: } \quad \dfrac{d}{dt}E_{\mathrm{SC}} - \left(P_{\mathrm{bat}} - P_{\mathrm{trac}}\right)\eta^{-k_{\mathrm{SC}}}_{\mathrm{SC}} &= 0 \\ P_{\mathrm{bat\_max}} - P_{\mathrm{bat}} &\geq 0 \\ P_{\mathrm{bat}} - P_{\mathrm{bat\_min}} &\geq 0 \\ \dfrac{1}{2}C_{\mathrm{SC}}\left(0.5u_{\mathrm{SC\_nom}}\right)^2 - E_{\mathrm{SC}} &\geq 0 \\ E_{\mathrm{SC}} - \dfrac{1}{2}C_{\mathrm{SC}}u_{\mathrm{SC\_nom}}^2 &\geq 0 \\ E_{\mathrm{SC}}(T) - E_{\mathrm{SC}}(0) &= 0. \end{aligned} {} \end{aligned} $$

(31)

In the next subsection, we will apply DP to solve this optimal control problem for each value of α; then the set of optimal solutions with 0 ≤ α ≤ 1 forms the Pareto front.

4.2 Dynamic Programming

Here, DP is used at the tactical layer to deduce the optimal solution for each particular dynamic optimization problem given by each weighting factor value. DP is based on the Bellman principle of optimality that leads to an effective numerical searching technique to find the optimal control law for a dynamic system [27]. Considering the above general system model (1) in the discrete form, DP is expressed by Bellman equation as follows:

(32)

in which the subscript k, N denotes the procedure going from the stage k ^th to the final stage N ^th, similar for k + 1, N and g _D is the discrete form of the function g mentioned in (4). Figure 6 illustrates the solving procedure for an arbitrary scalar component of state vector $\underline {x}$. It is to find the optimal path from the current state x _i(k) to the final state x(N). The optimal paths from all possible next states x(k + 1) to x(N) must be determined in advance. The operation of DP is to repeat this procedure from x(N) to the initial state x(0). Due to computation in discrete time, the system must be discretized and quantized. It is noteworthy that unlike real-time control, stability is not an issue of the optimal control methods like DP. The offline optimal control law is obtained considering a priori known disturbance and respecting the control and state constraints which often reflect the physical limitations keeping the system stable. Hence, it is unnecessary to analyze the stability of DP because the proposed approach is for offline benchmark comparison but not for real-time control.

Fig. 6

Illustration of dynamic programming computation procedure

DP is of interest because of its natural ability of dealing with the control- and state-constrained problems applied for various sorts of nonlinear systems. Thanks to its ability to generate global optimal solutions regarding all types of constraints for all types of dynamical systems, DP is the most used method to deduce the optimal benchmark for energy management problems. The drawback of DP is that it is heavy in term of computation. Moreover, this method requires the a priori known disturbances; thus, DP is only validated by offline simulations. In this study, we use the dpm MATLAB function introduced in [36] to implement DP in the inner loop (Algorithm 1), while the outer loop is the iteration of the weighting factor α as illustrated in Fig. 4.

Algorithm 1 System model implementation for DP computation using the dpm function introduced in [36]

5 Results and Discussions

This section presents the numerical validation of the proposed approach. The simulation configuration and scenario will be described and then followed by the results of Pareto front to serve as a multi-objective optimal benchmark. Finally, representative cases regarding the different weighting factor values will be given and discussed to show the pros of the proposed EMS.

5.1 Simulation Setup

The simulation is carried out using the parameters of eCommander EV available at the e-TESC laboratory, University of Sherbrooke [37], as the reference vehicle (Fig. 7). The vehicle total mass, including the HESS and the driver, is 871 kg. Nine SC modules Maxwell BMOD0058 E016 B02 are connected as three modules in series forming a branch and three branches in parallel. The SCs are linked to a DC/DC converter having an average efficiency of 95%. The SC subsystem is directly connected to a battery composed of 12 Valence U24-12XP Li-ion modules, in which 4 modules are in series and 3 branches are in parallel (4s/3p arrangement).

Fig. 7

The eCommander EV with the associated Valence U24-12XP Li-ion battery and Maxwell BMOD0058 E016 B02 SC modules of e-TESC laboratory, University of Sherbrooke, as the reference model

The full dynamical model, local control, and filtering-based strategy are simulated in MATLAB/Simulink environment. A real-world driving cycle recorded in the campus of our university is used as the vehicle speed reference (see Fig. 8)¹ with the length of 199.4 s. The discretization step, i.e., sampling time, of the problem is 0.1 s. Hence, there are 1994 time steps to be computed. The upper and lower boundaries of the state variable E _SC are based on the SC voltage limitations of 45 V and 22.5 V, respectively. The maximum and minimum battery power constraints are set as 6 kW of discharging for traction and −1 kW of charging for regenerative braking. The quantization of both E _SC and P _bat is 200 steps.

Fig. 8

The real-world driving cycle obtained in the University of Sherbrooke campus with the studied eCommander vehicle

Two main results are given. First, it is the Pareto front generated with the weighting factor α varying from zero to one. Results of filtering-based strategy are given to illustrate the benchmark role of the generated Pareto front. The second main result is the energy and power trajectories of the studied HESS with some specific values of α.

5.2 Pareto Front as a Multi-Objective Optimal Benchmark

The Pareto front generated from multi-objective optimal EMS is given in Fig. 9. Since DP is the global optimization method, this front can be used as a benchmark to evaluate the performance of sub-optimal strategies. The well-distributed convex form of the generated Pareto front verifies the validation of weighted sum scalarization.

Fig. 9

Pareto front benchmark generated from multi-objective optimal EMS

To give an example for the benchmark role of the generated Pareto front, results of the filtering-based strategy are used. Two typical values of the LPF cutoff frequency f _c1 = 50 mHz and f _c2 = 10 mHz are studied. With the f _c1, the EMS causes low SC system losses but reduces less battery stress demands. By contrast, with the f _c2, it is better for battery lifetime (less stress) but forces the SC system working exhaustively causing higher losses. Both are fairly far from the optimal solutions set. For better evaluation of filtering-based strategy, a set of LPF cutoff frequencies with 5 mHz step is examined as given in Fig. 9. This proposed set corresponds in fact to nine different filtering-based strategies. Also, Fig. 9 shows that the results of filtering-based strategy are distant from the Pareto front.

Advanced EMS giving results closer to the Pareto front are therefore preferred. It is supposed that an EMS giving results between the Pareto front and the curve of filtering strategy could be considered as better than this one. For instance, in [21], an optimization-based real-time strategy has been developed based on an adaptation of PMP to deduce a closed-loop control scheme of the SC voltage. Simulation and experimental validations have been carried out to verify the superiority of that EMS to the filtering strategy. Moreover, appropriate methods used for energy management of HEVs could be adapted for HESS due to their analogy in terms of power flow model. For example, the recent work [29] has proposed a linear quadratic regulator (LQR)-based EMS for a parallel hybrid powertrain of which the performance has been proven to be close to DP results. It could therefore be of interest to extend this strategy to energy management of EVs supplied by HESS.

In this case, solutions to the multi-objective optimization problem are computed by means of solving weighted sum with well-dispersed set of weights. In addition, the L ₁ (Manhattan metric) and L _∞ (Chebyshev metric) distances to reference points can be added to the designer define which level of each objective function would like to attain [26].

For instance, to identify more suitable Pareto optimal solutions, the L _∞ metric enables to compute unsupported solutions (i.e., non-dominated solutions which are convexly dominated) besides supported non-dominated solutions resulting from weighted sum scalar function and the L ₁ metric. Moreover, these different computation processes will offer to the benchmarking process different insights of the possible trade-offs regarding the tuning and evaluation of different real-time strategies.

5.3 Typical Cases

In these scenarios, the weighting factor α is chosen as {0, 0.25, 0.75, 1} respecting the priorities given to the purpose of battery lifetime extension. Figure 10 shows the SC energy E _SC and the HESS power profiles of the studied cases. They include the traction power P _trac which is the disturbance and the battery power P _bat which is the control variable.

Fig. 10

SC energy and HESS power trajectories with typical values of α. (a) α = 1. (b) α = 0. (c) α = 0.75. (d) α = 0.25

In all scenarios, the state variable E _SC is constrained between the maximum and minimum limitations. The final state E _SC(T) is controlled to be equal to the initial state E _SC(0) which means SCs charge sustaining. The P _bat is kept within its constraints as expected. In traction mode, the SCs support the battery to make the P _bat smoother and having lower peak values. In regenerative braking mode, all the energy is charged to the SCs as the expectation of almost EMS. More detailed discussions on each case follow.

The case α = 1 given in Fig. 10a means that all the priority is put on battery degradation reduction. In fact, this is the common case when the mono-objective approach is applied to the main source. The battery current is kept very smooth around a small average value. Most of the requested power is provided by SCs. It is worth to note that to provide the same power, the SCs with the lower voltage, i.e., lower energy, must give the higher current. This may put a heavy duty on the power electronics converter, especially on the stability issue, the magnetic saturation of the power inductor, and the efficiency of the converter. High Joule losses are also the consequence. The results of this case are used as the normalization factor for the scalarization of the SC objective function.

By contrast, in the case α = 0 plotted in Fig. 10b, the only objective is to minimize the SC system losses while receiving all regenerative energy as the constraints of the battery current. The SCs, therefore, support the battery to reduce only the peak power demand which is higher than its power constraint. Like the previous case of SCs, the battery objective function is normalized by using these results.

Between the two above extreme cases, either major or minor priority can be given to each objective. The two scenarios where α = {0.25, 0.75} are presented in Fig. 10c, d, respectively. They are the trade-off between battery stresses and SC system losses. The higher the weighting factor α is, the lower and smoother the battery power is, because in this study α is introduced as the priority given to the objective of battery power smoothing. Meanwhile, the SC power is in the inverse proportion. The smoothness and the reduction of battery power depend upon the chosen value of α which could be based on the expertise of the strategy designer.

6 Conclusion

This chapter has presented a systematic approach to develop multi-objective optimal EMS for HESS-based EVs. The SC subsystem losses are taken into account in addition to the main objective of extending battery life-span. The hierarchical structure has been employed that the EMS is considered as decomposing into strategic and tactical layers. At the strategic level, the multi-objective optimal control problem has been dealt with by using the weighted sum scalarization method. Afterward DP has been used at the tactical level for problem-solving, thanks to its ability of giving the global optimal solution. Consequently, a Pareto front has been generated as a multi-objective EMS benchmark of which the advantages are validated via numerical evaluations with intensive analyses. We have illustrated the benchmarking role of the Pareto front by comparing it to the well-known filtering strategy as a real-time EMS for a real EV.

The proposed methodology is not limited to the studied battery/SC system but can be extend for the other hybridized systems such as hybrid electric vehicles (HEVs) or fuel cell/battery/SC HESS. The optimal EMS can also be combined with component sizing to form a strategy/sizing bi-level optimization problem which is of interest for future study. Furthermore, using advanced scalarization methods such as L ₁ and L _∞ metric may enrich the Pareto front for maximizing the benchmarking assessment.