Categorical Commutator Theory

Abstract

In these notes, we introduce the reader to the categorical commutator theory (of subobjects), following the formal approach given by Mantovani and Metere in 2010. Such an approach is developed along the lines provided by Higgins, based on the notion of commutator word, introduced by the author in the context of varieties of $\Omega$-groups (groups equipped with additional algebraic operations of signature $\Omega$). An internal interpretation of the commutator words is described, providing an intrinsic notion of Higgins commutator, which reveals to have good properties in the context of ideal determined categories. Furthermore, we will illustrate some applications of commutator theory in categorical algebra, such as a useful way to test the normality of subobjects on one side, and the construction of the abelianization functor on the other.

Introduction

The theory of commutators [9] can be considered as an extension of the classical commutator theory for groups to more general varieties of algebras. A description of commutator of congruences in Mal’tsev varieties was developed by Smith [20], and then extended to a categorical context by Pedicchio [19], while a first categorical notion of commutator of subobjects was given by Huq in [13].

In these notes, following [18], we first recall the Higgins commutator, based on the notion of commutator word, introduced by Higgins [12] in the context of varieties of $\Omega$-groups (groups equipped with additional algebraic operations of signature $\Omega$). We will describe also the internal interpretation of these commutator words given in [12] by means of the so-called formal commutator, which allows us to provide an intrinsic notion of Higgins commutator [H, K] of two subobjects H, K of A in any regular and unital category with finite colimits (see Definition 3.2). Such a commutator [H, K] is not in general a normal subobject of A (see Example 2.6), but if we move into the context of ideal determined categories [15], we easily see that such a commutator is always normal in the join $H\vee K$ of H and K in A.

In Sect. 4, we revisit also Huq commutator [13], showing that in a unital and normal category [16], Huq commutator is nothing but the normal closure of Higgins commutator. The two commutators are different in general, even in the category of groups, if H and K are not normal in A, as Example 1.2 shows. But they coincide when one of the two subobjects is the whole A.

The case with $H = A$ is special also for another reason. In the category of groups, the commutator [A, K] can be used to test whether the subgroup K of A is normal in A. Actually K is normal in A if, and only if, [A, K] is a subgroup of K. A natural question is to ask if the internal formulation of this connection is still valid in a categorical setting. In Proposition 3.7 we recall from [18] that, in an ideal determined and unital category $\mathscr {C}$, any normal subobject K of A contains the commutator [A, K]. In order to get the converse, we need to move into the world of semi-abelian categories [14], where the full characterization of normality via commutators holds.

Furthermore, in Sect. 5, we recall from [2] the categorical notions of commutative and abelian object and how they are related to the previous notion of commutator. Referring to [6], we show in Theorem 5.8 that, in the realm of pointed Mal’tsev categories, the two notions coincide. We conclude by describing how to obtain the abelianization functor (left adjoint to the inclusion of the subcategory of abelian objects), by means of the cokernel of the commutator [X, X] over X, in any pointed normal Mal’tsev category.

1 Commutators of Groups

We begin by recalling the notion of commutator of two elements in a group and of two subgroups. All the material of this section can be found in any textbook about group theory. Let G be a group, and let $g, h \in G$. The commutator of g and h is the element

$$\begin{aligned}{}[g, h] = ghg^{-1}h^{-1}. \end{aligned}$$

If H and K are subgroups of G, the commutator of H and K is the subgroup of G generated by all the elements of the form [h, k] with $h \in H$ and $k \in K$:

$$\begin{aligned}{}[H, K] = \langle [h, k] \ | \ h \in H, k \in K \rangle . \end{aligned}$$

In particular, the subgroup [G, G] is called the derived subgroup of G. It is clear that G is an abelian group if and only if $[G, G] = 0$, where 0 denotes the trivial group. More generally, given $h, k \in G$, one has $[h, k] = 1$ if and only if h and k permute: $hk=kh$.

Remark 1.1

Given two subgroups H and K of a group G, if we denote by $H \vee K$ the smallest subgroup of G containing both H and K (namely the supremum of H and K in the lattice of subgroups of G), then we have that the commutator [H, K] is a normal subgroup of $H \vee K$.

Proof  If $hkh^{-1}k^{-1}$ is a generator of [H, K] and $\bar{h} \in H$, then

$$\begin{aligned} \bar{h} (hkh^{-1}k^{-1}) \bar{h}^{-1} = \bar{h} h k h^{-1} \bar{h}^{-1} \bar{h} k^{-1} \bar{h}^{-1} \end{aligned}$$

$$\begin{aligned} = \bar{h} h k h^{-1} \bar{h}^{-1} k^{-1} k \bar{h} k^{-1} \bar{h}^{-1} = ((\bar{h} h) k (\bar{h} h)^{-1} k^{-1})(k \bar{h} k^{-1} \bar{h}^{-1}) \in [H, K], \end{aligned}$$

since both $(\bar{h} h) k (\bar{h} h)^{-1} k^{-1}$ and $k \bar{h} k^{-1} \bar{h}^{-1}$ belong to [H, K]. Similarly, if $\bar{k} \in K$, then $\bar{k} (hkh^{-1}k^{-1}) \bar{k}^{-1} \in [H, K]$, and this is enough to conclude.    $\square$

However, if H and K are not normal subgroups of G, [H, K] is not normal in general. The following example is borrowed from Alan Cigoli’s Ph.D. thesis [7]:

Example 1.2

Let G be the alternating group $A_5$ and let H and K be the following subgroups of G:

$$\begin{aligned} H = \langle (12)(34) \rangle , \quad K = \langle (12)(45) \rangle . \end{aligned}$$

These subgroups are not normal in $A_5$ (actually $A_5$ is a simple group, i.e. it has no non-trivial subgroups). Let us put $h = (12)(34)$ and $k = (12)(45)$. Then $h=h^{-1}$ and $k=k^{-1}$ and so

$$\begin{aligned}{}[h, k] = hkhk = (12)(34)(12)(45)(12)(34)(12)(45) \end{aligned}$$

$$\begin{aligned} = (34)(45)(34)(45) = (354)(354) = (345). \end{aligned}$$

So, $[H, K] = \langle (345) \rangle$ is not normal in $A_5$.

The situation improves when H and K are normal subgroups of G. Indeed, the following property holds:

Proposition 1.3

If H and K are normal subgroups of G, then [H, K] is normal in G as well.

Proof  If $h \in H$, $k \in K$ and $g \in G$, then $ghg^{-1} = \bar{h} \in H$ and $gkg^{-1} = \bar{k} \in K$. Hence

$$\begin{aligned} g(hkh^{-1}k^{-1})g^{-1} = (ghg^{-1})(gk^{-1}g^{-1})(gh^{-1}g^{-1})(gk^{-1}g^{-1}) = \bar{h} \bar{k} \bar{h}^{-1} \bar{k}^{-1} \in [H, K]. \end{aligned}$$

   $\square$

We will come back later, in a more general framework, to this last property, which will be called normality of the Higgins commutator. For the moment, we observe that this property allows one to get two important chains of normal subgroups of G, namely the derived series:

$$\begin{aligned} G \rhd [G, G] \rhd [[G, G], [G, G]] \rhd [[[G, G], [G, G]], [[G, G], [G, G]]] \rhd \ldots \end{aligned}$$

and the lower central series:

$$\begin{aligned} G \rhd [G, G] \rhd [[G, G], G] \rhd [[[G, G], G], G] \rhd \ldots \end{aligned}$$

The derived series allows one to define solvable groups: a group is solvable if its derived series reaches the trivial group after a finite number of steps. Similarly, the lower central series allows one to define nilpotent groups: a group is nilpotent if its lower central series reaches the trivial group after a finite number of steps.

Before moving to a more general context than the one of groups, we list some important properties of the commutator of subgroups. Their proofs are left to the reader.

Proposition 1.4

• 1. Given a subgroup K of G, K is normal in G if and only if $[K, G] \subseteq K$.

• 2. If $H, K, H', K'$ are subgroups of G, with $H \subseteq H'$ and $K \subseteq K'$, then $[H, K] \subseteq [H', K']$.

• 3. $f :G \rightarrow G'$ is a surjective group homomorphism, and H and K are subgroups of G, then $f([H, K]) = [f(H), f(K)]$.

2 The Case of $\Omega$-groups

In order to extend, in a unified way, the notions of ideal and commutator to a wide range of algebraic structures, Higgins introduced in [12] the notion of $\Omega$-group. An $\Omega$-group G is a group $(G, +, -, 0)$ (written in additive notation, although it is not necessarily abelian) equipped with a set $\Omega$ of additional operations, of finite arity $n \ge 1$, such that, for all $\omega \in \Omega$:

$$\begin{aligned} \omega (0, 0, \ldots 0) = 0. \end{aligned}$$

For any fixed $\Omega$, we get a variety in the sense of universal algebra. We will denote by $\Omega$-$\mathrm{\mathsf Grp}$ the category whose objects are the $\Omega$-groups (for the fixed $\Omega$) and whose morphisms are the group homomorphisms that preserve any $\omega \in \Omega$. Every such category is pointed, with the initial and terminal object given by $0 = \{0\}$.

Let X be a set of indeterminates and let $\underline{x}$ denote a finite sequence $(x_1,x_2,...,x_n)$ of elements of X. A word in X is an expression obtained by formally applying the operations $\omega \in \Omega , +, -$ to elements of X and to 0 a finite number of times. As it usually happens for varieties of universal algebras, considering words is the first step in order to build the free $\Omega$-group on the set X (some identifications, according to the equations of the corresponding variety, will be needed). Now we can consider two special families of words:

Definition 2.1

Let $f(\underline{x}, \underline{y})$ be a word in two disjoint sets of indeterminates X and Y. We shall say that

• 1. $f(\underline{x}, \underline{y})$ is an ideal word of X w.r.t. Y if $f(\underline{x}, \underline{y})$ satisfies the equation $f(\underline{0}, \underline{y}) = 0$, where $f(\underline{0}, \underline{y})$ is the word obtained from $f(\underline{x}, \underline{y})$ by replacing every $x_i$ in $\underline{x}$ by 0.

• 2. $f(\underline{x}, \underline{y})$ is a commutator word in X and Y if $f(\underline{0}, \underline{y}) = f(\underline{x}, \underline{0}) = 0$.

We will denote by $X^Y$ the set of ideal words of X w.r.t. Y, and by [X, Y] the set of commutator words in X and Y. It is clear that $[X, Y] = X^Y \cap Y^X$.

Example 2.2

In the variety $\mathrm{\mathsf Grp}$ of groups (and, more generally, in every variety of $\Omega$-groups), the word $y + x -y$ is an ideal word of $\{x\}$ w.r.t. $\{y\}$, and $x+y-x-y$ is a commutator word in $\{x\}$ and $\{y\}$. In the variety $\mathrm{\mathsf Rng}$ of (non-unitary) rings, the word xy is both an ideal and a commutator word in $\{x\}$ and $\{y\}$.

The reason for the name ideal word is that, given an $\Omega$-group G and an $\Omega$-subgroup H of G, H is an ideal (i.e. the kernel of a morphism) if and only if, for any ideal word $f(\underline{h}, \underline{g})$ in H and G, one has that $f(\underline{h}, \underline{g}) \in H$ (where, now, we do not see $f(\underline{h}, \underline{g})$ as a formal combination of elements, but we compose the symbols using the operations in G). Following the same spirit, given two $\Omega$-subgroups H and K of G, we will denote by [H, K] the set of the realizations in G of all the commutator words $f(\underline{h}, \underline{k})$ in H and K. In the variety of groups, it is not difficult to see that

$$\begin{aligned}{}[H, K] = \langle [h, k] \ | \ h \in H, k \in K \rangle , \end{aligned}$$

while, in the variety $\mathrm{\mathsf CRng}$ of commutative rings

$$\begin{aligned}{}[H, K] = HK. \end{aligned}$$

In general, we have the following:

Lemma 2.3

[12, Lemma 4.1] [H, K] is an $\Omega$-subgroup of G. Moreover, it is an ideal in the join $H \vee K$ of H and K in G.

In the particular case of distributive $\Omega$-groups, namely those $\Omega$-groups in which every $\omega \in \Omega$ is distributive w.r.t. $+$:

$$\begin{aligned} \forall a_1, \ldots a_n, b \quad \omega (a_1, \ldots a_i + b, \ldots a_n) = \omega (a_1, \ldots a_i, \ldots a_n) + \omega (a_1, \ldots b, \ldots a_n), \end{aligned}$$

there is an easy description of ideals:

Theorem 2.4

[12, Theorem 4a] If G is a distributive $\Omega$-group and H is an $\Omega$-subgroup of G, H is an ideal of G if and only if it is a normal subgroup of G and, for all $g_1, \ldots g_n \in G$, $h \in H$ and $\omega \in \Omega$, $\omega (g_1, \ldots g_{i-1}, h, g_{i+1}, \ldots g_n) \in H$.

If, moreover, we suppose that the group operation $+$ is commutative, then there is also an easy description of the commutator of two subobjects:

Theorem 2.5

[12, Theorem 4c] If G is a distributive $\Omega$-group, with $+$ commutative, and H and K are $\Omega$-subgroups of G, then [H, K] consists of all polynomials in elements of H and K each term of which contains both a factor from H and a factor from K.

In the previous section, we observed that the commutator subgroup [H, K], of two normal subgroups H and K of a group G, is always normal in G. It is a natural question whether the same property holds for $\Omega$-groups. Unfortunately, the answer is negative, even for distributive $\Omega$-groups, as the following example shows:

Example 2.6

Consider the variety of abelian groups endowed with an additional binary operation $*$ which is distributive w.r.t. the group operation $+$. Consider the free abelian group on three elements $A = \mathbb {Z}_x + \mathbb {Z}_y + \mathbb {Z}_t$ with the operation $*$ defined in the following way on the generators:

Then the free abelian subgroup $K = \mathbb {Z}_x + \mathbb {Z}_y$ is an ideal of A, since any product which involves elements of K still belongs to K, but the commutator $[K, K] = \mathbb {Z}_x$ is not an ideal of A, because, for instance, $x * t$ does not belong to $\mathbb {Z}_x$.

3 The Categorical Higgins Commutator

In this section we extend the commutator defined by Higgins for $\Omega$-groups to a categorical context. For this purpose, we will consider a pointed category $\mathscr {C}$ with finite limits and finite colimits. In this context, for any pair of objects H and K of $\mathscr {C}$, we get canonical inclusions

determined by the universal property of the product. Similarly, we have canonical morphisms

determined by the universal property of the coproduct. Combining them, we get a canonical morphism

$$\begin{aligned} \Sigma :H+K \rightarrow H \times K. \end{aligned}$$

If $\mathscr {C}$ is the category $\mathrm{\mathsf Grp}$ of groups, $H+K$ is the free product of H and K, while $H \times K$ is the usual direct product. Then $\Sigma$ is defined as follows:

$$\begin{aligned} \Sigma (h_1, k_1, h_2, k_2, \ldots h_n, k_n) = (h_1 h_2 \ldots h_n, k_1 k_2 \ldots k_n), \end{aligned}$$

where $h_i \in H$, $k_i \in K$ and the chain $h_1, k_1, h_2, k_2, \ldots h_n, k_n$ is a word in the alphabet $H \cup K$, which represents an element of $H+K$. In $\mathrm{\mathsf Grp}$ such a morphism $\Sigma$ is always surjective. In $\mathrm{\mathsf Grp}$, for a morphism being surjective is equivalent to being a regular epimorphism (i.e. the coequalizer of a pair of morphisms) and to being a normal epimorphism (i.e. the cokernel of a morphism). Moreover, a morphism of groups f is surjective if and only if it is an extremal epimorphism: this means that, if $f = mg$, with m a monomorphism, then m is an isomorphism. Let us give a name to those categories for which the canonical morphism $\Sigma$ is always an extremal epimorphism:

Definition 3.1

[3] Let $\mathscr {C}$ be a pointed category with finite limits and finite colimits. $\mathscr {C}$ is unital if, for every pair of objects H and K, the canonical morphism $\Sigma$ is an extremal epimorphism.

Actually, the definition of a unital category can be given even in absence of finite coproducts. Indeed, it suffices to ask that, for every pair of objects H and K, the canonical morphisms $\langle 1, 0 \rangle :H \rightarrow H \times K$ and $\langle 0, 1 \rangle :K \rightarrow H \times K$ are jointly extremal epimorphic: if they factor through a common monomorphism m, then m is an isomorphism.

Let us now consider the kernel of $\Sigma :H+K \rightarrow H \times K$. We will denote it by $H \diamond K$ (it was introduced in [5] under the name cosmash product of H and K). It is not difficult to show that, in $\mathrm{\mathsf Grp}$, $H \diamond K$ is given by commutator words in H and K. To see this, one can consider what is the image under $\Sigma$ of words of the form $h_1, k_1, h_2, k_2$: they are sent to the neutral element of $H \times K$ if and only if $h_1h_2 = 1$ and $k_1k_2 = 1$, i.e. $h_2 = h_1^{-1}$ and $k_2 = k_1^{-1}$. Actually the same fact holds in every category of $\Omega$-groups. For this reason, we can call $H \diamond K$ the formal commutator of H and K.

Let us now assume that the category $\mathscr {C}$ is not only unital, but also regular [1]. This means that every morphism f in $\mathscr {C}$ admits a pullback-stable factorization $f = m e$, where e is a regular epimorphism and m is a monomorphism (for further information about regular categories, the reader is addressed to the chapter An introduction to regular categories of this book). In this setting, consider two subobjects $h :H \rightarrowtail A$ and $k :K \rightarrowtail A$ of the same object A. These two arrows induce a morphism $(h, k) :H+K \rightarrow A$, which we call the realization map. The name comes from the fact that, in the case of varieties of universal algebra, this arrow turns a formal word belonging to $H+K$ into the element in A obtained by realizing such word w.r.t. the operations in A. Consider then the following commutative square:

where (e, m) is the (regular epi, mono) factorization of the restriction of (h, k) to $H \diamond K$, i.e. of the composite $(h, k) \mathrm{ker}(\Sigma )$.

Definition 3.2

The object [H, K] defines the categorical Higgins commutator of H and K in A.

Once the categorical version of the Higgins commutator is defined, our goal becomes to check which of the properties the classical commutator in $\mathrm{\mathsf Grp}$ has, still hold in this setting. First of all, we ask ourselves whether the commutator [H, K] of two subobjects in A is a normal subobject of the join $H \vee K$ (by “normal subobject” we simply mean a kernel of a morphism. This notion should not be confused with the one of subobject normal to an internal equivalence relation in the sense of Bourn (see [2])). In order to answer this question, we first need to recall how the join can be constructed in our categorical setting. It is obtained as the monomorphic part of the (regular epi, mono) factorization of $(h, k) :H+K \rightarrow A$ given by:

Clearly H is a subobject of $H \vee K$, because we have the following commutative diagram:

and the same holds for K. Moreover, if Z is a subobject of A having both H and K as subobjects, as in the following diagram:

then we get the commutative diagram

By the uniqueness, up to isomorphisms, of the (regular epi, mono) factorization, we obtain that (a, b) factors through $H \vee K$, which is then a subobject of Z:

and this tells us that $H \vee K$ is the smallest subobject of A containing both H and K. In order to show that the commutator [H, K] is normal in $H \vee K$ (i.e. it is the kernel of a morphism with domain $H \vee K$), we need a further assumption on our category $\mathscr {C}$, namely that it is ideal determined [15]:

Definition 3.3

A pointed regular category $\mathscr {C}$ with finite colimits is ideal determined if the following two conditions hold:

• 1. $\mathscr {C}$ is normal in the sense of [16], which means that every regular epimorphism in $\mathscr {C}$ is a normal epimorphism (i.e. the cokernel of a morphism);

• 2. the regular image of a normal monomorphism is a normal monomorphism. This means that, given a commutative square

  

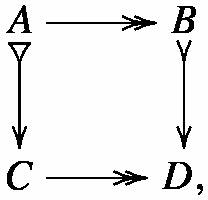
  where the horizontal arrows are regular epimorphisms and the vertical ones are monomorphisms, if the left vertical arrow is normal, then the right one is normal as well.

It is immediate to see that, in an ideal determined category, the commutator [H, K] is a normal subobject of the join $H \vee K$; it suffices to consider the following commutative square:

Let us now explore more in detail the second condition defining ideal determined categories. Let $h :H \rightarrow X$ be a normal subobject, and let $f :X \rightarrow Y$ be a regular epimorphism in an ideal determined category $\mathscr {C}$. If we consider the (regular epi, mono) factorization of fh:

we know, from Condition 2, that k is a normal subobject. So it will be the kernel of its cokernel. The cokernel of k can be built in the following way: let $q :X \rightarrow Q$ be the cokernel of h, and consider the pushout of q along f:

from which we get $q' k = 0$, since $f_1$ is an epimorphism. Moreover, if $t :Y \rightarrow T$ is such that $tk = 0$, then

$$\begin{aligned} 0 = tk f_1 = tfh. \end{aligned}$$

Since q is the cokernel of h, there exists a unique morphism $t' :Q \rightarrow T$ such that $tf = t' q$. Finally, by the universal property of the pushout, we get a unique $s :Q' \rightarrow T$ such that $s q' = t$ (and $s f' = t'$). Hence $q'$ is the cokernel of k.

Thanks to this observation, we can give an alternative characterization of ideal determined categories [17, Proposition 3.1]:

Proposition 3.4

Let $\mathscr {C}$ be a normal category with finite colimits. $\mathscr {C}$ is ideal determined if and only if, for any commutative diagram

such that the lower square is a pushout of regular epimorphisms, $h = \mathrm{ker}(q)$ and $k = \mathrm{ker}(q')$, one has that $f_1$ is a regular epimorphism, too.

Proof  Suppose $\mathscr {C}$ is ideal determined and the diagram (5.3.i) is given. Consider the (regular epi, mono) factorization of fh:

From what we observed before, we obtain that $k'$ is the kernel of its cokernel, which is necessarily $q'$. Then k and $k'$ are isomorphic, and so $f_1$ is a regular epimorphism.

Conversely, let $h :H \rightarrow X$ be the kernel of its cokernel $q :X \rightarrow Q$, and let $f :X \rightarrow Y$ be a regular epimorphism. Considering the pushout of f along q:

and completing the diagram with $k = \mathrm{ker}(q')$ and with the morphism $f_1$ induced by the universal property of the kernel (since $q' f h = f' q h = 0$), we obtain a diagram like (5.3.i). By assumption, $f_1$ is a regular epimorphism. Hence the regular image of the normal monomorphism h is the normal monomorphism k, and the category is ideal determined.    $\square$

Another property of the commutator we already observed for groups is the following: a subgroup K of A is normal if and only if the commutator [A, K] is a subgroup of K. In order to see if this property still holds in our general context, we first need to recall some facts concerning the construction of cokernels. Given a subobject $k :K \rightarrow A$, one way to build its cokernel in $\mathscr {C}$ is by means of the pushout

Another one (see [18]) is via the following, alternative pushout:

Indeed, from the equality $p (1, 0) = q (1, k)$ we get, precomposing with the first coproduct inclusion $\iota _A :A \rightarrow A+K$:

$$\begin{aligned} p = p (1, 0) \iota _A = q (1, k) \iota _A = q. \end{aligned}$$

Moreover, precomposing with the second coproduct inclusion $\iota _K :K \rightarrow A+K$, we obtain

$$\begin{aligned} 0 = p (1, 0) \iota _K = q (1, k) \iota _K = qk = pk, \end{aligned}$$

and, for every morphism $t :A \rightarrow T$ such that $tk = 0$, one has $t (1, 0) = t(1, k)$ and so, by the universal property of the pushout, there is a unique $s :Q \rightarrow T$ such that the following diagram commutes:

Hence $p=q$ is the cokernel of k.

The latter construction of the cokernel as a pushout gives an easy description of the normal closure of a subobject $k :K \rightarrow A$ (i.e. of the smallest normal subobject $\overline{k} :\overline{K} \rightarrow A$ containing K): it is the kernel of the cokernel of k. It is clear that a subobject is normal if and only if it coincides with its normal closure.

Let us now denote by $A \flat K$ the kernel of the canonical morphism $(1, 0) :A+K \rightarrow A$, where $k :K \rightarrow A$ is a subobject of A. Considering the following diagram

we see that, in an ideal determined category $\mathscr {C}$, the normal closure $\overline{K}$ of K is the regular image of the kernel $A \flat K$ of the canonical morphism $(1, 0) :A+K \rightarrow A$. Such object $A \flat K$ represents the “formal conjugator” of A over K: indeed, in the category $\mathrm{\mathsf Grp}$ of groups, $A \flat K$ is the subgroup of the free product $A + K$ formed by the ideal words in K and A, and it is generated by words of the form $(a, k, a^{-1})$ with $a \in A$ and $k \in K$. The fact that $A \flat K$ is the subalgebra of the coproduct formed by the ideal words actually holds in every category of $\Omega$-groups (see [12]). It is easy to see that the following fact, already observed for $\Omega$-groups, holds also in our categorical context:

Remark 3.5

Given two subobjects $h :H \rightarrow A$ and $k :K \rightarrow A$ of the same object A, one has

$$\begin{aligned} H \diamond K = (H \flat K) \cap (K \flat H). \end{aligned}$$

Moreover, the normal closure $\overline{K}$ of K is obtained from $A \flat K$ via the realization morphism, which, in $\mathrm{\mathsf Grp}$, sends the word $(a, k, a^{-1})$ to the element $aka^{-1} \in A$. Using this fact, one can prove the following result (whose proof is omitted, and can be found in [18, Proposition 5.10]):

Proposition 3.6

Given a subobject $k :K \rightarrow A$ in a unital, ideal determined category $\mathscr {C}$, one has that $[A, K] = [A, \overline{K}]$.

Now we are ready to prove the following

Proposition 3.7

[18, Proposition 6.1] Given a unital, ideal determined category $\mathscr {C}$, if K is a normal subobject of A, then [A, K] is a subobject of K.

Proof  Since $\mathscr {C}$ is ideal determined, we already know that [A, K] is a normal subobject of $A \vee K = A$. Consider then the following commutative diagram:

where the squares (1) and (2) are pushouts. Then the rectangle $(1) + (2)$ is a pushout as well. Moreover, $\pi _A \Sigma = (1, 0) :A+K \rightarrow A$, and we denote by p the composite $q' q$. Thanks to the previous observation, we have that p is the cokernel of $k :K \rightarrow A$. Since K is normal in A, $K = \overline{K}$, and so k is the kernel of p. To conclude that [A, K] is a subobject of K, it suffices to observe that $pj = 0$, because already $qj = 0$.    $\square$

The converse implication does not hold, in general, in a unital, ideal determined category. In order to recover it, we need to add a third condition, usually called Hofmann axiom, to the two conditions defining ideal determined categories. Hofmann axioms says that, given a commutative square

where the horizontal arrows are regular epimorphisms, the vertical ones are monomorphisms and $x'$ is normal, if $k = \mathrm{ker}(f)$ factors through x, then x is normal as well.

Definition 3.8

[14] An ideal determined category $\mathscr {C}$ which satisfies the Hofmann axiom is called a semi-abelian category.

Among the many examples of semi-abelian categories there are the category $\mathrm{\mathsf Grp}$ of groups, as well as the category $\mathrm{\mathsf Rng}$ of (not necessarily unitary) rings and every category of $\Omega$-groups. Further examples are the dual of the category of pointed sets and every abelian category. Actually the following characterization of abelian categories holds:

Remark 3.9

[14] A category $\mathscr {C}$ is abelian if and only if both $\mathscr {C}$ and its dual $\mathscr {C}^{\mathrm{op}}$ are semi-abelian.

The previous remark explains the name “semi-abelian”. Semi-abelian categories have many good properties. One of them is that they are always exact in the sense of Barr [1]: a category is Barr-exact if it is regular and, moreover, every internal equivalence relation is effective (which means that it is the kernel pair of a morphism). Another interesting property of semi-abelian categories is that they are Mal’tsev categories: we will explain this notion in the next section. Semi-abelian categories can be characterized as follows:

Proposition 3.10

A pointed, Barr-exact category $\mathscr {C}$ with finite coproducts is semi-abelian if and only if the short five lemma holds in it: given a commutative diagram

whose rows are short exact sequences, if $\alpha$ and $\gamma$ are isomorphisms, then $\beta$ also is.

In the setting of semi-abelian categories we can state the converse of Proposition 3.7. We are not going to give a proof, which can be found in [18, Theorem 6.3].

Theorem 3.11

In a semi-abelian category $\mathscr {C}$, a subobject K of an object A is normal if and only if [A, K] is a subobject of K.

Remark 3.12

This way to test the normality of a subobject K of A via the commutator [A, K] actually provides a characterization of semi-abelian categories among finitely cocomplete homological categories, as proved in [11].

4 The Huq Commutator

The aim of this section is to introduce another notion of commutator in a categorical context, and to compare it with the Higgins commutator we studied in the previous section. This alternative notion of commutator was first considered by Huq in [13] and further studied in the context of unital categories in [4]. Before going to our general categorical context, let us start with an observation in the case of groups:

Proposition 4.1

Given two subgroups H and K of the same group A, one has that $[H, K] = 0$ if and only if there exists a (necessarily unique) morphism $\varphi :H \times K \rightarrow A$ such that the following diagram commutes:

Proof  Since every element $(h, k) \in H \times K$ can be decomposed as $(h, k) = (h, 1) \cdot (1, k)$, a morphism $\varphi$ making the diagram above commute must satisfy the following equality:

$$\begin{aligned} \varphi (h, k) = \varphi ((h, 1) \cdot (1, k)) = \varphi (h, 1) \cdot \varphi (1, k) = \varphi \langle 1, 0 \rangle (h) \cdot \varphi \langle 0, 1 \rangle (k) = hk. \end{aligned}$$

This shows that such a morphism, when it exists, is uniquely determined. Let us now prove that $\varphi$ is a morphism if and only if $[H, K] = 0$. Given $h, h' \in H$ and $k, k' \in K$, one has

$$\begin{aligned} \varphi (h, h') \cdot \varphi (k, k') = hh'kk', \quad \text {while} \quad \varphi ((h, h') \cdot (k, k')) = hkh'k' \end{aligned}$$

and it is clear that the two expressions are equal for all $h, h' \in H$ and $k, k' \in K$ if and only if $[H, K] = 0$.    $\square$

With this property of groups in mind, we can give the following categorical definition:

Definition 4.2

[4] Let $\mathscr {C}$ be a unital category. Two subobjects $h :H \rightarrow A$ and $k :K \rightarrow A$ of the same object A are said to cooperate if there exists a morphism $\varphi :H \times K \rightarrow A$ such that diagram (5.4.i) commutes.

The morphism $\varphi$ as above, when it exists, is called the cooperator of h and k. It is always unique; indeed, if two morphisms $\varphi$ and $\varphi '$ make diagram (5.4.i) commute, then

$$\begin{aligned} \varphi \Sigma = \varphi ' \Sigma , \end{aligned}$$

since $\Sigma$ is induced by $\langle 1, 0 \rangle$ and $\langle 0, 1 \rangle$. But, in a unital category, $\Sigma$ is an extremal epimorphism, and this implies $\varphi = \varphi '$.

Let us see when two subobjects cooperate in the category $\mathrm{\mathsf Rng}$ of rings. Using the same argument we explained for groups, one can conclude that, if a cooperator $\varphi$ between subrings H and K of A exists, then it must be defined by $\varphi (h, k) = h+k$ for all $h \in H, k \in K$. But then

$$\begin{aligned} hk = \varphi (h, 0) \varphi (0, k) = \varphi (0, 0) = 0, \end{aligned}$$

and, in the same way, $kh = 0$. It is not difficult to check that the converse is also true. So, H and K cooperate if and only if $hk = kh = 0$ for all $h \in H, k \in K$.

We observe that, in order to Definition 4.2 make sense, there is no need that the morphisms h and k are monomorphisms. So, the definition can be extended to the one of cooperating morphisms with the same codomain, and no other restriction:

Definition 4.3

Let $\mathscr {C}$ be a unital category. Two morphisms $f :H \rightarrow A$ and $g :K \rightarrow A$ with the same codomain cooperate if there exists a morphism $\varphi :H \times K \rightarrow A$ such that the diagram

commutes.

Actually, if the category $\mathscr {C}$ is normal, this last definition is not really more general than Definition 4.2. In fact, the following Proposition holds:

Proposition 4.4

Let $\mathscr {C}$ be a normal and unital category. Two morphisms $f :H \rightarrow A$ and $g :K \rightarrow A$ cooperate if and only if their regular images cooperate as subobjects of A.

Proof   Consider the following commutative diagram:

and suppose that f(H) and g(K) cooperate as subobjects of A. Then there is a cooperator $\varphi :f(H) \times g(K) \rightarrow A$. It is immediate to check that, composing it with the morphism $\overline{f} \times \overline{g} :H \times K \rightarrow f(H) \times g(K)$, one gets a cooperator for f and g (see the diagram below).

Conversely, suppose that there is a cooperator $\psi :H \times K \rightarrow A$. The morphism $\overline{f} \times \overline{g}$ is a regular epimorphism, hence it is the cokernel of its kernel (because the category is normal). It is immediate to check that its kernel is $x \times y :N_H \times N_K \rightarrow H \times K$. Since

$$\begin{aligned} \psi (x \times y) \langle 1, 0 \rangle = 0 = \psi (x \times y) \langle 0, 1 \rangle \end{aligned}$$

and the category is unital, one has $\psi (x \times y) = 0$. Then, by the universal property of  the cokernel, one gets a unique morphism $\varphi \, :f(H) \times g(K) \rightarrow A$ such that $\varphi (\overline{f} \times \overline{g}) = \psi$. It is easy to check that such a morphism is a cooperator for f(H) and g(K) as subobjects of A.    $\square$

Now we have everything we need to define the Huq commutator:

Definition 4.5

Let $h :H \rightarrow A$ and $k :K \rightarrow A$ be two subobjects of the same object A in a normal and unital category $\mathscr {C}$. The Huq commutator of h and k, denoted by $[H, K]_{\mathrm{Huq}}$, is the smallest normal subobject $n :N \rightarrow A$ of A such that, denoting by $q :A \rightarrow A/N$ the cokernel of n, the morphisms qh and qk cooperate.

First of all, we should show that such smallest normal subobject always exists. In order to do that, consider the following pushout:

We want to show that $[H, K]_{\mathrm{Huq}}$ is the kernel of q. Let us complete the previous diagram as follows:

First of all, we observe that $\varphi$ is the cooperator of qh and qk, because $\Sigma = (\langle 1, 0 \rangle , \langle 0, 1 \rangle )$, and the commutativity of the pushout square says precisely that $\varphi (\langle 1, 0 \rangle , \langle 0, 1 \rangle ) = (qh, qk)$. Moreover, if $n :N \rightarrow A$ is a normal subobject of A such that ph and pk cooperate (where p is a cokernel of n), one has a cooperator $\psi :H \times K \rightarrow A/N$, which is a morphism such that $\psi \Sigma = p (h, k)$. The universal property of the pushout gives then a unique morphism $\gamma :Q \rightarrow A/N$ such that $\gamma q = p$ (and $\gamma \varphi = \psi$). From the universal property of n as a kernel of p, we get a unique $\beta :[H, K]_{\mathrm{Huq}} \rightarrow N$ such that $n \beta = \alpha$, and such a $\beta$ is necessarily a monomorphism.

Proposition 4.6

[18] Let $h :H \rightarrow A$ and $k :K \rightarrow A$ be two subobjects of the same object A in a normal and unital category $\mathscr {C}$. The Huq commutator $[H, K]_{\mathrm{Huq}}$ is the normal closure of the Higgins commutator [H, K] of h and k.

Proof  It suffices to consider the following commutative diagram:

where the lower square is a pushout, and to observe that q is the cokernel of m.    $\square$

So, if [H, K] is normal in A (in particular, when $A = H \vee K$), then $[H, K] = [H, K]_{\mathrm{Huq}}$. However, as we observed in the case of groups, it can be $[H, K] \ne [H, K]_{\mathrm{Huq}}$ if H and K are not normal in A. In our general categorical context, it can happen that $[H, K] \ne [H, K]_{\mathrm{Huq}}$ even if H and K are normal in A. We will say that the category $\mathscr {C}$ satisfies the condition of normality of the Higgins commutator if the Higgins commutator [H, K] of two normal subobjects of an object A is normal in A. The category $\mathrm{\mathsf Grp}$ has this property. We refer to [8] for more examples and counterexamples of semi-abelian categories with respect to this property.

5 Abelian Objects

The aim of this section is to introduce the notions of commutative and abelian object in a categorical context, and to compare them. We start talking about commutative objects.

Definition 5.1

An object X in a unital category $\mathscr {C}$ is commutative if the identity morphism $1_X$ cooperates with itself.

Thanks to the observations at the end of the previous section, we can conclude that, in a normal and unital category, an object X is commutative if and only if the Huq commutator $[X, X]_{\mathrm{Huq}}$ is the zero object. Moreover, since $X \vee X = X$ and X is clearly normal in itself, we have that the Higgins commutator [X, X] coincides with $[X, X]_{\mathrm{Huq}}$, and so X is commutative if and only if $[X, X]=0$. Another characterization of commutative objects, in terms of internal algebraic structures, is possible. In order to describe it, we first need to recall the following definition:

Definition 5.2

An internal unitary magma in a category $\mathscr {C}$ with finite limits is a triple (X, m, e), where X is an object of $\mathscr {C}$, and $m :X \times X \rightarrow X$, $e :1 \rightarrow X$ are morphisms in $\mathscr {C}$ (by 1 we denote the terminal object of $\mathscr {C}$) such that e “behaves like a unit for the internal operation m”, namely the following diagram commutes:

Proposition 5.3

An internal unitary magma structure on an object X in a unital category $\mathscr {C}$, when it exists, is unique. It exists if and only if the object X is commutative.

Proof  Since a unital category is pointed, the morphism $e :1=0 \rightarrow X$ is uniquely determined and, moreover, we have the following commutative triangles:

Hence the multiplication m of an internal unitary magma (X, m, e) must make the following diagram commute:

and so m must be a cooperator for the pair $(1_X, 1_X)$. Then it is unique, when it exists. Moreover, it exists if and only if $1_X$ cooperates with itself, i.e. if and only if X is commutative.    $\square$

Actually we can say more:

Proposition 5.4

Every internal unitary magma structure (X, m, e) in a unital category $\mathscr {C}$ is an internal commutative monoid structure, i.e. the internal multiplication m is associative and commutative.

Proof  In order to prove the associativity of m, we need to show that the following square commutes:

or, in other terms, that $m (m \times 1_X) = m (1_X \times m)$. To do that, we will show that $m (m \times 1_X)$ and $m (1_X \times m)$ are cooperators for the same pair of morphisms. Consider the following diagram:

The lower left-hand side triangle clearly commutes, the lower right-hand side one also does, since m is a cooperator for the pair $(1_X, 1_X)$, as observed in the proof of the previous proposition. For the same reason, the upper right-hand side triangle commutes as well. To check whether the remaining triangle commutes, we precompose with the jointly epimorphic pair of morphisms $\langle 1, 0 \rangle , \langle 0, 1 \rangle :X \rightarrow X \times X$. We have

$$\begin{aligned} (1_X \times m) \langle 1_{X \times X}, 0 \rangle \langle 1, 0 \rangle = (1_X \times m) \langle 1, 0, 0 \rangle = \langle 1, 0 \rangle \end{aligned}$$

and

$$\begin{aligned} (1_X \times m) \langle 1_{X \times X}, 0 \rangle \langle 0, 1 \rangle = (1_X \times m) \langle 0, 1, 0 \rangle = \langle 0, 1 \rangle , \end{aligned}$$

again using the fact that m is a cooperator for the pair $(1_X, 1_X)$. Hence the whole diagram commutes, and this tells us that $m (1_X \times m)$ is a cooperator for the pair $(m, 1_X)$. In a similar way, one can check that $m (m \times 1_X)$ is a cooperator for the same pair, and so these two morphisms coincide.

In order to show that m is commutative, we have to check that $m = m \circ tw$, where $\mathrm{tw}= \langle \pi _2, \pi _1 \rangle :X \times X \rightarrow X \times X$ is the “twisting” isomorphism (in set-theoretic terms, it sends a pair (x, y) to the pair (y, x)). We have the following commutative diagram:

which tells us that $m \circ \mathrm{tw}$ is a cooperator for the pair $(1_X, 1_X)$, as well as m, hence these two morphisms coincide.    $\square$

Once we know that every commutative object in a unital category has a (unique) structure of internal commutative monoid (and conversely), a natural question arises: to understand when these internal commutative monoids are internal abelian groups. Internal abelian groups deserve a specific name:

Definition 5.5

An abelian object in a unital category $\mathscr {C}$ is an object X equipped with a (necessarily unique) structure of internal abelian group.

The terminology is justified by the fact that, in the category $\mathrm{\mathsf Grp}$ of groups, the abelian objects are precisely the abelian groups. So, in $\mathrm{\mathsf Grp}$, commutative objects and abelian objects coincide. Unfortunately this is not true in every unital category: there can be commutative objects that are not abelian. In order to get the equivalence between the two notions, we need to impose further assumptions on our category. Before doing it, we recall some terminology.

Given two sets X and Y, a relation R from X to Y is difunctional if the following condition holds:

$$\begin{aligned} \forall \ x, x' \in X, y, y' \in Y \quad xRy', x'Ry', x'Ry \ \Longrightarrow \ xRy. \end{aligned}$$

This notion is important because, for example, it allows an easy characterization of equivalence relations among reflexive ones. Indeed, a reflexive relation on a set X is an equivalence relation if and only if it is difunctional. We can actually talk about relations internally to every category with finite limits (the reader may again refer to the chapter An introduction to regular categories of this volume for a full treatment of relations in regular categories). Indeed, an internal relation between two objects X and Y in a finitely complete category $\mathscr {C}$ is nothing but a subobject of $X\times Y$, which can be represented by a monomorphism $R \rightarrowtail X \times Y$. All the classical properties of relations can be easily expressed categorically. For instance, an internal relation R on an object X is reflexive if the diagonal morphism $\langle 1, 1 \rangle :X \rightarrow X \times X$ factors through R. An internal relation $R \rightarrowtail X \times Y$ is difunctional if, considering the commutative diagram

where $r_1 :R \rightarrow X$ and $r_2 :R \rightarrow Y$ are the composites of the monomorphism $R \rightarrowtail X \times Y$ with the product projections on X and Y, respectively, $\mathrm{tw}$ is the twisting isomorphism, and both squares are pullbacks, one has that the canonical inclusion $S \cap T \rightarrowtail S$ is an isomorphism. However, for our purposes, this internal description of difunctionality is not so important. Indeed, the notion of internal relation, as well as the main properties of relations (like reflexivity or difunctionality), can be expressed only by means of finite limits. Hence, if these properties of relations hold in the category $\mathrm{\mathsf Set}$ of sets, then they hold in every category with finite limits (we do not enter the details of this fact; the interested reader can find a self-contained explanation of this in Chapter 0 of [2]).

Now we have everything we need to give the following

Definition 5.6

[6] A finitely complete category $\mathscr {C}$ is a Mal’tsev category if every internal relation in $\mathscr {C}$ is difunctional.

In fact, one can define equivalently Mal’tsev categories as those finitely complete categories in which every internal reflexive relation is an equivalence relation (see [2]). The first property of Mal’tsev categories we are interested in is the following:

Proposition 5.7

Every pointed Mal’tsev category is unital.

Proof  Let $\mathscr {C}$ be a pointed Mal’tsev category. For any pair of objects X, Y in $\mathscr {C}$, we have to show that the morphisms

are jointly extremal epimorphic. So, suppose they both factorize through a common monomorphism $m :R \rightarrowtail X \times Y$.

Such an m gives rise to an internal relation R in $\mathscr {C}$, which is then difunctional. The fact that $\langle 1, 0 \rangle$ and $\langle 0, 1 \rangle$ factor through R can be expressed in set-theoretic terms saying that for all $x \in X$ and $y \in Y$ one has xR0 and 0Ry. By difunctionality we get

$$\begin{aligned} xR0, \ 0R0, \ 0Ry \quad \Longrightarrow \quad xRy. \end{aligned}$$

Hence R coincides, up to an isomorphism, with the total relation $X\times Y$. This means that m is an isomorphism, proving that $\langle 1, 0 \rangle$ and $\langle 0, 1 \rangle$ are jointly extremal epimorphic.    $\square$

Every semi-abelian category is a Mal’tsev category (see, for example, [2]). So, $\mathrm{\mathsf Grp}$, $\mathrm{\mathsf Rng}$, as well as every category of $\Omega$-groups in the sense of [12] are Mal’tsev categories.

Theorem 5.8

[6] Every commutative object in a pointed Mal’tsev category is abelian.

Proof  Let X be a commutative object in a pointed Mal’tsev category $\mathscr {C}$, and let (X, m, e) be its unique internal commutative monoid structure. We have to show that this structure is the one of an internal abelian group, i.e. there exists a morphism $i :X \rightarrow X$ making the following diagram commute:

We use again the elementwise approach. First of all, we show that the multiplication m satisfies the two following conditions:

• (i)   $\, m(x, y) = m(x, z) \quad \Longrightarrow \quad y=z$;

• (ii)   $\, m(y, x) = m(z, x) \quad \Longrightarrow \quad y=z$.

In order to do that, consider the relation R from $X \times X$ to X defined by

$$\begin{aligned} (y, z) R x \quad \Longleftrightarrow \quad m(x, y) = m(x, z). \end{aligned}$$

Suppose that $m(x, y) = m(x, z)$. Denoting by 0 the neutral element of m, we have that:

• (y, z)Rx, since $m(x, y) = m(x, z)$;

• (0, 0)Rx, since $m(x, 0) = m(x, 0) = x$;

• (0, 0)R0, since $m(0, 0) = m(0, 0) = 0$.

By difunctionality we get that (y, z)R0, which means that $y = m(0, y) = m(0, z) = z$. This proves (i); the proof of (ii) is analogous.

Let us now define another relation S on X by putting xSy if and only if there exists z such that $m(z, y) = x$. Such a z is unique because of (i) above. We have xSx, with $z=0$, since $m(0, x) = x$. Moreover, xS0, with $z=x$, since $m(x, 0) = x$, and finally 0S0. By difunctionality, we conclude that 0Sx, i.e. there exists a (unique) z such that $m(z, x) = 0$. This element z allows us to define the morphism i we are looking for.    $\square$

We conclude by observing that, in a pointed, normal Mal’tsev category $\mathscr {C}$, the full subcategory $\mathrm {Ab}(\mathscr {C})$ of abelian objects is reflective. The reflection is performed by the so-called abelianization functor

$$\begin{aligned} \mathrm{ab}:\mathscr {C}\rightarrow \mathrm {Ab}(\mathscr {C}). \end{aligned}$$

It is obtained as follows: given an object X of $\mathscr {C}$, $\mathrm{ab}(X) = \frac{X}{[X, X]_{\mathrm{Huq}}}$ as in the following pushout:

Indeed, we already observed that $[X, X]_{\mathrm{Huq}}$ is the smallest normal subobject of X such that the pair $(1_X, 1_X)$, composed with the projection q, commutes in $\frac{X}{[X, X]_{\mathrm{Huq}}}$. Hence, being $\mathscr {C}$ Mal’tsev, the object $\frac{X}{[X, X]_{\mathrm{Huq}}}$ is abelian. The functoriality of this construction is obvious. Let us check that it has the universal property of the reflection. Given a morphism $f :X \rightarrow A$, where A is an abelian object, we have that f cooperates with itself in A. Indeed, if m is the internal multiplication of A, $\psi = m \circ (f \times f)$ is a cooperator for the pair (f, f), because the following diagram commutes:

Then, by the universal property of the pushout, we get a unique $\overline{f} :[X, X]_{\mathrm{Huq}} \rightarrow A$ making the following diagram commute:

Whence the universality of the abelianization.