Waveform Relaxation for Low Frequency Coupled Field/Circuit Differential-Algebraic Models of Index 2

Abstract

Motivated by the task to design quench protection systems for superconducting magnets in particle accelerators we address a coupled field/circuit simulation based on a magneto-quasistatic field modeling. We investigate how a waveform relaxation of Gauß-Seidel type performs for a coupled simulation when circuit solving packages are used that describe the circuit by the modified nodal analysis. We present sufficient convergence criteria for the coupled simulation of FEM discretised field models and circuit models formed by a differential-algebraic equation (DAE) system of index 2. In particular, we demonstrate by a simple benchmark system the drastic influence of the circuit topology on the convergence behavior of the coupled simulation.

1 Introduction

Lumped circuit models, such as modified nodal analysis (MNA), are well-established in electrical engineering. However, they neglect the spatial dimension and therefore distributed phenomena like the skin effect. For certain devices, this may lead to inaccuracies of unacceptable magnitude in the simulation, e.g. for electric machines [14] or the quench protection system of superconducting magnets in particle accelerators [1]. These cases call for field/circuit coupling [2, 16]. To solve such coupled systems, it is often advisable to use waveform relaxation (WR) [7], since this iterative method allows for dedicated step sizes and suitable solvers for the different subsystems, and even for the use of proprietary blackbox solvers. The coupled field/circuit model considered here is a DAE in the time domain after space discretisation of the field system. It is well-known that WR can suffer from instabilities for DAEs unless an additional contraction criterion is satisfied [7, 12]. This work presents coupled field/circuit models, which are DAEs of index 2 [5], for the case where WR is convergent and the case where it diverges. Furthermore, generalizing a convergence criterion of [12], a topological and easy-to-check criterion is provided. Finally, we present numerical simulations verifying the topological convergence criterion.

2 Field/Circuit Model

To describe the electromagnetic (EM) field part, we consider a magnetoquasistatic approximation of Maxwell’s equations in a reduced magnetic vector potential formulation [4]. This leads to the curl-curl eddy current partial differential equation (PDE). The circuit side is formulated with the MNA [6]. For the numerical simulation of the coupled system, the method of lines is used with a finite element (FE) discretisation. Altogether, this leads to a time-dependent coupled system of DAE initial value problems (IVPs), described by

$$\displaystyle \begin{aligned} M\dot a+K(a)a-Xi_m&=0,& X^\top \dot a&=v_c, \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} E(x)\dot x+f(t,x)&=Pi_m, & P^\top x-v_c&=0. \end{aligned} $$

(2)

The first Eq. (1) represents the space-discrete field model based on the matrices

$$\displaystyle \begin{aligned} (M)_{ij} = \int_{\varOmega} \sigma \omega_i \cdot \omega_j\,\mathrm{d}\mathrm{V}, && (K(a))_{ij} = \int_{\varOmega} \nu(a) \nabla\times\omega_i \cdot \nabla\times \omega_j\,\mathrm{d}\mathrm{V}\;, \end{aligned} $$

(3)

which follow from the Ritz-Galerkin approach using a finite set of Nédélec basis functions ω _i [10] defined on the domain Ω; σ denotes the space-dependent electric conductivity and ν(a) the magnetic reluctivity that can additionally depend nonlinearly on the unknown magnetic vector potential a. The current through the field device is described by i _m. The excitation matrix is computed from a winding density function χ _j modelling the j-th stranded conductor [15] as

$$\displaystyle \begin{aligned} (X)_{ij} = \int_{\varOmega} {\chi}_j\cdot \omega_i \,\mathrm{d}\mathrm{V}\;. \end{aligned} $$

(4)

Definition 1

A function $f:\mathbb {R}^n\to \mathbb {R}^n$ is strongly monotone and a square matrix M(x) is uniformly positive definite, if

$$\displaystyle \begin{aligned} \exists \mu_f:&& (x_2-x_1)^\top(f(x_2)-f(x_1))\geq &\mu_f\|x_2-x_1\|{}^2, \ &\forall x_1,x_2\in\mathbb R^n,\\ \exists \mu_M:&& y^\top M(x)y \geq &\mu_M\|y\|{}^2,\ &\forall x\in\mathbb{R}^n,y\in\mathbb R^m. \end{aligned} $$

The space-discretization is supposed to meet the following properties.

Assumption 2

It holds (a) M is symmetric, (b) the matrix pencil λM + K is symmetric and positive definite for λ > 0, (c) X has full column rank and (d) the function a↦K(a)a is strongly monotone.

The assumptions are in agreement with previous formulation in the literature, e.g. [3, 15]. The first Assumption 2a follows naturally if a Ritz-Galerkin formulation (3) is chosen. The second Assumption 2b will be guaranteed by appropriate boundary and gauging conditions. Thirdly, the full column rank Assumption 2c follows from the fact that the columns are discretisations of different coils that are located in spatially disjoint subdomains. Finally, the monotonicity Assumption 2d follows from the strong monotonicity of the underlying nonlinear material law, i.e. the BH-curve [13]. In general, the field model is a multiport element such that the circuit coupling is established via multiple currents and voltages, i.e., vector-valued i _m and v _c. However, for simplicity of notation we assume a two-terminal device in the following.

The circuit Eq. (2) can be expanded into

$$\displaystyle \begin{aligned} { E(x) =\begin{pmatrix}\mathscr L_C(e)&0&0\\0&-L(i_L)&0\\ 0&0&0\end{pmatrix},\; f(t,x) = \begin{pmatrix}g_R(e)+A_L i_L+A_V i_V+q_i(t)\\A_L^\top e\\A_V^\top e - q_v(t)\end{pmatrix},\; P=\begin{pmatrix}A_m\\0\\0\end{pmatrix}} \end{aligned} $$

(5)

using the definitions $\mathscr L_C(e):=A_C C(A_C^\top e)A_C^\top$, $g_R(e):=A_R g(A_R^\top e)$ and x = (e, i _L, i _V) where A _⋆ are the usual incidence matrices and L(⋅), C(⋅) are state-dependent square matrices describing inductances and capacitances. The position of the field device in the circuit is described by A _m, and the voltage over the device by v _c. The function g(⋅) describes the voltage–current relation of resistive elements and q _i, q _v are the input current and voltage. Finally, x collects all node potentials e, currents through branches with voltage sources i _V and inductors i _L. The circuit system shall fulfill the following properties:

Assumption 3

It holds (a) g, C and L are Lipschitz continuous, g is strongly monotone and C, L are uniformly positive definite, (b) q _i and q _v are continuously differentiable, (c) A _V has full column rank and $\begin {pmatrix}A_C&A_V&A_R&A_L\end {pmatrix}$ has full row rank.

Assumption 3a reflects the global passivity of the respective elements [8]. Considering well-known relations between incidence matrices and circuit topology, Assumption 3c excludes the electrically forbidden configurations of loops of voltage sources and cutsets of current sources [5].

3 Waveform Relaxation and Convergence

We consider the Gauß-Seidel WR method. Applied to the coupled system (1)–(2) for given consistent initial values, this yields the scheme

$$\displaystyle \begin{aligned}M\dot a^k+K(a^k)a^k-Xi_m^k&=0,&\ X^\top \dot a^k&=v_c^{k-1}, \end{aligned} $$

(6)

$$\displaystyle \begin{aligned}E(x^k)\dot x^k+f(t,x^k)&=Pi_m^k,&\ P^\top x^k-v_c^k&=0. \end{aligned} $$

(7)

The coupling variables are the current through and the voltage over the field device i _m and v _c, where $i_m^k$ is computed in (6) and is then given to (7) as input, and vice versa for $v_c^k$. The superscript k denotes the iteration index. A common choice for the initial guess $v_c^{0}$ is constant extrapolation of the initial value.

We shall proceed as follows:

• 1. Lemmata 4 and 6 provide a DAE-decoupling of the EM field DAE (1) and the MNA DAE (2), respectively.

• 2. Definition 5 introduces the concept of parallel CVR paths. Assuming their existence and exploiting the previous decoupling Lemmata, Lemma 7 yields a DAE-decoupling of the coupled WR iteration (6)–(7). Notably, it reveals the structure of its inherent ODE, given by ϕ in Eq. (11).

• 3. The convergence Theorem 8 is a simple consequence of the previous Lemmata; it shows that the existence of parallel CVR paths guarantees convergence of the WR scheme (6)–(7).

For visual reasons, we shall write column vectors as (a, b, c).

Lemma 4

Let Assumption 2 hold. Then, for a given source term v _c , there exists a coordinate transformation (w, u) = T ⁻¹ a and a system of the form

$$\displaystyle \begin{aligned}\dot u+A_1u&=A_2v_c,&\ w&=Bu,&\ i_m=G_1u+G_2v_c \end{aligned} $$

(8)

such that (a, i _m) solves Eq. (1) if and only if (u, w, i _m) solves Eq. (8).

Proof

For better readability and shortness we present the proof only for the slightly more restrictive case where X ^⊤ M = 0, which is usually satisfied.

We equivalently transform the field DAE with new coordinates Tα = a:

$$\displaystyle \begin{aligned}{} T^\top M T\dot\alpha+ T^\top K(T\alpha)T\alpha- T^\top Xi_m&=0,\\ X^\top T\dot\alpha&=v_c. \end{aligned} $$

(9)

The transformation matrix $T:=(T_{\ker }\ X\ T_\perp )$ is constructed such that the columns of $T_{\ker }$ and T _⊥ form a basis of $\ker M\cap \ker X^\top$ and $(\ker M)^\perp$, respectively. It is nonsingular indeed, since its construction and Assumption 2 combined with X ^T M = 0 guarantee that $\text{im}X\perp \text{im}T_{\ker }$ and $\text{im}T_\perp \perp \text{im}(T_{\ker }\ X)$.

With α = (w, u) and u = (u ₁, u ₂), the transformed DAE (9) has the detailed form

$$\displaystyle \begin{aligned} \underline{T_{\ker}^\top K(T\alpha)T_{\ker}}w+T_{\ker}^\top K(T\alpha)(X\ \ T_\perp)u&=0,\\ X^\top K(T\alpha)T\alpha-\underline{X^\top X}i_m&=0,\\ \underline{T_\perp^\top M T_\perp} \dot u_2+T_\perp^\top K(T\alpha)T\alpha&=0,\\ \underline{X^\top X}\dot u_1&= v_c. \end{aligned} $$

The underlined matrices are nonsingular due to Assumption 2, and Eq. (8) is obtained by inversion and insertion.

Definition 5

A CVR path in a circuit is a path which consists of only capacitances, voltages sources and resistances. An element has a parallel CVR path, if its incident nodes are connnected by a CVR path.

Lemma 6

Let Assumption 3 hold. Then, for a given source term i _m , there exists a coordinate transformation (y, z ₁, z ₂) = T ⁻¹ x and a system of the form

$$\displaystyle \begin{aligned} \dot {y}&= f_0(t,y,z,z_2,u),& z_1&=g_1(t,y,z_2,\dot z_2,u),& z_2&=g_2(t)+QPi_m, \end{aligned} $$

(10a)

$$\displaystyle \begin{aligned} &&&&v_c&=P^\top T(y,z_1,z_2) \end{aligned} $$

(10b)

with f ₀, g ₁, g ₂ uniformly globally Lipschitz continuous ∀t and g ₂ ∈ C ¹ such that

• 1. (x, v _c) solves Eq. (2) if and only if (y, z ₁, z ₂, v _c) solves Eq. (10),

• 2. QP = 0 if each EM field element has a parallel CVR-path.

A detailed proof can be found in [11], where Q is shown to have the form (Q ₁  ∗ ∗) with $\text{im}Q_1=\ker (A_C\ A_V\ A_R)^\top$. Hence, if each field element has a parallel CVR-path, each column of A _m can be written as a sum of columns of (A _C A _V A _R) and it follows Q ₁ A _m = 0, thus QP = 0.

Lemma 7

Let Assumptions 2 and 3 hold. If each EM field element has a parallel CVR path, then there exists a coordinate transformation (r, s) = T ⁻¹(a, x) and a system of the form

$$\displaystyle \begin{aligned} \dot s^k=\phi(t,s^k,s^{k-1}),\qquad r^k=\varphi(t,s^k) \end{aligned} $$

(11)

with ϕ uniformly globally Lipschitz continuous ∀t and ϕ, φ continuous such that $(a^k,i_m^k,x^k,v_c^k)$ solves Eqs. (6)–(7) if and only if (s ^k, r ^k) solves Eq. (11).

Proof

We apply Lemmata 4, 6 to the iterated subsystems (6), (7). This yields an equivalent system

$$\displaystyle \begin{aligned} \dot u^k&=-A_1u^k+A_2v_c^{k-1}, & w^k&=Bu^k, & i_m^k&=G_1u^k+G_2v_c^{k-1}, \end{aligned} $$

(12)

$$\displaystyle \begin{aligned} \dot y^k &= f_0(t,y^k,z^k,z_2^k,u^k), & z_1^k&=g_1(t,y^k,z_2^k,\dot z_2^k,u^k), & z_2^k&=g_2(t), \end{aligned} $$

(13)

$$\displaystyle \begin{aligned} && &&v_c^k &=P^\top T(y^k,z_1^k,z_2^k). {} \end{aligned} $$

(14)

Since each field element has a parallel CVR path, $z_2^k=g(t)$ does not depend on u ^k anymore.

We insert $v_c^{k-1}=P^\top x^{k-1}=P^\top T(y^{k-1},z_1^{k-1},z_2^{k-1})$ and $z_1^{k-1}$ and $z_2^{k-1}$ therein to obtain, with $\tilde g_1(t,y^{k-1},u^{k-1})=g_1(t,y^{k-1},g_2(t),\dot g_2(t),u^{k-1})$,

$$\displaystyle \begin{aligned} \dot u^k=\phi_2(t,u^k,y^k,u^{k-1},y^{k-1})\quad :=-A_1u^k+A_2P^\top T(y^{k-1},\tilde g_1(t,y^{k-1},u^{k-1}),g_2(t)). \end{aligned} $$

Insertion of $z_1^k,z_2^k,\dot z_2^k$ into f ₀ yields

$$\displaystyle \begin{aligned} \dot y^k=\phi_1(t,u^k,y^k)\quad :=f_0(t,y^k,g_1(t,y^k,g_2(t),\dot g_2(t),u^k),g_2(t),u^k). \end{aligned} $$

Hence, defining s ^k := (u ^k, y ^k) and ϕ := (ϕ ₁, ϕ ₂), the sequence (u ^k, y ^k) is given implicitly by an ODE recursion of the form $\dot s^k=\phi (t,s^k,s^{k-1})$.

The algebraic constraint of Eq. (11) is obtained with $r^k=(w^k,i^k,z_1^k,z_2^k,v_c^k)$, s ^k = (u ^k, y ^k) and

$$\displaystyle \begin{aligned} \varphi(t,s)=(Bu,Gu,g_1(t,y,g_2(t),\dot g_2(t),u),g_2(t)). \end{aligned} $$

Clearly, (s ^k, r ^k) solves Eq. (11) if and only if $\tilde \alpha ^k:=(u^k,w^k,i_m^k,y^k,z_1^k,z_2^k,v_c^k)$ solves Eqs. (12)–(14), and $\tilde \alpha ^k$ solves (12)–(14) if and only if $(a^k,i_m^k,x^k,v_c^k)$ solves Eqs. (6)–(7).

We deduce the main result of this work:

Theorem 8

If each EM field element of the coupled system (1)–(2) has a parallel CVR path, then the WR scheme (6)–(7) is uniformly convergent to the exact solution of (1)–(2).

Proof

The ODE part of Eq. (11) is a WR scheme for ODEs with Lipschitz continuous vector field ϕ. It is well-known that such schemes are unconditionally convergent on bounded time intervals [7]. The convergence of s ^k clearly implies the convergence of (s ^k, r ^k) defined by (11). Due to the equivalence provided by Lemma 7, it follows that the original scheme (6)–(7) is convergent.

Remark 9

The convergence result holds for arbitrary continuous initial guesses x ⁰ and for bounded intervals of arbitrary size, see e.g. [7, 11].

Remark 10

The MNA decoupling given in Lemma 6 shows that g ₁ depends on z ₂ and the derivative $\dot z_2$. Hence, the system is most sensitive to perturbations of z ₂. The input of the EM field subsystem in the WR scheme is in fact a perturbation. Therefore, the condition QP = 0 from Lemma 6 is crucial to derive Theorem 8. If at least one EM field element has no parallel CVR path, then QP ≠ 0. Then, analogously to Lemma 7 and its proof, we find $\dot s^k=\phi (t,s^k,s^{k-1},\dot s^{k-1})$, which is guaranteed to converge only if ϕ is contractive in $\dot s^{k-1}$, see [7, 11].

4 Numerical Examples

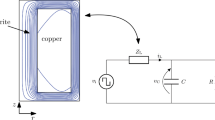
To illustrate the convergence behaviour of the WR scheme according to the derived criteria, we consider the toy example circuits in Fig. 2a and b. Both are described with MNA (2) and the (arbitrary) parameters R = 1Ω, L = 5H, C = 1F, $i_{\mathrm {s}}(t)=\sin {}(2t)+5\sin {}(20t)$ and $v_{\mathrm {s}}(t)=\sin {}(t)+\sin {}(20t)$ are set. The eddy current Eq. (1) is solved on the single phase isolation transformer shown in Fig. 1. For simplicity, a zero current is imposed on the secondary coil (dark orange) and only the primary coil is coupled to the circuit.

Fig. 1

Single phase isolation transformer (‘MyTransformer’), see [9]

Fig. 2

Field/circuit coupling with model from Fig. 1 (CVR path is dashed). (a) Convergent case. (b) Divergent case

The WR algorithm is applied on the simulation time window $\mathscr {I} = [0\;0.8]\,$s and the internal time integration is performed with the implicit Euler scheme with time step size δt = 10⁻² s. The theoretical result is illustrated by the successful simulation, see Fig. 3a, of the model shown in Fig. 2a which satisfies the convergence criterion of Theorem 8. However, numerical simulations of the model shown in Fig. 2b show that WR can diverge indeed if the criterion is not satisfied (Fig. 3).

Fig. 3

Monolithic (“mon”) and WR solution for k = 1, 2 iterations. (a) Convergent case. (b) Divergent case

5 Conclusions

In this work, we have presented a space-discretised coupled field/circuit model, which is a DAE of index 2, and a simulation of this model by means of WR. Furthermore, we have provided an easy-to-check topological convergence criterion for a class of coupled DAE/DAE systems of index 2.