1 What Makes Galaxy Clusters Interesting for Testing Gravity?

Put simply, a galaxy cluster is a self-gravitating system built out of dark matter, hot gas and baryonic tracers in the form of galaxies. What makes galaxy clusters attractive as tests of gravity is that they lie on the borderline between astrophysical and cosmological scales, allowing to test different aspects and predictions of gravity theories.

Traditionally, the combination of kinematical/dynamical measurements in a cluster with lensing observations allows to reconstruct the underlying mass distribution. In General Relativity (GR) the two are expected to be the same, however, this is no longer true within general families of theories beyond GR which predict that pressureless matter and light respond differently to gravity, in turn implying different predictions for the cluster’s inferred dynamical/kinematical and lensing mass profiles. This idea has formed the basis for the construction of consistency checks studied predominantly within scalar-tensor theories such as f(R), Brans–Dicke and (Beyond Horndeski) theories.

Disentangling genuine gravitational effects from the complicated astrophysical processes at cluster scales is, however, a subtle task and requires an adequate knowledge of the underlying systematics. In addition, since the bulk of the cluster’s mass comes from dark matter, an adequate modelling of the dark matter density distribution is necessary, which proves challenging without knowledge of the actual physics of the dark sector. Therefore, the underlying assumptions for constraints on gravity in this regard have to be challenged and testes before conclusive statements are to be made.

Our goal here is to briefly review progress on the methods and constraints on theories beyond GR with the physics of galaxy clusters, along with a discussion on the associated hurdles from astrophysical and observational systematics.

2 Consistency Conditions Based on the Mass Profiles of Galaxy Clusters

2.1 Generalities

It is instructive to start with a recap of some useful concepts from cosmological perturbation theory. In galaxy clusters, matter collapses in a non-linear fashion, however, gravity remains linear implying that, the gravitational wells are sufficiently small for linear perturbation theory to hold. In this regard, the Poisson equation relates the Newtonian potential \(\Psi \) to the matter density as \(\nabla ^2 \Psi = 8 \pi G_N \rho _{m}\), while the gravitational slip parameter relates \(\Psi \) to the relativistic potential \(\Phi \) through the gravitational slip parameter \(\eta \equiv \Psi /\Phi \). The weak-lensing potential satisfies a Poisson-like equation as \(\nabla ^{2}(\Phi + \Psi ) = 8 \pi G_N \rho _{lens}\), where \(\rho _{lens}\) is the matter density inferred through lensing probes—we will get back to this later.

Hydrostatic equilibrium in a galaxy cluster is achieved through the balance between gravity and the gas pressure as

$$\begin{aligned} \frac{d P_{\text {tot.}}}{dr} = \rho _{\text {gas}}\frac{d \Psi }{dr}, \end{aligned}$$
(36.1)

with the total pressure given by the sum of thermal and non-thermal pressure \(P_{\text {tot.}} = P_{\text {therm.}} +P _{\text {non-therm.}}\). The thermal pressure comes predominantly from the hot gas, as \(P_{\text {therm.}} = n_{\text {gas}} k T_{\text {gas}}\). Writing \(d \Psi /dr = G_N M(r)/r^2\), Eq. (36.1) then provides a definition of the (non-)thermal mass profile. The bulk of the pressureless matter sourcing the potential \(\Psi \) comes from dark matter. The most popular density profile to model it is the Navarro–Frenk–White (NFW), which is a 2-parameter profile depending on a characteristic density and radius as

$$\begin{aligned} \rho _{\text {NFW}} = \frac{\rho _{s}}{(r/r_s)(1 + r/r_s)^2}, \; \; \; \; \rho _s \equiv \frac{1}{3} \cdot \frac{\rho _{c}(z) \Delta _{\text {vir}} \cdot c^3}{\log (1+c) - c(1+c)^{-1}}, \end{aligned}$$
(36.2)

with \(\rho _{c} \equiv 3H^{2}(z)/(8 \pi G_N)\) corresponds to the critical density of the Universe. The concentration parameter, \(c \equiv r_{\text {vir}}/r_{s}\), relates the viral radius with the scale \(r_s\), with the former defining the region of the cluster that encloses a mean over density equal to \(\rho _{c} \Delta _{\text {vir}}\). The popularity of the NFW profile relies in that it provides a good fit to haloes within N-body simulations, and for large range of masses both in Newtonian and modified gravity. In particular, Ref. [1] showed that the NFW profile provides equally good fits to N-body simulations in f(R) gravity as the standard Newtonian case, which was later confirmed by Ref. [2] considering the particular case of the Hu-Sawicki f(R) model. Since here we will be mostly interested in constraints on the theory space of modified gravity, for more details on actual the hallo modelling beyond GR we refer to [1,2,3,4,5].

2.2 Probes Based on Mass Profiles from Galaxy Kinematics and Lensing

Under the assumption of spherical symmetry, the Poisson equations for the potentials \(\Psi \) and \(\Phi + \Psi \) allow us to derive the following expressions

$$\begin{aligned}&\Psi (r) = G_N \int _{r_0}^{r} \frac{ds}{s^2} M_{dyn}(s), \end{aligned}$$
(36.3)
$$\begin{aligned}&\Phi (r) = G_N \int ^r \frac{ds}{s^2} \left( 2M_{lens} - M_{dyn} \right) . \end{aligned}$$
(36.4)

Equation (36.3) serves as a definition of the dynamical mass of the cluster, i.e the mass inferred from dynamical probes, while it is easy to see that for the lensing mass \(M_{lens} = \frac{r^2}{2G} \frac{d}{dr} (\Phi + \Psi )\). Assuming that member galaxies are collision less tracers of the underlying gravitational field \(\Psi \), their velocity dispersion field satisfyies the Jeans equation

$$\begin{aligned} \frac{\partial (\nu \sigma _r^2)}{\partial t}+2\beta (r)\frac{\nu \sigma ^2_r}{r}=-\nu (r)\frac{\partial \Psi }{\partial r} \, , \end{aligned}$$
(36.5)

where \(\nu (r)\) is the number density of tracers, \(\sigma ^2_r\) the velocity dispersion along the radial direction and \(\beta \equiv 1-(\sigma _{\theta }^2+\sigma ^2_{\phi })/2\sigma ^2_r\) the velocity anisotropy profile. The latter, accounts for the neglected velocity component in along-the-light-of-sight observations, and it introduces an important source of uncertainty which has to be accounted for, as we will discuss in Sect. 36.3. In principle, the choice of \(\nu (r)\) is also model dependent and its effect on any constraints needs to be investigated.

The combination of lensing and dynamics of a galaxy cluster can provide a powerful test based on the gravitational slip parameter \(\eta \). Combining (36.3) and (36.4) we may derive an expression for the gravitational slip in terms of the dynamical and lensing mass profiles as

$$\begin{aligned} \eta (r) =\frac{\int ^r \frac{ds}{s^2}\left[ 2M_{\text {lens}}(s)-M_{\text {dyn}}(s)\right] }{\int ^r \frac{ds}{s^2}M_{\text {dyn}}(s)} \, . \end{aligned}$$
(36.6)

Therefore, the existence of gravitational slip can be viewed as a consistency condition between the dynamical and lensing mass of the cluster—In GR, and in the presence of perfect fluid matter, it is \(M_{dyn} = M_{lens}\) and \(\eta = 1\), but this is not true anymore as soon as gravity is modified. In this view, the existence of new gravitational degrees of freedom will manifest itself as a tension in the mass profile inferred from kinematics and lensing.

The above idea formed the basis of Ref. [6] which combined kinematical and lensing observations of the relaxed cluster MACS J1206.2-0847 (hereafter MACS 1206), at redshift \(z=0.44\) (at redshift \(z = 0.44\)) from the CLASHFootnote 1 and CLASH-VLTFootnote 2 surveys to reconstruct the slip parameter \(\eta \) as a function of the distance from the cluster’s center. In particular, it considered line-of-sight velocity measurements and projected positions for 592 member galaxies to perform a phase-space analysis using the code MAMPOSSt of Ref. [7], which solves the Jeans equation (36.5) to provide a maximum likelihood fit to the mass profile parameters. Assuming an NFW profile, a model for \(\beta (r)\), and a Newtonian form for \(\Psi \), combination of dynamics and lensing led to the constraint

$$\begin{aligned} \eta (r = 1.96 \text {Mpc}) = 1.00^{+0.31}_{-0.28} \; (\text {statistical}) \pm 0.35 \; (\text {systematic}). \end{aligned}$$
(36.7)

The assumption of the NFW profile for the total matter distribution was challenged by repeating the analysis with an Hernquist and Burkert profile, where it was found that NFW provided the highest likelihood fit to the kinematic data. The same concept was followed in Ref. [8], which forecasted the ability of galaxy clusters to constraint \(\eta \) using the procedure outlined above. In particular, dynamical mass profiles were re-constructed from a set of 15 spherical mock clusters in equilibrium solving (36.5), followed by a maximum likelihood analysis for the NFW parameters \((r_s, r_{200})\). Lensing information was simulated from the based on the observations of MACS 1206. Results showed that \(\eta \) can be constrained at the \({\sim }9 \%\) level (\(2 \sigma \)) when assumed to be scale-independent, and at \(21 \%\) when scale-dependence is accounted for.

Reference [9] implemented a similar combination of kinematics and lensing for MACS1206 with real data, but introducing the effect of the fifth-force in the gravitational potential within f(R) gravity and a simplified approach for screening. Under the assumption of an NFW profile and the form of the anisotropy profile, it quoted the upper bound on the fifth force’s Compton wavelength as

$$\begin{aligned} \lambda _{f(R)} \le 1.61\; (\text {statistical}) + 0.30 \; (\text {systematic}) \; \; \text {Mpc}. \end{aligned}$$
(36.8)

Notice that, \(\lambda _{f(R)}\) is related to the mass of the scalar field as \(\lambda _{f(R)} \sim 1/ m^{2}_{f(R)} \sim f_{RR}\).

We notice that, constraints on gravity from statistics of a sample of galaxy clusters should be in principle weighted over an appropriate mass function. In fact, the abundance of clusters in modified gravity have provided tight constraints on the allowed theory space of f(R) scalar-tensor theories, since the fifth force modifies the collapse of matter at large scales, leading to an enhancement of the mass function. This has been the topic of investigation in Refs. [10,11,12,13,14,15,16]. In particular, Ref. [12] combined geometrical probes with CMB and cluster abundance data to quote an upper bound on the parameter B related to the scalaron’s Compton wavelengthFootnote 3 for the so-called designer f(R) model as \(B(z = 0) < 1.1 \cdot 10^{-3}\) (\(95 \% \; \text {C.L}\)). An updated analysis using a similar combination of observables and galaxy clusters up to \(z \sim 0.5\) derived the tighter constraint \(B(z= 0) < 1.78 \cdot 10^{-4}\) (\(95.4 \% \; \text {C.L}\)) [14]. It should be noticed that, the designer model does not assume a fixed, a priori functional form for f(R), but rather fixes it implicitly by requiring that the predicted background evolution of the Universe matches with observations.

2.3 Probes Based on Thermal and Lensing Mass Profiles

An alternative route to test scalar-tensor theories with a conformal coupling between the scalar field and curvature, such as Brans–Dicke or f(R) theories, can be followed through the construction of tests based on the cluster’s thermal and lensing mass. In particular, the coupling between the scalar field and matter is expected to have a direct impact on the cluster’s inferred thermal mass, but not on the lensing one, since photons travel on null geodesics. This is the main idea followed in [17], which considered the phenomenological implications of the coupling between the chameleon scalar field with the baryonic and dark matter component in the cluster.

The chameleon field is sourced by the scalar potential and matter density according to

$$\begin{aligned} \nabla ^2 \phi = \frac{\partial V(\phi )}{\partial \phi } + \beta \sqrt{8\pi G_N} \rho e^{\beta \sqrt{8\pi G_N} \phi }, \end{aligned}$$
(36.9)

with \(\beta \) a dimensionless coupling strength, and \( \beta = 1/\sqrt{6}\) for the case of f(R) gravity. Sufficiently deep within the cluster, \(\nabla ^2 \phi \approx 0\), and the scalar field acquires a minimum, \(\phi _{0}\). In this region, the fifth-force is screened. Towards the outskirts of the cluster, a sizeable field gradient builds up, leading to a fifth-force effect with \(F_{\phi } = - \beta \sqrt{8\pi G_N} \frac{d\phi }{dr}\). The contribution of the fifth-force to the r.h.s of the hydrostatic equilibrium (36.1) will in turn affect the gas and temperature profiles of the cluster. Typically, one assumes that outside the cluster the chameleon scalar acquires its ambient cosmological value, \(\phi _{cosm.}\), which is the free, model parameter to be constrained. In the language of f(R) gravity,

$$\begin{aligned} \frac{\partial f}{\partial R} \equiv f_{R} = - \sqrt{\frac{16\pi G_N}{3}} \phi . \end{aligned}$$
(36.10)

Reference [17] started with a generalised NFW profile for dark matter, \(\rho = \rho _{s}/\left[ (r/r_s) (1 + r/r_s)\right] ^b\), and a polytropic one for the gas. In the presence of the chameleon field, the gas distribution becomes steeper at the outskirts of the cluster (compared to GR), where the fifth force is operative. From an observational viewpoint, this in turn causes a decrease in the predicted X-ray surface brightness of the cluster at large radii. Using the X-ray temperature profile observations from the Hydra A cluster, Ref. [17] was able to derive the bound \(\phi _{cosm.} < 10^{-4}/\sqrt{8\pi G_N}\) (at redshift \(z = 0\)) assuming \(\beta = 1\). Notice that, this result is insensitive to the details of the potential \(V(\phi )\).

The case of f(R) gravity (\(\beta = 1/\sqrt{6}\)) was studied with a more thorough analysis in [18] adopting a conceptually similar strategy. The work reconstructed the 3-dimensional X-ray temperature and surface brightness profiles, as well as the expected Sunyaev–Zel’dovich (SZ) effect in the presence of the chameleon force under sufficiently general assumptions for the modeling of the gas temperature profile and pressure. With the aid of an MCMC analysis, and the observations of the Coma cluster, the best-fit values for the gas/dark-matter and modified gravity parameter space were inferred, leading to the \(2\sigma \) constraints \(\phi _{cosm.} \lesssim 7 \cdot 10^{-5} /\sqrt{8\pi G_N}\). Under (36.10) this translates to

$$\begin{aligned} f_{R_0} \lesssim 6 \cdot 10^{-5}. \end{aligned}$$
(36.11)

In a similar context, Ref. [19] extended the analysis for multiple clusters, analysing 58 stacked cluster profiles observed within \(0.1< z < 1.2\), using X-ray and lensing data from the XMM Cluster Survey and the Canada France Hawaii Telescope Lensing Survey respectively. It is important that, the clusters were found to be living in unscreened environments, since otherwise the fifth force would be environmentally screened. The analysis concluded that, \(f_{R_0} \lesssim 6 \cdot 10^{-5}\) at \(2\sigma \). The methodology of the latter works was further verified in [20], through the study of hydrodynamical simulations in f(R) gravity. Most notably, it confirmed the validity of the NFW profile when modelling weak-lensing mass profiles in f(R) gravity and the spherical symmetry of the stacked cluster profiles.

Galaxy clusters have been also employed to probe a broader part of the theory space of scalar-tensor theories, beyond a conformal coupling. In particular, the so-called Beyond Hortndeski theories have been shown to exhibit an intriguing breaking of the Vainshtein mechanism within compact matter sources such as stars or galaxy clusters. A fundamental difference with conformally-coupled theories is that, here, lensing is directly affected by the fifth force. In particular, for the Beyond Horndeski theories exhibiting a breaking of the Vainshtein mechanism, the two scalar gravitational potentials within a compact object  can be shown to be,

$$\begin{aligned}&\frac{d \Psi (r)}{dr} = - \frac{G_N M(r)}{r^2} + \frac{Y_{1} G_N}{4} \cdot \frac{d^{2} M(r)}{dr^2}, \end{aligned}$$
(36.12)
$$\begin{aligned}&\frac{d \Phi (r)}{dr} = - \frac{G_N M(r)}{r^2} + \frac{5 Y_{2} G_N}{4 r} \cdot \frac{d M(r)}{dr}, \end{aligned}$$
(36.13)

where \(Y_1\) and \(Y_2\) are dimensionless couplings. For \(Y_1 = 0 = Y_2\) the standard expressions are recovered. The gas in the cluster responds to \(\Psi \), hence will be sensitive to \(Y_1\), whereas the lensing potential will probe both \(Y_1, Y_2\). Reference [21] used the same data and methodology of [19] for the modelling of the X-ray and lensing profiles to produce stacked profiles of 58 clusters. A simultaneous fit of the X-ray and lensing to the data with an MCMC analysis, lead to the following constraints for the fifth-force couplings,

$$\begin{aligned} Y_{1} = -0.11^{+0.93}_{-0.67} \; \; \; \text {and} \; \; \; Y_{2} = -0.22^{+1.22}_{-1.19}. \end{aligned}$$
(36.14)

In the context of Beyond Horndeski theories it has been also investigated whether the fifth force associated with the breaking of Vainshtein mechanism could mimic the effect of dark matter in galaxy clusters. In particular, Ref. [22] considered a sample of galaxy clusters from the CLASH survey, and reconstructed their gas density from the observed X-ray profiles. It was then shown that for the particular sample of clusters, and assuming a \(\Lambda CDM\) background cosmology, the model can provide a good fit to the lensing of observations without the introduction of dark matter component. In a similar follow up analysis by the same authors, and assuming that \(Y_1 = Y_2\), an upper bound at \(2\sigma \) was derived as [23]

$$\begin{aligned} Y_{1} \le 0.16. \end{aligned}$$
(36.15)

3 A Brief Discussion on Systematics

The previously discussed constraints rely on various simplifications regarding the modeling of the cluster, e.g the assumption of relaxation. Departures from these assumptions in realistic observations introduce systematics which need to be accounted for, if constraints need to be consistent and robust. Here, we will briefly discuss the impact of such systematics.

The Jean’s equation is a powerful method to infer the local potential \(\Phi \) in the cluster, however, applications of the method are limited by observational constraints, such as the fact that only the velocity dispersion along the line of sight \(\sigma ^2_r\) and the projected number density profile of galaxies can be measured directly. Tangential velocities are generally small and direct measurements of the velocity anisotropy are complicated. To infer \(\beta (r)\) one can proceeds parametrically, assuming a model for the anisotropy and determining the parameters of the profile along with the mass profile with a Maximum Likelihood fit to the data (see e.g. Ref. [24]). Nevertheless, some non-parametric techniques based on inverting the Jeans’ equation can be found in literature (e.g., Refs. [25, 26]), but their application generally requires additional information and assumptions. From both observations of galaxy clusters (e.g., Ref. [27]) and analyses of halos in cosmological simulations (e.g., Refs. [28, 29]) it has been found that generally orbits tend to be isotropic in the center (i.e. \(\beta =0\)) while the anisotropy grows with radius.

Fig. 36.1
figure 1

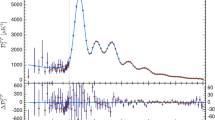
From Fig. 3 of Ref. [30]: constraints on \(\eta (r)\) obtained for the CLASH galaxy cluster MACS 1206 combining lensing and dynamics mass profile determinations. The mass profile is parametrized as a NFW model; different lines correspond to different ansatz in the velocity anisotropy parametrisation. The red shaded area indicates the region between the 16th and 84th percentile for the reference model, “O” profile

Full size image

In Fig. 36.1 (right panel of Fig. 3 in Ref. [30]) we show the constraints on the gravitational slip, obtained by combining lensing and dynamics mass profiles of the cluster MACS 1206 by Ref. [30], changing the parametrisation of the velocity anisotropy profile in the dynamical analysis. All the three models used in the fit—the constant anisotropy “C”, the Tiret model “T” of Ref. [31] and the Opposite model “O” of Ref. [24]—produce bounds on \(\eta \) in agreement within the 68% C.L. given the current uncertainties. However, with the expected precision achievable from future surveys (see below), these effects would become a relevant source of systematics.

A natural question arising when reconstructing mass profiles through a Jeans analysis is the dependence of the results on the number of tracers considered, since realistic observations typically come with a restricted number of spectroscopic velocity measurements. In addition, understanding of this may aid the optimisation of future cluster surveys. This question was investigated [8] in the context of forecasting constraints on \(\eta \) with future surveys, through a combination of simulated kinematical and lensing information. It was found that, keeping the NFW parameters fixed and assuming a scale-independent \(\eta \), the effect on the forecasted errors is moderate when varying the tracers number between \(100 \le N_{\text {galaxies}} \le 500\), while it becomes practically negligible for \(N_{\text {galaxies}} > 500\).

Departures from dynamical relaxation and spherical symmetry produce a bias in the estimation of the mass profile, introducing systematics in the constraints of modified gravity parameters. In particular, this has been shown in Ref. [32], which performed a detailed study on cosmological N-body simulations showing a strong correlation between the constraints in modified gravity models and the effect of the aforementioned departures; the analysis further identified two observational criteria, linked to the cluster’s dynamical properties, to be used in the selection of those clusters suitable for the application of this kind of methods. Moreover the assumption of dynamical equilibrium limits the validity of the Jeans’ equation out to the virial radius, which at \(z=0\) corresponds to the radius \(r_{200}\). It is possible to employ other techniques which doesn’t rely on the dynamical state of the cluster and thus they can be used to reconstruct the mass profile in more external regions \(r>r_{200}\) (e.g., the Caustic method of Ref. [33]); nevertheless, these methods suffer different kinds of systematics, and the application can be more or less appropriate with respect to the Jeans’ analysis depending on the case studied.

It is worth to notice that since both galaxies and the hot X-ray emitting gas of the Intra Cluster Medium (ICM) perceive the same gravitational potential, the two methods for reconstructing the mass profile are sensitive in the same way to modification of gravity. However, diffuse gas and galaxies dynamics suffer different systematics; for instance non-thermal pressure, e.g. associated with unthermalized gas motions, leads to a biased estimate of the cluster mass from X-ray analyses compared to other methods (see, e.g., Ref. [34] and references therein, Ref. [35]), especially in the cluster outskirts where the contribution of non-thermal pressure becomes large (e.g., Ref. [36]).

Moreover, analyses based on the dynamics of cluster member galaxies allow to constrain the gravitational potential out to the virial radius \(r_{200}\) (or beyond, as discussed above) while X-ray observations are generally limited to \(r_{500}\); in addition, gas clumping produces biased X-ray measurements in the outskirt of galaxy clusters (see, e.g., Ref. [37]). Clearly, combined X-ray and Jeans’ analyses to infer the gravitational potential in the central region of relaxed clusters could in principle help in tightening the constraints on the inner shape of the mass profile and to break possible degeneracies between the dynamical parameters and additional degrees of freedom in non-standard theories of gravity.

Finally, as regards tests based on the slip parameter \(\eta \), it is worth pointing out that \(\eta = 1\) in GR only if relativistic corrections to the gravitational potentials \(\Psi \) and \(\Phi \) can be neglected. In fact, future constraints of \(\eta \) based on galaxy cluster observations are expected to bring the statistical uncertainties down to few percents. At this level of precision, tiny departures form \(\Psi =\Phi \) sourced by non-linear effects in GR, and not by a modification of gravity, are no more negligible and could constitute a severe limitation of the measurements of \(\eta \). The contribution of these relativistic terms should be taken into account as systematic effect from future analyses.

4 Future Outlook

In the next years, new generation surveys will provide a significant amount of imaging and spectroscopic data covering a large portion of the sky, within a broad redshift range. Both ground-based (e.g., LSST and space-borne telescopes (e.g., Euclid are expected to observe several billions galaxies in different bands, aiming at probing the nature of dark energy and gravity at large scales. In particular, the forecasting analysis of Ref. [38] showed that Euclid’s weak lensing measurements will be able to tighten the constraints on MG parameters placed by the Planck satellite mission by two orders of magnitude.

As for mass determinations of galaxy clusters, the combination of data from the aforementioned surveys with spectroscopic observations coming from next generation high-multiplexing spectrographs on 8m-class telescopes will provide joint dynamics and lensing mass reconstruction of thousands clusters. The signal-to-noise ratio will be much lower than what has been already achieved by current surveys such as the CLASH and CLASH-VLT. Therefore, a good understanding of systematic effects, as discussed in the previous section, is required in order to take full advantage of galaxy cluster analyses for testing gravity on cosmological scales.