Abstract
Protecting the privacy of voters is a basic requirement of any electronic voting scheme, and formal definitions can be used to prove that a scheme satisfies privacy. In this work, we provide new game-based definitions of ballot secrecy for electronic voting schemes. First, we propose an intuitive definition in the honest model, i.e., a model in which all election officials are honest. Then, we show that this definition can be easily extended to the malicious ballot box setting and a setting that allows for a distributed tallier. In fact, to the best of our knowledge, we provide the first game-based definition of ballot secrecy that models both a malicious ballot box and a malicious subset of talliers. We demonstrate that our definitions of ballot secrecy are satisfiable, defining electronic voting scheme constructions which we prove satisfy our definitions. Finally, we revisit existing definitions, exploring their limitations and contextualising our contributions to the field.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Voter privacy ensures that a voter can participate in democratic processes without risk of intimidation or blackmail, and is regarded as a basic requirement in many elections.Footnote 1 At a fundamental level, voter privacy is defined as ballot secrecy, which intuitively states that a voter’s vote remains secret throughout the election, except when the result of the election reveals the vote, for example, in the event of a unanimous result. Stronger notions of privacy exist [23], including receipt-freeness and coercion-resistance but, in this work, we restrict discussion to the basic requirement of ballot secrecy.
Rigorous definitions of privacy have been proposed in the literature, the most common of which are game-based definitions. Early game-based definitions [4, 5] follow the well-established route of indistinguishability experiments (such as, for example, \(\mathsf {IND}\text {-}\mathsf {CPA}\) for public key encryption [27]). That is, an adversary must distinguish two different election views, when provided with a result computed with respect to the viewed election. Informally, we refer to this approach as the Benaloh approach, recognising the fact that Benaloh established this approach in early works [4, 5].Footnote 2 The Benaloh approach is utilised in a number of ballot secrecy definitions [10, 11, 19, 30]. However, to address the fact that the Benaloh approach limits the class of voting result functions that can be considered (see Sect. 5), a separate line of research departed from this approach, focusing instead on definitions that provide an adversary with a view of a ‘real’ election or a ‘fake’ election [7,8,9, 16, 20]. Here, the adversary is always provided with a tally computed with respect to the ‘real’ election. In particular, this approach is favoured by \(\mathsf {BPRIV}\) [7], a highly-regarded definition of ballot secrecy. More generally, the majority of game-based definitions of ballot secrecy position themselves in the so-called honest model. That is, they consider all election officials to be trusted. With respect to formal definitions, the consideration of the malicious setting is a young area of research and has focused on a malicious ballot box [11, 19, 20].
1.1 Our Contributions
New Definitions of Ballot Secrecy. In this work, we revisit the approach taken in [5] and present new definitions of ballot secrecy. We choose this approach due to the well-established, intuitive nature of indistinguishability experiments. Moreover, though we recognise that the Benaloh approach limits the class of result functions considered, an issue that we explore in Sect. 3 and Sect. 5, the Benaloh approach, and our definitions specifically, provides a number of advantages over existing definitions, which we discuss below.
First, we define \(\mathsf {BS}\), a definition of ballot secrecy in the honest model (Sect. 3). \(\mathsf {BS}\) builds upon [5], capturing several additional functionalities. First of all, \(\mathsf {BS}\) models e-voting schemes with a registration phase. That is, eligible voters are provided with a credential that is required to cast a ballot. Voter registration is not modelled in [5] or subsequent, related, definitions [10, 11] and, hence, \(\mathsf {BS}\) is the first definition that follows this approach to model voter registration. This reflects how advanced e-voting schemes are modelled, for example, Belenios [2, 17] and Civitas [14, 15]. Secondly, \(\mathsf {BS}\) allows for adaptive corruption of voters. Previous game-based definitions that model registration of voters are limited to static corruption of voters only [16, 19] or allow for voters to cast only a single ballot [30]. Therefore, \(\mathsf {BS}\) improves upon existing definitions in the honest model by modelling registration of voters and adaptive corruption of voters.
Our second definition, \(\mathsf {mbbBS}\), extends \(\mathsf {BS}\) to the malicious ballot box setting (Sect. 4.1). \(\mathsf {mbbBS}\) is similar to the definition presented in [11], which also adopts the approach of [5]. However, contrary to [11], and similarly to \(\mathsf {BS}\), \(\mathsf {mbbBS}\) models registration of voters. Our model for \(\mathsf {mbbBS}\) captures static corruption of voters only, a consequence of using the Benaloh approach, as we will explain in Sect. 4.1. We note, however, that all ballot secrecy definitions that model voter registration in the malicious ballot box setting only capture static voter corruption [19, 20].
Finally, we define \(\mathsf {dtBS}\), which, to the best of our knowledge, is the first ballot secrecy definition that models a malicious ballot box and a distributed tallier, in which the adversary corrupts a subset of talliers (Sect. 4.2). \(\mathsf {dtBS}\) extends \(\mathsf {mbbBS}\) to model an adversary that corrupts a subset of talliers. Like \(\mathsf {mbbBS}\), \(\mathsf {dtBS}\) considers static corruption of voters. Given that the malicious setting has received significantly less attention than the honest model, and a malicious tallier has not been explored, we believe that definitions in the malicious model, such as \(\mathsf {dtBS}\), are valuable and desirable. In particular, Helios [28] distributes the role of the tallier, yet proofs of ballot secrecy for Helios model the tallier as a single entity [7, 17]. As such, we see \(\mathsf {dtBS}\) as an important step towards formal proofs of security under realistic trust assumptions.
Feasibility of Our Definitions. For all of our definitions, we show feasibility, proving that our definitions can be satisfied. Specifically, we define an e-voting scheme \(\varGamma _{\mathsf {mini}}\), and prove it satisfies \(\mathsf {BS}\) and \(\mathsf {mbbBS}\). We then extend \(\varGamma _{\mathsf {mini}}\) to a setting with a distributed tallier, in a construction that we call \(\varGamma _{\mathsf {mini}}'\), and prove that it satisfies \(\mathsf {dtBS}\). Our scheme \(\varGamma _{\mathsf {mini}}\) is a simple construction; specifically, it is not verifiable. However, \(\varGamma _{\mathsf {mini}}\) can be used to prove the security of real, verifiable, e-voting schemes, similarly to how minivoting was used to prove ballot secrecy of Helios in [8].Footnote 3 Indeed, using the technique of [8], \(\varGamma _{\mathsf {mini}}\) can also be extended to a generic, Helios-like, e-voting protocol which can be shown to satisfy our notions of ballot secrecy if \(\varGamma _{\mathsf {mini}}\) satisfies ballot secrecy (and the verification process is secure). As such, though we simply demonstrate feasibility, our definitions can be applied to practical e-voting schemes.
Contextualising Our Definitions. Finally, we compare ballot secrecy definitions, with the goal of better understanding the limitations of definitions. In particular, we discuss related work and place our definitions in the context of the existing literature in Sect. 5. It emerges that our definitions provide an advantage with respect to extendibility, when compared to \(\mathsf {BPRIV}\). Moreover, our definitions improve upon existing definitions that follow the Benaloh approach, particularly with respect to the attacker model.
2 Preliminaries
Notation. We write \(x\leftarrow X\) to denote assignment of X to x. We use standard set notation and write \(\{\{x_1,\dots ,x_n\}\}\) to denote a multiset consisting of elements \(x_1,\dots ,x_n\), writing \(\{\{\}\}\) to denote the empty multiset. Additionally, we write \(L=(x_1,\dots ,x_n)\) to denote a list L with entries \(x_1,\dots ,x_n\), and write \(L\leftarrow L||y\) to denote appending y to the list L. We let \(A(x_1, \dots , x_n; c)\) denote the output of algorithm A on inputs \(x_1, \dots , x_n\) and coins c. Generally, we omit coins and simply write \(A(x_1, \dots , x_n)\). Moreover, we write \(A^\mathcal {O}\) to denote algorithm A with oracle access to \(\mathcal {O}\).
We provide syntax for a single-pass e-voting scheme, which requires a voter to post a single message in order to cast a vote. We consider that an e-voting scheme is defined relative to a result functionFootnote 4 \(f: (\mathcal {V}\times \mathcal {C})^*\rightarrow R\), where \(\mathcal {V} = \{id_1, \dots , id_{n_v}\}\) is the set of \(n_v\) eligible voters, \(\mathcal {C}=\{1,\dots ,n_c\}\) is the set of \(n_c\) candidates, and R is the result space of the election. Informally, our syntax captures an e-voting scheme with the following structure. Firstly, an election administrator publishes public parameters of the scheme. Then, a registrar provides eligible voters with a public and private credential and adds public credentials to a set \(\mathcal {L}\). Voters cast ballots that are linked to their public credential, and a ballot box manager processes and posts ballots to a ballot box \(\mathcal {BB}_{}\). We assume that the ballot box is private and the ballot box manager publishes a public view of the ballot box, known as the bulletin board, \(\mathcal {PBB}_{}\). Finally, the tallier computes and publishes the result of the election with a proof of correct tallying that can be verified by anyone. We formally define the syntax of an e-voting scheme, adapted from the syntax of [7, 12], in Definition 1.
Definition 1
(E-voting scheme). An e-voting scheme \(\varGamma \) for a result function f is a tuple of probabilistic polynomial-time (PPT) algorithms \((\mathsf {Setup},\mathsf {Register},\mathsf {Vote},\mathsf {Valid},\mathsf {Append},\mathsf {Publish},\mathsf {Tally},\mathsf {Verify})\) such that:
-
 On input security parameter
On input security parameter
 , algorithm \(\mathsf {Setup}\) initialises set \(\mathcal {L}\) and ballot box \(\mathcal {BB}_{}\) as empty. \(\mathsf {Setup}\) outputs an public/private election key pair (pk, sk). We assume that pk includes the sets \(\mathcal {V}\) and \(\mathcal {C}\).
, algorithm \(\mathsf {Setup}\) initialises set \(\mathcal {L}\) and ballot box \(\mathcal {BB}_{}\) as empty. \(\mathsf {Setup}\) outputs an public/private election key pair (pk, sk). We assume that pk includes the sets \(\mathcal {V}\) and \(\mathcal {C}\). -
\(\mathsf {Register}(id_{},\mathcal {L},pk)\) On input voter identity \(id_{}\), set \(\mathcal {L}\) and pk, algorithm \(\mathsf {Register}\) outputs a public/private credential pair \((pk_{id_{}},sk_{id_{}})\) and updates set \(\mathcal {L}\) with \(pk_{id_{}}\) such that \(\mathcal {L}\leftarrow \mathcal {L}\cup \{pk_{id_{}}\}\).
-
\(\mathsf {Vote}(v,pk_{id_{}},sk_{id_{}},pk)\) On input vote v, \(pk_{id_{}}\), \(sk_{id_{}}\) and pk, algorithm \(\mathsf {Vote}\) outputs a ballot b that includes the voter’s public credential.
-
\(\mathsf {Valid}(b,\mathcal {BB}_{,}\mathcal {L},pk)\) On input ballot b, ballot box \(\mathcal {BB}_{,}\) set \(\mathcal {L}\) and pk, algorithm \(\mathsf {Valid}\) outputs 1 if ballot b is accepted to ballot box \(\mathcal {BB}_{}\), and 0 otherwise.
-
\(\mathsf {Append}(b,\mathcal {BB}_{},\mathcal {L},pk)\) On input b, \(\mathcal {BB}_{,}\) set \(\mathcal {L}\) and pk, algorithm \(\mathsf {Append}\) outputs the updated ballot box to include ballot b.
-
\(\mathsf {Publish}(\mathcal {BB}_{})\) On input \(\mathcal {BB}_{,}\) algorithm \(\mathsf {Publish}\) outputs bulletin board \(\mathcal {PBB}_{.}\)
-
\(\mathsf {Tally}(\mathcal {BB}_{,}\mathcal {L},sk)\) On input \(\mathcal {BB}_{,}\) set \(\mathcal {L}\) and sk, algorithm \(\mathsf {Tally}\) computes and outputs the election result \(r\in R\) with a proof \(\pi \) that the result is correct.
-
\(\mathsf {Verify}(\mathcal {BB}_{,}\mathcal {L},r,\pi ,pk)\) On input \(\mathcal {BB}_{,}\) set \(\mathcal {L}\), result \(r\), proof \(\pi \) and pk, algorithm \(\mathsf {Verify}\) outputs 1 if the election result verifies, and 0 otherwise.
E-voting schemes must satisfy correctness, which requires that the result output by algorithm \(\mathsf {Tally}\) is equivalent to result function f applied to all votes input to algorithm \(\mathsf {Vote}\).
Definition 2
(Correctness). An e-voting scheme \(\varGamma \) defined with respect to a result function f is correct if, for any set of \(n_v\) voters \(\mathcal {V} = \{id_1, \dots , id_{n_v}\}\) and votes \(v_1,\dots ,v_{n_v}\in \mathcal {C}\), there exists a negligible function
 such that
such that

3 Ballot Secrecy in the Honest Model
We introduce \(\mathsf {BS}\), a definition of ballot secrecy in which an adversary can adaptively corrupt voters, submitting ballots on their behalf, and can submit two votes (the left and right vote) on behalf of honest voters. Thus, \(\mathsf {BS}\) describes an experiment in which an adversary is provided with access to a bulletin board, and the corresponding election result, that consists of ballots for the left or right vote submitted on behalf of honest voters, in addition to ballots submitted on behalf of corrupted voters. If the adversary cannot determine whether the bulletin board and result contains the left or right votes submitted by honest voters, a scheme is said to satisfy \(\mathsf {BS}\).
\(\mathsf {BS}\) requires a balancing condition to ensure that the adversary cannot trivially distinguish views. For example, an adversary in the \(\mathsf {BS}\) experiment could submit ‘0’ as the left vote and ‘1’ as the right vote on behalf of all honest voters. Then, the election result allows the adversary to trivially distinguish the two possible views. We define our balancing condition to prevent such trivial distinctions, and to model adaptive voter corruption. We first describe \(\mathsf {BS}\), followed by details of our balancing condition.
The \(\mathsf {BS}\) experiment
 for adversary
for adversary  , formally defined in Fig. 1, proceeds as follows. A challenger initialises sets \(V_0\) and \(V_1\), required to model the balancing condition, as empty, generates the election key pair (pk, sk), and chooses a bit \(\beta \). Adversary
, formally defined in Fig. 1, proceeds as follows. A challenger initialises sets \(V_0\) and \(V_1\), required to model the balancing condition, as empty, generates the election key pair (pk, sk), and chooses a bit \(\beta \). Adversary  is given public key pk and proceeds to query a number of oracles, formally defined in Fig. 1 and described as follows. We write \(\mathcal {O}\textsf {x}_{(y_1,\dots ,y_n)}(z_1,\dots ,z_n)\) to denote oracle \(\mathcal {O}\textsf {x}\) parametrised by \(y_1,\dots ,y_n\) that takes as input \(z_1,\dots ,z_n\).
is given public key pk and proceeds to query a number of oracles, formally defined in Fig. 1 and described as follows. We write \(\mathcal {O}\textsf {x}_{(y_1,\dots ,y_n)}(z_1,\dots ,z_n)\) to denote oracle \(\mathcal {O}\textsf {x}\) parametrised by \(y_1,\dots ,y_n\) that takes as input \(z_1,\dots ,z_n\).
-
\(\mathcal {O}\mathsf {reg}_{(pk,\mathcal {L}\mathcal {Q}\mathsf {reg})}(id_{})\) registers an eligible voter. If \(id_{}\) is in the set of eligible voters \(\mathcal {V}\), oracle \(\mathcal {O}\mathsf {reg}\) runs algorithm \(\mathsf {Register}\) on behalf of \(id_{}\) and returns the voter’s public credential \(pk_{id_{}}\) to
 . Oracle \(\mathcal {O}\mathsf {reg}\) additionally updates a list of queries \(\mathcal {Q}\mathsf {reg}\) to include the tuple \((id_{},pk_{id_{}},sk_{id_{}})\).
. Oracle \(\mathcal {O}\mathsf {reg}\) additionally updates a list of queries \(\mathcal {Q}\mathsf {reg}\) to include the tuple \((id_{},pk_{id_{}},sk_{id_{}})\). -
\(\mathcal {O}\mathsf {corrupt}_{(\mathcal {Q}\mathsf {reg},\mathcal {Q}\mathsf {corrupt})}(id_{})\) corrupts a voter. If \(id_{}\) is a registered voter, oracle \(\mathcal {O}\mathsf {corrupt}\) returns the voter’s private credential \(sk_{id_{}}\) to
 , and updates a list of queries \(\mathcal {Q}\mathsf {corrupt}\) to include the tuple \((id_{},pk_{id_{}},sk_{id_{}})\).
, and updates a list of queries \(\mathcal {Q}\mathsf {corrupt}\) to include the tuple \((id_{},pk_{id_{}},sk_{id_{}})\). -
\(\mathcal {O}\mathsf {vote}_{(pk,\mathcal {L},\mathcal {BB}_{},\mathcal {Q}\mathsf {reg},\mathcal {Q}\mathsf {corrupt},V_0,V_1)}(pk_{id_{}},v_0,v_1)\) produces and submits a ballot for vote \(v_\beta \) on behalf of an uncorrupted voter. If voter \(pk_{id_{}}\) is registered but not corrupt, and \(v_0,v_1\) are valid vote choices, oracle \(\mathcal {O}\mathsf {vote}\) runs algorithms \(\mathsf {Vote}\) and \(\mathsf {Append}\) on behalf of voter \(pk_{id_{}}\) and vote \(v_\beta \). Oracle \(\mathcal {O}\mathsf {vote}\) also updates sets \(V_0\) and \(V_1\) to include votes \(v_0\) and \(v_1\) respectively, and removes any previous entries for \(pk_{id_{}}\), modelling an e-voting scheme with a last-vote-counts revote policy.
-
\(\mathcal {O}\mathsf {cast}_{(pk,\mathcal {L},\mathcal {BB}_{},V_0,V_1)}(pk_{id_{}},b)\) submits a ballot on behalf of a voter. If ballot b is valid and created for voter \(pk_{id_{}}\), and ballot b does not exist in \(\mathcal {BB}_{}\), oracle \(\mathcal {O}\mathsf {cast}\) appends ballot b to ballot box \(\mathcal {BB}_{}\). Oracle \(\mathcal {O}\mathsf {cast}\) also removes any entries in sets \(V_0\) and \(V_1\) for \(pk_{id_{}}\).
-
\(\mathcal {O}\mathsf {board}_{\mathcal {BB}_{}}()\) returns bulletin board \(\mathcal {PBB}_{}\) to
 .
.
Adversary  outputs state information st, indicating that the experiment should transition to the tallying phase. Upon receiving the result \(r\) and proof of correct tallying \(\pi \),
outputs state information st, indicating that the experiment should transition to the tallying phase. Upon receiving the result \(r\) and proof of correct tallying \(\pi \),  outputs a bit \(\beta '\). The experiment returns 1 if \(\beta '=\beta \) and the balancing condition is satisfied.
outputs a bit \(\beta '\). The experiment returns 1 if \(\beta '=\beta \) and the balancing condition is satisfied.
Definition 3
( \(\mathsf {BS}\) ). An e-voting scheme \(\varGamma \) satisfies \(\mathsf {BS}\) if, for any PPT adversary  , there exists a negligible function
, there exists a negligible function
 such that
such that

where
 is the experiment defined in Fig. 1.
is the experiment defined in Fig. 1.
3.1 Our Balancing Condition
Following a query to oracle \(\mathcal {O}\mathsf {vote}\), sets \(V_0\) and \(V_1\) are updated to contain tuples \((pk_{id_{}},v_0)\) and \((pk_{id_{}},v_1)\) respectively. After the result of the election is announced, multisets \(V_0'\) and \(V_1'\) are defined to contain the votes \(v_0\) and \(v_1\) from sets \(V_0\) and \(V_1\) respectively. Our balancing condition, \(V_0'=V_1'\), ensures that, for every left-hand vote of an honest voter, there exists an honest voter for whom the same vote is submitted as their right-hand vote. Thus, we prevent trivial distinctions.
This notion of balance is inspired by Benaloh and Yung’s early definition of ballot secrecy [5] and is used by Bernhard and Smyth in their ballot secrecy definition \(\mathsf {IND-SEC}\) [10]. However, in comparison to \(\mathsf {BS}\), neither \(\mathsf {IND-SEC}\) nor Benaloh and Yung’s approach model registration of voters. It transpires that, to capture registration of voters and, in particular, to capture revoting and adaptive corruption of voters for e-voting schemes with voter registration, the balancing condition described above must include more complex features. We describe these subtleties and demonstrate their necessity through examples.
Eliminating Entries from \(\mathcal {O}\mathsf {vote}\). We require that, following a query to \(\mathcal {O}\mathsf {vote}\) on behalf of a voter \(pk_{id_{}}\), previous entries containing \(pk_{id_{}}\) are removed from sets \(V_0\) and \(V_1\). Else, it is possible that an adversary can submit oracle queries that allow trivial distinctions, even if a scheme is intuitively ballot secret. Consider an e-voting scheme that employs a last-vote-counts revote policy and allows voters to cast a ballot for ‘0’ or ‘1’. Let the election result be a vector of size two, indicating the number of votes cast for each candidate. Assume that \(\mathcal {O}\mathsf {vote}\) does not remove any entries from sets \(V_0\) or \(V_1\). Then an adversary in the \(\mathsf {BS}\) experiment can query \(\mathcal {O}\mathsf {vote}(pk_{id_{1}},0,1)\), \(\mathcal {O}\mathsf {vote}(pk_{id_{2}},1,0)\), \(\mathcal {O}\mathsf {vote}(pk_{id_{1}},1,0)\) and \(\mathcal {O}\mathsf {vote}(pk_{id_{3}},0,1)\) for \(pk_{id_{1}}\), \(pk_{id_{2}}\) and \(pk_{id_{3}}\) obtained via queries to \(\mathcal {O}\mathsf {reg}\) such that \(V_0=\{(pk_{id_{1}},0),(pk_{id_{2}},1),(pk_{id_{1}},1),(pk_{id_{3}},0)\}\) and \(V_1=\{(pk_{id_{1}},1),(pk_{id_{2}},0),(pk_{id_{1}},0),(pk_{id_{3}},1)\}\). Subsequently, \(V_0'=V_1'\) and the balancing condition is satisfied. However, if \(\beta =0\), \(r=(1,2)\) and, if \(\beta =1\), \(r=(2,1)\). Then the adversary trivially distinguishes the two views and succeeds in the \(\mathsf {BS}\) experiment. Therefore, it is essential that \(\mathcal {O}\mathsf {vote}\) removes previous entries that contain \(pk_{id_{}}\) from sets \(V_0\) and \(V_1\). Indeed, if the first entry of \(V_0\) and \(V_1\) is removed, the balancing condition is not satisfied and the adversary cannot succeed in the \(\mathsf {BS}\) experiment.
Eliminating Entries from \(\mathcal {O}\mathsf {cast}\). Similarly, following a query to \(\mathcal {O}\mathsf {cast}\) on behalf of voter \(pk_{id_{}}\), it is essential that entries containing \(pk_{id_{}}\) are removed from sets \(V_0\) and \(V_1\). In fact, rather than the second two queries to \(\mathcal {O}\mathsf {vote}\) in the example above, the adversary can query \(\mathcal {O}\mathsf {cast}(pk_{id_{1}},b)\) where b encodes a vote for ‘1’. Then, if \(\mathcal {O}\mathsf {cast}\) does not remove the previous entry for \(pk_{id_{1}}\), the balancing condition is satisfied. Yet, the result \(r=(0,2)\) (if \(\beta =0\)) or \(r=(1,1)\) (if \(\beta =1\)). Under static corruption of voters, removal of entries is not necessary as an adversary cannot make a query to \(\mathcal {O}\mathsf {vote}\) on behalf of a corrupted voter, i.e., voter \(pk_{id_{1}}\) in the example. Thus, removal of previous entries is key to ensure that our balancing condition allows for adaptive corruption of voters.
Voting Policies. Our balancing condition models a last-vote-counts revote policy, a policy applied to implemented e-voting schemes, for example, the Estonian i-Voting scheme [25]. On the other hand, it is common to implement an e-voting scheme with a no revote policy. For instance, Helios [1, 28] allows for both a last-vote-counts and a no revote policy. For this reason, we briefly describe how our balancing condition can be modified in a straightforward way to account for a no revote policy as follows. \(\mathcal {O}\mathsf {vote}\) does not remove previous entries containing \(pk_{id_{}}\) from sets \(V_0\) and \(V_1\) following a query on behalf of voter \(pk_{id_{}}\). Additionally, \(\mathcal {O}\mathsf {vote}\) adds new entries to sets \(V_0\) and \(V_1\) only if the sets do not contain an entry on behalf of \(pk_{id_{}}\). Finally, \(\mathcal {O}\mathsf {cast}\) does not update sets \(V_0\) and \(V_1\).
3.2 Satisfiability of \(\mathsf {BS}\)
We demonstrate satisfiability of \(\mathsf {BS}\) by constructing an e-voting scheme \(\varGamma _{\mathsf {mini}}\), defined formally in Fig. 2. \(\varGamma _{\mathsf {mini}}\) relies on a homomorphic public key encryption scheme \(\varPi \) and a signature of knowledge \(\mathsf {SOK}\), both of which are formally defined in Appendix A. A voter with credential pair \((pk_{id_{}},sk_{id_{}})\)Footnote 5 casts a ballot for \(v\in \{0,1\}\)Footnote 6 by producing an encryption, denoted c, of v under \(\varPi \), and generating a signature of knowledge, denoted \(\sigma \), that the resulting ciphertext encrypts \(v\in \{0,1\}\) using their private credential under \(\mathsf {SOK}\). The form of a ballot b is \((pk_{id_{}},c,\sigma )\). If ciphertext c does not appear in a ballot on the ballot box, and signature of knowledge \(\sigma \) verifies, the ballot is appended to the ballot box. The ballot box and the bulletin board are identical in this scheme. To compute the result, ciphertext c is extracted from the final ballot cast by each voter. The extracted ciphertexts are homomorphically tallied and the homomorphic ciphertext is decrypted, giving the result of the election. As we do not focus on verifiability, we simply define algorithm \(\mathsf {Tally}\) to output \(\bot \) in place of a proof of correct tallying, and algorithm \(\mathsf {Verify}\) is defined to always return 1.
To satisfy \(\mathsf {BS}\), we require that \(\varPi \) satisfies non-malleable-CPA security [3], \(\mathsf {NM}\text {-}\mathsf {CPA}\), and \(\mathsf {SOK}\) satisfies extractability [13]. We define these security properties in Appendix A. We obtain the result in Theorem 1.
Theorem 1
\(\varGamma _{\mathsf {mini}}\) (Fig. 2) satisfies \(\mathsf {BS}\) if public key encryption scheme \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) and signature of knowledge \(\mathsf {SOK}\) satisfies extractability.
We formally prove Theorem 1 in Appendix B. Informally, assuming that an adversary queries \(\mathcal {O}\mathsf {vote}\) and \(\mathcal {O}\mathsf {cast}\) such that \(V_0'=V_1'\), the result computed over \(\mathcal {BB}_{}\) in the \(\mathsf {BS}\) experiment for \(\beta =0\) is indistinguishable from the result for \(\beta =1\). In fact, with respect to the ballots included in the election result, \(\mathcal {BB}_{}\) contains the same number of votes for each candidate, regardless of \(\beta \). Moreover, an adversary cannot distinguish whether \(\mathcal {BB}_{}\) contains ballots for a left- or right-hand vote on behalf of honest voters if \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\). Finally, \(\mathsf {NM}\text {-}\mathsf {CPA}\) security of \(\varPi \) and extractability of \(\mathsf {SOK}\) ensures that an adversary cannot submit ballots on behalf of a corrupt voter that are meaningfully related to the ballots of honest voters, thus skewing the result and allowing the adversary to distinguish views [21].
3.3 Limitation of \(\mathsf {BS}\)
For transparency, we elaborate on an aspect of \(\mathsf {BS}\) that limits the class of e-voting schemes that can be captured by \(\mathsf {BS}\). We believe that such discussion is essential to understand security definitions for e-voting and ensure that, to prove security of an e-voting scheme, the most relevant definition is chosen based on the nuances of the scheme. In Sect. 5, we elaborate on the complexities and limitations of ballot secrecy definitions in the literature, further casting light on the applicability of definitions.
Our balancing condition limits the class of result functions that can be captured. In particular, consider an e-voting scheme in which a voter can submit a score for a candidate, e.g., \(\mathcal {C}=\{0,1,2\}\), and the result consists of the sum of all scores submitted. In [7], the authors show that Benaloh and Yung’s ballot secrecy definition [5], upon which \(\mathsf {BS}\) is based, does not capture this result function. Specifically, [5] and \(\mathsf {BS}\) do not model an attacker that can distinguish different vote assignments that lead to the same result, for example, two voters voting 0 and 2 respectively, and both voters voting 1. Despite this, common result functions, such as plurality voting, are within the scope of our definition.
4 Extending \(\mathsf {BS}\) to the Malicious Setting
Corrupt election officials can break ballot secrecy. In particular, a malicious ballot box can ‘stuff’ the ballot box with ballots, which can lead to attacks against ballot secrecy [21]. Furthermore, a malicious tallier can potentially reveal the votes of all honest voters, for example, if ballots consist of a vote encrypted under the tallier’s public key, such as in our construction \(\varGamma _{\mathsf {mini}}\). To overcome this, many e-voting schemes distribute the role of the tallier [29, 31] and assume that a proportion of talliers are honest. We define \(\mathsf {mbbBS}\), a definition that extends \(\mathsf {BS}\) to the malicious ballot box setting, and \(\mathsf {dtBS}\), an extension of \(\mathsf {mbbBS}\) in which the adversary can further corrupt a subset of talliers where the role of the tallier is distributed. In doing so, we provide definitions that allow a scheme designer to prove ballot secrecy in the event of an attacker that can corrupt the ballot box and a proportion of talliers.
4.1 Malicious Ballot Box Manager
We extend \(\mathsf {BS}\) to \(\mathsf {mbbBS}\), defining an adversary that arbitrarily constructs the ballot box, obtaining ballots for honest voters that correspond to either a left or right vote submitted to an oracle \(\mathcal {O}\mathsf {vote}\). Hence, \(\mathsf {mbbBS}\) models a corrupt ballot box, but considers all other election entities to be honest. We note that, in this setting, the adversary can only statically corrupt voters, a common restriction [16, 20]. This arises as a consequence of the balancing condition, which we elaborate on following the formal definition.
The \(\mathsf {mbbBS}\) experiment
 for adversary
for adversary  , formally defined in Fig. 3, registers all \(n_v\) eligible voters and provides the adversary
, formally defined in Fig. 3, registers all \(n_v\) eligible voters and provides the adversary  with the set of public credentials \(\mathcal {L}\) and the election public key pk.
with the set of public credentials \(\mathcal {L}\) and the election public key pk.  selects a subset of public credentials \(\mathsf {corr}\mathcal {L}\) to corrupt and
selects a subset of public credentials \(\mathsf {corr}\mathcal {L}\) to corrupt and  receives a list of corresponding private credentials \(\mathsf {c}\mathcal {L}\). Adversary
receives a list of corresponding private credentials \(\mathsf {c}\mathcal {L}\). Adversary  is provided with access to an oracle \(\mathcal {O}\mathsf {vote}_{(pk,\mathcal {L},\mathsf {corr}\mathcal {L},V)}(pk_{id_{}},v_0,v_1)\) that returns ballots for \(v_\beta \) on behalf of honest voters, and constructs a ballot box \(\mathcal {BB}_{}\), which may include both honestly and maliciously generated ballots. Upon receiving the result r computed over \(\mathcal {BB}_{}\) and a proof of correct tallying \(\pi \),
is provided with access to an oracle \(\mathcal {O}\mathsf {vote}_{(pk,\mathcal {L},\mathsf {corr}\mathcal {L},V)}(pk_{id_{}},v_0,v_1)\) that returns ballots for \(v_\beta \) on behalf of honest voters, and constructs a ballot box \(\mathcal {BB}_{}\), which may include both honestly and maliciously generated ballots. Upon receiving the result r computed over \(\mathcal {BB}_{}\) and a proof of correct tallying \(\pi \),  outputs a bit \(\beta '\). If \(\beta '=\beta \) and the balancing condition is satisfied, the experiment returns 1. We observe that the adversary does not require access to oracles \(\mathcal {O}\mathsf {reg}\) and \(\mathcal {O}\mathsf {corrupt}\), as defined for \(\mathsf {BS}\), because voters are statically corrupted. Moreover, the adversary does not require access to an oracle \(\mathcal {O}\mathsf {cast}\) because
outputs a bit \(\beta '\). If \(\beta '=\beta \) and the balancing condition is satisfied, the experiment returns 1. We observe that the adversary does not require access to oracles \(\mathcal {O}\mathsf {reg}\) and \(\mathcal {O}\mathsf {corrupt}\), as defined for \(\mathsf {BS}\), because voters are statically corrupted. Moreover, the adversary does not require access to an oracle \(\mathcal {O}\mathsf {cast}\) because  constructs the ballot box.
constructs the ballot box.
Definition 4
( \(\mathsf {mbbBS}\) ). An e-voting scheme \(\varGamma \) satisfies \(\mathsf {mbbBS}\) if, for any PPT adversary  , there exists a negligible function
, there exists a negligible function
 such that
such that

where
 is the experiment defined in Fig. 3.
is the experiment defined in Fig. 3.
Our Balancing Condition.
\(\mathsf {mbbBS}\) maintains a list of queries to \(\mathcal {O}\mathsf {vote}\) in a set V such that each entry in V consists of a tuple \((pk_{id_{}},v_0,v_1,b)\). Then, if b appears on ballot box \(\mathcal {BB}_{}\) and the tuple contains the final ballot that appears on \(\mathcal {BB}_{}\) with respect to voter \(pk_{id_{}}\), the experiment adds \(v_0\) (resp., \(v_1\)) to a multiset \(V_0\) (resp., \(V_1\)). In other words, multisets \(V_0\) and \(V_1\) contain only the final vote for every honest voter such that a corresponding ballot is appended to \(\mathcal {BB}_{}\).Footnote 7
As a result of our balancing condition, \(\mathsf {mbbBS}\) considers static corruption of voters. Indeed, if \(\mathsf {mbbBS}\) allows adaptive corruption of voters, a trivial distinguishing attack is possible. To demonstrate this, we recall our construction \(\varGamma _{\mathsf {mini}}\) (Fig. 2) and assume that an adversary in the \(\mathsf {mbbBS}\) experiment can adaptively corrupt voters. That is, the adversary has access to oracles \(\mathcal {O}\mathsf {reg}\) and \(\mathcal {O}\mathsf {corrupt}\) as defined in Fig. 1. Then, the adversary queries \(b_1\leftarrow \mathcal {O}\mathsf {vote}(pk_{id_{1}},0,1)\) and \(b_2\leftarrow \mathcal {O}\mathsf {vote}(pk_{id_{2}},1,0)\) for \(pk_{id_{1}}\) and \(pk_{id_{2}}\) obtained via queries to \(\mathcal {O}\mathsf {reg}\). Voter \(pk_{id_{1}}\) is corrupted via a query to \(\mathcal {O}\mathsf {corrupt}\) and the adversary appends \(b_1\), \(b_2\) and \(b_3\), a ballot for ‘1’ on behalf of \(pk_{id_{1}}\), to \(\mathcal {BB}_{}\). The balancing condition is satisfied but, if \(\beta =0\) (resp., \(\beta =1\)), \(r=(0,2)\) (resp., \(r=(1,1)\)), and the adversary can trivially distinguish the two views. Consequently, we restrict \(\mathsf {mbbBS}\) to allow only static corruption of voters. Then, if the adversary wishes to corrupt \(pk_{id_{1}}\), they cannot make queries to \(\mathcal {O}\mathsf {vote}\) on behalf of \(pk_{id_{1}}\) and, in the example above, the balancing condition is not satisfied. Therefore, the adversary does not succeed in the \(\mathsf {mbbBS}\) experiment.
Satisfiability of \(\mathsf {mbbBS}\). We show that our e-voting construction \(\varGamma _{\mathsf {mini}}\) (Fig. 2) satisfies \(\mathsf {mbbBS}\) under the same conditions that \(\varGamma _{\mathsf {mini}}\) satisfies \(\mathsf {BS}\). Indeed, we design the ballots in \(\varGamma _{\mathsf {mini}}\) to be non-malleable, which is required to satisfy \(\mathsf {mbbBS}\), a fact that we elaborate on following our formal result. In other words, we intentionally design \(\varGamma _{\mathsf {mini}}\) to satisfy stronger notions of ballot secrecy than \(\mathsf {BS}\). We require a \(\mathsf {NM}\text {-}\mathsf {CPA}\) secure public key encryption scheme and a signature of knowledge that satisfies extractability. We obtain the result in Theorem 2.
Theorem 2
\(\varGamma _{\mathsf {mini}}\) (Fig. 2) satisfies \(\mathsf {mbbBS}\) if public key encryption scheme \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) and signature of knowledge \(\mathsf {SOK}\) satisfies extractability.
We formally prove Theorem 2 in Appendix B. The proof of Theorem 2 is very similar to the proof that \(\varGamma _{\mathsf {mini}}\) satisfies \(\mathsf {BS}\) (Theorem 1). In particular, an adversary cannot distinguish whether \(\mathcal {O}\mathsf {vote}\) returns a ballot corresponding to \(v_0\) or \(v_1\) as a result of \(\mathsf {NM}\text {-}\mathsf {CPA}\) security of \(\varPi \). Moreover, the ballots returned by \(\mathcal {O}\mathsf {vote}\) cannot be modified by the adversary in a meaningful way due to non-malleability of the ballot, provided by extractability of \(\mathsf {SOK}\) and \(\mathsf {NM}\text {-}\mathsf {CPA}\) security of \(\varPi \). Thus, any ballot in \(\mathcal {BB}_{}\) is either a ballot of a corrupt voter that is independent of any other ballot, or an output of oracle \(\mathcal {O}\mathsf {vote}\). Then, if the balancing condition is satisfied, the result computed over \(\mathcal {BB}_{}\) constructed by the adversary is indistinguishable for \(\beta =0\) or 1.
As noted, ballots must be non-malleable to satisfy \(\mathsf {mbbBS}\). Intuitively, if an attacker with control of the ballot box can transform ballots, then they can append ballots to the ballot box that are meaningfully related to the vote of an honest voter such that the result reveals the honest voter’s vote. We demonstrate this by describing an attack against our e-voting scheme \(\varGamma _{\mathsf {mini}}\) where we replace the signature of knowledge with a standard digital signature scheme. An adversary in the \(\mathsf {mbbBS}\) experiment can query \(b_1\leftarrow \mathcal {O}\mathsf {vote}(pk_{id_{1}},0,1)\), \(b_2\leftarrow \mathcal {O}\mathsf {vote}(pk_{id_{2}},1,0)\) and \(b_3\leftarrow \mathcal {O}\mathsf {vote}(pk_{id_{3}},0,1)\), appending ballots \(b_1\) and \(b_2\) to \(\mathcal {BB}_{}\). Let \(b_3=(pk_{id_{3}},c_3,\sigma _3)\). The adversary produces a signature \(\sigma _4\) for ciphertext \(c_3\) for a corrupt voter \(pk_{id_{4}}\) and appends the modified ballot \(b^*=(pk_{id_{4}},c_3,\sigma _4)\) to \(\mathcal {BB}_{}\). The balancing condition is satisfied, yet, if \(\beta =0\), \(r=(2,1)\) and, if \(\beta =1\), \(r=(1,2)\), which allows
 to distinguish the two views. This attack is possible because the ballot is malleable. In contrast, if \(\sigma \) is a signature of knowledge, the adversary requires knowledge of the plaintext encrypted by \(c_3\) in order to construct a signature of knowledge for \(pk_{id_{4}}\). Therefore, we conclude that e-voting schemes that allow malleable ballots cannot satisfy \(\mathsf {mbbBS}\).
to distinguish the two views. This attack is possible because the ballot is malleable. In contrast, if \(\sigma \) is a signature of knowledge, the adversary requires knowledge of the plaintext encrypted by \(c_3\) in order to construct a signature of knowledge for \(pk_{id_{4}}\). Therefore, we conclude that e-voting schemes that allow malleable ballots cannot satisfy \(\mathsf {mbbBS}\).
We recognise that there exists e-voting schemes for which the ballots are malleable, for example, e-voting schemes that include a timestamp in the ballot. An adversary in the \(\mathsf {mbbBS}\) experiment can modify the timestamp in a ballot output by \(\mathcal {O}\mathsf {vote}\) and append the modified ballot to \(\mathcal {BB}_{}\). Then, the result trivially reveals \(\beta \) and the balancing condition holds. However, there may not be a ballot secrecy issue with the scheme in practice. Therefore, if a scheme produces ballots that contain a malleable part, the scheme does not satisfy \(\mathsf {mbbBS}\), despite the fact that it is intuitively ballot secret. Despite this, we believe that non-malleable ballots are desirable. For example, if a ballot includes a malleable timestamp, an attacker with control of the ballot box can modify the timestamp, potentially ensuring that a ballot is not included in the result of the election. Furthermore, ballots with malleable elements can be modified to ensure non-malleability. For instance, a ballot can include a signature of knowledge or proof of knowledge that ties the signature or proof to the malleable element, ensuring that the malleable element cannot be modified without detection (which, in turn, ensures that a modified ballot is not valid).
4.2 Distributed and Malicious Tallier
We now consider an extension of \(\mathsf {mbbBS}\) for e-voting schemes with a distributed tallier, that is, we write tallier \(\mathcal {T}\) as \(\mathcal {T}=(\mathcal {T}_1,\dots ,\mathcal {T}_{n})\). In this case, we consider an election private key that is distributed amongst n talliers such that \(sk=(sk_{\mathcal {T}_1},\dots ,sk_{\mathcal {T}_{n}})\) and at least t shares are required to reconstruct sk where \(t\le n\).Footnote 8 We extend \(\mathsf {mbbBS}\) to a definition \(\mathsf {dtBS}\) that models a corrupt ballot box and a subset of corrupt talliers. In particular, we model an attacker that obtains the private key share of up to \(t-1\) talliers. As with \(\mathsf {mbbBS}\), we consider other election entities to be honest and only allow the static corruption of voters.
The corruption strategy captured by \(\mathsf {dtBS}\) does not model an attacker that generates key shares for corrupt talliers. In fact, we consider that all key shares are generated honestly. In other words, the attacker corrupts talliers after key generation and, therefore, cannot influence the generation of key shares. As \(\mathsf {dtBS}\) is a preliminary exploration of ballot secrecy with a malicious ballot box and tallier, we consider the attack strategy captured by \(\mathsf {dtBS}\) to be appropriate and leave the case of stronger attacker models as an open problem.
We define the \(\mathsf {dtBS}\) experiment
 , parametrised by the number of talliers n and the number of shares required to reconstruct the election private key t, as the \(\mathsf {mbbBS}\) experiment, defined in Fig. 3, but with the following modifications. In addition to statically corrupting a subset of voters, adversary
, parametrised by the number of talliers n and the number of shares required to reconstruct the election private key t, as the \(\mathsf {mbbBS}\) experiment, defined in Fig. 3, but with the following modifications. In addition to statically corrupting a subset of voters, adversary
 corrupts \(t-1\) talliers. That is,
corrupts \(t-1\) talliers. That is,
 submits \(t-1\) unique indices \(\{i_1,\dots ,i_{t-1}\}\) and obtains the set of private key shares \(\{sk_{\mathcal {T}_{i_1}},\dots ,sk_{\mathcal {T}_{i_{t-1}}}\}\). Additionally, algorithm \(\mathsf {Tally}\) takes as input t private key shares that include the \(t-1\) shares returned to
submits \(t-1\) unique indices \(\{i_1,\dots ,i_{t-1}\}\) and obtains the set of private key shares \(\{sk_{\mathcal {T}_{i_1}},\dots ,sk_{\mathcal {T}_{i_{t-1}}}\}\). Additionally, algorithm \(\mathsf {Tally}\) takes as input t private key shares that include the \(t-1\) shares returned to
 . In all other respects, the \(\mathsf {dtBS}\) experiment is identical to the \(\mathsf {mbbBS}\) experiment.
. In all other respects, the \(\mathsf {dtBS}\) experiment is identical to the \(\mathsf {mbbBS}\) experiment.
Definition 5
( \(\mathsf {dtBS}\) ). An e-voting scheme \(\varGamma \) for n talliers and threshold t, where election private key \(sk=(sk_{\mathcal {T}_1},\dots ,sk_{\mathcal {T}_{n}})\), satisfies \(\mathsf {dtBS}\) if, for any PPT adversary  , there exists a negligible function
, there exists a negligible function
 such that
such that

where
 is the \(\mathsf {mbbBS}\) experiment defined in Fig. 3 for
is the \(\mathsf {mbbBS}\) experiment defined in Fig. 3 for  provided with \(t-1\) private key shares of their choice and where algorithm \(\mathsf {Tally}\) takes as input the \(t-1\) private keys provided to
provided with \(t-1\) private key shares of their choice and where algorithm \(\mathsf {Tally}\) takes as input the \(t-1\) private keys provided to
 .
.
Satisfiability of \(\mathsf {dtBS}\). To illustrate satisfiability of \(\mathsf {dtBS}\), we consider a modification to \(\varGamma _{\mathsf {mini}}\) (Fig. 2) that uses a (t, n)-threshold public key encryption scheme [24], \(\varPhi \), which we define in Appendix A. We call our modified construction \(\varGamma _{\mathsf {mini}}'\). Formally, \(\varGamma _{\mathsf {mini}}'\) is identical to \(\varGamma _{\mathsf {mini}}\) with the exceptions of the following modifications to algorithms \(\mathsf {Setup}\), \(\mathsf {Vote}\) and \(\mathsf {Tally}\). We write that \(\mathsf {Setup}\) takes additional input t and n and, rather than running algorithm \(\varPi .\mathsf {Gen}\), \(\mathsf {Setup}\) runs algorithm \(\varPhi .\mathsf {Gen}\) to generate a public key \(pk_\phi \) and n private keys \(sk_{\phi _1},\dots ,sk_{\phi _n}\). Each tallier is provided with a private key. Algorithm \(\mathsf {Vote}\) encrypts vote v by running \(\varPhi .\mathsf {Enc}\), rather than \(\varPi .\mathsf {Enc}\). Finally, algorithm \(\mathsf {Tally}\) requires interaction between t talliers. In detail, any tallier can produce the homomorphic ciphertext \(\mathsf {cipher}\), and, then, t talliers each produce a partial decryption of \(\mathsf {cipher}\) by running algorithm \(\varPhi .\mathsf {Dec}\). The final result r is computed by running algorithm \(\varPhi .\mathsf {Combine}\) on input of the t partial decryptions.
As for our previous results, to satisfy \(\mathsf {dtBS}\), we require that \(\varPhi \) satisfies \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) security and \(\mathsf {SOK}\) satisfies extractability. We define \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) security for a (t, n)-threshold encryption scheme in Appendix A. Briefly, security of a (t, n)-threshold encryption scheme is defined as a natural extension of security for a standard encryption scheme with the exception that the adversary can statically corrupt \(t-1\) decryption servers, see, for example [26, 32]. Therefore, \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) security for \(\varPhi \) is equivalent to \(\mathsf {NM}\text {-}\mathsf {CPA}\) security for a standard public key encryption scheme but the adversary obtains the private keys of \(t-1\) decryption servers of their choice. We obtain the result in Theorem 3.
Theorem 3
\(\varGamma _{\mathsf {mini}}'\) satisfies \(\mathsf {dtBS}\) if (t, n)-threshold public key encryption scheme \(\varPhi \) satisfies \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) and signature of knowledge \(\mathsf {SOK}\) satisfies extractability.
We formally prove Theorem 3 in Appendix B. The proof of this result follows largely from the fact that \(\varGamma _{\mathsf {mini}}\) satisfies \(\mathsf {mbbBS}\) and, as such, the result and output of \(\mathcal {O}\mathsf {vote}\) is indistinguishable for \(\beta =0\) or 1. Moreover, by \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) security of the threshold encryption scheme, access to \(t-1\) private keys does not provide the adversary with any more information about the votes of honest voters.
5 A Comparison of Ballot Secrecy Definitions
In this section, we provide a comparison of existing game-based definitions, grouping them according to their underlying intuition. In particular, we identify two types of definitions: those that tally the ‘real’ election, and those that rely on a balancing condition and tally the viewed election. We place our definitions (Definitions 3–5) in context, highlighting our contribution to the area.
5.1 Tally the ‘Real’ Election
Recall from the introduction that definitions in this category provide the adversary with a view of a real or fake election, depending on the value of a coin flip, and always compute the tally for the real election. This approach to defining ballot secrecy was introduced in [8], and refined in [9]. In [7], Cortier et al. reviewed ballot secrecy definitions from the literature and defined \(\mathsf {BPRIV}\) as an alteration of [8, 9], avoiding weaknesses found in both previous, related, definitions.Footnote 9 Arguably, \(\mathsf {BPRIV}\) has since become the most well-known and widely used definition of ballot secrecy in the literature. In fact, in [6], it was used to prove the security of Helios and has been extended to capture receipt-freeness [12]. Moreover, it has been extended to model e-voting schemes with registration of voters [16] and to capture a malicious ballot box [20]. As \(\mathsf {BPRIV}\) is the state-of-the-art definition in this category, we focus on \(\mathsf {BPRIV}\) and its extensions from [16] and [20]. \(\mathsf {BPRIV}\) avoids the limitations of existing definitions, including those definitions that follow the ‘tally the viewed election’ approach (see Sect. 5.2). Moreover, \(\mathsf {BPRIV}\) is shown to imply a simulation-based notion of ballot secrecy [7], reinforcing the correctness and strength of the \(\mathsf {BPRIV}\) approach. Despite this, we highlight two drawbacks of this approach.
Need for Additional Properties. \(\mathsf {BPRIV}\) is strong and well-established, yet, as a stand-alone definition, it is subject to attacks, as highlighted by Cortier et al., the authors of \(\mathsf {BPRIV}\) [7]. Specifically, \(\mathsf {BPRIV}\) does not capture an attacker that can cause the rejection of honestly created ballots, which can violate ballot secrecy. Cortier et al. define an e-voting scheme such that ballots are appended with a bit, 0 or 1, where algorithm \(\mathsf {Vote}\) always appends a 0. Then, if there exists a ballot in \(\mathcal {BB}_{}\) that is appended with 1, all subsequent ballots are rejected. As \(\mathsf {BPRIV}\) always computes the result of the ‘real’ election, such a scheme satisfies \(\mathsf {BPRIV}\). Yet, an attacker can ensure that a majority of honestly created ballots are rejected, potentially revealing the votes of a small subset of honest voters. Therefore, Cortier et al. define strong correctness, an additional property required to prevent such attacks. Our definition \(\mathsf {BS}\), and other definitions in the same category [4, 5, 10, 11, 19, 30], on the other hand, capture this attack. In fact, the balancing condition of \(\mathsf {BS}\) ensures that votes of honest voters are added to multisets \(V_0'\) and \(V_1'\), even if the ballot is rejected by algorithm \(\mathsf {Valid}\), yet the votes contained in these multisets will not necessarily be included in the result. As a consequence, the adversary can output a ballot box such that the balancing condition is satisfied, and determine \(\beta \) from the result computed over \(\mathcal {BB}_{}\).
Furthermore, Cortier et al. highlight that \(\mathsf {BPRIV}\) is subject to another attack in which the ballots of honest voters are not included in the result, potentially revealing the vote of an honest voter, and describe an e-voting scheme for a referendum that rejects the ballot of the first voter if the ballot is for a specified candidate [7]. Then, depending on whether the ballot is included in the result, it is possible to determine how the first voter voted. This scheme satisfies \(\mathsf {BPRIV}\) despite the fact that, intuitively, it is not ballot secret. Therefore, \(\mathsf {BPRIV}\) must be accompanied by a second additional property, strong consistency, that prevents this attack. By contrast, \(\mathsf {BS}\) and [4, 5, 10, 11, 19, 30] capture this attack. By defining an adversary that submits a query to \(\mathcal {O}\mathsf {vote}\) such that the left-hand vote is for the specified candidate and the right-hand vote is for a second candidate, the balancing condition can be satisfied and the result returned to the adversary in the \(\mathsf {BS}\) experiment reveals whether the first ballot was removed. We additionally note that definitions derived from \(\mathsf {BPRIV}\) [12, 16, 20] also require strong consistency and strong correctness to capture the two attacks outlined above.
Extendibility. For schemes with a registration phase, \(\mathsf {BPRIV}\) has been extended to static voter corruption only [16]. In fact, extending \(\mathsf {BPRIV}\) to an e-voting scheme with a registration phase is non-trivial and attempting to model adaptive corruption of voters in a logical fashion (e.g., by providing access to a corrupt oracle as in our definition \(\mathsf {BS}\)) results in a definition that is too strong [16]. By contrast, \(\mathsf {BS}\) captures adaptive corruption.
\(\mathsf {BPRIV}\) is also difficult to extend to the malicious ballot box setting, though a recent attempt was made in [20]. There, \(\mathcal {BB}_{\beta }\) is the ballot box created by the adversary in the \(\mathsf {BPRIV}\) experiment for \(\beta \in \{0,1\}\). Briefly, if \(\beta =0\), the result and tallying proof are returned for \(\mathcal {BB}_{0}\). If \(\beta =1\), the experiment returns the tally computed over \(\mathcal {BB}_{0}\) such that \(\mathcal {BB}_{0}\) is transformed according to the ways in which the adversary tampers with the ballots on \(\mathcal {BB}_{1}\). This ensures that the result returned to the adversary corresponds to the actions taken by the adversary when constructing the ballot box. To achieve this, the extension defines an algorithm that detects the ways in which an adversary can tamper with ballots in the ballot box (e.g., the algorithm can be defined to include one or more of the following actions: delete, modify, re-order ballots). In doing so, the definition is flexible, capable of capturing different potential attack scenarios. However, this means that, before applying the definition, it is necessary to first define an algorithm, presenting an opportunity for flawed security proofs if the algorithm is not defined correctly. On the other hand, \(\mathsf {BS}\) can be easily extended to \(\mathsf {mbbBS}\) and does not require additional algorithms, providing a simple-to-apply definition in the malicious setting. Further, \(\mathsf {BPRIV}\) cannot be easily extended to a setting in which the tallier is distributed and a subset of talliers can be corrupted. Indeed, in [22], del Pino et al. state that it is difficult to adapt \(\mathsf {BPRIV}\) to this setting because corrupted talliers must participate in the tallying stage of the election for both ballot boxes, yet \(\mathsf {BPRIV}\) only ever returns the result for the ballot box corresponding to the ‘real’ election. To overcome this, like our definition \(\mathsf {dtBS}\), del Pino et al. also rely on a balancing condition, effectively departing from \(\mathsf {BPRIV}\)’s approach.
5.2 Tallying the Viewed Election
Recall that the second type of approach, introduced in [4, 5], tallies the ballot box corresponding to the bulletin board viewed by the adversary. The definitions in [4] and [5] have been adopted in subsequent definitions and extended to the malicious ballot box setting. Namely, [4] (respectively, [5]) has been adopted by [30] (respectively, [10]) and extended to the malicious ballot box setting in [19] (respectively, [11]). The definitions that follow this approach require a balancing condition. The approaches defined in [4] and [5] differ with respect to the balancing condition. We choose to follow [5] to avoid the requirement of a partial tally assumption, which we describe in this section, and which is required by definitions that follow [4]. As a result, the definitions presented in this paper are close in spirit to [5, 10, 11]. However, our definitions are distinct. In fact, our definitions extend to e-voting schemes with voter registration, and avoid an incompatibility issue found with [10] and outlined below. We now discuss some of the benefits and limitations of this approach and, in particular, we elaborate on the features that set \(\mathsf {BS}\) apart from other definitions that follow this approach.
Restricted Result Functions. The balancing condition required in this style of definition restricts the class of result functions that can be captured, a criticism that does not apply to \(\mathsf {BPRIV}\). Some definitions [4, 19, 30] define the balancing condition such that the output of the result function applied to each of the two multisets is equal, i.e., \(f(V_0)=f(V_1)\). It is well-known that this approach requires a partial tally assumption [7, 19]. That is to say, where a set of votes can be written as \(V=V'\cup V''\), the partial tally assumption states that \(f(V)=f(V')* f(V'')\). We avoid the partial tally assumption by following the approach of [5, 10, 11], and require that two sets, when viewed as multisets, are equal (we additionally extend this to e-voting schemes with a registration phase). However, this approach does still restrict the class of result functions. In fact, as we discuss in Sect. 3.3, our definitions, and those in [5, 10, 11], do not capture result functions that allow different vote assignments that lead to the same result. Despite this, we note that common result functions, such as plurality voting, are within the scope of our definitions.
Extendibility. Unlike \(\mathsf {BPRIV}\), it has been shown that definitions in this category can be easily extended to the malicious setting. In particular, Bernhard and Smyth [11] and Cortier and Lallemand [19] extend this approach to the malicious ballot box setting in an intuitive way. Our definitions \(\mathsf {mbbBS}\) and \(\mathsf {dtBS}\) also demonstrate how this approach can be extended to the malicious ballot box and distributed tallier settings respectively.
On the other hand, extending to model e-voting schemes with a registration phase is not as well understood. Definitions in this category that model voter registration either allow static corruption of voters only [19], or allow adaptive corruption but only allow the adversary to submit a single left- and right-hand vote on behalf of each honest voter [30]. In this paper, we show that it is possible to model adaptive corruption of voters and allow the adversary to submit an arbitrary number of votes on behalf of each voter, capturing e-voting schemes with revoting policies. Thus, \(\mathsf {BS}\) models an attack strategy that has not yet captured been captured by any previous definition.
Compatibility with Verifiability. Though in this paper we focus on privacy for e-voting, it is desirable that a ballot secrecy definition is compatible with verifiability [18]. In [7] it was discovered that \(\mathsf {IND-SEC}\) [10], a ballot secrecy definition that relies on a balancing condition that is very similar to ours, is not compatible with verifiability. \(\mathsf {IND-SEC}\), like \(\mathsf {BS}\), requires that the multisets of left- and right-hand votes submitted on behalf of honest voters are equal. However, if these two multisets are not equal, \(\mathsf {IND-SEC}\) returns the result and accompanying tallying proof computed over the ballot box corresponding to the \(\mathsf {IND-SEC}\) experiment where \(\beta =0\). In [7], Cortier et al. prove that an e-voting scheme cannot simultaneously satisfy \(\mathsf {IND-SEC}\) and tally uniqueness, a minimal property required to ensure verifiability of an e-voting scheme, as a result of the actions performed when the multisets are not equal. We refer the reader to [7] for full details of this result. A fix to \(\mathsf {IND-SEC}\) was put forth in [33] to overcome this weakness, proposing that, if the multisets are not equal, the \(\mathsf {IND-SEC}\) experiment still returns the result computed over \(\mathcal {BB}_{}\) for \(\beta =0\), but not the tallying proof. However, a definition that does not return a tallying proof does not capture verifiable voting schemes. Instead, our definitions avoid the verifiability compatibility issue of both versions of \(\mathsf {IND-SEC}\) [10, 33] by restricting the adversary and requiring that the two multisets are equal, i.e., the experiment returns 0 otherwise.
5.3 Summarising Our Contributions
Game-based definitions of ballot secrecy in the honest model are well-studied. \(\mathsf {BPRIV}\), in particular, has received a lot of attention and is often regarded as the de facto definition of ballot secrecy. In contrast, the ballot secrecy definitions introduced in this paper follow the approach of [5]. Consequently, our definitions are not affected by the limitations of \(\mathsf {BPRIV}\), namely, the need for additional properties in order to prove security of an e-voting scheme, and the difficulties of extendibility. In fact, our definitions inherit the benefits of the Benaloh approach, that is, our definitions are intuitive, based on long-established techniques for indistinguishability experiments, and are well-suited to extensions into the malicious setting. Moreover, our definitions differ from existing definitions that also follow this approach. In particular, our definitions model e-voting schemes with a registration phase and, in comparison to existing definitions, \(\mathsf {BS}\) captures adaptive voter corruption in an e-voting scheme with a registration phase, whilst also modelling revoting policies. Moreover, though we do restrict the set of result functions that can be considered, we do not require a partial tally assumption. We believe that, to model realistic attack scenarios, the way forward is ballot secrecy definitions that model corrupted election officials. Our definitions \(\mathsf {mbbBS}\) and \(\mathsf {dtBS}\) model such attack scenarios and provide a spring-board for future research in this direction. Finally, we comment that, in light of current restrictions on movement caused by global pandemics, and the potential that democratic processes could move on-line as a result, we believe it is an apt time to revisit existing approaches and explore new definitions of ballot secrecy.
Notes
- 1.
Though the focus of this paper is privacy, another basic property of e-voting schemes is verifiability, by which any interested party can check that the result of the election is computed correctly. For a full discussion of this notion, including formal definitions, the interested reader can consult [18].
- 2.
- 3.
In fact, in [8], Bernhard et al. introduce minivoting, a simple e-voting scheme in which voters simply encrypt their vote and a tallier decrypts each ciphertext and computes the result from the resulting plaintext votes. Like \(\varGamma _{\mathsf {mini}}\), mini-voting is not verifiable. However, Bernhard et al. prove that mini-voting satisfies a notion of ballot secrecy and subsequently build a generic, verifiable, e-voting scheme with homomorphic tallying that also satisfies ballot secrecy. Helios is an instantiation of this generic e-voting scheme and, therefore, Helios can be shown to satisfy ballot secrecy if the underlying mini-voting construction is ballot secret.
- 4.
Our result function, similar to the result function in [7], determines how the result of the election is computed.
- 5.
We write that credential pairs are generated by a one-way function f.
- 6.
- 7.
As with \(\mathsf {BS}\), our balancing condition can be modified to model a no-revote policy.
- 8.
We note that, specifically, \(t=n\) is possible. That is, all n shares are required to reconstruct the private key.
- 9.
References
Adida, B.: Helios: web-based open-audit voting. In: USENIX 2008, vol. 17, pp. 335–348 (2008)
Belenios voting system. https://www.belenios.org/index.html
Bellare, M., Desai, A., Pointcheval, D., Rogaway, P.: Relations among notions of security for public-key encryption schemes. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 26–45. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055718
Benaloh, J.: Verifiable secret-ballot elections. Ph.D. thesis (1987)
Benaloh, J., Yung, M.: Distributing the power of a government to enhance the privacy of votes. In: PODC 1986, pp. 52–62 (1986)
Bernhard, D., Cortier, V., Galindo, D., Pereira, O., Warinschi, B.: A comprehensive analysis of game-based ballot privacy definitions. ePrint Report 2015/255 (2015)
Bernhard, D., Cortier, V., Galindo, D., Pereira, O., Warinschi, B.: SoK: a comprehensive analysis of game-based ballot privacy definitions. In: S&P 2015, pp. 499–516 (2015)
Bernhard, D., Cortier, V., Pereira, O., Smyth, B., Warinschi, B.: Adapting helios for provable ballot privacy. In: Atluri, V., Diaz, C. (eds.) ESORICS 2011. LNCS, vol. 6879, pp. 335–354. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23822-2_19
Bernhard, D., Pereira, O., Warinschi, B.: How not to prove yourself: pitfalls of the Fiat-Shamir heuristic and applications to helios. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 626–643. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_38
Smyth, B., Bernhard, D.: Ballot secrecy and ballot independence coincide. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 463–480. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40203-6_26
Bernhard, D., Smyth, B.: Ballot secrecy with malicious bulletin boards. ePrint Report 2014/822 (2014)
Chaidos, P., Cortier, V., Fuchsbauer, G., Galindo, D.: BeleniosRF: a non-interactive receipt-free electronic voting scheme. In: CCS 2016, pp. 1614–1625, New York (2016)
Chase, M., Lysyanskaya, A.: On signatures of knowledge. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 78–96. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_5
Civitas voting system. www.cs.cornell.edu/projects/civitas/
Clarkson, M.R., Chong, S., Myers, A.C.: Civitas: toward a secure voting system. In: S&P 2008, pp. 354–368. IEEE (2008)
Cortier, V., Dragan, C.C., Dupressoir, F., Warinschi, B.: Machine-checked proofs for electronic voting: privacy and verifiability for Belenios. In: CSF 2018, pp. 298–312 (2018)
Cortier, V., Galindo, D., Glondu, S., Izabachène, M.: Election verifiability for helios under weaker trust assumptions. In: Kutyłowski, M., Vaidya, J. (eds.) ESORICS 2014. LNCS, vol. 8713, pp. 327–344. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11212-1_19
Cortier, V., Galindo, D., Küsters, R., Müller, J., Truderung, T.: SoK: verifiability notions for e-voting protocols. In: S&P 2016, pp. 779–798 (2016)
Cortier, V., Lallemand, J.: Voting: you can’t have privacy without individual verifiability. In: CCS 2018, pp. 53–66, New York (2018)
Cortier, V., Lallemand, J., Warinschi, B.: Fifty shades of ballot privacy: privacy against a malicious board. ePrint Report 2020/127 (2020)
Cortier, V., Smyth, B.: Attacking and fixing helios: an analysis of ballot secrecy. In: CSF 2011, pp. 297–311 (2011)
del Pino, R., Lyubashevsky, V., Neven, G., Seiler, G.: Practical quantum-safe voting from lattices. In: CCS 2017, pp. 1565–1581, New York (2017)
Delaune, S., Kremer, S., Ryan, M.: Coercion-resistance and receipt-freeness in electronic voting. In: CSFW 2006, pp. 12–42 (2006)
Desmedt, Y., Frankel, Y.: Threshold cryptosystems. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 307–315. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_28
Fouque, P.-A., Poupard, G., Stern, J.: Sharing decryption in the context of voting or lotteries. In: Frankel, Y. (ed.) FC 2000. LNCS, vol. 1962, pp. 90–104. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45472-1_7
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Helios voting system. heliosvoting.org/
Juels, A., Catalano, D., Jakobsson, M.: Coercion-resistant electronic elections. In: Chaum, D., et al. (eds.) Towards Trustworthy Elections. LNCS, vol. 6000, pp. 37–63. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12980-3_2
Kiayias, A., Zacharias, T., Zhang, B.: End-to-end verifiable elections in the standard model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 468–498. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_16
Pereira, O.: Internet voting with helios. Real-World Electronic Voting, pp. 277–308 (2016)
Shoup, V., Gennaro, R.: Securing threshold cryptosystems against chosen ciphertext attack. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 1–16. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054113
Smyth, B., Bernhard, D.: Ballot secrecy and ballot independence: definitions and relations. ePrint Report 2013/235 (2013)
Acknowledgement
This work is partly supported by the EPSRC and the UK government as part of the Centre for Doctoral Training in Cyber Security at Royal Holloway, University of London (EP/P009301/1)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Building Blocks for our Constructions
1.1 A.1 Public-Key Encryption
Definition 6
(PKE scheme) A public key encryption scheme \(\varPi \) is a tuple of PPT algorithms \((\varPi .\mathsf {Gen}, \varPi .\mathsf {Enc}, \varPi .\mathsf {Dec})\) such that
-
 On input security parameter
On input security parameter
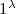 , algorithm \(\varPi .\mathsf {Gen}\) outputs a key pair \((pk_\varPi ,sk_\varPi )\).
, algorithm \(\varPi .\mathsf {Gen}\) outputs a key pair \((pk_\varPi ,sk_\varPi )\). -
\(\varPi .\mathsf {Enc}(pk_\varPi ,m)\) On input public key \(pk_\varPi \) and message m, algorithm \(\varPi .\mathsf {Enc}\) outputs a ciphertext c.
-
\(\varPi .\mathsf {Dec}(sk_\varPi ,c)\) On input private key \(sk_\varPi \) and ciphertext c, algorithm \(\varPi .\mathsf {Dec}\) outputs a message m.
Definition 7
( \(\mathsf {NM}\text {-}\mathsf {CPA}\) ). A public key encryption scheme \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) if, for any PPT adversary  , there exists a negligible function
, there exists a negligible function
 such that
such that

where
 is the experiment defined in Fig. 4.
is the experiment defined in Fig. 4.
1.2 A.2 Threshold Public Key Encryption
Definition 8
(Threshold PKE scheme) A (t, n)-threshold public key encryption scheme \(\varPhi \) is a tuple of PPT algorithms \((\varPhi .\mathsf {Gen}, \varPhi .\mathsf {Enc}, \varPhi .\mathsf {Dec}, \varPhi .\mathsf {Combine})\) such that
-
 On input security parameter
On input security parameter
 , threshold t and n, algorithm \(\varPhi .\mathsf {Gen}\) outputs a public key \(pk_\varPhi \) and n private keys, \(sk_{\varPhi _1}, \dots , sk_{\varPhi _n}\).
, threshold t and n, algorithm \(\varPhi .\mathsf {Gen}\) outputs a public key \(pk_\varPhi \) and n private keys, \(sk_{\varPhi _1}, \dots , sk_{\varPhi _n}\). -
\(\varPhi .\mathsf {Enc}(pk_\varPhi ,m)\) On input public key \(pk_\varPhi \) and message m, algorithm \(\varPhi .\mathsf {Enc}\) outputs a ciphertext c.
-
\(\varPhi .\mathsf {Dec}(pk_\varPhi ,i,sk_{\varPhi _i},c)\) On input public key \(pk_\varPhi \), an index \(1\le i\le n\), private key \(sk_{\varPhi _i}\) and ciphertext c, algorithm \(\varPhi .\mathsf {Dec}\) outputs a decryption share \(c_i\).
-
\(\varPhi .\mathsf {Combine}(pk_\varPhi ,c,c_1,\dots ,c_t)\) On input public key \(pk_\varPhi \), ciphertext c and t decryption shares \(c_1,\dots ,c_t\), algorithm \(\varPhi .\mathsf {Combine}\) outputs a message m.
Definition 9
( \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) ). A (t, n)-threshold public key encryption scheme \(\varPhi \) satisfies \(t\text {-}\mathsf {NM}\text {-}\mathsf {CPA}\) if, for any PPT adversary  , there exists a negligible function
, there exists a negligible function
 such that
such that

where
 is the experiment defined in Fig. 4.
is the experiment defined in Fig. 4.
1.3 A.3 Signature of Knowledge
Definition 10
(Signature of knowledge). A signature of knowledge \(\mathsf {SOK}\) is a tuple of algorithms \((\mathsf {SoK.Setup},\mathsf {SimSetup},\mathsf {SoK.Sign},\mathsf {SimSign},\mathsf {SoK.Verify})\) relative to a relation \(\mathcal {R}\) such that
-
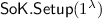 : on input security parameter
: on input security parameter
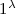 , algorithm \(\mathsf {SoK.Setup}\) outputs public parameters pp.
, algorithm \(\mathsf {SoK.Setup}\) outputs public parameters pp. -
 : on input security parameter
: on input security parameter
 , algorithm \(\mathsf {SimSetup}\) outputs public parameters pp and trapdoor \(\tau \).
, algorithm \(\mathsf {SimSetup}\) outputs public parameters pp and trapdoor \(\tau \). -
\(\mathsf {SoK.Sign}(pp,s,w,m)\): on input pp, statement s, witness w and message m, algorithm \(\mathsf {SoK.Sign}\) outputs a signature \(\sigma \) if \((s,w)\in \mathcal {R}\).
-
\(\mathsf {SimSign}(pp,s,\tau ,m)\): on input pp, s, \(\tau \) and m, algorithm \(\mathsf {SimSign}\) outputs a signature \(\sigma \).
-
\(\mathsf {SoK.Verify}(pp,s,m,\sigma )\): on input pp, s, m and \(\sigma \), algorithm \(\mathsf {SoK.Verify}\) outputs 1, if the signature verifies and 0 otherwise.
Definition 11
(Extractability). Let \(\mathsf {Extract}\) be a PPT algorithm such that
-
\(\mathsf {Extract}(pp,\tau ,s,m,\sigma )\): on input public parameters pp, trapdoor \(\tau \), statement s, message m and signature \(\sigma \), algorithm \(\mathsf {Extract}\) outputs a witness w.
Then signature of knowledge \(\mathsf {SOK}\) satisfies extractability if, for all PPT adversaries
 , there exists a negligible function
, there exists a negligible function
 such that
such that

where
 is the experiment defined in Fig. 5.
is the experiment defined in Fig. 5.
B Ballot Secrecy of our Constructions
1.1 B.1 Proof of Theorem 1
Let
 be an adversary in the experiment
be an adversary in the experiment
 where \(\varGamma _{\mathsf {mini}}\) is the construction in Fig. 2. Assume that
where \(\varGamma _{\mathsf {mini}}\) is the construction in Fig. 2. Assume that
 can output a bit \(\beta '\) such that \(\beta '=\beta \) and
can output a bit \(\beta '\) such that \(\beta '=\beta \) and
 queries \(\mathcal {O}\mathsf {vote}\) and \(\mathcal {O}\mathsf {cast}\) such that \(V_0'=V_1'\). Then
queries \(\mathcal {O}\mathsf {vote}\) and \(\mathcal {O}\mathsf {cast}\) such that \(V_0'=V_1'\). Then
 succeeds in experiment
succeeds in experiment
 with probability non-negligibly greater than \(\frac{1}{2}\). We note that, throughout the experiment,
with probability non-negligibly greater than \(\frac{1}{2}\). We note that, throughout the experiment,
 can only gain information about \(\beta \) through access to the bulletin board \(\mathcal {BB}_{}\) and the election result r.
can only gain information about \(\beta \) through access to the bulletin board \(\mathcal {BB}_{}\) and the election result r.
Let \(\mathsf {Forge}\) denote the event that
 submits a valid ballot \(b=(pk_{id_{}},c,\sigma )\) to \(\mathcal {O}\mathsf {cast}\) where \((\cdot ,pk_{id_{}},\cdot )\in \mathcal {Q}\mathsf {reg}\setminus \mathcal {Q}\mathsf {corrupt}\). We write that b is valid if \(\mathsf {Valid}(b,\mathcal {BB}_{},pk,\mathcal {L})=1\) which requires, in particular, that \(\mathsf {SoK.Verify}(pp,(c,pk_\varPi ,pk_{id_{}}),c,\sigma )=1\). Moreover, let \(\mathsf {Success}\) denote the event that experiment
submits a valid ballot \(b=(pk_{id_{}},c,\sigma )\) to \(\mathcal {O}\mathsf {cast}\) where \((\cdot ,pk_{id_{}},\cdot )\in \mathcal {Q}\mathsf {reg}\setminus \mathcal {Q}\mathsf {corrupt}\). We write that b is valid if \(\mathsf {Valid}(b,\mathcal {BB}_{},pk,\mathcal {L})=1\) which requires, in particular, that \(\mathsf {SoK.Verify}(pp,(c,pk_\varPi ,pk_{id_{}}),c,\sigma )=1\). Moreover, let \(\mathsf {Success}\) denote the event that experiment
 returns 1. Note that,
returns 1. Note that,

We show that  and
and  . The result of the Theorem then follows.
. The result of the Theorem then follows.
First, we show that  . In fact, we show that, if
. In fact, we show that, if
 can submit a valid ballot to \(\mathcal {O}\mathsf {corrupt}\), then
can submit a valid ballot to \(\mathcal {O}\mathsf {corrupt}\), then
 can be used to construct an adversary \(\mathcal {B}\) in the extractability experiment
can be used to construct an adversary \(\mathcal {B}\) in the extractability experiment
 , where \(\mathcal {B}\) plays the role of the challenger in the \(\mathsf {BS}\) experiment and \(\mathcal {C}\) is the challenger in the extractability experiment. In detail, we construct adversary \(\mathcal {B}\) as follows.
, where \(\mathcal {B}\) plays the role of the challenger in the \(\mathsf {BS}\) experiment and \(\mathcal {C}\) is the challenger in the extractability experiment. In detail, we construct adversary \(\mathcal {B}\) as follows.
-
1.
\(\mathcal {B}\) obtains public parameters pp for signature of knowledge \(\mathsf {SOK}\) from \(\mathcal {C}\) and runs
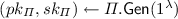 , and performs the setup of \(\varGamma _{\mathsf {mini}}\), providing
, and performs the setup of \(\varGamma _{\mathsf {mini}}\), providing  with pk. \(\mathcal {B}\) additionally performs the initialisation steps of the \(\mathsf {BS}\) experiment and selects a bit \(\beta \leftarrow \{0,1\}\).
with pk. \(\mathcal {B}\) additionally performs the initialisation steps of the \(\mathsf {BS}\) experiment and selects a bit \(\beta \leftarrow \{0,1\}\). -
2.
\(\mathcal {B}\) answers queries to \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\) and \(\mathcal {O}\mathsf {board}\) as described in the \(\mathsf {BS}\) experiment. Moreover, \(\mathcal {B}\) computes the election result as described in algorithm \(\mathsf {Tally}\).
-
3.
For queries to \(\mathcal {O}\mathsf {vote}(pk_{id_{}},v_0,v_1)\), \(\mathcal {B}\) computes \(c\leftarrow \varPi .\mathsf {Enc}(pk_\varPi ,m_\beta ;r)\) and queries \(\mathcal {O}_{pp,\tau }((c,pk_\varPi ,pk_{id_{}}),(sk_{id_{}},r),c)\) in the extractability experiment, receiving a signature of knowledge \(\sigma \). \(\mathcal {B}\) constructs ballot \(b\leftarrow (pk_{id_{}},c,\sigma )\) and appends the ballot to \(\mathcal {BB}_{}\).
-
4.
\(\mathcal {B}\) answers queries to \(\mathcal {O}\mathsf {cast}\) as described in the \(\mathsf {BS}\) experiment. By assumption that event \(\mathsf {Forge}\) occurs, \(\mathsf {SoK.Verify}\) returns 1 for at least one tuple \((pk_{id_{}},b)\) queried to \(\mathcal {O}\mathsf {cast}\) such that \(pk_{id_{}}\in \mathcal {Q}\mathsf {reg}\setminus \mathcal {Q}\mathsf {corrupt}\). We denote this ballot as \((pk_{id_{}}^*,c^*,\sigma ^*)\). Then, \(\mathcal {B}\) output \(((c^*,pk_\varPi ,pk_{id_{}}^*),c^*,\sigma ^*)\) in the extractability experiment.
\(\mathcal {B}\) perfectly simulates the role of the challenger in the \(\mathsf {BS}\) experiment to
 . In fact, \(\mathcal {B}\) trivially simulates oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\) and \(\mathcal {O}\mathsf {board}\), and trivially computes the result of the election and returns r to
. In fact, \(\mathcal {B}\) trivially simulates oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\) and \(\mathcal {O}\mathsf {board}\), and trivially computes the result of the election and returns r to
 . Moreover, when
. Moreover, when
 queries \(\mathcal {O}\mathsf {vote}\), \(\mathcal {B}\) returns a ciphertext consisting of an encryption c that is identical to the encryption viewed by
queries \(\mathcal {O}\mathsf {vote}\), \(\mathcal {B}\) returns a ciphertext consisting of an encryption c that is identical to the encryption viewed by
 in the \(\mathsf {BS}\) experiment and obtains a signature of knowledge from \(\mathcal {O}\mathsf {}\) in the extractability experiment that is identical to the signature viewed by
in the \(\mathsf {BS}\) experiment and obtains a signature of knowledge from \(\mathcal {O}\mathsf {}\) in the extractability experiment that is identical to the signature viewed by
 in the \(\mathsf {BS}\) experiment. Therefore, \(\mathcal {B}\) perfectly simulates \(\mathcal {O}\mathsf {vote}\) to
in the \(\mathsf {BS}\) experiment. Therefore, \(\mathcal {B}\) perfectly simulates \(\mathcal {O}\mathsf {vote}\) to
 . Furthermore, \(\mathcal {B}\) perfectly simulates \(\mathcal {O}\mathsf {cast}\) to
. Furthermore, \(\mathcal {B}\) perfectly simulates \(\mathcal {O}\mathsf {cast}\) to
 and, if event \(\mathsf {Forge}\) occurs,
and, if event \(\mathsf {Forge}\) occurs,
 successfully creates a valid signature of knowledge without witness \((sk_{id_{}},r)\), and, therefore, \(\mathcal {B}\) can output this signature in the extractability experiment and succeeds. By assumption, the signature of knowledge \(\mathsf {SOK}\) satisfies extractability, and hence, we conclude that
successfully creates a valid signature of knowledge without witness \((sk_{id_{}},r)\), and, therefore, \(\mathcal {B}\) can output this signature in the extractability experiment and succeeds. By assumption, the signature of knowledge \(\mathsf {SOK}\) satisfies extractability, and hence, we conclude that  .
.
We now show that  . That is, we show that, if
. That is, we show that, if
 succeeds in the \(\mathsf {BS}\) experiment without event \(\mathsf {Forge}\) occurring, we can use
succeeds in the \(\mathsf {BS}\) experiment without event \(\mathsf {Forge}\) occurring, we can use
 to construct an adversary \(\mathcal {B}'\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment
to construct an adversary \(\mathcal {B}'\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment
 , where \(\mathcal {B}'\) plays the role of the challenger in the \(\mathsf {BS}\) experiment and \(\mathcal {C}\) is the challenger in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment against scheme \(\varPi \). In detail, we construct adversary \(\mathcal {B}'\) as follows.
, where \(\mathcal {B}'\) plays the role of the challenger in the \(\mathsf {BS}\) experiment and \(\mathcal {C}\) is the challenger in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment against scheme \(\varPi \). In detail, we construct adversary \(\mathcal {B}'\) as follows.
-
1.
\(\mathcal {B}'\) obtains a public key \(pk_\varPi \) for public key encryption scheme \(\varPi \) from \(\mathcal {C}\), runs
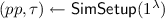 , and performs the setup of \(\varGamma _{\mathsf {mini}}\), providing
, and performs the setup of \(\varGamma _{\mathsf {mini}}\), providing  with pk. \(\mathcal {B}'\) additionally performs the initialisation steps of the \(\mathsf {BS}\) experiment.
with pk. \(\mathcal {B}'\) additionally performs the initialisation steps of the \(\mathsf {BS}\) experiment. -
2.
\(\mathcal {B}'\) answers queries to oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\), \(\mathcal {O}\mathsf {cast}\) and \(\mathcal {O}\mathsf {board}\) as described in the \(\mathsf {BS}\) experiment.
-
3.
For queries \(\mathcal {O}\mathsf {vote}(pk_{id_{}}, v_0,v_1)\), \(\mathcal {B}'\) queries \((m_0=v_0,m_1=v_1)\) to oracle \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment and receives a ciphertext c of \(m_\beta \). \(\mathcal {B}'\) then computes \(\sigma \leftarrow \mathsf {SimSign}(pp,(c,pk_\varPi ,pk_{id_{}}),\tau ,c)\) and appends ballot \(b=(pk_{id_{}},c,\sigma )\) to \(\mathcal {BB}_{}\).
-
4.
\(\mathcal {B}'\) computes the election result. Throughout, \(\mathcal {B}'\) keeps track of tuples \((pk_{id_{}},b)\) queried by
 to \(\mathcal {O}\mathsf {cast}\), such that the query results in a ballot that will be included in the result. We denote by B the set of all tuples of the form \((pk_{id_{}},b)\). \(\mathcal {B}'\) constructs a vector \(\mathbf {c}\) that consists of the ciphertext element of each ballot in B and submits \(\mathbf {c}\) to \(\mathcal {C}\). \(\mathcal {C}\) returns a vector of plaintexts \(\mathbf {m}\) (i.e., the plaintext votes encoded in ballots submitted to \(\mathcal {O}\mathsf {cast}\)) to \(\mathcal {B}'\). For each tuple \((pk_{id_{}},b)\in B\), \(\mathcal {B}'\) replaces ballot b with the corresponding plaintext included in vector \(\mathbf {m}\). \(\mathcal {B}'\) then computes the result r by computing the result function \(f(V_0\cup B)\).
to \(\mathcal {O}\mathsf {cast}\), such that the query results in a ballot that will be included in the result. We denote by B the set of all tuples of the form \((pk_{id_{}},b)\). \(\mathcal {B}'\) constructs a vector \(\mathbf {c}\) that consists of the ciphertext element of each ballot in B and submits \(\mathbf {c}\) to \(\mathcal {C}\). \(\mathcal {C}\) returns a vector of plaintexts \(\mathbf {m}\) (i.e., the plaintext votes encoded in ballots submitted to \(\mathcal {O}\mathsf {cast}\)) to \(\mathcal {B}'\). For each tuple \((pk_{id_{}},b)\in B\), \(\mathcal {B}'\) replaces ballot b with the corresponding plaintext included in vector \(\mathbf {m}\). \(\mathcal {B}'\) then computes the result r by computing the result function \(f(V_0\cup B)\). -
5.
\(\mathcal {B}'\) returns the bit \(\beta '\) output by
 .
.
We show that \(\mathcal {B'}\) perfectly simulates the role of the challenger in the \(\mathsf {BS}\) experiment to
 . Trivially, \(\mathcal {B}'\) simulates oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\), \(\mathcal {O}\mathsf {cast}\) and \(\mathcal {O}\mathsf {board}\) to
. Trivially, \(\mathcal {B}'\) simulates oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\), \(\mathcal {O}\mathsf {cast}\) and \(\mathcal {O}\mathsf {board}\) to
 . Additionally, \(\mathcal {B}'\) answers queries to \(\mathcal {O}\mathsf {vote}\) by obtaining a ciphertext from \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment that is identical to the encryption viewed by
. Additionally, \(\mathcal {B}'\) answers queries to \(\mathcal {O}\mathsf {vote}\) by obtaining a ciphertext from \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment that is identical to the encryption viewed by
 in the \(\mathsf {BS}\) experiment and constructs a signature of knowledge that is identical to that viewed by
in the \(\mathsf {BS}\) experiment and constructs a signature of knowledge that is identical to that viewed by
 . Consequently, the ballot obtained by \(\mathcal {B}'\), and subsequently appended to the ballot box, is identical to the ballot computed by \(\mathcal {O}\mathsf {vote}\). Therefore, \(\mathcal {B}'\) perfectly simulates \(\mathcal {O}\mathsf {vote}\). Finally, \(\mathcal {B}'\) computes the result function for set \(V_0\) (and B). By the assumption that event \(\mathsf {Forge}\) does not occur, B cannot contain ballots meaningfully related to the votes of honest voters. Moreover, by assumption that
. Consequently, the ballot obtained by \(\mathcal {B}'\), and subsequently appended to the ballot box, is identical to the ballot computed by \(\mathcal {O}\mathsf {vote}\). Therefore, \(\mathcal {B}'\) perfectly simulates \(\mathcal {O}\mathsf {vote}\). Finally, \(\mathcal {B}'\) computes the result function for set \(V_0\) (and B). By the assumption that event \(\mathsf {Forge}\) does not occur, B cannot contain ballots meaningfully related to the votes of honest voters. Moreover, by assumption that
 succeeds in the \(\mathsf {BS}\) experiment, \(V_0=V_1\) and, as such, \(\mathcal {B}'\) perfectly simulates algorithm \(\mathsf {Tally}\) to
succeeds in the \(\mathsf {BS}\) experiment, \(V_0=V_1\) and, as such, \(\mathcal {B}'\) perfectly simulates algorithm \(\mathsf {Tally}\) to
 . Moreover, we have that \(\beta '\) output by \(\mathcal {B}'\) is equal to the bit \(\beta \) chosen by \(\mathcal {C}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. In particular, if
. Moreover, we have that \(\beta '\) output by \(\mathcal {B}'\) is equal to the bit \(\beta \) chosen by \(\mathcal {C}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. In particular, if
 correctly guesses \(\beta '\) in the \(\mathsf {BS}\) experiment,
correctly guesses \(\beta '\) in the \(\mathsf {BS}\) experiment,
 correctly determines whether \(\mathcal {BB}_{}\) contains ballots corresponding to left- or right-hand votes submitted via \(\mathcal {O}\mathsf {vote}\). As these ballots are created by calling \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment where the bit \(\beta \) is chosen by the \(\mathsf {NM}\text {-}\mathsf {CPA}\) challenger, \(\mathcal {B}'\) succeeds in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. However, by assumption, \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) security and we conclude that
correctly determines whether \(\mathcal {BB}_{}\) contains ballots corresponding to left- or right-hand votes submitted via \(\mathcal {O}\mathsf {vote}\). As these ballots are created by calling \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment where the bit \(\beta \) is chosen by the \(\mathsf {NM}\text {-}\mathsf {CPA}\) challenger, \(\mathcal {B}'\) succeeds in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. However, by assumption, \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) security and we conclude that  . \(\square \)
. \(\square \)
1.2 B.2 Proof of Theorem 2
The details of this result follow largely from the proof of Theorem 1. We let
 be an adversary in the experiment
be an adversary in the experiment
 where \(\varGamma _{\mathsf {mini}}\) is the construction in Fig. 2. We assume that
where \(\varGamma _{\mathsf {mini}}\) is the construction in Fig. 2. We assume that
 succeeds in experiment
succeeds in experiment
 with probability non-negligibly greater than \(\frac{1}{2}\), that is,
with probability non-negligibly greater than \(\frac{1}{2}\), that is,
 outputs a bit \(\beta '\) such that \(\beta '=\beta \) and constructs ballot box \(\mathcal {BB}_{}\) such that \(V_0=V_1\). Throughout the experiment,
outputs a bit \(\beta '\) such that \(\beta '=\beta \) and constructs ballot box \(\mathcal {BB}_{}\) such that \(V_0=V_1\). Throughout the experiment,
 obtains information about \(\beta \) through ballots output by \(\mathcal {O}\mathsf {vote}\) and the election result r.
obtains information about \(\beta \) through ballots output by \(\mathcal {O}\mathsf {vote}\) and the election result r.
Let \(\mathsf {Forge}\) denote the event that
 posts a valid ballot \(b=(pk_{id_{}},c,\sigma )\) to \(\mathcal {BB}_{}\) where \(pk_{id_{}}\in \mathcal {L}\setminus \mathsf {corr}\mathcal {L}\) and b is not the output of \(\mathcal {O}\mathsf {vote}\). We write that b is valid if \(\mathsf {SoK.Verify}(pp,(c,pk_\varPi ,pk_{id_{}}),\sigma ,c)=1\). Moreover, let \(\mathsf {Success}\) denote the event that experiment
posts a valid ballot \(b=(pk_{id_{}},c,\sigma )\) to \(\mathcal {BB}_{}\) where \(pk_{id_{}}\in \mathcal {L}\setminus \mathsf {corr}\mathcal {L}\) and b is not the output of \(\mathcal {O}\mathsf {vote}\). We write that b is valid if \(\mathsf {SoK.Verify}(pp,(c,pk_\varPi ,pk_{id_{}}),\sigma ,c)=1\). Moreover, let \(\mathsf {Success}\) denote the event that experiment
 returns 1. As before,
returns 1. As before,

We show that  and
and  . The result of the Theorem then follows.
. The result of the Theorem then follows.
First, we show that  . In fact, we show that, if
. In fact, we show that, if
 can post a valid ballot to \(\mathcal {BB}_{}\) for an honest voter (without calling \(\mathcal {O}\mathsf {vote}\)), then
can post a valid ballot to \(\mathcal {BB}_{}\) for an honest voter (without calling \(\mathcal {O}\mathsf {vote}\)), then
 can be used to construct an adversary \(\mathcal {B}\) in the extractability experiment
can be used to construct an adversary \(\mathcal {B}\) in the extractability experiment
 , where \(\mathcal {B}\) plays the role of the challenger in the \(\mathsf {mbbBS}\) experiment and \(\mathcal {C}\) is the challenger in the extractability experiment. The detailed construction of \(\mathcal {B}\) is very similar to the adversary \(\mathcal {B}\) described in the proof of Theorem 1, and we refer the reader to this proof for full details. We describe the following changes to the adversary \(\mathcal {B}\):
, where \(\mathcal {B}\) plays the role of the challenger in the \(\mathsf {mbbBS}\) experiment and \(\mathcal {C}\) is the challenger in the extractability experiment. The detailed construction of \(\mathcal {B}\) is very similar to the adversary \(\mathcal {B}\) described in the proof of Theorem 1, and we refer the reader to this proof for full details. We describe the following changes to the adversary \(\mathcal {B}\):
-
1.
In step 2, \(\mathcal {B}\) does not answer queries to oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\) or \(\mathcal {O}\mathsf {board}\) as
 does not have access to these oracles in the \(\mathsf {mbbBS}\) experiment.
does not have access to these oracles in the \(\mathsf {mbbBS}\) experiment. -
2.
In step 4, by assumption that event \(\mathsf {Forge}\) occurs, \(\mathsf {SoK.Verify}\) returns 1 for at least one ballot, which we denote \(b^*=(pk_{id_{}}^*,c^*,\sigma ^*)\), that appears on \(\mathcal {BB}_{}\) such that \(pk_{id_{}}\in \mathcal {L}\setminus \mathsf {corr}\mathcal {L}\) and b is not the output of \(\mathcal {O}\mathsf {vote}\). Then, \(\mathcal {B}\) output \(((c^*,pk_\varPi ,pk_{id_{}}^*),c^*,\sigma ^*)\) in the extractability experiment.
\(\mathcal {B}\) perfectly simulates the role of the challenger in the \(\mathsf {mbbBS}\) experiment to
 . As in the proof of Theorem 1, \(\mathcal {B}\) perfectly simulates \(\mathcal {O}\mathsf {vote}\) to
. As in the proof of Theorem 1, \(\mathcal {B}\) perfectly simulates \(\mathcal {O}\mathsf {vote}\) to
 . Furthermore, if event \(\mathsf {Forge}\) occurs,
. Furthermore, if event \(\mathsf {Forge}\) occurs,
 successfully creates a valid signature without witness \((sk_{id_{}},r)\), and, therefore, \(\mathcal {B}\) can output this signature in the extractability experiment and succeeds. By assumption, the signature of knowledge \(\mathsf {SOK}\) satisfies extractability, and hence, we conclude that
successfully creates a valid signature without witness \((sk_{id_{}},r)\), and, therefore, \(\mathcal {B}\) can output this signature in the extractability experiment and succeeds. By assumption, the signature of knowledge \(\mathsf {SOK}\) satisfies extractability, and hence, we conclude that  .
.
We now show that  . That is, we show that, if
. That is, we show that, if
 succeeds in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment without event \(\mathsf {Forge}\) occurring, we can use
succeeds in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment without event \(\mathsf {Forge}\) occurring, we can use
 to construct an adversary \(\mathcal {B}'\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment
to construct an adversary \(\mathcal {B}'\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment
 , where \(\mathcal {B}'\) plays the role of the challenger in the \(\mathsf {mbbBS}\) experiment and \(\mathcal {C}\) is the challenger in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. Again, the detailed construction of \(\mathcal {B'}\) is very similar to the adversary \(\mathcal {B}'\) described in the proof of Theorem 1, and we describe the following changes to \(\mathcal {B'}\):
, where \(\mathcal {B}'\) plays the role of the challenger in the \(\mathsf {mbbBS}\) experiment and \(\mathcal {C}\) is the challenger in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. Again, the detailed construction of \(\mathcal {B'}\) is very similar to the adversary \(\mathcal {B}'\) described in the proof of Theorem 1, and we describe the following changes to \(\mathcal {B'}\):
-
1.
Step 2 is no longer required as
 does not have access to oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\) or \(\mathcal {O}\mathsf {board}\) in the \(\mathsf {mbbBS}\) experiment.
does not have access to oracles \(\mathcal {O}\mathsf {reg}\), \(\mathcal {O}\mathsf {corrupt}\) or \(\mathcal {O}\mathsf {board}\) in the \(\mathsf {mbbBS}\) experiment. -
2.
For queries to \(\mathcal {O}\mathsf {vote}(pk_{id_{}},v_0,v_1)\), rather than appending ballot b to \(\mathcal {BB}_{}\), \(\mathcal {B}'\) outputs b to
 .
. -
3.
To compute the election result, \(\mathcal {B}'\) creates a set B that consists of tuples \((pk_{id_{}},b)\) such that ballot b, submitted on behalf of voter credential \(pk_{id_{}}\), appears on \(\mathcal {BB}_{}\), is not an output of \(\mathcal {O}\mathsf {vote}\), and will be included in the result (i.e., is the last ballot cast for voter \(pk_{id_{}}\)). \(\mathcal {B}'\) then constructs vector \(\mathbf {c}\) from set B and proceeds to compute the election result as described in Step 4 in the proof of Theorem 1.
\(\mathcal {B}'\) perfectly simulates the role of the challenger in the \(\mathsf {mbbBS}\) experiment to
 . In particular, the ballot output by \(\mathcal {B}'\) following a query to \(\mathcal {O}\mathsf {vote}\) is identical to the ballot output by \(\mathcal {O}\mathsf {vote}\) because \(\mathcal {B}'\) obtains the ballot by querying \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. Moreover, as in the proof of Theorem 1, \(\mathcal {B}'\) perfectly simulates algorithm \(\mathsf {Tally}\) to
. In particular, the ballot output by \(\mathcal {B}'\) following a query to \(\mathcal {O}\mathsf {vote}\) is identical to the ballot output by \(\mathcal {O}\mathsf {vote}\) because \(\mathcal {B}'\) obtains the ballot by querying \(\mathcal {O}\mathsf {Encrypt}\) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. Moreover, as in the proof of Theorem 1, \(\mathcal {B}'\) perfectly simulates algorithm \(\mathsf {Tally}\) to
 as we assume that \(V_0=V_1\) and, as such, the results computed for \(\beta =0\) and \(\beta =1\) are identical. \(\mathcal {B}'\) outputs \(\beta '=\beta \) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. That is, if
as we assume that \(V_0=V_1\) and, as such, the results computed for \(\beta =0\) and \(\beta =1\) are identical. \(\mathcal {B}'\) outputs \(\beta '=\beta \) in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. That is, if
 outputs \(\beta '=\beta \) in the \(\mathsf {mbbBS}\) experiment,
outputs \(\beta '=\beta \) in the \(\mathsf {mbbBS}\) experiment,
 correctly determines whether \(\mathcal {O}\mathsf {vote}\) returns a ballot corresponding to the left- or right-hand vote. As the ballot is constructed by calling \(\mathcal {O}\mathsf {Encrypt}\), where \(\beta \) is chosen by the challenger \(\mathcal {C}\), \(\mathcal {B}'\) succeeds in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. By assumption, \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) security and we conclude that
correctly determines whether \(\mathcal {O}\mathsf {vote}\) returns a ballot corresponding to the left- or right-hand vote. As the ballot is constructed by calling \(\mathcal {O}\mathsf {Encrypt}\), where \(\beta \) is chosen by the challenger \(\mathcal {C}\), \(\mathcal {B}'\) succeeds in the \(\mathsf {NM}\text {-}\mathsf {CPA}\) experiment. By assumption, \(\varPi \) satisfies \(\mathsf {NM}\text {-}\mathsf {CPA}\) security and we conclude that  . \(\square \)
. \(\square \)
1.3 B.3 Proof of Theorem 3
The details of this result follow largely from the proof of Theorem 2. We focus on the changes to the proof of Theorem 2. We let
 be an adversary in the experiment
be an adversary in the experiment
 where \(\varGamma _{\mathsf {mini}}'\) is the construction described in Sect. 4.2. We assume that
where \(\varGamma _{\mathsf {mini}}'\) is the construction described in Sect. 4.2. We assume that
 succeeds in experiment
succeeds in experiment
 with probability non-negligibly greater than \(\frac{1}{2}\). We define events \(\mathsf {Forge}\) and \(\mathsf {Success}\) as in the proof of Theorem 2 and we show that
with probability non-negligibly greater than \(\frac{1}{2}\). We define events \(\mathsf {Forge}\) and \(\mathsf {Success}\) as in the proof of Theorem 2 and we show that  and
and  . The result of the Theorem then follows.
. The result of the Theorem then follows.
First, we show that  . This part of the proof is identical to the proof of Theorem 2, with the following exceptions. In step 1 of the description of adversary \(\mathcal {B}\), \(\mathcal {B}\) runs
. This part of the proof is identical to the proof of Theorem 2, with the following exceptions. In step 1 of the description of adversary \(\mathcal {B}\), \(\mathcal {B}\) runs  and provides
and provides
 with \(t-1\) private keys of
with \(t-1\) private keys of
 choice. Additionally, \(\mathcal {B}\) computes the result using the \(t-1\) private keys given to
choice. Additionally, \(\mathcal {B}\) computes the result using the \(t-1\) private keys given to
 plus one other private key. As in the proof of Theorem 2, \(\mathcal {B}\) perfectly simulates the role of the challenger in the \(\mathsf {dtBS}\) experiment to
plus one other private key. As in the proof of Theorem 2, \(\mathcal {B}\) perfectly simulates the role of the challenger in the \(\mathsf {dtBS}\) experiment to
 . In particular, \(\mathcal {B}\) generates the keys for \(\varPhi \) and provides
. In particular, \(\mathcal {B}\) generates the keys for \(\varPhi \) and provides
 with \(t-1\) private keys as expected. This concludes the first part of the proof.
with \(t-1\) private keys as expected. This concludes the first part of the proof.
We now show that  . We describe the following change to adversary \(\mathcal {B}'\). In step 1, \(\mathcal {B}'\) requests the \(t-1\) private keys from \(\mathcal {C}\) that
. We describe the following change to adversary \(\mathcal {B}'\). In step 1, \(\mathcal {B}'\) requests the \(t-1\) private keys from \(\mathcal {C}\) that
 requests, and \(\mathcal {B}'\) returns the private keys provided by \(\mathcal {C}\) to
requests, and \(\mathcal {B}'\) returns the private keys provided by \(\mathcal {C}\) to
 . Specific to the proof of this result, \(\mathcal {B}'\) returns private keys to
. Specific to the proof of this result, \(\mathcal {B}'\) returns private keys to
 that are identical to the private keys output to
that are identical to the private keys output to
 in the \(\mathsf {dtBS}\) experiment. Therefore, the second part of the proof holds. \(\square \)
in the \(\mathsf {dtBS}\) experiment. Therefore, the second part of the proof holds. \(\square \)
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Fraser, A., Quaglia, E.A. (2021). Protecting the Privacy of Voters: New Definitions of Ballot Secrecy for E-Voting. In: Dunkelman, O., Jacobson, Jr., M.J., O'Flynn, C. (eds) Selected Areas in Cryptography. SAC 2020. Lecture Notes in Computer Science(), vol 12804. Springer, Cham. https://doi.org/10.1007/978-3-030-81652-0_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-81652-0_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81651-3
Online ISBN: 978-3-030-81652-0
eBook Packages: Computer ScienceComputer Science (R0)





 On input security parameter
On input security parameter
 , algorithm
, algorithm  . Oracle
. Oracle  , and updates a list of queries
, and updates a list of queries  .
.
 where
where  has access to oracles
has access to oracles 

 where
where  has access to oracle
has access to oracle  On input security parameter
On input security parameter
 , algorithm
, algorithm 
 for public key encryption scheme
for public key encryption scheme  for (t, n)-threshold public key encryption scheme
for (t, n)-threshold public key encryption scheme  On input security parameter
On input security parameter
 , threshold t and n, algorithm
, threshold t and n, algorithm 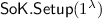 : on input security parameter
: on input security parameter
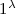 , algorithm
, algorithm  : on input security parameter
: on input security parameter
 , algorithm
, algorithm 
 for signature of knowledge
for signature of knowledge 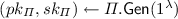 , and performs the setup of
, and performs the setup of  with pk.
with pk. 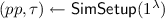 , and performs the setup of
, and performs the setup of  with pk.
with pk.  to
to  .
. does not have access to these oracles in the
does not have access to these oracles in the  does not have access to oracles
does not have access to oracles  .
.