Keywords

1 Introduction

Boolean functions are widely used in cryptography, error correction codes [2] and signal sequence design [7]. Their applications in cryptographic systems have been studied for more than three decades. Some important properties of these functions, including balance, nonlinearity and algebraic immunity, are obtained. Walsh transform is a powerful tool to study the properties of Boolean functions in the application of cryptography and coding theory. The Walsh transform of a Boolean function, a discrete Fourier transform, can be used to express the cryptographic properties of a Boolean function.

Bent functions proposed by [14] are Boolean functions with two different Walsh transform values and implements the maximum Hamming distance function to all the affine Boolean functions. Bent functions exist only with even number of variables. Bent functions have been extensively studied because of their interesting algebraic and combinatorial properties and it have received a lot of attention in the literature on communications, because of their multiple applications in cryptography [1], the fields of coding theory [8] and sequence design [13].

No bent function is balanced. As generalizations of bent functions, [5] introduced the concept of semi-bent functions and obtained the balancedness and good nonlinearity in both even and odd number of variables. Moreover, [17, 18] proved that bent functions and semi-bent functions are particular cases of the so-called plateaued functions. Like bent functions, semi-bent functions are also widely studied in cryptography. Because they have low Walsh transform values which can provide protection against fast correlation attacks [12] and linear cryptanalysis [9], they can possess desirable properties such as low autocorrelation, propagation criteria, resiliency, and high algebraic degree. Several new families of semi-bent functions were proposed by [3, 4, 6, 10, 15].

In 2014, [11] provided several new effective constructions of bent functions, and then gave several new infinite families of bent functions by adding a product of two linear functions to some known bent functions and their duals. After that, by adding a product of three linear functions to some known bent functions, [16] presented several classes of bent functions. Inspired by those results, in this paper, we firstly add a product of three linear functions to some known bent functions, and then add another product of three linear functions to which one (the added two products are related each other), so we obtain a class of bent functions and their duals. On the other hand, we promote a class of semi-bent functions and some classes of Boolean functions with five-valued Walsh spectra. Finally, a spectrum distribution of some class of Boolean functions with five-valued Walsh spectra is presented.

The paper is organized as follows. In Sect. 2, we introduce some notations and preliminaries. In Sect. 3, we present some bent functions, semi-bent functions and some functions with five-valued Walsh spectra. In Sect. 4, a spectrum distribution of the Boolean functions obtained in Sect. 3 is given. Section 5 concludes the paper.

2 Preliminaries

For a positive integer n,  let be the finite field with \(2^n\) elements, \(Tr_1^n\) denotes the absolute trace function from onto

Thus the Walsh transform of a Boolean function f on \(\mathbb {F}_{2^n}\) is defined by

Let \(N_i\) be the number of such that \(\hat{f}(\alpha )=v_i,\) i.e., where and t is a positive integer. By the properties of Walsh transform, we have the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{l} \sum \limits _{i=1}^tN_i=2^n,\\ \sum \limits _{i=1}^tN_iv_i=2^n(-1)^{f(0)},\\ \sum \limits _{i=1}^tN_iv_i^2=2^{2n}, \end{array}\right. \end{aligned}$$
(1)

A Boolean function (n even) is said to be bent if \(\hat{f}(\omega )=\pm 2^{\frac{n}{2}}\) for all \(\omega \in \mathbb {F}_{2^n}.\) Bent functions occur in pair. In fact, given a bent function f over we define its dual function, denoted by \(\tilde{f}\), when considering the signs of the values of the Walsh transform of f. More precisely, \(\hat{f}\) is defined by

$$\begin{aligned} \hat{f}(x)=2^{\frac{n}{2}}(-1)^{\tilde{f}(x)}. \end{aligned}$$
(2)

A Boolean function is said to be semi-bent if \(\hat{f}(\omega )\in \{0, \pm 2^{\frac{n+2}{2}}\}\) and if \(\hat{f}(\omega )\in \{0, \pm 2^{\frac{n+1}{2}}\}\) for all corresponding to n even and n odd, respectively. It is well known that the algebraic degree of a bent or semi-bent function defined on is at most \(\frac{n}{2}\) [2].

Let \(n=2m\) be a positive even integer and h be the monomial Niho quadratic function

$$\begin{aligned} h(x)=Tr_1^m(\lambda x^{2^m+1}), \end{aligned}$$
(3)

with . It is well known that h is bent, and its dual function \(\tilde{h}\) is given (see [11]) by

$$\begin{aligned} \tilde{h}(x)=Tr_1^m(\lambda ^{-1}x^{2^m+1})+1. \end{aligned}$$
(4)

Below we always let \(n=2m\) be an even and

3 Infinite Families of Bent, Semi-bent and Five-Valued Functions from Monomial Bent Functions

In this section, we give a class of bent functions, its dual function, a class of semi-bent functions and some classes of five-valued Walsh spectra.

We begin with the result presented by [11] that plays an important role. Let \(f_1, f_2\) and \(f_3\) be three pairwise distinct Boolean functions. Then define :

$$\begin{aligned} g(x)=f_1(x)f_2(x)+f_1(x)f_3(x)+f_2(x)f_3(x). \end{aligned}$$
(5)

Lemma 1

[11] Let \(f_1, f_2\) and \(f_3\) be three pairwise distinct bent functions over such that \(\psi =f_1+f_2+f_3\) is bent. Let g be a Boolean function defined by Eq. (5). Then g is bent if and only if \(\tilde{f_1}+\tilde{f_2}+\tilde{f_3}+\tilde{\psi }=0.\) Furthermore, if g is a bent function, then \(\tilde{g}\) is given by

[11] provides several new effective constructions of bent functions based on Eq. (5). Let be three bent functions given by

where \(a_1, a_2\) and \(a_3\) are pairwise distinct elements of After a simple calculation, Mesnager obtained that the Boolean function \(g(x)=f_1(x)f_2(x)+f_1(x)f_3(x)+f_2(x)f_3(x) = Tr_1^m(\lambda x^{2^m+1})+Tr_1^n(ax)Tr_1^n(bx)+Tr^n_1(a_1x),\) where \(a = a_1+a_3, b = a_1+a_2.\) In the next lemma, Mesnager pointed out that g(x) is a bent function under some conditions.

Lemma 2

[11] Let such that \(a\ne b\) and \(Tr_1^n(\lambda ^{-1}b^{2^m}a)=0.\) Then the Boolean function g defined on as \(g(x)=Tr_1^m(\lambda x^{2^m+1})+Tr_1^n(ax)Tr_1^n(bx),\) it is a bent function of algebraic degree 2 and its dual function \(\tilde{g}\) is given by

$$\begin{aligned} \tilde{g}(x)= & {} 1+Tr_1^m(\lambda ^{-1}x^{2^m+1})+\Big (Tr_1^m(\lambda ^{-1}a^{2^m+1})+Tr_1^n(\lambda ^{-1}a^{2^m}x)\Big )\\&\cdot \Big (Tr_1^m(\lambda ^{-1}b^{2^m+1})+Tr_1^n(\lambda ^{-1}b^{2^m}x)\Big ). \end{aligned}$$

Then one constructs a new class of Boolean functions and invests their properties by the two lemmas above. Let

$$\begin{aligned} f_i(x)=Tr_1^m(\lambda x^{2^m+1})+Tr_1^n(ax)Tr_1^n(a_ix), \end{aligned}$$

where \(a, a_1, a_2, a_3\) are pairwise distinct elements of  Hence by Eq. (5), one can obtain

$$\begin{aligned} f(x)= & {} f_1(x)f_2(x)+f_2(x)f_3(x)+f_1(x)f_3(x) \nonumber \\= & {} Tr_1^m(\lambda x^{2^m+1})+Tr_1^n(ax)Tr_1^n(a_1x)Tr_1^n((a_2+a_3)x)\nonumber \\&+Tr_1^n(ax)Tr_1^n(a_2x)Tr_1^n(a_3x). \end{aligned}$$
(6)

Motivated by [16, Lemma 1], we get the following result.

Lemma 3

Let h(x) be a Boolean function on and \(a, a_1, a_2, a_3\) are pairwise distinct elements of  If f(x) is defined as follows

$$\begin{aligned} f(x)=h(x)+Tr_1^n(ax)Tr_1^n(a_1x)Tr_1^n((a_2+a_3)x)+Tr_1^n(ax)Tr_1^n(a_2x)Tr_1^n(a_3x), \end{aligned}$$

then for any

$$\begin{aligned} \hat{f}(b)= & {} \frac{1}{4}\Big (2\hat{h}(b)+\sum \limits _{i=1}^3\hat{h}(b+a_i)-\hat{h}(b+\sum \limits _{i=1}^3a_i)+2\hat{h}(a+b)\\&-\sum \limits _{i=1}^3\hat{h}(a+b+a_i)+\hat{h}(a+b+\sum \limits _{i=1}^3a_i)\Big ). \end{aligned}$$

Proof

For any we define the set

and integer

$$S_{(\varepsilon _1, \varepsilon _2, \varepsilon _3)}(b)=\sum \limits _{x\in T(\varepsilon _1, \varepsilon _2, \varepsilon _3)}(-1)^{h(x)+Tr_1^n(bx)}.$$

Then for any and we have

(7)

One can immediately have \(wt(\varepsilon _1, \varepsilon _2, \varepsilon _3)\) is the Hamming weight of the vector \((\varepsilon _1, \varepsilon _2, \varepsilon _3).\)

From the definitions of \(S_{(\varepsilon _1, \varepsilon _2, \varepsilon _3)}(b)\) we have

(8)

for substitute \(a+b\) for b in the above equation, we get

(9)

Applying Eqs. (8) and (9) to Eq. (7), and after a simple calculation, we get

$$\begin{aligned} 4\hat{f}(b)= & {} 2\hat{h}(b)+\sum \limits _{i=1}^3\hat{h}(b+a_i)-\hat{h}(b+\sum \limits _{i=1}^3a_i)+2\hat{h}(a+b)\\&-\sum \limits _{i=1}^3\hat{h}(a+b+a_i))+\hat{h}(a+b+\sum \limits _{i=1}^3a_i). \end{aligned}$$

This completes the proof.    \(\square \)

In the following, we assume that \(A=Tr_1^m(\lambda ^{-1}b^{2^m+1}).\) Replace h(x) with \(Tr_1^m(\lambda x^{2^m+1})\) in Lemma 3, which happens to be Eq. (6), then after a tedious calculation by using Eqs. (2)–(4), we obtain

(10)

where

$$\begin{aligned} \begin{array}{ll} c_i=Tr_1^m(\lambda ^{-1}(b^{2^m}a_i+ba_i^{2^m}+a_i^{2^m+1})), &{} c_4=Tr_1^m(\lambda ^{-1}(b^{2^m}a+ba^{2^m}+a^{2^m+1})), \\ t_1=Tr_1^n(\lambda ^{-1}a_1^{2^m}a_{2}), &{} t_2=Tr_1^n(\lambda ^{-1}a_2^{2^m}a_{3}),\\ t_3=Tr_1^n(\lambda ^{-1}a_3^{2^m}a_{1}), &{} t_{i+3}=Tr_1^n(\lambda ^{-1}a^{2^m}a_i),\\ \end{array} \end{aligned}$$

for

Remark 1

In fact, since \(a, a_1, a_2, a_3\) are pairwise distinct elements of if \(a, a_1, a_2, a_3\) are linear dependent over we have the following two cases holds:

  1. (1)

    If \(a+a_i+a_j=0, i\ne j,\) then the three cases are corresponding to the result with [11].

  2. (2)

    If \(\sum \limits _{i=1}^3a_i=0\) or \(a+\sum \limits _{i=1}^3a_i=0,\) then the two cases are the same with the result of [16].

Below we always put \(t_0=\sum \limits _{i=1}^3t_i\) modulo 2.

Now we discuss the properties of the function defined in Eq. (6).

Theorem 1

With the notation as above. Let \(a, a_1, a_2, a_3\) are linear independent over If \((t_4, t_5, t_6)=(0, 0, 0),\) then f(x) in Eq. (6) is a bent function if and only if \(t_0=0.\) Furthermore, the dual function \(\tilde{f}(x)\) of the bent function f(x) in Eq. (6) is given by

Proof

Let \(\varphi (x)=\sum \limits _{i=1}^3f_i(x)=Tr_1^m(\lambda x^{2^m+1})+Tr_1^n(ax)Tr_1^n(\sum \limits _{i=1}^3a_ix).\) Since \(t_4=t_5=t_6=0,\) i.e., \(Tr_1^n(\lambda ^{-1}a^{2^m}a_i)=0\) for by Lemma 2 we find that \(f_1, f_2, f_3, \varphi \) are all bent functions and their dual functions \(\tilde{f_1}, \tilde{f_2}, \tilde{f_3}, \tilde{\varphi }\) are given by

$$\begin{aligned} \tilde{f_i}(x)= & {} 1+Tr_1^m(\lambda ^{-1}x^{2^m+1})+Tr_1^m(\lambda ^{-1}a^{2^m+1})\\&+Tr_1^n(\lambda ^{-1}a^{2^m}x)\Big (Tr_1^m(\lambda ^{-1}a_i^{2^m+1})+Tr_1^n(\lambda ^{-1}a_i^{2^m}x)\Big ), \end{aligned}$$

and

$$\begin{aligned} \tilde{\varphi }(x)= & {} 1+Tr_1^m(\lambda ^{-1}x^{2^m+1})+Tr_1^m(\lambda ^{-1}a^{2^m+1})+Tr_1^n(\lambda ^{-1}a^{2^m}x)\\&\Big (Tr_1^m(\lambda ^{-1}(\sum \limits _{i=1}^3a_i)^{2^m+1})+Tr_1^n(\lambda ^{-1}(\sum \limits _{i=1}^3a_i)^{2^m}x)\Big ). \end{aligned}$$

Assume that \(0=\sum \limits _{i=1}^3\tilde{f_i}(x)+\tilde{\varphi }(x),\) which is equivalent to

$$\begin{aligned}&\Big (Tr_1^n(\lambda ^{-1}a^{2^m+1})+Tr_1^n(\lambda ^{-1}a^{2^m}x)\Big ) \Big (\sum \limits _{i=1}^3Tr_1^m(\lambda ^{-1}a_i^{2^m+1}\Big ) \\+ & {} Tr_1^m(\lambda ^{-1}(\sum \limits _{i=1}^3a_i)^{2^m+1})\Big )=0, \end{aligned}$$

for all hence the equation holds if and only if \(Tr_1^n(\lambda ^{-1}(a_1^{2^m}a_2+a_1^{2^m}a_3+a_2^{2^m}a_3))=0.\) Thus the result follows from Lemma 1.

The dual function \(\tilde{f}\) of the bent function f(x) then follows from Lemmas 1–2.    \(\square \)

Remark 2

The condition \(t_0=0\) in Theorem 1 implies that \((t_{1}, t_{2}, t_{3})\in \{(1, 1, 0), (0, 1,1), (1, 0, 1), (0, 0, 0)\}.\) Thus, if \((t_{1}, t_{2}, t_{3}) = (0, 0, 0),\) then Theorem 1 can be easily obtained by [19, Corollary 4.2]. Even though the function constructed in Eq. (6) is contained in the function in [19, Corollary 4.2], where the other three cases are not discussed.

Theorem 2

Let \(a, a_1, a_2, a_3\) are linear independent over If \((t_0, t_4, t_5, t_6)=(0, 1, 1, 1),\) then f(x) in Eq. (6) is a semi-bent function.

Proof

If \((t_0, t_4, t_5, t_6)=(0, 1, 1, 1),\) then Eq. (10) can be written as

$$\begin{aligned} \hat{f}(b)= & {} \frac{1}{4}(-2^m)(-1)^{A}\Big (2+2(-1)^{c_4}+\sum \limits _{i=1}^3(-1)^{c_i}-(-1)^{\sum \limits _{i=1}^3c_i}\\&-\sum \limits _{i=1}^3(-1)^{c_i+c_4+1}+(-1)^{\sum \limits _{i=1}^4c_i+1}\Big ). \end{aligned}$$

So if \(c_4=0,\) we have

and if \(c_4=1\), we have

$$\begin{aligned} \hat{f}(b)= & {} \frac{1}{4}(-2^m)(-1)^{A}(0)=0. \end{aligned}$$

According to the definition of semi-bent function, we find that f(x) is a semi-bent function.    \(\square \)

Theorem 3

With the notation defined as above, we have

  1. (1)

    If \((t_0, t_4, t_5, t_6)=(1, 1, 1, 1),\) then f(x) in Eq. (6) is five-valued and the Walsh spectrum of f is \(\{0, \pm 2^m, \pm 3\cdot 2^m\}.\)

  2. (2)

    If then f(x) is five-valued and the Walsh spectrum of f is \(\{0, \pm 2^m, \pm 2^{m+1}\}.\)

Proof

We only give the proof for the case of (1) since the other case can be proved in the same manner.

  1. (1)

    If \((t_0,t_4, t_5, t_6)=(1, 1, 1, 1),\) then Eq. (10) can be reduced as

    $$\begin{aligned} \hat{f}(b)= & {} \frac{1}{4}(-2^m)(-1)^{A}\Big (2+2(-1)^{c_4}+\sum \limits _{i=1}^3(-1)^{c_i}-(-1)^{\sum \limits _{i=1}^3c_i+1}\\&-\sum \limits _{i=1}^3(-1)^{c_i+c_4+1}+(-1)^{\sum \limits _{i=1}^4c_i}\Big ). \end{aligned}$$

    Thus if \(c_4=0,\) we have

    And if \(c_4=1,\) we have

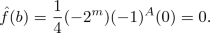
The remaining cases of proof are similar to that of \((t_0, t_4, t_5, t_6)=(1, 1, 1, 1),\) so we omit it here.    \(\square \)

Let \(m=6\) and \(\xi \) be a primitive element in such that \(\xi ^6+\xi ^4+\xi ^3+\xi +1=0.\)

Example 1

Let \(\lambda =a=1, a_1=\xi , a_2=\xi ^{5}, a_3=\xi ^{7}.\) Then we have \((t_0, t_4, t_5, t_6) =(0, 0, 0, 0)\) and it was verified by a Magma program that

$$f(x)=Tr_1^3(x^9)+Tr_1^6(x)Tr_1^6(\xi x)Tr_1^6((\xi ^{5}+\xi ^{7})x)+Tr_1^6(x)Tr_1^6(\xi ^{5}x)Tr_1^6(\xi ^{7}x)$$

is a bent function. This is consistent with our result in Theorem 1.

Example 2

Let \(\lambda =a=1, a_1=\xi ^3, a_2=\xi ^{6}, a_3=\xi ^{12}.\) Then we have \((t_0, t_4, t_5, t_6) =(0, 1, 1, 1)\) and it was verified by a Magma program that

$$f(x)=Tr_1^3(x^9)+Tr_1^6(x)Tr_1^6(\xi ^3x)Tr_1^6((\xi ^{6}+\xi ^{12})x)+Tr_1^6(x)Tr_1^6(\xi ^{6}x)Tr_1^6(\xi ^{12}x)$$

is a semi-bent function. This is consistent with our result in Theorem 2.

Example 3

(1) If \(\lambda =1, a=\xi , a_1=\xi ^3, a_2=\xi ^{9}, a_3=\xi ^{13},\) then we have \((t_0, t_4, t_5, t_6)=(1, 1, 1, 1)\) and it was verified by a Magma program that

$$f(x)=Tr_1^3(x^9)+Tr_1^6(\xi x)Tr_1^6(\xi ^3x)Tr_1^6((\xi ^{5}+\xi ^{13})x) +Tr_1^6(\xi x)Tr_1^6(\xi ^{5}x)Tr_1^6(\xi ^{13}x)$$

has \(\{0, \pm 2^3, \pm 3\cdot 2^3\}\) five-valued Walsh spectra.

(2) If \(\lambda =a=1, a_1=\xi , a_2=\xi ^{2}, a_3=\xi ^{4},\) then we have \((t_0, t_4, t_5, t_6)=(1, 0, 0, 0)\) and it was verified by a Magma program that

$$f(x)=Tr_1^3(x^9)+Tr_1^6(x)Tr_1^6(\xi x)Tr_1^6((\xi ^{2}+\xi ^{4})x)+Tr_1^6(x)Tr_1^6(\xi ^{2}x)Tr_1^6(\xi ^{4}x)$$

has \(\{0, \pm 2^3, \pm 2^4\}\) five-valued Walsh spectra.

4 The Walsh Spectrum of the Functions Given in Section 3

In this section, we give a spectrum distribution of the Boolean functions proposed in Sect. 3 with five-valued Walsh spectra.

Theorem 4

Let \(a, a_1, a_2, a_3\) are linear independent over . Then for f(x) given by Eq. (6), the following statements hold:

(1) If \((t_0, t_4, t_5, t_6)=(1, 1, 1, 1),\) then the spectrum distribution of f(x) is

$$ \hat{f}(b) =\left\{ \begin{array}{ll} (-1)^A3\cdot 2^{m}, &{} {2^{n-5}+(-1)^A2^{m-4}(1+\sum \limits _{i=1}^3(-1)^{t_{i}})}~ \mathrm {times},\\ (-1)^A2^{m}, &{}{7\cdot 2^{n-5}+(-1)^A2^{m-4}(5-3\sum \limits _{i=1}^3(-1)^{t_{i}}})~ \mathrm {times},\\ 0, &{}{2^{n-1}}~\mathrm {times}. \end{array} \right. $$

(2) If \((t_0, t_4, t_5, t_6)=(1, 0, 0, 0),\) then the spectrum distribution of f(x) is

$$ \hat{f}(b)=\left\{ \begin{array}{ll} (-1)^A2^{m+1}, &{} {2^{n-4}}~ \mathrm {times},\\ (-1)^A2^{m}, &{}{2^{n-2}+(-1)^A2^{m-1}}~ \mathrm {times},\\ 0, &{}{3\cdot 2^{n-3}}~ \mathrm {times}. \end{array} \right. $$

(3) For other cases, the spectrum distribution of f(x) is

$$ \hat{f}(b) =\left\{ \begin{array}{ll} (-1)^{A+1}2^{m+1}, &{} {2^{n-4}+(-1)^{A+1}2^{m-3}(1-(-1)^{\delta })}~ \mathrm {times},\\ (-1)^A2^{m}, &{}{2^{n-2}+(-1)^A2^{m-2}(1+(-1)^{\delta })}~ \mathrm {times},\\ 0, &{}{3\cdot 2^{n-3}}~ \mathrm {times}, \end{array} \right. $$

with

Proof

We only prove \((t_0, t_4, t_5, t_6)=(0, 0, 0, 1),\) i.e., \(\delta =t_1\) in (3), since the other cases can be proved in the same method. If \((t_0, t_4, t_5, t_6)=(0, 0, 0, 1)\), then from Eq. (10) we have

$$\begin{aligned} \hat{f}(b)= & {} \frac{1}{4}(-2^m)(-1)^{A}(2+2(-1)^{c_4}+\sum \limits _{i=1}^3(-1)^{c_i}+(-1)^{\sum \limits _{i=1}^3c_i+1}\\&+\sum \limits _{i=1}^2(-1)^{c_i+c_4+1}+(-1)^{c_3+c_4}+(-1)^{\sum \limits _{i=1}^4c_i+1}). \end{aligned}$$

So if \(c_4=0,\) we have

(11)

and if \(c_4=1,\) we have

(12)

Now we figure out the number of such that \(\hat{f}(b)=2^{m+1},\) i.e., \(c_4=0, A=1.\) Let \(N_1\) denote the number of such that \((c_1, c_2, c_3, c_4, A)\in \{(1, 0, 0, 0, 1), (0,1, 0, 0, 1)\}.\) Then we have

To calculate \(N_1\), we first consider and from the definitions of we have

Note that \(a_1, a_2, a_3\) and a are linear independent, that is, we have \(\sum \limits _{i=1}^3d_ia_i+d_4a\ne 0\) if and only if \((d_1, \cdots , d_4)\ne (0, \cdots , 0).\) If then we have

since \(\lambda \ne 0.\) Therefore, we obtain

Then by a similar argument, we can also have \(N_{12}=N_{11}.\)

Now we considered then we have

Note that from the bentness of \(Tr_1^m(\lambda ^{-1}x^{2^m+1}).\) Thus, one can obtain that \(N_{13}\) can expressed as

So we get

$$\begin{aligned} N_1= & {} \frac{1}{2^5}(N_{11}+N_{12}+N_{13})\\= & {} 2^{n-4}+2^{m-4}\Big (3-(-1)^{t_4}+\sum _{i=5}^6(-1)^{t_i}-(-1)^{t_3}-(-1)^{t_1}+(-1)^{t_2}\\&-(-1)^{t_3+t_4+t_6}-(-1)^{t_0}+(-1)^{t_2+t_5+t_6}-(-1)^{t_1+t_4+t_5}-(-1)^{\sum \limits _{i=1}^6t_i}\Big )\\= & {} 2^{n-4}+2^{m-3}(1-(-1)^{t_1}). \end{aligned}$$

Let \(N_2\) denote the number of such that \(\hat{f}(b)=0.\) It then follows from Eqs. (11) and (12) that \(\hat{f}(b)=0\) for any \((c_1, c_2, c_3, c_4)\in \{(1, 0, 1, 0), (0, 1, 1, 0), (0, 1, 0, 1), (0, 1, 1, 1), (1, 0, 0, 1), (1, 0, 1, 1)\}.\) It is the same as the calculation of \(N_{11},\) we have

Let and Then from Eq. (1) we have

$$\begin{aligned} \left\{ \begin{array}{ll} 2^n=n_1+n_2+n_3+2^{n-4}+2^{m-3}-2^{m-3}(-1)^{t_1}+3\cdot 2^{n-3},\\ 2^n=2^m\cdot n_1-2^m\cdot n_2-2^{m+1}\cdot n_3+2^{m+1}\cdot (2^{n-4}+2^{m-3}-2^{m-3}(-1)^{t_{1}}),\\ 2^{2n}=(2^m)^2\cdot (n_1+n_2)+(-2^{m+1})^2\cdot n_3 +(2^{m+1})^2 \\ \cdot (2^{n-3}+2^{m-3}-2^{m-3}(-1)^{t_{1}}). \end{array} \right. \end{aligned}$$

After a simple calculation, we have

$$\begin{aligned} \left\{ \begin{array}{ll} n_1=2^{n-4}+2^{m-3}+2^{m-3}(-1)^{t_{1}},\\ n_2=2^{n-4}-2^{m-3}-2^{m-3}(-1)^{t_{1}},\\ n_3=2^{n-4}-2^{m-3}+2^{m-3}(-1)^{t_{1}}. \end{array} \right. \end{aligned}$$

   \(\square \)

5 Conclusion

In this paper, a class of bent functions and their dual functions are constructed according to [11]. In addition, we obtain a class of semi-bent functions and some classes of five-valued Walsh spectra. Then according to the Magma program, we can see that the conclusion is consistent with our result in this paper.