Methods and Algorithms for Calculating Nonlinear Oscillations of Rotor Systems

Abstract

In the article, linear and nonlinear parameter identification methods were described relating to mathematical models of rotor oscillations for centrifugal pumps and turbochargers. For solving a nonlinear estimation problem, the combined use of several methods at each iteration step was proposed. In this regard, the determination of initial values for the estimated parameters was based on both the finite element and the discrete models. For studying the nonlinear rotor oscillations, a method for designing the discrete mathematical models was proposed based on the linear identification of equivalent masses using data obtained by the calculation of eigenfrequencies and mode shapes as a result of the finite element analysis. Using the artificial neural network, the methodology for estimating the inertia coefficients of rotor systems based on measurements of oscillation amplitudes at the frequency close to the critical one was developed. Finally, the proposed techniques were developed by implementing both quasilinear regression analysis and the artificial intelligence system. The corresponding program techniques were proved by the experimental research data of rotor oscillations using the accelerating and balancing stand with the vacuum camera. The developed methods and related program applications help evaluate the dynamic characteristics of pumps and turbochargers.

1 Introduction

The problem of parameter identification for mathematical models as an essential scientific direction in modeling dynamic systems is exceptionally urgent. In this regard, it should be emphasized that the scientific and theoretical fundamentals for implementation of the parameter identification of centrifugal machines’ rotors were developed and presented in the article [1].

Notably, oscillations of rotors of centrifugal power machines are polyharmonic ones [2]. This fact is due to the nonlinear behavior of the interaction between a rotor and a stator in bearing supports [3], sealing systems, and in the flow path. Even if neglecting these disturbances and consider only the influence of imbalances, oscillations, along with direct synchronous precession, will have asynchronous sub- and super-harmonic components [4]. According to the experimental research, these components reach significant values [5], and in some cases, they lead to a loss of rotation stability [6].

Therefore, to calculate the vibrations and stability of rotor systems and evaluate the critical frequencies and corresponding mode shapes, it is advisable to calculate the spectra of forced vibrations. The last one can be obtained by considering discrete models based on the system of nonlinear differential.

One of the ways to implement such calculations realizes by evaluating a discrete multi-mass model. This evaluation is carried out by eigenfrequencies and mode shapes obtained using the finite element model. Traditionally, such analyses contain the following stages. Firstly, the parameters of the conservative linear model of free oscillations are calculated [7]. After, linear components of the reactions from bearing supports [8], sealing elements [9], and flow paths [10] are added to the resulting equations. This model can be used for obtaining rotation stability regions [11]. At the next step, nonlinear components of the reactions from the rotor’s interaction with the stator [12, 13] are added to the obtained equations. The rotor system’s obtained nonlinear model [14] can be numerically integrated using the numerical simulation methods [15]. Finally, spectral analysis [16] of the received oscillation response is performed.

2 Literature Review

Plenty of scientific research works in rotor dynamics highlight the scientific novelty of the stated problem. Particularly, P. Dang et al. [17] studied static characteristics of the system “rotor – bearings” using the finite element method. As a result, the corresponding mathematical model was developed for the case of a rigid rotor-bearing system.

Liang [18] investigated the impact of rolling bearings on rotors’ nonlinear dynamics. For this purpose, the nonlinear response was calculated using the Newmark-β integration method [19].

Kubyshkin [20] studied self-excited oscillations of rotor systems. Notably, the nonlinear mathematical model with distributed parameters considering the material’s internal friction [21] was proposed. As a result of using the modified Galerkin method [22], the method of invariant manifolds [23], and the bifurcation theory [24], the stability conditions were found.

K. Lu et al. [25] proposed applying the proper orthogonal decomposition (POD) method in dual rotor-bearing systems considering the coupling misalignment. As a result, for verifying the higher computational efficiency of this method for the dimension reduction, it was compared with both the reduced-order model (ROM) [26] and the full-order model (FOM) [27].

Numerous applications of the rotor systems highlight the practical importance of the stated problem. Particularly, the ways for ensuring the reliability of rotors for hydraulic drives were described in papers [27,28,30]. Technologies for protecting contacting surfaces of sliding bearing for multistage centrifugal machines were presented in the research work [31].

A general approach for the vibration diagnostics of turbine bearings was developed in the article [32]. A particular case for calculating and designing rotodynamic pumps was presented in the paper [33]. Additionally, ways for ensuring the vibration reliability of turbopump units using artificial neural networks were proposed in the article [34]. Moreover, an engineering methodology for evaluating the reliability of rotor bearing supports was developed in the research works [35, 36]. Finally, a methodology for nonlinear simulations of hydraulic drives was developed in the paper [37].

As a result of the critical analysis of the research mentioned above works, the article aims at ensuring the vibration reliability of rotor systems in centrifugal machines. The following objectives have been formulated to achieve this goal. Firstly, a general approach for reducing degrees of freedom for discrete systems should be proposed. Secondly, linear and nonlinear evaluation of masses for the discrete mathematical model should be developed using both the linear regression procedure and artificial neural networks. Thirdly, the mathematical model of rotor oscillations should be developed based on the proposed discrete model considering linear and nonlinear reactions in a flow path, bearings, and sealing systems. Finally, the proposed mathematical model’s reliability should be proved numerically for an example of rotor oscillation for a particular centrifugal machine.

3 Research Methodology

3.1 The Conservative Discrete Model

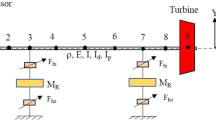
It is sufficient for most pumps and turbochargers to consider a three-mass model [38] for describing the rotor oscillations. In this case, the design scheme of the conservative discrete model is presented in Fig. 1.

Fig. 1.

The design scheme of the conservative discrete model.

According to D’Alembert’s principle [39], the matrix equation of free oscillations in reverse form is as follows:

$$ x_{i} = \sum\nolimits_{j = 1}^{n} {\beta_{ij} F_{j} = - \sum\nolimits_{j = 1}^{n} {\beta_{ij} m_{j} \ddot{x}_{j} } } . $$

(1)

where i, j – node number (i, j = 1, 2, …, n); n – total number of discrete masses;

x_i – displacement of i-th node; ${F}_{j}=-{m}_{j}{\ddot{x}}_{j}$ – inertia forces; β_ij – compliances as deflections of i-th node from the j-th node’s unit force F_j = 1 determined using the authors’ file “Forced oscillation of the rotor” (Reg. No. 61788, 23.09.2015, Ukraine), which implements the finite element method.

For the case of free oscillations, the substitution of the expression x_i = B_i·sin $\omega t$ in Eq. (1), after identical transformations allows obtaining the system of linear homogeneous equations for determining eigenfrequencies and mode shapes:

$$ B_{i} = {\upomega }^{2} \sum\nolimits_{j = 1}^{3} {\beta_{ij} m_{j} B_{j} .} $$

(2)

Models (1) and (2) are a system of equations for free oscillation of a beam with stiffness properties equivalent to an actual rotor’s finite element model. The discrete masses m_i are evaluated by the following methods: the linear parameter identification based on the condition for the maximum coincidence of eigenfrequencies and mode shapes of finite element model and the discrete model; the nonlinear parameter identification using the artificial neural network.

3.2 The Linear Parameter Identification

The method of linear parameter identification is used to estimate the discrete masses. Introduction of the parameter z = 1/ω² and dimensionless amplitudes U_j = B_j/B₁ (in this case, U₁ = 1) allows obtaining the system of n = 3 homogeneous equations:

$$ \sum\nolimits_{j = 1}^{n} {\left( {\beta_{ij} m_{j} - \delta_{ij} z} \right)U_{j} = 0,} $$

(3)

where δ_ij – Cronecker symbol [40] (δ_ij = 1 for i = j; δ_ij = 0 for i ≠ j).

Since the finite element model allows evaluating eigenfrequencies ω_j (or parameters ${z}_{j}=1/{\omega }_{j}^{2}$) and the relative amplitudes of the mode shapes ${U}_{i}^{<j>}$ ($i$ – mass number; $j$ – eigenfrequency number), the problem of identifying a discrete model can be considered. In this case, the discrete masses m_i are the estimated parameters.

Using the calculation data for the first n = 3 eigenfrequencies and mode shapes, Eq. (3) can be rewritten in the following matrix form:

$$ \left[ {\overline{D}} \right]\left\{ {\overline{m}} \right\} = \left\{ {\overline{C}} \right\}, $$

(4)

where: $\left[ {\overline{D}} \right] = \left[ {\left[ {\overline{D}^{\left\langle 1 \right\rangle } } \right]^{T} ,\left[ {\overline{D}^{\left\langle 2 \right\rangle } } \right]^{T} , \ldots ,\left[ {\overline{D}^{\left\langle n \right\rangle } } \right]^{T} } \right]^{T}$ – matrix of dimension (n² × n), elements of the submatrix of which $\overline{D}_{ij}^{\left\langle k \right\rangle } = \beta_{ij} U_{i}^{\left\langle k \right\rangle }$ (k = 1, 2, …, n); $\left\{ {\overline{m}} \right\}$ – column-vector of n estimated masses; $\left\{ {\overline{C}} \right\} =$$\left\{ {\left\{ {\overline{C}^{\left\langle 1 \right\rangle } } \right\}^{T} ,\left\{ {\overline{C}^{\left\langle 2 \right\rangle } } \right\}^{T} , \ldots ,\left\{ {\overline{C}^{\left\langle n \right\rangle } } \right\}^{T} } \right\}^{T}$ – column-vector of the right parts of dimension (n² × 1), elements of subvectors of which $\left\{{\overline{C} }^{<k>}\right\}={z}_{k}{U}_{i}^{<k>}$.

Equivalent masses of the discrete model are evaluated using the linear regression formula [41]:

$$ \left\{ {\overline{m}} \right\} = \left( {\left[ {\overline{D}} \right]^{T} \left[ {\overline{D}} \right]} \right)^{ - 1} \left[ {\overline{D}} \right]^{T} \left\{ {\overline{C}} \right\}. $$

(5)

To check the estimation accuracy, the eigenfrequencies of the discrete model ${\omega }_{k} = 1/\sqrt{{z}_{k}}$ are evaluated from the condition for the existence of non-trivial solutions of the homogeneous system (3):

$$ \det \left[ {\mathop {\sum\nolimits_{j = 1}^{3} {\left( {\beta_{ij} \overline{m}_{j} - \delta_{ij} z_{k} } \right)U_{j}^{\left\langle k \right\rangle } } }\limits_{{}}^{{}} } \right] = 0. $$

(6)

The corresponding algorithm for implementing the proposed linear parameter identification method of discrete masses is graphically presented in Fig. 2a.

3.3 The Nonlinear Parameter Identification Using the Artificial Neural Network

For a more precise solving of the estimation problem, an approach for nonlinear estimation of discrete masses is applied using the artificial neural network [42]. The corresponding algorithm is presented in Fig. 2b.

Fig. 2.

The algorithms of linear (a) and nonlinear (b) parameter identification.

This algorithm is fundamentally different from the linear regression procedure since estimating discrete masses does not involve dimensionless displacements as mode shapes’ amplitudes. Thus, the discrete masses are estimated directly from the available set of the first three eigenfrequencies of the rotor system.

3.4 The Nonlinear Discrete Model

The design scheme of the tree-mass nonlinear non-conservative discrete model of rotor oscillations is presented in Fig. 3.

Fig. 3.

The design scheme of the nonlinear discrete model.

The following general equations describe the oscillation equations of the discrete rotor model:

$$ \left\{ {\begin{array}{*{20}c} {x_{i} = \sum\nolimits_{j = 1}^{n} {\beta_{ij} F_{jx} ;} } \\ {y_{i} = \sum\nolimits_{j = 1}^{n} {\beta_{ij} F_{jy} ,} } \\ \end{array} } \right\} $$

(7)

where x_i, y_i – nodal displacements in directions of x- and y-axis, respectively;

F_jx, F_jy – projections of j-th nodal forces on the x- and y-axis, respectively:

$$\begin{array}{c}\begin{array}{c}{F}_{\mathrm{1,3}x}=-{m}_{1}{\omega }_{0}\frac{{d}^{2}{x}_{\mathrm{1,3}}}{d{\tau }^{2}}-{d}_{b}{\omega }_{0}\frac{d{x}_{\mathrm{1,3}}}{d\tau }-f\left({x}_{\mathrm{1,3}}^{2}+{y}_{\mathrm{1,3}}^{2}\right){x}_{\mathrm{1,3}}-{q}_{b}{y}_{\mathrm{1,3}};\\ {F}_{\mathrm{1,3}y}=-{m}_{1}{\omega }_{0}\frac{{d}^{2}{y}_{\mathrm{1,3}}}{d{\tau }^{2}}-{d}_{b}{\omega }_{0}\frac{d{y}_{\mathrm{1,3}}}{d\tau }-f\left({x}_{\mathrm{1,3}}^{2}+{y}_{\mathrm{1,3}}^{2}\right){y}_{\mathrm{1,3}}+{q}_{b}{x}_{\mathrm{1,3}};\end{array}\\ \begin{array}{c}{F}_{2x}=-{m}_{2}{\omega }_{0}\frac{{d}^{2}{x}_{2}}{d{\tau }^{2}}+{m}_{2}e{\overline{\omega }}^{2}{\omega }_{0}^{2}\mathrm{cos}\overline{\omega }\tau -{q}_{0}{y}_{2};\\ {F}_{2y}=-{m}_{2}{\omega }_{0}\frac{{d}^{2}{y}_{2}}{d{\tau }^{2}}+{m}_{2}e{\overline{\omega }}^{2}{\omega }_{0}^{2}\mathrm{sin}\overline{\omega }\tau +{q}_{0}{x}_{2}.\end{array}\end{array}$$

(8)

These expressions contain the following parameters: ω – rotor frequency, rad/s; ω₀ – nominal operation frequency; $\overline{\omega } = \omega /\omega_{n}$ – dimensionless frequency; τ = ω_n·t – dimensionless time; e – eccentricity; f – coefficient of nonlinear stiffness of bearing supports, N/m³; d_b – damping factor of bearings; q_b = δ·ω·d_b – circulating force coefficient in bearing supports (δ – dimensionless factor of the circulating force); q₀ – circulating force coefficient in the flow path. Notably, the coefficients f, d_b, q_b are taken the same for both bearing supports.

The nonlinear differential Eqs. (8) system can be further used to study the rotor’s polyharmonic oscillation response.

4 Results

4.1 Description of the Design Model

As an example of using the proposed methodology, the analysis of forced oscillations and stability of the rotor’s rotation of a centrifugal compressor for underground gas storages with 25 MW power is considered. The nominal frequency of the rotor ω_n = 785 rad/s.

Figure 4a presents the main view of the studied compressor unit. The cross-section of the rotor and its finite element model is shown in Fig. 4b–c.

Fig. 4.

The compressor S325GC-650/6-56M12 for underground gas storages: photo (a); cross-section (b); design scheme (c).

4.2 Evaluation of the Discrete Masses

As a result of numerical simulation using the author’s file “Critical frequencies of the rotor” of the computer algebra system MathCAD (Reg. No. 59855, 27.05.2015, Ukraine), which implements the finite element method, the first three eigenfrequencies have been obtained: $\omega_{1}^{*}$ = 307 rad/s, $\omega_{2}^{*}$ = 991 rad/s, and $\omega_{3}^{*}$ = 1689 rad/s. The corresponding mode shapes are presented in Fig. 5.

Fig. 5.

1st (1), 2nd (2), and 3rd (3) mode shapes of the rotor.

With the use of the regression algorithms mentioned above, the following equivalent masses have been evaluated: $\overline{m}_{1}$ = 183 kg, $\overline{m}_{2}$ = 1333 kg, and $\overline{m}_{3}$ = 725 kg.

The reliability of the obtained three-mass discrete model of the rotor oscillations is verified by comparing the corresponding eigenfrequencies. In this case, the relative error is as follows:

$$ \varepsilon_{i} = \left| {\frac{{\omega_{i} }}{{\omega_{i}^{*} }} - 1} \right|\cdot100{\text{ \% }}, $$

(9)

where ω_i – eigenfrequencies of the discrete three-mass rotor system.

The discrete model’s eigenfrequencies determined from the non-trivial solution conditions to a homogeneous system (3) are as follows: ω₁ = 308 rad/s, ω₁ = 933 rad/s, and ω₃ = 1876 rad/s. In this case, the following relative errors are calculated: ε₁ = 0.3%, ε₂ = 5.8%, and ε₃ = 11.1%.

4.3 Harmonic Analysis of the Nonlinear Discrete System

As an example of the studying polyharmonic oscillations of the rotor system, below are presented results obtained during solving a system of nonlinear differential Eqs. (8).

The time characteristics and the spectrum of rotor oscillations for 2nd mass in directions of the x-axis (a) and y-axis (b) in the case of the stable rotation (d_b = 0.35·10⁵ N·s/m; δ = 0.3; q = 0; ω = ω_n) are shown in Fig. 6.

An indication of the stability loss is the occurrence of the subharmonic component. However, rotor oscillations can still be within acceptable limits. Particularly, for parameters causing instability (d_b = 0.35·10⁵ N·s/m; δ = 0.3; q = 2·10⁶ N/m; ω = 1030 rad/s), the time characteristics, the spectrum, and the orbit are presented in Fig. 7.

Fig. 6.

The time characteristics (a, b) and the spectrum (c) of rotor oscillations for 2nd mass in directions of the x-axis (a) and y-axis (b) in the case of stable rotation (ω = ω₀ = 785 rad/s).

Fig. 7.

The time characteristics (a, b), the spectrum (c), and the orbit (d) of rotor oscillations for 2nd mass in directions of the x-axis (a) and y-axis (b) in the case of the unstable rotation.

4.4 Dynamic Stability of the Rotor System

According to calculations of different combinations of practically varying bearing parameters d_b, δ, and f, the circulating force’s effect on the rotation stability has been investigated. In this case, the coefficient of the circulating force q₀ has varied within limits, which are acceptable for actual operational practice.

The boundaries for the stability regions (Fig. 8) reflect the circulating forces’ influence on the rotor stability. Based on these data, it can be concluded that the stability is provided quite reliably in the range of the operating frequencies.

Fig. 8.

The stability regions for different values of the circulating force q, N/m: 0 (1), 1·10⁶ (2), 2·10⁶ (3), and 3·10⁶ (4).

5 Conclusions

Thus, a general approach for reducing degrees of freedom for rotor dynamics has been proposed. As a result, the three-mass discrete model has been developed. The algorithms for linear and nonlinear parameter identification of the proposed model’s inertia coefficients have been developed based on linear regression and artificial neural networks. Notably, for the practical case of the compressor S325GC-650/6-56M12 for underground gas storage with the power of 25 MW and the operation frequency of 785 rad/s, the system of three discrete masses 183 kg, 1333 kg, and 725 kg have been evaluated.

The reliability of the proposed methodology has been proved by relatively small errors in calculating critical frequencies. Notably, for the particular case study, the first three critical frequencies 307 rad/s, 991 rad/s, and 1689 rad/s have been calculated using the authors’ file of the computer-algebra system. After implementing the parameter identification algorithms, the discrete three-mass rotor system’s eigenfrequencies vary from these values insignificantly for practical purposes. Notably, the relative errors are 0.3%, 5.8%, and 11.1% for different mode shapes.

After evaluating discrete masses, the nonlinear mathematical model of rotor oscillations was developed based on the proposed discrete model considering linear and nonlinear reactions in bearings, flow paths, and sealing systems.

The main advantages of the proposed methodology are due to the following facts. Firstly, the proposed mathematical model allows analytically studying forced oscillations of rotor systems considering the nonlinear components of reaction forces in a flow path, bearings, and sealing systems. Additionally, the proposed discrete model allows for studying the stability of the nonlinear dynamic system.

Overall, the developed methodology will help scientists and practicians ensure the vibration reliability of centrifugal pumps and compressors.