A Maximum-Flow Model for Digital Elastica Shape Optimization

Abstract

The Elastica is a curve regularization model that integrates the squared curvature in addition to the curve length. It has been shown to be useful for contour smoothing and interpolation, for example in the presence of thin elements.

In this article, we propose a graph-cut based model for optimizing the discrete Elastica energy using a fast and efficient graph-cut model. Even though the Elastica energy is neither convex nor sub-modular, we show that the final shape we achieve is often very close to the globally optimal one.

Our model easily adapts to image segmentation tasks. We show that compared to previous works and state-of-the-art algorithms, our proposal is simpler to implement, faster, and yields comparable or better results.

1 Introduction

The Elastica model and associated energy is a curve regularisation problem with a rich history [12, 15], which involves the squared curvature. It was introduced in computer vision in [16] as a means to regularize edges or segmentation boundaries with an explicit curvature component. Being associated with second-order derivatives, the notion of curvature is difficult to compute and optimize in a regularisation framework.

Multiple attempts have been made by prominent researchers to introduce an explicit curvature term in curve regularizers using various methods and approaches. Even early active contour models [10] had an elasticity component equivalent to a notion of curvature. Similarly, with level-set methods, local curvature can readily be estimated as in [13]. However these approaches typically optimise a non-convex local energy by gradient descent, and most were non-geometric, i.e. discretization-dependent. In contrast [5] proposed a geometric level-set segmentation method, but using only the perimeter as a regularizer, and was still non-convex. All the numerous approaches based on total-variation minimization for image restoration or segmentation [19] and even the Mumford-Shah functional [17] use this quite elementary regularizer, probably because optimizing it in an exact manner was already a challenge for a long time [2, 4, 6], whether in the discrete or continuous cases.

In more recent works, optimizing the Elastica, which is a geometric regularizer, has seen renewed interest. In [14], authors successfully use a computational geometry approach to perform image restoration with the Elastica as regularizer. In [7], authors compute an approximate discrete version of the Elastica and optimize it with discrete calculus. In [18], an efficient, discrete approximation of curvature is optimized with a specific solver using local submodular approximations [8]. However, in these works, the poor quality of the curvature approximation may limit accuracy and hence the quality of the result.

In a previous work [1] we proposed to formulate a digital flow that approximates an Elastica-related flow using a multigrid-convergent curvature estimator, within a discrete variational framework. We also presented an application of this model as a post-processing step to a segmentation framework.

In this work, we propose a novel approach that still uses a multigrid-convergent estimation of curvature, but we optimize using a maximal flow algorithm.

1.1 Multigrid Convergent Estimators

Geometric measurements in digital objects can be tricky. Intuitively, a good estimator should converge to its continuous counterpart value as the grid resolution is refined. The criterion that formalizes this intuition is the multigrid convergence property.

Definition 1

(Multigrid convergence). Let $\mathcal {F}$ a family of shapes in the plane and Q a global measurement (e.g., perimeter, area) on members of $\mathcal {F}$. Additionally, denote $D_h(S)$ a digitization of shape S in a digital grid of resolution h. The estimator $\hat{Q}$ of Q is multigrid convergent for the family $\mathcal {F}$ if and only if for every shape $S \in \mathcal {F}$, there exists $h_S > 0$ such that

$$\begin{aligned} \forall h \le h_S, \quad |\hat{Q}(D_h(S),h) - Q(S)| \le \tau _S(h), \end{aligned}$$

where $\tau _S:\mathbb {R}_+\setminus \{0\} \rightarrow \mathbb {R}_+$ tends to zero as h tends to zero and is the speed of convergence of $\hat{Q}$ towards Q for S.

Tangent and curvature are examples of local properties computed along the boundary of some shape S in the plane. We need a slightly different definition of multigrid convergence in order to map points of the Euclidean boundary to those in the digital contour.

Definition 2

(Multigrid convergence for local geometric quantities). Let $\mathcal {F}$ a family of shapes in the plane and Q a local measurement along the boundary $\partial S$ of $S \in \mathcal {F}$. Additionally, denote $D_h(S)$ a digitization of S in a digital grid of resolution h and $\partial _h S$ its digital contour. The estimator $\hat{Q}$ of Q is multigrid convergent for the family $\mathcal {F}$ if and only if for every shape $S \in \mathcal {F}$, there exists $h_S > 0$ such that the estimate $\hat{Q}(D_h(S),p,h)$ is defined for all $p \in \partial _h S$ with $0< h < h_S$, and for any $x \in \partial S$,

$$\begin{aligned} \forall p \in \partial _h S \text { with } \Vert p-x\Vert _{\infty } \le h,\quad | \hat{Q}(D_h(S),p,h) - Q(S,x) | \le \tau _S(h), \end{aligned}$$

where $\tau _S:\mathbb {R}_+\setminus \{0\} \rightarrow \mathbb {R}_+$ has null limit at 0. This function defines the speed of convergence of $\hat{Q}$ towards Q for S.

We now recall the notion of Elastica, as well as its digital counterpart.

1.2 Digital Elastica

Letting $\kappa$ be the curvature function along some Euclidean shape $S \subset \mathbb {R}^2$. The elastica energy of S with parameters $\boldsymbol{\theta }=(\alpha \ge 0, \beta \ge 0)$ is defined as

$$\begin{aligned} E_{\boldsymbol{\theta }}(S)&= \int _{\partial S}{ \alpha + \beta \kappa (s)^2 ds}. \end{aligned}$$

Similarly, the digital elastica $\hat{E}_{\boldsymbol{\theta }}$ of some digitization $D_h(S)$ of S is defined as

$$\begin{aligned} \hat{E}_{\boldsymbol{\theta }}( D_h(S) ) = \sum _{\dot{\boldsymbol{e}} \in \partial _h S}{ \hat{s}( \dot{\boldsymbol{e}})\left( \; \alpha + \beta \hat{\kappa }^2(D_h(S),\dot{\boldsymbol{e}},h) \; \right) }, \end{aligned}$$

(1)

where $\dot{\boldsymbol{e}}$ denotes the center of the linel $\boldsymbol{e}$ and the estimators of length $\hat{s}$ and curvature $\hat{\kappa }$ are multigrid convergent.

1.3 A Multigrid-Convergent Estimation of Curvature

Let S be an arbitrary shape. The following definition yields a curvature estimation at every point of its boundary.

Definition 3

(Integral Invariant Curvature Estimator). Let $D_h(S)$ a digitization of $S \subset \mathbb {R}^2$ and $B_r(p)$ the Euclidean disk of radius r centered at p. The integral invariant curvature estimator is defined for every point $p \in \partial _h S$ as

$$\begin{aligned} \hat{\kappa }_{r}(D_h(S),p,h) := \frac{3}{r^3} \left( \frac{\pi r^2}{2} - \widehat{\text {Area}} \left( D_h\big ( B_{r} ( p ) \big ) \cap D_h(S), h \right) \right) . \end{aligned}$$

(2)

where $\widehat{\text {Area}}( D,h )$ estimates the area of D by counting its grid points and then scaling them by $h^2$. This estimator is multigrid convergent for the family of compact shapes in the plane with 3-smooth boundary. It converges with speed $O(h^\frac{1}{3})$ for radii chosen as $r=\varTheta (h^\frac{1}{3})$ [11].

In the expression above, we will substitute an arbitrary subset $D$ of $\mathbb {Z}^2$ to $D_h(S)$ since the continuous shape S is unknown. In the following we omit the grid step h to simplify expressions (or, putting it differently, we assume that the shape of interest is rescaled by 1/h and we set $h=1$).

2 Digital Elastica Minimization via Graph Cuts

In this section we present a graph cut model that converges to the optimum digital shape under digital elastica regularization. Moreover, the model is easily adapted to image segmentation tasks.

2.1 Balance Coefficient

In the core of the model is the notion of balance coefficient. We are going to extend Eq. 2 to the whole digital domain. In fact, since we are more interested in the balance of intersected and non-intersected points, we slightly change Eq. 2 and give it another name. We define the balance coefficient as

$$\begin{aligned} u_r(D,p)&= \left( \frac{\pi r^2}{2} - \widehat{\text {Area}}(B_r(p) \cap D) \right) ^2. \end{aligned}$$

The balance coefficient at p gives us as an approximation of the new squared curvature value when the shape is perturbed a little around p. Therefore, it is reasonable to evolve the shape towards the zero level set of the balance coefficient function (see Fig. 1).

Fig. 1.

Balance coefficient zero level set. We notice that evolving the initial contour (colored in white) to the zero level set of the balance coefficient (colored in magenta) regularizes the shape with respect to the squared curvature. (Color figure online)

2.2 Model Overview

Let $D^{(0)}$ be the initial digital set. The GraphFlow model produces a sequence of digital shapes $D^{(k)}$ by executing two main steps:

• Candidate selection: We associate to $D^{(k)}$ a set of neighbor shapes $\mathcal {P}(D^{(k)})$. For each $D' \in \mathcal {P}(D^{(k)})$ we construct the capacitated graph $\mathcal {G}_{D'}$ such that its minimum cut Q minimizes the candidate function.

  $$\begin{aligned} cand(D)&= data(D) + \sum _{p \in D'}\sum _{q \in \mathcal {N}_{4}(p)}{ u_r(D,p) +u_r(D,q) }. \end{aligned}$$

  (3)

  The proposition mincut(Q, G) indicates that Q is a minimum cut of G.

• Validation: Each minimum cut Q computed in the previous step induces a solution candidate $D_{Q}$. We group the solution candidates in the set $sol(D^{(k)})$ and we choose the one that minimizes the validation energy

  $$\begin{aligned} val(D)&= data(D) + \hat{E}_{\boldsymbol{\theta }}( D ). \end{aligned}$$

  (4)

The candidate function is computed on a band around the contour of $D^{(k)}$. Let $d_{D}:\varOmega \rightarrow \mathbb {R}$ be the signed Euclidean distance transformation with respect to shape D. The value $d_{D}(p)$ gives the Euclidean distance between $p \notin D$ and the closest point in D. For points $p \in D$, $d_{D}(p)$ gives the negative of the distance between p and the closest point not in D.

Definition 4

(Optimization band). Let $D \subset \varOmega \subset \mathbb {Z}^2$ a digital set and natural number $n>0$. The optimization band $O_n(D)$ is defined as

$$\begin{aligned} O_n(D)&:=\left\{ p \in \varOmega \; | \; -n \le d_{D}(p) \le n \right\} . \end{aligned}$$

We use as the neighborhood of shapes the a-probe set

Definition 5

(a-probe set). Let $D\subset \varOmega \subset \mathbb {Z}^2$ a digital set and a some natural number. The a-probe set of $D$ is defined as

$$\begin{aligned} \mathcal {P}_a(D)&= D\cup \bigcup _{a' < a}{D^{+a'} \cup D^{-a'}}, \end{aligned}$$

where $D^{+a}$($D^{-a}$) denotes a dilation(erosion) by a disk of radius a.

2.3 Shape Optimization

We are going to evolve the initial contour $\partial D$ of some digital shape D to the zero level set of its balance coefficient by computing the minimum cut of the candidate graphs. In this experiment, the data term in both candidate and validation functions equal to zero.

Definition 6

Candidate graph. Let $D \subset \varOmega \subset \mathbb {Z}^2$ a digital set and natural number $n>0$. We define $\mathcal {G}_D(\mathcal {V},\mathcal {E},c)$ as the candidate graph of D with optimization band n such that

$$\begin{aligned} \mathcal {V}&= \big \{\; v_p \; | \; p \in O_n(D) \;\} \cup \{s,t \big \} \\ \mathcal {E}&= \big \{ \; \{v_p,v_q\} \; | \; p \in O_n(D) \text { and } q \in \mathcal {N}_4(p) \; \big \} \cup \mathcal {E}_{st}\\ \mathcal {E}_{st}&= \big \{\; \{s,v_p\} \; | \; d_D(p)=-n \; \big \} \cup \big \{\; \{v_p,t\} \; | \; d_D(p)=n \; \big \}. \end{aligned}$$

The vertices s, t are virtual vertices representing the source and target vertices as it is usual in a minimum cut framework. In particular, after the minimum cut is computed, vertices connected to the source will define the new digital shape. The innermost (resp. outermost) pixels of the optimization band are connected to the source (resp. target), and we identify such vertices as

$$\begin{aligned} \mathcal {V}_s&:=\left\{ v_p \in \varOmega \; | \; d_{D}(p) = -n \right\} \\ \mathcal {V}_t&:=\left\{ v_p \in \varOmega \; | \; d_{D}(p) = n \right\} . \end{aligned}$$

The set $\mathcal {E}_{st}$ comprises all the edges having the source as their starting point or the target as their endpoint. Next, we describe how to set the edges’ capacities.

Edge e	c(e)	For
$\{v_p, v_q\}$	$u_r(D,p) + u_r(D,q)$	$\{v_p,v_q\} \in \mathcal {E}_{u}$
$\{v_p, s\}$	M	$v_p \in \mathcal {V}_{s}$
$\{v_p, t\}$	M	$v_p \in \mathcal {V}_{t}$

Here M is twice the highest value of the balance coefficient plus one, i.e.

$$\begin{aligned} M&= 1+\max _{p \in O_n(D)} 2*u_r(D,p). \end{aligned}$$

2.4 Image Segmentation

The GraphFlow model is suitable for image processing tasks. We present our experiments using the data term employed by Boykov-Jolly (BJ) graph cut model described in [3]. Let $\boldsymbol{x} \in [0,1]^{|D|}$ represent the label of each pixel (0 for background and 1 for foreground). Then, we define the data term as

$$\begin{aligned} data(D)&= \gamma _r \sum _{p \in D}{ \psi _p(x_p) } + \gamma _b \sum _{p \in D'}\sum _{q \in \mathcal {N}_{4}(p)}{\psi _{p,q}(x_p,x_q)}, \end{aligned}$$

where $\gamma _r \ge 0$ and $\gamma _b \ge 0$ are parameters controlling the influence of the data and space coherence terms, respectively. Given the image $I:\varOmega \rightarrow [0,1]^3$, the unary and pairwise terms are defined as

$$\begin{aligned} \psi _p(x_p)&= \left\{ \begin{array}{ll} -\ln H_{bg}\big ( I(p) \big ), &{} \text {if } x_p=0 \\ -\ln H_{fg}\big ( I(p) \big ), &{} \text {if } x_p=1, \end{array}\right. \\[1em] \psi _{p,q}(x_p,x_q)&= \left\{ \begin{array}{ll} \displaystyle \exp { \left( - \frac{1}{ |(p,q)| }\frac{(I(p) - I(q))^2}{2\sigma ^2} \right) }, &{} q \in \mathcal {N}_4(p) \\ 0, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

The terms $H_{bg}$ and $H_{fg}$ are mixed Gaussian distribution constructed from foreground and background seeds given by the user.

2.5 Elastica GraphFlow Algorithm

The GraphFlow algorithm implements a local-search strategy to minimize (4) with a search space given by the solution of the candidates set defined in the previous section. We choose to let the model flow even in the case where the next shape $D^{(k+1)}$ has a higher energy than the previous shape $D^{(k)}$. It is a simple strategy to escape local minima. In the implementation presented here, the only stopping condition is the number of iterations. This strategy could be tailored to a specific application.

The Elastica GraphFlow algorithm has two fundamental steps. In the candidate selection, we build the solution of the candidates set from the minimum cuts of the candidate graphs. Next, in the validation step, we choose the digital set with minimum value for (4). If we interpret the balance coefficient minimization as the best move one can make towards digital elastica minimization, the solution of the candidates set can be seen as the neighboring shapes with highest potential to minimize the elastica energy for the given a-probe set.

Some results of Algorithm 1 are shown in the next section.

3 Results and Discussion

We first present some of our own results, then some comparison with our previous work and with the reference implementation of [20].

3.1 Results

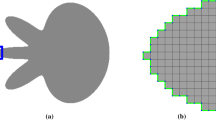
The GraphFlow algorithm produces a flow that is in accordance with expectations for a flow guided by the elastica energy. In particular, it grows and shrinks in accordance with the $\alpha$ coefficient in the digital elastica (see Fig. 2) for a-probe sets such that $a>0$. If we use a 0-probe set, we recover a flow similar to the curve-shortening flow [9].

Fig. 2.

GraphFlow results. The GraphFlow algorithm can shrink and grow in accordance with length penalization and it converges to a shape close to the theoretical global optimum (green curve) in the free elastica problem. We are using $n=2,a=2$ and shapes are displayed every 10 iterations. (Color figure online)

Fig. 3.

GraphFlow segmentation. Given foreground (green) and background (gray) seeds in picture (a); Graph cut produces picture (b) which is used as input of the GraphFlow algorithm; in pictures (c) and (d) we display the output of our Elastica GraphFlow algorithm with and without the squared curvature term in the regularization. (Color figure online)

Fig. 4.

GraphFlow and completion property. The oversegmented picture on the left was obtained with no squared curvature regularization, while the picture on the right was obtained by setting $\beta =1.0$. (Color figure online)

Table 1. Running time for the image segmentation problem.

The solutions are very similar to those achieved in [1], but with the advantage of producing smoother flows and up to $100 \times$ faster. In Fig. 3, we show that our algorithm can easily be used for segmentation, and that it produces results that are parametrically smoother than those of the BJ model.

In Fig. 4, we can observe that the Elastica GraphFlow presents the completion property, i.e., it tends to return a segmentation with fewer disconnected components.

3.2 Comparisons

In this section we compare our proposed results for segmentation with several state-of-the-art results in Fig. 5: the reference BJ segmentation method; the linear relaxation methods by Schoeneman et al.; and our previous results. We observe that our results are smoother than BJ, as in the previous figure. They are very similar to our previous results, and much better than the reference SCLR method from literature.

Fig. 5.

Segmentation results comparison. Top row, Graph-Cut BJ results; second row: references SCLR results; third row: previous results from [1]; last row: proposed method.

All the experiments were executed on a 32-core 2.4 GHz CPU. According to Table 1, our proposed method is significantly faster than our previous work, and much faster than the reference SLCR method.

4 Conclusion

In this article, we described a graph cut model for optimizing the Elastica energy that is suitable for both discrete curve evolution and image segmentation. The evolution produced by the Elastica GraphFlow responds to the length penalization term $\alpha$, i.e., the shape tends to grow (shrink) for lower (higher) values of $\alpha$ and to the curvature penalization $\beta$. Furthermore we observe a convergence to a shape that appears close to the expected, theoretical global optimum of the Elastica model in the cases where this globally optimal curve can be computed. Our Elastica GraphFlow algorithm is significantly faster and simpler to implement than the previous models presented in the literature.

In our method, we need to use a family of shapes (a-probes). In future work, we plan to use a dynamic family with the help a parameter-free estimator. In the same vein, a multi-resolution approach would be very useful, in particular for dealing with very thin portions of the image. We also note that a globally optimal solution with multigrid convergent estimators is yet to be proposed.