Keywords

1 Introduction

In the field of Evolutionary Multi-objective Optimization (EMO), new algorithms are proposed every year. In general, these algorithms are classified into three categories: Pareto dominance-based (e.g., NSGA-II [5]), decomposition-based (e.g., MOEA/D [18]), and indicator-based (e.g., SMS-EMOA [2, 7]). Among these three categories, indicator-based EMO algorithms transform a multi-objective optimization problem into a single-objective optimization problem where the single-objective is to optimize the value of an indicator (e.g., GD [16], IGD [3], Hypervolume [19], R2 [8]). The performance of EMO algorithms is usually evaluated by indicators. Each indicator-based EMO algorithm is likely to achieve a good performance with respect to the indicator used in the algorithm. That is, an IGD-based algorithm is likely to achieve a good IGD performance, and a hypervolume-based algorithm is likely to achieve a good hypervolume performance. This is the main advantage of the indicator-based algorithms.

Among different indicators, the hypervolume indicator is the most popular one in the EMO community since it has solid theoretical foundations and is comprehensively investigated [14]. The hypervolume-based EMO algorithms use the hypervolume indicator as the optimization criterion, which have been successfully applied to solve multi- and many-objective optimization problems. Some representative hypervolume-based algorithms are SMS-EMOA [2, 7], FV-MOEA [11], HypE [1], and R2HCA-EMOA [12]. SMS-EMOA and FV-MOEA use the exact hypervolume calculation. The advantage of these two algorithms is that a good hypervolume performance can be achieved. The main disadvantage of these two algorithms is that the exact hypervolume calculation is very time-consuming in high-dimensional objective spaces. Thus, their efficiency is very low when solving many-objective problems.

In order to solve the above issue, HypE and R2HCA-EMOA are proposed. These two algorithms use hypervolume approximation methods in the algorithm implementations, and thus they can solve many-objective problems efficiently. Since the hypervolume is approximated in these two algorithms, their hypervolume performance is worse than SMS-EMOA and FV-MOEA. As reported in [12], R2HCA-EMOA is able to run faster and at the same time achieve better hypervolume performance than HypE. Thus, R2HCA-EMOA is more efficient and effective than HypE for solving many-objective problems.

However, compared with other popular EMO algorithms (e.g., NSGA-II, MOEA/D, NSGA-III [4]), R2HCA-EMOA is still not very efficient (i.e., slower than those algorithms). Thus, the question is whether we can further improve the efficiency of R2HCA-EMOA without sacrificing its high performance. In this paper, we investigate this issue and propose two strategies to further improve the efficiency of R2HCA-EMOA. The improved version of R2HCA-EMOA is more efficient and its performance is not deteriorated. That is, the improved version is more attractive for practical use.

The rest of the paper is organized as follows. R2HCA-EMOA is briefly introduced in Sect. 2. Two efficiency improvement strategies are presented in Sect. 3. Numerical experiments are conducted in Sect. 4. The conclusions are drawn in Sect. 5.

2 R2HCA-EMOA

R2HCA-EMOA follows the framework of SMS-EMOA. In each generation, one offspring is generated and added into the population. Then one individual with the least hypervolume contribution in the last front is removed from the population. The main difference between R2HCA-EMOA and SMS-EMOA is that the hypervolume contribution is approximated in R2HCA-EMOA instead of exactly calculated. The pseudocode of R2HCA-EMOA is shown in Algorithm 1.

figure a

In R2HCA-EMOA, the hypervolume contribution is approximated by an R2 indicator variant, and a utility tensor structure is used to facilitate the calculation of the R2 indicator variant. Next, the R2 indicator variant and the utility tensor structure are briefly explained.

2.1 R2-Based Hypervolume Contribution Approximation

In R2HCA-EMOA, an R2 indicator variant is used to approximate the hypervolume contribution of a solution \(\mathbf {s}\) to a solution set A in an m-dimensional objective spaceFootnote 1:

$$\begin{aligned} \begin{aligned}&R^{\text {HCA}}_2(\mathbf {s})=\frac{1}{|\varLambda |}\sum _{\varvec{\lambda }\in \varLambda }\min \left\{ \min _{\mathbf {a}\in A{\setminus } \{\mathbf {s}\}}\left\{ g^{\text {*2tch}}(\mathbf {a}|\varvec{\lambda },\mathbf {s})\right\} ,g^{\text {mtch}}(\mathbf {r}|\varvec{\lambda },\mathbf {s})\right\} ^m, \end{aligned} \end{aligned}$$
(1)

where A is a non-dominated solution set with \(\mathbf {s}\in A\), \(\varLambda \) is a direction vector set, each direction vector \(\varvec{\lambda }=(\lambda _1,\lambda _2,...,\lambda _m)\in \varLambda \) satisfies \(\left\| \varvec{\lambda } \right\| _2 = 1\) and \(\lambda _i\ge 0\) for \(i = 1,...,m\), and \(\mathbf {r}\) is the reference point.

The \(g^{\text {*2tch}}(\mathbf {a}|\varvec{\lambda },\mathbf {s})\) function is defined for minimization problems as

$$\begin{aligned} g^{\text {*2tch}}(\mathbf {a}|\varvec{\lambda },\mathbf {s})= \max _{j\in \{1,...,m\}}\left\{ \frac{a_j-s_j}{\lambda _j}\right\} . \end{aligned}$$
(2)

For maximization problems, it is defined as

$$\begin{aligned} g^{\text {*2tch}}(\mathbf {a}|\varvec{\lambda },\mathbf {s})= \max _{j\in \{1,...,m\}}\left\{ \frac{s_j-a_j}{\lambda _j}\right\} . \end{aligned}$$
(3)

The \(g^{\text {mtch}}\) function is defined for both minimization and maximization problems as

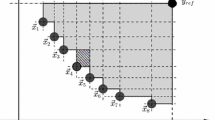
$$\begin{aligned} g^{\text {mtch}}(\mathbf {r}|\varvec{\lambda },\mathbf {s})=\min _{j\in \{1,...,m\}}\left\{ \frac{|s_j-r_j|}{\lambda _j}\right\} . \end{aligned}$$
(4)

The geometric meaning of the R2 indicator variant is illustrated in Fig. 1. Given a non-dominated solution set \(\{\mathbf {a}^1,\mathbf {a}^2,\mathbf {a}^3\}\) and a set of line segments with different directions in the hypervolume contribution region of \(\mathbf {a}^2\), the R2 indicator variant in (1) is calculated as \(R^{\text {HCA}}_2(\mathbf {a}^2)=\frac{1}{|\varLambda |}\sum _{i=1}^{|\varLambda |} l_i^m\) where \(l_i\) is the length of the ith line segment. For more detailed explanations of the R2 indicator variant, please refer to [13].

Fig. 1.
figure 1

An illustration of the geometric meaning of \(R^{\text {HCA}}_2\) for the hypervolume contribution approximation.

Full size image

2.2 Utility Tensor Structure

In R2HCA-EMOA, a utility tensor structure is introduced to facilitate the calculation of \(R^{\text {HCA}}_2\). From the definition of \(R^{\text {HCA}}_2\) in (1), we can see that in order to compute the \(R^{\text {HCA}}_2\) value of a solution \(\mathbf {s}\in A\), we need to compute \(g^{\text {*2tch}}(\mathbf {a}|\varvec{\lambda },\mathbf {s})\) for all \(\mathbf {a}\in A{\setminus } \{\mathbf {s}\}\) and all \(\varvec{\lambda }\in \varLambda \), and \(g^{\text {mtch}}(\mathbf {r}|\varvec{\lambda },\mathbf {s})\) for all \(\varvec{\lambda }\in \varLambda \). Thus, we can store \(g^{\text {*2tch}}\) and \(g^{\text {mtch}}\) values in a matrix \(\mathbf {M}\) as follows:

$$\mathbf {M}=\begin{bmatrix} g^{\text {*2tch}}(\mathbf {a}_1|\varvec{\lambda }_1,\mathbf {s}) &{} g^{\text {*2tch}}(\mathbf {a}_1|\varvec{\lambda }_2,\mathbf {s}) &{} \cdots &{}g^{\text {*2tch}}(\mathbf {a}_1|\varvec{\lambda }_{|\varLambda |},\mathbf {s}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ g^{\text {*2tch}}(\mathbf {a}_{|A|-1}|\varvec{\lambda }_1,\mathbf {s}) &{} g^{\text {*2tch}}(\mathbf {a}_{|A|-1}|\varvec{\lambda }_2,\mathbf {s}) &{}\cdots &{} g^{\text {*2tch}}(\mathbf {a}_{|A|-1}|\varvec{\lambda }_{|\varLambda |},\mathbf {s})\\ g^{\text {mtch}}(\mathbf {r}|\varvec{\lambda }_1,\mathbf {s}) &{} g^{\text {mtch}}(\mathbf {r}|\varvec{\lambda }_2,\mathbf {s}) &{} \cdots &{} g^{\text {mtch}}(\mathbf {r}|\varvec{\lambda }_{|\varLambda |},\mathbf {s}) \end{bmatrix}_{|A|\times |\varLambda |}$$

After obtaining the above matrix, we can calculate \(R^{\text {HCA}}_2(\mathbf {s})\) as follows:

$$\begin{aligned} R^{\text {HCA}}_2(\mathbf {s}) = \frac{1}{|\varLambda |}\sum _{j=1}^{|\varLambda |}\left( \min _{i=\{1,2,...,|A|\}}M_{ij}\right) ^m. \end{aligned}$$
(5)

Since we need to calculate \(R^{\text {HCA}}_2\) for each \(\mathbf {s}\in A\), we need to have |A| matrices for all solutions in A. These |A| matrices form a tensor

$$\mathbf {T}=\left[ \mathbf {M}_1,\mathbf {M}_2,...,\mathbf {M}_{|A|}\right] ,$$

where \(\mathbf {M}_k\) is the matrix for \(\mathbf {a}_k\in A\).

We use tensor \(\mathbf {T}\) as a memory to store useful information for the calculation of \(R^{\text {HCA}}_2\). As shown in Algorithm 1, since only one offspring is generated and one individual is removed in each generation, we do not need to recalculate tensor \(\mathbf {T}\) in each generation. Instead, we only update \(\mathbf {T}\) with respect to the changed elements to maximize the efficiency. Furthermore, if all the solutions in the current population are non-dominated, we can use (5) to calculate \(R^{\text {HCA}}_2\). However, if there are some dominated solutions, we need to extract useful information from \(\mathbf {T}\) to calculate \(R^{\text {HCA}}_2\) for the last front. For more detailed explanation of tensor \(\mathbf {T}\) and its operations, please refer to [12].

3 Efficiency Improvement Strategies

In this section, we propose two strategies to further improve the efficiency of R2HCA-EMOA. The first strategy is to simplify the environmental selection, and the second strategy is to change the number of direction vectors depending on the state of evolution.

3.1 Simplify the Environmental Selection

The first strategy is to simplify the environmental selection in R2HCA-EMOA. As explained in the previous section, we use tensor \(\mathbf {T}\) to calculate \(R^{\text {HCA}}_2\) values, i.e., the approximated hypervolume contributions. If there are dominated solutions, we cannot directly use tensor \(\mathbf {T}\) to calculate \(R^{\text {HCA}}_2\) for the last front. Thus, a tensor extraction is performed to get a subtensor \(\mathbf {T}'\). This will lower the efficiency of R2HCA-EMOA.

The idea is to simplify the environmental selection when there are dominated solutions. Instead of extracting a subtensor \(\mathbf {T}'\) and calculating \(R^{\text {HCA}}_2\) for the last front, we simply randomly remove one solution from the last front. In this way, we can avoid the tensor extraction procedure and the algorithm efficiency can be improved. To be more specific, lines 8–15 in Algorithm 1 are replaced by the following lines:

figure b

Footnote 2

The question is whether this simple strategy can deteriorate the performance of R2HCA-EMOA. The answer is NO (which will be verified in the experiments). The reason can be explained as follows. In many-objective optimization, all or almost all solutions in the current population are non-dominated. In this situation, it is not likely that dominated solutions play an important role in multi-objective evolution. That is, it is likely that all dominated solutions in the current population are almost equally useless (if compared with the non-dominated solutions). As a result, it is not needed to carefully evaluate each dominated solution to identify the worst one with the least contribution.

3.2 Change the Number of Direction Vectors

The second strategy is to dynamically change the number of direction vectors used in R2HCA-EMOA. As discussed in [12], the worst-case time complexity of one generation of R2HCA-EMOA is \(O(N^2|\varLambda |)\). We can see that the time complexity is related to the number of direction vectors \(|\varLambda |\). We can improve the efficiency of R2HCA-EMOA by decreasing the value of \(|\varLambda |\). However, a smaller value of \(|\varLambda |\) means a lower approximation quality of \(R^{\text {HCA}}_2\). Thus, if we simply set \(|\varLambda |\) as a small value, the performance of \(R^{\text {HCA}}_2\) may be deteriorated.

The idea is to use a small number of \(|\varLambda |\) in the early stage of the evolution and use a large number of \(|\varLambda |\) in the late stage of the evolution. In the early stage of the evolution, we do not need a very high approximation quality of \(R^{\text {HCA}}_2\) since the main focus is the convergence of the population. Also, as we discussed in the first strategy, the solutions in the last front are randomly removed. In this case, we do not need to calculate \(R^{\text {HCA}}_2\). In the late stage of the evolution, we use a large number of \(|\varLambda |\) to achieve a good hypervolume performance.

The question is the timing to change the number of direction vectors. Ideally, the timing for the change is when the population has converged to the Pareto front. However, the Pareto front is usually unknown in practice. Thus, we need to have a mechanism to decide the timing for the change. In this paper, we use the following mechanism:

$$\begin{aligned} |\varLambda | = \left\{ \begin{array}{lc} \text {a small number,} &{} \text {if } \text {FEs}\le \theta \text {FEs}^{\text {max}} \\ \text {a large number,} &{} \text {otherwise} \end{array}\right. \end{aligned}$$
(6)

where \(\theta \in [0,1]\) is a timing control parameter. The small number and the large number are set to 10 and 100, respectively, in our experiments.

We need to note that when \(|\varLambda |\) is changed, the direction vector set \(\varLambda \) is regenerated, and tensor \(\mathbf {T}\) needs to be reinitialized since the size of \(\mathbf {T}\) is also changed.

4 Experiments

In this section, we examine the effect of the proposed two strategies on the performance of R2HCA-EMOA through computational experiments.

4.1 Experimental Settings

  1. 1.

    Platforms. Our experiments are performed on PlatEMO [15], which is a MATLAB-based open source platform for evolutionary multi-objective optimization. The source code of R2HCA-EMOA is available at https://github.com/HisaoLabSUSTC/R2HCA-EMOA. The hardware platform is a PC equipped with Intel Core i7-8700K CPU@3.70 GHz, 16 GB RAM.

  2. 2.

    Test Problems. DTLZ1-4 [6], WFG1-9 [9], and their minus versions (i.e., MinusDTLZ1-4 and MinusWFG1-9) [10] are selected as test problems in our experiments. The number of objectives is set to \(m=5\). The number of decision variables is set to \(m+4\) for DTLZ1 and MinusDTLZ1, and \(m+9\) for the other DTLZ and MinusDTLZ problems. For WFG and MinusWFG problems, the distance and position decision variables are set to 24 and \(m-1\), respectively.

  3. 3.

    Parameter Settings. The population size N is set to 100. For DTLZ1, DTLZ3, WFG1 and their minus versions, the maximum function evaluations \(\text {FEs}^{\text {max}}\) is set to 100,000, while \(\text {FEs}^{\text {max}}\) is set to 30,000 for the other test problems. The simulated binary crossover (SBX) and the polynomial mutation are adopted in the algorithms where the distribution index is specified as 20 in both operators. The crossover and mutation rates are set to 1.0 and 1/n respectively, where n is the number of decision variables. Each algorithm is run 20 time independently on each test problem.

  4. 4.

    Performance Metrics. The hypervolume indicator is used to evaluate the performance of the algorithms, and the runtime is recorded to evaluate the efficiency of the algorithms. We employ the WFG algorithm [17] to calculate the exact hypervolume of the obtained solution sets. The hypervolume is calculated as follows. First, using the true ideal point \(\mathbf {z}^*\) and the true nadir point \(\mathbf {z}^{\text {nad}}\) calculated from the true PF, the objective space is normalized, i.e., the two points \(\mathbf {z}^*\) and \(\mathbf {z}^{\text {nad}}\) are (0, ..., 0) and (1, ..., 1) after the normalization. Then, the reference point \(\mathbf {r}\) is specified as (1.1, ..., 1.1) to calculate the hypervolume of the obtained solution set in the normalized objective space.

  5. 5.

    Algorithm Configurations. The compared algorithms are R2HCA-EMOA and its improved version (denoted as R2HCA-EMOA-II) equipped with the two strategies. For R2HCA-EMOA, the number of direction vectors \(|\varLambda |\) is set to 100. For R2HCA-EMOA-II, \(|\varLambda |\) is initially set to 10, and finally changed to 100 according to (6). The timing control parameter \(\theta \) is set to \(\{0.0, 0.3, 0.5, 0.8\}\), i.e., we examine the effect of different \(\theta \) values. All the results are analyzed by the Wilcoxon rank sum test with a significance level of 0.05. ‘\(+\)’, ‘−’ and ‘\(\approx \)’ indicate that R2HCA-EMOA-II is ‘significantly better than’, ‘significantly worse than’ and ‘statistically similar to’ the original R2HCA-EMOA, respectively.

4.2 Results

The mean hypervolume results and the mean runtime results over 20 runs are shown in Table 1 and Table 2, respectively.

Table 1. Statistical results of hypervolume values obtained by R2HCA-EMOA and R2HCA-EMOA-II. The best result for each test problem is shaded.
Full size table
Table 2. Statistical results of runtime (in seconds) of R2HCA-EMOA and R2HCA-EMOA-II. The best result for each test problem is shaded.
Full size table

From Table 1, we can see that R2HCA-EMOA-II achieves a comparable hypervolume performance to R2HCA-EMOA when \(\theta =0.0,0.3\). When \(\theta =0.0\) (i.e., we only consider the first strategy), R2HCA-EMOA-II is significantly better on WFG9. When \(\theta =0.3\), it is significantly better on WFG6 and significantly worse on WFG8, and has no significant difference on all the other test problems. It should be noted that the difference in the average hypervolume value between the two algorithms is very small even when there exists a statistically significant difference (see the results on WFG6, WFG8 and WFG9). When \(\theta =0.5\), R2HCA-EMOA-II is slightly worse than R2HCA-EMOA. It is significantly worse on 3 out of the 26 test problems, and has no significant difference on all the other test problems. When \(\theta =0.8\), the performance of R2HCA-EMOA-II is clearly deteriorated. It is significantly worse on 10 out of the 26 test problems. From these results, we can see that the first strategy does not degrade the performance of R2HCA-EMOA-II (i.e., when \(\theta =0.0\)). We can also see that the second strategy has a large effect on the performance of R2HCA-EMOA-II depending on the value of \(\theta \). A too large \(\theta \) value can deteriorate the performance of R2HCA-EMOA-II. In our results, \(\theta =0.5\) is an acceptable value since the performance of R2HCA-EMOA-II is almost the same as that of R2HCA-EMOA.

From Table 2, we can see that the efficiency of R2HCA-EMOA-II is slightly improved by the first strategy when \(\theta =0.0\). The runtime of R2HCA-EMOA-II is significantly better on 2 out of the 26 test problems. This is because the first strategy only works when there exist dominated solutions. If all the solutions are non-dominated, the two algorithms are exactly the same. It is very likely that the first strategy only works for a small number of generations. For the second strategy, the efficiency of R2HCA-EMOA-II is significantly improved compared with R2HCA-EMOA. We can also see that R2HCA-EMOA-II runs faster as \(\theta \) increases. Take DTLZ1 as an example, when \(\theta =0.3\), the runtime of R2HCA-EMOA-II is about 0.78 times that of R2HCA-EMOA. When \(\theta =0.5\), the runtime of R2HCA-EMOA-II is about 0.61 times that of R2HCA-EMOA. When \(\theta =0.8\), this number is about 0.37. Similar results are obtained for other test problems.

Based on Table 1 and Table 2, we can see that if \(\theta \) is properly specified (e.g., \(\theta =0.3,0.5\)), we can improve the efficiency of R2HCA-EMOA without sacrificing its performance, which suggests the usefulness of the proposed two strategies.

5 Conclusions

In this paper, we proposed two strategies to further improve the efficiency of R2HCA-EMOA. The first strategy is to randomly remove one individual in the last front when there are dominated solutions. The second strategy is to use a small number of direction vectors in the early stage and a large number of direction vectors in the late stage of the evolution. The experimental results verified the effectiveness of the proposed two strategies. The efficiency of R2HCA-EMOA was improved without sacrificing its hypervolume performance. The results in this paper make R2HCA-EMOA more attractive for practical use.

In the future, the improved R2HCA-EMOA can be tested on more test problems and real-world problems. It is also interesting to propose other strategies to further improve the efficiency of R2HCA-EMOA. For example, removing the non-dominated sorting procedure and using the R2 indicator variant (i.e., \(R^{\text {HCA}}_2\)) to evaluate all the solutions (not only the solutions in the last front) is an interesting way to go.