On Predicting Principal Components Through Linear Mixed Models

Abstract

This work introduces a Principal Component Analysis of data given by the Best Predictor of a multivariate random vector. The mixed linear model framework offers a comprehensive baseline to get a dimensionality reduction of a variety of random-effects modeled data. Alongside the suitability of using model covariates and specific covariance structures, the method allows the researcher to assess the crucial changes of a set of multivariate vectors from the observed data to the Best Predicted data. The estimation of the parameters is achieved using the extension to the multivariate case of the distribution-free Variance Least Squares method. An application to some Well-being Italian indicators shows the changeover from longitudinal data to the subject-specific best prediction by a random-effects multivariate Analysis of Variance model.

1 Introduction

Principal Component Analysis (PCA) is one of the best established methods for dimension reduction. Principal Components (PCs) lead to a better assessment of the available information, by summarizing and visualizing data, and at the same time, minimizing the loss of information [6, 7].

Given a p-variate centered random vector $\mathbf {y}_i$ $(i = 1, \dots , n)$ and an $n\times p$ matrix of observed data $\mathbf {Y}$ from $\mathbf {y}$, the PCA of $\mathbf {y}$ can be obtained by a Singular Value Decomposition (SVD) of $\mathbf {Y}$ into the matrix product $\mathbf {Y}=\mathbf {P}\mathbf {L}_{s}\mathbf {Q}^{\prime }+\mathbf {N}=\mathbf {C}^{s}\mathbf {Q}^{\prime }+\mathbf {N}$, where: (i) $\mathbf {P}$ is the s-reduced rank orthogonal matrix of the first s eigenvectors (the left singular vectors) of the symmetric matrix $\mathbf {YY^{\prime }}$ ($r=1,...,s,...,p,\quad s\ll p$), (ii) $\mathbf {L}_{s}$ is the diagonal matrix of the first s singular values, and (iii) $\mathbf {Q}$ is the s-reduced rank matrix of the eigenvectors (the right singular vectors) of the symmetric covariance matrix $\mathbf {S}_{y}=\frac{1}{n}\mathbf {Y^{\prime }Y}$. The $n\times s$ matrix $\mathbf {C}^{s}=\mathbf {PL}_{s}$ gives the first s principal components, and the $n\times p$ matrix $\mathbf {N}$ reports the cross-product minimum norm matrix of residuals. Given the s-dimensional subspace representation of the observed data, we have $\left\| \mathbf { N^{\prime }N}\right\| ^{2}=tr(\mathbf {N^{\prime }N})=\min$ (here tr is the trace of a square matrix).

For decades, PCA has undergone many generalizations and adjustments to the needs of specific research goals. One of them brings into play the role of prediction by the linear statistical models. Bair et al. [1] provided a supervised PCA to address the high dimensional issue that arises when the number of predictors, p, far exceeds the number of observations, n-seeking linear combinations with both high variance and significant correlation with the outcome.

Tipping and Bishop [13] had already introduced the notion of prediction for the PCs. They called Probabilistic PCA (probPCA) the model behind the PCA, in which parameters are estimated by means of the Expectation-Maximization algorithm. The “noisy” PC model (nPC), proposed by Ulfarsson and Solo (see [13, 14] for details) has a quite similar formulation respect to the probPC model, providing—in a similar way—the nPC prediction once the model estimates have been given [2, 10].

Unlike the fixed effects PCs, as the traditional linear regression PCA model assumes, the probPC (or nPC) are random variables. This condition suggests, on the one hand, the adoption of the Bayesian approach to handle the estimates for the probPC linear model and, on the other hand, to predict PCs under its meaning within the random linear models theory [9].

The Bayesian approach to the estimation requires an expectation of some model parameters that are random, conditionally to the observed data. Given normality of the error ${\boldsymbol{\varepsilon }} \sim N(0,\sigma ^{2}\mathbf {I})$, for a linear model $\mathbf {\tau } =\mathbf {B}\mathbf {\lambda } +{\boldsymbol{\varepsilon }}$—in case of the vector $\mathbf {\lambda }$ random—the likelihood is based on the conditional distribution $\mathbf {\lambda } |\mathbf {\tau } \sim N[E(\mathbf {\lambda } |\mathbf {\tau } ),var(\mathbf {\lambda } |\mathbf {\tau } )]$. Moreover, it is known [8, 9, 11] that $E(\mathbf {\lambda } |\mathbf {\tau } )=\mathbf {\widetilde{\lambda }}$ is the Best Prediction (BP) estimate, with $var(\mathbf {\widetilde{\lambda }}-\mathbf {\lambda } )=E_{\mathbf {\tau } }[var(\mathbf {\lambda } |\mathbf {\tau } )]$. This is somewhat different from the standard linear regression model, where the prediction is given by $E(\mathbf {\tau }|\mathbf {\lambda })$. Therefore, given a Linear Mixed Model (LMM) for $\mathbf {\tau }$, with $E(\mathbf {\tau }| \mathbf {\lambda })) =\mathbf {\lambda }$, the model parameters become realizations of random variables. The BP of a linear combination of the LMM fixed and random effects (i.e., linear in $\mathbf {\tau }$, with $E[E(\mathbf {\tau }|\mathbf {\lambda })]=0$) gives the Best Linear Unbiased Prediction (BLUP) estimates [3, 8, 11].

LMM’s are particularly suitable for modeling with covariates (fixed and random) and for specifying model covariance structures [3]. They allow researchers to take into account special data, such as hierarchical, time-dependent, correlated, covariance patterned models. Thus, given the BP estimates of the nPC $\mathbf {\lambda }$, $\widetilde{\mathbf {\lambda }} = E(\mathbf {\lambda } | \mathbf {\tau })$, the vector $\widetilde{\mathbf {\tau }} = \mathbf {B} \widetilde{\mathbf {\lambda }}$ represents the best prediction of the p-variate vector (in the way of the BP).

In general, it is convenient to employ the LMM’s to assess how the most relevant parameters affect the linear model assumed for $\mathbf {y}_{i}$: we acknowledge the difficulty of including in the probPC model some of the typical LMM parameters. For this reason, this work proposes to reverse the BP estimation typical of the probPC model, in the sense that the data from the p-vector may produce itself the BP estimates $\mathbf {\widetilde{y}}_{i}$ by a multivariate BLUP. Afterwards, ordinary PCs can be obtained by the matrix of the n realizations $\mathbf {\widetilde{y}}_{i}$. Using the predictive variance of $(\mathbf {y}_{i}-\widetilde{\mathbf {y}}_{i})$, we can configure a double set of analyses analogous to the Redundancy Analysis [12, 15], the last based on the eigenvalue-eigenvector decomposition of the multivariate regression model predictions and errors. Therefore, we have a constrained analysis, based on the eigenvalue-eigenvector decomposition of $cov(\widetilde{\mathbf {y}}_{i})$, and an unconstrained analysis of the Best Prediction model error covariance, $cov(\mathbf {y}_{i}-\widetilde{\mathbf {y}}_{i})$.

The main advantage with respect to Redundancy Analysis is that the novel method may works also without model covariates. This is because the largest part of the multidimensional variability is due to the covariance of the same random effects among the components of the multivariate data vectors. We call this analysis a predictive PCA (predPCA), because the PCs are given by the BP data vectors of the subjects.

The proposed procedure would be particularly worthwhile with typically correlated observations, like repeated measures surveys, clustered, longitudinal, and spatially correlated multivariate data. Although the PCA operates only as a final step, this type of analysis can be valuable when the reduction of dimensionality aims to be investigated on data predicted by the sample, rather than the PCA of the sample data by themselves. Usually, the BLUP estimation of the p-variate random effects request iterative procedures in case of likelihood-based methods: the larger is the number of the model parameters, the more computationally expensive is to obtain the estimates to the normal variate covariance components of the LMM model.

Given that the general BLUP estimator has the same form of the BP under normality [8, 11], it is proposed to estimate the model covariance parameters, defining a distribution-free estimator of the BLUP. We introduce a multivariate extension of the Variance Least Squares (VLS) estimation method [4] for the variance components. Because of the specific aspects related to the multivariate case, this method changes from non-iterative to iterative, depending on alternating the minimization procedure from knowing, in turn, one of the two covariance matrices involved in the linear model. For this reason, we obtain an iterative version of the VLS: the Iterative Variance Least Squares (IVLS) method.

When the linear model for $\mathbf {y}_{i}$ is a population model without fixed covariates, the predPCA is equivalent to a PCA of the n realizations of the p-vector, $\mathbf {\widetilde{y}}_{i}$. Thus, the linear mixed model is a Multivariate Analysis of Variance (MANOVA) with variance components.

The paper is organized as follows: the first part is dedicated to the predPCA method, together with some explanations about the IVLS estimation. Then, an application of the predPCA method to some Well-being Italian indicators is presented. Two Appendices report some backgrounds and the proof of the Lemma given in the paper.

2 Predictive Principal Components Analysis

Given a p-variate random vector $\mathbf {y}_{ij}$, $i=1,...,m$, $j=1,...,k$, consider the case when $\mathbf {y}$ is partitioned in m subjects, each of them with k individuals (balanced design). If $\mathbf {\mu ^{\prime }}=(\mathbf {\mu } _{1},...,\mathbf {\mu } _{p})$ is the vector of the p means, a random-effects MANOVA model is given by

$$\begin{aligned} \mathbf {y}_{ij}-\mathbf {\mu } =\mathbf {a}_{i} + \mathbf {e}_{ij}, \end{aligned}$$

(1)

where $\mathbf {a}_{i}\overset{ind}{\sim }N_{p}(0,\Sigma _{a})$ is the p-variate random effect and $\mathbf {e}_{ij}\overset{ind}{\sim }N_{p}(0,\Sigma _{e})$ is the model error. Given $n=m\times k$ data from $\mathbf {y}$, we write the model (1) in the LMM standard matrix form $\mathbf {Y}=\mathbf {XB}+\mathbf {ZA}+\mathbf {E}$, where $\mathbf {Y}$ is the $n\times p$ matrix of data from $\mathbf {y}$, $\mathbf {X}$ is a $n\times l$ matrix of explanatory variables, $\mathbf {B}$ the $l\times p$ matrix of the l fixed effects, $\mathbf {Z}$ the $n\times m$ design matrix of random effects, $\mathbf {A}$ is the $m\times p$ matrix of random effects, $\mathbf {E}$ the $n\times p$ matrix of errors.

For the random-effects MANOVA model (1), we have that $\mathbf {X}$ is a column of ones (i.e., $l=1$), and $\mathbf {B}$ the row vector $\mathbf {\overline{\mu }^{\prime }}$ of sample means:

$$\begin{aligned} \mathbf {Y}-\mathbf {1}_{n\times 1}\mathbf {\overline{\mu }}_{1\times p}^{\prime }=(\mathbf {I}_{m}\otimes \mathbf {1}_{k})\times (\mathbf {a}_{1}...,\mathbf {a}_{p})_{m\times p}+\mathbf {E}, \end{aligned}$$

(2)

where $\otimes$ is the Kronecker product, $\mathbf {Z}=(\mathbf {I}_{m}\otimes \mathbf {1}_{k})$, $\mathbf {A}=(a_{1},...,a_{r},...,a_{p})$. Furthermore, the data $\mathbf {Y}$ and the error matrices have the structure

$\mathbf {Y}_{mk\times p} =(\mathbf {y}_{11},\mathbf {y}_{12},...,\mathbf {y}_{1k},...,\mathbf {y}_{m1},\mathbf {y}_{m2},...,\mathbf {y}_{mk})^{\prime }$

$\mathbf {E}_{mk\times p} =(\mathbf {e}_{11},\mathbf {e}_{12},...,\mathbf {e}_{1k},...,\mathbf {e}_{m1},\mathbf {e}_{m2},...,\mathbf {e}_{mk})^{\prime }.$

By centering the data $\mathbf {Y}$, with $\mathbf {Y}-\mathbf {1}_{n\times 1}\mathbf {\overline{\mu }} _{1\times p}^{\prime }=\mathbf {Y}^{*}$, and remembering that $E(\mathbf {\overline{\mu }} )=\mathbf {\mu }$, the p-vector population model (1) becomes $\mathbf {y}_{ij}^{*}=\mathbf {a}_{i}+\mathbf {e}_{ij}$. The BP estimation of the p-vector $\mathbf {a}_{i}$ in the LMM is given by [3, 8, 11]

$$\begin{aligned} \mathbf {\widetilde{a}} _{i}=E(\mathbf {a}_{i}|\mathbf {y}_{i}^{*})=cov(\mathbf {a}_{r},\mathbf {y}_{i}^{*})[var(\mathbf {y}_{i}^{*})]^{-1}[\mathbf {y}_{i}^{*}-E(\mathbf {y}_{i}^{*})] \end{aligned}$$

(3)

Reducing the LMM to the random-effects MANOVA model, we have by the Eq. (2): $E(\mathbf {y}_{i})=\mathbf {B}^{\prime }\mathbf {x}_{i}=\mathbf {\mu }$. It is well-known [8] that the variance of the LMM model is $cov[vec(\mathbf {Y})]=\mathbf {V}=\mathbf {D}+\mathbf {U}$, with $\mathbf {D}=\mathbf {Z}\times cov[vec(\mathbf {A})]\times \mathbf {Z}^{\prime }$ and $\mathbf {U}=cov[vec(\mathbf {E})]$. The variance matrix $\mathbf {V}$ allows to define a variety of typical linear models, by setting the parameters vector $\mathbf {\theta } =(\mathbf {\theta }_{1},...,\mathbf {\theta }_{q})$ inside the components $\mathbf {D}$ and $\mathbf {U}$. The estimation of these parameters is done by standard methods (e.g., Maximum Likelihood, Restricted Maximum Likelihood, Moment Estimator). Given the parameters estimate $\mathbf {\widehat{\theta }}$, and then the variance $\mathbf {\widehat{V}}=\mathbf {V}\mathbf {(\widehat{\theta }})$, the fixed effects estimate is given by the General Least Squares estimate $\mathbf {\widehat{B}}=\mathbf {\widehat{B}}_{GLS}=(\mathbf {X}^{\prime }\mathbf {V}^{-1}\mathbf {X})^{-1}X^{\prime }\mathbf {V}^{-1}\mathbf {Y^{*}}$. The random effects  (3) estimate $\mathbf {\widetilde{A}}=(\mathbf {\widetilde{a}}_{1}...,\mathbf {\widetilde{a}}_{r},...,\mathbf {\widetilde{a}}_{p})$, $\mathbf {\widetilde{a}}_{r}={\text {col}}(\mathbf {\widetilde{a}}_{ri})$, $r=1,...,p$, completes the so-called Empirical BLUP (EBLUP) $\mathbf {\widetilde{Y}^{*}}=\mathbf {X}\mathbf {\widehat{B}}+\mathbf {Z}\mathbf {\widetilde{A}}$. We assume for the model  (2) the more simple structure, with a single random effect by the i-th subject. Furthermore, an equicorrelation between these random effects is employed. Some further computational details for the specification of the model  (2) are given in Appendix 1.

We introduce an iterative multivariate variance least squares estimation (IVLS) for the estimation of the vector of parameters $\mathbf {\theta }$. The objective function to minimize is $VLS=trace(\Xi -\mathbf {U}-\mathbf {D})^{2}$, with $\Xi _{|mkp\times mkp}$ the empirical model covariance matrix. The algorithm is based on alternating least squares in a two-step iterative optimization process. At every iteration, the IVLS procedure first fixes $\mathbf {U}$ and the solves for $\mathbf {D}$, and then it fixes $\mathbf {D}$ and solves for $\mathbf {U}$. Since the LS solution is unique, at each step the VLS function can either decrease or stay unchanged but never increase. Alternating between the two steps iteratively guarantees convergence only to a local minimum, because it ultimately depends on the initial values for $\mathbf {U}$. Being $\Xi$ the matrix of the multivariate OLS cross-products of residuals, the VLS iterations are given by the following steps: (a) starting from the separate subject (group)-specific empirical covariance matrices $\mathbf {U}_{ri}$, first minimize VLS to obtain the estimate of the random-effects covariance $\mathbf {D}$, then (b), given the matrix $\mathbf {\widehat{B}}_{GLS}$%, minimize VLS, setting the same error covariance matrix among the subjects, and (c), iterate (a) and (b), until convergence to the minimum. The number of iterations may vary, depending on the choice of the specific model variance structure for the random effects and error covariance matrices.

Applications of the predPCA may be related to different types of available data, and then may accommodate a variety of patterned covariance matrices. Further, groups can be dependent or independent, even in space, time, and space-time correlated data.

The IVLS estimator at each step is unbiased, as discussed in the following Lemma:

Lemma

(Unbiasedness of the IVLS estimator) Under the balanced p -variate variance components MANOVA model $\mathbf {Y}^{*}=\mathbf {Z}\mathbf {A}+\mathbf {E}$, with $\mathbf {Z}$ the design matrix of random effects, $\mathbf {E}$ the matrix of errors, and covariance matrix $\mathbf {D}+\mathbf {U}$, $\mathbf {D}=(\mathbf {I}\otimes \mathbf {Z})cov[vec(\mathbf {A})](\mathbf {I}\otimes \mathbf {Z}^{\prime })$, $\mathbf {U}=cov[vec(\mathbf {E})]$, and known matrix $\mathbf {U}$, for the IVLS estimator of the parameters $\mathbf {\theta }$ in $\mathbf {D}$ we have $E[\mathbf {D}=\mathbf {D}(\mathbf {\widehat{\theta }}_{IVLS})]=\mathbf {D}\mathbf {(\theta )}.$

The proof is given in Appendix 2.

Finally, a SVD of the matrix $\widetilde{\mathbf {Y}}$ from the p-dimensional $\widetilde{\mathbf {y}}$ vector is obtained, in order to give a PC decomposition of the subject data involved by the linear model. The predPC are generated by the eigenvalue-eigenvector decomposition of the covariance matrix of the predicted data, i.e., $(\widetilde{\mathbf {Y}} - \mathbf {XB}(\widehat{\mathbf {\theta }}))^{\prime }(\widetilde{\mathbf {Y}} - \mathbf {XB}(\widehat{\mathbf {\theta }}))$.

3 An Application to Some Well-Being Indicators

The introduced predPCA is applied here for the analysis of some Equitable and Sustainable Well-being indicators (BES), annually provided by the Italian Statistical Institute [16].

The discussed IVLS estimation procedure is adopted.

According to recent law reforms, these indicators should contribute to define the economic policies which largely affect some fundamental dimensions of the quality of life. In this case study, we present an application of predPCA to 5 of the 12 BES indicators available in the years 2013–2016, collected at the level of NUTS2 (Nomenclature of Territorial Units for Statistics). We use the random-effect MANOVA model, where the random multivariate vector $\mathbf {Y}$ includes the repeated observations of all the Italian regions in the 4 time instants ($\mathbf {X}$). We do not consider model covariates, allowing predictors to be derived only by the covariance structure. We assume equicorrelation both of the multivariate random effects and of the residual covariance (see Appendix 1 for details). The random-effects MANOVA model is then given by a balanced design, with an AR(1) error structure.

Table 1 IVLS fixed effects estimates of the random-effect MANOVA model (centered data)

The fixed effects estimates, obtained through both the OLS and GLS estimators, are provided in Table 1. We have that the GLS estimates outperform the OLS estimates in terms of coefficient’s interpretability. The GLS estimate of the variable “Lack of Safety” highlights the greater change in value respect to the OLS mean estimate. This means that this indicator plays the most important role in highlighting the adjustment provided by the model prediction with respect to the observed data. Furthermore, this implies that the Lack of Safety will be the most influential indicator in terms of shifting the statistical units (i.e., the administrative Regions) from their observed position in the factorial plane.

Table 2 Iterative variance least squares estimates of the random-effects MANOVA model

Table 2 shows the IVLS estimation results of the mixed MANOVA model parameters, reporting the estimated variance and correlation among indicators ($\sigma _a$, $\rho _a$) and regression errors ($\sigma _e$, $\rho _e$), in the $\Sigma _a$ and $\Sigma _e$ matrices, respectively. We find a negative covariance between the BES indicators, together with a positive covariance between the regression errors among indicators. Finally, the time autocorrelation between units is estimated as slightly positive, independently from the nature of the BES indicator.

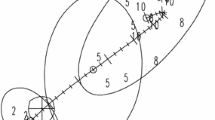
Finally, in order to visualize simultaneously the first factorial axes of the four years on a common factorial plane, for both observed and predicted variables, we performed a Multiple Factor Analysis (MFA) on a matrix obtained by juxtaposing the BES indicators with their IVLS prediction. Figure 1 shows the MFA biplot, where observed factor loadings and scores for each year (dashed lines) and predicted loadings and scores (plain lines) for each indicator are jointly represented with the observed and predicted (in rectangles) regions.

Fig. 1

Multiple Factor Analysis (MFA), observed factor loadings and scores per year (dashed lines); predicted loadings and scores (plain lines) in the space of the MFA

On this plan, it is possible to see how the axes change over years (among groups), and at the same time, to foresee how they could change in a new situation (in this example on a new year), comparing the position of the observed variable with their IVLS prediction.

Looking at the biplot, the horizontal axis clearly represents the well-being, being positively correlated with the variables GDP, Education and training (E&T), Job satisfaction and Investment in research and development (R&I), and having the variable Lack of Safety always a high negative coordinate. As expected, the Southern Italian regions are concentrated on the left side of the plane.

What is interesting to see is that most of the Southern regions, e.g., Puglia, Campania, Sicily, show a general improvement in terms of predicted values along this axis: the coordinates generally move towards the origin, foreseeing a decrease in the Lack of Safety, (i.e., an increase in their Well-being).

4 Conclusions and Perspectives

This paper introduces PCA of a multivariate predictor to perform an exploratory survey of sample data. The predPCA provides a new tool for interpreting a factorial plan, by enriching the factorial solution with the projection of the trends included in the observations. Given a multivariate vector with independent groups, and a random-effects population model, the predPCA relies on the assumption that the linear model itself is able to predict accurately specific subjects or group representatives, even in time and spatial dependent data. The use of the PCA is given afterward when the model has provided data predictions. Substantially, predPCA is a model-based PCA where the data are supplied by the model best predictors.

The advantage in using the predPCA, with respect to the PC-based models, is given by accommodating more easily a variety of structured data by the linear model itself. After using a linear mixed model, the PredPCA explores predicted data that originates in part from the regressive process and in part from the observed ones to understand the contribution of the observed to predictions.

We note that this approach is able to work out simultaneously the issues related to the use of model covariates and specific patterned covariance matrices. The impact of choosing the model structure is easily recognizable when we investigate changes in the factor data description. The reduction of dimensionality of the Best Prediction of a variety of linear models, some of them designed for grouped and correlated data, represents an important issue.

A forthcoming careful consideration will be made against Common Principal Components [5], as a comparative study in terms of a simultaneous representation of different data submatrices. Future studies can accommodate spatial and spatio-temporal data, bringing out the predictive ability of the general linear mixed models, by pivoting on specific covariance structures of the data.

Appendix 1

To accommodate a variety of random effects and error covariance matrices, it is appropriate to refer to the general LMM, as the generalization of the MANOVA variance components model given by Eq. (1):

$$\begin{aligned} \mathbf {Y}=\widetilde{\mathbf {X}}\mathbf {B}+\widetilde{\mathbf {Z}}\mathbf {A}+\mathbf {E}. \end{aligned}$$

We use the vector operator $vec(\mathbf {S})$, that converts the matrix $\mathbf {S}$ in a column vector. Then we have $\mathbf {y}=vec(\mathbf {Y})=\mathbf {X}\mathbf {\beta } +\mathbf {Z}\mathbf {a}+\mathbf {e}, \mathbf {y}_{mkp\times 1}=vec(\mathbf {Y}_{mk\times p}), \widetilde{\mathbf {X}}_{mk\times 1}=\mathbf {1}_{p}^{\prime }\otimes \mathbf {1}_{mk}, \mathbf {B}_{1\times p}=(\mathbf {\beta } _{01},...,\mathbf {\beta } _{0p}), \mathbf {X}_{mkp\times p}=\mathbf {I}_{p}\otimes \mathbf {X}=\mathbf {I}_{p}\otimes \mathbf {1}_{mk}, \mathbf {\beta } =vec(\mathbf {B}_{1\times p}), \widetilde{\mathbf {Z}}_{mk\times pm}=\mathbf {1}_{p}^{\prime }\otimes \mathbf {Z}_{r}, \mathbf {Z}_{i}=\mathbf {1}_{k}, \mathbf {Z}_{r}=\mathbf {I}_{m}\otimes \mathbf {Z}_{i}=\mathbf {I}_{m}\otimes \mathbf {1}_{k}, \mathbf {Z}_{p(mk\times m)}=diag(\mathbf {Z}_{1},...,\mathbf {Z}_{p}), \mathbf {A}_{mp\times p}=diag(\mathbf {a}_{1},...,\mathbf {a}_{p}), \mathbf {a}_{r}= {\text {col}}(\mathbf {a}_{r1},...,\mathbf {a}_{rm}), \mathbf {a}_{pm\times 1}={\text {col}}({\text {col}} (\mathbf {a}_{r1},...,\mathbf {a}_{rm}))$, and $\mathbf {E}_{mk\times p}=(\mathbf {e}_{1},...,\mathbf {e}_{p}), \mathbf {e}={\text {col}} (\mathbf {e}_{1},...,\mathbf {e}_{p})={\text {col}}({\text {col}}({\text {col}}(\mathbf {e}_{rm1},...,\mathbf {e}_{rmk})))$.

The BLUP for the j-th group (subject) and r-th response variable is given by $\widetilde{\mathbf {a}}_{ri}=E(\mathbf {a}_{ri}|\mathbf {y}_{ri})=cov(\mathbf {a}_{ri},\mathbf {y}_{ri})[var(\mathbf {y}_{ri})]^{-1}[\mathbf {y}_{ri}-E(\mathbf {y}_{ri})]$, with $\mathbf {U}_{ri}$ the covarince matrix of the residual errors for the i-th group and the r-th variable ($r=1,...,p$). The fixed effects estimates are given by the matrix $\widehat{\mathbf {B}}_{GLS}=(\mathbf {X}^{\prime }\mathbf {V}^{-1}\mathbf {X})^{-1}\mathbf {X}^{\prime }\mathbf {V}^{-1}\mathbf {Y}$, where $\mathbf {V}$ is the model covariance. In the case the variance components MANOVA model (1), if $\mathbf {G}$ is the $p\times p$ covariance matrix of random effects, with $\mathbf {D}=\mathbf {Z}\mathbf {G}\mathbf {Z}_{mkp\times mkp}^{\prime }=\mathbf {G}\otimes \mathbf {Z}_{r}\mathbf {Z}_{r}^{\prime }$, $\mathbf {U}_{ri}=\sigma _{ri}^{2}\mathbf {I}_{k}$, $\mathbf {U}_{r}=diag(\mathbf {U}_{r1},...,\mathbf {U}_{rm})$, $\mathbf {U}_{mkp\times mkp}=diag(\mathbf {U}_{1},...,\mathbf {U}_{p})$, and the model covariance matrix $\mathbf {V}_{mkp\times mkp}=cov(vec\mathbf {Y})=cov(\mathbf {y})=\mathbf {Z}\mathbf {G}\mathbf {Z}^{\prime }+\mathbf {U}=\mathbf {D}+\mathbf {U}$, we get a “constrained” PCA by the predictors, as the SVD of the estimates $\mathbf {Y}-\mathbf {1}\widehat{\mathbf {\mu } } _{GLS}^{\prime }=(\mathbf {I}_{m}\otimes \mathbf {1}_{k})\times (\widetilde{\mathbf {a}}_{1},..., \widetilde{\mathbf {a}}_{p})$. Further, an “unconstrained” analysis by the scores of the model conditional residuals $\mathbf {Y}-\widetilde{\mathbf {Y}}=\mathbf {Y}-\mathbf {1}\widehat{\mathbf {\mu } } _{GLS}^{\prime }-(\mathbf {I}_{m}\otimes \mathbf {1}_{k})\times (\widetilde{\mathbf {a}}_{1},..., \widetilde{\mathbf {a}}_{p})$ is done. To get the BLUP estimates $\widetilde{\mathbf {a}}_{ri}$, we must know the parameters of the MANOVA model inside the covariance matrix $\mathbf {D}=\mathbf {Z}\times cov(vec(\mathbf {A}))\times \mathbf {Z}_{mkp\times mkp}^{\prime }$, that is equal to:

$$\begin{aligned} \mathbf {D}=\Sigma _{a}\otimes (\mathbf {I}_{m}\otimes \mathbf {1}_{k})(\mathbf {I}_{m}\otimes \mathbf {1}_{k}^{\prime })=\Sigma _{a}\otimes (\mathbf {I}_{m}\otimes \mathbf {1}_{k}\mathbf {1}_{k}^{\prime }). \end{aligned}$$

Then: $vec(\mathbf {Y}) =(\mathbf {I}_{p}\otimes 1_{mt})vec(\mathbf {B})+(\mathbf {I}_{p}\otimes Z)vec(\mathbf {A})+vec(\mathbf {E})$ ; $\mathbf {y}^{*} =vec(\mathbf {Y}), \mathbf {X}^{*}=(\mathbf {I}_{p}\otimes \mathbf {X})=(\mathbf {I}_{p}\otimes \mathbf {1}_{mt})$, $\mathbf {\beta } ^{*} =vec(\mathbf {B})$, $\mathbf {Z}^{*}\mathbf {a}^{*}=(\mathbf {I}_{p}\otimes \mathbf {Z})vec(\mathbf {A})$.

Further, given the IVLS estimates $\widehat{\theta }$, we have $cov[(\mathbf {{y}}^{*}(\widehat{\theta }))]=(\mathbf {I}_{p}\otimes \mathbf {I}_{m}\otimes \mathbf {1}_{k})(\Sigma _{a}(\widehat{\theta })\otimes \mathbf {I}_{m})(\mathbf {I}_{p}\otimes \mathbf {I}_{m}\otimes \mathbf {1}_{k}^{\prime }){+}cov(vec(\mathbf {E})){=}\Sigma _{a}(\widehat{\theta })\otimes (\mathbf {I}_{m}\otimes \mathbf {1}_{k}\mathbf {1}_{k}^{\prime }){+}(\Sigma _{e}(\widehat{\theta })\otimes \mathbf {I}_{n})\otimes \Omega (\widehat{\theta })$. Finally, after the iterative VLS estimation, the predictor is given by $\mathbf {\widetilde{y}}^{*}(\widehat{\theta })=\mathbf {X}^{*}\mathbf {\widehat{\beta }}_{GLS}^{*}+\mathbf {Z}^{*} \mathbf {\widetilde{a}}^{*}=\Gamma \mathbf {y}^{*}(\widehat{\theta })+(\mathbf {I}-\Gamma )\mathbf {X}^{*}\mathbf {\widehat{\beta }} _{GLS}^{*}$, $\Gamma =(\Sigma _{a}(\widehat{\theta })\otimes \mathbf {ZZ}^{\prime })cov[(\mathbf {{y}}^{*}(\widehat{\theta }))]^{-1}$. Note that the matrix $\Gamma$ specifies both the contribution of the regression model and the observed data to the prediction.

We assume equicorrelation both of the multivariate random effects and the residual covariance, together with the AR(1) structure of the error:

$$\begin{aligned} \Sigma _{a}&=\sigma _{a}^{2}\times \left[ \begin{array}{cccc} 1 &{} \rho _{a} &{} \cdots &{} \rho _{a} \\ \rho _{a} &{} 1 &{} \cdots &{} \rho _{a} \\ \vdots &{} \cdots &{} \ddots &{} \vdots \\ \rho _{a} &{} \rho _{a} &{} \cdots &{} 1 \end{array} \right] _{5\times 5} \qquad \qquad \Sigma _{e}&=\sigma _{e}^{2}\times \left[ \begin{array}{cccc} 1 &{} \rho _{e} &{} \cdots &{} \rho _{e} \\ \rho _{e} &{} 1 &{} \cdots &{} \rho _{e} \\ \vdots &{} \cdots &{} \ddots &{} \vdots \\ \rho _{e} &{} \rho _{e} &{} \cdots &{} 1 \end{array} \right] _{5\times 5} \\ \end{aligned}$$

$$\begin{aligned} \Omega= & {} \frac{1}{1-\rho _{t}^{2}}\left( \begin{array}{cccc} 1 &{} \rho _{t} &{} \rho _{t}^{2} &{} \rho _{t}^{3} \\ \rho _{t} &{} 1 &{} \rho _{t} &{} \rho _{t}^{2} \\ \rho _{t}^{2} &{} \rho _{t} &{} 1 &{} \rho _{t} \\ \rho _{t}^{3} &{} \rho _{t}^{2} &{} \rho _{t} &{} 1\end{array}\right) _{4\times 4} \end{aligned}$$

Appendix 2

Lemma

(Unbiasedness of the IVLS estimator) Under the balanced p -variate variance components MANOVA model $\mathbf {Y}^{*}=\mathbf {Z}\mathbf {A}+\mathbf {E}$, with $\mathbf {Z}$ the design matrix of random effects, $\mathbf {E}$ the matrix of errors, and covariance matrix $\mathbf {D}+\mathbf {U}$, $\mathbf {D}=(\mathbf {I}\otimes \mathbf {Z})cov[vec(\mathbf {A})](\mathbf {I}\otimes \mathbf {Z}^{\prime })$, with known matrix $\mathbf {U}=cov[vec(\mathbf {E})]$, for the IVLS estimator of the vector of parameters $\mathbf {\theta }$ in $\mathbf {D}$ we have $E[\mathbf {D}=\mathbf {D}(\widehat{\mathbf {\theta } }_{IVLS})]=\mathbf {D}(\mathbf {\theta } )$.

Proof

With m groups ($i=1,...,m$), each of k individuals ($j=1,...,k$), for the multivariate mixed model we have the vector representation $\mathbf {y}=\mathbf {X}^{*}\mathbf {\beta } +\mathbf {Z}^{*}\mathbf {a}+\mathbf {e}$, with $\mathbf {y}=vec(\mathbf {Y})$, $\mathbf {X}^{*}=(\mathbf {I}\otimes \mathbf {X})$, $\mathbf {\beta } =vec(\mathbf {B})$, $\mathbf {Z}^{*}=(\mathbf {I}\otimes \mathbf {Z})$, $\mathbf {a}=vec(\mathbf {A})$, $\mathbf {e}=vec(\mathbf {E})$, and $\mathbf {\eta } =\mathbf {Z}^{*}\mathbf {a}+\mathbf {e}$, $\widehat{\mathbf {B}}=\widehat{\mathbf {B}}_{OLS}$. Defining $\widehat{{\boldsymbol{\varepsilon }} }=\mathbf {y}-\mathbf {X}^{*}\widehat{\mathbf {\beta } }=\mathbf {X}^{*}\mathbf {\beta } +\mathbf {\eta } -\mathbf {X}^{*}\widehat{\mathbf {\beta } }=\mathbf {\eta } -\mathbf {X}^{*}(\widehat{\mathbf {\beta } }-\mathbf {\beta } )$, by standard results on multivariate regression we write $\widehat{\mathbf {\beta } } -\mathbf {\beta } =\left\{ \mathbf {I}\otimes (\mathbf {X}^{\prime }\mathbf {X})^{-1}\mathbf {X}^{\prime }\right\} \mathbf {y}-\mathbf {\beta } =\mathbf {C}\times (\mathbf {X}^{*}\mathbf {\beta } +\mathbf {\eta } )-\mathbf {\beta }$. Thus: $\mathbf {X}^{*}(\widehat{\mathbf {\beta } } -\mathbf {\beta } )=\mathbf {X}^{*}\mathbf {C}\mathbf {X}^{*}\mathbf {\beta } +\mathbf {X}^{*}\mathbf {C}\mathbf {\eta } -\mathbf {X}^{*}\mathbf {\beta }$, and noticing that $\mathbf {C}\mathbf {X}^{*}=\left\{ \mathbf {I}\otimes (\mathbf {X}^{\prime }\mathbf {X})^{-1}\mathbf {X}^{\prime }\right\} \mathbf {X}^{*}=\left\{ \mathbf {I}\otimes (\mathbf {X}^{\prime }\mathbf {X})^{-1}\mathbf {X}^{\prime }\right\} (\mathbf {I}\otimes \mathbf {X})=\mathbf {I}\otimes (\mathbf {X}^{\prime }\mathbf {X})^{-1}\mathbf {X}^{\prime }\mathbf {X}=\mathbf {I}$, we get: $\mathbf {X}^{*}(\widehat{\mathbf {\beta } }-\mathbf {\beta } )=\mathbf {X}^{*}\mathbf {\beta } +\mathbf {X}^{*}\mathbf {C}\mathbf {\eta } -\mathbf {X}^{*}\mathbf {\beta } =\mathbf {X}^{*}\mathbf {C}\mathbf {\eta }$, and $\widehat{\mathbf {\varepsilon }}=\mathbf {y}-\mathbf {X}^{*}\widehat{\mathbf {\beta } }=\mathbf {\eta } -\mathbf {X}^{*}\mathbf {C}\mathbf {\eta }$.

Setting for the MANOVA model $\mathbf {Y}^{*}=\mathbf {Y}-\mathbf {X}\mathbf {B}$, $\mathbf {X}=\mathbf {1}_{mk\times 1}$, $\mathbf {B}=\mathbf {\mu } _{1\times p}^{\prime }$, to stack matrices by ordering subjects (groups), assume $\mathbf {y}^{**}=vec(\mathbf {Y}^{*\prime })=(\mathbf {Z}\otimes \mathbf {I})vec(\mathbf {A})+vec(\mathbf {E}^{\prime })=\mathbf {Z}^{*}\mathbf {a}+\mathbf {e}=\mathbf {\eta }$, with $\mathbf {Z}^{*}$ the design matrix of the multivariate random effects. Given $\widehat{{\boldsymbol{\varepsilon }} }=vec(\mathbf {Y}^{\prime }-\widehat{\mathbf {B}}^{\prime }\mathbf {X}^{\prime })=\widehat{\mathbf {y}}^{**}$, $\widehat{\mathbf {B}}=\widehat{\mathbf {B}}_{OLS}=\mathbf {\mu } ^{\prime }$, the VLS estimator finds the minimum of $VLS(\mathbf {\theta } )=tr(\mathbf {T}^{2})=tr\left\{ \widehat{{\boldsymbol{\varepsilon }}}\widehat{\mathbf {\varepsilon }}^{\prime }-cov(vec(\mathbf {\eta } )\right\} ^{2}=\Sigma \mathbf {T}_{ij}^{2}$. Now denoting $cov(\mathbf {a})=\mathbf {G}=\mathbf {G}(\mathbf {\theta } )$, $\mathbf {g}^{*}=vec(\mathbf {G})$, $\mathbf {u}^{*}=vec(\mathbf {U})$, and differentiating the VLS function with respect to $\mathbf {G}$, we have the following derivatives:

$$\begin{aligned} \frac{\partial }{\partial \mathbf {G}}VLS(\mathbf {\theta } )= & {} \mathbf {Z}^{*\prime }\widehat{ {\boldsymbol{\varepsilon }} }\widehat{\mathbf {\varepsilon } }^{\prime }\mathbf {Z}^{*}-\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\mathbf {G}\mathbf {Z}^{\prime }\mathbf {Z}-\mathbf {Z}^{*\prime }\mathbf {U}\mathbf {Z}^{*}=0 \\ (\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\otimes \mathbf {Z}^{*\prime }\mathbf {Z}^{*})\mathbf {g}^{*}+(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })\mathbf {u}^{*}= & {} (\mathbf {Z}^{*\prime } \widehat{{\boldsymbol{\varepsilon }}})\otimes (\mathbf {Z}^{*\prime }\widehat{\mathbf {\varepsilon }}). \end{aligned}$$

Then: $\widehat{\mathbf {g}}^{*}=\mathbf {g}^{*}(\widehat{\mathbf {\theta } })=(\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\otimes \mathbf {Z}^{*\prime }\mathbf {Z}^{*})^{-1}\left\{ (\mathbf {Z}^{*\prime }\widehat{{\boldsymbol{\varepsilon }} })\otimes (\mathbf {Z}^{*\prime }\widehat{{\boldsymbol{\varepsilon }} })-(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime }) \mathbf {u}^{*}\right\}$.

Remembering that $(\mathbf {Z}^{*\prime }\widehat{{\boldsymbol{\varepsilon }} })\otimes (\mathbf {Z}^{*\prime }\widehat{\mathbf {\varepsilon }})=(\mathbf {Z}^{*\prime }\mathbf {\eta } )\otimes (\mathbf {Z}^{*\prime }\mathbf {\eta } )$, $cov(\mathbf {a},\mathbf {e})=0$, and taking the expectation of $\mathbf {\eta } \otimes \mathbf {\eta }$:

$$\begin{aligned} E(\mathbf {\eta } \otimes \mathbf {\eta } )= & {} E(vec(\mathbf {\eta } \mathbf {\eta } ^{\prime }))=E(vec\left\{ (\mathbf {Z}^{*}\mathbf {a}+\mathbf {e})(\mathbf {Z}^{*}\mathbf {a}+\mathbf {e})^{\prime }\right\} ) \\= & {} E\left\{ (\mathbf {Z}^{*}\otimes \mathbf {Z}^{*})vec(\mathbf {a}\mathbf {a}^{\prime })+(\mathbf {e}\otimes \mathbf {Z}^{*})\mathbf {a}+(\mathbf {Z}^{*}\otimes \mathbf {e})\mathbf {a}+vec(\mathbf {e}\mathbf {e}^{\prime })\right\} \\= & {} (\mathbf {Z}^{*}\otimes \mathbf {Z}^{*})\mathbf {g}^{*}+0+0+\mathbf {u}^{*}. \end{aligned}$$

Since $(\mathbf {Z}^{*\prime }\mathbf {\eta } )\otimes (\mathbf {Z}^{*\prime }\mathbf {\eta } )=(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })(\mathbf {\eta } \otimes \mathbf {\eta })$, the expectation become:

$$\begin{aligned}&E\left\{ (\mathbf {Z}^{*\prime }\widehat{{\boldsymbol{\varepsilon }} })\otimes (\mathbf {Z}^{*\prime }\widehat{{\boldsymbol{\varepsilon }} })\right\} \\= & {} E\left\{ (\mathbf {Z}^{*\prime }\mathbf {\eta } )\otimes (\mathbf {Z}^{*\prime }\mathbf {\eta } )\right\} =(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })E(\mathbf {\eta } \otimes \mathbf {\eta } ) \\= & {} (\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })(\mathbf {Z}^{*}\otimes \mathbf {Z}^{*})\mathbf {g}^{*}+(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })\mathbf {u}^{*} \\= & {} (\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\otimes \mathbf {Z}^{*\prime }\mathbf {Z}^{*})\mathbf {g}^{*}+vec(\mathbf {Z}^{*\prime }\mathbf {U}\mathbf {Z}^{*}). \end{aligned}$$

Hence: $E[\mathbf {g}^{*}(\widehat{\mathbf {\theta } }_{IVLS})] {=}(\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\otimes \mathbf {Z}^{*\prime }\mathbf {Z}^{*})^{-1}\left\{ E \left[ (\mathbf {Z}^{*\prime }\widehat{\mathbf {\varepsilon }})\otimes (\mathbf {Z}^{*\prime } \widehat{{\boldsymbol{\varepsilon }} })\right] {-}(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })\mathbf {u}^{*}\right\} =(\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\otimes \mathbf {Z}^{*\prime }\mathbf {Z}^{*})^{-1}\left\{ (\mathbf {Z}^{*\prime }\mathbf {Z}^{*}\otimes \mathbf {Z}^{*\prime }\mathbf {Z}^{*})\mathbf {g}^{*}+vec(\mathbf {Z}^{*\prime }\mathbf {U}\mathbf {Z}^{*})-(\mathbf {Z}^{*\prime }\otimes \mathbf {Z}^{*\prime })\mathbf {u}^{*}\right\} =\mathbf {g}^{*}(\mathbf {\theta } )$.