Keywords

1 Introduction

The properties of laboratory, thermonuclear (tokamak), laser-produced, astrophysical plasmas have drawn considerable attention over the last decades [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76]. It is known that atomic ions play an important role in the diagnostics of a wide variety of plasmas [1,2,3,4,5,6,7,8,9,10]. Electron-ion collisions involving multiply charged ions, as well as various radiation and radiation-collisional processes, predetermine the quantitative characteristics of the energy balance of the plasmas [1,2,3,4,5,6, 15,16,17,18,19,20]. For this reason, the plasmas modelers and diagnosticians require absolute cross sections for these processes. The cross sections for electron-impact excitation of ions are needed to interpret spectroscopic measurements and for simulations of plasmas using collisional-radiative models. The electron-ion collisions play a major role in the energy balance of plasmas (e.g. [1,2,3,4,5,6,7,8,9,10]). Different theoretical methods were employed along with the Debye screening to study plasma medium.

In the case of solving collision problems involving multi-electron atomic systems, as well as low-energy processes, etc., the structure of atomic systems should be described on the basis of rigorous methods of quantum theory. As a rule, the Hartree-Fock (HF) or Hartree-Fock-Slater (HFS) models implemented in the tight-binding approximation were used to describe the wave functions of the bound states of atoms and ions. Another direction is the models of the central potential (model potential, pseudopotential) implemented in the distorted wave approximation (DWA).

It should be mentioned the currently widespread and widely used R-matrix method and its various promising modifications, as well as a generalization of the well-known Dirac-Fock method for the case of taking into account multipolarity in the corresponding operators (see, e.g., [1,2,3,4,5,6,7]). It should be noted that, depending on the perturbation theory (PT) basis used, different versions of the R-matrix method received the corresponding names. For example, in specific calculations such versions as R-MATR-CI3-5R and R-MATR-41 R-matrix method were used using respectively wave functions in the multiconfiguration approximation, in particular, 5- and 41-configuration wave functions.

As numerous applications of the R-matrix method have shown, it has certain advantages in terms of accuracy and consistency over such popular approaches as the first-order PT method, as well as the distorted wave approximation taking into account configuration interaction (CI-DWBA), approximation of distorted waves using the HF basis (HF-DWBA), finally, the relativistic approximation of distorted waves with a 1-configuration and multi-configuration wave function of the ground state (SCGS-RDWA, MCGS-RDWA, etc.). Improved models have also appeared in theories of the coupled-channel (VC) type VCDWA (Variational Continuum Distorted Wave), for example, a modification of the Vraun-Scroters type and others (see [1,2,3,4,5]). Various cluster methods have also been widely used (see in more detail Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]).

Earlier we have developed a new version of a relativistic energy approach combined with the many-body perturbation theory (RMBPT) for multi-quasiparticle (QP) systems to study spectra of plasma of the multicharged ions, electron-ion collisional parameters [24,25,26,27,28,29]. The method is based on the Debye shielding model and energy approach. A new element of this paper is in using the effective optimized Dirac-Kohn-Sham method in general relativistic energy approach to collision processes in the Debye plasmas.

In this paper, which goes on our work [8,9,10,11, 24,25,26,27,28], we present the results of computing the transition probabilities and lifetimes for different excited states in spectrum of the Li-like calcium for different values of the plasmas screening (Debye) parameter (respectively, electron density, temperature) and compared with available alternative spectroscopic data.

The computational approach used is based on the generalized relativistic energy approach combined with the optimized RMBPT with the Dirac-Debye shielding model as zeroth approximation, adapted for application to study the spectral parameters of ions in plasmas. An electronic Hamiltonian for N-electron ion in plasmas is added by the Yukawa-type electron-electron and nuclear interaction potential.

The results of relativistic calculation (taking into account the exchange and correlation corrections) of the electron collision cross-sections (strengths) of excitation of the transition between the fine-structure levels (2P3/2 − 2P1/2) of the ground state of F-like ions with Z = 19–26 and of the [2s2 1S − (2s2p 1P)] transition in the B-like O4+ are presented and analyzed.

It should be emphasized that an accurate treating the gauge dependent lowest perturbation theory multielectron contributions to radiation widths of atomic levels or radiation transitions probabilities is a fundamental requirement in order to construct the optimized one-electron representation in the many-body perturbation theory zeroth approximation. One could remember that the known relativistic many-body perturbation theory formalism is constructed with using the same ideas as the well-known perturbation theory approach with the model potential zeroth approximation by Ivanov-Ivanova et al. [31,32,33,34,35,36,37,38,39,40,41,42]. But unlike the method by Ivanova et al. and similar method by Glushkov et al. [43,44,45,46,47,48,49,50], the PT zeroth approximation in our method is the Dirac-Debye-Hückel one. Computing the radiative and collisional characteristics of atoms and ions is performed within a gauge-invariant version of relativistic energy approach [43].

2 Advanced Relativistic Energy Approach in Electron-Collisional Spectroscopy

The detailed description of our approach was earlier presented (see, for example, Refs. [24,25,26,27,28,29]). Therefore, below we are limited only by the key points. The generalized relativistic energy approach combined with the RMBPT has been in detail described in Refs. [7, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. It generalizes earlier developed energy approach. The key idea is in calculating the energy shifts ΔE of degenerate states that is connected with the secular matrix M diagonalization. To construct M, one should use the Gell-Mann and Low adiabatic formula for ΔE.

The whole calculation is reduced to calculation and diagonalization of the complex matrix M and definition of matrix of the coefficients with eigen state vectors \(B_{ie,iv}^{IK}\) [7, 24, 25]. To calculate all necessary matrix elements one must use the bases of the 1QP relativistic functions. Within an energy approach the total energy shift of the state is usually presented as [31, 32]:

$$\Delta {\text{E }} = {\text{ Re}}\Delta {\text{E }} + {\text{ i}}\varGamma /{ 2},$$
(1)

where Γ is interpreted as the level width and decay (transition) possibility P = Γ. The imaginary part of electron energy of the system, which is defined in the lowest PT order as [31, 32]:

$${\text{Im}}\Delta E(B) = - \frac{{e^{2} }}{4\pi }\sum\limits_{\begin{subarray}{l} \, \alpha > n > f \\ \left[ {\alpha < n \le f} \right] \end{subarray} } {V_{\alpha n\alpha n}^{{\left| {\omega_{\alpha n} } \right|}} }$$
(2)
$$V_{ijkl}^{\left| \omega \right|} = \iint {dr_{1} dr_{2} \varPsi_{i}^{*} (r_{1} )\varPsi_{j}^{*} (r_{2} )\frac{{\sin \left| \omega \right|r_{12} }}{{r_{12} }}(1 - \alpha_{1} \alpha_{2} )\varPsi_{k}^{*} (r_{2} )\varPsi_{l}^{*} (r_{1} )}$$
(3)

where \(\sum\nolimits_{\alpha > n > f} {}\) for electron and \(\sum\nolimits_{\alpha < n < f} {}\) for vacancy. The separated terms of the sum in (2) represent the contributions of different channels.

According to the definition, a lifetime of some excited state f is defined as follows (included all possible transition channels) for the transition rate \(P_{f - i}^{A}\) due to a radiative operator A:

$$\tau_{f} = 1/\sum\limits_{A,i} {P_{f - i}^{A} }$$
(4)

The transition rates via various multipole channels are determined as follows:

$$P_{f - i}^{E1} = \frac{{2.02613 \cdot 10^{18} }}{{\lambda^{3} (2J_{f} + 1)}}S_{f - i}^{E1}$$
(5a)
$$P_{f - i}^{M1} = \frac{{2.69735 \cdot 10^{13} }}{{\lambda^{3} (2J_{f} + 1)}}S_{f - i}^{M1}$$
(5b)
$$P_{f - i}^{E2} = \frac{{ 1. 1 1 9 9 5\cdot 10^{18} }}{{\lambda^{5} (2J_{f} + 1)}}S_{f - i}^{E2}$$
(5c)

where λ is the wavelength (Å), Jf is the total angular momentum of the f state, \(S_{f - i}^{A}\) ~ ImΔE is a line strength due to the corresponding transition operator A (the decay channels E1, M1 and E2 represent the electric dipole, magnetic dipole, and electric quadrupole transition channels respectively).

It is known [31, 32] that the matrix elements computed with using the length gauge expressions converge faster than the velocity ones with respect to the configuration space of the orbital bases.

This phenomenon is directly linked with a correct accounting for the correlation effects and using the optimized basis of electron wave functions. In [31, 32] it has been proposed an effective relativistic approach to construction of the optimized electron orbitals basis set.

The key idea of this approach is linked with search of minimum contribution into an imaginary part of the atomic level energy shift due to the gauge dependent multielectron contribution, provided by the QED perturbation theory fourth order (second order of atomic perturbation theory) exchange-correlation Feynmann diagrams [43].

One should note that this effective approach has been successfully used while solving multiple problems of modern atomic, nuclear and molecular optics and spectroscopy (see details, for example, in Refs. [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90]).

Further let us firstly consider the Debye shielding model according to Refs. [25, 26]. What is known from the classical theory of plasmas developed by Debye-Hückel, the interaction potential between two charged particles is modeled by the Yukawa-type potential, which contains the shielding parameter μ. There is a direct link between the parameter μ and the plasma parameters (temperature T and the charge density n)

$$\mu \sim \sqrt {e^{2} (1 + Z)n_{e} /k_{B} T_{e} }$$

The useful estimates for the shielding parameter for different plasmas types and conditions are listed in Refs. [25, 26].

The electronic Hamiltonian for N-electron ion in a plasma with using special Yukawa-type e-N and e-e interaction potentials can be constructed as follows [25, 26] (in atomic units):

$$H = \sum\limits_{i} {\{ \alpha cp_{i} - \beta c^{2} - Z \cdot \exp ( - \mu r_{i} )/r_{i} \} } + \sum\limits_{i > j} {{\text{exp(}} - \mu r_{ij} )(1 - \alpha_{i} \alpha_{j} )/r_{ij} } ,$$
(6)

where αi,αj are the Dirac matrices, c is the velocity of light and Z is a charge of an ionic nucleus.

To generate the wave functions basis we use the optimized Dirac-Kohn-Sham potential with one parameter [43], determined on the basis of a relativistic energy formalism [31]. Modified PC numerical code ‘Superatom’ is used in all calculations. Other details can be found in Refs. [24,25,26,27,28,29,30,31,32,33,34,35, 91,92,93,94,95,96,97,98,99,100].

Certain ideas of a relativistic energy formalism in application to a quantum scattering topics have been presented in a literature (e.g., [7, 43,44,45]). The important quantity is a scattered part of energy shift Im ΔE. It can be presented in the form of integral over the scattered electron energy εsc:

$$\int {d\varepsilon_{sc} G(\varepsilon_{iv} ,\varepsilon_{ie} ,\varepsilon_{in} ,\varepsilon_{sc} )/} (\varepsilon_{sc} - \varepsilon_{iv} - \varepsilon_{ie} - \varepsilon_{in} - i0)$$
(7)
$${\text{Im}}\Delta = \pi G(\varepsilon_{iv} ,\varepsilon_{ie} ,\varepsilon_{in} ,\varepsilon_{sc} )$$
(8)

where εin and εsc are the energies of the incident and scattered electrons and G is a definite squired combination of the two-electron matrix elements.

Further one could easily determine the collisional cross-section σ = −2 ImΔE (the details can be found in Refs. [6, 25, 26]). In particular, the collisional de-excitation cross section can be written in the following form [6, 25]:

$$\begin{aligned} \sigma (IK \to 0) & = 2\pi \sum\limits_{{j_{in} ,j_{sc} }} {(2j_{sc} + 1)} \\ & \quad * \left\{ {\sum\limits_{{j_{ie,} j_{iv} }} { < 0|j_{in} ,j_{sc} |j_{ie} ,j_{iv} ,J_{i} > {B_{ie,iv}^{IK}}^{2} } } \right\} \\ \end{aligned}$$
(9a)
$$\begin{aligned} & \left\langle {0|j_{in} ,j_{sc} |j_{ie} ,j_{iv} ,J_{i} } \right\rangle \\ & \quad = \sqrt {(2j_{ie} + 1)(2j_{iv} + 1)} ( - 1)^{{j_{ie} + 1/2}} \times \sum\limits_{\lambda } {( - 1)^{{\lambda + J_{i} }} } \\ & \quad \quad \times \{ \delta_{{\lambda ,J_{i} }} /(2J_{i} + 1)Q_{\lambda } (sc,ie;iv,in) \\ & \quad \quad + \left[ \begin{aligned} j_{in} \ldots j_{sc} \ldots J_{i} \hfill \\ j_{ie} \ldots j_{iv} \ldots \lambda \hfill \\ \end{aligned} \right]Q_{\lambda } (ie;in;iv,sc)\} \\ \end{aligned} ,$$
(9b)

Here the quantity Qλ can be expressed thorough the known Coulomb-Yukawa (CY) and Breit (Br) matrix elements combinations [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]:

$$Q_{\lambda } = Q_{\lambda }^{{\text{CY}}} + Q_{\lambda }^{Br}$$
(10)

The \(Q_{\lambda }^{{\text{CY}}} ,Q_{\lambda }^{Br}\) quantities contain the corresponding radial Wλ and angular Yλ integrals as follows:

$$\begin{aligned} Q_{\lambda }^{{\text{CY}}} & = \left\{ {W_{\lambda } \left( {1243} \right)Y_{\lambda } \left( {1243} \right) + W_{\lambda } \left( {\tilde{1}24\tilde{3}} \right)Y_{\lambda } \left( {\tilde{1}24\tilde{3}} \right)} \right. \\ \\ & \quad \left. { + W_{\lambda } \left( {1\tilde{2}\tilde{4}3} \right)Y_{\lambda } \left( {1\tilde{2}\tilde{4}3} \right) + W_{\lambda } \left( {\tilde{1}\tilde{2}\tilde{4}\tilde{3}} \right)Y_{\lambda } \left( {\tilde{1}\tilde{2}\tilde{4}\tilde{3}} \right)} \right\}. \\ \end{aligned}$$
(11)

where the tilde designates that the large radial Dirac component f must be replaced by the small Dirac component g (other details can be found in Refs. [25, 26]). It should be noted that the Breit quantity can be analogically expressed thorough the same integrals.

The effective collision strength \(\varOmega (I \to F)\) is associated with a collisional cross section σ as follows (in the Coulomb units):

$$\begin{aligned} \sigma (I \to F) & = \varOmega (I \to F) \cdot \pi \\ & \quad /\{ (2J_{i} + 1)\varepsilon_{in} [(\alpha Z)^{2} \varepsilon_{in} + 2]\} , \\ \end{aligned}$$
(12)

where α is the fine structure constant.

Other details can be found in Refs. [8,9,10,11, 14,15,16,17,18,19,20, 24,25,26,27,28,29,30,31, 91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,124,124]. All computing is performed with using the modified PC atomic code “Superatom-ISAN” (the modified version 93).

3 Results and Conclusions

Below we present the results of computing the energy, spectroscopic characteristics of some Li-like, B-like and F-like ions. The sought objects of research, firstly, belong to the class of complex relativistic many-electron atomic systems, in connection with which the approbation of the theory is extremely important and indicative just for such systems. Secondly, the sought multiply charged ions are of great interest for a number of applications in the field of laser physics and quantum electronics, in particular, the use of the plasma of the corresponding ions as an active medium for short-wavelength lasers, further in the field of diagnostics of astrophysical, laboratory plasma and plasma of a fusion reactor, tokamak and EBIT devices, as well as, of course, laser plasma.

Firstly, we present our results on the transition probabilities and lifetimes for some excited states of the Li-like ion of calcium. The spectroscopic properties for plasma-isolated ion with μ = 0 have been considered. In Tables 1 and 2 there are listed probabilities values for transitions (E1, M1, and E2 channels) from the excited states to the low-lying states of Ca XVIII.

Table 1 The transition probabilities (P) for some transitions in spectrum of Ca XVIII: RCC—relativistic coupled-cluster (RCC) method [3]; This—our work
Full size table
Table 2 The transition probabilities (P) for some transitions in spectrum of Ca XVIII (our data)
Full size table

Using these values, one could calculate the corresponding lifetimes of the excited states. The analysis shows that the presented data are in physically reasonable agreement with the NIST experimental data and theoretical results by relativistic coupled-cluster (RCC) method calculation (e.g. [3, 24, 25]). However, some difference between the corresponding results can be explained by using different relativistic orbital bases and by difference in the model of accounting for the screening effect as well as some numerical differences.

In Tables 3 and 4 we list the numerical variations in the lifetimes of the 2p1/2, 3s1/2, 3p1/2, 3d3/2, and 4s1/2 states in Ca XVIII for different µ values.

Table 3 The dependence of the lifetimes (ps) of the 2p1/2 state in the Ca XVIII spectrum upon the screening parameter µ: RCC—relativistic coupled-cluster (RCC) method [3]; This—our work
Full size table
Table 4 The dependence of the lifetimes (ps) of the 3lj, 4lj states in the Ca XVIII spectrum upon the parameter µ (this work)
Full size table

It is worth to note that our computing oscillator strengths within energy approach with different forms of transition operator (i.e. using the photon propagators in the form of Coulomb, Feynman or Babushkin) gives very close results.

In Table 5 we present the results of our relativistic calculation (taking into account the exchange and correlation corrections) of the electron collision strengths of excitation the transition between the fine-structure levels (2P3/2 − 2P1/2) of the ground state of F-like ions with Z = 19–26.

Table 5 The electron collision strengths of excitation the transition between the fine-structure levels (2P3/2 − 2P1/2) of the ground state of F-like ions with Z = 19–26
Full size table

The energy of the incident electron is εin = 0.1294 · Z2 eV, T = z2 keV (z is the core charge), Ne = 1018 cm−3. For comparison, in Table 5 there are also listed the calculation results based on the most advanced versions of the R-matrix method, nonrelativistic calculation data in the framework of the energy approach, and also the available experimental data (e.g. [1,2,3, 24, 25]).

The analysis shows that the presented data are in physically reasonable agreement, however, some difference can be explained by using different relativistic orbital basises and different models for accounting for the plasma screening effect. This circumstance is mainly associated with the correct accounting of relativistic and exchange-correlation effects, using the optimized basis of relativistic orbitals (2s2 2p5; 2s 2p6 2s2 2p4 3l, l = 0–2) and, to a lesser extent, taking into account the effect of the plasma environment.

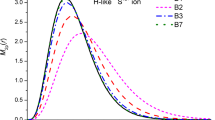
The electron-ion collision characteristics for Be-like ions are of great interest for applications such as the diagnosis of astrophysical, laboratory, and thermonuclear plasmas, as well as EBIT plasmas (see, for example, [4, 5]). In the latter case, the characteristic values ​​of electron density turn out to be significantly (several orders of magnitude) less than those considered above (1015–1017). In particular, the so-called MEIBEL (the merged electron-ion beams energy-loss) experiment (1999), the results of which for a Be-like oxygen ion are presented in Fig. 1. In this figure there also listed the cross section (10−16 cm3) of the electron-collision excitation of the [2s2 1S − (2s2p 1P)] transition in the spectra of Be-like oxygen together with the data from an alternative 3-configuration R-matrix calculation [4]. At energies below 20 eV there is a reasonable agreement between the theoretical and experimental, but, above 20 eV there is a discrepancy, which is due to different degrees of allowance for correlation effects (interaction of configurations) due to the difference in the bases used.

Fig. 1
figure 1

Cross section for electron-collision excitation of the [2s2 1S − (2s2p 1P)] transition in the spectra of B-like O4+: Experiment MEIBEL—points; Theory: R-matrix—solid line; our theory—dashed line

Full size image

To conclude, we have presented an effective relativistic approach to computing energy and spectroscopic characteristics of the multicharged ions in plasmas. It is consistently based on the generalized relativistic energy approach combined with the optimized relativistic many-body perturbation theory with the Dirac-Debye shielding model as zeroth approximation. The important theoretical aspect is connected with construction of an electronic Hamiltonian for N-electron ion in plasmas with addition of the Yukawa-type electron-electron and nuclear interaction potentials.

As an illustration, the approach has been applied to computing probabilities and lifetimes for different excited states in spectrum of the Li-like calcium as well as the electron collision cross-sections (strengths) of excitation of the transition between the fine-structure levels (2P3/2 − 2P1/2) of the ground state of F-like ions with Z = 19–26 and the [2s2 1S − (2s2p 1P)] transition in the B-like O4+ The presented approach and obtained data can be used in different applications, namely, in atomic, molecular and laser physics, quantum electronics, astrophysical, laboratory, thermonuclear plasmas physics etc. (e.g. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21, 43]).