1 Introduction

We are concerned with the effect of unsteady free-stream disturbances on laminar to turbulent transition in supersonic boundary layer flows. For low free-stream disturbances levels (say less than 1%) the transition usually results from a series of events beginning with the so-called receptivity process that refers to the generation of spatially growing instability waves by acoustic and/or vortical disturbances in the free-stream. The most fundamental receptivity mechanism arguably results from the nonparallel leading edge flow and the focus here is, therefore, on that case.

For incompressible flows, Goldstein [1] showed that there is an overlap domain where appropriate asymptotic solutions to the forced boundary layer equations match onto the so-called Tollmien-Schlichting (TS) waves that satisfy the Orr-Sommerfeld equation further downstream. Ricco and Wu [2] extended the analysis of Goldstein [1] to subsonic and supersonic boundary layers and showed that the coupling is more intense in supersonic flows and that the instability can either be of the viscous TS type or of the purely inviscid Rayleigh type when the mean boundary layer flow has a generalized inflection point. The coupling mechanism can be of the viscous type considered in [3] or of the inviscid type considered by Fedorov and Khokhlov [4]. The latter mechanism tends to be dominant when the flow is hypersonic and the obliqueness angle \(\theta \) of the disturbance differs from the critical angle \(\theta _c=\cos ^{-1}(M_\infty ^{-1})\) by an \(\mathcal {O}(1)\) amount [4] (\(M_\infty \) is the free-stream Mach number).

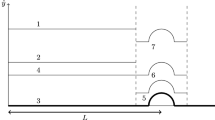
Reference [3] shows that the instability occurs too far downstream to be of practical interest at the moderately supersonic Mach numbers being considered here when \(\Delta \)\(\theta =0(1)\) but can occur much further upstream when \(\Delta \theta \) is sufficiently small. Figure 1 shows that the theoretical results of Fedorov and Khokhlov [4] are in good agreement with experimental data when \(\Delta \)\(\theta =\theta _c-\theta =\mathcal {O}(1)\) but the agreement breaks down when \(\theta \rightarrow \theta _c\). Reference [3] extended that analysis to small values of \(\Delta \theta \) and showed that the instability can occur much further upstream when \(\Delta \theta \) is sufficiently small. But there is a smallest value of \(\Delta \)\(\theta \) for which the instability wave coupling can occur.

Smith [5] showed that viscous instabilities exhibiting the same triple-deck structure as the subsonic TS waves can also occur at supersonic speeds when the obliqueness angle \(\theta \) is larger than the critical angle \(\theta _c\). But their phase speeds are very small and they must therefore be produced by a viscous wall layer mechanism identified in [1]. It therefore makes sense to treat both the viscous and the small-\(\Delta \) \(\theta \) inviscid mechanisms at the moderately supersonic Mach number considered here. Further details can be found in [3, 6].

Fig. 1
figure 1

Comparison of the Fedorov/Khokhlov solution with experimental data [7]

Full size image

2 Free-Stream Disturbances

Since the boundary layer is believed to be convectively unstable, the receptivity phenomena are best illustrated by considering a small amplitude harmonic distortion with angular frequency \(\omega ^*\) superimposed on a moderately supersonic Mach number flow of an ideal gas past an infinitely thin flat plate with uniform free-stream velocity \(U_\infty ^*\), temperature \(T_\infty ^*\), dynamic viscosity \(\mu _\infty ^*\) and density \(\rho _\infty ^*\). The velocities, pressure fluctuations, temperature and dynamic viscosity are normalized by \(U_\infty ^*\), \(\rho _\infty ^* U_\infty ^*\), \(T_\infty ^*\), and \(\mu _\infty ^*\), respectively. The time t is scaled by \(\omega ^*\) and the Cartesian coordinates x, y, and z are scaled by \(L=U_\infty ^*/\omega \) with x being in the meanflow direction and y being normal to the plate.

We require that the Reynolds number \(Re=\rho ^* U_\infty ^* L^*/\mu _\infty ^*\) be large or, equivalently, that the frequency parameter \(\mathcal {F}=Re^{-1}\) be small, and we use asymptotic theory to explain how the imposed harmonic distortion generates oblique instabilities at large downstream distances in the viscous boundary layer that forms on the surface of the flat plate. The expansion parameter is taken to be \(\epsilon =\mathcal {F}^{-1/6}\). The free-steam disturbances will be inviscid at the lowest order of approximation and can be decomposed into an acoustic component that carries no vorticity, and vortical and entropic components that produce no pressure fluctuations. But only the first two will be considered here.

The vortical velocity \(\mathbf{u} _v\) is given by

$$\begin{aligned} \mathbf{u} _v = \{u_v, v_v, w_v\} = \hat{\delta }\{u_\infty , v_\infty , w_\infty \} \exp \left[ i(x-t+\gamma y+\beta z) \right] , \end{aligned}$$
(1)

where \(\hat{\delta }\ll 1\) and \(u_\infty , v_\infty , w_\infty \) satisfy the continuity condition

$$\begin{aligned} u_\infty + \gamma v_\infty + \beta w_\infty =0 \end{aligned}$$
(2)

but are otherwise arbitrary constants while the acoustic component is governed by the linear wave equation which has a fundamental plane wave solution

$$\begin{aligned} \{\mathbf {u}_a,p_a\} = \{u_a, v_a, w_a, p_a\} = \frac{\hat{\delta } p_\infty }{1-\alpha } \{\alpha , \gamma , \beta , 1-\alpha \} \exp [ i(\alpha x+\gamma y+\beta z-t)], \end{aligned}$$
(3)

for the velocity and pressure perturbations. More details are found in §2 of [3].

3 Boundary Layer Disturbances Generated by Free-Stream Vorticity

We begin by considering the fluctuations imposed on the boundary layer by the free-stream vortical disturbance. These disturbances will generate oblique TS instability waves which are known to exhibit a triple-deck structure in the vicinity of their lower branch which lies at an \(\mathcal {O}\left( \epsilon ^{-2}\right) \) distance downstream of the leading edge in the high Reynolds number flow being considered here. They will have \(\mathcal {O}\left( \epsilon ^{-1}\right) \) spanwise wavenumbers and we therefore require that

$$\begin{aligned} \overline{\beta } \equiv \epsilon \beta = \mathcal {O}(1) \end{aligned}$$
(4)

since the spanwise wavenumber is assumed to remain constant as the disturbances propagate downstream. The continuity condition (2) and the obliqueness restriction \(v_\infty /w_\infty \ll 1\) will be satisfied if we put

$$\begin{aligned} \overline{w}_\infty \equiv \frac{w_\infty }{\epsilon } = \mathcal {O}(1), \overline{v}_\infty \equiv \frac{v_\infty }{\epsilon } = \mathcal {O}(1), \overline{\gamma } \equiv \epsilon \gamma = \mathcal {O}(1). \end{aligned}$$
(5)

The vortical velocity (1) will then interact with the plate to produce an inviscid velocity field that generates a slip velocity at the surface of the plate which must be brought to zero in a thin viscous boundary layer whose temperature, density and streamwise velocity, say \(T(\eta ),\rho (\eta ), U(\eta )\) respectively, are assumed to be functions of the Dorodnitsyn-Howarth variable

$$\begin{aligned} \eta \equiv \frac{1}{\epsilon ^3 \sqrt{2 x}} \int _0^y \rho \left( x,\tilde{y}\right) \mathrm {d}y \end{aligned}$$
(6)

and are determined from the similarity equations given in Stewartson [8].

We begin by considering the flow in the vicinity of the leading edge where the streamwise length scale corresponds to \(x=\mathcal {O}(1)\). Since the inviscid velocity field can only depend on the streamwise coordinate through this relatively long streamwise length scale the solution for the velocity and temperature perturbation \(\{u,v,w,\vartheta \}\) in this region of the boundary layer is given by [2]

$$\begin{aligned} \begin{aligned} \{u,v,w,\vartheta \} =&\left\{ F'(\eta ),\frac{\epsilon ^3\,T}{\sqrt{2 x}}\left( \eta _c F' - F \right) ,0,T \right\} + \\&\tilde{\delta }\left\{ \overline{u}_0(x,\eta ), \epsilon ^3 \sqrt{2 x} \overline{v}_0(x,\eta ), \epsilon \overline{w}_0(x,\eta ), \overline{\vartheta }_0(x,\eta ) \right\} e^{i\left( \overline{\beta } z/\epsilon - t\right) }, \end{aligned} \end{aligned}$$
(7)

where \(\eta _c \equiv T(\eta )^{-1} \int _0^\eta T(\tilde{\eta }) \mathrm {d} \tilde{\eta }\).

The vector \(\left\{ \overline{u}_0(x,\eta ), \epsilon ^3 \sqrt{2 x} \overline{v}_0(x,\eta ), \epsilon \overline{w}_0(x,\eta ), \overline{\vartheta }_0(x,\eta )\right\} \) is determined by the linearized boundary layer equations and \(\left\{ \overline{u}_0, \overline{v}_0, \overline{w}_0, \overline{\vartheta }_0\right\} \) can be divided into the following two components [9]

$$\begin{aligned} \left\{ \overline{u}_0, \overline{v}_0, \overline{w}_0, \overline{\vartheta }_0\right\} {=} \overline{u}_\infty \left\{ \overline{u}, \overline{v}, 0, \overline{\vartheta }\right\} + i \overline{\beta } \left( \overline{w}_\infty + i \overline{v}_\infty \right) \left\{ \overline{u}^{(0)}, \overline{v}^{(0)}, -i \overline{w}^{(0)}/\overline{\beta }, \overline{\vartheta }^{(0)}\right\} , \end{aligned}$$
(8)

where \(\left\{ \overline{u}^{(0)}, \overline{v}^{(0)}, \overline{w}^{(0)}, \overline{\vartheta }^{(0)}\right\} \) satisfy the three-dimensional compressible linearized boundary layer equations subject to the boundary conditions [2]

$$\begin{aligned} \overline{u}^{(0)} \rightarrow 0, \quad \overline{w}^{(0)} \rightarrow e^{i x}, \quad \overline{\vartheta }^{(0)} \rightarrow 0 \quad \text{ as } \quad \eta \rightarrow \infty , \end{aligned}$$
(9)

while the two-dimensional solution \(\{\overline{u},\overline{v},0,\overline{\vartheta }\}\) satisfies the two-dimensional linearized boundary layer equations. The downstream asymptotic solutions to the boundary-layer equations are discussed in detail in [3, 6]. A key point is that it is only necessary to consider the lowest-order asymptotic mode because that is the only one that matches onto a spatially growing oblique TS wave further downstream. The receptivity problem can then be solved by combining the numerical boundary layer solutions with appropriate matched asymptotic expansions to relate the instability wave amplitude to that of the free-stream disturbance.

4 Boundary Layer Disturbances Generated by the Fedorov/Khokhlov Mechanism at Near Critical Obliqueness Angles

Fedorov and Khokhlov [4], whose focus was on hypersonic flows, analyzed the generation of Mack mode instabilities in flat plate boundary layers by oblique acoustic waves of the form (3) where the incidence angle \(\gamma \) is equal to zero. They showed that diffraction of the slow acoustic wave by the nonparallel mean boundary layer flow can produce a first Mack mode instability in the downstream region where \(x=\mathcal {O}(\epsilon ^{-6})\) when its obliqueness angle \(\theta \) is less than the critical angle \(\cos ^{-1}(M_\infty ^{-1})\) and the deviation \(\Delta \theta =\theta _c-\theta \) is \(\mathcal {O}(1)\).

But as noted in the introduction the instability emerges too far downstream to be of practical interest when scaled up to actual flight conditions at the low supersonic Mach numbers being considered here. It will however emerge much further upstream when \(\Delta \theta \ll 1\). Reference [3] extended the result of Fedorov and Khokhlov [4] to the small-\(\Delta \theta \) regime and showed that

$$\begin{aligned} \beta = \beta _1 = \frac{\tilde{\beta }}{\Delta \theta }, \quad \alpha = \frac{\tilde{\alpha }}{\Delta \theta } + {\tilde{\alpha }}_1+..., \end{aligned}$$
(10)

where \(\tilde{\alpha }\), \(\tilde{\beta }\), \(\tilde{\alpha }_1=\mathcal {O}(1)\) and \(\Delta \theta \ll 1\), which means that \(\alpha \) and \(\beta \) become large when \(\Delta \theta \rightarrow 0\). Reference [3] also shows that the relevant solution has a triple-deck structure: an outer diffraction region and a viscous wall layer in which the unsteady, convective and viscous terms all balance and a main boundary layer region where the solution is of the form

$$\begin{aligned} \begin{aligned} \{u,v,w,\vartheta ,p\}{=}&\{1,0,0,1,1\} {+} \hat{\delta }\left\{ u_2(x_2,y_2),\epsilon ^{3/2}v_2(x_2,y_2),w_2(x_2,y_2),\vartheta _2(x_2,y_2),\right. \\&\left. p_2(x_2)\right\} \exp \left\{ i\left[ \left( \frac{\tilde{\alpha }}{\Delta \theta } + {\tilde{\alpha }}_1 \right) x + \frac{{\tilde{\beta }} z}{\Delta \theta } - t \right] \right\} , \end{aligned} \end{aligned}$$
(11)

where

$$\begin{aligned} x_2 \equiv x \epsilon ^3 = \mathcal {O}(1), \quad y_2 \equiv y \epsilon ^{3/2} = \mathcal {O}(1) \end{aligned}$$
(12)

and the surface pressure \(p_2(x_2)\) behaves like

$$\begin{aligned} p_2\left( {\tilde{\tilde{x}}}_2 \right) \sim \exp \left[ \gamma _0^2 \pi \left( {\tilde{\tilde{x}}}_2\right) ^2 \right] \quad \text{ as } \quad {\tilde{\tilde{x}}}_2 \rightarrow \infty , \end{aligned}$$
(13)

where

$$\begin{aligned} \gamma _0 \equiv \frac{{\tilde{\tilde{x}}}_2 \left( {\tilde{\alpha }}^2 + {\tilde{\beta }}^2\right) {\tilde{\alpha }}^{1/2} T_w^2}{\lambda \sqrt{2 \pi i\left( M_\infty ^2 -1 \right) }}. \end{aligned}$$
(14)

The acoustically and vortically generated boundary layer disturbance considered in this section eventually evolve into propagating eigensolutions in regions that lie further downstream. The resulting flow will have a triple-deck structure of the type considered in [2, 5, 10] in the former (i.e. vortically generated) case. But the acoustically generated disturbance will only develop an eigensolution structure in a region that lies much further downstream. This region will be closest to the leading edge when \(\Delta \theta = \mathcal {O}(\epsilon ^{2/3})\). We begin by considering the triple-deck region.

5 The Viscous Triple-Deck Region

As shown by [2, 5, 10] the linearized Navier-Stokes equations possess an eigensolution of the form

$$\begin{aligned} \left\{ u,v,w,p\right\} = \hat{\delta }{\boldsymbol{\Phi }} (y,\epsilon ) \exp \left\{ i\left[ \frac{1}{\epsilon ^3} \int _0^{x_1} \kappa \left( x_1,\epsilon \right) \mathrm {d}x_1 +\overline{\beta }\overline{z} - t \right] \right\} \end{aligned}$$
(15)

in the triple-deck region where

$$\begin{aligned} x_1 \equiv \epsilon ^2 x = \mathcal {O}(1) \end{aligned}$$
(16)

and \(\overline{z} \equiv z/\epsilon = z^* \omega ^*/(\epsilon U_\infty ^*)\) is a scaled transverse coordinate. As noted in [1], \(\kappa \) has the expansion \(\kappa \left( x_1,\epsilon \right) = \kappa _0\left( x_1\right) + \epsilon \kappa _1\left( x_1\right) + \epsilon ^2 \kappa _2\left( x_1\right) +..., \) where the lowest order term in this expansion satisfies the following dispersion relation

$$\begin{aligned} \kappa _0^2 + \overline{\beta }^2 = \frac{1}{\left( i \kappa _0\right) ^{1/3}} \left( \frac{\lambda }{\sqrt{2 x_1}}\right) ^{5/3} \left( \frac{\mu _w}{T_w^7}\right) ^{1/3} \frac{\left[ \overline{\beta }^2 - \left( M_\infty ^2-1\right) \kappa _0^2\right] ^{1/2}\text{ Ai }'\left( \xi _0\right) }{\int _{\xi _0}^\infty \text{ Ai }\left( q\right) \mathrm {d}q} \end{aligned}$$
(17)

and

$$\begin{aligned} \xi _0 = - i^{1/3} \left( \frac{\sqrt{2 x_1}}{\kappa _0 \lambda }\right) ^{2/3} \left( \frac{T_w}{\mu _w}\right) ^{1/3}, \end{aligned}$$
(18)

which is easily obtained by rewriting Eq. (5.2) of [2] or Eq. (3.17) of [10] in the present notation. The solution must satisfy the inequality \(\mathfrak {R}\left\{ \left[ \overline{\beta }^2 - \left( M_\infty ^2-1\right) \kappa _0^2\right] ^{1/2}\right\} \ge 0\) in order to exclude solutions exhibiting unphysical wall-normal exponential growth.

This requirement will be satisfied for all \(M_\infty < 1\) but will only be satisfied at supersonic Mach numbers when the obliqueness angle \(\theta \) is greater than the critical angle \(\theta _c=\cos ^{-1}(M_\infty ^{-1})\). Equations (17) and (18) can be satisfied at small values of \(x_1\) if \(\kappa _0 \sim \sqrt{x_1}\) and \(\xi _0 \rightarrow \zeta _n\) for \(n=0,1,2,...\) as \(x_1 \rightarrow 0\) where \(\zeta _n\) is the nth root of

$$\begin{aligned} \text{ Ai }'(\zeta _n)=0 \quad \text{ for } \quad n=0,1,2,3..., \end{aligned}$$
(19)

as discussed in [3]. Inserting these expressions of \(\kappa _0\) and \(\xi _0\) into (17) shows that \(\kappa _0 \rightarrow \left( 2 T_w x_1/i \mu _w \right) ^{1/2} / \lambda \zeta _n^{3/2}\) as \(x_1 \rightarrow 0\), which, as shown in [2, 3], matches onto the downstream asymptotic limit of the boundary layer solution.

5.1 Numerical Results

The dispersion relation (17), which determines the complex wavenumber of the triple-deck instabilities, is expected to have at least one root corresponding to each of the infinitely many roots of the Lam-Rott dispersion relation (19), as discussed in [3]. But only the lowest order \(n=0\) root can produce the spatially growing modes of (17). The wall temperature \(T_w\) and viscosity \(\mu _w\) can be scaled out of this equation by introducing the rescaled variables \(\kappa _0^\dagger =\kappa _0 T_w^{1/2} \mu _w^{1/6}, x_1^\dagger =x_1 T_w^2/\mu _w^{2/3}, {\overline{\beta }}^\dagger =\overline{\beta } T_w^{1/2}\mu _w^{1/6}\).

Fig. 2
figure 2

\(-\mathfrak {I}\left( \kappa _0^\dagger \right) \) as a function of the scaled streamwise coordinate \(x_1^\dagger \) calculated from the dispersion relation (17) together with the asymptotic initial condition found at the end of §5 for \(M_\infty =2,3,4\) (double dot dashed, dot dashed, and solid lines, respectively) and three values of the scaled transverse wavenumber \(\overline{\beta }^\dagger \ge 2\)

Full size image

Figure 2 are plots of the negative imaginary parts of the scaled wavenumber \(\kappa _0^\dagger \) as a function of the scaled streamwise coordinate \(\overline{x}_1^\dagger \) calculated from (17) for \(M_\infty =2,3,4\) and three values of the frequency scaled transverse wavenumber \(\overline{\beta }^\dagger \ge 2\). The inset is included to more clearly show the changes at small \(\overline{x}_1^\dagger \). The red dashed curves in the inset denote the imaginary parts of the small-\(\overline{x}_1^\dagger \) asymptotic formula found at the end of §5. The composite Lam-Rott triple-deck eigensolution can undergo a significant amount of damping before it turns into a spatially growing instability wave at the lower branch with the amount of damping determined by the upstream behavior of the triple-deck solution (15) since this solution actually contains the Lam-Rott solution as an upstream limit. The inset in Fig. 2 is particularly relevant because it shows that the length \(\Delta x_1^\dagger =0.01\) of this upstream region is very short and therefore that the damping is relatively small in the supersonic case being considered here. The leading edge receptivity mechanism is therefore expected to be much more efficient than in the incompressible case considered in [1].

6 The Inviscid Triple-Deck Region

The acoustically driven solution will only match onto an eigensolution in a region that lies downstream of the viscous triple-deck region considered above and will have an inviscid structure. The relevant dispersion relation is given by

$$\begin{aligned} {\overline{\kappa }_0}^2 + \overline{\overline{\beta }}^2 = \frac{\lambda \left[ \overline{\overline{\beta }}^2 - \left( M_\infty ^2-1\right) \overline{\kappa }_0^2\right] ^{1/2}}{\overline{\kappa }_0 \sqrt{2 {\hat{x}}_1} T_w^2} \end{aligned}$$
(20)

where the square root \(\left[ \overline{\overline{\beta }}^2 - (M_\infty ^2 - 1)\overline{\kappa }_0^2\right] ^{1/2}\) is required to remain finite as \(\epsilon \rightarrow 0\). Our papers [3, 6] show that the lowest order wave number \(\kappa _0\) is purely real, which means that exponential growth (if it occurs) can only occur at higher order. The key result is that the acoustically generated instabilities will be less significant than the vortically-generated instabilities that are generated upstream.

7 Next Stage of Evolution

References [3, 6] also show that the viscous and the inviscid triple-deck solutions both evolve into reduced Rayleigh modes further downstream. The wall-normal velocity component satisfies the reduced Rayleigh equation

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\eta } \left( \frac{1}{T^2} \frac{\mathrm {d}\overline{v}}{\mathrm {d}\eta } \right) + \left[ \frac{\overline{\alpha }}{1-\overline{\alpha } U} \left( \frac{U'}{T^2} \right) ' - \left( \overline{\overline{\beta }} \sqrt{2\overline{x}_1}\right) ^2 \right] \overline{v} = \mathcal {O}\left( \epsilon ^{2(1-r)}\right) , \end{aligned}$$
(21)

and the following boundary conditions

$$\begin{aligned} \overline{v} \sim e^{-\overline{\overline{\beta }}\overline{y}} \quad \text{ for } \quad \overline{y} \rightarrow \infty \quad \text{ and } \quad \overline{v}=0 \quad \text{ at } \quad \overline{y} =0. \end{aligned}$$
(22)

Figure 3 shows the downstream evolution of the growth rate at different Mach numbers. The red dashed lines demonstrate how the Rayleigh solutions match the triple-deck solutions as the leading edge is approached.

Fig. 3
figure 3

\(|\mathfrak {I}\left( \bar{\alpha }\right) |\) versus \(\widehat{\beta }\) calculated from the reduced Rayleigh solution. The dashed lines in the inset are \(|\mathfrak {I}\left( \bar{\alpha }\right) |=C \widehat{\beta }\), where the following values for the scale factor C were obtained by optimizing the fit to the computations: C=36 for \(M_\infty \)=2, C=129.4 for \(M_\infty \)=3, and C=340.1 for \(M_\infty \)=4

Full size image

8 Conclusions

This paper uses high Reynolds number asymptotics to study the nonlocal behavior of boundary layer instabilities generated by small amplitude free-stream disturbances at moderately supersonic Mach numbers. The appropriate small expansion parameter turns out to be \(\epsilon =\mathcal {F}^{-1/6}\), where \(\mathcal {F}\) denotes the frequency parameter. The oblique first Mack mode instabilities generated by free-stream acoustic disturbances are compared with those generated by elongated vortical disturbances. The focus is on explaining the relevant physics and not on obtaining accurate numerical predictions. The free-stream vortical disturbances generate unsteady flows in the leading edge region that produce short spanwise wavelength instabilities in a viscous triple-deck region which lies at an \(\mathcal {O}(\epsilon ^{-2})\) distance downstream from the leading edge. The mechanism was first considered for two-dimensional incompressible flows in reference [1], but the instability onset occurs much further upstream in the supersonic case and is, therefore, much more likely to be important at the higher Mach numbers considered in this paper. The lowest order triple-deck solution does not possess an upper branch and evolves into an inviscid first Mack mode instability with short spanwise wavelength at an \(\mathcal {O}(\epsilon ^{-4})\) distance downstream. Fedorov and Khokhlov [4] used asymptotic methods to study the generation of inviscid instabilities in supersonic boundary layers by fast and slow acoustic disturbances in the free stream whose obliqueness angle \(\theta \) deviated from its critical value by an \(\mathcal {O}(1)\) amount and showed that slow acoustic disturbances generate unsteady boundary layer disturbances that produce \(\mathcal {O}(1)\) spanwise wavelength inviscid first Mack mode instabilities at a much larger \(\mathcal {O}(\epsilon ^{-6})\) distance downstream. But the calculations in our paper [3] show that the physical streamwise distance \(x^* (U_\infty ^*)^3/(\omega ^*)^2 \nu _\infty ^*\) corresponding to this scaled downstream location is at least equal to about 7 m for the typical supersonic flight conditions at \(M_\infty =3\) (\(U_\infty ^*=800\), \(\nu _\infty ^*=0.000264\)m\(^2\)/s) end an altitude of 20 km with an upper bound of 100 kHz for the characteristic frequency. This means that this instability occurs too far downstream to be of any practical interest at the moderately low supersonic Mach numbers considered here. But, the inviscid instability, which first appears at an \(\mathcal {O}(\epsilon ^{-(4+2/3)})\) distance downstream when \(\Delta \theta \) is reduced to \(\mathcal {O}(\epsilon ^{-(4+2/3})\) can be significant when scaled to flight conditions. We therefore compared the vortically-generated instabilities with the instabilities generated by oblique acoustic disturbances with obliqueness angles in this range.