Keywords

1 Introduction

The description of metal deformation processes based on the approaches of crystal plasticity requires a large number of numerical experiments. Some experiments are necessary to determine a large number of parameters of the developed models. When we find them, it is possible to solve applied problems, i.e. determine the mechanical response of materials and structures. It should also be noted that multilevel models have recently been developed to describe inelastic deformation of metals. Due to the multilevel description, a more detailed process description is possible, as the built hierarchical system with large scale elements contains those of smaller scales, and enables a physically-based description of the material structure, provided that the relations between the levels are correctly described. The disadvantages of the multilevel models include massive computing resources for the implementation of numerical experiments. This fact reveals the need to optimize the program code, to implement the parallel execution of the model algorithm in the areas where it does not contradict with the numerical schemes and the structure of the mathematical model. At the same time, the studies including the numerical implementation of the multilevel models may unlock a deeper understanding of the studied area by being not only a substitute for natural experiments but also offering predictive opportunities.

The phenomenon of serrated yielding (the Portevin–Le Chatelier (PLC) effect) as a manifestation of the instability of inelastic deformation has been found for a number of metals and alloys in certain ranges of strain rates and temperatures under different loading programs. On deformation curves, serrated yielding manifests itself in the form of repetitive inhomogeneities, i.e. steps or teeth of various types depending on a type of loading. The localization laws of plastic deformation in a sample under loading, as noted in a number of works [1,2,3,4,5], and often correlate with the discontinuous nature of the deformation curve, with each jump in the uniaxial loading diagram (stress σ - deformation ε) associated with the emergence or propagation of a deformation band visible on the lateral surface of the sample.

The aim of studying the PLC effect when it comes to deformation of metals and alloys is to predict how temperatures and deformations influence behaviors of structures. Most structural metals and alloys in certain temperature-strain rate ranges of deformation demonstrate the manifestation of the PLC effect. Aluminum alloys have been recently used for critical structures and their parts operating in extreme conditions, as they own high strength characteristics but are subjected to the PLC effect. In this regard, it is a priority to solve the problem of establishing the ranges within which serrated yielding is realized, in order to exclude them from the list of manufacturing modes of processing metal products (especially at finishing operations).

The results of numerous field experiments on serrated yielding allow us to conclude that a discontinuous, irregular response of the material under monotonic impacts is caused by the presence of inhomogeneities in material properties and features of motion of large dislocation arrays (i.e., their coordinated motions) at various scale levels. These inhomogeneities can develop in a cascade manner from nanosizes to values comparable with the sizes of macrosamples.

The processes of inelastic deformation and properties of polycrystalline materials at the macrolevel are largely determined by the state of the evolving meso- and microstructure of a material. Dynamic strain aging (SDS) associated with the effect of the agglomeration of impurities near dislocations is assumed to be the major mechanism resulting in the PLC effect. The stress fields from point defects interact with the stress fields of dislocations, hindering the movement of dislocations until the current barrier (critical stress) is overcome, at which the dislocations are detached from the clouds of the impurity atoms, which is the main factor of the occurring serrated area on the deformation curve.

To describe the dynamic strain aging and the effects associated with it, most researchers (A. Benallal, A. Bertram, T. Böhlke, X. Chen, Y. Estrin, S. Graff, P. Hähner, O. Hopperstad, S.Y. Hu, L.P. Kubin, R. Larsson, C.P. Ling, P.G. McCormick, E. Rizzi, S. Zhang, S.-Y. Yang, D. Yu, etc.) [1,2,3,4,5] use macrophenomenological models of inelastic deformation [6].

L.P. Kubin and Y. Estrin [7] proposed one of the well-known phenomenological viscoplastic models, which takes into account strain aging and focuses on describing the PLC effect under uniaxial loading. The strain rate sensitivity of the material is determined by the sum of two parts, i.e. the one independent and dependent on deformation aging. The latter is established using the dislocation submodel, which includes evolutionary equations for scalar densities of mobile and forest (immobile) dislocations. It is noted that the model makes it possible to determine the critical values of accumulated strains (of the beginning and end of serrated yielding) that are actually observed in the experiments.

The macrophenomenological model proposed in [8] is based on a qualitative analysis of the physical processes responsible for the start of serrated yielding. The model is focused on describing uniaxial loading. An evolutionary equation for the flow stress is proposed which includes the terms responsible for strain and rate hardening, as well as for the change in flow stress due to strain aging. The latter takes into account the competition between hardening due to an interaction of the impurity atoms with dislocations and softening due to a separation of dislocations from the atmospheres.

The paper in [9] describes the macrophenomenological elastoviscoplastic model and the results obtained with its help in studying the deformation of specimens cut at different angles (related to the direction of rolling) from rolled sheets of aluminum alloy AA5083-H116. The constitutive relations are based on the McCormick model [10], in which the flow stress, along with the terms characterizing the strain and rate hardening, also includes a term describing the change in the flow stress with time due to strain aging.

Macrophenomenological models based on the macrosample experiments set dependences between the parameters of the macrolevel, without in-depth issues of a material microstructure evolution. In particular, the disadvantage of these models is that they are not suitable for predicting properties of designed materials. Also they do not make it possible to determine the main parameters of unstable deformation (width, propagation rate and value of deformation in localization bands). It is necessary to study the material behavior at structural-scale levels lower than the macrolevel to get a correct description of plastic deformation and its inhomogeneity, to consider the most significant physical mechanisms that determine it and accompany it.

Models based on crystal plasticity (J. Alcala, H. Askari, R.A. Austin, D.L. McDowell, J. Balik, P. Lukac, M.S. Bharathi, etc.) do not include disadvantages of the macrophenomenological models, which are based on an explicit consideration of deformation mechanisms at meso- and microscales.

The work in [11] suggests using a 2-level elastoplastic model to study the PLC effect. In order to describe the PLC effect, an evolutionary equation for critical stresses was formulated, which includes additive terms responsible for a change in the resistance to deformation due to athermal (strong) barriers, strain hardening (which also takes into account softening by dynamic recovery, rate hardening (excluding dynamic aging), and a separate term reflecting the effects of strain aging. The results using the specified elastoviscoplastic physical model to analyze the deformation of flat specimens from the Al-2.5% Mg alloy are presented.

The paper in [12] presents a constitutive plastic model describing the behavior of polycrystalline heat-resistant nickel-based alloys. Three scale levels are considered, the macrolevel corresponding to the representative volume of the polycrystal, the mesoscale (or the level of an individual grain), and the level of subgrains. The model studies monotonic loading. At the mesoscale, the structure of the nickel-based alloy is modeled using an additional plastic submodel using the finite element method.

A model proposed in [13] to determine the resistance to deformation is presented in the form of a simultaneous integro-differential equations describing the material hardening as a result of an increment in dislocation density and blocking of the motion of mobile dislocations by grain and subgrain boundaries taking into account softening due to recovery and recrystallization. It is proposed to describe the physical processes of hardening and softening, which determine the physical and mechanical properties of alloys by changing the shape of the deformation curve. To determine the resistance to deformation, additional internal parameters were introduced into the model, which are responsible for blocking the motion of mobile dislocations by the impurity atoms and inclusions. The model allows one to describe the resistance to deformation of alloys under high-temperature deformation taking into account the combined effect of hardening, recovery, recrystallization and barrier effects (blocking of free dislocations by the impurity atoms) as well as the Portevin–Le Chatelier effect. The parameters of the model were determined by identifying them according to the experimental data obtained under uniaxial tension of the specimens from the AMg6 alloy in the range of deformation rates from 5 to 25 s−1 and temperatures of 400 and 500 °C.

Some authors [14, 15] offer a review of theoretical works based on crystal plasticity and a description of deformation properties of alloys in temperature-rate ranges, in which diffusion processes have a significant effect on the material behavior. Particular attention is paid to the Portevin–Le Chatelier (PLC) effect. The disadvantages of models based on crystal plasticity include the problem of closing the set of relations, a large number of parameters and difficulties in identifying them, and the complexity of their numerical implementation.

1.1 Interaction of Impurity Atoms and Dislocations

It is known that the motion of dislocations is not continuous; it has a jump-like nature, while free motion alternates with stops at localized obstacles during a certain waiting time [16]. As the processes of inelastic deformation at the macrolevel are largely determined by the state of the evolving meso- and microstructure of the material, which may finally lead to a spontaneous deformation localization, both Russian and foreign researchers attempted to construct mathematical models by taking into account the dislocation dynamics (A. Alankar, A. Arsenlis, K.M. Davoudi, L. Kiely, D. Li, H. Zbib, C. Reuber, M. Zecevic, M. Knezevic, M. Lebedkin et al.).

A big part of the monograph in [17] refers to analyzing the interaction of impurities with dislocations. The impurity atoms move to the immobile dislocations by diffusion and are located along the dislocation lines in positions with the maximum binding forces. For mobile dislocations, two options are possible. Firstly, it refers to stresses exceeding a certain limit, in this case, dislocations can detach from the atmospheres formed around them. Secondly, it refers to low stresses, thus low velocities of motion, when dislocations can carry the atmospheres of the impurity atoms with them.

In [18], along with the inflow of atoms to a dislocation due to the interaction of stress fields, diffusion is taken into account due to the concentration gradient of the impurity atoms. To consider the processes over long periods of time, the author introduces the concept of the so-called average capture radius. It is the radius of a cylindrical region, which (in case of a specific problem) has the same probability of capturing the diffusing atoms just like the dislocation with its inherent stress field. Analytical solutions are obtained to determine the temporal and spatial evolution of the impurity atoms’ concentration in the neighborhood of the single edge and screw dislocations. An analytical solution is obtained for the fraction of the deposited impurity atoms on an array of the parallel dislocations, which is described by a single dislocation and a cylindrical region with an average capture radius.

A detailed consideration of the interaction of point defects with dislocations is given in [19] with a brief overview of earlier works in this area. A variety of interactions of the point defects with the dislocations is noted, i.e. those determined by the stress fields of the dislocations during the introduction of defects with sizes different from lattice atoms, chemical and electrical effects, and vibrations of the defects. It is noted that the interaction of the point defects with the dislocations due to their own stress fields is the most important one.

A model based on considering the interaction of the dislocations with the impurity atoms was proposed in [20,21,22]. It is assumed that the flow stress is equal to the sum of the resistance to deformation from the interaction of the dislocations with the forest dislocations and the friction stress from the interaction of the dislocations with the impurity atoms, which depends on the concentration of the latter. It is assumed that the dislocations in motion can capture the impurity atoms and move together with them. The captured impurity atoms are capable of intensively diffusing along the lines of the dislocation nuclei up to a certain saturation limit. The dependences of the average velocities of motion of the dislocations and stress of resistance to flow on the concentration of the impurities and temperature are obtained; on the basis of which the existence of a temperature interval is shown where the negative sensitivity of the resistance to deformation on the strain rate takes place.

2 Concept and Mathematical Setting

In this work we used a model based on crystal plasticity (CP). The model was built using an approach based on the introduction of internal variables (internal parameters of the system state). The material’s reaction at each instant of time is completely determined by the values of the tensor thermomechanical characteristics of the material and a finite set of internal variables, parameters of physical and mechanical effects and their time derivatives of the required order at the instant of time under study.

Some of the internal variables included in the constitutive relations of the level under consideration are called explicit internal variables. They include parameters characterizing yield stress, etc. The second group of the internal variables is an implicit one, that is, characterizing the evolution of the material structure and processes at lower scale levels of the model. By analyzing the existing material models and physical mechanisms of the inelastic deformation of a wide range of structural materials, it becomes possible to propose a constitutive model structure which includes constitutive relations, evolutionary and closing equations.

The positive aspects of using this approach include a clearer physical interpretation of the internal variables, the possibility of comparing it with the real material structure, great possibilities of processing the obtained data, as well as the fact that it is based on the fundamental physical laws [9].

2.1 General Structure of the Model

This work considers the macrolevel, meso-1, and meso-2 as structural-scale levels to describe the behavior of the polycrystalline specimen. The key mechanism of the inelastic deformation in this work is assumed to be the motion of the edge dislocations. At the mesoscale-2, its description is carried out using the introduction of the dislocation densities on slip systems (SS) and their velocities. At mesoscale-1, the inelastic deformation is considered in terms of shear rates along the crystallographic SS. To connect the submodels of different levels, the explicit internal variables are introduced into the structure of the constitutive relations at each of the scale levels, which are determined by the closing equations describing the deformation processes at deeper scale levels with respect to the considered one. At the macrolevel, the behavior of the material representative volume is described in terms of the elastic and plastic components of the strain tensor and stress tensor. The element of the macrolevel (macropoint, representative macrovolume) is hierarchically senior in relation to a certain set of elements of the meso-1. The hierarchical structure of the model makes it possible to simultaneously calculate the stress-strain state in all the elements of the underlying level, have a further volume averaging. This fact allows using parallel execution schemes when implementing this model. As an effect on the mesolevel-1 from the macrolevel, kinematic effects are transmitted (Voigt’s hypothesis about the equality of the velocity gradients of the displacements of the two levels is accepted). A macropoint can be used to solve the boundary value problem; the inelastic component of the strain rate tensor of the macrolevel is determined by averaging the rates of inelastic deformations of the meso-1 elements. In describing the deformation of a crystallite, the mesoscale-1 model and meso-2 submodel are used. At the meso-1, the mechanical state of the crystallite is described. The tangential stresses on the slip systems determined at the mesoscale-1 are transmitted as an action on the mesoscale-2, where the evolution of defect densities is considered, changes in the concentration fields of the impurity atoms are calculated, hardening is described, the velocities of dislocations motion are determined, as well as shear rates along the SS. From the mesoscale-2 to the mesoscale-1, shear rates are transmitted along the slip systems.

The problem of describing the behavior of alloys under loading taking into account the evolution of the microstructure can be subdivided into several interconnected (sub) problems, namely, the problem of determining the stress-strain state (SSS), the problem of thermal conductivity, the problem of diffusion of the impurity atoms, i.e., the related problem splits according to the physical processes. To simplify the model, an assumption is introduced that the process under consideration is isothermal.

The mesoscale-2 model uses the distribution of the dislocation densities for the slip systems into positive and negative (according to a predetermined rule, depending on the direction of the extraplane). The mesoscale-2 variables are dislocation densities (positive and negative), the density of the dislocation sources on the SS, and the concentration of the impurity atoms for each SS. Internal variables of the mesoscale-1 include shear rates along the slip systems and critical stresses, which are determined by the dislocation substructure with allowance for interactions with the impurity atoms at the mesoscale-2. In the mesoscale-2 model, in addition to the interaction of dislocations with each other, the interaction of the dislocations with the impurity atoms is introduced, and the process of redistributing the edge dislocations over the SS is described.

The fundamental hypothesis in this work is a detailed physically justified description of the dislocation slip, the interaction of dislocations with each other, as well as the interaction of the dislocations with the impurity atoms. The latter makes a significant contribution to the motion of the dislocations due to the formation of clouds of the impurity atoms. Depending on the dislocation velocities, the clouds of the impurity atoms change in the volume and the contribution of the impurity atoms to the critical shear stresses along the SS changes.

3 Mathematical Setting

The strain rates are transferred from the macrolevel to the meso-1 level using the Voigt hypothesis:

$$ {\mathbf{z}}\text{ = }{\mathbf{Z}}{\mathbf{.}} $$
(1)

At the mesolevel-1 we determine the plastic part of the strain rate measure \( {\mathbf{z}}^{in} \), \( {\varvec{\upsigma}} \) stress tensor components, the acting shear stresses being found \( \tau^{\left( k \right)} \) are transmitted from the mesolevel-1 to the mesolevel-2. Shear rates \( \dot{\gamma }^{\left( k \right)} \) are found at the mesolevel-2 by the velocities of the motion of the dislocations and are used to calculate the inelastic component of the measure of the strain rate at the mesolevel-1. The submodel of the mesolevel-1 includes the following system of equations:

$$ \left\{ {\begin{array}{*{20}l} {{\dot{\mathbf{\sigma }}} + {\varvec{\upsigma}} \cdot {\varvec{\upomega}} - {\varvec{\upomega}} \cdot {\varvec{\upsigma}} = {\boldsymbol{{{\uppi}}}}:({\mathbf{z}} - {\mathbf{z}}_{{}}^{in} - {\varvec{\upomega}}),} \hfill \\ {{\mathbf{z}} = {\mathbf{z}}^{e} + {\mathbf{z}}^{in} } \hfill \\ {{\varvec{\upomega}} = {\dot{\mathbf{o}}}\, \cdot \,{\mathbf{o}}^{\text{T}} } \hfill \\ {{\mathbf{z}}^{in} = \sum\limits_{k = 1}^{n} {\dot{\gamma }^{(k)} {\mathbf{b}}^{(k)} {\mathbf{n}}^{(k)} } } \hfill \\ {\tau^{(k)} = {\mathbf{b}}^{(k)} {\mathbf{n}}^{(k)} :{\varvec{\upsigma}}} \hfill \\ \end{array} } \right., $$
(2)

where \( {\mathbf{b}} \) is the unit vector in the direction of the Burgers vector of the edge dislocation, \( {\mathbf{n}} \) is the normal to the plane of the dislocation slip, k is the number of the slip system (SS), \( {\varvec{\upomega}} \) is the lattice spin. The description of the evolution of the microstructure is made at the mesoscale-2. The explicit internal variables (IV) of the mesoscale-1 include \( {\varvec{\upsigma}} \), the stress tensor at the mesolevel-1.

The evolutionary equations for the dislocation densities on the SS describe the nucleation of the dislocations due to the operation of the Frank-Read sources, the annihilation of the dislocations of different signs on one SS. The critical stresses on the SS are determined by the current density of defects on all the systems. The explicit internal variables at the mesoscale-2 include the average shear rates of \( V_{ + - }^{{{\prime }\left( k \right)}} \) dislocations depending on the tangential stresses τ, critical shear stresses τc and temperature θ, the density of the positive and negative dislocations on SS \( \rho_{ + }^{\left( k \right)} ,\,\rho_{ - }^{\left( k \right)} \).

The average velocities of dislocation motion are determined by the acting stresses and defect densities. Shear rates are determined using Orowan’s velocity form equation. The meso-2 submodel is represented by the following system of equations:

$$ \left\{ {\begin{array}{*{20}l} {V_{ \pm }^{'(k)} = \pm f_{1} (\tau^{(k)} ,\tau_{c}^{(k)} ,\theta )sign(\tau^{(k)} ),} \hfill \\ {{\dot{\gamma }}^{(k)} = (\rho_{ + }^{(k)} V_{ + }^{'(k)} - \rho_{ - }^{(k)} V_{ - }^{'(k)} )\left| {\mathbf{b}} \right|_{{}}^{(k)} ,} \hfill \\ {\uprho^{(k)} = f_{2} (\tau^{(k)} ,\tau_{c}^{(k)} ,\theta ,\uprho^{(k)} ,\uprho_{bar}^{(k)} ),} \hfill \\ {\uprho_{bar}^{(kl)} = f_{3} (\tau^{(k)} ,\tau_{c}^{(k)} ,\theta ,\uprho^{(k)} ,\uprho_{bar}^{(k)} ),} \hfill \\ {\tau_{c}^{(k)} = f_{4} (\rho ,\rho_{bar} ,).} \hfill \\ \end{array} } \right. $$
(3)

The average velocities of dislocations (\( V_{ + }^{{{\prime }\left( k \right)}} ,\,V_{ - }^{{{\prime }\left( k \right)}} \)) play an important role for the description of the dislocation reactions, the most important role is played by the average velocities of the dislocations. In this case the velocities of motion of the dislocations of opposite signs may differ in sign and magnitude.

To determine the shear rates along the SS at the mesoscale-1, the rate form of the Orowan equation is used, including the densities of the positive and negative dislocations, the average slip velocities of dislocations (determined in the laboratory coordinate system (LCS)) and the modulus of the Burgers vector of dislocations:

$$ {\dot{\gamma }}^{(k)} = (\rho_{ + }^{(k)} V_{ + }^{'(k)} - \rho_{ - }^{(k)} V_{ - }^{'(k)} )\left| {\mathbf{b}} \right|_{{}}^{(k)} . $$
(4)

The average velocities of motion of the dislocations are expressed by the following relation:

$$ \left\{ {\begin{array}{*{20}l} {V_{ + }^{'(k)} = l^{k} v\,\exp ( - \Delta G_{*}^{k} /k_{B} \theta )sign(\tau^{(k)} )} \hfill \\ {V_{ - }^{'(k)} = - l^{k} v\,\exp ( - \Delta G_{*}^{k} /k_{B} \theta )sign(\tau^{(k)} ).} \hfill \\ \end{array} } \right. $$
(5)

The sign of the first factor in determining the average shear rates depends on the sign of the dislocations for which they are determined, e.g. for positive dislocations, the default sign will be a plus, for negative dislocations, it will be a minus.

3.1 Work of Dislocation Sources

As a rule, during plastic deformation, there is an increase in the density of dislocations on the SS. The Frank-Read sources that generate closed expanding dislocation loops are distinguished as intragranular dislocation sources. It is known experimentally that a source can generate a limited number of loops. The densities of the Frank-Read sources are introduced in the work. Until the critical stresses of the source are reached, no new loops are generated:

$$ \begin{array}{*{20}l} {\rho_{0src}^{(k)} = \rho_{0src} ,} \hfill \\ {\dot{\rho }^{(k)}_{src} = L\uprho_{bar}^{kl} \rho^{l} [l^{k} v\,\exp ( - \Delta G_{*}^{k} /k_{B} \theta )],} \hfill \\ {\tau_{src} = \frac{A\mu b}{2\pi L}\left( {\ln \frac{L}{{r_{0} }} + B} \right),} \hfill \\ \end{array} $$
(6)

where \( \mu \) is the shear modulus, \( R_{s} \) is the average width of the fixed area (depends on the density of defects), \( b \) is the value of the Burgers vector, \( a \) is a dimensionless parameter. The contribution to the increase of the dislocation densities is proportional to the current density of the dislocation loops; and it is nonzero only when the acting stresses exceed the critical ones:

$$ {\dot{\uprho }}_{nuc}^{(k)} = k\rho_{src} H(\tau^{(k)} - \tau^{(k)}_{src} ). $$
(7)

3.2 Annihilation of Dislocations

Occurs as a result of a reaction on two dislocations with one SS and different extraplanes (in terms of the model, these are positive and negative dislocations).

This reaction is possible if two dislocations of the opposite signs are at a small distance from each other. The dislocation annihilation is most often observed in the experiments with reverse loading. The dislocations of the opposite signs in the same slip system attract. When the dislocations are located on the parallel slip systems, they can also creep towards each other, thus annihilating when approaching by the annihilation distance \( h_{ann} \). The number of the reacted dislocations is proportional to the swept volume and dislocation density on the slip systems. To describe annihilation in the work, it is proposed to use the following relation:

$$ {\dot{\rho }}_{ \pm }^{(k)ann} = - h_{ann}^{{}}\uprho_{ + }^{(k)}\uprho_{ - }^{(k)} \left| {V_{ + }^{'(k)} - V_{ - }^{'(k)} } \right|. $$
(8)

3.3 Impurity Atoms

In the mesoscale-2 model, in addition to the interaction of the dislocations with each other, the interaction of the dislocations with the impurity atoms is introduced. The total amount of the impurity atoms is constant and can be distributed between the dislocations on the slip systems. We consider the interaction of the dislocations with the impurity atoms precipitated during the motion of the latter and being at the current time in the capture tube, which slow down the motion of the dislocations. Depending on the velocities of the dislocation motion, the concentration of the impurity atoms changes in the volume of the capture tube, so the contribution to the critical shear stresses along the SS from the action of the impurity atom changes. The change in the concentration of the impurity atoms captured by the dislocations on the k-th slip system is determined according to the two scenarios.

The First Scenario.

If the average velocity of dislocations \( V_{{}}^{(k)} \) is lower than the impurity atoms velocity caused by self-diffusion \( V_{diff.} \) at a given temperature, and the current concentration of the impurity atoms \( c_{capt}^{(k)} \) captured by the dislocation is lower than the critical concentration \( c_{crit}^{(k)} \) (the highest concentration of the atoms that the dislocation can hold), in this case the dislocation collects the impurity atoms in its capture tube. A new concentration of the captured and free impurity atoms is calculated depending on the value of the dislocation velocity. In this case, the greater the dislocation velocity, the more impurity atoms the dislocation collects per unit time. However the concentration of the captured atoms cannot exceed the critical one. The change in the concentration of the captured atoms in this case can be expressed by the following relation:

$$ \dot{c}_{capt1.1}^{(k)} = c_{free}^{(k)} \frac{{V_{{}}^{(k)} }}{R}H\left( {V_{diff.} - \left| {V_{{}}^{(k)} } \right|} \right)H\,\left( {c_{crit.}^{(k)} \text{-}\varepsilon {-}c_{capt.}^{(k)} } \right), $$
(9)

where ε is a small positive value, for example, 0.1% of the critical concentration.

If the average velocity of the dislocation motion \( V_{{}}^{(k)} \) is lower than the impurity atoms velocity caused by self-diffusion \( V_{diff.} \) and the current concentration of the impurity atoms \( c_{capt.}^{(k)} \) captured by the dislocation equals to the critical concentration \( c_{crit.}^{(k)} \), in this case the dislocation moves together with the cloud of the impurity atoms of a constant (equal to the limit one) concentration. At this time, the cloud is simultaneously resupplied with new captured impurity atoms, and it releases excessive atoms, then both processes are continuous. The concentration of the captured and free impurity atoms remains the same, so the rate of changing the number of the captured atoms should become zero, which is described by relation (8). As soon as the concentration of the captured atoms becomes critical (taking into account the introduced tolerance), due to the second Heaviside function, the source capture is set to zero.

The Second Scenario.

If the average velocity of the dislocation \( V_{{}}^{(k)} \) is higher than the impurity atoms velocity caused by self-diffusion \( V_{diff.} \), then there is a new calculation of the concentration of the captured and free impurity atoms depending on the value of the dislocation velocity. The higher the dislocation velocity, the more impurity atoms throw off the dislocation per unit time. When moving, the front wall of the capture tube sweeps a certain volume per unit time, in which there are impurity atoms with the concentration of free atoms. In other words, it determines the intensity of the source of absorption by the capture tube per unit time. The back wall also sweeps a certain volume, in which the impurity atoms remain with a concentration equal to the concentration of the captured atoms at the current time. This determines the intensity of the sink of the impurity atoms from the capture tube (the amount is equal to the product of the concentration of the captured atoms by the noticeable volume) and is described by the relation in (9):

$$ \dot{c}_{capt2}^{{}} = \left( {c_{free} - c_{capt} } \right)\frac{{V^{(k)} }}{R}H\left( {\left| {V_{{}}^{(k)} } \right| - V_{diff.} } \right). $$
(10)

The general system of equations determining the contribution from the interaction of the dislocations with the impurity atoms is as follows:

$$ \left\{ \begin{aligned} & \dot{c}_{capt.}^{(k)} = c_{free.}^{(k)} \frac{{V^{(k)} }}{R}H\,\left( {c_{\kappa crit.}^{(k)} \text{-}\varepsilon {-}c_{capt.}^{(k)} } \right)H\left( {V_{diff.} - \left| {V^{(k)} } \right|} \right) + \\ & + \left( {c_{free} - c_{capt} } \right)\frac{{V^{(k)} }}{R}H\left( {\left| {V^{(k)} } \right| - V_{diff.} } \right), \\ & c_{{}}^{(k)} = c_{capt.}^{(k)} + c_{free.}^{(k)} = \text{const}, \\ & \dot{\tau }_{imp}^{(k)} = \alpha \tau^{\prime}\frac{{\dot{c}_{capt.}^{(k)} }}{{c^{(k)} }}. \\ \end{aligned} \right. $$
(11)

3.4 Hardening Law

A hypothesis is accepted about the possibility of an additive decomposition of the critical stresses of the SS into contributions from the lattice resistance (constant value), from the stress fields of the dislocations and impurity atoms:

$$ \begin{aligned} & \tau_{c0}^{(k)} = \tau_{lat}^{(k)} , \\ & \dot{\tau }_{c}^{(k)} = \dot{\tau }_{disl}^{(k)} + { \dot{\tau }}_{imp}^{(k)} , \\ & \dot{\tau }_{disl}^{(k)} = \alpha \sum\limits_{i = 1}^{n} {M^{ik} \dot{\rho }_{{}}^{i} } , \\ & \dot{\tau }_{imp}^{(k)} = \alpha \tau^{\prime}\frac{{\dot{c}_{capt.}^{(k)} }}{{c^{(k)} }}. \\ \end{aligned} $$
(12)

4 Model Implementation Algorithm

Computations based on the model algorithm at all scale levels are implemented in terms of physical time. The stability of the numerical solution depends on the choice of the time step. The considered model can be integrated into the general model for solving boundary value problems of loading structures. In this case the element of the macrolevel will describe the mechanical response of the element of the considered finite element mesh. An algorithm for the implementation of one step (in time) of the deformation process will be described below. It should be noted that the plastic deformation does not usually occur immediately. To begin the plastic deformation, it is necessary to fulfill a certain criterion, the first stages of deformation usually occur in an elastic manner. Such staging imposes restrictions on the size of the time step, and may also require its significant reduction at the time of changing modes. The model is formulated in a velocity form, for integration over time a step-by-step process and integration by the Euler method are used.

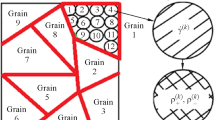
At the macrolevel, the deformation of the representative macrovolume of the material (macrodot) is considered. The macrolevel parameters include components of the Cauchy stress tensor (current value and rate of change at the current time step) and components of the spin tensor. Structurally, the macrolevel consists of a set of mesoscale-1 elements, while each element has its own characteristics, such as the orientation of the lattice in space, stress, etc. Deformations are prescribed to the macrodot, by using the Voigt hypothesis, the deformations are transferred to the mesoscale-1. In each element of the meso-1, stresses, the rate of rotation of the lattice, and the magnitude of plastic deformations are determined. By averaging the characteristics of the meso-1 elements (the averaging assumes the equality of the representatives of the meso-1 included in the macrolevel, i.e., the averaging over the representative macrovolume takes place), the stresses at the macrolevel are determined (Fig. 1).

Fig. 1.
figure 1

A schematic representation of a macrolevel element consisting of a set of the meso-1 elements.

Full size image

At the meso-1, the mechanical behavior of the crystallite is described, that is a region with a uniform crystal lattice. The mesoscale-1 parameters include the components of the Cauchy stress tensor (at the current step and in velocities), shear rates at the SS of the current step, the components of the spin tensor at the current step, and the values of shear stresses at each SS. At the mesoscale-1, it is assumed that the mesostresses, the rate of rotation of the lattice, and the rates of shear along the SS are homogeneous. The input variables are the components of the strain rate tensor, the response is the Cauchy stress tensor and the rate of the lattice rotation. At the mesoscale-1, the characteristics of the stress-strain state of the crystallite are determined, the magnitude of inelastic deformations, using Hooke’s law in the rate relaxation form, the stress changing rate and stress at the current step are determined. The value of the stress tensor (calculated in the previous step) is used to determine the magnitude of the shear stresses that are subsequently transmitted to the meso-2 level. From the mesoscale-2 to the mesoscale-1, shear rates are transmitted along the SS, determined from the velocities of motion and dislocation densities (Fig. 2).

Fig. 2.
figure 2

A schematic representation of the relation between elements of the meso-1 and meso-2.

Full size image

At the mesoscale-2, the evolution of densities and the kinetics of structural defects (edge dislocations and impurity atoms) are described. The mesoscale-2 parameters include the dislocation densities along the SS (in velocities and absolute values), critical stresses at each SS (at velocities and absolute values), average slip velocities of the dislocations at each SS, temperature, the concentrations of the free atoms and impurities. From the shear stresses transferred from the meso-1 and critical stresses from the previous step, we determined the average slip velocities of dislocations, the number of dislocation sources formed, the rate of change in the density of dislocations emitted by the sources, the rate of change in density due to the annihilation of the dislocations, the number of fixed and free impurity atoms. The rates and the absolute value of critical stresses for the next integration step are determined from the rates of change in the dislocation densities and the concentrations of the captured impurities. The absolute dislocation densities along the SS are found, using the Orowan equation, in the velocities, the shear rates transmitted to the meso-1 are determined.

In accordance with the structure of the model, the algorithm for its implementation is carried out by a stepwise (in physical time) solution of the following set of equations:

$$ \begin{array}{*{20}l} {\text{Macrolevel:}} \hfill \\ {\text{input}\;\text{:}\;{\mathbf{Z}}\text{,} - \text{ > }\text{Meso1;}} \hfill \\ {\text{Meso1}:|} \hfill \\ {{\mathbf{z}} = {\mathbf{Z}}} \hfill \\ {\tau^{{(\text{k})}} = {\mathbf{b}}^{{(\text{k})}} {\mathbf{n}}^{{(\text{k})}} :{\varvec{\upsigma}}\text{,} - > \text{Meso}2;} \hfill \\ {\text{Meso}2:} \hfill \\ {\text{V}_{ \pm }^{{'(\text{k})}} = \pm \text{f}\left( {\tau^{{(\text{k})}} ,\tau_{\text{c}}^{{(\text{k})}} \varvec{,}\theta } \right)\text{sign}\left( {\tau^{{(\text{k})}} } \right)\text{,}} \hfill \\ {{\dot{\rho }}_{ \pm }^{{(\text{k})}} = {\dot{\rho }}_{muc \pm }^{{(\text{k})}} + {\dot{\rho }}_{{\text{ann}}}^{{(\text{k})}} ,} \hfill \\ {{\dot{\rho }}_{muc}^{{(\text{k})}} = \text{f}\left( {\uprho_{\varvec{s}}^{{(\text{k})}} ,\tau^{{(\text{k})}} \varvec{,}\theta } \right),} \hfill \\ {{\dot{\rho }}_{ \pm }^{{(\text{k})\text{ann}}} = - \text{h}_{{\text{ann}}}\uprho_{ + }^{{(\text{k})}}\uprho_{ - }^{{(\text{k})}} \left| {\text{V}_{ + }^{{'(\text{k})}} - \text{V}_{ - }^{{'(\text{k})}} } \right|} \hfill \\ {{\dot{c}}_{{\text{capt.}}}^{{(\text{k})}} = \text{c}_{{\text{free.}}}^{{(\text{k})}} \frac{{\text{V}^{{(\text{k})}} }}{\text{R}}H\left( {\text{c}_{{\text{crit.}}}^{{(\text{k})}} - \varepsilon - \text{c}_{{\text{capt.}}}^{{(\text{k})}} } \right)\text{H}\left( {\text{V}_{{\text{diff.}}} - \left| {\text{V}^{{(\text{k})}} } \right|} \right) + \left( {\text{c}_{{\text{free}}} - \text{c}_{{\text{capt}}} } \right)\frac{{\text{V}^{{(\text{k})}} }}{\text{R}}\text{H}\left( {\left| {\text{V}^{{(\text{k})}} } \right| - \text{V}_{{\text{diff.}}} } \right),} \hfill \\ {\dot{\tau }_{{\text{disl}}}^{{(\text{k})}} = \alpha \sum\limits_{{\text{i = 1}}}^{\text{n}} {\text{M}^{{\text{ik}}} \dot{\rho }^{\text{i}} ,} } \hfill \\ {\dot{\tau }_{{\text{imp}}}^{{(\text{k})}} = \alpha \tau '\frac{{{\dot{c}}_{{\text{cap.}}}^{{(\text{k})}} }}{{\text{c}^{{(\text{k})}} }}.} \hfill \\ {\dot{\tau }_{\varvec{c}}^{{(\text{k})}} = \dot{\tau }_{{\text{dis}}}^{{(\text{k})}} + \dot{\tau }_{{\text{imp}}}^{{(\text{k})}} ,} \hfill \\ {{\dot{\gamma }}^{{(\text{k})}} = \left( {\rho_{\text{ + }}^{{(\text{k})}} \text{V}_{ + }^{{'(\text{k})}} - \rho_{ - }^{{(\text{k})}} \text{V}_{ - }^{{'(\text{k})}} } \right)\left| {\mathbf{b}} \right|^{{(\text{k})}} , - \varvec{ > }\text{Meso1}} \hfill \\ {\text{Meso1:}} \hfill \\ {{\mathbf{z}}^{{\text{in}}} = \sum\limits_{{\text{k} = 1}}^{\text{K}} {{\dot{\gamma }}^{{(\text{k})}} {\mathbf{b}}^{{(\text{k})}} {\mathbf{n}}^{{(\text{k})}} ,} } \hfill \\ {{{{\mathbf{\omega}} = \dot{{\mathbf{o}}}}} \cdot {\mathbf{o}}^{\varvec{T}} ,} \hfill \\ {{\mathbf{z}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\nabla } \text{v}^{\text{T}} - {\varvec{\upomega}},} \hfill \\ {{\varvec{\upsigma}}^{cr} =\Pi :\left( {{\mathbf{z}} - {\mathbf{z}}^{{\text{in}}} } \right), - \text{ > }\;\text{Macrolevel}} \hfill \\ \end{array} $$
(13)

It should be noted that the elements of the meso-1 and meso-2 in this formulation can be implemented simultaneously for one macrovolume, which makes it possible to implement the parallel algorithm for these elements.

5 Determining Model Parameter Values

Benefits of the physically-oriented models include the possibility of determining the values of parameters from numerical experiments on simplified research objects. Often, such work is carried out using mathematical packages implemented in functional programming languages, for example Wolfram Mathematica, Matlab, etc. The disadvantages of these tools include an inconvenience for implementing large algorithms, the complexity of implementing modular programs. To solve small applied problems, the mathematical packages offer great advantages; they have great function libraries, offer an easy visualization of results, as well as all the advantages of the high-level paradigm of the package implementation.

Additional numerical processes were used to determine some of the parameters. When determining the critical stresses, which depend on the interaction of the edge dislocations with each other, the solution is used for an isotropic elastic medium with a fixed single dislocation:

$$ \left\{ \begin{aligned} & \sigma_{xx} = - L \cdot \frac{{y(3x^{2} + y^{2} )}}{{(x^{2} + y^{2} )^{2} }}; \\ & \sigma_{yy} = - L \cdot \frac{{y(x^{2} - y^{2} )}}{{(x^{2} + y^{2} )^{2} }}; \\ & \sigma_{xy} = - L \cdot \frac{{x(3x^{2} - y^{2} )}}{{(x^{2} + y^{2} )^{2} }}; \\ & \sigma_{zz} = \nu (\sigma_{xx} + \sigma_{yy} );\sigma_{xz} = \sigma_{yz} = 0. \\ \end{aligned} \right. $$
(14)

The dislocations from another SS were introduced into the neighborhood of the fixed dislocation segment, and the forces of interaction of such segments were estimated. The forces with which two dislocations interact were considered (in the case of dislocations, the dislocation segments were taken from different SSs), and the possible variants of their interposition at different distances were taken into account. By averaging these forces, we could estimate the interaction forces between the dislocations on the fixed SS and introduced dislocations, and to construct a matrix describing the interaction intensity of the dislocations with different SSs. When determining the components of this matrix, the Wolfram Mathematica application package was used.

The stresses generated by the deposition of the impurity atoms on the edge dislocations were determined in a similar way, and the characteristics of the process of capturing the impurity atoms by the edge dislocations were determined.

6 Software Implementation, Results

The above model was implemented in C ++ in a procedure-oriented paradigm. The results of applying the algorithm to describe the evolution of the defects density in a crystallite (the meso-1 and meso-2 systems) and a polycrystalline aggregate of 64 elements (the macrolevel, the meso-1 and meso-2) are presented. To describe all the main processes, separate functions were used; for all real values, the double-precision double type was used. The results visualization is done in the packages Wolfram Mathematica and VeusZ.

The implementation of the parallel computations was made using the Intel c ++ compiler, the elements of the meso-1 and meso-2, as well as a number of procedures, were subject to parallel execution. The developed algorithm can be built into the finite element software products, which allows us to solve applied problems to describe the response of structures.

In the numerical implementation, a time step of 0.001 s−1 was used. The elastoplastic deformation of the AMg6 alloy was simulated, and the strain rates for shear (\( \text{z}_{{\text{12}}} = \text{z}_{{\text{21}}} = 1 \cdot 10^{ - 4} \text{s}^{{\text{{-}1}}} \)) were set as the loading. In the reference configuration, the crystallographic coordinate system was assumed to coincide with the laboratory one. Some of the parameters were taken from references; others were determined by an additional research. The deformation was performed until the intensity of the accumulated deformation reached 10%.

The numerical implementation of the model allows one to analyze the magnitude of all the variables during the deformation, which makes it possible to analyze the evolution mechanisms of the lattice defects (Fig. 3).

Fig. 3.
figure 3

The dependence of stresses on deformations (a single crystal, experiment 1).

Full size image

During deformation, the main attention was paid to the fixation and release of the edge dislocations from the impurity atoms. The existing model makes it possible to analyze all the parameters of the system during the plastic deformation, as well as to analyze the influence of all the evolution mechanisms of the defect densities. After a hundred of iterations, the main characteristics of the system were recorded in a file, which made it possible to further analyze them, as well as debug the program code. After the onset of the plastic deformation, an increase in the dislocation densities and an active redistribution of the concentration of the impurity atoms on the active SS were observed in both experiments (Fig. 4).

Fig. 4.
figure 4

A dependence of stresses on deformations (polycrystal, 64 crystallites, experiment 2).

Full size image

In the experiments with polycrystals, a higher level of stress jumps was observed, which is explained by the gradual accumulation of the impurity atoms on the dislocations in many crystallites, and then by their release in an avalanche-like manner (Fig. 5).

Fig. 5.
figure 5

Kinetics of the pinning of the impurity atoms on the dislocations of the considered SS.

Full size image

When analyzing the processes of pinning and releasing the impurity atoms, the dependence of the concentration of the impurity atoms fixed on the SS on the accumulated deformation was considered. Let us note that this process is more active at the initial stage of the plastic deformation. Qualitatively, this phenomenon is observed under plastic loading in field experiments.

7 Conclusion

This article gives an overview of the models describing the Portevin - Le Chatelier effect and outlines the main advantages and disadvantages of the existing models. An attempt has been made to use a common approach including the multilevel models based on crystal plasticity to describe the discontinuous plasticity effect. The model previously developed by the team of authors was modified taking into account the presence of the impurity atoms in the alloy and their interaction with the edge dislocations, which affects the critical slip stresses. A detailed description of the direct elastoviscoplastic model is given including the relations describing different structural levels. Also the relations between them have been described.

The model implementation algorithm for the material representative volume at all scale levels is given. This model is a part of the software package that is implemented and developed in a modular structure that allows one to describe a wide range of physical and mechanical effects. To determine the values of a number of parameters, the additional package of Wolfram Mathematica for the mathematical calculations was used.

We identified the model parameters, carried out a number of studies and showed the qualitative agreement of the results with the data of the field experiments. Some of the computation results using this model are considered, the main evolution mechanisms of the microstructure are described. The calculations were made using an algorithm implemented in the C++ language in the VisualStudio 2012 series environment; the Intel Parallel Studio development package was used to implement the parallel computing procedures.