Minimising Cycle Time in Assembly Lines: A Novel Ant Colony Optimisation Approach

Abstract

We investigate the problem of mixed model assembly line balancing with sequence dependent setup times. The problem requires that a set of operations be executed at workstations, in a cyclic fashion, and operations may have precedences between them. The aim is to minimise the maximum cycle time incurred across all workstations. The simple assembly line balancing problem (with precedence constraints) is proven to be NP-hard and is consequently computationally challenging. In addition, we consider setup times and mixed model product types, thereby further complicating the problem. In this study, we propose a novel ant colony optimisation (ACO) based heuristic, which unlike previous approaches for the problem, focuses on learning permutations of operations. These permutations are then mapped to workstations using an efficient assignment heuristic, thereby creating feasible allocations. Moreover, we develop a mixed integer programming formulation, which provides a basis for comparing the quality of solutions found by ACO. Our numerical results demonstrate the efficacy of ACO across a number of problems. We find that ACO often finds optimal solutions for small problems, and high quality solutions for medium-large problem instances where mixed integer programming is unable to find any solutions.

1 Introduction

Assembly line balancing deals with subdividing a manufacturing process into simple operations and to assign those operations to workstations to produce goods in an optimal fashion. Assembly lines generally consist of a set of workstations connected by material handling systems including moving belts or robots [12]. Finding an optimal assignment of operations to workstations considering precedences between operations, operation durations and the availability of workstations is called an assembly line balancing problem (ALBP) [11]. The problem has several categories depending on line layouts, variability of durations, objective functions, and so forth. For example, a type I ALBP (ALBP-I) tries to minimise the number of workstations for given cycle time. In contrast, a type II ALBP (ALBP-II) minimises the cycle time or maximises the throughput for a given number of workstations. Moreover, there are other types, namely E and F, where type F focuses on maximising an effectiveness measure and type E is used when there is no specific objective  [3].

Assembly line problems are also categorised based on the number of models processed on a line. A single model problem (SALBP), an early variant, aimed to address a high volume of demand for a particular product. To respond to diversified customer requirements for products and to avoid constructing multiple assembly lines, the multi-model and mixed model variants (MMALBP) variants emerged. Here, several models of a product are considered simultaneously but still only a single assembly line [11]. Production systems differ substantially, thus leading to new problem variants. The various ALBP type problems include general (GALBP), resource constrained (RCALBP), robotic (RALBP), worker assignment (ALWABP), robotic (RMMALBP), etc. Of particular interest in this study are the type II SALBP and MMALBP problems with setup times, which are abbreviated as SALBPS and MMALBPS, respectively [1, 3, 17].

ALBP, in its simplest form, is known to be computationally intractable or NP-hard [7]. A large body of research is devoted to solve the problem in a time efficient manner. Several exact algorithms have been proposed for the problem, but to deal with its complexity, incomplete approaches including dynamic programming, heuristics and meta-heuristics have been attempted [12, 15]. Simaria and Vilarinho [14] maximise the production rate of a line (equivalent to minimising cycle time of a line) in a MMALBP with parallel workstations for a pre-determined number of operators using a genetic algorithm. The studies by Kilincci [9] and Hossain [8] investigate SALBP-II, where the first study proposes bounded exact methods while the second study proposes a progressive modelling approach. Seyed-Alagheband et al. [13] propose a simulated annealing algorithm to solve a general assembly line balancing problem with setups (GALBPS-II) by using the Taguchi method. In this work, the author represented the problem as an object-oriented graph. Zheng et al. [20] proposed a version of ant colony optimisation (ACO) method in solving a type II ALBP which essentially searches for different combinations of tasks for each workstation. Despite several approaches (exact and incomplete) being proposed for variants of the ALBP, there is still substantial room for improvement.

In this study, we propose a novel ACO based heuristic and adapt a mixed integer programming approach for tackling the MMALBPS.¹ Previous studies with the MMALBPS have focused on either modifying solutions based on a neighbourhood structure [19] or the assignment of operations to workstations [1, 10]. In contrast to these approaches (including also ACO), our ACO approach splits the solution creation into two components. The motivation for this is that ACO is very effective at ‘sequence learning’ but not as effective in dealing with complex constraints. Hence, the first component learns sequences (or equivalently permutations) of operations (which ACO is very effective at) and the second component takes a sequence and maps it into a feasible assignment of operations to workstations. We show that this approach is indeed very effective for MMALBPS, and our results demonstrate that ACO can find high quality (often optimal) solutions in short time-frames. Moreover, ACO scales very efficiently with problem size.

The paper is organized as follows: Sect. 2 defines the MMALBPS problem and provides its mixed integer programming (MIP) formulation. Section 3 discusses the ACO-based heuristic specifically designed for this problem. Section 4 details the experimental setting followed by a presentation of the results. Section 5 concludes the paper and provides some insights into future work.

2 Problem Definition and Mathematical Model

The MMALBPS can be formally described as follows. We are given N operations which must complete M models of a product in a manufacturing system. The operations are allowed to use W workstations.² The assignment of operations to workstations (sequencing) must satisfy precedence relations $P_{ij}$ (an indicator variable), where $P_{ij}=1$ if operation i must precede operation j. An operation $i \in N$ in model $m \in M$ occupies a workstation $s \in W$ that it is allocated to for a duration $T_{im}$ (process time of operation i in model m). Moreover, when two operations i and j are allocated sequentially to the same workstation, they incur a forward setup³ time $F_{ij}^m$ (setup time between operations i and j in model m). In this paper we aim to solve an MMALBPS with parameters (N, M, W, $P_{ij}$, $T_{im}$, $F_{ij}^m)$, which seeks an optimal assignment of N operations pertaining to M models to workstations so that the maximum cycle time (sum of durations and setup times) of any workstation is minimised. When $M=1$, we are dealing with the SALBP.

Given the problem definition above, we define the following MIP. Note, we have adapted the MIP from the study of Akpinar [2] where we relax the constraints on cycle time but rather impose constraints on the number of machines. In the following discussion we provide the list of decision variables and detail the objective function and the constraints of the MIP model. In addition to the parameters specified above, we make use of an indicator variable $Q_{im}$, which is 1 if $T_{im}>0$.

The model makes use of binary variables y, w and x. $y_{is}$ is 1 if operation i is assigned to workstation s, $w_{ijs}$ is 1 if operation i precedes operation j at machine s and $x_{ijms}$ is 1 if operation j directly follows operation i of model m at workstation s. Additionally, the variable c represents the cycle time.

$$\begin{aligned} \begin{aligned} {{\textit{\textbf{Minimize }}}} c = \max \limits _{s\in W,m\in M} \Bigg \{ \sum \limits _{i=1}^N \left( y_{is}T_{im} + \sum \limits _{j=1}^N (x_{ijms}F_{ijm}) \right) \Bigg \} \end{aligned} \end{aligned}$$

(1)

$$\begin{aligned} \begin{aligned} {{\textit{\textbf{subject }}} {\textit{\textbf{to }}}} \sum \limits _{s=1}^W y_{is}=1&\forall i \in N \end{aligned} \end{aligned}$$

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

The objective function minimises the cycle time of the assembly line as given in (1), which is the maximum cycle time across all workstations. Constraints sets (2–3) assign tasks to workstations ensuring that the precedence relations are satisfied. Constraints sets (4–9) order the assigned tasks to each workstation ensuring that the precedence relations within a workstation are satisfied. The constraint set (10) determines the number of orderings between all pairs of tasks at each workstation. Constraints sets (11–13) guarantee that each task can have a single immediate successor in a workstation. Finally, the constraint set (14) determines the immediate successor of each task and relevant setup operation that should be performed between them.

3 Ant Colony Optimisation

The ACO variant used in this study is ant colony system (ACS)  [5]. ACS is proven as one of the most practically effective ACO methods. In particular, its convergence characteristics are a lot more effective on a range of problems compared to that of the original Ant System [5].

We use $\pi$ – a permutation that represents a solution to the problem. The permutation has an associated assignment $\hat{\pi }$, which takes the operations in the permutation and assigns them one-by-one in the order they appear into workstations. This assignment heuristic (Sect. 3) ensures that precedence feasible solutions are constructed, and hence the permutation does not need to be precedence feasible.

An ACS implementation for the MMALBPS is shown in Algorithm 1. The algorithm has the following inputs: (a) an MMALBPS problem instance, (b) a terminating criteria, we use a time limit ($t_{max}$) for this study, (c) the number of permutations $n_s$ to be constructed at each iteration of the algorithm and (d) a pre-defined parameter $q_0$ that specifies the level of deterministic selection. In the first step of the algorithm, the pheromone trails are initialised (Initialise($\mathcal {T}$)). Here, we set $\tau _{ij} = \frac{1}{|N|}$ $\forall i,j \in N$, where $\tau _{ij}$ is the desirability of picking $\pi _i = j$.

The algorithm executes Lines 4–9 until a terminating criteria, or in this study, until a time limit expires. Within this time limit, a number of iterations are executed. In an iteration, the first step is to construct $n_{s}$ solutions from scratch. Each solution is built by starting out with an empty permutation, and adding operations in successive positions of the permutation using the pheromone trails (ConstructSequence($\mathcal {T}$, $q_0$ )). In the usual ACS way, operations are selected either deterministically or stochastically. For this purpose, a random number q is generated from the interval (0, 1] and is compared to the pre-defined parameter $q_0$. If $q < q_0$, operation k is chosen in position i of the permutation as:

$$\begin{aligned} k = \mathop {\text {arg}\text {max}}\limits _{j \in N} \{ \tau _{ij} \cdot \eta _{ij} \} \end{aligned}$$

(15)

If $q \ge q_0$, the operation is selected stochastically according to:

$$\begin{aligned} P(\pi _i=k) = \frac{\tau _{ik} \cdot \eta _{ik}}{\sum _{j\in N}\,\tau _{ij}\cdot \eta _{ij}} \end{aligned}$$

(16)

where a heuristic $\eta _{ik}$ is used to bias the selection of operation i in position k. In preliminary testing, we investigated several heuristics, for example setup times $\mu$, but the most effective choice was found to be $\eta _{ij} = \frac{1}{T_{im}}$.

In ACS, a local pheromone update is used at every selection step as a mean to reduce the chance of making a repeated selection. That is, when an operation j is selected at position i the pheromones are updated according to:

$$\begin{aligned} \tau _{ij} = \max \{\tau _{ij} \cdot (1.0-\rho ), \tau _{min}\} \end{aligned}$$

(17)

where, to ensure that no selection of an operation to a position becomes too low, we set $\tau _{min} = 0.0001$. This ensures that operation j at least has a small chance of being selected in position i.

A complete permutation can be mapped in a greedy way to a feasible assignment of operations to workstations in AssignOperation($\pi _j$) (Sect. 3). In Line 7, an iteration best solution is selected as one that minimises the cycle time across all workstations. In Line 8, $\pi ^{bs}$ is updated to $\pi ^{ib}$ if $\pi ^{ib}$ is an improvement. The final step is to update the pheromone trails ($\mathcal {T}:=$ PheromoneUpdate($\pi ^{bs}$)) for those solution components seen in $\pi ^{bs}$:

$$\begin{aligned} \tau _{ij} = \tau _{ij} \cdot (1.0-\rho ) + \delta \end{aligned}$$

(18)

where the reward factor $\delta = Q/f(\pi ^{bs})$ applies to all solution components and Q is a normalising factor that is chosen to ensure that the reward, relative to the pheromone values, is always between $0.01 \le \delta \le 0.1$. For the evaporation rate, it was found that a value of 0.1 is very effective. This is not unusual as for ACO implementations with relatively short run-times (as is the case in this study), a high reward is favourable.

Assigning Operations to Workstations Previous studies in scheduling have demonstrated the efficacy of learning permutations and mapping these to a schedule [4, 18]. Using this idea as a guide, we develop an assignment heuristic, which maps operations in a permutation to workstations.

The high-level algorithm is shown in Algorithm 2. Starting with a permutation $\pi$ (input), the heuristic assigns operations to workstations ensuring that a minimum cycle time is always maintained. The first step is to initialise the following data structures: (a) $\hat{\pi }$ - the assignment of operations to workstations, (b ) W - a waiting list and (c) g - the workstation cycle times. The main loop starts in Line 3 where, for each operation, a feasible assignment to a workstation is found. The operation is tested to see if its preceding operations have been completed (Lines 5–7), and if not, it is put on a waiting list W. If the precedences are satisfied, then the operation is assigned to the workstation with the minimum overall cycle time divided by the number of jobs on the workstation - that is, workstation j is chosen for operation i under mode m:

$$\begin{aligned} j = \mathop {\text {arg}\text {min}}\limits _{s \in S} \left\{ \frac{\hat{C}_s+T_{im}+F_{i-1,i,m}}{|N_s|} \right\} \end{aligned}$$

(19)

where $\hat{C}_s$ is the current cycle time of workstation s and $|N_s|$ is the number of operations already allocated to station s. In Line 10, the final assignment $\hat{\pi }$ and cycle time of workstation s are updated. An assignment of an operation leads to examining W, to determine if any other operations can now be assigned (Lines 12–15). The procedure completes by returning the final precedence-feasible assignment.

Fig. 1.

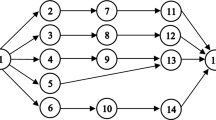
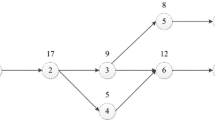
An example of an assignment of operations to workstations. The figure on the left shows a permutation of 7 operations and 5 workstations. The figure in the middle shows that the first 5 operations are placed in each available workstation (height of a job is its duration). The figure on the right shows that Operation 6 ($O_6$) is assigned to the workstation with the shortest cycle time (Station 3 here). A setup time $ST_{31}$ is required between the two operations on the workstation.

Figure 1 illustrates how the heuristic works. The figure on the left shows a permutation of operations and 5 workstations. The operations are assigned in order to workstations while workstations still do not have operations in them (Fig. 1 – middle). In the figure on the right we see that a new operation is added to a workstation when an operation is already assigned to it. In this case, the operation is assigned to the workstation with the lowest overall cycle time.

4 Experimental Setting and Results

ACS for MMALBPS was implemented in C++ and compiled in GCC-5.4.0. The MIP was implemented in Gurobi 9.0.1 (http://www.gurobi.com/). The experiments were conducted on MonARCH - a Linux cluster at Monash University.⁴

Table 1. The details of the problem instances; n is the number of operations and W the number of workstations; The workstation levels are also provided.

To investigate the performance of the algorithms, we consider the problem instances from [2]. We made two changes: (a) remove the constraint on cycle time and (b) specify the number of workstations as a function of the number of operations n: $\{ \frac{n}{2},\frac{2 \cdot n}{2},\frac{3 \cdot n}{4} \}$.⁵ The details of these problem instances are shown in Table 1. The table shows, for each problem, the number of operations (n), the number of workstations (W) split by levels (WL). Overall, we have a total of 120 problem instances, with 60 per model type. For ACS, we allow a run-time of 2 min and conduct 30 runs per instance. The MIP executes only once per instance (as it is deterministic) and will allow a time limit of 10 min.⁶ ACS is memory efficient requiring only up to 1 GB memory, while the MIP often used up to 10 GB for the large instances.

We used a subset of the problem instances to tune the parameters of ACS. For $\rho$, we tested values in the range $\{0.2,0.1,0.0.5,0.01\}$ and found that 0.01 was most effective. For $q_0$ we tested $\{0.5,0.2,0.1,0.01\}$ and found that 0.1 was best. $\tau _{min} = 0.0001$ was used to ensure that an operation at a workstation will always have some small chance of being selected.

In the following, we use workstation level (WL) to denote the varying level of workstations: 1 = $\frac{n}{2}$, 2 = $\frac{2 \cdot n}{2}$ and 3 = $\frac{3 \cdot n}{4}$. Here, WL = 1 can be thought of as the hardest problem consisting of the fewest machines. The instances are numbered such that the number of workstations increases with increasing numbers.

Table 2 shows a comparison of ACS and the MIP solver. The results are split by model M (single = 1, two = 2), workstation level WL and solver type. The table shows the cycle time obtained by the MIP, and for ACS, the best, mean and standard deviations of 30 runs are reported. The best solutions found are marked in boldface. When a method fails to find a feasible solution (only in the case of the MIP) it is marked by a “-”.

Table 2. The results the cycle times obtained by the MIP and ACS. Since ACS is run 30 times on each problem instance, the best, average and standard deviations are shown. The results are split by model type (single or two model) - M - and three workstation levels (WL); the values in boldface indicate the best solution found for a problem instance; “-” indicates that no feasible solution was found; b is the best solution, $\mu$ is the average solution and sd is the standard deviation considering 30 runs.

For small problem instances, the MIP can often find optimal solutions (up to problem 8 for single model problems). On instances with many workstations, i.e., WL = 2,3, ACS often finds the optimal solution (on average). In fact for a few small problem instances with two models (e.g., Problem 5), ACS outperforms the MIP. However, for these instances the ACS solutions are not provably optimal. When the problem size increases (${\ge }$9), ACS easily proves to be the best method, where the MIP is unable to even find a feasible solution on most occasions. Even when solutions are found (e.g.. Problem 10 - Model 1 - WL 2), they have very large cycle times. Interestingly, splitting by models, we see that ACS performs better when there are two models compared to one despite the instances with two models being more complex. These results overall demonstrate that despite running ACS for short run-times, we see very good results.

Fig. 2.

The performance of ACS on single model and two model instances.

We now delve into the results by focusing on ACS in Fig. 2. The left axis represents the cycle time, the right axis shows the number of workstations and the horizontal axis represents the instances. The bars in these plots show the number of machines. The figure on the left shows the results for single models while the figure on the right shows the same for two models. The ACS run is indicated by the green line. An obvious pattern we see is that the variation in single model problems is much larger than two model problems, demonstrating the usefulness of ACS in dealing with increased complexity.

For single model instances, the cycle times tend to increase when the problem consist of 20–30 stations (problem instances 11–16 where the number of tasks are between 28–45). However, for problems with more than 30 stations, the cycle times return to previous levels (900–1500 time units). A similar effect is seen for two model problems at around 35 stations. While this aspect warrants further investigation (e.g.. examining the proportion of operations to workstations or precedence graphs), we leave this to further work due to space limitations.

Fig. 3.

The performance of ACS with 120 s execution time cap with different workstation levels.

In Fig. 3 we focus on ACS with respect to the level of workstations WL. Like with Fig. 2, the cycle time is presented on the left, the number of workstations on the right and the instances on the horizontal axis. The plots show a split of the performance of ACS depending on the number of workstations. We see that, for single and two models with WL = 1, the cycle times are large and also have high variability. This is not surprising since the instances with a small number of workstations are the hardest ones in the sense of minimising cycle times. In fact, when the instances are “easy”, ACS find very low cycle times consistently (a number of which are provably optimal, see Table 2). The large spikes in cycle times seen in Fig. 2 are attributable to those problem instances with relatively few workstations (where workstations were selected as $n \div 2$) for both models.

5 Conclusion and Future Work

We investigate the multi-model assembly line balancing problem with setup times, and propose a novel ant colony system based heuristic for solving it. In comparison to previous ACS methods on similar problems, we focus on learning permutations of operations, which are then mapped to workstations via an efficient assignment heuristic. We compare ACS to a mixed integer programming model and find that ACS performs well overall. In particular, ACS demonstrates clear advantages in three aspects: (a) high quality solutions are found in short time-frames when the number of work stations increase compared to the MIP, (b) improved performance on two model problems compared to single model problems (c) outperforms the MIP for all medium to large problem instances.

While the proposed ACS approach is effective, there are areas where its performance can certainly be improved. This is especially in the case where there are a small number of workstations leading to large cycle times. For example, the assignment heuristic could be enhanced with probabilistic selection for operations to stations. Furthermore, time-based MIP models could prove very effective, leading to decompositions [6] and hybrid approaches [16].