Keywords

1 Introduction

Plate-type structures are key components in many engineering applications [1,2,3]. The real-time damage assessment of plate structure is of great importance. Vibration-based structural health monitoring (SHM) is one of the most promising methods due to the low-cost and reliable industrialized accelerometers are available on the market [4,5]. Due to the difficulty of accurate damage assessment with a limited number of sensors, the studies on damage detection for plate structures are relatively limited.

Typical dynamic parameters used for damage assessment are natural frequency, modes shape and mode shape curvatures (MSC). Frequency-based methods are more suitable for the application with a stable environment [6]. On the other hand, mode shape and MSC based methods are more robust against the environment [7,8]. Nonetheless, they need a large number of sensors to cover the whole surface of the structure.

Some studies [9,10] showed that the node displacement (NODIS) of vibrational mode shapes is an efficient damage indicator. The method needs a small number of sensors attached to the vibrational nodal points. Moreover, the environment has less influence on the method comparing to frequency. However, due to the limited number of noisy measurements, the damage detection is often an ill-posed of ill-conditioned problem. The Bayesian probabilistic approach is widely used to deal with this problem by describing the uncertainties in damage detection [11,12,13].

As the posterior probability distribution is intractable due to the computational effort, the damage parameter can be estimated based on samples drawn numerically using a Markov chain Monte Carlo (MCMC) sampling technique [14,15,16]. A candidate sample is drawn each time and is either accepted or rejected according to a certain acceptance rate. After sufficient sampling times, the samples automatically form a distribution that corresponds to the Bayesian posterior of the problem.

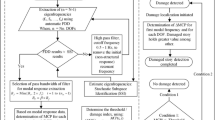
This paper proposes an MCMC-based Bayesian probabilistic damage detection method using NODIS for plate structures. The adaptive Metropolis algorithm is adopted in the MCMC sampling. The principle of the NODIS method for the plate is first elaborated with the response surface. Then the MCMC-based Bayesian framework and the adaptive Metropolis algorithm are explained in detail. At last, the proposed method is validated with FE models.

2 Principles of NODIS Method for Plate Structure

In this paper, the NODIS represents the out-of-plane displacement at vibration nodal points. When a damage is introduced on the plate, the mode shape is changed and the NODIS is therefore changed. Thus, the damage parameter can be inferred from the changed NODIS. In this section, the response of NODIS under different damage location and severity is studied with a four-sides-clamped plate with single damage.

A numerical model of an aluminum plate is simulated in Abaqus, as illustrated in Fig. 1. The dimension of the plate is 500 mm × 500 mm × 5 mm and four sides are all clamped. The damage is simulated with a stiffness loss in the highlighted area. The plate is partitioned into 50 × 50 sections. Each section can have different stiffness. A Python script is developed to assign different stiffness at different locations. Then, modal analysis is conducted for each damage case. Thus, the mode shape and NODIS can be extracted. The range of the damage center \(\left({\xi }_{x}, {\xi }_{y}\right)\) in X- and Y-direction are both from 15 mm to 485 mm with an interval of 10 mm. The size of the damage is 30 mm × 30 mm. The range of the relative stiffness loss \(\varepsilon \) is from 0.1 to 0.5 with an interval of 0.1. Thus, a total number of 11520 samples of the NODIS are acquired.

Fig. 1.
figure 1

A sketch of the plate partition, damage information and location of nodes.

Full size image
Fig. 2.
figure 2

Mode shape of interest (a) first mode and (b) second mode and the location of selected nine nodes N1–N9.

Full size image

The first and second mode of interest are selected, as illustrated in Fig. 2. As the four nodes in the second mode share the same location as the nodes in the first mode, only five sensors are needed to acquire the nine NODIS. With the database of NODIS under different damage parameters, the NODIS response surfaces can be acquired. Figure 3 shows an example under the stiffness loss of 0.1. Each sub-figure represent a response surface of a node. The X- and Y-axis represent the center coordinates of the damage. The color represents the amplitude of the out-of-plane displacement. As the pattern of each NODIS response surface is different, they have the potential to be adopted for damage characterization.

Fig. 3.
figure 3

The NODIS response surfaces constructed from FE models with damage location (ε = 0.1) (a)–(i): N1–N9.

Full size image

3 MCMC-Based Bayesian Framework with NODIS

The goal of the Bayesian framework is to obtain a probability distribution of the unknown damage parameter given a limited number of noisy NODIS measurements. The likelihood function can capture the information implicitly offered by the measurement. Then, a posterior probability distribution over the damage parameter can be acquired by combining the likelihood function and a prior distribution. However, the integration of the probability distribution is not feasible. Thus, an MCMC sampling technique is needed to estimate the distribution of the damage parameter.

3.1 Bayesian Statistical Inference

The Bayesian inference will calculate the probability distribution of damage parameter \({\varvec{\Theta}}=\left\{{\xi }_{x}, {\xi }_{y},\varepsilon \right\}\). Given a measurement \(\mathbf{D}={\left\{{z}_{i}^{e}\right\}}_{i=1}^{N}\) which contains \(N\) measured NODIS values, the posterior probability density function (PDF) can be given as

$$P\left({\varvec{\Theta}}|\mathbf{D}\right) = \frac{P\left({\varvec{\Theta}}\right)P\left(\mathbf{D}|{\varvec{\Theta}}\right)}{\int P\left({\varvec{\Theta}}\right)P\left(\mathbf{D}|{\varvec{\Theta}}\right)\mathrm{d}{\varvec{\Theta}}}$$
(1)

where \(P\left(\mathbf{D}|{\varvec{\Theta}}\right)\) is the likelihood function which represents the probability of measuring the data \(\mathbf{D}\) given a damage parameter \({\varvec{\Theta}}\). The denominator, which is the marginal likelihood, can be considered to be a normalization factor. And \(P\left({\varvec{\Theta}}\right)\) is the prior which can be set based on the expert opinion or practical experience.

Under a damage parameter \({\varvec{\Theta}}\), it is common to assume that the measured NODIS is polluted with a random noise which is independent and identically distributed according to a zero-mean normal distribution

$${z}_{i}^{e}={z}_{i}\left({\varvec{\Theta}}\right)+{\eta }_{i}, {\eta }_{i}\sim N(0,{\sigma }_{i}^{2})$$
(2)

where \({\sigma }_{i}\) is the standard deviation of the i-th measurement. Then, the likelihood function of each measurement for a given damage parameter can be written as

$$P\left({z}_{i}^{e}|{\varvec{\Theta}}\right)=\mathcal{N}\left({z}_{i}\left({\varvec{\Theta}}\right),{\sigma }_{i}^{2}\right)$$
(3)

The likelihood function of the measured NODIS values \(\mathbf{D}\) can be formulated as a joint probability

$$P\left(\mathbf{D}|{\varvec{\Theta}}\right)=\prod_{i=1}^{N}P\left({z}_{i}^{e}|{\varvec{\Theta}}\right)=\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi }{\sigma }_{i}}\mathrm{exp}\left(-\frac{{{(z}_{i}^{e}-{z}_{i}\left({\varvec{\Theta}}\right))}^{2}}{2{\sigma }_{i}^{2}}\right)$$
(4)

3.2 The MCMC Sampling Technique

The calculation of the posterior Eq. (1) often involves multidimensional integrals is intractable. MCMC can be used for sampling high dimensional and complex distributions. After collecting samples drawn from \(P\left({\varvec{\Theta}}|\mathbf{D}\right)\), the damage parameter can be estimated. Most features, such as expectation and variance, can be determined from expectations of \(f({\varvec{\Theta}})\), thus

$$\mathbf{E}\left[f({\varvec{\Theta}})\left|\mathbf{D}\right.\right] =\int f({\varvec{\Theta}})P\left({\varvec{\Theta}}|\mathbf{D}\right)\mathrm{d}{\varvec{\Theta}}= \int \frac{f({\varvec{\Theta}})P\left({\varvec{\Theta}}\right)P\left(\mathbf{D}|{\varvec{\Theta}}\right)}{\int P\left({\varvec{\Theta}}\right)P\left(\mathbf{D}|{\varvec{\Theta}}\right)\mathrm{d}{\varvec{\Theta}}}\mathrm{d}{\varvec{\Theta}}$$
(5)

For simplicity, \(P\left({\varvec{\Theta}}\right)P\left(\mathbf{D}|{\varvec{\Theta}}\right)\) is replaced with an arbitrary distribution \(\pi (\mathrm{X})\). The key point of the MCMC sampling technique is to generate a sequence of samples of \(\mathrm{X}\), according to the target distribution \(\pi \left(\mathrm{X}\right).\) This sequence is denoted as \(\{{\mathrm{X}}_{t}, t=1, 2, \dots , n\}\). After sampling, the distribution \(\pi \left(\mathrm{X}\right)\) can be visualized by summing up the frequency of each value of \(\mathrm{X}\) in the sequence into a histogram. The features can be determined using Monte-Carlo integration

$$\mathbf{E}\left[f\left(\mathrm{X}\right)\right]= \frac{\int f\left(\mathrm{X}\right)\pi \left(\mathrm{X}\right)\mathrm{d}{\varvec{\Theta}}}{\int \pi \left(\mathrm{X}\right)\mathrm{d}{\varvec{\Theta}}}\approx \frac{1}{n}\sum_{t=1}^{n}f\left({\mathrm{X}}_{t}\right)$$
(6)

At any step \(t\), a candidate \(\mathrm{Y}\) is first proposed based on the current state \({\mathrm{X}}_{t}\) according to a proposal distribution \(\mathrm{Y }\sim q\left(\mathrm{Y}|{\mathrm{X}}_{t}\right)\). Then the candidate \(\mathrm{Y}\) is accepted with a probability called the acceptance rate \(\mathrm{\alpha }({\mathrm{X}}_{\mathrm{t}},\mathrm{Y})\), or else it will be rejected. The most common choice of the proposal distribution is called the Metropolis algorithm. Under this condition, the acceptance rate can be written as

$$\mathrm{\alpha }\left(\mathrm{X},\mathrm{Y}\right)=\mathrm{min}\left(1,\frac{\pi \left(\mathrm{Y}\right)}{\pi \left(\mathrm{X}\right)}\right)$$
(7)

The Gaussian proposal distribution is adopted in this paper

$$q\left(\mathbf{Y}|\mathbf{X}\right)= \frac{1}{\sqrt{{\left(2\pi \right)}^{n}\left|\Sigma \right|}}\mathrm{exp}\left(-\frac{{\left(\mathbf{Y}-\mathbf{X}\right)}^{\mathrm{T}}{\Sigma }^{-1}\left(\mathbf{Y}-\mathbf{X}\right)}{2}\right)$$
(8)

where \(n\) is the dimension of the sampled vector, and \(\Sigma \) is the covariance matrix of the Gaussian distribution. \(\Sigma \) is a free parameter in the algorithm that plays a key role in the ergodicity performance of the MCMC chain.

Then, the Adaptive Metropolis (AM) MCMC technique to achieve an automatic adaptation of the covariance matrix during the sampling process. The formula used for calculating each time’s covariance matrix can be simplified in most practical cases as

$${\Sigma }_{n}={s}_{d}\mathrm{Cov}\left({\mathrm{X}}_{0},{\mathrm{X}}_{1},\dots ,{\mathrm{X}}_{n-1}\right)$$
(9)

where \({s}_{n}=5.76/n\) is a scaling parameter suggested by a lot of researchers [15].

It can be seen from Eq. (9), that when the covariance of the past samples decreases (which is mainly because of the repeating of samples due to high rejection rates), the ‘step length’ \(\Sigma \) automatically becomes smaller to generate more ‘prudent’ proposals in order to increase the acceptance rate. On the other hand, if the step length is getting too small, the proposal gradually becomes ‘bolder’ according to the formula. In this way, an automatic adaptation of the sampling is realized. The algorithm of the adaptive Metropolis MCMC algorithm is summarized as follows.

figure a

4 Numerical Validations

The MCMC framework is realized with MATLAB, Python and Abaqus. In each step, a sample of the damage parameters is drawn. In order to calculate the acceptance rate, the posterior distribution has to be evaluated for the proposed sample. At this point, the MATLAB code generates a parameter file. A python code reads this file. The python code organizes the necessary information for an FE simulation, such as the geometry configuration of the plate and the damage position.

Then the python code starts an FE simulation in Abaqus with the information collected. The results of the simulation are saved in another file. Then, the python code read this file and extract the node displacement values from it. These values are sent back to MATLAB, where they are further processed to NODIS indexes and used in the calculation of the acceptance rate of the proposed sample. Finally, the samples generated with MCMC are processed in MATLAB to reconstruct the distribution. The calculation of the distribution features with the samples is also done in MATLAB.

To validate the proposed MCMC framework, four damage cases, as listed in Table 1, are adopted. The NODIS value acquired from the FE model with a 30% noise is considered as the measurement. By adopting the proposed MCMC framework, the posterior distribution of the damage parameter can be acquired, as illustrated in Fig. 4. It can be seen that that location and severity of the damage can be identified. The estimated damage parameter is listed in Table 1, and the normalized error is below 12%.

Table 1. Damage parameter and estimates
Full size table
Fig. 4.
figure 4

Posterior distribution under different damage cases (a)–(d): case 1 – case 4.

Full size image

5 Conclusion

In this paper, an MCMC-based probabilistic damage detection method using NODIS is proposed for plate structures. First, The NODIS response surfaces are elaborated with FE models. Then, the MCMC-based Bayesian framework is presented. Furthermore, the algorithm of the adaptive Metropolis MCMC is explained in detail. Finally, the validation results show that the proposed method can identify the damage parameter with a probability distribution and the normalized errors are limited to 12%.