CFD Modelling and Simulation of Drilled Cuttings Transport Efficiency in Horizontal Annulus During Gas Drilling Process: Effect of Gas Injection Method

Abstract

Gas drilling, such as the air or nitrogen drilling, can improve the drilling efficiency and effectively protect the oil and gas reservoir from the lost circulation during the drilling process. However, a major disadvantage of the gas drilling is the severe deposition of the drilled cuttings, especially in the horizontal gas drilling, which mainly caused by the poor transport capacity of the gas phase due to its low density and viscosity. Generally, the solution is increasing the gas injection rate, but it will lead to a higher cost and may cause ice-balling of the drill bit. In this paper, a pulsed gas injection method is proposed to overcome the shortcoming, leading to cost reduction and efficiency increase. The Eulerian-Eulerian two-fluid approach with the kinetic theory of granular flow is employed to simulate the gas-solid two-phase flow in a 3D eccentric horizontal annulus using CFD modelling. The RNG k-ε turbulence model is adopted to describe the turbulence behavior of the gas phase. The effects of various gas injection methods on the gas inlet velocity, pressure drop, cuttings volume fraction, granular temperature, turbulence kinetic energy, and turbulence dissipation rate are systematically investigated. The results show that almost no stationary cuttings bed is formed in the annulus under the pulsed gas injection condition. The cuttings particles are conveyed out within the wave-like moving cuttings bed. Compared with the constant-rate gas injection method, the pulsed gas injection method provides a much better cuttings transport efficiency at the identical condition of gas injection volume.

1 Introduction

Since the first air drilling operation was conducted in the early 1860s, the gas drilling has gradually been a popular alternative technique for drilling a well. Briefly, gas drilling, also known as the underbalanced drilling (UBD), is a technique to generate a pathway connecting the reservoir to the surface equipment, in which commonly compressed gases are applied to remove the cuttings and cool the bit instead of the conventionally used fluids. Over the past 70 years, several types of gas drilling have emerged with the advancement of the industry, such as mist drilling [1, 2], foam drilling [3, 4], and aerated drilling [5, 6]. In these methods, the compressed gases are injected into the well combined with the incompressible liquids, generally water, surfactants, and drilling muds. Due to the significantly increased viscosity of the mixture compared with the single gas phase, the gas injection rate or method becomes a less important parameter in cuttings transport. Therefore, the term of gas drilling in this work denotes only the drilling method using the compressed gas (air, nitrogen, or natural gas) as the sole circulating medium.

Gas drilling has many advantages, such as increasing the rate of penetration, reducing the formation damage (especially the water-sensitive formation), reducing the risk of lost circulation, and improving the drill bit life, etc. [7]. However, a major disadvantage of the gas drilling is the severe deposition of the drilled cuttings, especially in the horizontal gas drilling, which mainly caused by the poor transport capacity of the gas phase due to its low density and viscosity. Generally, the solution is increasing the gas injection rate. But if the gas injection rate is too high, the cost due to the higher gas injection volume and the investment of the surface equipment will increase accordingly. Besides, the high gas injection rate may cause ice-balling of the drill bit [8, 9]. On the contrary, a too low gas injection rate means a low cuttings transport efficiency, which may lead to a series of potential downhole problems, such as the dill pipe sticking and bore-hole instability.

To the best of our knowledge, most of the papers focus on the effects of the rate of penetration (ROP), drill pipe rotation speed, fluid flow rate, fluid viscosity, and cuttings sphericity, etc. on the cuttings transport efficiency [10,11,12,13]. The effects of different gas injection methods on the cuttings transport efficiency are seldom reported. In this paper, a pulsed gas injection method is proposed to overcome the shortcoming of the low cuttings transport efficiency in horizontal gas drilling. The pulsed gas injection method based on different pulse amplitudes and pulse repetition frequencies has the same gas injection volume with the constant-rate gas injection method, but has a wider velocity range due to the velocity fluctuation. The Eulerian-Eulerian two-fluid approach with the kinetic theory of granular flow is employed to simulate the gas-solid two-phase flow in a 3D eccentric horizontal annulus using CFD modelling. The RNG k-ε turbulence model is adopted to describe the turbulence behavior of the gas phase. The effects of various gas injection methods on the gas inlet velocity, pressure drop, cuttings volume fraction, granular temperature, turbulence kinetic energy, and turbulence dissipation rate are systematically investigated. The results can provide a reference for the petroleum engineers in using this pulsed gas injection method for horizontal gas drilling.

2 Mathematical Formulation

2.1 Continuity Equation

No mass exchange takes place between the gas and solid phase. Thus, the volume fraction of each phase can be obtained through the mass conservation equations as follows:

$$ \frac{\partial }{\partial t}\left( {\alpha_{g} \rho_{g} } \right) + \nabla \cdot \left( {\alpha_{g} \rho_{g} \vec{v}_{g} } \right) = 0 $$

(1)

$$ \frac{\partial }{\partial t}\left( {\alpha_{s} \rho_{s} } \right) + \nabla \cdot \left( {\alpha_{s} \rho_{s} \vec{v}_{s} } \right) = 0 $$

(2)

where $\alpha_{g}$ is the volume fraction of gas phase, $\alpha_{s}$ is the volume fraction of solid phase, $\rho_{g}$ is the gas phase density, $\rho_{s}$ is the solid phase density, $\vec{v}_{g}$ is the velocity of gas phase, and the $\vec{v}_{s}$ is the velocity of solid phase.

2.2 Momentum Equation

The added-mass force, lift force, Magnus force, Basset force, and Saffman force can be neglected in a gas-solid flow system. Consequently, the momentum conservation equations of the gas and solid phases can be described as follows:

$$ \frac{\partial }{\partial t}\left( {\alpha_{g} \rho_{g} \vec{v}_{g} } \right) + \nabla \cdot \left( {\alpha_{g} \rho_{g} \vec{v}_{g} \vec{v}_{g} } \right) = - \alpha_{g} \nabla p + \nabla \cdot \overline{\overline{\tau }}_{g} + \alpha_{g} \rho_{g} \vec{g} + K_{gs} \left( {\vec{v}_{g} - \vec{v}_{s} } \right) $$

(3)

$$ \frac{\partial }{\partial t}\left( {\alpha_{s} \rho_{s} \vec{v}_{s} } \right) + \nabla \cdot \left( {\alpha_{s} \rho_{s} \vec{v}_{s} \vec{v}_{s} } \right) = - \alpha_{s} \nabla p - \nabla p_{s} + \nabla \cdot \overline{\overline{\tau }}_{s} + \alpha_{s} \rho_{s} \vec{g} + K_{gs} \left( {\vec{v}_{g} - \vec{v}_{s} } \right) $$

(4)

where $p$ is the pressure shared by gas and solid phases, $p_{s}$ is the solids pressure, $\overline{\overline{\tau }}_{g}$ is the stress-strain tensor of gas phase, $\overline{\overline{\tau }}_{s}$ is the stress-strain tensor of solid phase, $\vec{g}$ is the acceleration due to gravity, and $K_{gs}$ is the gas-solid interphase momentum exchange coefficient. Here,

$$ \overline{\overline{\tau }}_{q} = \alpha_{q} \mu_{q} \left( {\nabla \vec{v}_{q} + \nabla \vec{v}_{q}^{T} } \right) + \alpha_{q} \left( {\lambda_{q} - \frac{2}{3}\mu_{q} } \right)\nabla \cdot \vec{v}_{q} \overline{\overline{I}} \, \left( {q = g,s} \right) $$

(5)

where $\lambda_{q}$ is the bulk viscosity of phase $q$, $\mu_{q}$ is the shear viscosity of phase $q$, and $\overline{\overline{I}}$ is the unit tensor.

2.3 Gas-Solid Exchange Coefficient

The Gidaspow model is employed to describe the gas-solid exchange coefficient:

$$ K_{gs} = \frac{3}{4}C_{D} \frac{{\alpha_{s} \alpha_{g} \rho_{g} \left| {\vec{v}_{s} - \vec{v}_{g} } \right|}}{{d_{s} }}\alpha_{g}^{ - 2.65} \,\,\left( {\alpha_{g} > 0.8} \right) $$

(6)

$$ K_{gs} = 150\frac{{\alpha_{s} \left( {1 - \alpha_{g} } \right)\mu_{g} }}{{\alpha_{g} d_{s}^{2} }} + 1.75\frac{{\rho_{g} \alpha_{s} \left| {\vec{v}_{s} - \vec{v}_{g} } \right|}}{{d_{s} }} \,\, \left( {\alpha_{g} \le 0.8} \right) $$

(7)

where $d_{s}$ is the diameter of solid particles, and $C_{D}$ is the drag function respect to the relative Reynolds number ($Re_{s}$).

$$ C_{D} = \frac{24}{{\alpha_{g} Re_{s} }}\left[ {1 + 0.15\left( {\alpha_{g} Re_{s} } \right)^{0.687} } \right] $$

(8)

$$ Re_{s} = \frac{{\rho_{g} d_{s} \left| {\vec{v}_{s} - \vec{v}_{g} } \right|}}{{\mu_{g} }} $$

(9)

2.4 Closure Model

In order to close the fundamental equations of mass and momentum conservation, several specific properties of the granular phase, such as the granular viscosity, granular bulk viscosity, granular temperature, solids pressure, and radial distribution, are required to be described mathematically.

The granular viscosity is expressed as given in [14] as:

$$ \mu_{s} = \frac{{10\rho_{s} d_{s} \sqrt {\varTheta_{s} \pi } }}{{96\alpha_{s} \left( {1 + e_{ss} } \right)g_{{_{0} ,ss}} }}\left[ {1 + \frac{4}{5}g_{{_{0} ,ss}} \alpha_{s} \left( {1 + e_{ss} } \right)} \right]^{2} $$

(10)

The granular bulk viscosity has the following form introduced by Lun et al. [15]:

$$ \lambda_{s} = \frac{4}{3}\alpha_{s}^{2} \rho_{s} d_{s} g_{{_{0} ,ss}} \left( {1 + e_{ss} } \right)\left( {\frac{{\varTheta_{s} }}{\pi }} \right)^{1/2} $$

(11)

The solids pressure is calculated as:

$$ p_{s} = \alpha_{s} \rho_{s} \varTheta_{s} + 2\rho_{s} \left( {1 + e_{ss} } \right)\alpha_{s}^{2} g_{{_{0} ,ss}} \varTheta_{s} $$

(12)

The radial distribution is defined as:

$$ g_{{_{0} ,ss}} = \left[ {1 - \left( {\frac{{\alpha_{s} }}{{\alpha_{s,max} }}} \right)^{{\frac{1}{3}}} } \right]^{ - 1} $$

(13)

where $e_{ss}$ is the restitution coefficient for the collisions between particles, and $e_{ss}$ = 0.9; $\alpha_{s,max}$ is the packing limit for the granular phase which is equal to 0.63. The granular temperature transport equation can be derived from the kinetic theory of granular flow:

$$ \frac{3}{2}\left[ {\frac{\partial }{\partial t}\left( {\alpha_{s} \rho_{s} \varTheta_{s} } \right) + \nabla \cdot \left( {\alpha_{s} \rho_{s} \vec{v}_{s} \varTheta_{s} } \right)} \right] = \left( { - p_{s} \overline{\overline{I}} + \overline{\overline{\tau }}_{s} } \right):\nabla \vec{v}_{s} + \nabla \cdot \left( {k_{{\varTheta_{s} }} \nabla \varTheta_{s} } \right) - \gamma_{{\varTheta_{s} }} + \varphi_{gs} $$

(14)

where $\left( { - p_{s} \overline{\overline{I}} + \overline{\overline{\tau }}_{s} } \right):\nabla \vec{v}_{s}$ is the generation of energy by the solid stress tensor, $k_{{\varTheta_{s} }} \nabla \varTheta_{s}$ is the diffusion of energy, $\gamma_{{\varTheta_{s} }}$ is the collisional dissipation of energy, and $\varphi_{gs}$ is the energy exchange between the gas and solid phase.

In this work, the granular temperature transport equation adopts a simplified algebraic form which neglects the convection and diffusion contributions as follows:

$$ 0 = \left( { - p_{s} \overline{\overline{I}} + \overline{\overline{\tau }}_{s} } \right):\nabla \vec{v}_{s} - \gamma_{{\varTheta_{s} }} + \varphi_{gs} $$

(15)

where,

$$ \gamma_{{\varTheta_{s} }} = \frac{{12\left( {1 - e_{ss}^{2} } \right)g_{0,ss} }}{{d_{s} \sqrt \pi }}\alpha_{s}^{2} \rho_{s} \varTheta_{s}^{3/2} $$

(16)

$$ \varphi_{gs} = - 3K_{gs} \varTheta_{s} $$

(17)

2.5 Turbulence Model

The RNG $k$-$\varepsilon$ model is used to characterize the turbulence kinetic energy ($k$) of the gas phase and its dissipation rate ($\varepsilon$) through the following transport equations:

$$ \frac{\partial }{\partial t}\left( {\rho_{g} k} \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho_{g} kv_{g}^{i} } \right) = \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{k} \mu_{g,eff} \frac{\partial k}{{\partial x_{j} }}} \right) + G_{k} - \rho_{g} \varepsilon $$

(18)

$$ \frac{\partial }{\partial t}\left( {\rho_{g} \varepsilon } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho_{g} \varepsilon v_{g}^{i} } \right) = \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{\varepsilon } \mu_{g,eff} \frac{\partial \varepsilon }{{\partial x_{j} }}} \right) + \frac{\varepsilon }{k}\left( {C_{1\varepsilon } G_{k} - C_{2\varepsilon } \rho_{g} \varepsilon } \right) - R_{\varepsilon } $$

(19)

where $\alpha_{k}$ and $\alpha_{\varepsilon }$ are the inverse effective Prandtl numbers for $k$ and $\varepsilon$, $\mu_{g,eff}$ is the effective viscosity of gas phase, $G_{k}$ is the generation of turbulence kinetic energy due to the mean velocity gradients, $R_{\varepsilon }$ is the rate of strain, and $C_{1\varepsilon }$ and $C_{2\varepsilon }$ are constants equal to 1.42 and 1.68, respectively. $\alpha_{k}$ and $\alpha_{\varepsilon }$ can be calculated from the following formula:

$$ \left| {\frac{\alpha - 1.3929}{{\alpha_{0} - 1.3929}}} \right|^{0.6321} \left| {\frac{\alpha + 2.3929}{{\alpha_{0} + 2.3929}}} \right|^{0.3679} = \frac{{\mu_{g} }}{{\mu_{g,eff} }} $$

(20)

where $\alpha_{0}$ = 1.0. In the low-Reynolds number limit, the effective viscosity of the gas phase ($\mu_{g,eff}$) is given by:

$$ d\left( {\frac{{\rho_{g}^{2} k}}{{\sqrt {\varepsilon \mu_{g} } }}} \right) = 1.72\frac{{\widehat{v}}}{{\sqrt {\widehat{v}^{3} - 1 + C_{v} } }}d\widehat{v} $$

(21)

where

$$ \widehat{v} = \frac{{\mu_{g,eff} }}{{\mu_{g} }} $$

(22)

$$ C_{v} \approx 100 $$

(23)

In the high-Reynolds number limit, the effective viscosity of the gas phase ($\mu_{g,eff}$) is calculated as:

$$ \mu_{g,eff} = \rho_{g} C_{\mu } \frac{{k^{2} }}{\varepsilon } $$

(24)

where $C_{\mu }$ = 0.0845. The term $G_{k}$ is defined as:

$$ G_{k} = - \rho_{g} \overline{{v_{g}^{i'} v_{g}^{j'} }} \frac{{\partial v_{g}^{j} }}{{\partial x_{i} }} $$

(25)

The rate of strain ($R_{\varepsilon }$) in the $\varepsilon$ equation is computed by:

$$ R_{\varepsilon } = \frac{{C_{\mu } \rho_{g} \eta^{3} \left( {1 - \eta /\eta_{{_{0} }} } \right)}}{{1 + \beta \eta^{3} }}\frac{{\varepsilon^{2} }}{k} $$

(26)

where $\eta_{0}$ = 4.38, $\beta$ = 0.012, and $\eta$ is expressed as:

$$ \eta = \frac{k}{\varepsilon }\left[ {\frac{{\partial v_{g}^{i} }}{{\partial x_{j} }}\left( {\frac{{\partial v_{g}^{i} }}{{\partial x_{j} }} + \frac{{\partial v_{g}^{j} }}{{\partial x_{i} }}} \right)} \right]^{1/2} $$

(27)

2.6 Initial and Boundary Conditions

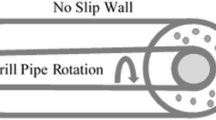
The physical model refers to a 3D horizontal eccentric annulus of 12 m in length as shown schematically in Fig. 1. The diameters of the wellbore and drill pipe are devised following the API standard, which are 244.5 and 127.0 mm, respectively. The drill pipe eccentricity is 0.5 with a rotation speed of 120 rpm. The drill cuttings particle has a diameter of 3 mm and density of 2600 kg/m³. The volume fraction of the injected cuttings is constant with the value of 0.03. Nitrogen is used as the drilling fluid and its velocity is a function of time, pulse amplitude, and pulse repetition frequency as follows:

Fig. 1.

Schematic of horizontal annulus.

$$ \mu_{g,in} = \mu_{i} + \mu_{A} sin\left( {2\pi ft} \right) $$

(28)

where $\mu_{g,in}$ is the nitrogen injection velocity, $\mu_{A}$ is the pulse amplitude, and $f$ is the pulse repetition frequency; $\mu_{i}$ = 20 m/s, $\mu_{A}$ = 2.5, 5, 10 m/s, and $f$ = 1.0, 2.0, 4.0 Hz.

At the walls of the wellbore and drill pipe, the no-slip boundary conditions are applied for the gas and solid phases. The restitution coefficient for the collisions between the cuttings particles is specified as 0.9.

2.7 Solution Procedure

In order to simulate the drill pipe rotation, the sliding mesh model is enabled for the drill pipe cell zone. The Phase Coupled SIMPLE (Semi-Implicit Method for Pressure Linked Equations), which is an extension of the SIMPLE algorithm [16], is adopted as the pressure-velocity coupling scheme. The QUICK (Quadratic Upstream Interpolation for Convective Kinematics) spatial discretization scheme is selected to solve all the convection-diffusion equations. A fixed time step of 5 × 10⁻⁴ s is used for the transient flow calculations which are performed for a time period of 50 s. The simulations are run on a high-performance computer with the 28-core Intel® Xeon® W-3175X processor (38.5 M Cache, 3.1 GHz) and 64 GB RAM.

3 Results and Discussion

3.1 Nitrogen Injection Velocity and Pressure Drop

Figure 2 shows the effect of gas injection method on the nitrogen inlet velocity and pressure drop. The constant-rate gas injection method has a gas inlet velocity of 20 m/s. The parameters of the gas inlet velocity of the pulsed gas injection method are composed of different pulse amplitudes ranged from 2.5 to 10 m/s and different pulse repetition frequencies ranged from 1.0 to 4.0 Hz. It is evident that the nitrogen inlet velocity and pressure drop oscillate in different sinusoidal waves based on various pulse amplitudes and pulse repetition frequencies. Moreover, the pressure drop across the annulus increases with the gas inlet velocity and decreases with the decrease of the gas inlet velocity. The cumulative gas injection volume is the integral of the flow rate (the product of the gas velocity and cross-sectional area) with respect to time. Consequently, the cumulative gas injection volumes are identical within the time of the integer multiple of one second during the multiphase flow processes of different gas injection methods. Compared with the constant-rate gas injection method, the pressure drop under the pulsed gas injection method can be divided into two portions. One is the high pressure drop section and the other is the low pressure drop section. This can be attributed to the fluctuation of the frictional resistance which caused by the gas velocity variation and its induced changes in the cuttings volume fraction. Hence, the pulsed gas injection method certainly will contribute the improvement of the cuttings transport efficiency under the same condition of gas injection volume.

Fig. 2.

Profiles of nitrogen injection velocity and pressure drop.

3.2 Cuttings Volume Fraction

Cuttings transport efficiency can be quantitatively characterized by the cuttings volume fraction within the annulus of the wellbore during the drilling operation. Briefly, the lower the concentration of the drilled cuttings, the higher the cuttings transport efficiency is. Figure 3 illustrates the cuttings volume fraction as a function of time under different methods of gas injection. The constant-rate gas injection method has a gas inlet velocity of 20 m/s. The parameters of the gas inlet velocity of the pulsed gas injection method are composed of different pulse amplitudes ranged from 2.5 to 10 m/s and different pulse repetition frequencies ranged from 1.0 to 4.0 Hz. It is obvious that the cuttings volume fraction under the pulsed gas injection method is lower than that using the constant-rate gas injection method. As the pulse amplitude increases from 2.5 to 10 m/s, the average cuttings volume fraction drastically decreases from 0.0635 to 0.0462. Additionally, increasing the pulse repetition frequency from 2.0 to 4.0 Hz leads to a further reduction of the average cuttings volume fraction from 0.0462 to 0.0433. That is to say, the higher pulse amplitude and pulse repetition frequency produce a better cuttings transport efficiency. Figure 4 shows the effect of pulse amplitude and pulse repetition frequency on the average cuttings volume fraction under the pulsed gas injection method. The fit lines demonstrate that the reduction extent of the average cuttings volume fraction increases with the pulse amplitude and decreases with the increase of the pulse repetition frequency. Therefore, the magnitude of the pulse amplitude is the dominant factor in the enhancement of the cuttings transport efficiency utilizing the pulsed gas injection method.

Fig. 3.

Effect of gas injection method on cuttings volume fraction.

Fig. 4.

Effect of pulse amplitude and pulse repetition frequency on average cuttings volume fraction under pulsed gas injection method.

Figures 5 and 6 are the contour plots of the distribution of the cuttings volume fraction at the outlet of the eccentric horizontal annulus under different gas injection methods. The gas inlet velocity of the constant-rate gas injection method is equal to 20 m/s. The parameters of the gas inlet velocity of the pulsed gas injection method contain different pulse amplitudes ranged from 2.5 to 10 m/s with a fixed pulse repetition frequency equal to 2.0 Hz, or different pulse repetition frequencies ranged from 1.0 to 4.0 Hz with a fixed pulse amplitude equal to 10 m/s. It can be intuitively discerned by the chromatism in the contour plots that the thickness and width of the cuttings bed significantly decrease with the increase of the pulse amplitude and pulse repetition frequency. Figure 7 depicts the axial distribution of the drilled cuttings in the eccentric horizontal annulus under different gas injection methods. A gas inlet velocity of 20 m/s is used in the constant-rate gas injection method. Meanwhile, a pulse amplitude of 10 m/s and a pulse repetition frequency of 2.0 Hz are employed in the pulsed gas injection method. In the conventional horizontal gas drilling operation using the constant-rate gas injection method, the drilled cuttings will gradually deposit on the bottom of the wellbore inevitably, as seen in the left panel of Fig. 7. As the drilling process proceeds further, the cuttings will tend to densely deposit together and irreversibly form a stationary cuttings bed beneath the moving cuttings bed. The cuttings in the stationary cuttings bed can hardly be conveyed out. A series of potential downhole problems, such as the dill pipe sticking and borehole instability, may occur accordingly. However, as shown in the right panel of Fig. 7, there almost no stationary cuttings bed exists in the horizontal annulus while utilizing the pulsed gas injection method. Besides, a wave-like moving cuttings bed can be seen in the annulus. The reason can be attributed to the fact that the drilled cuttings particles are more energetic under the pulsed gas injection condition, which can prevent the cuttings from depositing. As a result, only very few cuttings particles are settled, and most of the drilled cuttings will move forward in a pulsed way (wave-like). In view of the above considerations, the pulsed gas injection method will substantially reduce the cuttings concentration in the annulus during horizontal gas drilling process. Compared with the constant-rate gas injection method, the pulsed gas injection method provides a much better cuttings transport efficiency.

Fig. 5.

Contour plots of cuttings volume fraction at outlet of annulus (t = 40 s) using a constant-rate gas injection method (μ_g,in = 20 m/s) and pulsed gas injection method with different pulse amplitudes: b 2.5 m/s, c 5 m/s, and d 10 m/s (f = 2.0 Hz).

Fig. 6.

Contour plots of cuttings volume fraction at outlet of annulus (t = 40 s) using a constant-rate gas injection method (μ_g,in = 20 m/s) and pulsed gas injection method with different pulse repetition frequencies: b 1.0 Hz, c 2.0 Hz, and d 4.0 Hz (μ_A = 10 m/s).

Fig. 7.

Axial distribution of drilled cuttings in horizontal annulus under different gas injection methods (t = 40 s).

3.3 Granular Temperature, Turbulence Kinetic Energy, and Turbulence Dissipation Rate

Table 1 gives the effect of different gas injection methods on the average granular temperature, turbulence kinetic energy, and turbulence dissipation rate. The gas inlet velocity of the constant-rate gas injection method is equal to 20 m/s. The parameters of the gas inlet velocity of the pulsed gas injection method contain different pulse amplitudes ranged from 2.5 to 10 m/s with a fixed pulse repetition frequency equal to 2.0 Hz, or different pulse repetition frequencies ranged from 2.0 to 4.0 Hz with a fixed pulse amplitude equal to 10 m/s. It is apparent that the average granular temperature under the pulsed gas injection method is higher than that under the constant-rate gas injection method. With the pulse amplitude increasing from 2.5 to 10 m/s, the average granular temperature increases from 0.0429 to 0.0440 m²/s². Moreover, with the pulse repetition frequency increasing from 2.0 to 4.0 Hz, the average granular temperature further increases from 0.0440 to 0.0483 m²/s². The granular temperature is proportional to the kinetic energy of the random motion of the drilled cuttings particles [17]. During the gas drilling procedure using the pulsed gas injection method, most of the cuttings transport in a wave-like pattern, as indicated in the preceding subsection (Fig. 7). The more flowing cuttings particles can remarkably increase the number of the collisions between the particles and thus their random-motion kinetic energy. Therefore, the average granular temperature of the whole annulus will be increased accordingly.

Table 1. Effect of gas injection method on average granular temperature, turbulence kinetic energy, and turbulence dissipation rate (en dash means using constant-rate gas injection method).

As present in Table 1, obviously, the average turbulence kinetic energy and turbulence dissipation rate are also higher under the pulsed gas injection condition than that under the constant-rate gas injection condition. As the pulse amplitude alters from 2.5 to 10 m/s, the average turbulence kinetic energy increases from 15.469 to 19.449 m²/s², and the average turbulence dissipation rate increases from 17249 to 29757 m²/s³. Additionally, as the pulse repetition frequency changes from 2.0 to 4.0 Hz, the average turbulence kinetic energy further increases from 19.449 to 19.739 m²/s². However, the average turbulence dissipation rate decreases from 29757 to 21641 m²/s³. The turbulence dissipation rate is the rate at which the turbulence kinetic energy cascades down from larger to smaller eddies until it is ultimately converted into heat due to viscous forces. In the case of gas drilling, the higher average turbulence dissipation rate denotes that the gas-solid mixture has a better mixing characteristic which benefits to the cuttings transport. Meanwhile, the higher average turbulence dissipation rate also indicates a higher energy transmission efficiency from the pulse generator to the cuttings conveyance. On the contrary, the low average turbulence dissipation rate stands for a poor mixing of the two phases and a low energy transmission efficiency. This can explain why the gradient of the reduction in cuttings volume fraction descends with the increase of the pulse repetition frequency (Fig. 4). Hence, one can infer that the pulse repetition frequency of the pulsed gas injection method should not be too high.

4 Conclusion

In this work, a numerical model is developed for the simulation of the cuttings transport in a 3D eccentric horizontal annulus during the gas drilling process. The effects of different gas injection methods on the gas inlet velocity, pressure drop, cuttings volume fraction, granular temperature, turbulence kinetic energy, and turbulence dissipation rate are systematically investigated. These following conclusions are derived from the data and results in the present research. (1) The cuttings volume fraction under the pulsed gas injection method is lower than that under the constant-rate gas injection method. (2) The higher the pulse amplitude and pulse repetition frequency, the lower the cuttings volume fraction is. Nevertheless, the pulse repetition frequency should not be too high, which may result in the poor mixing of the gas-solid mixture and the low energy transmission efficiency. (3) Almost no stationary cuttings bed is found under the pulsed gas injection condition, the cuttings particles are conveyed out within the wave-like moving cuttings bed. (4) Compared with the constant-rate gas injection method, the pulsed gas injection method provides a much better cuttings transport efficiency at the same condition of the gas injection volume.