Ensemble Kalman Filter Optimizing Deep Neural Networks: An Alternative Approach to Non-performing Gradient Descent

Abstract

The successful training of deep neural networks is dependent on initialization schemes and choice of activation functions. Non-optimally chosen parameter settings lead to the known problem of exploding or vanishing gradients. This issue occurs when gradient descent and backpropagation are applied. For this setting the Ensemble Kalman Filter (EnKF) can be used as an alternative optimizer when training neural networks. The EnKF does not require the explicit calculation of gradients or adjoints and we show this resolves the exploding and vanishing gradient problem. We analyze different parameter initializations, propose a dynamic change in ensembles and compare results to established methods.

1 Introduction

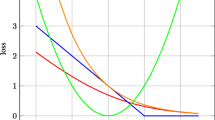
The performance of deep multilayered neural networks is very susceptible to the initialization of weights and the selected activation functions [10, 31]. For example, non-optimally chosen parameters in the initialization stage may lead to a loss of input information in the feed-forward step or to the well known problem of exploding and vanishing gradients during the backpropgation phase [2, 3, 13, 29]. An example of this problem is illustrated in Fig. 1, which depicts the test error of a convolutional network trained for 10 epochs on the MNIST dataset (see Sect. 2.2 for details). The figure shows that, if the initialization is not done in an optimal way, the stochastic gradient descent (SGD) algorithm is not able to train the network. Further, training with ADAM [17] is heavily slowed down depending on the choice of the algorithmic parameters (c.f. Sects. 3.1 and 3.2). The vanishing gradient problem has been explored analytically in detail [9, 24, 26]. Although substantial work has been done regarding activation functions and initializations, most of the studies investigate the problems using gradient descent and backpropagation as optimization procedure. The aforementioned drawbacks are related to gradients obtained within deep neuronal networks [13].

Fig. 1.

Mean test error (dark line) of the network in % for 10 runs trained for one epoch using different optimizers. The shaded area is the standard deviation of the runs. The standard deviation of the normal distribution when initializing the weights is set as $\sigma = 1$. The test is performed on a separate test dataset while the training is ongoing.

Since, in general, optimal parameters can only be determined by successive testing, we are interested in alternative robust numerical methods for training deep neural networks. Hence, in this work we utilize a method that does not rely on gradient information (see Fig. 1). An advantage of this approach is that it also allows for non differentiable activation functions without introducing additional smoothing.

Dealing with Non Differentiability and the Vanishing Gradient Problem. Many of the recent approaches for training deep networks counteract against non differentiability by applying smoothing to the rectified linear unit (ReLU) [22], e.g. the exponential linear unit (ELU) [5]. This may also lead to numerical instability due to possible singular limits for small smoothing parameters. Other approaches have been suggested to circumvent the problem observed in Fig. 1. In particular, different initialization schemes like the Xavier [30] or Kaiming-initialization [11]. The latter incorporates the number of incoming or outgoing connections to or from the neurons of the next or previous layer, to stabilize the training by normalizing the weights. Sussillo and Abbott [28] showed that gradients scale only as the square root of the depth of the network. Based on this observation they proposed a heuristic for initializing networks with a procedure called Random Walk Initialization. They observe satisfactory performance under those modifications.

The role of the activation function and its properties have been investigated with regards to their influence on the training procedure. Lecun et al. [19] discuss that the logistic function will slow down training since it induces a slower convergence. Based on [19] Glorot et al. [30] investigate the selection of activation functions regarding the saturation of the gradients. Many studies remark the logistic function is not suitable for training deep networks [19, 24, 30].

In this paper we investigate the problem of training neural networks within ill-conditioned settings. Our starting point is that a possible explanation of the difficulties of the previous methods when training the networks could be related to the dependence on explicit gradient information. To diminish this dependence we explore the effects of using a particle based method, in particular, the Ensemble Kalman Filter (EnKF). The EnKF has been widely studied in engineering literature [1, 7, 15, 27] as well as recently in the mathematical community [12, 25]. We refer to [16] for a comprehensible introduction and [6, 14] for more details on the method. However, it has only been recently shown that EnKF could also be applied to solve inverse problems and we formulate the training procedure as such a problem. The EnKF does not require to calculate gradients explicitly and omits the backpropagation step. Furthermore, this method does not require a particular form of the activation function. We follow the formulation of the EnKF proposed in [14]. In contrast to previous work having a similar setting such as in [8, 18] we emphasize that the scope of our contribution does not focus on achieving high benchmark performance on the investigated datasets. Instead, our objective is to provide an analysis based on numerical solutions regarding the ability of the EnKF to cope with problems where gradient based algorithms fail, are very sensitive to initial conditions or provide a poor performance in general.

Among other results, we show that a classification problem can be solved using the EnKF as an optimizer, the logistic function as activation function and a normal distributed initialization of the weights. The method is shown to be independent to different realizations when initializing the weights. In contrast, the same network is not able to achieve sufficient performance in the task when optimized by SGD as indicated in Fig. 1. Since the EnKFdepends among other parameters on the chosen number of ensembles we propose a dynamic adaption of algorithmic parameters depending on the reached training accuracy indicated in Algorithm 1 and with corresponding results presented in Fig. 10.

2 Ensemble Kalman Filter Optimizing Neural Networks

The EnKF is a well-known iterative numerical method for nonlinear dynamic filtering problems under noise and has been applied more recently to inverse problems [25] as well. The parameter estimation problem is a particular inverse problem and we apply the EnKF here. When training a deep neural network only the evaluation of the feed-forward propagation is required, thus omitting the backpropagation. Further, the EnKF is easily parallelizable in contrast to gradient based approaches. First results on training deep neural networks and recurrent neural networks with the EnKF can be found in [18, 21].

2.1 Description and Properties of the Ensemble Kalman Filter

Training a neural network to learn its weights and biases can be formulated as an optimization problem. Kovachki et al. [18] describe the training as a minimization problem for $\varPhi$ given by

$$\begin{aligned} \varPhi (\mathbf {u},\mathbf {y}) = \left\| \mathcal {G}(\mathbf {u}) - \mathbf {y} \right\| ^{2}_{\varGamma } \end{aligned}$$

(1)

where $\mathcal {G}(\mathbf {u})$ is the model output and $\mathbf {y}$ is the target or label to optimize for.

We introduce briefly the EnKF following the formulation from [14]:

$$\begin{aligned} \mathbf {u}_j^{n+1} = \mathbf {u}_j^{n}+\mathbf {C}(\mathbf {U}^{n})\left( \mathbf {D}(\mathbf {U}^n) + \varvec{\varGamma }^{-1}\right) ^{-1} \left( \mathbf {y} - \mathcal {G}(\mathbf {u}_j^{n})\right) \end{aligned}$$

(2)

where $\mathbf {U}^n = \{\mathbf {u}_j^n\}_{j=1}^{J}$ is the set of all ensembles, n is the iteration index, J is number of ensembles. In our setting, the ensemble $\mathbf {u}_j$ corresponds to the weights of the network (c.f. Sect. 2.2). $\varvec{\varGamma }$ is the covariance matrix related to the measurement of noise, in our case we use $\varvec{\varGamma }$ as an identity matrix multiplied with a small scalar, i.e. $\varvec{\varGamma } = \gamma \mathbf {I}$. The hyper-parameters $J, \gamma , \text {and } n$ are the only hyper-parameters of the EnKF.

The matrices $\mathbf {C}(\mathbf {U}^n)$ and $\mathbf {D}(\mathbf {U}^n)$ are covariance matrices defined by:

$$\begin{aligned} \begin{gathered} \mathbf {C}(\mathbf {U}) = \dfrac{1}{J} \displaystyle \sum _{j=1}^{J}(\mathbf {u}_j - \mathbf {\overline{u}}) \otimes (\mathcal {G}(\mathbf {u}_j) - \mathcal {\overline{G}})^{T},\\ \mathbf {D}(\mathbf {U}) = \dfrac{1}{J} \displaystyle \sum _{j=1}^{J} \left( \mathcal {G}(\mathbf {u}_j\right) - \mathcal {\overline{G}})\otimes \big (\mathcal {G}(\mathbf {u}_j) - \mathcal {\overline{G}}\big )^{T}, \\ \mathbf {\overline{u}} = \dfrac{1}{J} \displaystyle \sum _{j=1}^{J}\mathbf {u}_j, \mathcal {\overline{G}} = \dfrac{1}{J} \displaystyle \sum _{j=1}^{J} \mathcal {G}(\mathbf {u}_j) \end{gathered} \end{aligned}$$

(3)

where $\otimes$ is the tensor-product. In [18] it was shown that under simplifed assumptions we have $\mathbf {\overline{u}^{\star }} =\text {arg min}(\varPhi (\mathbf {u},\mathbf {y}))$ and $\frac{1}{N}\sum _{j=1}^J \mathbf {u}_j^n \xrightarrow {n \rightarrow \infty } \mathbf {\overline{u}}^*$.

2.2 Experimental Setup

In this section we present the network architecture and the training procedure for the Ensemble Kalman Filter and the backpropagation optimizers. All simulations were performed on a compute node with a NVIDIA Tesla K20c graphic cards, Intel i7-4770 CPU and Scientific Linux 7.4 as an operating system.

Network Architecture. The network (see also Fig. 2) we use in all of our experiments consists of two convolutional layers and a fully connected layer and the logistic function ($f(x) = 1/(1+ e^{-x})$) applied on the output of the convolutional layers. The kernel size of the convolution for both layers is $5 \times 5$ with stride 1. Max pooling is applied on both convolutional layers with a kernel size of 2 and a stride of 2. The implementation is done with the PyTorch¹ [23] library.

Fig. 2.

Workflow depicting a training phase of a convolutional network optimized by an Ensemble Kalman Filter using adaptive choice of EnKF parameters.

Training with the Ensemble Kalman Filter. The training of the Convolutional Neural Network using the EnKF is shown in Fig. 2 as a workflow². The experiments have been designed using the MNIST dataset [20]. In Sect. 3.3 we show classification results obtained on the letter dataset [4]. First we initialize the biases to be 0 and the weights $\mathbf {W}=(W_{i,k})_{i,k}$ for each layer as

$$\begin{aligned} W_{i,k} \sim \mathcal {N} (\mu , \sigma ^2) \end{aligned}$$

(4)

with $\mu =0, \,\sigma \in [0.01, 10]$, where $\mathcal {N}$ is the normal distribution with mean $\mu$ and variance $\sigma .$

The initialization $n=0$ and $\mathbf {u}_j^0$ is done J times, i.e. a single member j of the ensemble $\mathbf {u}_j$ corresponds to a random weight matrix $\mathbf {W}$ according to the normal distribution $\mathcal {N} (\mu , \sigma ^2).$ This matrix is assigned to the ensemble $\mathbf {u}^0_j := \mathbf {W} \in \mathbb {R}^{\text {layer}\times \text {weights}}$ for $j=1,\ldots ,J$. After that $\mathbf {u}_j^n$ for $n>0$ is obtained by the iterative Formula (2). We choose $J=5000$ ensembles as a basis. Different settings are discussed in Sect. 3. Additionally, the EnKF Formula (2) requires the model outputs $\mathcal {G}(\mathbf {u})$, i.e. the feed-forward network output. Thus, for J iterations we initialize the j-th ensemble as weights for the network and apply one classification step for a given mini-batch of size 64. The scaling factor $\gamma$ is set constant for all experiments, $\gamma =0.01$.

The output of the network and the targets are fed into the iterative EnKF update formula, where a new set of ensembles J is calculated according to Eq. (2). We observed that a repetitive presentation of the images before switching to new samples helped the network to converge faster and reach a better performance. We verified the number of repeated presentations required to reach a high accuracy on the training mini-batch was 8 repetitions. This number can be set less or omitted after 500 iterations when a high test accuracy is reached (see Fig. 8). Every 500th iterations, after the training is completed, we obtain the test errors. We initialize one network by setting the weights of the network with the mean vector $\overline{\mathbf {u}}$ of the ensembles. A test set of data images with corresponding targets are forwarded as the input to the network and the classification error is evaluated. We also extended the setting with an adaptive mechanism to change the number of ensembles, iterations and repetitions depending on the test accuracy. For details we refer to Sect. 3.3.

Training with Backpropagation. Backpropagation is performed using SGD or ADAM on mini-batches of size 64. The training is completed using a similar strategy as described for the EnKF. The loss is calculated using the Cross Entropy Loss³, which is a combination of the negative log-likelihood and log softmax applied on the model output $\mathbf {z}_j = \mathcal {G}(\mathbf {u}_j)$, i.e.

$$\begin{aligned} \sigma (\mathbf {z}_j) = -\log \left( \frac{e^{z_j}}{\sum _i{e^{z_i}}} \right) . \end{aligned}$$

(5)

Note that, if the network is optimized using SGD no learning effect or improvement can be observed for longer runs (c.f. Sect. 3.1).

3 Numerical Results

In this section we discuss how gradients and activation values vanish or saturate by initialization schemes described in Sect. 2.2 with focus on SGD and ADAM. Afterwards we show that different sigmoidal activation functions (Logistic function, ReLU, Tanh) and variying number of ensembles influence the performance of the EnKF on the basis of the test error. Furthermore, we present results obtained when training the network on the letters dataset [4].

3.1 Non Evolving Gradients and Activation Values with SGD

When SGD is applied as an optimizer in our experimental setting (see Sect. 2.2) the units saturate in the early training phase and they cannot recover, as it can be observed from Fig. 3 (left). Here, the evolution of the mean (dark blue, orange and green lines) and standard deviation (light blue, orange and green vertical bars) of the activation values obtained after the logistic function on the hidden layer are shown over all mini-batch iterations. For layer 1 and 2 the activation values saturate close to 200 iterations, with mean activation value of layer 1 of 0.4597, standard deviation of 0.2976 and a value for the mean activation of layer 2 of 0.3178 and 0.4624 standard deviation. The mean activation value in layer 3 (0.1) stays constant from the first iteration on and has a standard deviation of 0.2908. Saturation is clearly reflected in the gradients as depicted in Fig. 3 (right). The distribution shows that after 800 mini-batch iterations the distribution didn’t change and the mean of the gradients is close to zero, confirming saturated gradients.

Fig. 3.

Left: Mean and standard deviation of the activation values during training for the three hidden layers of the network. SGD is applied as optimizer. Note: only every 8th entry is shown. Right: normalized histogram depicting a distribution of the gradients with a mean value of 0 for all three layers. Iterations are one epoch run with a mini-batch size of 64.

If the training is run for more epochs (e.g. 50 epochs) the network is still not able to learn. This is depicted in Fig. 4 (left) where the gradients stay at zero mean for all three layers. Only layer 3 has an oscillating standard deviation around the value 0.1. The same situation is presented for the activation functions as it can be seen in Fig. 4, in which the distribution of the mean activation is depicted. For layer 1 there is a very small shift of the mean from 0.475 towards 0.5, but the values of the other layers still do not change.

Fig. 4.

Left: Mean (blue, orange and green lines) and standard deviation (blue, orange and green vertical bars) of the backpropagated gradients for all three layers for 50 epochs. Right: Mean distributions of activation values over 50 epochs for all three layers using SGD as optimizer. (Color figure online)

Fig. 5.

Test error of the network trained for 50 epochs on the MNIST dataset. Different values for the standard deviation $\sigma$ are used when initializing the weights.

3.2 Slowly Evolving Gradients and Activation Values with ADAM

In our experiments we observe that ADAM is more robust when optimizing the network compared to SGD in terms of performance. When the weights are initialized with $\sigma =1$ the network will slowly start to correctly classify the dataset. Within 10 epochs it reaches more than 95% of test accuracy (see also Fig. 5). When fixing $\sigma = 3$ a similar behavior to the SGD setting is observable in the first epochs (c.f. Fig. 5). When looking at the mean and standard deviation of the activation values within in the first epoch a fast saturation is not observed for layer 1 (c.f. Fig. 6 (left)). We see an increase of the mean value of the activation values from 0.49 up to 0.53 (overall mean value of 0.5124), with standard deviation of 0.2860. This indicates a slow saturation in the longer run, which can be verified by analyzing layer 2. Layer 2 also increases it’s mean activation value (0.47) from the first iteration to the value 0.5, but stagnates at around the 400th iteration with a value of 0.5 (overall mean is 0.4957, standard deviation is 0.4965). The mean value of layer 3 stays constant at 0.1.

Fig. 6.

Left: Mean (dark blue, orange and green lines) and standard deviation (light blue, orange and green vertical bars) of the activation values during training for the three hidden layers of the network in one epoch. ADAM is applied as optimizer. Right: Normalized histogram depicting a distribution of the gradients with a mean value of 0 for all three layers. Iterations are one epoch run with a mini-batch size of 64. (Color figure online)

Fig. 7.

Left: Mean (line) and standard deviation (vertical bar) of the backpropagated gradients for all three layers for 50 epochs. Right: Mean distributions of activation values over 50 epochs for all three layers using ADAM as optimizer.

Figure 7 (left) shows the progress of the mean activation values over 50 epochs. An acceptable learning performance with regards to the test accuracy is achieved after 30 epochs. This is reflected especially in layer 1: here, we observe how the mean evolves over the epochs. While in epoch 1 the distribution is around 0.49, we can see after 40 epochs that the distribution evolves around 0.56. On the other hand the distribution of the activation values of layer 2 and 3 stay constant (around 0.5 and 0.0). The mean distribution of gradients obtained by backpropagation after one epoch is close to zero for all layers as one can observe in Fig. 6 (right). However, in the long run (i.e. after 30 epochs) the network starts to perform better (up to 84% accuracy). In Fig. 7 (left) the mean and standard deviations of the backpropagated gradients in layer 1 and layer 2 do not vary strongly up to epoch 10. Until then, the network shows no learning capability (test accuracy under 10%). Mean values in the first epochs for layer 1 are between $-0.3$ and 0.2 and standard deviations are between $-0.8$ and 0.6 showing a decreasing trend. For layer 2 mean values are between $-0.1$ and 0.1 and standard deviations are between $-0.2$ and 0.2. From epoch 10 up to epoch 28 both mean and standard deviation of layer 1 and 2 decrease and stay constant close to zero for both values. After the 28th epoch the network starts to learn. An increase and a small variance in the mean and standard deviations of both layers 1 and 2 can be observed again (layer 1 means in $[-0.02, 0.02]$, standard deviations in $[-0.01, 0.06]$; layer 2 means in $[-0.01, 0.01]$, standard deviation in $[-0.01, 0.03]$). The mean activation value of layer 3 stays constant in all iterations at a very small value close to zero, in contrast to the standard deviation which starts in the first epoch at 0.16 and decreases to 0.01. We offer the following interpretation. First, this shows that a network can recover from the saturation of its gradients given enough time to train. Secondly, a good performance shows that the network converges to a suitable classification with high accuracy only for suitable initial settings.

3.3 Performance of the Ensemble Kalman Filter

Given the same setup using the Ensemble Kalman Filter enables the network to perform well (see Figs. 8 and 9). After the first epoch the network has a test error of 3.8% when classifying the MNIST dataset. In the following we analyze in detail the performance with varying number of ensembles and its sensitivity to different activation functions.

Fig. 8.

Left: Test error during training on the MNIST dataset for different activation functions optimized by EnKF. Right: Test error during training on the MNIST dataset for different ensemble sizes within one epoch. Every 500th iteration is shown.

Different Activation Functions. We investigated the network training for different activation functions such as ReLU: $\text {ReLU}(x) = \max (0,x)$, Tanh: $\text {tanh}(x)=\dfrac{e^x - e^{-x}}{e^x + e^{-x}}$ and a Logistic Function: $f(x) = \dfrac{1}{1+ e^{-x}}$. Figure 8 (left) depicts the test errors in % using different activation functions over iterations. The test errors do not change strongly when ReLU or Logistic Function as activation functions are applied. There is a small gap of 0.45% error after the 500th iteration (test errors with Logistic Function: 6.11%, ReLU: 6.56%). The test error after one epoch is 3.8% when Logistic Function is applied and 3.75% for ReLU. If Tanh is used as activation function the performance is slightly worse, in the 500th iteration the error is at 8.15%, while after 7500 iterations it is 4.51%. The discrepancy may be induced because of the range of the Tanh function which is in $[-1, 1]$, whereas the images are normalized between [0, 1] (c.f. [19]). Due to the fast convergence the EnKF reaches a suitable accuracy already after 500 iterations. This behavior results in a slower improvement of the accuracy between the 500th and the 7500th iteration, approximately 3%.

EnKF-NN Training on Letters Dataset. Figure 9 presents the test error on the letters dataset using the EnKF optimizer. The parameter-setting is the same as in Sect. 2.2. We use 5000 and 10000 ensembles during the training. We observe a higher number of ensembles achieves a slightly better classification with a test error 15.1% within one epoch. With 5000 ensembles the test error is at 16.32%. We can conclude that a higher number of ensembles enables a better performance but is not necessarily an overall solution to increase the accuracy. To this point we didn’t test if there is a smaller ensemble size than 10000 which achieves the same error rate.

Fig. 9.

Test error during training on the letters dataset for different ensemble sizes within one epoch. Every 500th iteration is shown.

A hyperparameter for the EnKF is the number of ensembles. The convergence behavior of the EnKF is strongly influenced by this value. The test error for a different number of ensembles is depicted in Fig. 8 (right). A small size of a few hundred ensembles is not sufficient to optimize the network to perform with a suitable accuracy. Here, the test error stagnates around 47% which is just above chance level when classifying the test dataset. In contrast, a higher number of ensembles, e.g. 5000 ensembles, is sufficient to achieve a good performance on the test set. The test error after 7500 iterations is at 3.8%. Having even more ensembles decreases the test error slightly, e.g. with 10000 ensembles the error drops to 3%.

Adaptive Changes. The results of the previous sections indicate a possible reduction of ensembles, repetitions and iterations. To achieve these reductions we implemented an adaptive mechanism. The main idea is based on comparing the actual with the previous test accuracy ($t_n, t_{n-1}$) and deciding to change if the number stay in given upper and lower boundaries ($b_u, b_l)$. The algorithm is outlined in Algorithm 1.

Fig. 10.

Two runs on the MNIST dataset with (adaptive, orange graphs) and without (fixed, blue graphs) adaptive changes. In the adaptive setting, every 500 iteration the values of the parameters required by the EnKF are dynamically changed depending on the test errors. (Color figure online)

Figure 10 depicts two runs of the EnKF optimization on the MNIST dataset with the adaptive change (orange graphs, “adaptive”) and without (blue graphs, “fixed”). The fixed run follows the setting described in Sect. 2.2 and e.g. conducted for Fig. 8, the values of the parameters are fixed. The test error is shown on the left y-Axis and the number of ensembles and repetitions are on the right y-Axes. In every 500th iteration $\tau$ the test errors are evaluated and changes can be applied if $t_n < 10\%$. The test error of the fixed run is shown up to iteration 2500 as by then one epoch is reached with the adaptive setting. We observed that the adaptive changes (Fig. 10 left, orange line with dots) do not increase the test error while they reach the same accuracy as the fixed run (blue line with dots). Due to the fast convergence of the EnKF we were able decrease the repetitions r (Fig. 10 right, orange line with stars) by 1 in every 500th iteration. Additionally, we noticed that more repetitions do not increase the performance after a few iterations and after a satisfactory test accuracy is reached. After 1500 iterations the number of ensembles N (orange line with squares) are decreased by $\upsilon = 1000$. We were rather conservative by slowly increasing or decreasing all numbers. We decreased for instance the number of ensembles only by $\upsilon = 1000$ and not e.g. by half to ensure smaller changes and stability. The lower bound $b_l$ is set to minimal number of 1000 ensembles and the upper bound $b_u$is set to a maximal number of 10000 ensembles. For the same reasons we required that in order to decrease the values the test error has to be equal or less than $\kappa =1$ between the actual and previous test errors. This restrictive behavior causes the slow decrease of the number of ensembles after 1500 iterations. Since there was no increase in the test error an increase of the values did not occur.

4 Conclusions and Outlook

Network performance is susceptible to weight initialization and proper selection of activation functions. Improperly selected parameters cause the vanishing gradient problem especially when training with gradient descent and backpropagation. We have shown in Sect. 3 that also simple deep networks are affected by this problem. For a better understanding we investigated how gradients and activation function values vanish or saturate by analysing their distributions, mean and standard deviation per layer over iterations and epochs for different parameters. Our setting focused on SGD and ADAM as optimizers, random normal distributed weight initializations and the logistic function as activation function. The network was not able to learn or only very slowly on the MNIST classification task. In our experiments ADAM was more robust in contrast to SGD and performed better for different parameter settings. As an alternative to backpropagation we analyzed the use of the Ensemble Kalman Filter (EnKF), which omits the calculation of gradients and only requires the feed-forward step in the training phase.

Given the same settings, the EnKF is able to optimize the network on the MNIST and letters datasets and achieve a performance above 96% and 85%. We investigated the activation values of different network layers by analyzing the distribution, mean and standard deviations over several iterations within one epoch. Further, we experimented with the number of ensembles and concluded that a larger ensemble size does not necessarily give a significant better performance as one could expect (Sect. 3.3). Additionally, we investigated how different initializations of the weights influence the overall learning performance. Our study didn’t focus on reaching state of the art classification accuracy. Regarding solely the classification performance we refer to  [8, 18]. Due to the fast convergence of the EnKF the network was able to perform on the MNIST dataset already after 500 iterations. The fast convergence on the other hand may be problematic if the method is stuck in a local minimum and exploration of other possible minima is desirable. To counteract this issue it is possible to add noise to the ensembles in every update step as it was suggested in [18]. Another approach would be to adapt the scaling $\gamma$ of the covariance matrix $\mathbf {\varGamma }$ dynamically (see Eq. 3). To dynamically change the number of iterations, repetitions and ensembles we extended the setting with an adaptive algorithm to modify parameters depending on the test errors.

Our approach provides an alternative to optimization of multilayered neural networks which can overcome the problems introduced by different activation functions and initialization settings. This opens new avenues in research of the benefits of using these activation functions and initializations. It also provides a basis for new research on gradient free alternatives to optimize learning in neural networks.

In training neural networks there is a large number of variables which can affect the results. In our work we have chosen a narrow set of parameters to explore, while leaving everything else fixed. This approach allows us to control the conclusions we draw from these experiments. We consider our work a first step into exploring setups where using the EnKF can be beneficial and maybe even a unique option to deal with specific problems of interest to the scientific community.