Keywords

We solve a classification problem by using SVM [14]. The SVM have been shown effective in many applications including computer vision, natural language, bioinformatics, and finance [12]. There are three main performance measures for SVM : the generalization performance, sparsity of a decision boundary and computational performance of learning. SVM are in the group of the most accurate classifiers and are generally the most efficient classifiers in terms of overall running time [16]. They may be preferable due to its simplicity compared to deep learning approach for image data, especially when training data are sparse. One of the problem in the domain of SVM is to efficiently tune two hyperparameters: the cost C which is a trade-off between the margin and the error term; and \(\sigma \) which is a parameter of a Gaussian kernel, also called the radial basis function (RBF) kernel [14]. The grid search is the most used in practice due to its simplicity and feasibility for SVM , where only two hyperparameters are tuned. The generalization performance of sophisticated meta-heuristic methods for hyperparameter optimization for SVM , like genetic algorithms, particle swarm optimization, estimation of distribution algorithms is similar to simpler random search and grid search [9]. The random search can have some advantages over grid search when more hyperparameters are considered like for neural networks [1]. The random search still requires considerable fraction of the grid size. The problem with a grid search method is high computational cost due to exhaustive search of a discretized hyperparameter space.

In this article, we tackle the problem of improving performance of hyperparameter search for the cost C in terms of computational time while preserving sparsity and generalization. In [4], authors use a general approach of checking fewer candidates. They first use a technique for finding optimal \(\sigma \) value, then they use a grid search exclusively for C with an elbow method. The potential limitation of this method is that it still requires a grid search for C, and there is an additional parameter, tolerance for an elbow point. In practice, the number of checked values has been reduced to 5 from 15. In [3], authors use an analytical formula for C in terms of a jackknife estimate of the perturbation in the eigenvalues of the kernel matrix. However, in [9] authors find that tuning hyperparameters generally results in substantial improvements over default parameter values. Usually, a cross validation is used for tuning hyperparameters which additionally increases computational time.

Recently, an algorithm for solving SVM using SGD has been proposed [10] with interesting properties. We call it Stochastic Gradient Descent for Support Vector Classification (SGD-SVC) for simplicity. Originally, it was called OLLAWV. It always stops in the first epoch, which we call extreme early stopping and has a related property of not using a regularization term. The SGD-SVC is based on iterative learning. Online learning has a long tradition in machine learning starting from a perceptron [12]. Online learning methods can be directly used for batch learning. However, the SGD-SVC is not a true online learning algorithm, because it uses knowledge from all examples in each iteration. The SGD-SVC due to its iterative nature is similar to many online methods having roots in a perceptron, like the Alma Forecaster [2] that maximizes margin. Many perceptron-like methods have been kernelized, some of them also related to SVM like kernel-adatron [14]. In this article, we reformulate slightly the SGDSVC by replacing a hyperparameter C with a margin hyperparameter M. This parameter is mentioned as a desired margin in [14], def. 4.16. The margin plays a central role in SVM and in a statistical learning theory, especially in generalization bounds for a soft margin SVM. The reformulation leads to simpler formulation of a decision boundary with the same coefficients for any data set that differs only in kernel function values and the number of support vectors which is related to the margin M. Such simple reformulation of weights is close in spirit to the empirical Bayes classifier, where all weights are the same. It has been inspired by fast heuristics used by animals and humans in decision-making [6]. The idea of replacing the C hyperparameter has been mentioned in [13] and proposed as \(\nu \) support vector classification (\(\nu \)-SVC). The problem is that it leads to a different optimization problem and is computationally less tractable. The \(\nu \)-SVC has been also formulated as \(\nu \) being a direct replacement of \(C = 1/(n\nu )\) in [14], where n is the number of examples, with the same optimization problem as support vector classification (SVC). The margin classifier has been mentioned in [15], however, originally it has been artificially converted to the classifier with the regularization term. The statistical bounds for the margin classifier has been given in [5], but without proposing a solver based on these bounds. There is also a technique of solution/regularization path with a procedure of computing a solution for some values of C using a piecewise linearity property. However, the approach is complicated and requires solving a system of equations and several checks of O(n) [7]. In the proposed method, we use one solution for a particular M for generating all solutions for remaining values of M.

The outline of the article is as follows. First, we define a problem, then the methods and update rules. After that, we show experiments on real world data sets.

1 Problem

We consider a classification problem for a given sample data \(\mathbf {x_i}\) mapped respectively to \(y_i\in \{-1, 1\}\) for \(i=1, \ldots , n\) with the following decision boundary

$$\begin{aligned} f\left( \mathbf {x}\right) \equiv \mathbf {w} \cdot \varphi \left( \mathbf {x}\right) = 0 , \end{aligned}$$
(1)

where \(\mathbf {w} \in \mathbb {R}^m\) with the feature map \(\varphi (\cdot )\in \mathbb {R}^m\), \(f(\cdot )\) is a decision function. We classify data according to the sign of the left side \(f(\mathbf {x})\). This is the standard decision boundary formulation used in SVM with a feature map and without a free term b. The primal optimization problem for (C-SVC) is

Optimization problem (OP) 1.

$$\begin{aligned} \min _{\mathbf {w}} \frac{1}{2}\left\Vert \mathbf {w}\right\Vert ^2 + C\sum _{i=1}^n\max \left\{ 0, 1 - y_i\left( \mathbf {w}\cdot \varphi \left( \mathbf {x_i}\right) \right) \right\} , \end{aligned}$$
(2)

where \(C > 0\), \(\varphi \left( \mathbf {x_j}\right) \in \mathbb {R}^m\).

The first term in (2) is known as a regularization term (regularizer), the second term is an error term. The \(\mathbf {w}\) can be written in the form

$$\begin{aligned} \mathbf {w} \equiv \sum _{j=1}^n \beta _j \varphi \left( \mathbf {x_j}\right) , \end{aligned}$$
(3)

where \(\mathbf {\beta }\in \mathbb {R}^n\). We usually substitute (3) to a decision boundary and we get

$$\begin{aligned} \sum _{j=1}^n \beta _j \varphi \left( \mathbf {x_j}\right) \cdot \varphi \left( \mathbf {x}\right) = 0 . \end{aligned}$$
(4)

The optimization problem OP 1 is reformulated to find \(\beta _j\) parameters.

The SGD procedure for finding a solution of SVM proposed in [10], called here SGD-SVC is to update parameters \(\beta _k\) iteratively using the following update rule for the first epoch

$$\begin{aligned} \beta _{k} \leftarrow -\eta _k {\left\{ \begin{array}{ll} - Cy_{w(k)}, &{} \text {if}\ 1 - y_{w\left( k\right) }\sum _{j=1}^{k-1} \beta _j \varphi \left( \mathbf {x_{w\left( j\right) }}\right) \cdot \varphi \left( \mathbf {x_{w\left( k\right) }}\right) \ge 0 \\ 0, &{} \text {otherwise} \end{array}\right. } , \end{aligned}$$
(5)

where \(\eta _k\) is a learning rate set to \(\eta _k = 1/\sqrt{k}\) for \(k=1, \ldots , n\), all \(\beta _k\) are initialized with 0 before the first epoch. We set \(w(1) = 1\). We always stop in the first epoch, either when the condition in (5) is violated, or when we updated all parameters \(\beta _k\). The w(k) is used for selection of an index using the worst violator technique. It means that we look for the example among all remaining examples, with the worst value of the condition in (5). We check the condition only for the examples not being used in the iteration process before. The worst violators are searched among all remaining examples, so when one wants to use this method for online learning, it is still required to train the model in a batch for optimal performance. We use a version of SVM without a free term b for simplicity, which does not impact any performance measures. We update each parameter maximally one time. Finally, only parameters \(\beta _k\) for the fulfilled condition during the iteration process have nonzero values. The remaining parameters \(\beta _k\) have zero values. In that way, we achieve sparsity of a solution. The number of iterations \(n_c\) for \(\beta _k\) parameters with the fulfilled condition is also the number of support vectors. The derivation of an update rule has been already given in [10]. We call the algorithm that stops always in the first epoch as extreme early stopping.

The idea that we want to explore is to get rid of the C hyperparameter from the update rule and from the updated term for \(\beta _k\) (5).

2 Solution – Main Contribution

The decision boundary (4) for SGD-SVC can be written as

$$\begin{aligned} \sum _{k=1}^{n_c} Cy_{w\left( k\right) }\eta _k \varphi \left( \mathbf {x_{w\left( k\right) }}\right) \cdot \varphi \left( \mathbf {x}\right) = 0 , \end{aligned}$$
(6)

where \(n_c \le n\) is the number of support vectors. In the same way, we can write the margin boundaries

$$\begin{aligned} \sum _{k=1}^{n_c} Cy_{w\left( k\right) }\eta _k \varphi \left( \mathbf {x_{w\left( k\right) }}\right) \cdot \varphi \left( \mathbf {x}\right) = \pm 1 . \end{aligned}$$
(7)

When we divide by C, we get

$$\begin{aligned} \sum _{k=1}^{n_c} y_{w\left( k\right) }\eta _k \varphi \left( \mathbf {x_{w\left( k\right) }}\right) \cdot \varphi \left( \mathbf {x}\right) = \pm 1/C . \end{aligned}$$
(8)

The left side is independent of C, the right side is a new margin value. The new decision boundary can be written as

$$\begin{aligned} \sum _{k=1}^{n_c} y_{w\left( k\right) }\eta _k \varphi \left( \mathbf {x_{w\left( k\right) }}\right) \cdot \varphi \left( \mathbf {x}\right) = 0 . \end{aligned}$$
(9)

We propose a classifier based on a margin solving the following optimization problem

OP 2.

$$\begin{aligned} \min _{\mathbf {w}} \frac{1}{2}\left\Vert \mathbf {w}\right\Vert ^2 + \sum _{i=1}^n\max \left\{ 0, M - y_i\left( \mathbf {w}\cdot \varphi \left( \mathbf {x_i}\right) \right) \right\} , \end{aligned}$$
(10)

where \(M > 0\) is a desired margin – a hyperparameter that replaces the C hyperparameter. We call it M Support Vector Classification (M-SVC). The classifier with explicitly given margin has been investigated in [14]. In our approach, we tune a margin, unlike for standard SVM when the margin is optimized, see [14] page 220. We have the following proposition.

Proposition 1

The OP 2 is equivalent to OP 1.

Proof

We can write (10) as

$$\begin{aligned} \min _{\mathbf {w}} \frac{1}{2}\left\Vert \mathbf {w}\right\Vert ^2 + M\sum _{i=1}^n\max \left\{ 0, 1 - y_i\left( \frac{\mathbf {w}}{M}\cdot \varphi \left( \mathbf {x_i}\right) \right) \right\} . \end{aligned}$$
(11)

When we substitute \(\mathbf {w}'\rightarrow \mathbf {w}/M\), we get

$$\begin{aligned} \min _{\mathbf {w}'} \frac{1}{2}\left\Vert \mathbf {w}'M\right\Vert ^2 + M\sum _{i=1}^n\max \left\{ 0, 1 - y_i\left( \mathbf {w}'\cdot \varphi \left( \mathbf {x_i}\right) \right) \right\} , \end{aligned}$$
(12)

So we get

$$\begin{aligned} \min _{\mathbf {w}'} \frac{1}{2}\left\Vert \mathbf {w}'\right\Vert ^2 + \frac{1}{M}\sum _{i=1}^n\max \left\{ 0, 1 - y_i\left( \mathbf {w}'\cdot \varphi \left( \mathbf {x_i}\right) \right) \right\} . \end{aligned}$$
(13)

The M is related to C by

$$\begin{aligned} M = 1/C . \end{aligned}$$
(14)

It is a similar term as for \(\nu \)-SVC classifier given in [14], where \(C = 1/(n\nu )\) and \(\nu \in (0, 1]\). Because the optimization problems are equivalent, generally all properties of SVM in the form OP 2 applies also for M-SVC. In [14], page 211, authors stated an SVM version, where the margin M is automatically optimized as an additional variable. However, they still have the constant C. From the statistical learning theory point of view, the original bounds [14], page 211 applies for a priori chosen M.

We can derive the update rules for M-SVC similar as for SGD-SVC. The new update rules called (SGD-M-SVC) are

$$\begin{aligned} \beta _{k} \leftarrow -\eta _k {\left\{ \begin{array}{ll} - y_{w(k)}, &{} \text {if}\ M - y_{w(k)}\sum _{j=1}^{k-1} \beta _j \varphi \left( \mathbf {x_{w(j)}}\right) \cdot \varphi \left( \mathbf {x_{w(k)}}\right) \ge 0 \\ 0, &{} \text {otherwise} \end{array}\right. } . \end{aligned}$$
(15)

In the proposed update rules, there is no hyperparameter in the updated value, only in the condition, in opposite to (5). It means that for different values of a margin M, we get solutions that differ only in the number of terms. The corresponding values of parameters \(\beta _k\) are the same for each M value, so the ordering of corresponding parameters is the same. It means that we do not need to tune values of parameters \(\beta _k\), only the stopping criterion and thus the number of terms in a solution. When we have a set of M values, and we have a model for the \(M_{\max }\), we can generate solutions for all remaining M values just by removing the last terms in the solution for \(M_{\max }\). We have a correspondence between M value and the number of support vectors \(n_c\) stated as follows.

Proposition 2

After running the SGD-M-SVC for any two values \(M_1\) and \(M_2\), such as \(M_1 > M_2\), the number of support vectors \(n_c\) is bigger or equals for \(M_1\).

Proof

The \(n_c\) is the number of support vectors and also the number of terms. The stopping criterion is the opposite for the update condition (15) for the k-th iteration. Due to the form \(M < \cdot \), it is fulfilled earlier for \(M_2\). There is a special case when stopping criterion would not be triggered for both values, then we get the same model with n terms. Another special case is when only one condition is triggered, then we get model for \(M_2\) and for \(M_1\) with all n terms.

3 Theoretical Analysis

The interesting property of the new update rules is that we realize two goals with update rules: we decrease the objective function value (10) and simultaneously, we generate solutions for a set of given different values of a hyperparameter M, and all is done in the first epoch. We can say, that we solve a discrete non-convex optimization problem OP 2 where we can treat M as a discrete variable to optimize. The main question that we want to address is how is it possible, that we can effectively generate solutions for different values of M in the first epoch. First, note due to convergence analysis of a stochastic method, we expect that we improve the objective function value of (10) during the iteration process. We provide an argument that we are able to generate solutions for different values of M. The SVM can be reformulated as solving a multiobjective optimization problem [11] with two goals, a regularization term, and the error term (2). The SVM is a weighted (linear) scalarization with the C being a scalarization parameter. For the corresponding multiobjective optimization problem for OP 2, we have the M scalarization parameter instead. Due to convexity of the two goals, the set all solutions of SVM for different values of C is a Pareto frontier for the multiobjective optimization problem. We show that during the iteration process, we generate approximated Pareto optimal solutions. The error term for the t-th iteration of SGD-M-SVC for the example to be added \(\mathbf {x_{w\left( t+1\right) }}\) can be written as

$$\begin{aligned} \sum _{\begin{array}{c} i=1\\ i\ne t+1 \end{array}}^{n}\max \left\{ 0, M - y_{w\left( i\right) }f_t\left( \mathbf {x_{w\left( i\right) }}\right) \right\} + \max \left\{ 0, M - y_{w\left( t+1\right) }f_t\left( \mathbf {x_{w\left( t+1\right) }}\right) \right\} , \end{aligned}$$
(16)

where \(f_t(\cdot )\) is a decision function of SGD-M-SVC after t-th iteration. After adding \(t+1\)-th parameter, we get an error term

$$\begin{aligned} \begin{gathered} \sum _{\begin{array}{c} i=1 \\ i\ne t+1 \end{array}}^{n}\max \left\{ 0, M - y_{w\left( i\right) }f_{t}\left( \mathbf {x_{w\left( i\right) }}\right) -y_{w\left( i\right) }y_{w\left( t+1\right) }\frac{1}{\sqrt{t+1}}\varphi \left( \mathbf {x_{w\left( t+1\right) }}\right) \cdot \varphi \left( \mathbf {x_{w\left( i\right) }}\right) \right\} \\ +\max \left\{ 0, M - y_{w\left( t+1\right) }f_{t}\left( \mathbf {x_{w\left( t+1\right) }}\right) - \frac{1}{\sqrt{t+1}}\right\} \end{gathered} \end{aligned}$$
(17)

assuming that we replace a scalar product with an RBF kernel function. The update for the regularization term from (10) is

$$\begin{aligned} \left\Vert \mathbf {w_{t+1}}\right\Vert ^2 = \sum _{i=1}^{t+1}\sum _{j=1}^{t+1} y_{w\left( i\right) }y_{w\left( j\right) }\frac{1}{\sqrt{i}}\frac{1}{\sqrt{j}}\varphi \left( \mathbf {x_{w\left( i\right) }}\right) \cdot \varphi \left( \mathbf {x_{w\left( j\right) }}\right) . \end{aligned}$$
(18)

So we get

$$\begin{aligned} \left\Vert \mathbf {w_{t+1}}\right\Vert ^2 = \left\Vert \mathbf {w_{t}}\right\Vert ^2 + 2y_{w\left( t+1\right) }\frac{1}{\sqrt{t+1}}f_{t}\left( \mathbf {x_{w\left( t+1\right) }}\right) + \frac{1}{\sqrt{t+1}}\frac{1}{\sqrt{t+1}} . \end{aligned}$$
(19)

The goal of analysis is to show that during the iteration process, we expect decreasing value of an error term and increasing value of a regularization term. It is the constraint for generating Pareto optimal solutions. Due to Proposition 2, we are increasing value of M, which corresponds to decreased value of C due to (14). For SVM, oppositely, we are increasing value of a regularization term, when C is increased. We call this property a reversed scalarization for extreme early stopping. First, we consider the error term. We compare the error term after adding an example (17) to the error term before adding the example (16). The second term in (17) stays the same or it has smaller value due to the update condition for the \(t+1\)-th iteration

$$\begin{aligned} M - y_{w\left( t+1\right) }f_{t}\left( \mathbf {x_{w\left( t+1\right) }}\right) \ge 0 \end{aligned}$$
(20)

and due to the positive \(1/\sqrt{t+1}\). Moreover, the worst violator selection technique maximizes the left side of (20) among all remaining examples, so it increases the chance of getting smaller value. Now regarding the first term in (16). After update (17), we decrease a value of this term for examples already processed with same class so for which \(y_{w(i)} = y_{w(t+1)}\) for \(i\le t\). However, we increase particular terms for remaining examples with the opposite class. The worst violators will likely be surrounded by examples for an opposite class. So we expect bigger similarities to the examples with the opposite class, thus we expect \(\varphi \left( \mathbf {x_{w\left( t+1\right) }}\right) \cdot \varphi \left( \mathbf {x_{w\left( i\right) }}\right) \) to be bigger.

Regarding showing increasing values of (19) during the iteration process. The third term in (19) is positive. The second term in (19) can be positive or negative. It is closely related to the update condition (20). During the iteration process, we expect the update condition to be improved, because, we have an improved model. During the iteration process, the update condition starts to improving and there is a point for which

$$\begin{aligned} y_{w\left( t+1\right) }f_{t}\left( \mathbf {x_{w\left( t+1\right) }}\right) > -1/\sqrt{t+1} . \end{aligned}$$
(21)

Then the update for (19) becomes positive. We call this point a Pareto starter. So we first optimize the objective function value by minimizing the regularization term and minimizing the error term, then after Pareto starter we generate approximated Pareto optimal solutions, while still improving the objective function value by minimizing only the error term.

3.1 Bounds for M

We bound M by finding bounds for the decision function \(f(\cdot )\). Given \(\sigma \), we can compute the lower and upper bound for \(f(\cdot )\) for the RBF kernel for a given number of examples as follows

$$\begin{aligned} l = \left( -1\right) \exp \left( 0/\left( -2\sigma ^2\right) \right) \sum _{i=1}^n\frac{1}{\sqrt{i}}, u = \exp \left( 0/\left( -2\sigma ^2\right) \right) \sum _{i=1}^n\frac{1}{\sqrt{i}} = \sum _{i=1}^n\frac{1}{\sqrt{i}} . \end{aligned}$$
(22)

It holds that \(l\le f(\cdot ) \le u\). In the lower bound, we assume all examples with a class \(-1\). The upper bound is a harmonic number \(H_{n,0.5}\). The bounds capture cases when margin functions have all examples on the same side. For random classes for examples (with the Rademacher distribution), the expected value of l (with replaced \(-1\) with classes for particular examples) is 0. We also consider the case with one support vector with class 1 for capturing the error term close to 0. We have the error term \(1 - \exp \left( 1/\left( -2\sigma ^2\right) \right) \). Given \(\sigma _{\max }\) arbitrarily, we can compute \(\sigma _{\min }\) assuming one support vector according to the numerical precision. For simplicity, we can use one value, \(\sigma _{\max }\) for computing \(l_2\). Overall, we can compute bounds for \(f(\cdot )\) as the lower bound based on \(l_2\) and the upper bound based on u. For example, for \(n=100000\) and \(\sigma _{\max } = 2^9\), we get after rounding powers to integers \(\sigma _{\min } = 2^{-4}\), \(M_{\min } = 2^{-19}\), \(M_{\max } = 2^{10}\).

4 Method

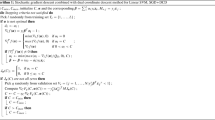
The SGD-M-SVC returns the equivalent solutions as SGD-SVC. However, it is faster for validating different values of M. First, we run a prototype solver SGD-M-SVC with \(M = M_{\max } = 2^{10}\) with provided a list of sorted \(M_i\) values as a parameter and with particular \(\sigma \) value. During the iteration process in the prototype solver, we store margin values defined as \(m_k \equiv y_{w(k)}f_{k-1}\left( \mathbf {x_{w(k)}}\right) \). Because sometimes it may happen that \(m_k < m_{k-1}\), then we copy a value of \(m_{k-1}\) to \(m_k\), so we have always a sorted sequence of \(m_k\) values. The size of \(m_k\) is \(n-1\) at most. We also store validation errors \(v_k\) that are updated in each iteration. The size of this list is the size of a validation set. We also update the map of \(M_i\) values to k indices during the iteration process. Then, we use a solver returning a validation error for particular \(M_i\) as specified in Algorithm 1. Given validation error, we can compare solutions for different hyperparameter values.

figure a

4.1 Computational Performance

The computational complexity of SGD-SVC based on update rules (5) is \(O(n_cn)\), when \(n_c\) is the number of iterations. It is also the number of support vectors. So sparsity influences directly computational performance of training. The requirement for computing the update rule for each parameter is a linear time. The update rules (5) are computed in each iteration in a constant time. However, a linear time is needed for updating values of a decision function for all remaining examples. The procedure of finding two hyperparameter values \(\sigma \) and C using the cross validation, a grid search method and SGD-SVC has the complexity \(O(n_c(n-n/v)v|C||\sigma | + n_cn|C||\sigma |)\) for v-fold cross validation, where |C| is the number of C values to check, \(|\sigma |\) is the number of \(\sigma \) values to check, \(n_c\) is the average number of support vectors. For each fold, we train a separate model. The first term is related to training a model. The second term is related to computing a validation error. The complexity of SGD-M-SVC is

$$\begin{aligned} O(n_{c,p}(n-n/v)v|\sigma | + n_{c,p}n|\sigma |) , \end{aligned}$$
(23)

where \(n_{c,p}\) is the number of support vectors for a prototype solver. We removed a multiplier |C| from the first term, that is related to the training complexity, and from the second term, that is related to the computation of a validation error.

5 Experiments

The M-SVC returns equivalent solutions to C-SVC. However, it is faster for validating different values of M. We validate equally distributed powers of 2 as M values from \(2^{-19}\) to \(2^{10}\) for integer powers, based on the analysis in the Sect. 3.1. We use our own implementation of both SGD-SVC and SGD-MSVC. We compare performance of both methods for real world data sets for binary classification. More details about data sets are on the LibSVM site ([8]). We selected all data sets from this site for binary classification. For all data sets, we scaled every feature linearly to \(\left[ 0, 1\right] \). We use the RBF kernel in a form \(K(\mathbf {x}, \mathbf {z}) = \exp (-\left\Vert \mathbf {x} - \mathbf {z}\right\Vert ^2/(2\sigma ^2))\). The number of hyperparameters to tune is 2, \(\sigma \) and M for SGD-M-SVC, and \(\sigma \) and C for SGD-SVC. For all hyperparameters, we use a grid search method for finding the best values. The \(\sigma \) values are integer powers of 2 from \(2^{-4}\) to \(2^9\). We use the procedure similar to repeated double cross validation for performance comparison. For the outer loop, we run a modified k-fold cross validation for \(k = 15\), with the optimal training set size set to 80% of all examples with maximal training set size equal to 1000 examples. We limit a test data set to 1000 examples. We limit all read data to 35000. When it is not possible to create the next fold, we shuffle data and start from the beginning. We use the 5-fold cross validation for the inner loop for finding optimal values of the hyperparameters. After that, we run the method on training data, and we report results on a test set.

The observations based on experimental results are as follows. The proposed method SGD-M-SVC is about 7.6 times faster SGD-SVC (see Table 1) for binary classification, with the same generalization performance and the number of support vectors. We have 30 values of M to tune. Some authors tune value of C with fewer values. Then the effect of this speed improvement may be smaller. We generally expect the accuracy performance to degrade slowly for smaller number of values of M. We also implemented the method for multiclass classification with similar results, however we do not report it here due to space constraints. We validated also theoretical results. We check Pareto frontier every 10 iterations. The results is that the approximated Pareto frontier is generated from almost the beginning of a data set after processing 0.05% examples on average (column pS in Table 1). Approximated Pareto frontier is generated perfectly for some data sets (1.0 in a column pU), on average in 75% updates. While we check Pareto updates every 10 iterations, it may be worth to check them only for selected solutions for given M, which are distributed differently. From the practical point of view, we recommend to use SGD-M-SVC instead of SGD-SVC due to speed performance benefits.

Table 1. Experiment 1. The numbers in descriptions of the columns mean the methods: 1 - SGD-SVC, 2- SGD-M-SVC. Column descriptions: dn – data set, size – the number of all examples, dim – dimension of the data set, err – misclassification error, sv – the number of support vectors, t – average training time per outer fold in seconds, the best time is in bold (last row is a sum), pU – Pareto optimal solutions ratio (last row is an average), pS – Pareto starter ratio (last row is an average).
Full size table

6 Conclusion

We proposed a novel method for SVC based on tuning margin M instead of C, with an algorithm SGD-M-SVC which improves substantially tuning time for the margin M hyperparameter compared to tuning the cost C in SGD-SVC. We provided theoretical analysis of an approximated Pareto frontier for this solver, which confirms the ability to generate solutions for different values of M during the first epoch.