Prediction of Strength-Band of Methane Hydrate-Bearing Sand by Elastoplastic Constitutive Model Considering Microstructure of Gas Hydrates

Abstract

In the present study, we propose a new elastoplastic constitutive equation with consideration of the hydrate morphology. Then, using the proposed constitutive equation, we investigate how large the strength and the volumetric strain change by the change in the hydrate morphology with the fixed total hydrate saturation. The result indicates that the strength and the positive dilatancy becomes the larger in the case where the morphology of the cementing-type is more dominant. Moreover, the strength curves predicted by the proposed model is in good agreement with the past experimental research. This makes it possible to predict the strength and the deformation behavior of MH-bearing sediments even in the area where there is a lack of research data.

1 Introduction

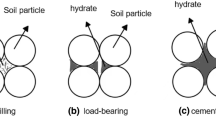
Many researchers have investigated mechanical properties of methane hydrate by means of triaxial compression tests. They have recently revealed that there are obvious differences in stress-strain relationship and dilatancy behavior among the MH-bearing specimens even though they have the same degree of hydrate saturation. Those differences may come from the microstructure of the hydrates particles in the pore space of the sand, that is, hydrate morphology. Some researchers have pointed that those differences of the mechanical properties of MH-bearing sediments may come from hydrate morphology in pore spaces, that is, the microstructure of hydrates and its interaction with soil particles. The hydrate morphology is basically divided into three types: pore filling (PF) type, load bearing (LB) type, and cementing (CM) type as shown in Fig. 1 (i.e., Waite et al. 2009).

Several effective constitutive models that can reproduce the mechanical behavior of gas hydrate-bearing soils have been proposed (i.e., Sánchez et al. 2017; Uchida et al. 2012) There are, however, few constitutive models that takes the effect of the hydrate morphology into account. In the present study, we propose a new elastoplastic constitutive equation with consideration of the hydrate morphology. Then, using the proposed constitutive equation, we investigate how large the strength and the volumetric strain change by the change in the hydrate morphology with the fixed total hydrate saturation.

Fig. 1.

Schematic view of hydrate morphology and interactions with soil particles

2 Elastoplastic Constitutive Model

The proposed model in the present study is based on the methane hydrate critical state (MHCS) model proposed by Uchida et al. (2012). The outline of the proposed model is introduced in the following.

2.1 Definition of Total Hydrate Saturation and Morphology Ratio

At first, the total hydrate saturation $S_{r}^{H}$ is defined as follows:

$$ S_{r}^{H} = {{V^{H} } \mathord{\left/ {\vphantom {{V^{H} } {V^{v} }}} \right. \kern-\nulldelimiterspace} {V^{v} }} $$

(1)

in which $V^{H}$ is the volume of the hydrate, and $V^{v}$ is the volume of void. In the proposed constitutive model, we assume that there are three different types of hydrate morphology: pore-filling (PF) type, load-bearing (LB) type, and cementing (CM) type, and the total hydrate saturation $S_{r}^{H}$ is expressed by the sum of the saturation of each hydrate morphology:

$$ S_{r}^{H} = S_{CM}^{H} + S_{LB}^{H} + S_{PF}^{H} $$

(2)

$$ S_{CM}^{H} = \alpha S_{r}^{H} ,\,\,\,S_{LB}^{H} = \beta S_{r}^{H} ,\,\,\,S_{PF}^{H} = \gamma S_{r}^{H} $$

(3)

in which α, β, γ are the ratio of each hydrate morphology with respect to the total hydrate saturation., and the summation should be equal to 1.

$$ \alpha + \beta + \,\gamma = 1\,\,\,\left( {0 < \alpha ,\,\,\beta ,\,\,\gamma < 1} \right) $$

(4)

2.2 Yield Function

The following yield function is used in the present model; Modified Cam-clay type of yield function is adopted.

$$ f = q^{2} + M^{2} p^{\prime}\left[ {p^{\prime} - R\left( {p^{\prime}_{c} + p^{\prime}_{CM} + p^{\prime}_{LB} } \right)} \right] $$

(5)

where q is the deviator stress, M is the stress ratio at the critical state of host geomaterial, p′ is the mean effective stress, $p^{\prime}_{c}$, $p^{\prime}_{CM}$, $p^{\prime}_{LB}$ are the hardening parameters that expand the original yield function, and the details of those parameters are explained in the next section. The parameter R is the sub-loading surface ratio proposed by Hashiguchi (1989) and its evolution law is given by:

$$ dR = - m_{R} \left\{ {{{\left( {p^{\prime}_{c} + p^{\prime}_{CM} + p^{\prime}_{LB} } \right)} \mathord{\left/ {\vphantom {{\left( {p^{\prime}_{c} + p^{\prime}_{CM} + p^{\prime}_{LB} } \right)} {p^{\prime}_{c} }}} \right. \kern-\nulldelimiterspace} {p^{\prime}_{c} }}} \right\}\ln R\,\,\left| {d{{\varvec{\upvarepsilon}}}^{p} } \right| $$

(6)

where $m_{R}$ is a fitting parameter and $d{{\varvec{\upvarepsilon}}}^{p}$ is the plastic strain increment vector.

The hardening and softening behavior is controlled by the hardening parameter $R\left( {p^{\prime}_{c} + p^{\prime}_{CM} + p^{\prime}_{LB} } \right)$ in Eq. (5).

In the present model, the associated flow rule is used; the plastic potential function g is the same as the yield function defined above. The plastic strain vector can be calculated by the following equation:

$$ \left\{ {d\varepsilon_{v}^{p} \,\,\,d\varepsilon_{d}^{p} } \right\}^{T} = \Lambda \left\{ {{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial p^{\prime}}}} \right. \kern-\nulldelimiterspace} {\partial p^{\prime}}}\,\,\,\,{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial q}}} \right. \kern-\nulldelimiterspace} {\partial q}}} \right\}^{T} \,\,\,\left( {g = f} \right) $$

(7)

2.3 Hardening Parameters

The hardening parameter $p^{\prime}_{c}$ is the conventional consolidation yield stress depending on the plastic volumetric strain $d\varepsilon_{v}^{p}$, and the its evolution law is given by:

$$ \frac{{dp^{\prime}_{c} }}{{p^{\prime}_{c} }} = \frac{1 + e}{{\lambda - \kappa }}d\varepsilon_{v}^{p} $$

(8)

in which e is void ratio, $\lambda$ is compression index, and $\kappa$ is swelling index.

In addition to the consolidation yield stress, the other two hardening parameters related to the hydrate morphology are introduced to the model in order to express the increase in the strength and the positive dilatancy, that is, $p^{\prime}_{CM}$ and $p^{\prime}_{LB}$. The different type of the hydrate morphology indicates the different hardening behavior. Hence, the parameter $p^{\prime}_{CM}$ and $p^{\prime}_{LB}$ are defined as the function of each hydrate morphology.

$$ p^{\prime}_{CM} = a_{CM} \left( {S_{CM}^{H} } \right)^{{b_{CM} }} = a_{CM} \left( {\alpha S_{r}^{H} } \right)^{{b_{CM} }} $$

(9)

$$ p^{\prime}_{LB} = a_{LB} \left( {S_{LB}^{H} } \right)^{{b_{LB} }} = a_{LB} \left( {\beta S_{r}^{H} } \right)^{{b_{LB} }} $$

(10)

in which $a_{CM}$, $b_{CM}$, $a_{LB}$, and $b_{LB}$ are the fitting parameters. These parameters are determined so that the material hardening of the CM-type becomes much larger than that of the LB-type.

The hardening parameters will change as the changes of not only the total hydrate saturatio $S_{r}^{H}$ but also each morphology ratio $\alpha ,\beta , {\rm{and}}\, \gamma$. The microstructure of hydrate particles and its interaction with soil particles may transform when hydrate-bearing soil is subjected to shearing. It is, therefore, necessary to consider incremental forms of the hydrate morphology ratio depending on the shear deformations. In regard to the morphology transition, the following assumptions are adopted:

Fig. 2.

CM-type morphology changes into LB-type due to breakage of hydrates by shearing

• (1) First, the CM-type of hydrate morphology changes into the LB-type due to crush or breakage of the hydrates bonding with soil particles, as shown in Fig. 2. Thus, the increment of the CM-type ratio $\alpha$ is given by the following equation as depending on the shear strain (Fig. 2).

$$ d\alpha = - m_{\alpha } \alpha \left| {d\varepsilon_{d}^{p} } \right| $$

(11)

where ${m_\alpha}$ is a material parameter which determines the transition rate from the CM-type to the LB-type.

• (2) Second, the LB-type and the PF-type of the hydrate morphology mutually changes with increase and decrease in the volume of void. The LB-type changes into the PF-type in the case of the volume expansion: positive dilatancy. In contrast, the PF-type changes into the LB-type when it is compression: negative dilatancy. This transition between the LB-type and the PF-type is schematically illustrated in Fig. 4.

Fig. 3.

LB-type and PF-type change into with each other depending on the volume of void

The increment of the PF-type ratio $\gamma$ is given by the following equation as depending on the plastic volumetric strain (positive in compression).

$$ d\gamma = - m_{\gamma } \gamma d\varepsilon_{v}^{p} $$

(12)

where m_γ is a material parameter which determines the transition rate between the PF-type and the LB-type. The increment of the LB-type ratio can be described as the following equation by considering Eq. (4), (11) and (12).

$$ d\beta = - d\alpha - d\gamma $$

(13)

Considering Eq. (9)–(13), the evolution laws for the hardening parameters $p^{\prime}_{CM}$ and $p^{\prime}_{LB}$ can be given as the following equations.

$$ dp^{\prime}_{CM} = a_{CM} b_{CM} \left( {\alpha S_{r}^{H} } \right)^{{b_{CM} - 1}} \left( {\alpha dS_{r}^{H} - m_{\alpha } \alpha \left| {d\varepsilon_{d}^{p} } \right|S_{r}^{H} } \right) $$

(14)

$$ dp^{\prime}_{LB} = a_{LB} b_{LB} \left( {\beta S_{r}^{H} } \right)^{{b_{LB} - 1}} \left\{ {\beta dS_{r}^{H} - \left( {d\alpha + d\gamma } \right)S_{r}^{H} } \right\} $$

(15)

3 Conditions of Model Analysis

In applying the proposed model to the past experimental results, it is necessary to determine the initial morphology ratio α₀, β₀, γ₀. It is preferable to determine the actual initial morphology ratio by visualizing microscopic structures of soil particles and hydrates, however, it is quite difficult to do so because we do not have any way to know the actual existence form of hydrate particles in pore space. In addition to that, the in-situ MH-bearing sediments is highly heterogeneous, and the various morphology of MHs exist complicated. It is almost impossible to determine the actual hydrate morphology ratio uniquely. Therefore, in this section, the constitutive model is used to examine the range in which the strength and dilatancy change when the morphology ratio changes with a certain total hydrate saturation. The material parameters are listed in Table 1. In Table 1, from the initial mean effective stress to the initial yield stress were determined based on the experimental data of Hyodo et al. (2013). As for the other parameters, we treated them as just fitting parameters so that the stress-strain curve and the volumetric strain curve fit well with the experimental results of MH-bearing sand specimens.

Table 1. Material parameters for the constitutive model

4 Simulation Results

The following Fig. 4 and Fig. 5 show the simulation results that the total hydrate saturation is fixed at 10% and 50%, respectively. The case of ($\alpha , \beta , \gamma$) = (0.0, 0.0, 0.0) means the soil without MHs. Basically, the stress-strain curve becomes larger with increase in the ratio of the CM-type ($\alpha$) and the LB-type ($\beta$), and the positive dilatancy also becomes more significant. The largest deviator stress can be found in the case of ($\alpha , \beta , \gamma$) = (1.0, 0.0, 0.0); all the MHs exist in the form of the CM-type. This tendency is the same for Fig. 5. However, as compared with the case where the total hydrate saturation is 10%, the degree of increase in the stress-strain relationship is greater in the case of 50%. For example, when the CM-type is the largest: ($\alpha , \beta , \gamma$) = (1.0, 0.0, 0.0), the maximum deviator stress is less than 5 MPa at 10% of the total hydrate saturation, but it reaches at 8.0 MPa in the case of 50%. The larger the total hydrate saturation, the more sensitive the strength increase with respect to changes in the hydrate morphology ratio. Here, the predicted curve of the maximum deviator stress of the MH-bearing sediments based on the experimental results proposed by Miyazaki et al. (2011) and Yoneda et al. (2015) and the strength-band calculated in the present study are compared in Fig. 6. The dashed line indicates the results of this analysis, and the solid line indicates the approximate curve obtained from the experimental results. In Fig. 6, the intersection of the curve with ($\alpha , \beta , \gamma$) = (0.5, 0.5, 0.0) and the curve obtained by Miyazaki et al. (2011) 16) is the point at which the total hydrate saturation is 40.0%. Similarly, it is around 55.0% of the total hydrate saturation in the case of Yoneda et al. (2015).

Fig. 4.

Range of the stress-strain relationship and the volumetric strain with the variation of hydrate morphology ratio with the total hydrate saturation of 10%

Fig. 5.

Range of the stress-strain and the volumetric strain with the variation of hydrate morphology ratio with the total hydrate saturation of 50%

Fig. 6.

Prediction curves of the maximum deviator stress (CD-test) of MH-bearing sediments

According to Waite et al. (2009), when the total hydrate saturation exceeds 40.0%–50.0%, the CM-type is more predominant to the-LB type or the PF-type ratio, and the strength of the MH-containing ground increases significantly. In the comparison results, the line predicted from the experiment exceeds the simulated line at which the CM-type ratio is 50% at around total the hydrate saturation of 40–50%, which is well consistent with the knowledge of Waite et al. (2009).

5 Conclusions

In the present study, the strength-band of MH-containing ground was predicted using the newly proposed constitutive equation considering the hydrate morphology. As a result, it was found that the larger the total hydrate saturation, the larger the strength increase with respect to the increase in the CM-type ratio. Furthermore, the prediction curve of the maximum deviator stress was consistent with past experimental results; the CM-type ratio increases as the total hydrate saturation increases, and then the strength also increases exponentially.