Keywords

1 Introduction

Due to their computational efficiency, continuum mechanics-based models are often used in practice to study complex geosystems such as wellbores interacting with natural faults, engineered and geological barriers in nuclear waste disposals, or soil-anchor systems. However, under high stress, geomaterials undergo localized damage and/or large deformation, which cannot be modeled in a continuum framework. Macro-fracture propagation results from micro-crack coalescence. Numerous numerical methods were proposed to model multiscale fracture propagation, including: (1) Direct numerical simulation, also known as full-scale simulation, e.g., with the Discrete Element Method or the Finite Element Method (FEM); (2) Homogenization-based multiscale approaches (e.g., Belytschko et al. 2008; Geers et al. 2010); (3) Phase-field methods (e.g., Verhoosel and de Borst 2013; Voyiadjis et al. 2013); and (4) Damage–fracture transition techniques. The latter consists in coupling a Continuum Damage Mechanics (CDM) model with a discrete fracture mechanics model through an advanced discretization method. It was found that the cohesive fracture model could be formulated as a nonlocal damage model (Planas et al. 1993). Then, an equivalence was established between the energy dissipated for opening a discrete fracture and the energy dissipated for producing a dilute distribution of micro-cracks (Mazars and Pijaudier–Cabot 1996). This energy equivalence was further used to construct a cohesive law from a nonlocal damage model (Cazes et al. 2010) and predict the transition from micro-crack propagation to cohesive fracture debonding, with the embedded crack method (Jirasek and Zimmermann 2001; Roth et al. 2015). Macro fractures were also represented with traction free surfaces instead of cohesive models, by means of the eXtended FEM (XFEM). For example, Simone and collaborators (2003) defined the threshold for macroscopic fracture propagation as a function of a gradient enhanced damage variable, while Comi and collaborators (2007) set the damage threshold in relation to the size of the element at the fracture tip. Energy equivalence is ensured by assigning the energy not yet dissipated by the damage model within the process zone to the cohesive zone model. Coupled CDM-XFEM approaches were later used for mixed mode fracture propagation (e.g.,Wang and Waisman 2015).

In the numerical methods reviewed above, the CDM model is usually isotropic and phenomenological, and the threshold between CDM and CZ models is not always precisely defined or calibrated. In this paper, we present a rigorous method to couple continuum mechanics and discrete fracture mechanics governing equations for simulating damage localization and subsequent propagation of “macroscopic” discontinuities, beyond the scale of the Representative Elementary Volume (REV). Constitutive relationships of CDM are out of the scope of this study. Section 2 introduces the hydro-mechanical governing equations. The corresponding weak formulation is presented in Sect. 3. FEM and XFEM discretization approaches are discussed in Sect. 4. Section 5 explains the calibration procedure in both approaches. We conclude on the performance of the CDM-CZ coupling methods in Sect. 6.

2 Meso-macro Governing Hydro-Mechanical Equations

Consider a fracture embedded in a Damageable Porous Continuum (DPC), in which micro-cracks are represented by a damage tensor ω, either defined as a convolution of moments of probabilities of crack descriptors (e.g., size, aspect ratio, orientation), or as a function of displacement jumps at crack faces (Arson 2020). The stiffness tensor is a function of damage, which translates stress or crack-induced anisotropy. Given the potential energy density Hs of a REV of DPC, the expressions of Biot’s effective stress tensor σ and of the porosity ϕ are found through thermodynamic conjugation relationships, as follows:

$$ \begin{array}{*{20}l} {\user2{\sigma = }\frac{{\partial H_{s} }}{\partial \varepsilon } = {\mathbb{C}}\left( {\varvec{\omega}} \right)\rm{:}\,{\varvec{\varepsilon} - \alpha }p} \hfill \\ {\phi - \phi_{0} = - \frac{{\partial H_{s} }}{\partial p} = {\varvec{\alpha}}:{\varvec{\varepsilon}} + \frac{p}{N}} \hfill \\ \end{array} $$
(1)

Where ε is the strain tensor, ϕ0 is the initial porosity, p is the fluid pressure, \({\mathbb{C}}({\varvec{\omega}})\) is the elastoplastic stiffness tensor, \({\alpha }_{ij}=-{\partial }^{2}{H}_{s}/\partial {\varepsilon }_{ij}\partial p\) is Biot’s coefficient tensor, and \(1/N=-{\partial }^{2}{H}_{s}/{\partial }^{2}p\) is the inverse of Biot’s skeleton modulus. Hs is also called Helmholtz free energy. Under the quasi-static condition, the momentum balance equation of the REV (made of the mixture solid and fluid) is:

$$\varvec{\nabla} .{\varvec{\sigma}}+\rho {\varvec{g}}=0$$
(2)

where ρ is the average mass density of the mixture, defined as \(\rho =(1-\phi ){\rho }_{s}+\phi {\rho }_{f}\), in which ρs (respectively ρf) stands for the mass density of the solid phase (respectively, the mass density of the fluid phase). g is the body force vector. From Eq. (1)–(2), the strong form of the governing equation for the mixture is:

$$ \varvec{{\nabla }}{\mathbf{.}}\left[ {{\mathbb{C}}{{(}}{\boldsymbol{\omega}}{\mathbf{)}}\varvec{:}\,\user2{\varepsilon - \alpha }p} \right] + \rho {\varvec{g}} = 0 $$
(3)

The mass balance equation for the fluid in the porous matrix of the DPC is:

$$\varvec{\nabla} .\left({\rho }_{f}{\varvec{v}}\right)+ \frac{\partial {m}_{f}}{\partial t} =0$$
(4)

where v is the velocity vector of the fluid, and mf is the mass of the fluid. Assuming that the DPC is saturated with one fluid phase, we have mf =  ρf ϕ. Moreover, from the state equation of the fluid, the mass density of the fluid is related to the pore pressure through the following equation:

$$\frac{{\varvec{d}}{\rho }_{f}}{{\rho }_{f}}= \frac{dp}{{K}_{f}}$$
(5)

where Kf is the bulk modulus of the fluid. We assume that fluid flow inside the porous matrix is laminar and that it is governed by Darcy’s seepage equation as:

$${\varvec{v}}=-\frac{{{\varvec{k}}}_{{\varvec{m}}}}{{\varvec{\mu}}}\left({\nabla} {\varvec{p}}-{\rho }_{f}{\varvec{g}}\right)\boldsymbol{ }$$
(6)

where μ is the dynamic viscosity of the fluid and km(ω) is the intrinsic anisotropic permeability tensor of the solid skeleton, which depends on damage. By substituting Eq. (1), (5) and (6) into Eq. (4), we get the governing equation for the fluid flow through the permeable porous medium surrounding the fracture, as follows:

$$\user2{\alpha }:\frac{{\partial \user2{\varepsilon }}}{{\partial t}} + \frac{\rm{1}}{{M}}\frac{{\partial p}}{{\partial t}}\user2{~} = \varvec{\nabla} .\frac{{\user2{k}_{\user2{m}} }}{\user2{\mu }}\left( {\varvec{\nabla} \user2{p} - \rho _{f} \user2{g}} \right)\user2{~} $$
(7)

where the spatial variability of the fluid mass density is assumed negligible (i.e., \(\varvec{\nabla} {\rho }_{f}=0\)). M is the so called Biot’s modulus, defined by \(1/M= 1/N + \phi /{K}_{f}\).

The fluid mass change per unit of time within the REV is equal to the variation of flow rate in the direction of the fracture flow, plus the variation of flow rate in the direction perpendicular to the fracture surfaces. The mass balance equation is thus expressed as:

$$ {\varvec{\nabla }}_{{\varvec{s}}} \left[ {\rho_{f} {\varvec{q}(\varvec{s})}} \right] + \left[\kern-0.15em\left[ {\rho_{f} {\varvec{\nu}}\left( {\varvec{s}} \right)} \right]\kern-0.15em\right].{\mathbf{n}}_{{\Gamma_{d} }} + \frac{\partial }{\partial t}\left( {\rho_{f} w} \right) = 0 $$
(8)

where \(\varvec{\nabla }_{{\varvec{s}}}\) represents the gradient in the tangent direction of the local fracture surface, in which s denotes the natural coordinate of the fracture. q is the flow rate inside the fracture. We note \( \left[\kern-0.15em\left[ {\user2{\nu }\left( \user2{s} \right)} \right]\kern-0.15em\right] \) the velocity jump across the fracture. The flow rate q is typically computed by the integral of the velocity over the thickness of the fracture. It can vary with the location s of the point on the fracture surface, and it is related to the pressure gradient in the fracture surface by the following law:

$${\varvec{q}}({\varvec{s}}) = -c({\varvec{s}})\left({\varvec{\nabla} }_{{\varvec{s}}}{\varvec{p}}({\varvec{s}})-{\rho }_{f}{\varvec{g}}\right)=-\frac{{w}^{3}({\varvec{s}})}{12\mu }\left({\varvec{\nabla} }_{{\varvec{s}}}{\varvec{p}}({\varvec{s}})-{\rho }_{f}{\varvec{g}}\right)$$
(9)

where c(s) is the hydraulic conductivity of the fracture at the natural coordinate s. Here, we use Poiseuille fluid flow equation and we calculate c(s) from the cubic law. By substituting the constitutive law (Eq. (9)) and the state equation (Eq. (5)) into Eq. (8), we get the governing equation for fluid flow in the fracture, as follows:

$$ {\left[\kern-0.15em\left[ {\user2{\nu }\left( \user2{s} \right)} \right]\kern-0.15em\right] }.{\varvec{n}}_{{\Gamma_{{d}} }} + \frac{{\partial w\left( {\varvec{s}} \right)}}{\partial t} + \frac{{w\left( {\varvec{s}} \right)}}{{K_{f} }}\frac{{\partial p\left( {\varvec{s}} \right)}}{\partial t} = \varvec{\nabla}_{{\varvec{s}}} .\left[ {\frac{{w^{3} \left( {\varvec{s}} \right)}}{12\mu }\left( {\varvec{\nabla}_{{\varvec{s}}} {\varvec{p}}\left( {\varvec{s}} \right) - \rho_{f} {\varvec{g}}} \right)} \right] $$
(10)

Equation (3), (7) and (10) are usually referred to as the u-p formulation.

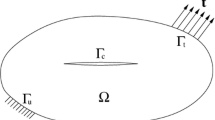
From a physics perspective, the existence of a fracture Γd in the domain Ω leads to a hydro-mechanical coupling between the fracture and the bounding matrix. Fluid flow along the fracture exerts pressure on the two fracture surfaces and pushes them apart, while the two surfaces transmit cohesive traction. Reversely, pressure gradients drive fluid flow into/out of the bounding matrix surrounding the fracture. The essential and natural boundary conditions at the interior boundary Γd are:

$$ \begin{array}{*{20}c} {\user2{\sigma }\user2{.n}_{{\Gamma _{d} }} = \user2{t}_{d} - p\user2{n}_{{\Gamma _{d} }} \;\;on\;\;\Gamma _{d} } \\ {\left( {\user2{\nu }^{ + } - \user2{\nu }^{ - } } \right).\user2{n}_{{\Gamma _{d} }} = \left[\kern-0.15em\left[ \user2{\nu } \right]\kern-0.15em\right].\user2{n}_{{\Gamma _{d} }} = q_{d} \;\;on\;\;{\rm{\Gamma }}_{d} } \\ \end{array} $$
(11)

in which the notations are explained in Fig. 1. td is the cohesive traction which governs the mechanical behavior of the macro-fracture once the fracture is initiated, and qd represents the fluid flow into the matrix, i.e., leak-off in the fracture flow model.

3 Weak Formulation

We first obtain the weak form of the mixture governing equation by multiplying Eq. 4 with a virtual displacement δu and by integrating over the whole domain Ω. After applying the divergence theorem and the boundary conditions, we have:

$$\begin{array}{*{20}c} {\int_{\Omega } {{\varvec{\nabla }}^{{\varvec{s}}} \delta {\varvec{u}}:{\mathbb{C}}({\varvec{\omega}}):} \varvec{\nabla}^{\varvec{s}} u\,d\Omega - \int_{\Omega } {{\varvec{\nabla }}^{{\varvec{s}}} \delta {\varvec{u}}:{\varvec{\alpha}}p{\varvec{d}}\Omega + \int_{{\Gamma_{d} }} {\delta \left[\kern-0.15em\left[ {\varvec{u}} \right]\kern-0.15em\right].\left( {{\varvec{t}}_{d} - {\varvec{pn}}_{{\Gamma_{d} }} } \right)} } {\varvec{d}}\Gamma } \\ { = \int_{{\Gamma_{t} }} {\delta {\varvec{u}}.\overline{\user2{t}}\;{\varvec{d}}\Gamma + \int_{\Omega } {\rho \delta {\varvec{u}}.{\varvec{gd}}\Omega } } } \\ \end{array} $$
(12)

where the kinematic strain-displacement relation \(\varvec{\nabla }^{{\varvec{s}}}{\varvec{u}}={\varvec{\varepsilon}}\) is used, and \(\varvec{\nabla }^{{\varvec{s}}}\) denotes the symmetric part of the gradient operator. We adopt Ritz method, in which the interpolation functions used to approximate the displacement field also serve as weight functions to calculate the weighted integral residuals.

Fig. 1.
figure 1

Boundary conditions on a domain Ω that contains a discontinuity Γd. Ω is subjected to boundary conditions, as follows: Γu (respectively, Γp) is subjected to displacement (respectively, pore pressure); and Γt (respectively, Γq) is subjected to traction (respectively, fluid flux). The discontinuity Γd is treated as an interior boundary with a positive surface Γd+ and a negative surface Γd−, subjected to cohesive traction td+ and td− respectively. Unit normal vectors are noted nΓd+ and nΓd- for the positive and negative fracture surface, respectively. Note that the level set function ϕ is defined so as that it is positive on the side of the domain that contains Γd+, and negative on the side of the domain that contains Γd−. Reprinted by permission from Springer Nature Customer Service Centre GmbH: Springer Nature, Acta Geotechnica, Fluid-driven transition from damage to fracture in anisotropic porous media: a multi-scale XFEM approach, W. Jin and C. Arson, 2020

Full size image

Similarly, the weak form of the governing equation of the fluid (Eq. (7)) is:

$$\begin{array}{c}{\int }_{\Omega }\updelta p\frac{1}{{\varvec{M}}}\frac{\partial p}{\partial t}\boldsymbol{ }\rm{d\Omega } + {\int }_{\Omega }\updelta p \boldsymbol{\alpha }:\varvec{\nabla }^{{\varvec{s}}}\frac{\partial {\varvec{u}}}{\partial t}\rm{d\Omega} + {\int }_{\Omega }\varvec{\nabla}\updelta p . \left(\frac{{{\varvec{k}}}_{{\varvec{m}}}\left({\varvec{\omega}}\right)}{{\varvec{\mu}}}\varvec{\nabla} p\right)\rm{d\Omega} \\ -{\int }_{{\Gamma }_{d}}\updelta p {q}_{d}d\Gamma = -{\int }_{{\Gamma }_{d}}\updelta p \stackrel{-}{q}d\Gamma + {\int }_{\Omega }\left(\frac{{\rho }_{f}{{\varvec{k}}}_{{\varvec{m}}}\left({\varvec{\omega}}\right)}{{\varvec{\mu}}}\right)\varvec{\nabla}\updelta p . {\varvec{g}}d\Omega \end{array}$$
(13)

Note that δp is the virtual pressure that satisfies \({\left.\delta p\right|}_{{\Gamma }_{p}}\boldsymbol{ }=0\). The boundary condition \(\frac{{{\varvec{k}}}_{{\varvec{m}}}}{\mu }\boldsymbol{ }\left(-\varvec{\nabla} {\varvec{p}}\boldsymbol{ }+\boldsymbol{ }{\rho }_{f}\,\boldsymbol{ }{\varvec{g}}\right).{\mathbf{n}}_{{\varvec{\Gamma}}}={\varvec{v}}.{\mathbf{n}}_{{\varvec{\Gamma}}}=\overline{{\varvec{q}}}\) is used for the exterior boundary Γq. In Eq. (13), the term \({\int }_{{\Gamma }_{d}}\updelta p\,\,\, {q}_{d}d\Gamma \) indicates that the velocity of the fluid normal to the fracture is discontinuous. According to Darcy’s law, that means that the gradient of fluid pressure along the normal to the fracture surface is also discontinuous. However, the fluid pressure field and the virtual pressure should be continuous across the fracture so that Darcy’s law can be applied. So, we use the same virtual pressure δp as in Eq. (13) to multiply the governing equation of the fluid flowing in the fracture (Eq. 10), and we integrate it over the fracture domain \({\Gamma }_{d}\) to obtain the following weak form:

$$ \begin{array}{*{20}c} {\int_{{\Gamma_{d} }} {\delta p\left[\kern-0.15em\left[ \nu \right]\kern-0.15em\right]} .{\varvec{n}}_{{\Gamma_{d} }} \,\rm{d}\Gamma = \int_{{\Gamma_{d} }} {\delta p\,q_{d} } \,\rm{d}\Gamma } =\\ { - \int_{{\Gamma_{d} }} {\delta p\frac{\partial w}{{\partial t}}} \,\rm{d}\Gamma - \int_{{\Gamma_{d} }} {\delta p} \frac{w}{{K_{f} }}\frac{\partial p}{{\partial t}}\,\rm{d}\Gamma - \int_{{\Gamma_{d} }} {\varvec{\nabla} m\,\delta p.\left[ {\frac{{w^{3} }}{12\mu }\varvec{\nabla} m\,p} \right]\rm{d}\Gamma + \delta p\left.\,\, {Q_{in} } \right|_{s = 0} } } \\ \end{array} $$
(14)

where \({\varvec{\nabla} }_{{\varvec{m}}}\) denotes the one-dimensional gradient along the fracture tangent direction (\({{\varvec{m}}}_{{\Gamma }_{d}}\), as shown in Fig. 1) and Qin is a fluid injection rate applied at the fracture mouth (s = 0). The width of the fracture is computed as:

$$ w = \left( {{\mathbf{u}}^{{\mathbf{ + }}} - {\mathbf{u}}^{{\mathbf{ - }}} } \right).\eta_{{\Gamma_{d} }} = \left[\kern-0.15em\left[ {\varvec{u}} \right]\kern-0.15em\right].\varvec{n}_{{\Gamma_{d} }} $$
(15)

The weak form of the governing equation for the fluid flow inside the fracture can be directly injected into the weak form of the governing equation for the fluid flowing in the matrix (Eq. 13), since the same virtual field δp is used.

4 Transition Between Continuum and Discrete

4.1 Finite Element Method (FEM) and Cohesive Zone (CZ) Elements

One way of coupling the evolution of damage in the DPC to the propagation of a macro-scale discontinuity is to formulate a constitutive law for a domain that contains a fraction of discrete fracture (closed or open) embedded in the DPC. The fracture is modeled by a CZ element, in which the hardening behavior is governed by a CDM model, up to a critical value of damage (e.g., the critical damage Ωcr shown in Fig. 2, which can represent an isotropic damage variable, or the norm of a damage tensor), while the post-peak softening behavior is governed by a softening traction-separation law, as illustrated in Fig. 2.

Fig. 2.
figure 2

Conceptual model of CDM – based cohesive law

Full size image

Cohesive elements have a reduced number of degrees of freedom, because only the normal and shear displacement jumps across the fracture are considered. For example, the 8-node 3-D cohesive element shown in Fig. 3 has only 12 degrees of freedom (dof): two shear jump dofs and one normal jump dof per pair of nodes, where a pair here is formed by two nodes separated by the element thickness. We can represent the 3-D 8-node cohesive element as a four-node 2-D plane element that lies in the so-called “mid-layer”. In the following, we derive the Jacobian matrix of the 8-node 3-D cohesive element. We note \((X,Y,Z)\) the global coordinate system, and (\(r,s,t)\) the local orthogonal coordinate system (Fig. 3). We introduce the natural coordinate system (\(\xi ,\eta , \zeta )\) to derive the equations of the standard (master) element.

Fig. 3.
figure 3

Geometry and coordinate systems in the thin layered element

Full size image

We define four vectors 2 \(\mathop{P}\limits^{\rightharpoonup} _{i} \left( {{\text{i }} = { }1,{ }2,{ }3,{ }4} \right)\) that provide the displacement jump of the element at each of the four nodes in the mid-layer. Linear interpolation functions are adopted. Therefore, the position vector [\(X,Y,Z]\) of a point inside the element can be described by the position vector of the mid-layer \(\left[ {\overline{X},\overline{Y},\overline{Z}} \right]\) and the vector \(\mathop{P}\limits^{\rightharpoonup} \):

$$ \left[ {X,Y,Z} \right] = \left[ {\overline{X},\overline{Y},\overline{Z}} \right] + \zeta \overline{P}_{i} $$
(16)

where the position vector \(\left[ {\overline{{X_{i} }} , \overline{{Y_{i} }} , \overline{{Z_{i} }} } \right]\) of a node in the mid-layer is calculated as the average position vector of the corresponding nodes in the upper and lower surfaces. We adopt the 2 \(\times \) 2 Gauss integration scheme for planar linear elements. The interpolation functions at the Gauss point are noted: \({\psi }_{1}=\frac{1}{4} (1-\xi )(1-\eta )\), \({\psi }_{2}=\frac{1}{4} (1+\xi )(1-\eta )\), \({\psi }_{3}=\frac{1}{4} (1+\xi )(1+\eta )\), \({\psi }_{4}=\frac{1}{4} (1-\xi )(1+\eta )\). The position vector for an integration point in the mid-layer can then be calculated as follows:

$$ \begin{array}{*{20}c} {\bar{X} = \sum\nolimits_{{i = 1}}^{4} {\psi _{i} ~\overline{{X_{i} ,}} } } & {\overline{Y} = \sum\nolimits_{{i = 1}}^{4} {\psi _{i} ~\overline{{Y_{i} }} } } \\ \end{array} $$
(17)

Since the thickness change of the element is small compared to the changes of length in the other directions, the third component of the position vector \((Z)\) of a point inside the element can be approximated as the position vector in the mid-layer \([\overline{X} , \overline{Y}, \overline{Z}]\), plus half of the vector of thickness direction \(\mathop{P}\limits^{\rightharpoonup} \), as follows:

$$ \left[ {X, Y,Z} \right] = \sum\nolimits_{i = 1}^{4} {\psi_{i} } ([\overline{X} , \overline{Y}, \overline{Z}] + \zeta \mathop{P}\limits^{\rightharpoonup} _{i} ) $$
(18)

The Jacobian matrix for a standard 3D linear element is given as (Reddy 2004):

$$J=\left[\begin{array}{ccc}\frac{\partial r}{\partial \xi }& \frac{\partial s}{\partial \xi }& \frac{\partial t}{\partial \xi }\\ \frac{\partial r}{\partial \eta }& \frac{\partial s}{\partial \eta }& \frac{\partial t}{\partial \eta }\\ \frac{\partial r}{\partial \zeta }& \frac{\partial s}{\partial \zeta }& \frac{\partial t}{\partial \zeta }\end{array}\right]={\left[\begin{array}{ccc}r& s& t\end{array}\right]}^{T} [\begin{array}{ccc}\frac{\partial }{\partial \xi }& \frac{\partial }{\partial \eta }& \frac{\partial }{\partial \zeta }\end{array}]$$
(19)

Notice that in the local coordinate system (\(r,s,t)\), the interpolation relationships still hold. Since t = 0 in the mid-layer, we have:

$$ \left[ {\begin{array}{*{20}c} r & s & t \\ \end{array} } \right]^{T} = \sum\nolimits_{i = 1}^{4} {\psi_{i} } \left( {\left[ {\begin{array}{*{20}c} {\overline{r}_{i} } & {\overline{s}_{i} } & 0 \\ \end{array} } \right]^{T} + \zeta \mathop{P}\limits^{\rightharpoonup} _{i} } \right) $$
(20)

where here, \(\mathop{P}\limits^{\rightharpoonup} \) is expressed in the local coordinate system. Substituting \(\left[ {\begin{array}{*{20}c} r & s & t \\ \end{array} } \right]^{T} = \sum\nolimits_{i = 1}^{4} {\psi_{i} } \left( {\left[ {\begin{array}{*{20}c} {\overline{r}_{i} } & {\overline{s}_{i} } & 0 \\ \end{array} } \right]^{T} + \zeta \mathop{P}\limits^{\rightharpoonup} _{i} } \right)\) into the expression of Jacobian, the Jacobian matrix of the 3-D cohesive element in local coordinates (\(r, s, t\)) is thus obtained as:

$$J={\left[\begin{array}{ccc}{\sum }_{i=1}^{4} {\left[\begin{array}{ccc}r\,\,\, s \,\,\,0\end{array}\right]}^{T}\frac{{\partial \psi }_{i}}{\partial \xi }+\zeta \frac{\partial \stackrel{-}{P}}{\partial \xi }, {\sum }_{i=1}^{4} {\left[\begin{array}{ccc}r\,\,\, s \,\,\,0\end{array}\right]}^{T}\frac{{\partial \psi }_{i}}{\partial \eta }+\zeta \frac{\partial \stackrel{-}{P}}{\partial \eta }, \overline{P}\end{array}\right]}^{T}$$
(21)

in which we note \(\sum\nolimits_{i = 1}^{4} {\psi_{i} } \mathop{P}\limits^{\rightharpoonup} _{l} = \overline{P}\). Notice that the local coordinates \({\left[\begin{array}{ccc}r& s& t\end{array}\right]}^{T}\) are transformed from the global coordinates \({\left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^{T}\) by using the transformation matrix \({\varvec{T}}\), as follows:

$${\left[\begin{array}{ccc}r& s& t\end{array}\right]}^{T}={{\varvec{T}}}^{T}{\left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^{T}$$
(22)

Let \(v={\left[\begin{array}{ccc}r& s& t\end{array}\right]}^{T}\), \({V=\left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^{T}\). The transformation matrix for a 2D plane in 3D space is: \({\varvec{T}}=[{V}_{r} {V}_{s} {V}_{t}]\), where \({V}_{r}, {V}_{s}, {V}_{t}\) are base vectors for the 2D plane and are expressed as (Kim et al. 2003):

$${V}_{r}=\frac{{V}_{\xi }}{{|V}_{\xi }|}, {V}_{s}={V}_{t}\times {V}_{r}, {V}_{t}=\frac{{V}_{\xi }\times {V}_{\eta }}{|{V}_{\xi }\times {V}_{\eta }|}$$
(23)

where \({V}_{\xi }={{\sum }_{i=1}^{4}\frac{\partial {\psi }_{i}}{\partial \xi } \left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^{T}\) and \({V}_{\eta }={{\sum }_{i=1}^{4}\frac{\partial {\psi }_{i}}{\partial \eta } \left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^{T}\). We now substitute \(v=\left[\begin{array}{ccc}{V}_{r}^{T}& {V}_{s}^{T}& {V}_{t}^{T}\end{array}\right] V\) into the expression of the Jacobian in local coordinates:

$$J=\left[\begin{array}{ccc}{V}_{r}^{T}({V}_{\xi }+\zeta \frac{\partial \overline{P}}{\partial \xi })& {V}_{s}^{T}({V}_{\xi }+\zeta \frac{\partial \overline{P}}{\partial \xi })& {V}_{t}^{T}({V}_{\xi }+\zeta \frac{\partial \overline{P}}{\partial \xi })\\ {V}_{r}^{T}({V}_{\eta }+\zeta \frac{\partial \overline{P}}{\partial \eta })& {V}_{s}^{T}({V}_{\eta }+\zeta \frac{\partial \overline{P}}{\partial \eta })& {V}_{t}^{T}({V}_{\eta }+\zeta \frac{\partial \overline{P}}{\partial \eta })\\ {V}_{r}^{T}\overline{P}& {V}_{s}^{T}\overline{P}& {V}_{t}^{T}\overline{P}\end{array}\right]$$
(24)

in which we used vector notations \({V}_{\xi }\) and \({V}_{\eta }\) for compactness.

4.2 EXtended Finite Element Method (XFEM) and CZ Segments

An alternative to inserting CZ elements between all finite elements is to discretize the governing equations with the XFEM. The Heaviside enrichment function is employed to account for the displacement jump across the macro-fracture. The approximate function of displacement \({{\varvec{u}}}^{{\varvec{h}}}({\varvec{x}},t)\) is expressed in the following form:

$$\begin{array}{c}{{\varvec{u}}}^{{\varvec{h}}}\left({\varvec{x}},{\varvec{t}}\right)\boldsymbol{ }=\boldsymbol{ }\sum_{{\varvec{i}}\in {\varvec{S}}}{N}_{ui}({\varvec{x}}){{\varvec{u}}}_{{\varvec{i}}}({\varvec{t}})\boldsymbol{ }+\boldsymbol{ }\sum_{{\varvec{i}}\in {{\varvec{S}}}_{{\varvec{H}}}}{N}_{ui}({\varvec{x}})\frac{1}{2}\left[{H}_{{\Gamma }_{d}}({\varvec{x}})-{H}_{{\Gamma }_{d}}({{\varvec{x}}}_{{\varvec{i}}})\right]{{\varvec{a}}}_{{\varvec{i}}}({\varvec{t}})\boldsymbol{ }\\ =\boldsymbol{ }{{\varvec{N}}}_{{\varvec{u}}}({\varvec{x}}){\varvec{U}}({\varvec{t}})\boldsymbol{ }+\boldsymbol{ }{{\varvec{N}}}_{{\varvec{a}}}({\varvec{x}}){\varvec{A}}({\varvec{t}})\end{array}$$
(25)

where Nui(x) is the standard shape function associated with node i, S is the set of all nodal points and SH is the set of enriched nodes, the supports of which are bisected by the fracture. ui(x) and ai(x) denote the nodal value of the displacement field associated with the standard and enriched degree of freedoms, respectively. The Heaviside jump function H(x) is defined as

$${H}_{{\Gamma }_{d}}({\varvec{x}})= \left\{\begin{array}{c}+1, \phi (\varvec{x}) > 0\\ -1, \phi (\varvec{x}) < 0\end{array}\right.$$
(26)

where ϕ(x) is the level set function, which is defined as the closest distance from the fracture surface, positive or negative, depending on which side of the fracture the point x is located (Fig. 1). The displacement jump across the fracture Γd is:

$$ \left[\kern-0.15em\left[ {{\varvec{u}}({\varvec{x}},{\varvec{t}})} \right]\kern-0.15em\right] = \sum\nolimits_{{{\varvec{i}} \in {\varvec{S}}_{{\varvec{H}}} }} {N_{ui} ({\varvec{x}}){\varvec{a}}_{{\varvec{i}}} ({\varvec{t}}) = {\varvec{N}}_{a} ({\varvec{x}}){\varvec{A}}({\varvec{t}})} $$
(27)

Note that the displacement jump is directly used to calculate the fracture aperture w in the fluid flow equation (Eq. (15)). For the fluid pressure field, enrichment is done with the distance function. The approximate pressure field is expressed as:

$$\begin{array}{c}{p}^{h}({\varvec{x}},{\varvec{t}})=\sum_{{\varvec{i}}\in {\varvec{S}}}{N}_{pi}({\varvec{x}}){p}_{i}({\varvec{t}})+\sum_{{\varvec{i}}\in {{\varvec{S}}}_{{\varvec{H}}}}{N}_{pi}({\varvec{x}})\left[{D}_{{\Gamma }_{d}}({\varvec{x}})-{D}_{{\Gamma }_{d}}({{\varvec{x}}}_{{\varvec{i}}})\right]{R({\varvec{x}}){\varvec{b}}}_{{\varvec{i}}}({\varvec{t}})\\ = {{\varvec{N}}}_{{\varvec{p}}}({\varvec{x}}){\varvec{P}}({\varvec{t}})+{{\varvec{N}}}_{{\varvec{b}}}({\varvec{x}}){\varvec{B}}({\varvec{t}})\end{array}$$
(28)

where Npi(x) is the standard finite element shape function associated with node i. Nodal sets S and SH are the same as for the displacement field. pi(t) and bi(t) denote the nodal value of the fluid pressure associated with the standard and enriched degree of freedom, respectively. \({D}_{{\Gamma }_{d}}({\varvec{x}})\) is the distance function, defined as

$${D}_{{\Gamma }_{d}}({\varvec{x}})= \left\{\begin{array}{c}+\phi (x), \phi (x) > 0\\ -\phi (x), \phi (x) < 0\end{array}\right.$$
(29)

The gradient of the distance function along the direction normal to the fracture is discontinuous, with: \({\nabla} {D}_{{\Gamma }_{d}}.{{\varvec{n}}}_{{\Gamma }_{d}}={H}_{{\Gamma }_{d}}\). As a result, enriching the FEM with the distance function for the pressure field ensures a continuous pressure field and a discontinuous gradient of pressure across the fracture. Thus, the fluid exchange between the fracture and the matrix can be accounted for. Similar to the displacement approximation, the shifted enrichment function \(\left[{D}_{{\Gamma }_{d}}({\varvec{x}})-{D}_{{\Gamma }_{d}}({{\varvec{x}}}_{{\varvec{i}}})\right]\) is used and R(x) is a weight function, defined as \(R({\varvec{x}}) = \sum_{i\in {S}_{H}}{N}_{pi}({\varvec{x}})\), as proposed by Mohammadnejad and Khoei (2013). It is worth noting that the pressure field at the tip of the fracture does not need to be enriched to satisfy the ‘‘no leakage flux’’ boundary condition. By substituting the approximations (Eqs. (25) and (28)) into the governing weak form equations (Eqs. (3), (7), (10)), we can obtain the discretized form of the governing equations, as follows:

$${{\varvec{K}}}_{{\varvec{u}}{\varvec{u}}}{\varvec{U}} + {{\varvec{K}}}_{{\varvec{u}}{\varvec{a}}}{\varvec{A}} - {{\varvec{Q}}}_{{\varvec{u}}{\varvec{p}}}{\varvec{P}} -{{\varvec{Q}}}_{{\varvec{u}}{\varvec{b}}}{\varvec{B}} - {{\varvec{F}}}_{{\varvec{u}}}^{{\varvec{e}}{\varvec{x}}{\varvec{t}}}=0$$
(30a)
$${{\varvec{K}}}_{{\varvec{u}}{\varvec{a}}}^{{\varvec{T}}}{\varvec{U}}\boldsymbol{ }+{{\varvec{K}}}_{{\varvec{a}}{\varvec{a}}}{\varvec{A}}\boldsymbol{ }-{{\varvec{Q}}}_{{\varvec{a}}{\varvec{p}}}{\varvec{P}}\boldsymbol{ }-{{\varvec{Q}}}_{{\varvec{a}}{\varvec{b}}}{\varvec{B}}\boldsymbol{ }-{{\varvec{Q}}}_{{\varvec{a}}{\varvec{d}}}{{\varvec{P}}}_{{\varvec{d}}}\boldsymbol{ }+{{\varvec{F}}}_{{\varvec{a}}}^{{\varvec{i}}{\varvec{n}}{\varvec{t}}}-{{\varvec{F}}}_{{\varvec{a}}}^{{\varvec{e}}{\varvec{x}}{\varvec{t}}}=\boldsymbol{ }0$$
(30b)
$${{\varvec{Q}}}_{{\varvec{u}}{\varvec{p}}}^{{\varvec{T}}}\dot{{\varvec{U}}}\boldsymbol{ }+{{\varvec{Q}}}_{{\varvec{a}}{\varvec{p}}}^{{\varvec{T}}}\dot{{\varvec{A}}}+{{\varvec{M}}}_{{\varvec{p}}{\varvec{p}}}\dot{{\varvec{P}}}\boldsymbol{ }+{{\varvec{M}}}_{{\varvec{p}}{\varvec{b}}}\dot{{\varvec{B}}}\boldsymbol{ }+\boldsymbol{ }{{\varvec{H}}}_{{\varvec{p}}{\varvec{p}}}{\varvec{P}}\boldsymbol{ }+{{\varvec{H}}}_{{\varvec{p}}{\varvec{b}}}{\varvec{B}}\boldsymbol{ }-{{\varvec{F}}}_{{\varvec{p}}}^{{\varvec{i}}{\varvec{n}}{\varvec{t}}}-{{\varvec{F}}}_{{\varvec{p}}}^{{\varvec{e}}{\varvec{x}}{\varvec{t}}}=\boldsymbol{ }0$$
(30c)
$${{\varvec{Q}}}_{{\varvec{u}}{\varvec{b}}}^{{\varvec{T}}}\dot{{\varvec{U}}}\boldsymbol{ }+{{\varvec{Q}}}_{{\varvec{a}}{\varvec{b}}}^{{\varvec{T}}}\dot{{\varvec{A}}}+{{\varvec{M}}}_{{\varvec{b}}{\varvec{p}}}\dot{{\varvec{P}}}\boldsymbol{ }+{{\varvec{M}}}_{{\varvec{b}}{\varvec{b}}}\dot{{\varvec{B}}}\boldsymbol{ }+\boldsymbol{ }{{\varvec{H}}}_{{\varvec{p}}{\varvec{b}}}^{{\varvec{T}}}{\varvec{P}}\boldsymbol{ }+{{\varvec{H}}}_{{\varvec{b}}{\varvec{b}}}{\varvec{B}}\boldsymbol{ }-{{\varvec{F}}}_{{\varvec{b}}}^{{\varvec{i}}{\varvec{n}}{\varvec{t}}}-{{\varvec{F}}}_{{\varvec{b}}}^{{\varvec{e}}{\varvec{x}}{\varvec{t}}}=\boldsymbol{ }0$$
(30d)

in which Nu(x) and Np(x) (respectively, Na(x) and Nb(x)) are the matrices of standard (respectively, enriched) shape functions for the displacement field u and for the pressure field p, respectively. U(t) and P(t) (respectively, A(t) and B(t)) are the vectors of the standard (respectively, enriched) displacement and pressure degrees of freedom, respectively. The expressions of the matrices in Eq. (30a, b, c, d) are explained in detail in (Jin and Arson, 2020). In order to simplify the notations, we condense the enriched and standard degrees of freedom for displacement and pressure as \({\mathbb{U}}({\varvec{U}},{\varvec{A}})\) and \({\mathbb{P}}({\varvec{P}},{\varvec{B}})\), respectively. The weak form of the governing equation discretized in space (Eq. (30)) can be rewritten as:

$$\begin{array}{c}{\varvec{K}}{\mathbb{U}}\boldsymbol{ }-\boldsymbol{ }{\varvec{Q}}{\mathbb{P}}+{{\varvec{F}}}_{\mathbb{U}}^{{\varvec{i}}{\varvec{n}}{\varvec{t}}}\left({\mathbb{U}},{\mathbb{P}}\right)\boldsymbol{ }-\boldsymbol{ }{{\varvec{F}}}_{\mathbb{U}}^{{\varvec{e}}{\varvec{x}}{\varvec{t}}}\boldsymbol{ }=\boldsymbol{ }0\\ {{\varvec{Q}}}^{{\varvec{T}}}{\mathbb{U}}\boldsymbol{ }+\boldsymbol{ }{\varvec{M}}{\mathbb{P}}\boldsymbol{ }+\boldsymbol{ }{\varvec{H}}{\mathbb{P}}-{{\varvec{F}}}_{\mathbb{P}}^{{\varvec{i}}{\varvec{n}}{\varvec{t}}}\left({\mathbb{U}},{\mathbb{P}}\right)\boldsymbol{ }-\boldsymbol{ }{{\varvec{F}}}_{\mathbb{P}}^{{\varvec{e}}{\varvec{x}}{\varvec{t}}}\boldsymbol{ }=\boldsymbol{ }0\end{array}$$
(31)

To solve the above equations, we use a linear time discretization scheme. After injecting the time discretization equations into the spatially discretized governing equations (Eq. 31), we obtain the residual at time step n + 1, as follows:

$$ \begin{array}{*{20}c} {{\varvec{R}}_{{{\mathbb{U}},{\varvec{n}} + 1}} \user2{ } = \user2{ K}{\mathbb{U}}_{{{\varvec{n}} + 1}} \user2{ } - \user2{ Q}{\mathbb{P}}_{{{\varvec{n}} + 1}} \user2{ } + \user2{ F}_{{{\mathbb{U}}_{{{\varvec{n}} + 1}} }}^{{{\varvec{int}}}} \user2{ } - \user2{ F}_{{{\mathbb{U}}_{{{\varvec{n}} + 1}} }}^{{{\varvec{ext}}}} = \user2{ }0} \\ {{\varvec{R}}_{{{\mathbb{P}},{\varvec{n}} + 1}} \user2{ } = \user2{ Q}^{{\varvec{T}}} {\mathbb{U}}_{{{\varvec{n}} + 1}} \user2{ } + \user2{ }\left( {{\varvec{M}} + \theta {\Delta }t{\varvec{H}}} \right){\mathbb{P}}_{{{\varvec{n}} + 1}} - \user2{ F}_{{{\mathbb{P}}_{{{\varvec{n}} + 1}} }}^{{{\varvec{int}}}} \user2{ } - \user2{ G}_{{{\mathbb{P}}_{{{\varvec{n}} + 1}} }} \user2{ } = \user2{ }0} \\ \end{array} $$
(32)

in which the weight θ can be any value between 0 and 1, and \({G}_{{\mathbb{P}}_{n+1}}\) is the vector of known values at time step n, expressed as:

$$\begin{array}{*{20}c} {G_{{\rm{\mathbb{P}}_{{\user2{n} + 1}} }} = \Delta \user2{t}\;\user2{F}_{{\rm{\mathbb{P}}_{{\user2{n} + 1}} }}^{{\user2{int}}} + \user2{Q}^{\user2{T}} \rm{\mathbb{U}}_{\user2{n}} + \left( {\user2{M} - \Delta \user2{t}(1 - \theta )\user2{H}} \right)\rm{\mathbb{P}}_{\user2{n}} + \int_{{\Gamma _{d} }} {\user2{N}_{\rm{\mathbb{P}}}^{\user2{T}} \frac{\user2{w}}{{\user2{K}_{\user2{f}} }}p_{n} \user2{d}\Gamma } } \\ { + \int_{{\Gamma _{d} }} {\user2{N}_{\rm{\mathbb{P}}}^{\user2{T}} \left[\kern-0.15em\left[ \user2{u} \right]\kern-0.15em\right]_{n} .\user2{n}_{{\Gamma _{d} }} \,\user2{d}\Gamma - } \Delta t\left( {1 - \theta } \right)\int_{{\Gamma _{d} }} {\varvec{\nabla}\user2{N}_{\rm{\mathbb{P}}}^{\user2{T}} .\user2{m}_{{\Gamma _{d} }} \,\frac{{w^{3} }}{{12\mu }}} \varvec{\nabla} p_{n} \user2{.m}_{{\Gamma _{d} }} \user2{d}\Gamma } \\ \end{array} $$
(33)

and \({F}_{{\mathbb{P}}_{n+1}}^{int}\) is the flux vector that accounts for the mass exchange between the matrix and the fracture at time step n + 1:

$$ \begin{array}{*{20}c} {{\varvec{F}}_{{{\mathbb{P}}_{{{\varvec{n}} + 1}} }}^{{{\varvec{int}}}} = - \int_{{\Gamma_{d} }} {{\varvec{N}}_{{\mathbb{P}}}^{{\varvec{T}}} \frac{{\varvec{w}}}{{{\varvec{K}}_{{\varvec{f}}} }}p_{n + 1} \,{\varvec{d}}\Gamma } - \int_{{\Gamma_{d} }} {{\varvec{N}}_{{\mathbb{P}}}^{{\varvec{T}}} \left[\kern-0.15em\left[ {\varvec{u}} \right]\kern-0.15em\right]_{n + 1} .{\varvec{n}}_{{\Gamma_{d} }} \,{\varvec{d}}\Gamma } } \\ { - \Delta t\,{\theta}\int_{{\Gamma_{d} }} \varvec{\nabla}{{\varvec{N}}_{{\mathbb{P}}}^{{\varvec{T}}} .{\varvec{m}}_{{\Gamma_{d} }} \frac{{w^{3} }}{12\mu }} \varvec{\nabla} p_{n + 1} \user2{.m}_{{\Gamma_{d} }} \,{\varvec{d}}\Gamma + \Delta t\,{\varvec{N}}_{{\mathbb{P}}} \left. {Q_{in} } \right|_{s = 0} } \\ \end{array} $$
(34)

The nonlinear system (Eq. (32)) is solved iteratively (Jin and Arson 2020). The transition between CDM and CZ is triggered when the invariants of the damage tensor meet a threshold condition (similar to a yield condition in plasticity). To compute the damage value at the crack tip, we adopt the method proposed by Wang and Waisman (2016) and Wells et al. (2002). As shown in Fig. 4, we assume that the fracture propagates when the maximum component of the weighted damage vector over the half-circle patch (shaded in blue) exceeds the threshold ωcrit.

The macro-fracture propagates in the direction \({\overline{{\varvec{d}}}}_{{\varvec{i}}}\), calculated as the weighted average of the damage directions in the half-circle patch, as follows:

$${\overline{{\varvec{d}}}}_{{\varvec{i}}}({{\varvec{x}}}_{{\varvec{t}}{\varvec{i}}{\varvec{p}}})={\int }_{{\Omega }_{T}}\alpha ({{\varvec{x}}}_{{\varvec{t}}{\varvec{i}}{\varvec{p}}},{\varvec{\xi}}){\omega }_{i}\left({\varvec{\xi}}\right)\frac{{\varvec{d}}}{\Vert {\varvec{d}}\Vert }{\varvec{d}}\rm{\Omega }_{T}\left({\varvec{\xi}}\right), (i=\mathrm{1,2})$$
(35)

where \({\varvec{d}} ={\varvec{\xi}}- {{\varvec{x}}}_{tip}\), as shown in Fig. 4. If the damage invariants meet the threshold function, we propagate the fracture in the direction of \({\overline{{\varvec{d}}}}_{{\varvec{i}}}\) with a user-defined growth length Δa. Since only the Heaviside function is used for XFEM discretization, no cohesive segment is inserted into the tip element if the fracture tip is located inside an element.

Fig. 4.
figure 4

Principle of the transition CDM model - CZ segment with the XFEM. Reprinted by permission from Springer Nature Customer Service Centre GmbH: Springer Nature, Acta Geotechnica, Fluid-driven transition from damage to fracture in anisotropic porous media: a multi-scale XFEM approach, W. Jin and C. Arson 2020

Full size image

It is worth noting that for a given time increment, the size of the zone in which damage satisfies the transition criterion may exceed the growth length Δa. Thus, we repeat the above calculation until the damage invariants meet the threshold criterion. Within a single time increment, the length of the propagated fracture equals several times Δa. Every time the fracture grows by a length Δa, we add extra degrees of freedom at the enriched nodes, and we add enriched shape functions for the elements that contain newly enriched nodes. In addition, to ensure consistent displacement jumps across the fracture, we adopt the classical sub-region quadrature technique to divide a quadrilateral element into multiple triangles, as illustrated in Fig. 4. We use three Gauss points within each triangle to calculate the Jacobian matrix and the residual. To transform the internal and state variables from the initial to the new set of Gauss points, we adopt the Super-convergent Patch Recovery (SPR) method proposed by Zienkiewicz and Zhu (1992). After remapping, we recheck the propagation criterion and repeat all the follow-up steps. If the propagation criterion is not satisfied, we march to the next increment and construct the global matrix equations, and the problem is iteratively solved. After convergence is reached and the results are postprocessed, the fracture propagation procedure is repeated.

5 Calibration

5.1 Finite Element Method (FEM) and Cohesive Zone (CZ) Elements

The FEM-based CZ model is calibrated in three steps: (i) CDM parameters in the hardening regime; (ii) Critical damage threshold; (iii) Softening parameters. Typically, the CDM parameters can be found iteratively by fitting simulated stress/strain curves to experimental data, e.g., triaxial compression results. We used parallel computing algorithms in MATLAB to accelerate the calibration process. The program keeps comparing the simulation results with stress-strain curves obtained from laboratory tests and gradually narrows down the searching range to obtain the set of parameters that can best predict the mechanical behavior of the tested material. The initial searching area still needs to be defined prior to the automatic calibration process. In the case of the DSID model (Xu and Arson 2014), which is an energy-based CDM model, we can observe that, for rock materials subjected to triaxial loading conditions: (1) The initial (reference, pre-loading) elastic modulus \({E}_{0}\) and Poisson’s ratio \({v}_{0}\) govern the mechanical behavior before damage occurs, so these two parameters can be estimated based on the linear portion of the experimental stress-strain curve; (2) The parameter \({a}_{2}\) that is needed to express the free energy and controls the evolution of the principal stress directions, has the most significant influence on rock damage; (3) The initial damage threshold parameter \({C}_{0}\) governs the initiation of damage. Therefore, the initialization of the parameters of the DSID model can be done by searching first the range of values of only four parameters: \({E}_{0}\), \({v}_{0}\), \({a}_{2}\) and \({C}_{0}\). After estimating these four parameters, the MATLAB program is used to find the other parameters and to refine the initial estimation of the four initialization parameters. After calibration of the CDM parameters, the material compression strength is found by calculating the peak stress. The corresponding damage tensor is set as the critical damage threshold. Lastly, the softening parameters are calibrated to minimize the distance between the experimental and simulated stress/strain curves. Figure 5 shows material-point simulation results obtained by coupling the DSID model to a linear softening CZ model. Damage initiation under tensile loading occurred at the very early stage of the loading and tensile strength is much lower than shear strength, as could be expected for a rock material. In Fig. 5.b, the same shearing deformation is applied under different levels of compressive strain (applied in the \(z\) – direction). It can be observed that, at a higher compressive strain, the mean stress level increases and so do the stiffness and shear strength. This is typical of most geomaterials, which exhibit material hardening. The approach used here can be extended to any CDM model and to any CZ softening model.

Fig. 5.
figure 5

One-element simulation results obtained with MATLAB for one CDM-based cohesive element on: (a) normal direction and (b) shearing direction.

Full size image

5.2 EXtended Finite Element Method (XFEM) and CZ Segments

In the XFEM-based coupling approach, the direction of propagation of the discrete fracture is not known a priori, and solving for the critical damage thresholds in several directions of space is usually not feasible. That is why a damage measure is often defined to set a threshold empirically. For example, the threshold can be found by calculating the values of the damage components beyond which the damaged stiffness components predicted by the CDM model depart from those predicted by a micro-mechanical model that accounts for micro-crack interaction (Jin et al. 2017, Jin and Arson 2019). In phenomenological CDM models, the damage threshold is typically reached when principal damage components equal a value between 0.1 and 0.3. The CDM and CZ parameters are calibrated in the same way as in the FEM-based coupling approach. First, a FEM model without discrete fractures is used to simulate laboratory tests and CDM parameters are adjusted to match numerical stress/strain curves to experimental results in the hardening regime. Then, the coupled CDM-CZ model is used to simulate the tests once more, and the CZ parameters are calibrated to match the stress/strain curve in the softening regime, beyond the critical damage threshold. Figure 6 shows an example of calibration simulation for a micromechanical damage model coupled with the Park–Paulino–Roesler CZ model (Park et al. 2009).

The tip of the macro cohesive fracture is behind the front of the process zone at all stages, which indicates a smooth transition from damage to fracture. The size of the process zone is constant throughout the simulation. All the simulated cases show that the evolution of energy follows three phases. In the initial phase, all the input work is transformed and stored as elastic energy within the system. In the second phase, energy is dissipated by micro-crack and macro-fracture propagation while the elastic energy of the system keeps increasing. In the final phase, most of the input work is dissipated immediately, and some of the stored elastic energy gets dissipated as well, to propagate the micro-cracks and the macro-fracture. The elastic energy of the system tends to zero. We can also note that the percentage of energy dissipated by micro-crack propagation (damage development) is significantly smaller than the amount of energy dissipated by macro-fracture surface formation.

Fig. 6.
figure 6

Simulation of a splitting wedge test with an XFEM-based CDM-CZ model. Left: Load vs. CMOD response: comparison of numerical and experimental results. Right: Contour of the damage component Ωy (horizontal micro cracks) and macro cohesive fracture path shown on the deformed mesh (displacements magnified x 5). Reprinted from Computer Methods in Applied Mechanics and Engineering, vol. 357, W. Jin and C. Arson, XFEM to couple nonlocal micromechanics damage with discrete mode I cohesive fracture, p.18, copyright 2019, with permission from Elsevier.

Full size image

6 Conclusions

The coupling between CDM and CZ models relies on an energy equivalence criterion to determine the cohesive strength and the cohesive energy release rate, such that the total dissipated energy by propagating macro-fracture and micro-cracks for a unit area equals the energy release rate measured in the laboratory. In the FEM approach, the critical damage threshold is calculated after calibrating the CDM parameters. In the XFEM approach, a weighted damage tensor is calculated around the tip area to determine the direction and length of the macro-fracture that propagates, and the SPR method is used to map state variables after remeshing. Results demonstrate that the XFEM-based CDM-CZ framework can successfully capture the propagation of a mode I microfracture within a damage process zone. Simulation results reveal that most of the energy is dissipated to create macro-fracture surfaces and that the amount of energy dissipated by damage development is negligible. However, the tangent Jacobian matrix cannot be calculated without the explicit expression of the damaged stiffness matrix, which can result in convergence issues for complex stress paths, and also restricts the type of CDM constitutive models that can be used in the coupled approach, hence limiting the type of fracture patterns that can be simulated. Furthermore, some discrepancies are noted with the XFEM approach, especially when both material and stress anisotropy are accounted for, because of the choice of the damage-to-fracture transition criterion, which cannot account for fracture branching (but works perfectly well for unidirectional fractures). On the one hand, a more detailed algorithm is needed to process the evolution of damage at the tip and predict branching paths; on the other hand, the level set method used to identify fracture paths in the XFEM has inherent limitations to account for multiple fracture branches and intersections, especially in 3D. The FEM approach based on the insertion of CZ elements shows great promise. The main challenges ahead are to parallelize FEM-CZM computations to reduce the computational cost, and to understand the dependency of predicted field variables and fracture patterns to spatial discretization.