Keywords

1 Introduction

Research and development of exoskeleton devices to mimic or assist walking have been ongoing since the 1960s [1]. The mechanical design and control strategies for these exoskeletons can vary widely. A collaborative team at Case Western Reserve University and the Cleveland Stokes Veteran’s Affairs (VA) hospital is currently developing a hybrid exoskeleton [2]. The exoskeleton is considered a hybrid because it combines functional electrical stimulation (FES) [3] of the user’s muscles with the bracing and power assistance of an exoskeleton [4]. Such an exoskeleton will enable patients to regain mobility and act as a form of physical therapy due to the physiological benefits of FES [5]. Specifically, paraplegic patients benefit from the exoskeleton’s powered joints that compensate for inadequate muscle activation when using FES.

Despite the progress of exoskeletons and biped robots to date, their movements remain in general less robust and adaptive compared to those of humans. The robustness and adaptation of human walking is due to the structure and function of the neural control networks within the nervous system. Decades of study in neuroscience and biology have begun to uncover how these controllers operate [6]. Controlling our exoskeleton with a computational model of these networks, which we call a “Synthetic Nervous System” (SNS) [7], may endow it with more robust and adaptive locomotion.

Our ultimate goal is to control our exoskeleton and FES with an SNS model that incorporates sensory feedback to coordinate the motion of different limb segments in a flexible framework that can be altered by descending influences in a task-dependent way. These two features have been shown to underlie periodic motor output in animals [8,9,10]. Neural models of animal locomotion in [11,12,13] can serve as a basis for the organization of our SNS model moving forward. However, with the actuators of the exoskeleton more closely resembling servomotors than antagonistic pairs of muscles, design of joint movement controls will be more in line with the design process outlined in [14]. Interjoint coordination will be relying on sensory feedback signals from the positions of other joints and forces on the leg [11, 15].

An expected hurdle to developing and tuning this SNS will be in the coordination of the multiple rhythmic systems, i.e. the oscillation of each joint. Inter-joint coordination arises from sensory pathways between leg joints adjusting the oscillatory phase of the other joints. For example, loading information from the foot adjusts the phase of the hip’s control network to generate propulsion [11]. But how should the strength of such pathways be tuned? One tool that quantifies how periodic trajectories are altered by perturbations is the infinitesimal phase response curve, or iPRC. An iPRC reveals how the cycle’s phase changes in response to perturbations applied to each of its state variables at different phases throughout its limit cycle. By locating the areas of higher and lower sensitivity, we may be able to design sensory pathways that exploit the oscillators’ phase-dependent sensitivity to inputs. In addition, understanding how sensory information alters the relative phase of the joints, we may be able to determine the stability of periodic trajectories (i.e. how the exoskeleton walks) and its robustness to system parameters.

Despite the potential benefits these iPRCs could provide, the process of finding the iPRCs via brute force guess-and-check can require long computation times, especially as the dimensionality of the SNS model grows. Analytical methods for generating iPRCs exist, which should be faster and computationally less expensive than brute force methods. However, such methods mostly consider smooth systems and tend to break down in non-smooth systems due to the Jacobian matrices of the system’s vector fields not being well defined [16]. Our model joint model system contains piecewise functions and certain hard boundaries (i.e. “sliding conditions”) that make it non-smooth. However, more recently developed analytical methods for finding iPRCs can treat systems whose dynamics contain piecewise functions and sliding conditions [16, 17]. In this work, we will apply these newer methods with a reduced model of our SNS exoskeleton controller to compute its iPRC numerically. We compare this iPRC to one generated via brute force (i.e. repeated perturbed simulation). We then discuss future applications for this work.

2 Methods

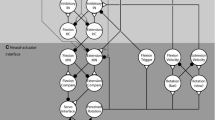
This work establishes a system wherein the direction, timing, and speed of the hip joint of a powered exoskeleton is controlled by simple neural network consisting of a central pattern generator (CPG), modeled using two non-spiking leaky neurons. The hip joint is powered by a DC motor with a gearbox, and the rotation of the joint provides feedback to the CPG.

2.1 Motor Dynamics

The hip power unit is the actuator driving the movement. It is composed of a DC motor paired with a transmission to produce a larger torque, while still being capable of outputting the needed speeds of the hip during walking locomotion. The power unit can be modeled as a motor.

Kirchhoff’s Current Law.

To model the electrical properties of the motor we use Kirchhoff’s Current Law,

$$ L\, \cdot \,\dot{I}\, = \,V_{in} \, - \,K_{v} \, \cdot \,\dot{\theta }\, - \,R_{m} \, \cdot \,I $$
(1)

Where \( L \) is the motor armature inductance, \( V_{in} \) is the motor voltage input, \( K_{v} \) is the motor speed constant, \( \dot{\theta } \) is the angular velocity, \( R_{m} \) is the motor terminal resistance, and \( I \) is the motor current. Equation 1 makes up the basis of our motor current state. Due to limitations of the motor controller and transmission inside the power unit, only a certain amount of current can be sourced at once. This restriction introduces a sliding condition to the state equation for current, where it can only reach a set maximum amount of current.

Newton’s Law of Motion.

To model the mechanical properties of the motor we use Newton’s Law of Motion resulting in

$$ J\, \cdot \,\ddot{\theta }\, = \,K_{t} \, \cdot \,I\, - \,B\, \cdot \,\dot{\theta }\, - \,sign\left( \theta \right)\, \cdot \,\tau_{ext} $$
(2)

where the \( J \) is the motor mass moment of inertia, \( K_{t} \) is the motor torque constant, \( B \) is the motor viscous friction, and \( \tau_{ext} \) is the external torque, which is used to account for the static friction. Equation 2 makes up the basis of the angular velocity state of the motor.

Angular Position.

To describe the dynamics in a state-space representation, we add a differential equation modeling the angular position of the motor,

$$ \dot{\theta }\, = \,\frac{d\theta }{dt} $$
(3)

2.2 Neural Dynamics

The neural dynamics contribute four state variables to the system. These variables model the activation level of the two neurons in our CPG, as well as those neurons’ persistent sodium channel inactivation.

Non-spiking Leaky Neuron Model.

The neurons are modeled as non-spiking Hodgkin-Huxley compartments with the substitution \( U\, = \,V\, - \,E_{r} \), as used in [7, 14] to simplify analysis, where \( E_{r} \) is the resting potential, \( V \) is the neuron voltage, and \( U \) is the activation level above the resting voltage. This gives us

$$ \begin{aligned} & C_{m} \, \cdot \,\dot{U}\, = \, - G_{m} \, \cdot \,U\, + \,G_{syn} \left( U \right)\, \cdot \,\left( {\Delta E_{syn} \, - \,U} \right)\, + \,G_{Na} \, \cdot \,m_{\infty } \left( U \right)\, \cdot \,h\, \cdot \,\left( {\Delta E_{Na} \, - \,U} \right) \\ & +\,I_{app} \, + \,I_{pert} \, + \,G_{fb} \, \cdot \,\left( {\Delta E_{fb} \, - \,U} \right) \\ \end{aligned} $$
(4)

where \( C_{m} \) is the membrane capacitance, \( G_{m} \) is the membrane conductance, \( G_{syn} \) is the instantaneous synaptic conductance, \( \Delta E_{syn} \) is the synaptic reversal potential, \( G_{Na} \) is the sodium conductance, \( m_{\infty } \) is a sigmoid for the persistent sodium channel activation, \( h \) is the persistent sodium channel inactivation, \( \Delta E_{Na} \) is the sodium channel reversal potential, \( I_{app} \) is the membrane applied current, and \( I_{pert} \) is a small current pulse that is only applied to one of the neurons at the beginning to create an offset to begin oscillation of the CPG. The terms \( G_{fb} \) and \( \Delta E_{fb} \) are feedback terms used to interface feedback pathways with the motor. \( G_{fb} \) is the feedback synapse conductance and \( \Delta E_{fb} \) is the feedback reversal potential.

Central Pattern Generator.

The central pattern generator is formed by mutual inhibition between two neurons with persistent sodium channels [14]. The synaptic conductance, \( G_{syn} \), of the inhibitory synaptic connections between the two neurons is described by the piecewise-linear function

$$ G_{syn} \left( U \right)\, = \, \left\{ {\begin{array}{*{20}c} {0,} \\ {g_{syn} \cdot \frac{U}{R},} \\ {g_{syn} ,} \\ \end{array} \, \begin{array}{*{20}c} {{\text{if}}\,U\, \le \,0} \\ {{\text{if}}\,0\, < \,U\, < \,R} \\ {{\text{if}}\,U\, \ge \,R} \\ \end{array} } \right. $$
(5)

where \( R \) is the expected range of voltage output from the neuron and \( g_{syn} \) is the maximum synaptic conductance. To have our network oscillate between the voltage range of \( 0 \) to \( R \) at steady state when one neuron is inhibited and the other is uninhibited, \( G_{Na} \) is found using

$$ G_{Na} \, = \,\frac{{G_{m} \, \cdot \,R}}{{m_{\infty } \left( R \right)\, \cdot \,h_{\infty } \left( R \right)\, \cdot \,\left( {\Delta E_{Na} \, - \,R} \right)}}. $$
(6)

The maximum synaptic conductance, \( g_{syn} \), is found using

$$ g_{syn} \, = \, \frac{{ - \delta \, - \,G_{Na} \, \cdot \,m_{\infty } \left( \delta \right)\, \cdot \,h_{\infty } \left( \delta \right)\, \cdot \,\left( {\delta \, - \,\Delta E_{Na} } \right)}}{{\delta \, - \,\Delta E_{syn} }}. $$
(7)

Here, \( \delta \) is a bifurcation parameter that represents the strength of the synaptic inhibition as the difference between the inhibited neuron’s resting potential and the lower threshold of the synapse [14]. The term \( h_{\infty } \) is another sigmoid, similar to \( m_{\infty } \), but for the sodium inactivation channel. The sigmoids are defined as

$$ m_{\infty } \left( V \right)\, = \,\frac{1}{{1\, + \,\exp \left( {S\, \cdot \,\left( {R\, - \,V} \right)} \right)}} $$
(8)
$$ h_{\infty } \left( V \right)\, = \,\frac{1}{{1\, + \,0.5\, \cdot \,\exp \left( {S\, \cdot \,V} \right)}} $$
(9)

where \( S \) is the maximum slope of the sigmoid.

Sodium Channel Inactivation.

The differential equation that governs the sodium channel inactivation term, \( h \), found in Eq. 4 is

$$ \dot{h}\, = \,\frac{{h_{\infty } \left( U \right)\, - \,h}}{{\tau_{h} \left( U \right)}} $$
(10)

where \( \tau_{h} \) is the sodium inactivation time constant found using

$$ \tau_{h} \left( V \right)\, = \,\tau_{h,max} \, \cdot \,h_{\infty } \left( V \right)\, \cdot \,\sqrt {0.5\, \cdot \,\exp \left( {S\, \cdot \,V} \right)} $$
(11)

2.3 Interfacing the Dynamics

With the motor and neural dynamics laid out in the sections above, we must establish coupling terms between them. Our goal is to use the neural states to specify position and velocity commands for the motor. For the CPG to be able to control the movement of the motor, the states of the neural dynamics are integrated in to the motor dynamics as inputs as well as having certain states from the motor dynamics used in new feedback pathways for the neurons.

Neuron Activation as Inputs to the Motor.

To have the CPG specify the velocity of the motor, the motor voltage input, \( \varvec{V}_{{\varvec{in}}} \), becomes a piecewise-linear function of the neuron activation states.

$$ V_{in} \left( {U_{1} ,\,U_{2} } \right)\, = \,P\, \cdot \,\hbox{min} (\hbox{max} \left( {U_{1} ,\,0} \right),\,R)\, - \,\hbox{min} (\hbox{max} \left( {U_{2} ,\,0} \right),\,R)) $$
(12)

where \( U_{1} \) and \( U_{2} \) represent the activation states of neurons 1 and 2, respectively. The term \( P \) is a gain term represented as

$$ P\, = \,\frac{{4\, \cdot \,K_{v} }}{1000\, \cdot \,R} $$
(13)

that limits the maximum commanded speed to \( 4\,\text{rads} /\text{s} \), since this is the approximate speed of the hip joint during walking locomotion found in [18].

Angular Position as Feedback for the Neurons.

The feedback synapse conductance, \( {G}_{{{fb}}} \), is set as a function of position \( {\theta} \). If neuron 1 \( \left( {{U}_{1} } \right) \) was active when \( {\theta} \) reaches a certain threshold, the feedback synapse conductance activates to allow a strong inhibitory current to inhibit \( {U}_{1} \). With \( {U}_{1} \) now inhibited, \( {U}_{2} \) is allowed to escape and become the active neuron in the CPG. This causes the angular velocity to switch signs due to Eq. 12, leading to a change in direction. \( {G}_{{{fb}}} \) for neurons 1 and 2 are represented by the following piecewise functions

$$ G_{fb,1} \left( \theta \right)\, = \,\left\{ {\begin{array}{*{20}c} {0, \,\theta \, < \,\theta_{FLX} } \\ {g_{FB} , \,\theta \, \ge \,\theta_{FLX} } \\ \end{array} } \right. $$
(14)
$$ G_{fb,2} \left( \theta \right)\, = \,\left\{ {\begin{array}{*{20}c} {0,\, \theta \, > \,\theta_{EXT} } \\ {g_{FB} , \,\theta \, \le \,\theta_{EXT} } \\ \end{array} } \right. $$
(15)

Where \( g_{FB} \) is the maximum feedback conductance, \( \theta_{FLX} \) is the flexion position trigger and \( \theta_{EXT} \) is the extension position trigger. The current model sets \( \theta_{FLX} \, = \,30 \) degrees and \( \theta_{EXT} \, = \, - 10 \) degrees based on hip angle ranges during locomotion found in [18]. For completeness, all state equations are listed in Table 1 and all variable values and units are shown in Table 2.

Table 1. State equations of the system
Full size table
Table 2. Parameter values and units.
Full size table

2.4 Deriving/Generating Analytically the Infinitesimal Phase Response Curves (IPRCs)

The system, governed by the state equations shown above in Table 1, exhibits a limit cycle with both piecewise functions and hard boundaries acting as sliding conditions. Deriving iPRCs for piecewise-linear and limit cycles with sliding conditions (LCSCs) have been treated in detail in [16, 17]. However, we will briefly summarize the process.

Finding the Infinitesimal Phase Response Curve via Brute Force.

To generate the iPRC of a system via brute force, the unperturbed system is simulated for at least one period. After obtaining this unperturbed limit cycle, the system is integrated up to given phases. Once reaching the given phase, the solution is halted, perturbed in the direction of a basis vector at a sufficiently small magnitude (1E-2–1E-4 are common values [17]) and re-initialized. The system is then integrated after this perturbation for a sufficiently long time (typically 10 times the period). The value of the iPRC for the phase at which the perturbation is applied is calculated as the difference between the duration of the unperturbed and perturbed limit cycles, divided by the magnitude of the perturbation.

Analytically Finding the Infinitesimal Phase Response Curve.

For a general smooth nonlinear system which produces a limit cycle, the iPRC can be found using an adjoint equation method [19]. The adjoint equation is

$$ \dot{z}\, = \, - \left( {DF\left( \gamma \right)} \right)^{T} \, \cdot \,z, $$
(16)

where \( z \) is the iPRC and \( DF\left( \gamma \right) \) is the Jacobian matrix evaluated on the limit cycle \( \gamma \). Usually, the adjoint equation cannot be used on nonsmooth systems due to the discontinuities present at the boundaries of piecewise functions or sliding conditions. However, [16, 17] introduce methods to account for these discontinuities.

To account for the discontinuities at the boundaries, jump matrices are calculated at each boundary crossing. These jump matrices capture the abrupt changes that happen to the vector field of the system at the boundaries. To use the jump matrices to properly calculate the iPRC, one evaluates the adjoint equation backwards in time. The adjoint equation is calculated backwards in time because the jump matrix at the liftoff point for sliding conditions would not be well defined otherwise, as detailed in Remark 3.9 and Theorem 3.7 in [16]. When a boundary is encountered, the iPRC just before (in forwards time) the boundary is calculated by

$$ z^{ - } \, = \,{\mathcal{J}}z^{ + } , $$
(17)

where \( z^{ - } \) is the iPRC just before the boundary, \( z^{ + } \) is the iPRC just after the boundary and \( {\mathcal{J}} \) is the jump matrix. How to calculate the jump matrix is detailed in Theorem 2.2 for piecewise smooth limit cycles in [17] and Remark 3.10 for LCSCs in [16]. Once \( z^{ - } \) is found, one re-initializes the adjoint equation using \( z^{ - } \) and continues to evaluate the adjoint equation backwards in time.

3 Results

3.1 Simulation of the Full System

The state equations shown in Table 1 were simulated in MATLAB (The Mathworks, Natick, MA) using its ODE15s solver with relative and absolute tolerances set at \( 1\, \times \,10^{ - 10} , \) for 5000 ms to produce Fig. 1. Figure 1 shows that the system is rhythmically oscillating. The flattening of the peaks in plot (c) in Fig. 1 verifies and displays the locations of the system’s sliding conditions, where the motor’s current draw is limited. Because the motor’s current draw is a dynamical state variable, this limitation represents a sliding condition, not a discontinuity. The period of the system was calculated as \( T\, \approx \,545 \text{ms} \).

Fig. 1.
figure 1

Simulation results of the SNS controlled hip power unit model. (a): Plot of neuron 1 \( \left( {U_{1} } \right) \) and neuron 2 activation \( \left( {U_{2} } \right) \) represented by black lines and dashed gray lines, respectively. (b): Plot of neuron 1 \( \left( {h_{1} } \right) \) and neuron 2 sodium channel inactivation \( \left( {h_{2} } \right) \) represented by black lines and dashed gray lines, respectively. (c): Plot of the motor current. Sliding conditions take place at the maximum and minimum allowable currents of magnitude \( 8.76 A \). (d): Plot of the angular position of the motor in degrees. (e): Plot of the angular velocity of the motor in radians per second.

Full size image

3.2 Infinitesimal Phase Response Curve

The brute force and analytical iPRCs of the limit cycle are displayed together in Fig. 2. The perturbation magnitude used for the brute force iPRC was calculated as \( 10^{ - 2} \) times the average absolute value of each state over one period. Two hundred fifty equally spaced given phase positions were used to generate the brute force iPRC. The Jacobian matrix \( DF \) used in the adjoint equation for the analytically obtained iPRC was calculated numerically by finite difference. Figure 2 shows good agreement between the brute force and analytical iPRCs. The runtime for the analytical solution was 28.65 s versus more than 5 h for the brute force solution, representing a massive speedup.

Fig. 2.
figure 2

The brute force (dots) and analytical (lines) iPRCs of the SNS controlled hip power unit model. (a): iPRC of \( U_{1} \) and \( U_{2} \) with the brute force iPRC represented by blue and green dots respectively, and the analytical iPRC represented by black and gray lines, respectively. (b): iPRC of \( h_{1} \) and \( h_{2} \) with the brute force iPRC represented by blue and green dots respectively, and the analytical iPRC represented by black and gray lines, respectively. (c): iPRC of the motor current. (d): iPRC of the angular position. (e): iPRC of the angular velocity. (Color figure online)

Full size image

4 Discussion

In this work, we present a model wherein the direction, timing, and speed of the hip joint of a powered exoskeleton are controlled by simple neural network consisting of a central pattern generator (CPG), modeled using two non-spiking leaky neurons. The model identifies the CPG, the plant, and the coupling between them in a control architecture directly reflecting the structure of biological motor systems [20]. For this system, we show that the analytical methods in [16, 17] for generating iPRCs of limit cycles containing piecewise-linear functions and sliding conditions agree with the iPRCs calculated for our system via brute force. This method will enable us to precisely tune the interjoint coordinating influences in our exoskeleton control model.

The analytical method for generating iPRCs will enable us to more rapidly tune the parameters of our system. One of our intended uses for the iPRCs is to find and evaluate ideal parameter values for interjoint coordinating influences in our networks. Proper walking emerges from sensory feedback pathways that synapse onto the CPGs to change their oscillation phases [8]. However, it is not clear which states should alter CPG phase, or how strong those influences should be. We can use iPRCs to determine at what phases a network is most sensitive to inputs, and exploit this knowledge to design locomotion-stabilizing coordination pathways. Even though this could be accomplished by generating iPRCs via simulation and brute force [14], the analytical iPRC method is faster and computationally less expensive, allowing quicker evaluation of possible changes to the system.

This analytical method for generating iPRCs will also enable us to determine synaptic sites for descending influences that alter locomotion. Descending influences from the brain are known to be critical for directing (but not necessarily generating) ongoing periodic motor output in all types of animals [9, 10]. However, it is not always clear what parts of the network descending commands modify to alter locomotion, or how strong those influences are. With the ability to rapidly generate iPRCs, we can identify how the parameters of a joint controller change its response to descending signals, and how the form and strength of those signals affect locomotion.

The ability of the analytical methods to account for piecewise and sliding conditions is also of great value. As shown in our methods and [14], the SNS can depend on piecewise equations to function correctly. Importantly, such piecewise equations enable the output of a neuron to be completely “shut off,” such as when a neuron stops firing action potentials. This effect cannot be produced by traditional recurrent neural networks with continuous synaptic activation functions [21]. As the system in this work is scaled up and developed for use as a controller for an assistive exoskeleton for walking gait rehabilitation, the discontinuous mechanics of walking will introduce more sliding conditions [22], such as making and breaking contact with the ground, which must be accounted for. We believe we can continue to scale this method up to more accurately and quickly predict how a dynamical system’s periodic orbit may be altered by perturbations in a phase-dependent way.

For future work we intend to continue development towards a larger and more realistic network for controlling our exoskeleton, that would include additional joints, as well as expanded sensory pathways and descending commands. We also plan to explore additional methods in [16] for analytically finding the infinitesimal shape response curves (iSRCs) for our systems. The iSRC would show how the values of each state change throughout its period when system parameters are perturbed from their baseline values for the duration of the limit cycle. Understanding how these lasting perturbations alter the periodic trajectory of the system will assist tuning of parameter values. Essentially, by perturbing one or more parameters for the full period of the limit cycle, their effects on the state values can be determined at each instance of the period. With this information, the proper parameter values needed for the trajectory to exhibit key features (i.e. level body height during the stance phase) can be found. We expect this analytical method to again be faster and computationally less expensive than solving the iSRC via brute force, allowing tuning to be done more quickly and efficiently.