A Refinement Calculus for Requirements Engineering Based on Argumentation Theory

Abstract

The Requirements Engineering (RE) process starts with initial requirements elicited from stakeholders – however conflicting, unattainable, incomplete and ambiguous – and iteratively refines them into a specification that is consistent, complete, valid and unambiguous. We propose a novel RE process in the form of a calculus where the process is envisioned as an iterative application of refinement operators, with each operator removing a defect from the current requirements. Our proposal is motivated by the dialectic and incremental nature of RE activities. The calculus, which we call CaRE, casts the RE problem as an iterative argument between stakeholders, who point out defects (ambiguity, incompleteness, etc.) of existing requirements, and then propose refinements to address those defects, thus leading to the construction of a refinement graph. This graph is then a conceptual model of an RE process enactment. The semantics of these models is provided by Argumentation Theory, where a requirement may be attacked for having a defect, which in turn may be eliminated by a refinement.

1 Introduction

The creation of software requirements is a very important initial stage of software development. The original core problem in Requirements Engineering (RE) consists of transforming the initial requirements R elicited from stakeholders—however informal, ambiguous, unattainable, etc.—through a systematic refinement process into a specification S that (a) consists of functional requirements, quality constraints and domain assumptions, such that (b) S is consistent, complete, and realizable, and (c) S fulfills R. Variants of this problem form the backbone of RE research, and since the late 1970’s it has been recognized that the resulting requirements document contains a conceptual model of the environment and the software-to-be [1, 2].

To begin with, consider two RE techniques that can be viewed as research baseline and analogues for our work. In each case, we mention 1) the basic ontology underlying the approach, 2) the refinement process by which the requirements are built, and 3) the “requirements document” resulting from the enactment of this process.

SADT (1977) [1] was the first widely known requirements specification notation and methodology. The modeling ontology of SADT consists of data and activity boxes, connected by input/output/control arrows. The refinement methodology is structured decomposition of non-atomic boxes into aptly named sub-boxes, which are interconnected by aptly-named arrows in appropriate ways. Therefore, the final requirements document/model consists of a number of pages, each describing the internal content of a box; all unexpanded boxes are viewed as atomic/realizable. Ross [1] explicitly stated that SADT can be used to describe not just software requirements but to communicate any idea/conceptual model, and showed how to describe the process of model building in SADT itself.

Basic Goal-Oriented RE—GORE (1993) [3, 4] is one of the most influential RE paradigms, and, in its simplest form, has an ontology consisting of goals, connected by reduction and conflict relations. The methodology suggests refining non-realizable goals (ones that cannot be implemented directly) using and/or decomposition. The final requirements model then consists of the graph of goal and decomposition nodes, with operationalisable goals as leafs.

The present paper, which extends and builds on initial work in [5], proposes an approach, called CaRE, whose ontology consists of goals/requirements, defects and refinements, the latter two of various sub-types. CaRE offers a novel calculus of operators that can be used to critique goals using various defect types, and to address such defects using various kinds of refinements. The CaRE refinement methodology suggests viewing the use of the operators as a dialectic argument between stakeholders, including requirements engineers. The result of enacting this argument will be a refinement graph, which records goals, defects and refinements, and for which we define a notion of “acceptability”. The set of defect subtypes in CaRE is inspired by the IEEE/ISO Standards on Software Requirements Specifications [6, 7]. The set of refinements addressing them is gathered from the RE literature, which contains many proposals for dealing with specific types of problems. These include techniques for eliminating forms of conflict, such as inconsistencies [8] and obstacles [9]. For example, the nonAtomic defect in CaRE marks a goal as non-operationalisable (in GORE terminology), and the reduce operator can be used to perform and-decomposition of the goal.

Prior RE approaches, starting with [10], viewed initial requirements R as being satisfied by specification S under domain assumptions A, if A and S together logically entailed R. This notion of fulfillment runs counter to requirements engineering practice, where stakeholder requirements are routinely weakened because they are unnecessarily strong (e.g., “system shall be available 7/24”), or even dropped altogether. Such refinements can’t be accounted for explicitly by proposals in the literature.

The CaRE process, in contrast, results in a refinement graph with nodes corresponding to requirements: some for the initial R, some for potential specifications S, and others for intermediate refinements. Some S, consisting of leaf nodes, is said to address R if there is an “acceptable argument” that involves refining S from R. This renders the derivation of S from R a Hegelian dialectic process of thesis-antithesis-synthesis [11], also similar in spirit to the inquiry cycle [12], though our proposal includes more structure, technical details, and reasoning support for the RE process. Addressing a given set of requirements by offering an acceptable argument is a weaker notion of fulfillment than satisfying it, because it allows a requirement to be weakened or altogether dropped, as long as there is an acceptable argument for this. Towards this end, we adopt argumentation semantics from Dung  [13].

The contributions of this work are:

• A comprehensive refinement calculus for RE, inspired by goal-oriented RE but which adds: (i) “defects” and “refinements” to its ontology, based on a full set of defect types from IEEE/ISO standards; (ii) a comprehensive set of refinement operators for defects; (iii) refinement graphs, which are conceptual models of the RE process enactment, and can serve as explanation/rationale for the specifications obtained.

• An argumentation-based semantics of what it means for a specification to address a set of stakeholder requirements The systematic process for constructing CaRE refinement graphs, inspired by its argumentation-based semantics, supports negotiation and convergence towards agreement between stakeholders. In contrast with most previous approaches, where only a requirement engineer conducts analysis, with CaRE all stakeholders are involved.

• Reasoning support that, given an initial set of requirements R and a constructed refinement graph, returns all specifications S that address R. This is implemented as a prototype tool that is available on the web.

2 CaRE Requirements Calculus

The proposed approach consists of a calculus and a systematic process for requirements elicitation, negotiation, and refinement. The calculus is based on a collection of defect types and of refinements. The defect types are inspired by the IEEE/ISO standards and represent issues that could be identified by stakeholders for one or more requirements. Refinements, on the other hand, are the means for fixing defects. By means of an iterative process of defect identification and refinement, a refinement graph is constructed and zero or more specifications are produced.

Defect Types: Defects can be found in individual requirements (single-target defects) or sets thereof (multi-target defects). The single target defects are

• nonAtomic: the requirement is not operationalisable. For example, $\langle g_1$: “System shall schedule a meeting upon request”$\rangle$ may not be atomic since there is no single action the system-to-be or an agent in the environment can perform to address it.

• ambiguous: the requirement admits many interpretations because it is vague, imprecise, or otherwise ambiguous. For example, $\langle g_2$: “The authentication process shall be easy”$\rangle$ is ambiguous since the term easy is vague.

• unattainable: the requirement is not feasible, i.e. doesn’t have a realistic solution. For example, $\langle g_3$: “The system shall be available at all times”$\rangle$ is unattainable because it assumes eternal availability of power and other resources.

• unjustified: the requirement does not have an explicit motivation. For example, $\langle g_4$: “The system shall run on Windows operating system”$\rangle$ is missing an explicit justification why other operating systems are not considered.

• incomplete: the requirement is missing information. For example, $\langle g_5$: “In case of fault, the system shall send an error message”$\rangle$ is incomplete because it does not specify a recipient for the message.

• tooStrong: the requirement is over-restrictive. For example, $\langle g_6$: “The website shall use HTTPS protocol”$\rangle$, may be too strong if there is no sensitive data.

• tooWeak: the requirement is too weak. For example, $\langle g_7$: “The DB system shall process 500 transactions/sec”$\rangle$ is too weak if the expected workload for the system-to-be is 1,000 transactions/sec.

• rejected: the requirement is rejected. For example, in the context of an app recommending nearby restaurants to users, a requirement such as $\langle g_8$: “The app shall support chatting between user and restaurant”$\rangle$ may be deemed unacceptable.

The multitarget defects are:

• mConflict: the full set of requirements doesn’t admit any solutions, even though subsets may do so. For example, the requirements $\langle g_9$: “The train control system shall stop the train if a red signal is missed”$\rangle$ and $\langle g_{10}$: “The train control system shall not apply brakes if the speed is below 30 km/h”$\rangle$ are conflicting, if the driver is in charge for speeds <30 km/h.

• mMissing: the set of requirements is incomplete. For example, a set of requirements for a social network platform is mMissing if it does not include any privacy requirement.

• mRedundant: here a set of requirements is too strong or redundant, as in $\langle g_{11}$: “The system shall support authentication through fingerprint recognition”$\rangle$ and $\langle g_{12}$: “The system shall support authentication through iris recognition”$\rangle$.

Refinement Operators: A refinement operator invocation, op(D, R), addresses a defect D of some existing requirements, offering alternative (presumably better) requirement(s) R that address the problem. Each operator takes a (set of) defective requirements, and is applicable to one or more defect types. Each defect type has at least one refinement operator that is applicable to it, i.e., can eliminate defects of that type. Defects of type rejected are an exception: in this case there is no possible fix, as the rejected requirement constitutes a dead end. Although some operators behave similarly, we have chosen to keep them, to make the calculus more readily usable. The operators are as follows:

Fig. 1.

Graphical notation

Fig. 2.

Refinement graph example

• weaken: introduces a weaker requirement. For example, the unattainable requirement $g_3$ may be weakened into $\langle g_{13}$: “The system shall be available at all times, with interruptions of $\le$2 h”$\rangle$. weaken is applicable to defects of type unattainable, and tooStrong.

• strengthen: introduces a stronger requirement. For instance, $g_7$ may be strengthened into $\langle g_{14}$: “The system shall process 1,200 tps”$\rangle$. strengthen is applicable to defects of type tooWeak.

• reduce: decomposes a requirement into a set $g_1, ..., g_n$ using and-refinement. reduce is applicable to defects of type nonAtomic.

• add: introduces new requirements, and is applicable to defects of type mMissing.

• clarify: is applicable to incomplete and ambiguous defects, and introduces a, presumably, improved requirement.

• justify: introduces a new requirement that represents an explicit motivation for another requirement, and is applicable to unjustified defects.

• resolve: applies to defects of type mConflict, typically moderating or dropping the original requirements.

• drop: given a set of mRedundant requirements, produces a proper subset not including redundant elements.

2.1 Incremental Construction of a Refinement Graph

The incremental CaRE requirements acquisition process starts with an initial set of requirements. These are critiqued by stakeholders and defects in the requirements are identified. Then, requirements – or sets of requirements – that have defects are refined by applying the different refinement operators, producing new requirements. If the new requirements are acceptable, i.e. have no defects, the original (defective) requirements are accepted. Otherwise, this process is repeated until no new defects are identified. Thus, the result of the process is a refinement graph in which all the leaf nodes are requirements that have no defects. Therefore, in a sense, the acceptability of requirements is propagated from the leaf nodes towards the higher-level nodes. Finally, specifications of a refinement graph are determined by identifying minimal sets of leaf nodes that make the initial requirements acceptable.

2.2 Graphical Notation and Running Example

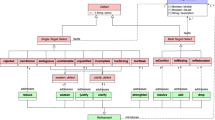
This section presents a simple example used to illustrate our proposal, and its graphical expression. The basic elements of the graphical notation are shown in Fig. 1, and consist of requirements, defects (single- and multi-target), and refinements. Each instance of these elements is associated with a unique id (REQ-id, DEF-id, REF-id in Fig. 1).

The example, which is based on a simple elicitation case, is represented by the refinement graph in Fig. 2. In the running example, a customer requires a new app to be installed on the tablets of factory workers, to be used for sharing workflow information. The customer requires that the app runs on Android (g00). Furthermore, the customer wants the system to be delivered within six months (g01). The requirements analyst asks why Android is required (unjustified(d00) defect), and the customer replies that the tablets currently used by the workers are all Android tablets (g10, introduced with the justify refinement r10). The requirements analyst knows that their software company has a very similar app for iOS, but that porting and adaptation would require twelve months. Hence, g00 and g01 are considered conflicting. In the refinement graph, an mConflict defect is specified, and a textual motivation (the optional <“claim”> in Fig. 1) is used to explain the nature of the defect: mConflict(d01:“cannot deliver Android app in 6 months”). To comply with the deadline, the requirements analyst suggests to develop the app for iOS (g20), so that its adaptation to the customer’s needs is feasible within 6 months (g21). However, this would require replacing the tablets at the factory with iPad tablets (g22). Alternatively, the requirements analyst suggests to develop the app for Android (g23), but to deliver it in twelve months (g24). These two options aim at resolving conflict d01, and are represented as alternative refinements r20 and r21. Assuming that no other defects are found, according to the approach provided in Sect. 2.1, we have two possible specifications: {g20, g21, g22} and {g23, g24}.

2.3 Discussion of Design Choices

Firstly, we gained a claim of completeness with respect to the defect types of our calculus by using the IEEE/ISO standards. However, there is no claim of minimality for defect types since, e.g., unattainable is a form of tooStrong. However, there’s been much research on how to recognize and deal with unattainable specifically – it is a special case of conflicting requirements and domain assumptions.

The set of refinement operators is not minimal since, e.g., add and justify modify the graph the same way. However, operators guide users on how to deal with defects. For example, if r is attacked as being incomplete with respect to privacy concerns, then use of add should introduce some privacy requirements. If, on the other hand, r is deemed unjustified, the new requirement introduced by justify should serve as justification for r. In short, add and justify do similar things, but for very different purposes.

CaRE might be criticized as too cumbersome for users compared to, say, GORE approaches. This may well be the case – we need empirical studies to judge this. However, as discussed above, CaRE is the only proposal in the RE literature for solving the requirements problem in its greater generality. And in any case, in addressing an open problem one may want to keep in mind Albert Einstein’s dictum “Make things as simple as possible, but not simpler”.

3 Argumentation Semantics

Dung  [13] introduced a formal Argumentation Framework (DAF), whose basic notions are arguments and attacks (conflicts between arguments), and where the key reasoning task is the acceptability of arguments, i.e, whether and which arguments should or should not be accepted by an intelligent agent. Sets of collectively acceptable arguments are called extensions.

The semantics of the CaRE calculus will be given in the form of a translation from a refinement graph into an argumentation theory, a structured variant of Dung’s DAF  [13]. The translation leads to arguments that represent requirements, defects and refinements. Informally, attacks between these arguments correspond to (i) the identification of a defect in a requirement or set of requirements, and (ii) the application of a refinement to address a defect. More precisely, in our formalisation, an argument d that represents a defect in a requirement g attacks the argument representing g; similarly, an argument r that represents a refinement to address a defect d attacks the argument representing d, thus possibly restoring the acceptability of the attacked requirement. The specifications resulting from a refinement graph are computed by considering all possible minimal extensions where the initial requirements are acceptable.

The formalization of CaRE using is motivated by (i) the dialectic nature of requirements engineering, for which argumentation theory is a natural formal choice; (ii) the flexibility of , being a meta-reasoning tool for reasoning over a freely chosen underlying logic, which enables us to easily consider more structured RE languages, e.g. [14], in the future; (iii) the non-monotonic nature of argumentation theories, which enables extending the framework to incorporate other important features, e.g., support of conflict and dependency relations between requirements  [15].

This section first introduces the formal definition of the structured argumentation framework, and the formal representation of a refinement graph and its well-formedness conditions. It then describes how a refinement graph is translated into an argumentation theory and, thereby, into a DAF. We define how this enables determining the acceptability of requirements and computing specification sets. Finally, we conclude by describing a prototype tool implementing our calculus.

3.1 Basics of Argumentation Theory

In a DAF, arguments have an abstract representation in the form of simple propositions, e.g., the argument “It is raining today, therefore I should stay home” can be represented using a simple propositional symbol a. Conflicts between arguments are given in a relation $\mathcal {D}$ over the set of arguments. For example, consider another argument b, “I have to buy food, so I must go to the store”, which obviously conflicts with a. In DAF’s terminology, this conflict is called an attack, and is represented in the form of a tuple (a, b) in $\mathcal {D}$. Given arguments and attacks, the acceptability of arguments can be determined, informally, as follows  [16]: an argument is IN (acceptable) if it is not attacked or if all its attackers are OUT (not acceptable). An argument is OUT if it is attacked by an argument that is IN. Otherwise, an argument is UNDECIDED.

Though powerful, the abstract representation of arguments in DAF makes it often less practical for modeling real-world problems. The framework for structured argumentation  [17]¹ therefore extends DAF to enable the representation of basic arguments in the form of inference rules, each having a set of premises and a conclusion. For example, argument a above can be represented using a (strict) inference rule, having a single premise “it is raining today” and a conclusion “I should stay home”. One advantage of this representation is that it explicates the structure of arguments and enables the automatic construction of complex arguments by chaining inference rules. relies on DAF to determine acceptability of arguments. In particular, given an argumentation theory that includes inference rules, identifies the different basic and complex arguments as well as conflicts between them. Then, it constructs a DAF and uses it to determine which arguments are accepted and which are not.

3.2 Formal Description of Refinement Graphs

A refinement graph $\mathrm {RG}$ is a tuple $\langle \mathrm {Req}, \mathrm {Defect}, \mathrm {Ref}\rangle$ where:

• $\mathrm {Req}\,\subseteq \,\mathrm {Id_g}\,\times \,\mathrm {Text}$ is a set of requirements. Each requirement has a unique identifier (in $\mathrm {Id_g}$) and a natural language text description (in Text).

• $\mathrm {Defect}\,\subseteq \,\mathrm {Id_d}\times \,\mathrm {DType}\,\times \,\mathcal {P}(\mathrm {Text})\,\times \,\mathcal {P}(\mathrm {Id_g})$ is a set of defects. A defect has (i) a unique identifier (in $\mathrm {Id_d}$); (ii) a defect type; (iii) some natural language explanations of the defect’s nature; and (iv) the identifier(s) of a set of requirements found to have the defect.

• $\mathrm {Ref}\subseteq \mathrm {Id_r}\times \mathrm {RType} \times \mathrm {Id_d} \times \mathcal {P}(\mathrm {Id_g})$ is a set of refinements. A refinement has (i) a unique identifier (in $\mathrm {Id_r}$); (ii) a refinement type; (iii) a defect that it aims at addressing, and (iv) a set of other requirements, which are meant to replace the defective one(s).

So, for example, from Fig. 2, we have the formal requirement $Req(g23,The app\ shall\$ $run\ on\ Android)$². The set of identifiers $\mathrm {Id_g}$, $\mathrm {Id_r}$, and $\mathrm {Id_d}$ are disjoint; henceforth, given a refinement graph $\mathrm {RG}$ = $\langle \mathrm {Req}, \mathrm {Defect}, \mathrm {Ref}\rangle$, the set $\mathrm {Id}_{\mathrm {RG}}$ is used to denote all identifiers of its elements, i.e., $\mathrm {Id}_{\mathrm {RG}}=\mathrm {Id_g}\cup \mathrm {Id_d}\cup \mathrm {Id_r}$.

A refinement graph is well-formed iff every refinement addressing a defect matches its type, as described in Sect. 2.

In addition, to make the semantics work out more easily, we assume in this conference paper that the refinement graph is acyclic. This means that if a requirement is to be re-used it must be given a new label.

3.3 Refinement Graph Semantics by Translation to Argumentation Theory

Each refinement graph $\mathrm {RG}$ has a corresponding argumentation theory representation, denoted $\mathcal {AT}(\mathrm {RG})$. An argumentation theory is a tuple $\langle \mathcal {L}{}, IR, \mathrm {name} \rangle$ where $\mathcal {L}{}$ is a logical language (in our case simple propositional symbols and their negation).

IR is a set of defeasible inference rules of the form $\varphi _1,...,\varphi _n \Rightarrow \varphi$, $n \ge 0$, where $\varphi _1,...,\varphi _n, \varphi$ are from $\mathcal {L}{}$. In case $n=0$, $\Rightarrow \varphi$ is equivalent to $true \Rightarrow \varphi$, and defeasibly asserts $\varphi$. The intended meaning of a defeasible rule is that if one accepts all antecedents/premises, then one must accept the consequent/conclusion unless there is sufficient reason to reject it. Defeasible rules with empty premises, of the form $\Rightarrow \varphi$, are called assumptions.

Finally, name is a partial function that gives names to (some) defeasible rules including assumptions. For convenience, we will write for a defeasible rule $\varphi _1,...,\varphi _n \Rightarrow \varphi$ whose name is $\mathrm {d}$.

Table 1. Mapping of elements of refinement graphs to argumentation theory.

Translation of Refinement Graphs to . The argumentation theory $\mathcal {AT}(\mathrm {RG})=\langle \mathcal {L}_{\mathrm {RG}}, \mathcal {IR}_{\mathrm {RG}}, \mathrm {name}_{\mathrm {RG}}\rangle$ corresponding to a refinement graph $\mathrm {RG}=\langle \mathrm {Req},\text {{Defect}},\mathrm {Ref}\rangle$ is constructed as follows³:

• The set of propositions $\mathcal {L}$ contains the elements of Text used in the graph, together with the identifiers in $\mathrm {RG}$, and their negations.

• The set of defeasible rules of $\mathcal {AT}(\mathrm {RG})$ is constructed on the basis of requirements, defects, and refinements of refinement graphs as described in Table 1.

Thus, the above formalization represents requirements and defects as antecedent-free rules, while refinements have premises which are the requirements that the refinement introduces.

Note that natural language statements of defects are not currently considered in the translation to argumentation theories. The inclusion of these elements as well as support/conflict relations between them represent future work.

Construction of Arguments and Attacks.  constructs arguments that take the form of inference trees. In our case, complex arguments start from leaves that are rules with antecedent true, and are put together into larger ones by chaining with inference rules. Due to space limitations, we do not present the rules of the construction of arguments. Interested readers are referred to [17, 18].

Figure 3 depicts the arguments constructed on the basis of the refinement graph shown in Fig. 2. The figure shows that all the requirements in the refinement graph correspond to arguments $\{G_0,G_1,G_2,G_3,G_4,G_5,G_6,G_7\}$ in the theory, and defects correspond to $\{D_0, D_1, D_2\}$. Refinements take the form of defeasible rules whose premises are (non-initial) requirements. These lead to inference trees where the premises are the leaves of the tree, as in $\{R_0,R_1,R_2\}$. Notice the structure of every argument: it includes a set of sub-conclusions, a (proper) conclusion, and a set of defeasible rules. For example, the sub-conclusions of argument $R_1$ are The app shall run on Android, The app shall be delivered in 12 months, and ${\lnot d01}$; the conclusion is ${\lnot d01}$; and it has a single defeasible rule r01.

Fig. 3.

Example of construction of arguments

Identification of Attacks. Given two arguments A and B, A attacks B if one of the conclusions of A conflicts with (the name of) one of the defeasible rules of B. Note that two formulas $\phi$ and $\psi$ conflict if they are contradictory, i.e., if $\phi =\lnot \psi$ or $\psi = \lnot \phi$.

According to the previous definition, defects attack requirements that they point to, whereas refinements attack defects that they address. So, for example, Fig. 3 shows that defect $D_0$ attacks requirement $G_0$, and then the refinement $R_0$ attacks the defect $D_0$.

Construction of DAFs. The purpose of argument construction and attack identification in is to enable the construction of a DAF.

We present the construction process by example here (for details, see  [17]): starting from the theory above, one obtains a DAF that can be represented graphically as in Fig. 4, where nodes represent arguments, and edges represent attacks. One can easily see in the graph how arguments {$D_0,D_1,D_2$}, representing defects, attack arguments {$G_0,G_1,G_2$}, representing requirements. Similarly, arguments {$R_0,R_1,R_2$}, denoting refinements, attack arguments {$D_0,$ $D_1,$ $D_2$}, denoting defects.

Fig. 4.

DAF example

Computation of DAF Extensions. The computation of the extensions of a DAF enables the determination of the acceptability of arguments, i.e., which arguments should be accepted and which should not. The computation of extensions is based on the following concepts and definitions.

• A set A of arguments is conflict-free if it does not include two arguments that attack each other.

• An argument a is acceptable w.r.t. to a set of arguments A iff whenever a is attacked by an argument b then b must be attacked by some element in A.

• A set of arguments A is admissible iff A is conflict-free and every argument $a\in A$ is acceptable w.r.t. A.

• A set of arguments is complete iff if is admissible and includes every argument a that is acceptable w.r.t. to it.

In this paper, we are interested in the computation of the so-called complete extensions. In the previous example, the only complete extension is the set {$G_0,G_1,G_2,G_3,G_4,$ $G_5,G_6,G_7,R_0,R_1,R_2$}. In general, if a DAF graph is acyclic then it is guaranteed to have a single complete extension. To avoid the complexity of multiple extensions, we assume in this conference paper that the original requirements graph is acyclic.

In general, the acceptable requirements in a refinement graph $\mathrm {RG}$, denoted by $AR(\mathcal {AT}(\mathrm {RG}))$, will be the set of requirements appearing in the conclusions of the arguments of its complete extension.

After the identification of acceptable arguments, we determine acceptable requirements by checking the ones that appear as conclusions of acceptable arguments. Thus, we determine that all the requirements are acceptable since they are the conclusions of arguments {$G_0$, ... , $G_7$}.

3.4 Identification of Specification Sets

The acceptability of requirements only indicates that either they are free of defects or their defects have been addressed. To determine the minimal sets of requirements necessary to make the initial requirements acceptable, we compute the minimal specification sets. In the following, suppose we are given a specific requirements graph $\mathrm {RG}$ = $\langle$Req, Defect, Ref$\rangle$.

The initial requirements ${\mathrm {InitR}}$ are those that are not introduced by a refinement. Formally, $\mathrm {InitR}\text {=}\{ txt \,| \, \lnot \exists RF , id \; . \;\text {{Ref}}( \_,\_,\_,RF )\; \wedge \; id \in RF \; \wedge \mathrm {Req}( id , txt ) \;\}$

The specification elements SpecE are the “leaves” of refinement graphs. More precisely, these requirement elements satisfy two conditions: (i) They have no defects other than mMissing, and hence have not been further refined; the rationale for this is that mMissing, in contrast to nonAtomic say, is dealt with by the add operator, which only leads to the introduction of other new necessary requirements as opposed to its replacement. This means that requirements found to be mMissing can still be leaves in refinement trees, if they have no other defects. (ii) And the leaves have not been introduced by a justify refinement, because those are (higher-level) goals.

Let a minimal set of requirements be a (minimal) subset of the requirements $\mathrm {Req}$ that lead to the acceptance of the initial requirements. Formally, it is one of the sets minimal w.r.t. set inclusion of the set $\mathrm {RR}$, defined as follows:

$\mathrm {RR}=\{R' \,|\, RG '=\langle R', \mathrm {Fault}, \mathrm {Ref}\rangle \,\wedge R'\subseteq \mathrm {Req} \,\wedge \, \mathrm {InitR}\in AR(\mathcal {AT}( RG '))\}$

Intuitively, the set $\mathrm {RR}$ is the set of all subsets of the requirements proposed during refinements that lead to the acceptance of the initial requirements. In the running example, the sets {$G_3,G_4,G_5$}, {$G_2,G_3,G_4,G_5$}, and {$G_2,G_3,G_4,G_5,G_6$} represent some of the elements of $\mathrm {RR}$. The minimal requirements sets are {$G_2,G_3,G_4$} and {$G_2,G_5,G_6,G_7$}. Finally, the specification sets, $\mathrm {SS}$, are identified by taking the intersection of specification elements and minimal requirements, i.e., $\mathrm {SS}=\{\mathrm {S}\,|\, \exists R.\mathrm {R}\in \mathrm {RR}\, ,\mathrm {S}=(\mathrm {R}\,\cap \,\mathrm {SpecE})$}. In the running example, the sets {$G_3,G_4$} and {$G_5,G_6,G_7$} represent the only specification sets.

3.5 Tool Description

We have implemented a prototype tool of the calculus. The tool aims at helping requirements engineers to systematically refine, negotiate, and document the requirements refinement process (in the form of a refinement graph). The tool also provides reasoning support by determining the acceptability of requirements and computing the minimal specifications. Due to space limitations, we only present a brief description of the tool below. The tool, as well a description of the examples in this paper and use instructions, can be downloaded at  [19] (requires Java SE Development Kit 9 to run). The tool’s input is a textual description of a refinement graph—a GUI is left as future work. An “Argumentation Theory Generator” module then generates an argumentation theory for every possible configuration of requirements. A requirements configuration is a subset of the requirements that could lead to the acceptance of the initial requirements. On the basis of these argumentation theories, an “ module” identifies the arguments, attacks, and generates a Dung Argumentation Framework (DAF). A “DAF module” then determines the acceptability of abstract arguments by computing the complete extensions of the DAF. Finally, a “Compute Minimal Specifications” module stores all (subsets of) requirements ($\mathrm {RR}$) that make the initial requirements acceptable and determines the minimal specification sets ($\mathrm {SS}$) by taking the intersection of specification elements and minimal requirements (as explained in Sect. 3.4).

4 Related Work

Since requirements engineering is dialectical by nature, argumentation frameworks have been previously used to formalise and support RE activities, including elicitation  [20], assessment  [21,22,23], and regulatory compliance  [24]. Some works focus on specific RE issues, such as security  [21, 22], or requirements conflicts  [25, 26]. The spirit of our work is analogous to the more comprehensive frameworks of Juret et al. [27], who support the definition of goal models through argumentation and Mirbel & Villeta  [15], who manage requirements artifacts based on argumentation-theory.

Finally, RationalGRL  [28, 29] captures not only traditional GORE model refinement, but also arguments about design decisions (e.g., “This refinement should be OR rather than AND”), and the rationale behind them. RationalGRL also proposes argumentation patterns to point out defects in goal models. Its laudable focus is making goal models and their evolution understandable to RE users.

The main feature distinguishing our work from all of the above is the intention: CaRE is an integrated calculus for deriving specifications from stakeholder requirements. Thus the defect types used by our framework are different and comprehensive, as are refinement operators addressing each specific defect type. Moreover, CaRE proposes its own unified representation (refinement graphs), with /AF only being used to give CaRE semantics rather than being an overt part of the framework.

The only work we know of that offers a refinement calculus for the requirements problem is the Desirée proposal [14], which generalizes GORE approaches with a rich set of operators for refinement and operationalization. The main differences between CaRE and Desirée are that CaRE (a) includes defects and defect types in its ontology, which Desiree does not, (b) casts the refinement process as a dialectic argument among stakeholders, and (c) gives a formal semantics of what does it mean for S to satisfy R based on Argumentation Theory.

5 Conclusion

This paper presents a novel calculus for RE through which initial stakeholder requirements can be refined into specifications through a dialectic process. A major advantage of our approach over existing proposals, notably GORE ones, is that it offers a comprehensive framework for introducing into the discussion the full range of defects recognized in RE standards, as opposed to the particular types considered so far. It also makes all of the stakeholders active participants in the refinement process, as opposed to traditional approaches where typically only the requirements analyst is responsible for refining the requirements and building models.

CaRE refinement graphs capture a more complete view of the RE process. Significantly, they provide a conceptual model of the enactment of our requirements engineering process. They offer excellent support for RE documentation, traceability, and change management since new defects or refinements can be added to the graph monotonically, without needing to revise its previous elements.

The semantics of the calculus is given in terms of argumentation theory, by defining a mapping from refinement graphs to constructs of the argumentation framework. Through this formalisation, we define what it means for a specification to make initial requirements acceptable. In our proposal, the notion of satisfaction, typical of earlier approaches, is replaced by the weaker notion of acceptability. Our contributions include a Java implementation of a prototype tool for the calculus A forthcoming paper will show the connection of the argumentation theoretic semantics here to abduction in an essentially propositional logic setting.

We have carried out a detailed scenario from the railway domain illustrating the elements of our calculus and how they can be used to derive specifications from requirements⁴. We still need a preliminary assessment of CaRE on an industrial case-study, and a consolidation assessment of domain experts using CaRE. Other future work includes adding further aspects of GORE ontologies (e.g., soft-goals, agents), and global consistency conditions on requirements graphs (e.g., can g be marked both tooStrong and tooWeak by the same person?).