Abstract
Development of efficient strategies for the rational design of materials involved in the production and storage of renewable energy is essential for accelerating the transition to a low-carbon economy. To contribute to this goal, we propose a novel workflow for the assessment and optimization of battery materials. The approach effectively combines quantum and atomistic modelling/simulations, enhanced by efficient sampling, Bayesian parameterization, and experimental information. It is implemented to study prospective materials for lithium and sodium batteries.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Nearly 30 years ago Sony Co. launched the first commercial lithium-ion battery (LIB) and changed the world [25]. LIBs powered the revolution in portable electronics, allowing the transformation of mobile phones into general purpose computers within a decade. Moreover, governments around the globe have gained awareness of the role greenhouse gases play in climate change, leading to incentives for the development of renewable energy technologies (solar, wind, etc.) and electric vehicles (EVs). For all of these technologies to be effectively implemented, energy storage systems are key enablers. As an example, the European Commission has set the target of achieving emission-free urban passenger transportation by 2050 (i.e. abandoning the use of conventionally fuelled cars in cities) and emission-free urban freight transportation by 2030 [15]. Consequently, research and development on LIBs have exploded (in the span of 7 years, researchers around the globe have added at least 119188 new publications on batteries from 2010 to 2017 [54]). A recognition of the current importance of the field comes from the 2019 Nobel Prize in Chemistry, awarded to John Goodenough, M. Stanley Whittingham and Akira Yoshino for the invention of the rechargeable LIB.
While the bulk of battery research is directed towards LIBs, it is important to consider that lithium is not regarded as an abundant element (the relative abundance of lithium in the Earth’s crust is only 20 parts per million). Moreover, lithium resources are greatly concentrated in South America, which means that regional politics can have an outsized effect on its price. The second-smallest alkali metal, sodium, constitutes 1% of the earth’s crust and is a strong candidate to substitute lithium in rechargeable batteries [78]. For this reason, sodium-ion batteries (NIBs) are one of the most widely investigated alternatives to LIBs, and commercial units are being produced already for systems with low energy density (e.g. e-bikes, e-scooters) [11]. For most applications, though, LIBs are yet to find a credible contender.
While advances in materials and battery design have been impressive, the fundamental purpose of battery research has remained unchanged over the years: to decrease the weight and volume of the battery, increase its durability (i.e. the number of charge/discharge cycles of the battery) and minimize its cost while maintaining safety. Achieving these objectives requires an interdisciplinary approach involving material scientists, chemists, physicists, and a growing army of applied mathematicians and computer scientists. Indeed, increasing computing power, and improving the algorithms for quantum, atomistic and continuous simulations are making the feedback loop between the chemistry lab and the laptop screen a practical reality. Still, the complex multiscale nature of LIBs and NIBs, involving solid state ionics, interface science, polymer physics and engineering, means that plenty of open problems remain to be satisfactorily tackled.
From a mathematical and computational perspective, the goals stated above often translate into answering the following questions: (i) is it possible to accurately and efficiently estimate the electronic and/or ionic conductivities of the materials involved, based on prior knowledge of their atomistic structure?; (ii) can the chemical composition be optimized to enhance desirable features such as conductivity, cyclability or energy density?; (iii) can the structure and transport properties of the interface between different components be predicted from models of the individual phases?; and (iv) how can all this information be integrated into the macroscopic model of a realistic battery? Our research program in the recent years has attempted to contribute to answering these questions.
One of the critical challenges involving the atomistic simulation of battery materials is the slow diffusion of charge carriers at room temperature. To tackle this issue, we have developed enhanced sampling methods and multi-stage integration schemes that are suitable for solid-state systems including polarizable atoms, allowing us to simulate the ionic transport in materials for LIBs and NIBs at realistic operating conditions [2, 6, 30, 32, 61]. In order to produce experimentally meaningful results, an accurate model of the interatomic interactions (a force field) must be first developed or adapted. For the specific case of polarizable systems, the development of a force field can be quite challenging and the resulting model might not be accurate or lead to instability at certain chemical compositions of interest. We have overcome this shortcomings by introducing composition dependant force fields, adjusted with respect to accurate quantum mechanical simulations and/or experimental data [18, 19, 34]. Also, we provided a simple solution to deal with the additional degrees of freedom posed by the core-shell polarizability model [18].
One promising way to reduce the costs associated with experimental synthesis and characterization of new materials is in-silico material discovery and optimization. Despite considerable progress and the seemingly unstoppable growth of computing power, novel techniques to perform this task that can efficiently incorporate experimental information are still needed [38, 57]. On this front, we have designed Bayesian inference algorithms coupled with multi-stage integrators that will combine incoming data from atomistic simulations and information from experiments to produce the distribution of compositions that is most likely to maximize the expectation of a desired set of macroscopic properties [6, 60].
The article summarizes these contributions and demonstrates some key examples involving state-of-the-art LIB and NIB components. In Sect. 2, we offer a short but necessary summary of the key fundamental aspects of rechargeable batteries. In Sect. 3, we provide a brief introduction to traditional atomistic simulation methods and present our enhanced sampling techniques for molecular simulation and computational statistics [60], along with the in-house advanced adaptive integration schemes for Hamiltonian dynamics [6]. In Sect. 4, we discuss the development of force fields for polarizable and non-polarizable materials. Sect. 5 presents our published applications of the discussed algorithms for modelling of sodium intercalation cathodes for NIBs and solid electrolyte garnets for LIBs [18, 19, 32, 41]. Finally, Sect. 6 provides concluding remarks and some future research directions. Specifically, we discuss the incorporation of the in-house Bayesian parameterization technique Mix & Match Hamiltonian Monte Carlo (MMHMC) [60] into the proposed framework for Bayesian materials screening and comment on the multiscale simulation of composite materials using the novel version of our Generalized Shadow Hamiltonian Monte Carlo (GSHMC) [2] that is specially adapted for sampling of coarse-grained systems (meso-GSHMC) [3].
2 Fundamental Aspects of LIBs and NIBs
We provide a summary of the key fundamental properties of the rechargeable batteries essential for this study.
2.1 Structure and Chemistry of Electrochemical Cells
The basic building blocks of any battery are the electrochemical cells (Fig. 1), in which charge carriers move from the anode (negative electrode) to the cathode (positive electrode) during the discharge. In LIBs, the carrier consists of positively charged lithium ions (Li+) and the process is reversible: when an external voltage above the cell potential is applied, Li+ is transferred from the cathode to the anode, charging the cell once again. The cathode and the anode are separated by the electrolyte containing dissociated lithium salts. In most commercial LIBs, electrolytes are comprised of organic liquid salts confined within a porous separator membrane, which avoids direct contact between the electrodes. When a lithium atom leaves the anode during the discharge, an electron is released to the outer circuit and performs electrical work. During the charge, electrons are injected into the anode from the external source, driving the release of Li+ from the cathode. Hence, it is clear that the electrolyte must be electronically insulating while constituting a good medium for the diffusion of Li+. In NIBs, the charge carriers are sodium ions (Na+).
Currently, cathode materials are made of electrochemically active metal oxide particles (such as XCoO2 and XFePO4, with X = Li for LIBs or X = Na for NIBs), an inert binder “gluing” them together and some electronically conductive coating (typically carbon). The key feature of the active particles is their ability to accept and release Li+ ions (lithiation/delithiation) with minimal changes to their crystal structure, through a process which Whittingham called the intercalation mechanism [76]. Anodes are most commonly made of graphite, because the lithiation/delithiation reaction is quite reversible without altering the mechanical and electrical properties of the material. On the first charge of the battery, a passivation layer, the so-called solid electrolyte interphase (SEI), forms from the decomposition of the electrolyte on the anode surface. This layer is of crucial importance for the battery operation in terms of safety, as it prevents the carbon from reacting with the electrolyte and helps avoiding graphite exfoliation [37, 54].
Important efforts have been made to replace liquid electrolytes with solids, due to the safety problems associated with the flammability of the organic salts that comprise them. Another driver is the impossibility to use metallic lithium (Li0) as the anode along with liquid electrolytes, because the fast and disorder electrodeposition of Li+ leads to the formation of Li0 filaments (dendrites) that can penetrate the separator and connect both electrodes, producing a short-circuit. Since Li0 anodes have a much higher energy density, their safe and efficient incorporation could greatly reduce battery volume/weight. Several solid and semi-solid electrolytes have been developed in recent years, including crystalline materials, polymers, gels, and composites mixing these three families [80]. Still, none has yet achieved the combination of ionic conductivity, thermal, mechanical and chemical stability and low cost necessary for widespread adoption.
While there are many factors influencing battery performance, we will focus on the one of particular importance: ionic conductivity.
2.2 Ionic Conduction in Battery Materials
The rate of X+ ion transfer between the electrodes is a multiscale variable depending on (i) the ionic diffusivity within the active electrode particle; (ii) the grain boundary resistance between adjacent electrode particles; (iii) the rate of interfacial exchange between electrode and electrolyte; (iv) the ionic diffusivity within the electrolyte and, for solid electrolytes, the grain boundary resistance between adjacent electrolyte particles; and (iv) the ionic diffusivity within the SEI (Fig. 2). It is still possible to subdivide these resistances further, as electrode particles may be agglomerated through a binder and contain some coating particles to enhance the electronic properties (see Fig. 2).
The several scales of ionic conduction in an electrochemical cell for LIBs. Cathode, anode and electrolyte (a solid one in the sketch) are composed of active particle agglomerates, presenting grain boundary resistances at the particle/particle interfaces. Often, these particles are glued by a polymeric binder and may be coated to enhance electronic conduction. These micro/meso structures (∼10−6–10−5 m) are generally isotropic. Within single active particle crystals, structural anisotropy can create preferential diffusion paths for Li+. In addition, only particular sites are capable of accepting Li+ ions, which means that intracrystalline Li+ motion occurs in discrete jumps between those sites. Individual jumps occur at the atomistic scale (∼10−10–10−9 m) and long range conduction happens over many such jumps (∼10−8–10−7 m). However, subatomic scale phenomena such as oxygen polarization (∼10−12 m) can strongly influence the energy barriers associated with the jumps
2.2.1 Ionic Conduction in Cathodes
Within the active particles of the cathode, insertion of an X+ leads to the reduction (acceptance of an electron) by the transition metal (M) (e.g. in LiFePO4, iron is reduced from Fe3+ to Fe2+). Clearly, the ease with which electrons can reach and reduce M and the ease with which X+ can travel from the surface to the bulk of the particle are of paramount importance. The latter is captured by the ionic conductivity tensor (σ X), which is defined as
where J is the electric current density transported by the charge carrier and E the electric field. Most active cathode particles, however, are orthotropic at the nanoscale (∼10−9 m) and only the diagonal components of σ X are needed. In addition, because cathodes are made of randomly oriented collections of active particles, mesoscopic ionic conduction is isotropic and the conductivity tensor at this scale reduces to a simple scalar σ X,meso.
Most experimental measurements are microscopic (∼10−6 m). Moreover, electron movement and reduction of M is comparatively fast compared to ionic diffusion, which means that the cathode conductivity reported in the literature normally corresponds to σ X,meso [10]. There are, nonetheless, single crystal measurement methods capable of capturing conductivity anisotropy [7]. In most atomistic studies (ours included), it is assumed that intraparticle diffusion dominates over interparticle diffusion, and σ X,meso is simply estimated as \(\sigma ^*_{\text{X,meso}}= \frac {1}{3} \mathrm {tr}(\boldsymbol {\sigma }_{\text{X}})\) [18, 19, 30, 70, 75]. This is not entirely correct, as grain boundary and other interfacial resistances can be quite significant and neglecting them leads to overestimated conductivities. In general terms, if the atomistically estimated conductivity is within an order of magnitude above the experimental values, the estimation is considered good enough. Extending atomistic methods to the mesoscale simulation of cathodes (coarse-graining) will provide powerful means for examining the impact of large-scale interfacial effects.
The self-diffusion coefficient for X+ in an orthotropic crystal is a diagonal tensor D X whose i-th entry is given by
where 〈 Δ2 r i(t)〉 is the mean square displacement of the ions in the i-th direction after time t, and t c is a characteristic diffusion time (for the cathode, it corresponds to the average interval between consecutive ionic jumps). D X,i is related to σ X,i through the corrected Nernst-Einstein equation:
where c X is the charge carrier concentration, Q X is its ionic charge, F is the Faraday’s constant, k B is the Boltzmann’s constant, T is the temperature and H r ≤ 1 is the Haven’s ratio. H r corresponds to the ratio of the charge carrier collective diffusivity to the self-diffusivity; it is unity in the small concentration limit. Above that, ionic displacements are correlated due to long-range Coulomb interactions and this correction is required [56].
2.2.2 Ionic Conduction in Electrolytes
In most electrolytes, positive ions (cations) move isotropically in all directions. However, in liquid and polymer electrolytes, X+ usually originates from the dissociation of a salt, which means that negative counterions (anions) are also present (e.g. standard Li salt LiPF6 dissociates into Li+ and PF\(^-_6\)). Since the mobility of anions and cations is different (the anion is always much heavier), the diffusivity of both species must be considered in the calculation of the conductivity:
where c tot is the total ionic concentration, Q v is the ionic charge of species v and D v,i its self-diffusivity in the i-th direction. v = + for the cation and v = − for the anion. Using atomistic simulations, it is straightforward to estimate the terms in equations (2) and (3) [20]. While for single ionic carriers it is often a reasonable approximation to take H r = 1, this almost always leads to large errors for dissolved salts, because of the strong tendency cations and anions have to cluster and behave in a collective fashion. Finally, in crystalline solid electrolytes such as Li7La3Zr2O12, X+ moves through a partially unoccupied lattice embedded within a crystalline framework [19, 41]. In these systems, ionic conduction occurs through discrete jumps between X sites. However, because the lattice contains vacancies, diffusion is somewhat more fluid than it is in typical cathode particles (there, diffusion requires the prior formation of a defect in order to produce a vacant site to which X+ can jump to). Since no counterions are present in crystalline solid electrolytes, Eq. (2) can be used to obtain the ionic conductivity.
2.2.3 Ionic Conduction in Anodes
Since we have not tackled yet the study of conduction in graphite anodes, we will not discuss it in detail. Suffice it to say that ion intercalation in graphitic anodes involves ion absorption and diffusion through the SEI, and the occurrence of phase transitions within the ordered graphite structure. As a consequence, it is rather complex and multiscale in nature. A recent review on advances in the modelling of anodes can be found in [58].
3 Sampling in Atomistic Simulation
Molecular dynamics (MD) and Metropolis Monte Carlo (MC) are traditional sampling techniques broadly used for solid-state atomistic simulation [39]. Recently, we have proposed the class of enhanced sampling methods [4] which combine the advantages of both MD and MC offering improved sampling efficiency and accuracy vital for the success of a molecular simulation. The methods utilize the modified Hamiltonians for sampling enhancement and hence the name of the class—Modified Hamiltonian Monte Carlo (MHMC). In this section, we briefly review the molecular dynamics and Monte Carlo approaches and discuss the main features of MHMC as well as the benefits of employing them in the study of battery materials.
3.1 Molecular Dynamics
Molecular Dynamics (MD) is a computer simulation approach in which the evolution in time of a group of interacting atoms is followed by integrating the Newtonian equations of motion. In general, MD is not trying to generate physically accurate trajectories: this is often an impossible task. Instead, quantities of interest are statistical averages computed during the sampling of phase space.
Let us denote the positions of a system of n particles as \(\mathbf {r} \in \mathbb {R}^{d}\), where d = 3n, and the velocities as \(\mathbf {v} \in \mathbb {R}^{d}\) and assume that the system is conservative, i.e. a potential energy function U exists such that
where F are the forces. The function U is also called a force field and it contains the contribution to the potential energy from all interatomic interactions. Then, for the classical n-body problem in MD-simulations, Newton’s second law can be expressed as
where \(M \in \mathbb {R}^{d\times d}\) is the (symmetric positive definite) mass matrix.
The Hamiltonian formulation of Newtonian mechanics (5) reads
Here \(\mathbf {p} = M \dot {\mathbf {r}}\),Footnote 1 \(\mathbf {p} \in \mathbb {R}^d\) is the linear momenta and the Hamiltonian or energy functional is defined as
where the super index T denotes the transpose vector. The equations in (6) are the Hamilton equations of motion. By introducing the 2d × 2d matrix \(J=\begin {bmatrix} 0_{d \times d} & -I_{d \times d}\\ I_{d \times d} & 0_{d \times d}\end {bmatrix}\), (6) can be rewritten as (cf. [65])
where
The space defined by the vectors (r, p) satisfying Eq. (8) is called the phase space. Under suitable conditions, there is a unique exact solution at a time t for every initial point (r(0), p(0)), and, for any time t, a flow map ϕ t can be defined as
Hamiltonian flows have a number of important properties, including (cf. [65]):
-
1.
Symplecticity: For all t, a flow map ϕ t is symplectic if, at each point (r, p) in phase space,
$$\displaystyle \begin{aligned} \phi^{\prime}_t(\mathbf{r}, \mathbf{p})^T J \phi^{\prime}_t(\mathbf{r}, \mathbf{p}) = J, \end{aligned}$$where \(\phi ^{\prime }_t(\mathbf {r}, \mathbf {p})\) is the 2d × 2d Jacobian matrix of ϕ t. An important consequence of symplecticity is phase volume preservation (oriented volume): If A represents a region in phase space, then the volume of ϕ t(A) is invariant in t.
-
2.
Time reversibility: The Hamiltonian system described by Eqs. (7)–(9) is time reversible; i.e., for all t, \(\phi _{t}^{-1} = \phi _{-t}\).
There are another two characteristics that do not apply generically to all Hamiltonian flows. However, they have been empirically observed in the flows arising from many systems in MD simulations (cf. [52]):
-
3.
Ergodicity: In statistical physics, ergodicity is defined to be the property that for any observable Ω, the time averages of Ω eventually converge to the average of Ω over the phase space. More precisely, for a probability measure π preserved under the Hamiltonian flow, ergodicity implies that
$$\displaystyle \begin{aligned} \lim_{T\to\infty}\frac{1}{T}\sum_{t=0}^{T} \Omega(\phi_t(\mathbf{r}, \mathbf{p})) = \lim_{T\to\infty} \frac{1}{T} \int_0^T \Omega(\mathbf{r}, \mathbf{p}) \mathrm{d}\pi(\mathbf{r}, \mathbf{p}). {} \end{aligned} $$(10)This is very useful for simulations, as it allows approximating the spatial averages by means of time-averages available through MD.
-
4.
Sensitive dependence on initial conditions (SDIC): In high-dimensional Hamiltonian systems, there are arbitrarily close points (r ′, p ′) to (r(0), p(0)), such that the positive orbit starting at (r ′, p ′) eventually diverges from the one starting at (r(0), p(0)). As a consequence, MD trajectories cannot be computed for long periods of time in a classical sense (that is, point-to-point matching between exact value and computed value), because even the unavoidable round-off error will naturally be magnified, thus potentially rendering computed values that are far from the actual values.
SDIC and ergodicity are two phenomena playing complementary roles in computing long-term trajectories of MD flow-maps: while SDIC prevents the computation of accurate trajectories, ergodicity allows the extraction of statistical information from the same computations. From a numerical standpoint, if a discretization ϕ L Δt of the flow map ϕ t (where L Δt is a trajectory length and Δt is a time step) is symplectic, then averages of an observable Ω calculated along orbits of ϕ L Δt will converge to the desired spatial average as the time step Δt tends to 0. Efficient and simple integrators providing symplecticity and time reversibility are available, the most popular of which are the Störmer-Verlet method and its extensions (leapfrog, velocity Verlet, etc.). Nonetheless, MD still suffers from several drawbacks:
-
(i)
As stated in Eq. (10), making use of ergodicity (if it exists) requires sufficiently long trajectories. In systems with large energy barriers such as the ones between adjacent sites in cathode materials, meaningful trajectories may need to be hundreds of nanoseconds long (∼10−7 s) to sample atomic jumps. Because time steps need to be small (typically ∼10−15 s), the number of steps required can be as high as L ∼ 108. For a tens-of-thousands atoms system this can be very demanding, even with robust computing architectures.
-
(ii)
Because MD only allows for slow exploration of configurational space through a sequence of many small steps, systematic discretization errors can be significant.
-
(iii)
In the absence of external forces, the flow defined by (9) is energy preserving: the dynamics occurs on a surface in \(\mathbb {R}^{2d}\) for which H is constant. The probability density arising from this condition is the so-called microcanonical ensemble. However, most practical applications occur either at constant number of particles, N, temperature, T, and volume V (the canonical or NVT ensemble) or at given N, T and pressure, P (the isothermal-isobaric or NPT ensemble). In the latter two ensembles, the Hamiltonian must be modified by adding additional degrees of freedom, which are coupled to the particle velocities (thermostatting) and simulation domain dimensions (barostatting), increasing computational cost and introducing additional sources of error.
One significant advantage of MD is the ability to capture dynamical properties, such as the diffusion coefficients in Eqs. (2) and (3). In addition, even though the true evolution of the system may not be captured, qualitative information regarding the underlying mechanisms of the physical processes can still be extracted.
3.2 Monte Carlo Simulations
While MD tries to estimate the value of the integral on the r.h.s. of Eq. (10) using a deterministic scheme, Monte Carlo (MC) simulations attempt to approximate the value of such integral using a stochastic approach. For simplicity, we will refer only to the canonical ensemble, for which the probability density distribution is
where β = (k B T)−1 is the thermodynamic beta. The position and momenta contributions to the Hamiltonian in Eq. (7) are separable. Moreover, the momenta part can be analytically integrated, which means that only the target distribution
needs to be sampled using the Metropolis-Hastings Markov chain MC algorithm [42]:
-
The current configuration in the chain r is randomly perturbed to generate a trial atomic configuration r ′. A typical perturbation might be a single-particle displacement: randomly pick an atom and displace its position by a small amount.
-
Accept the proposal configuration to become
 with probability $$\displaystyle \begin{aligned} \alpha = \min{\left\{1, \frac{\pi(\mathbf{r}')}{\pi(\mathbf{r})}\right\}} = \min\left\{1, \exp[-\beta(U(\mathbf{r'}) - U(\mathbf{r}))]\right\}. \end{aligned}$$
with probability $$\displaystyle \begin{aligned} \alpha = \min{\left\{1, \frac{\pi(\mathbf{r}')}{\pi(\mathbf{r})}\right\}} = \min\left\{1, \exp[-\beta(U(\mathbf{r'}) - U(\mathbf{r}))]\right\}. \end{aligned}$$Otherwise, dismiss r ′ and set
 to r.
to r. -
Repeat the two steps until the number of configurations reaches N.
Following this procedure, due to the law of the large numbers, the average of an observable Ω can be estimated as
where {r i} is the set of accepted configurations.
Metropolis MC has a number of advantages with respect to MD. Thus, MC does not have an equivalent of a time step error, its sampling is exact with only statistical errors involved. The method is flexible in the choice of sequences of steps which potentially can lead to rapid exploration of configurational space. However, it also has a number of important drawbacks: for systems with large numbers of degrees of freedom, such as biomolecules, it may become impractical due to the difficulties in specifying a physically meaningful move leading to high acceptance rates. In addition, the method does not provide dynamical information, which means that quantities such as diffusivities or conductivities (Eqs. (1)–(3)) cannot be estimated.
3.3 Modified Hamiltonian Monte Carlo Methods
Our choice of simulation techniques for the effective study of ion transport in bulk and nanostructured materials is based on four requirements critical for the success of the project. Such methods should (i) sample efficiently multidimensional space; (ii) reproduce dynamical properties of a simulated system; (iii) be able to detect rare events; and (iv) be easily extended to simulations on meso-scales.
The Modified Hamiltonian Monte Carlo (MHMC) methods were originally developed for atomistic simulations of complex systems [1, 2, 45, 68] and then adapted for multiscale [31] and mesoscale simulations [3]. They proved to be successful in the study of rare events in complex biological processes [3, 4, 31, 74] though never have been applied to solid-state chemistry until recently when we proposed using them for the simulation of battery materials [18, 19, 32, 41].
MHMC are importance sampling Hybrid Monte Carlo (HMC) methods [28] that achieve higher efficiency than MC, HMC or MD by sampling with respect to a modified Hamiltonian. Such methods are especially appropriate when exploring high-dimensional configurational spaces, helping in finding energy global minima and simulating rare events such as slow chemical reactions or phase transitions. Furthermore, the MHMC methods originated from the generalized hybrid Monte Carlo (GHMC) [44, 49] can keep the dynamic information throughout the sampling process similar to stochastic Langevin and Brownian dynamics simulations.
In general, to simulate the properties of physical systems, one collects samples with respect to a target distribution such as π(r) in (12). For that purpose, HMC methods are a suitable choice as a sampling technique. Given a separable Hamiltonian (7), HMC generates samples of configurations from the augmented canonical distribution (11). Then, marginalizing momenta variables out, one can obtain the samples with respect to the target distribution π(r) in (12).
Instead of sampling from the canonical distribution (11), MHMC methods sample from an importance canonical density
where \(\tilde {H}^{[k]}\) is the kth order truncation of the modified Hamiltonian which is preserved exactly by a symplectic integrator [65]. For certain H 2, H 3, …, a modified Hamiltonian reads as
where Δt is an integration time step. For an integrator of order m, \(\tilde {H} = H + \mathcal {O}(\Delta t^m)\), so that H 2, …, H m vanish. Thus, for k > m,
According to [6, 14], for a system of D particles, the expectation of the increments of H and \(\tilde {H}^{[k]}\) in an integration leg satisfy
and
respectively.
Let us now describe the algorithm of a generic MHMC method. Given a sample (r, p) from the distribution \(\tilde {\pi }\), the next configuration  is obtained as follows:
is obtained as follows:
-
Set up the new momentum p ∗ by applying a momentum refreshment procedure that preserves the importance density \(\tilde {\pi }\) (13).
-
Generate a proposal configuration (r ′, p ′) by simulating the Hamiltonian dynamics (6) with the Hamiltonian H in (7) and the initial condition (r, p ∗) using a symplectic and time-reversible numerical integrator Ψ (cf. [65]).
-
Accept the proposal configuration (r ′, p ′) to become
 with probability $$\displaystyle \begin{aligned} \alpha = \min{\left\{1, \frac{\tilde{\pi}(\mathbf{r}', \mathbf{p}')}{\tilde{\pi}(\mathbf{r}, {\mathbf{p}}^*)}\right\}}. \end{aligned}$$
with probability $$\displaystyle \begin{aligned} \alpha = \min{\left\{1, \frac{\tilde{\pi}(\mathbf{r}', \mathbf{p}')}{\tilde{\pi}(\mathbf{r}, {\mathbf{p}}^*)}\right\}}. \end{aligned}$$Otherwise, reject the proposal and perform a momentum flip, i.e.
 .
.
The reader should notice that
For comparison, in the Hybrid Monte Carlo algorithm, the corresponding ratio is given by
Therefore, since k > m, one can see from (15)–(18) that MHMC methods may provide higher acceptance rates than regular HMC methods. The fewer rejections has a positive impact not only on the sampling efficiency but also on the accuracy of dynamics since less momentum flips occur [2, 5]. Moreover, for very big systems, where performance of HMC degrades dramatically, MHMC algorithms may counterbalance the error introduced by the size D and maintain a high acceptance rate by choosing a bigger truncation order k without increasing the order of the integrator m [6].
Since in MHMC methods the samples are generated with respect to the importance density (13), the computation of averages of any observable Ω with respect to the canonical distribution (11) requires a reweighting. Given N samples of the observable Ωi, i = 1, 2, …, N along a trajectory (r i, p i) drawn from (13), the average of Ω with respect to (11) is calculated as
where the importance weights are computed as
A big variability among weights would mean that the canonical density π in (11) and the importance density \(\tilde {\pi }\) in (13) are not close. This would lead to errors in the averages, as many samples would not contribute significantly to the computation in (19). Such a situation is well controlled, however, in the MHMC methods through the appropriate choice of an integration step and an order of a modified Hamiltonian (cf. (14)). This makes samples of (13) an efficient means towards computing expectations with respect to (11).
The various algorithms in the MHMC class of methods may differ in the elements described above: refreshing the momenta, simulating the Hamiltonian dynamics or computing the modified Hamiltonians.
For our purposes here, the Generalized Shadow Hybrid Monte Carlo (GSHMC) method [2] is of special interest. As its predecessor the Targeted Shadowing Hybrid Monte Carlo (TSHMC) method [1], GSHMC takes advantage of a partial momentum update based on the ideas of Horowitz [44], which helps preserving partially dynamics and enhancing sampling efficiency:
where φ ∈ (0, π∕2] is a parameter and u a random noise drawn from \(\mathcal {N}(0, \beta ^{-1} M)\). The proposed refreshed momentum p r is accepted, i.e. p ∗ = p r, with the probability
where
In the case of rejection, we set p ∗ = p.
GSHMC was originally introduced for atomistic simulations in canonical ensembles [2, 30, 74] and then adapted to simulations in isobaric-isothermal ensembles [35].
Different extensions of GSHMC aiming at specific applications appeared recently. For meso-scale simulations, the meso-GSHMC method [3] was proposed. In coarse-grained mesoscopic models, the fluctuation-dissipation contributions should mimic the impact of non-resolved finer details of an atomistic model on the coarse grained length and time scales while maintaining the system at a desired temperature. For this purpose, the stochastic thermostat called Dissipative Particle Dynamics (DPD) [33] is used. The meso-GSHMC puts DPD in the GSHMC framework by introducing a DPD-type momentum update step which conserves total linear and angular momenta. Unlike original DPD, meso-GSHMC samples exactly from the canonical distribution (11) while dealing with the fluctuation-dissipation terms.
For multiscale simulations, a naturally possessed weak stochasticity of GSHMC can be combined with the modified impulse multi-time-stepping (MTS) molecular dynamics and the modified Hamiltonians specially derived for modified MTS integrators. The resulting MTS-GSHMC method [31] demonstrates the improved stability of the MTS integrators and superior sampling performance over multi-time-stepping molecular and Langevin dynamics.
More recently, the MHMC method for solid-state atomistic simulations called Randomized Shell Mass GSHMC (RSM-GSHMC) has been proposed [32]. In this algorithm, a mass randomization is implemented as part of the momentum update step in order to reduce the negative effect of a shell mass within a dynamical shell model on the kinetics of a simulated system. Before updating the momenta, a fraction of the atomic mass is redistributed between the core and the shell, maintaining the total mass constant. Apart from the study where the methodology was introduced [32], it has been also used in [18].
All variants of GSHMC described above posses the strongest features of GSHMC such as the enhanced sampling, ability to reproduce dynamical properties of simulated systems and rigorous temperature control. As demonstrated in the studies cited above (see also [6] and references therein) for different problems, the use of GSHMC methods resulted in a systematic improvement of the sampling efficiency and accuracy with respect to those observed with conventional sampling techniques, such as MD, MC, HMC or Langevin dynamics.
While GSHMC methods were designed for applications in the field of molecular simulation, the Mix & Match Hamiltonian Monte Carlo (MMHMC) [60] method has been recently proposed for Bayesian inference problems. In simple terms, MMHMC is an adaptation of GSHMC to computational statistics. It proved to be successful in the simulation of popular statistical models such as multivariate Gaussian, Bayesian Logistic Regression and Stochastic volatility [60].
Two possible strategies for enhancing performance of MHMC methods are (i) a suitable choice of the method-specific parameters; and (ii) an optimization of conservation properties of numerical integrators used for simulating the Hamiltonian dynamics. The latter is explored in the following section.
3.4 Modified Adaptive Integration Approach
In this study, we limit ourselves to separable Hamiltonians, such as the one in (7), meaning that the Hamiltonian can be written as a sum H ≡ A + B of two partial functions
which correspond to the kinetic and potential energies, respectively. Thus, the Hamilton equations of motion (6) can be rewritten as
These equations can be integrated analytically and their solution flows at a time t are given by (cf. (9))
and
These solution flows of the partial systems, for a time t, associate the exact solution value (r(t), p(t)) with each initial condition (r(0), p(0)).
A splitting integrator can be constructed as a palindromic composition of the solutions flows (22) and (23) of the partial systems (cf. [16]). Here, we limit our attention to the one-parameter family of two-stageFootnote 2 splitting integrators studied in detail in previous works [6, 17, 36]. The map that advances the solution over one step Δt is
where b ∈ (0, 1∕4] is the parameter that fully characterizes a two-stage integrator. Then, for a time τ = L Δt with \(L \in \mathbb {N}\), one can also define the transformation Ψτ as the composition

The integrators in (24) are symplectic because they are a composition of Hamiltonian flows [65]. Moreover, they are also time-reversible due to the palindromic structure of (24) [17].
The optimal choice of a parameter b in (24) has been thoroughly investigated for the HMC [36] and MHMC methods [6, 61]. The suggested criteria for such “optimality” is the maximization of acceptance rates in HMC or MHMC due to the conservation properties of a chosen integrator.
For MHMC, the focus is on those two-stage integration schemes ψ that provide the lowest expected error \(\Delta \tilde {H}^{[k]}\) in modified Hamiltonians with respect to a modified density (13). Here,
for a given time τ = L Δt. Thus, the acceptance criterion in (17) is integrator-dependent.
In contrast to the well established practice in molecular simulation to use the same integrator, usually Verlet/leapfrog, for a broad range of the simulated systems, in [6], it has been proposed to construct a system specific two-stage integrator prior to an MHMC simulation. The Modified Adaptive Integration Approach (MAIA), which realises this idea, adapts the parameter b to a given simulated system and a chosen by a user value of step size Δt in such a way that the expected value of (25), \(\mathbb {E}\left [\Delta \tilde {H}^{[k]}\right ]\), is minimal. Based on the detailed analysis of the one-dimensional harmonic oscillator, the MAIA approach provides the upper bound ρ(h, b) of \(\mathbb {E}\left [\Delta \tilde {H}^{[k]}\right ]\),Footnote 3 where h is a dimensionless step size related to Δt by
Here, \(\sqrt {3}\) is a safety factor used to avoid nonlinear resonances (cf. [6, 36, 67]) and \(\tilde {\omega }\) is the fastest angular frequency of the two-body interactions. Then, the value of b is found as the one that minimizes
where \(\tilde {h}\) is the dimensionless time step associated to a user defined Δt.
One should note that, for a realistic physical model consisting of D harmonic oscillators, \((0, \tilde {h})\) is the shortest interval that contains all \(h_i = \sqrt {3} \omega _i \Delta t\), where ω i are the D frequencies in the problem.
It has to be stated that MAIA is a never-fail strategy, meaning that it guarantees, by construction, that the numerical stability is not lost. For the biggest allowed integration step sizes, the parameter b in (24) becomes 1/4, which means that the integrator of choice is the two-stage version of the classic velocity Verlet. This integration scheme is known as the integrator with the largest stability interval among two-stage integrators, namely (0, 4).
The extended MAIA (e-MAIA) [6] is capable of keeping the momenta acceptance rate (21) at the user-desired level for any given problem through the intelligent choice of the parameter φ in the momentum update (20).
Both MAIA and e-MAIA proved their efficiency in simulations of complex molecular systems in Materials Science, Biology and Chemistry [6, 18, 19, 32, 41].
3.5 Software Implementation
The GSHMC methods for molecular simulation, i.e. GSHMC, meso-GSHMC, RSM-GSHMC, described in Sect. 3.3 have been implemented in the in-house software package MultiHMC-GROMACS [30, 35, 36] which is built on top of the popular suite of programs for molecular dynamics simulations GROMACS [12, 43]. GROMACS supports state-of-the-art molecular simulation algorithms and is well known for its computational efficiency and parallel scaling properties. These features are carefully maintained in MultiHMC-GROMACS.
Two-stage integrators (24) are implemented in MultiHMC-GROMACS as a concatenation of velocity Verlet stepsFootnote 4 [36]. The implementation is general enough to allow the use of all members of the family (24), including the adaptive integration schemes MAIA and e-MAIA (Sect. 3.4). The analysis required for the MAIA and e-MAIA methods is done within the GROMACS preprocessing module [6]. Thus, no computational overheads are introduced. Once the integrator parameter b and the angle φ (in the e-MAIA case) are obtained, they are passed to the running module prior to a simulation.
The package offers the efficient implementation of various formulations of modified Hamiltonians derived for the range of GSHMC methods and numerical integrators. In addition to the GSHMC methods, the HMC samplers have been included in MultiHMC-GROMACS as particular cases of GSHMC [36]. The user can select any GSHMC or HMC method from the code simply by predetermining appropriate parameters in the modified GROMACS input file. The same applies to numerical integrators.
A detailed description of the MultiHMC-GROMACS package may be found in [6, 30, 32, 35, 36].
The Mix & Match Hamiltonian Monte Carlo (Sect. 3.3), proposed for applications in computational statistics, is implemented in the in-house software package HaiCS [60]. The package is designed for statistical sampling of high dimensional, complex distributions and parameter estimation in different models by means of Bayesian inference using HMC-based methods. The code benefits from the efficient implementation of modified Hamiltonians, multi-stage splitting integrators [61], performance analysis tools compatible with CODA toolkit [59] and provides a user-friendly interface for implementing alternative HMC-type samplers, splitting integrators and statistical models.
Both MultiHMC-GROMACS and HaiCS are written in C and targeted to computers running UNIX certified operating systems.
4 Force Fields
As briefly introduced in Sect. 3.1, a force field is a mathematical expression describing the dependence of the energy of a system on the positions of its particles. It is fully defined by a functional form of the interatomic potential energy, U(r), and a set of parameters. There are several force fields in use addressed to particular families of materials (e.g. AMBER, for proteins and DNA [27] or CHARMM for polymers [24]). However, it is clear that for many specific materials and applications, custom force fields must be developed. Force field development has three fundamental requirements:
-
an appropriate functional form for the interaction potentials,
-
a training data set of structural, mechanical and/or thermodynamic properties (e.g. experimental, computed, etc.) to fit the model, and
-
an optimization strategy to perform the fitting.
Ideally, a force field must be simple enough to be evaluated quickly, but sufficiently detailed to reproduce the properties of interest. Below, we elaborate on each of these requirements, with particular focus on those interactions that are typical to intercalation in cathodes and solid electrolyte materials. Hence, metallic systems are not included in this discussion.
4.1 Functional Form of the Interaction Potentials
Let us denote a position of atom i in an n-particle system as r i, and the Euclidean distance between atoms i and j as r ij. The general expression for most force fields has the form:
Contributions to U bonded(r 1, …, r n) come from groups of chemically linked atoms (sharing electrons), and are typically divided into two-body bond-stretching potentials, three-body angular-bending potentials, and four-body dihedral potentials (Fig. 3a). For instance, the form of U bonded in the popular OPLS [48] and AMBER [27] force fields is:
where angle θ ijk = θ(r i, r j, r k) (analogously for proper dihedral ϕ ijkl), and {r 0,b}, {θ 0,a}, {k a}, {k b} and {k d,m} are positive force field parameters. There are no improper dihedrals in the original version of these force fields, but later updates have included them.
(a) Typical bonded interactions: bonding (U bond), angular (U angle), proper dihedral (U proper) and improper dihedral (U improper) interactions. U bonded = U bond + U angle + U proper + U improper. (b) Core-shell model of polarizability: the polarizable ion of mass m and charge Q is represented as a core (c) and a shell (s) with opposite charges Q c and Q s, respectively, interacting through a bond potential U cs (usually harmonic, U cs = k cs r cs). The mass of the ion is concentrated in the core (m = m c), to allow for instantaneous thermalization of the shell. In practice, however, it is better to choose a small shell mass (m s > 0, m s << m c) to boost computational efficiency
Polarizability is the ability for some atoms to form instantaneous dipoles. In many cases, its effect can be strong enough to significantly influence thermodynamic and transport properties [75, 79]. One of the simplest way to incorporate polarizability into the force field is the core–shell model suggested by Dick and Overhauser [26], in which a central core of a charge Q c and a shell of a charge Q s, with Q s Q c < 0, are introduced in such a way that the sum of these charges Q c + Q s equals the ion charge Q (Fig. 3b). The core and shell are coupled together in a unit via a bond potential (usually harmonic), which allows the shell to move with respect to the core, thus simulating a dielectric polarization. In the original proposal by Dick and Overhauser, the core mass m c was equal to the mass of the ion, m (i.e. the shell mass m s was zero), in order to enable instant thermalization of the shell. Mitchell [55] showed that taking a sufficiently small value for m s allowed simulating the core-shell system using conventional MD, as the thermal contribution from the shell was insignificant. This is called the cs-adiabatic scheme (cs-adi), which we have employed in our previous work [18]. The force field parameters for the harmonic cs-adi model, \(U_{cs}=k_{cs}r^2_{cs}\), are the spring constant k cs, Q s and m s.
The non-bonded interactions present in a typical force field are pairwise Coulomb, U Coul, and van der Waals, U vdW, interactions
acting over all atom pairs (i,j). In general, however, contributions from pairs already interacting through bonded potentials are totally or partially excluded. U Coul is given by
where 𝜖 is the vacuum permittivity and Q i the charge of atom i. Q i is a force field parameter, but in solid state systems its value is often taken as eZ i, where e is the electron charge and Z i the oxidation state of atom i. U vdW can take many possible forms, the simplest non-trivial of which is the hard-sphere potential. For battery materials, two types of vdW potentials are particularly common: the Lennard-Jones (LJ)-type potentials, U LJ (for liquid and polymeric electrolytes) and the softer Born potential U Born (for crystalline materials) [40]. The LJ potentials between i and j atoms is given by
where A ij > 0 and B ij > 0 are force field parameters. Powers (n, m) typically assume the values (9,6) or (12,6), but can also be taken as adjustable parameters. U Born,ij, on the other hand, is a softer potential, allowing for greater interatomic overlap:
where A ij, ρ ij, C ij and D ij are positive force field parameters. U vdW can, of course, be written as a combination of several types of potentials: e.g. when modelling polymer/garnet composite solid electrolytes, the LJ potentials can be employed to model the interactions in the polymer phase, while the Born potential can be used to model interactions within the garnet. In any scenario, \(U_{\text{vdW}}=\frac {1}{2}\sum _{i,j=1}^{n}U_{\text{vdW},ij}\).
4.2 Training Dataset
It is important to note that force fields partition the total electronic energy into well defined atom-atom contributions, such as Coulomb, polarization, dispersion, etc. However, it is impossible to fully separate the intricate electronic effects this way. The proper choice of a functional form of a force field and a set of data used to parameterize it (the training dataset, TD) usually makes it possible to generate a force field that is valid at least for specific problems and within the chemical and environmental constraints from the TD.
The TD typically comprises data obtained either from ab initio or semi-empirical quantum mechanical (QM) calculations, or from experimental measurements such as neutron, X-ray and electron diffraction, NMR, Raman spectroscopy, etc. Naturally, experiments can only probe a limited set of properties and their reliability depends on the quality of the experimental setup and the examined sample. The synthesis of many battery materials is by no means an exact science, and structural defects and impurities can be significant. That is why, it is expected that TDs from extensive QM calculations lead to more generally applicable force fields compared to those from experimental data. However, QM calculations still contain plenty of approximations, and a QM-based force field is of little or no use if it cannot reproduce experimental values or trends. In many cases, force fields trained through QM-based TDs are further fine-tuned with respect to experimental measurements.
4.3 Optimization Strategy to Perform the Fitting
The optimization strategy refers to the technique through which the set of optimal parameters is determined. When using an experimental TD, the general idea is to find the set of force field parameters γ 1, …, γ M that minimizes the scoring function
where \(\Omega ^0_i\) is the ith reference observation in the TD, 〈 Ω〉sim,i its atomistically simulated value with the trial force field, L the total number of observations, ω i is the weight given to observation i and ∥⋅∥ a suitable norm.
In exploiting a QM-based TD, the scoring function has a rather different form. While experimental TD’s are invariably composed of average properties (e.g. unit cell sizes, Young’s moduli, etc.) that result from a configurational average in a particular ensemble (even the fastest neutron scattering measurement results from averaging over an infinite number of configurations), QM-based TDs are normally composed of instantaneous snapshots of the equilibrated system. Hence, one can set up the particles in the exact positions provided by the snapshots, and then find the values of γ 1, …, γ M that achieve, for example, the total energy closest to the QM energy for each snapshot. This in fact is what most studies have done. A much more effective strategy is to additionally adjust {γ k} to multidimensional variables such as forces and stresses, which are also available from QM calculations. This is precisely what the so-called force-matching algorithm (FMA) does and what we employ in our study. For a training dataset consisting of L configurations, a suitable FMA scoring function is given by [22]
where n l is the number of particles in configuration l. {e l}, {s p,l, p = 1, …, 6} and {f i,l, i = 1, …, 3n l} are the energies, stresses and forces obtained with the trial force field, respectively. The superindex 0 denotes the reference values from the TD. ω e and ω s are user-defined weights to balance the amount of available information for each quantity. Such a scoring function has been proposed and implemented in the open software potfit, developed by Brommer et al. [22, 23]. We have adjusted this function to parametrization of a broader range of models by incorporating in it core-shell polarizable potentials and angular terms [18, 32].
The scoring functions (28) and (29) can be highly multidimensional and non convex. Occasionally, some of the force field parameters can be reliably set to known values from similar force fields, simplifying the problem and allowing the use of local optimization strategies [19]. In most cases, however, stochastic global optimization techniques, such as simulated annealing, are necessary to avoid local minima. This, of course, comes with the hurdle of finding suitable adjustable parameters for the algorithm itself.
5 Applications
Below, we summarize the highlights of recent work performed in our group on the atomistic simulation of battery materials for LIBS and NIBS, using the numerical schemes described above. Specifically, we focus on cathode material olivine NaFePO4 for NIBs, and solid electrolyte material Li7La3Zr2O12 for LIBs.
5.1 Na Diffusion in Cathode Material Olivine NaFePO4 for NIBS
Olivine LiFePO4 is likely the most studied commercial cathode for LIBs [73]. It provides high stability, rate capability, and sustained high voltage throughout the discharge cycle. In principle, one could expect NaFePO4 to inherit these properties from its isostructural lithium counterpart, making it a suitable cathode for NIBs. The first fundamental studies revealed that the intercalation mechanisms (see Sect. 2.1) of Li+ and Na+ in FePO4 are, however, significantly different [81]. While LixFePO4 (0 ≤ x ≤ 1) is stable at all values of x, NaxFePO4 is only stable at discrete Na+ contents: x ∈{0.0, 0.66, 0.83, 1.0} [66]. This means that during the discharge, the structure of NaxFePO4 evolves through combinations of these stable, highly organized phases (Fig. 4), adding another level of complexity to the study of Na+ intercalation as compared to that of Li+. This issue is particularly relevant when studying dynamic properties such as Na+ mobility using simulations, requiring large supercells and long simulation times to account for possible sodium orderings. These requirements make the use of first-principles methods, such as density functional theory (DFT), prohibitive in terms of computational cost. We addressed this computational challenge using atomistic simulations. Two key elements are required for this task: an accurate force field and an efficient sampling technique.
(a) The convex-hull (blue line) of NaxFePO4. At any x, all possible system structures will have an energy of formation above the convex hull. As a consequence, the most stable structure for a given x will be a segregated mixture of the structures corresponding to the closest vertices in the convex-hull. These vertices are located at x = 0.0, 0.66, 0.83, and 1.0 [66]. For instance, a mol of Na0.3FePO4 will comprise 0.45 moles of Na0.66FePO4 and 0.55 moles of FePO4. b Left: Structure of Na0.66FePO4: O2− in green, P5+ in purple, Fe2+ in blue and Fe3+ in red. Na+ is coordinated by six O2− atoms (yellow octahedra). The curved trajectory followed by Na+ along one of the channels in the main diffusion direction, y, is depicted as the solid orange line. Na+ vacancies and Fe3+ ions follow a highly organized banded arrangement (similarly for x = 0.83). Right-top: close up showing the characteristic Na+ jumping distance. Right-bottom: Cross section of a diffusion channel along y. The channels along x and z are much narrower, which means that jumps in these directions are rare. (Adapted with permission from [18]. Copyright (2018) American Chemical Society)
Whiteside et al. [75] developed a force field for the structural simulation of NaFePO4, incorporating the polarizability of the oxygen atoms through the core-shell model. We will denote such force field as Whiteside-ff from here on. However, removal of one Na+ ion leads to the oxidation of one iron (i.e. iron goes from Fe2+ to Fe3+), which means that NaxFePO4, with x < 1, contains a combination of both Fe2+ and Fe3+ (Fig. 4b). Whiteside-ff does not consider the presence of Fe3+ and, as a consequence, is not suitable for a general study of charge transport in NaxFePO4. To overcome this issue, we developed a new force field for this system, the Na x FePO 4 -ff, using accurate DFT calculations at the stable Na+ contents. The force field employs the cs-adi model described in Sect. 4.1 to incorporate polarizability in oxygen and iron atoms.
For configurational sampling of the system, conventional MD (see Sect. 3.1) has two key disadvantages. On the one hand, it requires many simulation steps for the estimation of the room temperature diffusivities. On the other hand, the cs-adi version of the core-shell polarizability model allows only for small time steps, increasing the computation time even further. In sight of this, we selected instead the in-house RSM-GSHMC technique as our simulation tool [32] (see Sect. 3.3), which simultaneously provides enhanced sampling while incorporating a scheme to minimize the computational impact of the small shell mass.
5.1.1 Force Field Development
5.1.1.1 Derivation
Ionic polarizability plays an important role in the dynamics of NaxFePO4. Similarly to Whiteside-ff [75], we divided the Fe2+ and O2− ions into polarizable core-shell units. Hereafter, Osh and Fesh will refer to the O2− and Fe2+ shells, respectively. For the bonded interactions, we considered only the angular potential between the covalently linked O-P-O ions in PO4 tetrahedra, following
where n a is the number of angles, and k a and θ 0 are force field parameters. Non-bonded interactions were represented by a sum of the Coulomb (26) and Born (27) potentials. Only interactions between X - O\(_{sh}^{2-}\) pairs were considered in the Born contribution (X = Fe\(^{2+}_{sh}\), Fe3+, Na+, P5+, O\(^{2-}_{sh}\)). The cores of Fe2+ and O2− only interacted electrostatically. The TD (see Sect. 4.2) comprised 58 olivine NaxFePO4 configurations consisting of (a) 11 quantum mechanically optimized structures at 0 K, ranging from 72 to 84 atoms, and (b) 58 equilibrated snapshots taken out of ab initio MD trajectories of an ideal NaFePO4 crystal at 500 and 1000 K. All TD configurations were computed with the plane wave DFT code VASP [50]. As an optimization strategy, we used the force-matching algorithm described in Sect. 4.3 with the scoring function (29) and the adaptive simulated annealing scheme implemented in the in-house extended version of the open source software potfit [18, 22, 23].
Since the core-shell unit is simply a construct to introduce polarizability within an empirical force field, the ab initio dataset does not provide information on how to specify the core and shell coordinates. For the core, a sensible solution consists in setting its position to that of the actual ion, because the core carries most of the core-shell unit mass. For the shell, its position should be selected in such a way that the total force on it is zero. We proposed a consistent approach to treat the shells positions, which have usually been randomly chosen in previous works [18]. We fix the spring constant and charge distribution for all core-shell units prior to starting the parameter estimation. Then, given that dispersion interactions in a core-shell unit l are assigned to a shell only, the total force on a core l, F l,core, becomes
where \({\mathbf {F}}_{l,\text{core}}^{\text{elect}}\) is the electrostatic force on a core l, and r l,core and r l,shell are the respective core and shell positions. Since the force on a shell must in principle be zero, F l,core should correspond to the force on the lth ion F l,ion, estimated from DFT. Thus, the shells must be allocated such that
\({\mathbf {F}}_{l,\text{core}}^{\text{elec}}\) depends only on the charge distribution and atom positions. Hence, expression (30) represents a system of 3L force field-independent equations and 3L unknown variables for the shells coordinates. In this work, the charge distribution and spring constants were taken from [75]. The equations in (30) were solved by a simple fixed-point iteration scheme. The schematic of the method is presented in Fig. 5.
5.1.1.2 Validation
The validation involved a comparison of experimental data outside the TD with the results obtained through atomistic simulations incorporating the proposed force field. To simulate the present system we chose the RSM-GSHMC simulation method, which helped to reduce potential negative effects on the kinetic properties of the system caused by the use of the cs-adi model. We further combined RSM-GSHMC with the MAIA integrator (Sect. 3.4) to achieve the highest possible integration accuracy when using two-stage splitting methods, including Verlet.
The final set of parameters of NaxFePO4-ff can be found in [18]. Figure 6 compares the accuracy of NaxFePO4-ff and Whiteside-ff. Figure 6a depicts the relative error ×100 for the unit cell parameters (a, b, c) with respect to experimental measurements at room temperature [66]. In the absence of Na+ (x = 0), Whiteside-ff leads to numerical instability and values cannot be extracted. For x = 0.66 and x = 0.83 both force fields display comparable levels of accuracy, and at x = 1.0, NaxFePO4-ff is clearly better. When comparing the volume divergence at room temperature, Fig. 6b shows that NaxFePO4-ff is clearly superior. The DFT data are calculated at 0 K and thus, its divergence is high. However, it is clear that NaxFePO4-ff follows the same trend as the DFT values. Finally, Fig. 6c presents the radial distribution functions between phosphorous atoms, g P−P(r), in the Na0.58FePO4 system after 10 ps at 300 K. The dashed line corresponds to the initial configurations, which are the same for both force fields. After 10 ps of simulation, there is a distortion in the position of the peaks for Whiteside-ff with respect to the initial g P−P(r), evidencing the additional repulsion between oxygens of adjacent tetrahedrals when a Na+ ion is removed. This is an anomalous effect not observed with NaxFePO4-ff due to the reoptimized parameters. Such an anomaly leads to errors in the diffusivities when using Whiteside-ff.
Force field validation. All simulated values in this figure were obtained by combining NaxFePO4-ff or Whiteside-ff with the RSM-GSHMC technique. In Whiteside-ff, the parameters involving Fe3+ were taken to be the same as those for Fe2+. (a) Relative error ×100 for the unit cell parameters (a, b, c) with respect to experimental measurements at room temperature [66]. (b) Relative volume divergence with respect to experimental results at room temperature. (c) Radial distribution functions for phosphorous atoms in a Na0.58FePO4 system after 10 ps at 300 K. The dashed line corresponds to the initial positions, which is the same for both force fields
5.1.2 MD vs. RSM-GSHMC
Figure 7a presents the MSD for Na+ at 700 K in the main diffusion direction, y, obtained from both traditional MD and RSM-GSHMC. Convergence to the equilibrium slope that provides the diffusion coefficient through Eq. (1) is reached nearly 2 ns quicker through RSM-GSHMC, demonstrating its ability to sample the configurational space more efficiently than MD. The noise in the MSD curves in Fig. 7 is at least partially due to the fact that a fraction of the Na+ atoms do not perform any jump or jumps only once. While the situation could be improved by extending the simulations, the cs-adi model severely limits the simulation time-step, and further increasing the simulation time comes with a significant increase in the computation time.
(a) MSD at 700 K in the main diffusion direction, y, using both traditional MD and RSM-GSHMC combined with NaxFePO4-ff. Convergence to the equilibrium slope is reached faster through RSM-GSHMC. (b) Three-dimensional diffusion coefficient as a function of temperature (legends indicate force field and sampler combinations) (Adapted with permission from [18]. Copyright (2018) American Chemical Society)
Figure 7b shows the three-dimensional diffusion coefficients of Na+, \(D=\frac {1}{3}(D_x+D_y+D_z)\), for a range of temperatures using RSM-GSHMC with both force fields. We also plot results for similar simulations using standard MD with NaxFePO4-ff. Comparison of the three curves suggests that not only does the force field affects the diffusion coefficients but the sampling efficiency of the chosen sampler also does. Indeed, at higher temperatures the computed diffusions using MD and RSM-GSHMC combined with the same force field (for equal simulation times) diverge visibly. This is a consequence of the higher sampling efficiency of GSHMC methods [2]. For longer simulation times, both methods are expected to converge [32].
5.1.3 Mechanism of Na+ Diffusion
Because RSM-GSHMC does a good job in preserving dynamical information, it allows an atom-eye perspective of the physics behind the diffusion dynamics of Na+ in NaxFePO4. We confirmed that the main transport mechanism involves single Na-ion hops through the one-dimensional channels along the y axis (the [010] crystallographic direction). Furthermore, we identified the novel Na-ion diffusion dynamics involving the formation and annihilation of Na+/Fe2+ antisite defects (the exchange of positions between Na+ and Fe2+ ions), which effectively facilitate the migration of Na-ions between adjacent y-oriented channels (see Fig. 8 for a detailed explanation). Na+/Fe2+ antisite defects were expected to block y channels and, therefore, hinder Na-ion mobility in the bulk material. In contrast, our results revealed that such defects can indeed favor Na-ion exchange between parallel y channels. This result is in general agreement with simulations of two-dimensional diffusion in LiFePO4 [69]: occasional jumps of charge carriers in the y axis can overcome (at a cost of reduced diffusivity) the damaging effect of antisite defects.
Two-dimensional trajectory at 700 K. At this temperature, the coordination polyhedra are slightly distorted. The red octahedra are Fe3+O6 units, the blue octahedra are Fe2+O6 units, and the tetrahedrals correspond to (PO4)−3 units. The green, pink, cyan and orange atoms are tagged Na+ ions; the remaining Na+ ions are colored in yellow. The numbers in the figure specify the order in which atomic jumps occurred. (a) Initial, defect-free configuration. The double arrow shows the diametrically opposed Fe3+ ions around an extrinsic vacancy. (b) Antisite-like defect. A Fe2+ atom (encircled in red in (a) and (b) moves to the adjacent extrinsic vacancy (jump 1), allowing the green Na+ to jump to the empty Fe2+ site (jump 2). (c) Since the central diffusion channel is blocked, the green Na+ transfers to an adjacent channel (jump 6), leading to the cascade of jumps 7–10. (d) After the defect in the Fe2+ site is removed (jump 13), one-dimensional diffusion is reestablished. Notice that Na+ diffuses through the extrinsic vacancies in single, long curvilinear jumps (4, 9, and 15) (Adapted with permission from [18]. Copyright (2018) American Chemical Society)
5.2 Li+ Diffusion in Cubic Ga/Al Substituted Li7La3Zr2O12 (LLZO) Solid Electrolyte
LLZO garnet is a strong solid electrolyte contender for all-solid-state LIBs, which can in principle eliminate the safety problems associated with current liquid electrolyte-based batteries [9, 62]. LLZO garnets can crystallize in at least two different crystal structures, a poorly Li-ion conductive tetragonal structure (t-phase) and a significantly more conductive cubic one (c-phase) (Fig. 9). The c-phase structure contains partially occupied Li-sites (at any given instant they may or may not contain a Li+) and is unstable at room temperature, but can be stabilized by substitution of, for instance, Li+ by Al3+ and Ga3+ ions [64]. Despite having the same formal charge, gallium substitution is found to lead to higher room temperature conductivities (∼10−3 S/cm) than aluminium substitution [13, 62, 63] (∼10−4 S/cm). However, the origin and degree of this phenomenon is yet to be fully understood.
Crystal structures of garnet-type LLZO. (a) c-phase. Li atoms are represented by partially filled spheres, indicating partial occupancy. (b) t-phase, containing an ordered distribution of fully occupied Li-sites (Li+ ions are shown in green). La dodecahedra and Zr octahedra are shown in blue and yellow, respectively. The red spheres correspond to oxygen atoms. (Reproduced with permission from [19]. Copyright (2019) Elsevier)
We tackled this question using atomistic simulations, performed with traditional MD and our in-house GSHMC simulation method (Sect. 3.3). For this study, the chosen force field was based on that from Jalem et al. [47], but further adjusted with respect to experimental structural data reported in [63]. Details on the fitting procedure can be found in [41]. Below, we will use the notation GayAlx-LLZO to denote Li7−3(x+y)GayAlxLa3Zr2O12.
5.2.1 MD vs. GSHMC
To compare the sampling efficiency of MD and GSHMC methods for the simulation of the substituted LLZO systems, we calculated the integrated autocorrelation functions (IACF) of the potential energy U
where ACF(l), l = 0, …, K ≤ K ′ is the standard autocorrelation function for the time series U k of K samples, k = 1, …, K. Lower values of IACF indicate a more efficient sampling, since it estimates the time required, on average, to generate an uncorrelated sample. In Fig. 10, we present the values of \(IACF^{U}_{\text{MD}}/IACF^{U}_{\text{GSHMC}}\) for Ga0Al0.10-LLZO and Ga0Al0.12-LLZO in the t-phase and Ga0Al0.20-LLZO and Ga0Al0.25-LLZO in the c-phase at room temperature in the NVT ensemble. GSHMC simulations exhibit a sampling performance up to 25 times better than MD for the tested systems in the t-phase. In contrast, for the c-phase the performance of both methods are comparable, because the intersite energy barriers are relatively low. Based on this analysis, we have used GSHMC for simulations of the t-phase [41], as well as for simulations of the c-phase below room temperature, where the intersite barriers are much more significant [19]. Otherwise, we chose to use the conventional MD approach in order to minimize the efforts required for tuning of the GSHMC parameters.
Relative IACF U with respect to GSHMC at T = 298 K achieved when calculating the potential energy during the equilibration stage with the MD method. (Reproduced with permission from [19]. Copyright (2019) Elsevier)
5.2.2 Simulation Results
5.2.2.1 Length and Time Scales of Li+ Diffusion in Cubic LLZO
A simple way to understand the Li+ lattice in the c-phase is to consider it as a three-dimensional diffusion network, in which each node is connected to its closest four neighboring nodes through one intermediate site. Those intermediate sites are coordinated by six oxygen atoms, and thus are called Octahedral Li-sites, O h. The nodes, in turn, are coordinated by four oxygen atoms, and thus are called tetrahedral sites, T d. Hence, a typical Li+ diffusion path involves a succession of jumps of the form O h → T d → O h → T d →…. In Fig. 11, we provide an atom’s eye view of Li-ion transport by considering a complete trajectory of a selected Li+ ion across simulations at different temperatures and total time lengths.
Simulated trajectories of an individual Li+ ion (orange) in the Ga0.2Al0.0-LLZO system at different temperatures. From top to bottom the temperature decreases, whereas from left to right the simulation time increases. Li, Zr, O and Ga ions are depicted in green, yellow, red and blue, respectively (La ions are not shown for simplicity) (Reproduced with permission from [41]. Copyright (2019) American Chemical Society)
Li-ion transport is isotropic. At 313 K, the selected Li+ crosses frequently different T d and O h sites in a relatively short lapse of time (80 ns). In addition, we notice that a Li+ ion can visit the same T d site several times. This is revealed by the presence of branches centered in the nodal T d sites along the diffusive path as shown in the inset of Fig. 11. When the temperature is decreased to 253 K, the distance covered by the Li+ ion in 80 ns decreases. In fact, even after 200 ns the number of T d and O h sites visited has decreased considerably in comparison with the simulation at 313 K, resulting as well in a lower number of branches along the diffusive path. Finally, at 193 K we see that diffusion is severely hindered, with the Li+ ion barely visiting more than one T d site in less than 80 ns.
5.2.2.2 Variation of Li+ Conductivity with Ga/Al in Cubic LLZO
Figure 12 depicts the variation of the ionic conductivity σ Li (calculated through (2)) with the inverse of temperature for Ga0.2−xAlx-LLZO and x = 0.0, 0.1 and 0.2. It is clear that for a constant concentration of substituents, increasing the ratio of Ga3+ to Al3+ has a positive effect on the conductivity. However, as temperature increases, the difference between Ga3+ and Al3+ vanishes, in agreement with recent experimental work [63]. This observation was explained on the grounds that a Ga3+ content above 0.15 leads to a phase change, in which shortcuts to the typical O h → T d → O h →… diffusion path appear. However, if this was the only explanation, the curves would not display the observed temperature dependance.
Calculated Li-ion conductivity as a function of inverse temperature for Ga0.2−xAlx ( x = 0.0, 0.1, 0.2). Filled data points refer to simulation data. Experimental values, represented by empty symbols, were taken from Ref. [63]. Notice that the simulated data overestimate the experimental values, because the boundary resistances discussed in Sect. 2.2.1 cannot be easily incorporated. Those resistances are particularly high in Ga0.0Al0.2-LLZO, which has a powdery macrostructure. However, the trends in the simulated and experimental curves are clearly consistent
Through a detailed analysis of the radial distribution functions (see [41] for details) we were able to determine that the local environment around Ga3+ and Al3+ cations disrupts active diffusion paths. Hence, regions within the crystal volume that do not contribute to Li-ion conduction arise. Figure 13 depicts volume density maps of mobile Li+ ions at 233 K in Ga0.2Al0.0-LLZO and Ga0.0Al0.2-LLZO, showing a depletion of active diffusion paths around Ga3+ and Al3+. However, because of the particular parameters of the Al3+–O2− interaction potential, the disruptive effect of Al3+ is more pronounced. As temperature increases, Li+ ions acquire enough thermal energy to overcome the barriers surrounding Ga3+ and Al3+ ions, eliminating the difference in performance between both cations.
Density volume maps at 233 K for all Li+ ions in Ga0.0Al0.2-LLZO (a), and only those Li+ ions jumping at least one T d site-T d site length after 190 ns (>4 Å) in Ga0.2Al0.0-LLZO (b) and Ga0.0Al0.2-LLZO (c). Al3+ and Ga3+ ions are represented by magenta and blue spheres, respectively. (a) Can be interpreted as the total available volume for Li-ion diffusion, while (b) and (c) correspond to the active volume where diffusion is actually occurring. Clearly, active diffusion paths avoid the vicinity of Al3+ and Ga3+ (see insets to the right of (b) and (c) but the disruption of diffusion paths in Ga0.0Al0.2-LLZO is much more severe (Reproduced with permission from [41]. Copyright (2019) American Chemical Society)
5.2.2.3 Variation of Conductivity in the Experimental Data for Ga0.0Alx-LLZO
There is significant variability in the literature regarding the conductivity of Gal0Alx-LLZO. Given the recently reported gradients in Al content within a single sample [72], one potential scenario is that Al-rich regions crystallize in the c-phase, while the Al-poor regions form the t-phase. The second potential scenario is that thermodynamic equilibrium can be established between the two phases at the same x. To the best of our knowledge, neither scenario can be categorically dismissed. Presuming that thermodynamic equilibrium exists between the c- and t-phases at some Al contents, we can estimate the proportion of each phase through an adequate mixing model. Assuming that both phases mix randomly and homogeneously at the microscopic scale (∼10−6 m), Bruggeman’s effective medium model [51] predicts that
where ν i is phase volume fraction, σ i is conductivity and i = {c, t, m} denotes the cubic, tetragonal, and mixed phases, respectively. By equating the c-phase volume fraction ν c to the experimental values, it is possible to determine the theoretical conductivity of the mixed c- and t-phases using (32). Considering the experimental works by Botros et al. [21] and Tsai et al. [71], who report weight percentages for mixed cubic/tetragonal samples, we estimated the corresponding mixed phase conductivities by using conductivities simulated over the range of Al content. The predictions are shown in Fig. 14 as red circles, while the measurements from [21] and [71] are highlighted through the empty circles. Our predictions are in good agreement with the conductivities provided by [21] and [71], reproducing the experimental results better than either of the pure phases at all Al contents. Thus, we provide a sound basis for the analysis of phase coexistence in substituted LLZO and similar polycrystalline solid electrolyte materials.
Experimental and simulated Li-ion conductivities, σ Li, of Alx-LLZO for x = [0.0, 0.10, 0.12, 0.15, 0.17, 0.20, 0.25] at room temperature. Cyan circles correspond to experimental data taken from several experimental studies (the complete list of references can be found in the caption of Fig. 8 in [19]). Empty and dotted circles correspond to the experimental conductivities from Botros et al. [21] and Tsai et al. [71], respectively, who provide the percentages of c- and t-phases present in their samples. Filled squares (triangles) correspond to σ Li for c-phase (t-phase) obtained in this work. Red filled and dotted circles correspond to the conductivities obtained by combining Bruggeman’s model in (32) with the simulated σ Li to represent the coexistence of t- and c-phases at the proportions reported in Botros et al. [21] and Tsai et al. [71] (Reproduced with permission from [19]. Copyright (2019) Elsevier)
6 Conclusions
In this work, we present a brief review of the work performed in our team towards multiscale modelling and simulation of advanced battery materials. We have attempted to make the current material self-contained, and thus we have included sections on the basic science and engineering aspects of LIBs and NIBs (Sect. 2), as well as a short discussion of conventional simulation methods (Sects. 3.1 and 3.2) and force field development (Sect. 4). These sections can be selectively avoided by experienced practitioners.
We focus on the family of Modified Hamiltonian Monte Carlo (MHMC) methods recently introduced for atomistic simulations of complex systems [1, 2, 4, 32, 45, 68] and later adapted to multiscale [31] and mesoscale simulations [3]. In particular, we have found members of this family, the Generalized Shadow Hybrid Monte Carlo (GSHMC) method [2] and its latest extension Randomized Shell Mass GSHMC (RSM-GSHMC) [32], to be powerful tools for unveiling the structural, thermodynamic and transport properties of solid state battery materials. As application examples, we present our recent results in the modelling of ionic conduction in NaFePO4 cathode material for NIBs and LLZO solid electrolyte material for LIBs [18, 19, 32, 41]. Future work will focus on two key areas: probabilistic screening of advanced energy materials and multiscale simulation of composite materials.
Probabilistic Screening of Advanced Energy Materials
There is a considerable activity in the field of materials discovery using high-throughput computing combined with statistical screening approaches. However, incorporating macroscopic materials properties of practical importance, such as ionic conductivity, tensile moduli or phase transition temperatures into a materials design scheme in an efficient way remains a standing challenge.
Bayesian parameterization provides a principled way of combining prior information with data, within a solid decision theoretical framework. Past information and experimental data can readily be accounted for and form a prior distribution for future analysis. Moreover, when new observations become available, the previous posterior distribution can be used as a prior. More importantly, it provides interpretable answers from an experimental standpoint, such as “the optimal compound has a probability of 0.95 of falling in a 95% credible interval”.
Our in-house Bayesian parameterization technique, the Mix & Match Hybrid Monte Carlo (MMHMC) method [60], will be at the core of a novel framework that will combine incoming data from atomistic simulations and information from experiments, in order to provide the distribution of compositions that is most likely to maximize the expectation of a desired set of macroscopic properties (Fig. 15).
Multiscale Simulation of Composite Materials
In Sect. 2, we have briefly mentioned that one strategy to develop novel battery components with properties that no individual material has, is through the combination of several types of materials into segregated multiphase components called composites. Often, one of the phases is organic (e.g. a polymer) that provides mechanical flexibility, while the other is composed by inorganic particles (e.g. ionic crystals) providing good conductivity. The atomistic simulation of diffusional exchange between the various phases in composite materials is a relatively new subject. Despite the difficulty to experimentally examine the interface (and hence validate computational studies), simulations can provide very useful insights regarding the main barriers to particle exchange, and how the chemistry and environmental conditions affect them. Moreover, with advanced sampling methods such as GSHMC combined with splitting integrators, it is feasible to test many realizations of the polymer/crystal interface and systematically study the impact of contact defects. However, simulating an entire inorganic particle surrounded by polymer remains a great computational challenge that has been attempted only with very small nanoparticles. We are working on the coarse-grained simulation of such a system using our in-house simulation technique meso-GSHMC [3]. The transport coefficients and selectivities obtained this way can be incorporated in continuous or effective medium approaches, providing a multiscale modelling framework for the modelling of composite materials.
Notes
- 1.
For simplicity, we use here the dot-notation for the derivatives in time.
- 2.
The stage notation first suggested by Blanes et al. [17] indicates the number of force evaluations performed per step.
- 3.
The expression for ρ(h, b) as well as the details of its derivation can be found in [6].
- 4.
The main idea is that, for every b, an integration step ψ Δt can be rewritten as \(\psi _{\Delta t} = \left (\phi _{b \Delta t}^B \circ \phi _{\Delta t/2}^A \circ \phi _{(1 - 2 b) \Delta t/2}^B\right ) \circ \left (\phi _{(1 - 2 b) \Delta t/2}^B \circ \phi _{\Delta t/2}^A \circ \phi _{b \Delta t}^B\right )\).
References
Akhmatskaya, E., Reich, S.: The targeted shadowing hybrid Monte Carlo (TSHMC) method. In: Leimkuhler, B., Chipot, C., Elber, R., Laaksonen, A., Mark, A., Schlick, T., Schütte, C., Skeel, R. (eds.) New Algorithms for Macromolecular Simulation, pp. 141–153. Springer, Heidelberg (2006)
Akhmatskaya, E., Reich, S.: GSHMC: an efficient method for molecular simulation. J. Comp. Phys. 227, 4934–4954 (2008)
Akhmatskaya, E., Reich, S.: Meso-GSHMC: a stochastic algorithm for meso-scale constant temperature simulations. Proc. Comp. Sci. 4, 1353–1362 (2011)
Akhmatskaya, E., Reich, S.: New Hybrid Monte Carlo methods for efficient sampling: from physics to biology and statistics. Prog. Nucl. Sci. Technol. 2, 447–462 (2012)
Akhmatskaya, E., Bou-Rabee, N., Reich, S.: A comparison of generalized hybrid Monte Carlo methods with and without momentum flip. J. Comp. Phys. 228, 2256–2265 (2009)
Akhmatskaya, E., Fernández-Pendás, M., Radivojević, T., Sanz-Serna, J.M.: Adaptive splitting integrators for enhancing sampling efficiency of modified Hamiltonian Monte Carlo methods in molecular simulation. Langmuir 33, 11530–11542 (2017)
Amin, R., Balaya, P., Maier, J.: Anisotropy of electronic and ionic transport in LiFePO4 single crystals. J. Power Sources 10, A13–A16 (2007)
Amores, M., Ashton, T.E., Baker, P.J.,Cussen, E.J., Corr, S.A.: Fast microwave-assisted synthesis of Li-stuffed garnets and insights into Li diffusion from Muon spin spectroscopy. J. Mater. Chem. A 4, 1729–1736 (2016)
Awaka, J., Kijima, N., Hayakawa, H., Akimoto, J.: Synthesis and structure analysis of tetragonal Li 7La 3Zr 2O 12 with the garnet-related type structure. J. Solid State Chem. France 182, 2046–2052 (2009)
Barsoukov, E., Macdonald, J.R.: Impedance Spectroscopy: Theory, Experiment, and Applications. Kluwer, Boston (2005)
Bauer, A., Song, J., Vail, S., Pan, W., Barker, J., Lu, Y.: The scale-up and commercialization of nonaqueous Na-Ion battery technologies. Adv. Ener. Mat. 8, 1702869 (2018)
Berendsen, H., van der Spoel, D., van Drunen, R.: GROMACS: a message-passing parallel molecular dynamics implementation. Comp. Phys. Commun. 91, 43–56 (1995)
Bernuy-Lopez, C., Manalastas, W., Lopez del Amo, J.M., Aguadero, A., Aguesse, F., Kilner, J.A.: Atmosphere controlled processing of Ga-substituted garnets for high Li-ion conductivity ceramics. Chem. Mater. 26, 3610–3617 (2014)
Beskos, A., Pillai, N., Roberts, G., Sanz-Serna, J.M., Stuart, A.: Optimal tuning of the hybrid Monte Carlo algorithm. Bernoulli 19, 1501–1534 (2013)
Biresselioglu, M.E., Kaplan, M.D., Yilmaz, B.K.: Electric mobility in Europe: a comprehensive review of motivators and barriers in decision making processes. Transp. Res. A: Policy Pract. 109, 1–13 (2018)
Blanes, S., Casas, F.: A Concise Introduction to Geometric Numerical Integration. Chapman and Hall, London (2016)
Blanes, S., Casas, F., Sanz-Serna, J.M.: Numerical integrators for the hybrid Monte Carlo method. SIAM J. Sci. Comput. 36, A1556–A1580 (2014)
Bonilla, M. R., Lozano, A., Escribano, B., Carrasco, J., Akhmatskaya, E.: Revealing the mechanism of sodium diffusion in NaxFePO4 using an improved force field. J. Phys. Chem. C. 122, 8065–8075 (2018)
Bonilla, M. R., García Daza, F. A., Carrasco, J., Akhmatskaya, E.: Exploring Li-ion conductivity in cubic, tetragonal and mixed-phase Al-substituted Li7La3Zr2O12 using atomistic simulations and effective medium theory. Acta Mater. 175, 426–435 (2019)
Borodin, O., Smith, G.D.: Na-ion mobility in layered Na2FePO4F and olivine Na[Fe,Mn]PO4. Macromolecules 39, 1620–1629 (2006)
Botros, M., Djenadic, R., Clemens, O., Möller, M., Hahn, H.: Assisted sintering of fine-grained Li7−3xLa3Zr2AlxO12 solid electrolyte and the influence of the microstructure on the electrochemical performance. J. Power Sources 309, 108–115 (2016)
Brommer, P., Gähler, F.: Potfit: effective potentials from ab initio data. Model. Simul. Mater. Sci. Eng. 15, 295 (2007)
Brommer, P., Kiselev, A., Schopf, D., Beck, P.: Classical interaction potentials for diverse materials from ab initio data: a review of potfit. Model. Simul. Mater. Sci. Eng. 23, 074002 (2015)
Brooks, B.R., Bruccoleri, R.E., Olafson, B.D., States, D.J., Swaminathan, S., Karplus, M.: CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4, 187–217 (1983)
Crabtree, G., Kocs, E., Trahey, L.: The energy-storage frontier: Lithium-ion batteries and beyond. MRS Bull. 40,1067–1076 (2015)
Dick, B.G., Overhauser, A.W.: Theory of the dielectric constants of alkali halide crystals. Phys. Rev. 112, 90–103 (1958)
Duan, Y., Wu, C., Chowdhury, S., Lee, M.C., Xiong, G., Zhang, W., Yang, R., Cieplak, P.: A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 24, 1999–2012 (2003)
Duane, S., Kennedy, A.D., Pendleton, B. J., Roweth, D.: Hybrid Monte Carlo. Phys. Lett. B 195, 216–222 (1987)
Duin, A. C.T., Dasgupta, S., Lorant, F., Goddard, W.A.: ReaxFF: a reactive force field for hydrocarbons. J. Phys. Chem. A 41, 9396–9409 (2001)
Escribano, B., Akhmatskaya, E., Mujika, J. I.: Combining stochastic and deterministic approaches within high efficiency molecular simulations. Centr. Eur. J. Math. 11, 787–799 (2013)
Escribano, B., Akhmatskaya, E., Reich, S., Azpiroz, J. M.: Multiple-time-stepping generalized hybrid Monte Carlo methods. J. Comp. Phys. 280, 1–20 (2015)
Escribano, B., Lozano, A., Radivojević, T., Fernández-Pendás, M., Carrasco, J., Akhmatskaya, E.: Enhancing sampling in atomistic simulations of solid-state materials for batteries: a focus on olivine NaFePO4. Theo. Chem. Acc. 136 (2017). Article number: 43
Español, P., Warren, P.: Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 30, 191–196 (1995)
Famprikis, T., Canepa, P., Dawson, J.A., Islam, M.S.: Fundamentals of inorganic solid-state electrolytes for batteries Nat. Mater. 18, 1278–1291 (2019)
Fernández-Pendás, M., Escribano, B., Radivojević, T., Akhmatskaya, E.: Constant pressure hybrid Monte Carlo simulations in GROMACS. J. Mol. Mod. 20, 2487 (2014)
Fernández-Pendás, M., Akhmatskaya, E., Sanz-Serna, J.M.: Adaptive multi-stage integrators for optimal energy conservation in molecular simulations. J. Comp. Phys. 327, 434–449 (2016)
Franco A.: Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: concepts, methods and challenges. RSC Adv. 3, 13027–13058 (2013)
Franco, A. A., Rucci, A., Brandell, D., Frayret, C., Gaberscek, M., Jankowski, P., Johansson, P.: Boosting rechargeable batteries R&D by multiscale modelling: Myth or reality?. Chem. Rev. 119, 4569 (2019)
Frenkel, D., Smit, B.: Understanding Molecular Simulation: From Algorithms to Applications. 2nd edn. Academic, San Diego (2002)
Fumi, F.G., Tosi, M.P.: Ionic sizes and born repulsive parameters in the NaCl-type alkali halides I. J. Phys. Chem. Solids 25, 31–43 (1964)
García Daza, F. A., Bonilla, M. R., Llordés, A., Carrasco, J., Akhmatskaya, E.: Atomistic insight into ion transport and conductivity in Ga/Al-substituted Li7La3Zr2O12 solid electrolytes. ACS Appl. Mater. Interfaces 11 (2019)
Hastings, W.K.: Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970)
Hess, B., Kutzner, C., van der Spoel, D., Lindahl, E.: GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theo.Comp. 4, 435–447 (2008)
Horowitz, A. M.: A generalized guided Monte Carlo algorithm. Phys. Lett. B 268, 247–252 (1991)
Izaguirre, J. A., Hampton, S. S.: Shadow hybrid Monte Carlo: an efficient propagator in phase space of macromolecules. J. Comp. Phys. 200, 581–604 (2004)
Izaguirre, J. A., Reich, S., Skeel, R. D.: Longer time steps for molecular dynamics. J. Chem. Phys. 110, 9853–9864 (1999)
Jalem, R., Rushton, M.J.D., Manalastas, W., Nakayama, M., Kasuga, T., Kilner, J.A., Grimes, R.W.: Effects of gallium doping in Garnet-type Li7La3Zr2O12 solid electrolyte. Chem. Mater. 27, 2821–2831 (2015)
Jorgensen, W.L., Maxwell, D.S., Tirado-Rives, J.: Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225–11236 (1996)
Kennedy, A.D., Pendleton, B.: Cost of the generalised hybrid Monte Carlo algorithm for free field theory. Nucl. Phys. B 607, 456–510 (2001)
Kresse, G., Hafner, J.: Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993)
Landauer, R.: Electrical conductivity in inhomogeneous media. J. AIP Conf. Proc. 40, 2–45 (1978)
Leimkuhler, B., Matthews, C.: Molecular dynamics with deterministic and stochastic numerical methods. In: Interdisciplinary Applied Mathematics, vol. 39. Springer, New York (2015)
Leimkuhler, B., Reich, S.: Simulating Hamiltonian dynamics. In: Cambridge Monographs on Applied and Computational Mathematics, vol. 14. University Press, Cambridge (2004)
Li, M., Lu, J., Chen, C., Amine, K.: 30 years of lithium-ion batteries. Adv. Mater. 30, 1800561 (2018)
Mitchell, P.J., Fincham, D.: Shell model simulations by adiabatic dynamics. J. Phys.: Condens. Matter 5, 1031 (1993)
Murch, G.: The haven ratio in fast ionic conductors. Solid State Ion. 7, 177–198 (1982)
Oganov, A.R., Kvashnin, A.G., Saleh, G.: Computational materials discovery: dream or reality? In: Oganov, A.R., Saleh, G., Kvashnin, A.G. (eds) Computational Materials Discovery, pp. 1–14. The Royal Society of Chemistry, London (2019)
Park, M., Zhang, X., Chung, M., Less, G.B., Sastry, A.M.: A review of conduction phenomena in Li-ion batteries. J. Power Sources 195, 794–7929 (2010)
Plummer, M., Best, N., Cowles, K., Vines, K.: CODA: Convergence diagnosis and output analysis for MCMC. R News 6, 7–1 (2006)
Radivojević, T., Akhmatskaya, E.: Modified Hamiltonian Monte Carlo for Bayesian inference. Stat. Comp. 30, 377–404 (2020)
Radivojević, T., Fernández-Pendás, M., Sanz-Serna, J.M., Akhmatskaya, E.: Multi-stage splitting integrators for sampling with modified Hamiltonian Monte Carlo methods. J. Comp. Phys. 373, 900–916 (2018)
Ramaswamy. M., Venkataraman, T., Werner, W.: Fast lithium ion conduction in Garnet-type Li7La3Zr2O12. Angew. Chem. Edn.: Int. 46, 7778—7781 (2007)
Rettenwander, D., Redhammer, G., Preishuber-Pflugl, F., Cheng, L., Miara, L., Wagner, R., Welzl, A., Suard, E., Doeff, M.M., Wilkening, M., Fleig, J., Amthauer, G.: Structural and electrochemical consequences of Al and Ga cosubstitution in Li7La3Zr2O12 solid electrolytes. Chem. Mater. 28, 2384–2392 (1998)
Rettenwander, D., Geiger, C.A., Tribus, M., Tropper, P., Amthauer, G.: A synthesis and crystal chemical study of the fast ion conductor Li7La3Zr2O12 with x = 0.08 to 0.84 in Li7La3Zr2O12 solid electrolytes. Chem. Mater. 53, 6264–6269 (2014)
Sanz-Serna, J.M., Calvo, M.P.: Numerical Hamiltonian Problems. Chapman and Hall, London (1994)
Saracibar, A., Carrasco, J., Saurel, D., Galceran, M., Acebedo, B., Anne, H., Lepoitevin, M., Rojo, T., Cabanas, M.C.: Investigation of sodium insertion-extraction in olivine NaxFePO4 (0 ≤ x ≤ 1) using first-principles calculations. Phys. Chem. Chem. Phys. 18, 13045–13051 (2016)
Schlick, T., Mandziuk, M., Skeel, R. D., Srinivas, K.: Nonlinear resonance artifacts in molecular dynamics simulations. J. Comp. Phys. 140, 1–29 (1998)
Sweet, C. R., Hampton, S. S., Skeel, R. D., Izaguirre, J. A.: A separable shadow Hamiltonian hybrid Monte Carlo method. J. Chem. Phys. 131, 174106 (2009)
Tealdi, C., Spreafico, C., Mustarelli, P.: Lithium diffusion in Li1−xFePO4: the effect of cationic disorder. J. Mater. Chem. 22, 24870–24876 (2012)
Tripathi, R. Wood, S. M., Islam, M. S. Nazar, L. F.: Na-ion mobility in layered Na2FePO4F and olivine Na[Fe,Mn]PO4. Energ. Environ. Sci. 6, 2257–2264 (2013)
Tsai, C.L., Dashjav, E., Hammer, E.M., Finsterbusch, M., Tietz, F., Uhlenbruck, S., Buchkremer, H.P.: High conductivity of mixed phase Al-substituted Li7La3Zr2O12. Nanoscale 35, 25–32 (2015)
Wachter-Welzl, A., Kirowitz, J., Wagner, R., Smetaczek, S., Brunauer, G.C., Bonta, M., Rettenwander, D., Taibl, S., Limbeck, A., Amthauer, G., Fleig, J.: The origin of conductivity variations in Al-stabilized Li7La3Zr2O12 ceramics. Solid State Ionics 319, 203–208 (1978)
Wang, J., Xueliang, S.: Olivine LiFePO4: the remaining challenges for future energy storage. Energy Environ. Sci. 8, 1110–1138 (2015)
Wee, C.L., Sansom, M.S.P., Reich, S., Akhmatskaya, E.: Improved sampling for simulations of interfacial membrane proteins: application of generalized shadow hybrid Monte Carlo to a peptide toxin/bilayer system. J. Phys. Chem. B 112, 5710–5717 (2008)
Whiteside, A., Fisher, C.A.J., Parker, S.C., Islam, M.S.: Particle shapes and surface structures of olivine NaFePO4 in comparison to LiFePO4. Phys. Chem. Chem. Phys. 39, 21788–21794 (2014)
Whittingham M.S.: Electrical energy storage and intercalation chemistry. Science 192, 1126–1127 (1976)
Wu, J.F., Chen, E.Y., Yu, Y., Liu, L., Wu, Y., Pang, W.K., Peterson, V.K., Guo,: X. Gallium-doped Li7La3Zr2O12 Garnet-type electrolytes with high lithium-ion conductivity. ACS Appl. Mater. Interfaces 9, 1542–1552 (2017)
Yabuuchi, N., Kubota, K., Dahbi, M., Komaba, S.: Research development on sodium-ion batteries. Chem. Rev. 114, 11636–11682 (2014)
Yan, T., Burnham, C.J., Del Pópolo, M.G., Voth, G.A.: Molecular dynamics simulation of ionic liquids: the effect of electronic polarizability. J. Phys. Chem. B. 108, 11877–11881 (2004)
Zheng, F., Kotobuki, M., Song, S., Lai, Man, O., Lu, L.: Review on solid electrolytes for all-solid-state lithium-ion batteries. J. Power Sources 389, 198–213 (2018)
Zhu, Y., Xu, Y., Liu, Y., Luo, C., Wang, C.: Comparison of electrochemical performances of olivine NaFePO4 in sodium-ion batteries and olivine LiFePO4 in lithium-ion batteries. Nanoscale 5, 780–787 (2013)
Acknowledgements
We acknowledge the financial support by the Ministerio de Economia y Competitividad (MINECO) of the Spanish Government through grants PID2019-104927GB-C22 and BCAM Severo Ochoa accreditation SEV-2017-0718. This work was supported by the BERC 2018e2021 Program and by ELKARTEK Program, grants KK-2020/00049 and KK-2020/00008, funded by the Basque Government. The research is partially supported by the Basque Government under the grant “Artificial Intelligence in BCAM number EXP. 2019/00432”. This work has been possible thanks to the support of the computing infrastructure of the i2BASQUE academic network, DIPC Computer Center and the technical and human support provided by IZO-SGI SGIker of UPV/EHU and European funding (ERDF and ESF).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Bonilla, M.R., García Daza, F.A., Fernández-Pendás, M., Carrasco, J., Akhmatskaya, E. (2021). Multiscale Modelling and Simulation of Advanced Battery Materials. In: Cruz, M., Parés, C., Quintela, P. (eds) Progress in Industrial Mathematics: Success Stories. SEMA SIMAI Springer Series(), vol 5. Springer, Cham. https://doi.org/10.1007/978-3-030-61844-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-61844-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-61843-8
Online ISBN: 978-3-030-61844-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




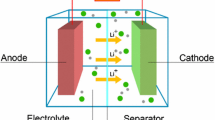


 with probability
with probability  to r.
to r. with probability
with probability  .
.











