Approximation of Fractional Order Dynamic Systems Using Elman, GRU and LSTM Neural Networks

Abstract

In the paper, authors explore the possibility of using the recurrent neural networks (RNN) - Elman, GRU and LSTM - for an approximation of the solution of the fractional-orders differential equations. The RNN network parameters are estimated via optimisation with the second order L-BFGS algorithm. It is done based on data from four systems: simple first and second fractional order LTI systems, a system of fractional-order point kinetics and heat exchange in the nuclear reactor core and complex nonlinear system. The obtained result shows that the studied RNNs are very promising as approximators of the fractional-order systems. On the other hand, these approximations may be easily implemented in real digital control platforms.

1 Introduction

The methods of the Fractional Order Calculus (FOC) involving, non-integer derivatives and integrals, have been known since XVII century but only in recent years have their technical applications been extensively reported in numerous fields of science and engineering [13]. Also, in the field of control systems, FOC has found its application that is mainly used for fractional-order modelling of complex system dynamics and the fractional-order control strategies synthesis. Literature studies demonstrate that the dynamics of many complex systems taking part in the field of control theory can be described more accurately with the differential equations of non-integer order. The fractional-order control strategies, with appropriate tuning and design methodologies, may achieve better control quality in various control systems (e.g. fractional-order PID controllers [17, 19]).

The fractional-order dynamic systems are characterised by infinite memory, or in other words, they are of infinite dimensions. Consequently, the mathematical models of such systems in the Laplace or $\mathcal {Z}$ domain are characterised by an irrational order and the discrete models by an infinite memory of processed samples. While the synthesis of systems based on fractional order operators is not particularly problematic, the implementation of such systems on digital control platforms (e.g. FPGA, DSP, PLC) is a demanding task. In the latter case, techniques that allow for the approximation of fractional systems are needed. Such approximation techniques most often lead to the identification of appropriate dynamic systems, which will be described by integer-order models or will use finite memory resources. The most popular and widely used approximations of fractional order systems include: continued fraction-based approximations, Oustaloup filters, frequency response fitting approach and many other [19].

Each of the mentioned approximation methods has its own cons and pros. Generally, they allow for an approximation of non-integer order operators with the use of structures of classical digital, mostly linear and sometimes nonlinear, filters. Especially in the case of approximation, the long memory length is needed what may cause problems during the real time implementation on the real digital control platforms. Moreover, resulting polynomials: (i) may be ill-conditioned (coefficients with very large values), which may lead to the computational instability and overflow errors on the digital platform, (ii) may contain internal instability related to the inappropriate location of polynomials zeros and poles, and additionally, (iii) the same approximation cannot be used if there are changes in the value of fractional-order of differentiation or integration operator, or characteristic system parameters in the time/frequency domain - the approximation procedure must be carried out again.

To more or less overcome these problems various authors propose in literature the use of Artificial Neural Networks to approximate the fractional-order operators or linear and nonlinear fractional-order systems [9, 18, 20]. Typically, various authors in their works use the feed-forward multi-layer perceptron structure of the ANN, to model fractional-order dynamic systems. In literature, the analysis of dynamics and stability of the fractional-order neural network with the structure of recurrent Hopfield network may be found [10].

In this paper, the authors explore the possibility of using some recent structures of recurrent neural networks (RNN), with dynamic memory, as a more natural substitute for the approximation of evolving process states according to various mathematical models of the dynamic systems which may be described by ordinary, and especially by the fractional-orders differential equations sets. Those RNN structures are: (i) Elman recurrent neural network [4], (ii) networks consisting of GRU cells [3], (iii) and networks consisting of LSTM cells [8].

The proposed RNN structures are verified based on a series of numerical experiments with fractional-order systems models in the form of: (i) a simple linear fractional first-order LTI system, (ii) a simple linear fractional secondorder LTI system, (iii) nonlinear fractional-order physical system of point kinetics and heat exchange in the nuclear reactor core [5, 14], (iv) and a complex nonlinear system [19].

The paper is organised as follows. In Sect. 2 the considered problem is described. In Sect. 3 the methodology used in the paper is presented. Section 4 presents the results of numerical simulations. Finally, Sect. 5 concludes the paper.

2 Problem Statement

The recurrent neural networks are known for their excellent approximation properties. Following [7, 12] it’s worthwhile to quote here the universal approximation theorem:

Theorem 1

Any nonlinear dynamic system may be approximated by a recurrent neural network to any desired degree of accuracy and with no restrictions imposed on the compactness of the state space, provided that the network is equipped with an adequate number of hidden neurons.

The quoted theorem about the universal approximation of systems using recurrent neural networks is the foundation on which the research presented in the paper is based. In the context of the usability of the above mentioned theorem, the following problems should be kept in mind:

• 1. selection of appropriate recursive network architecture i.e. selection of adequate number of neurons in the hidden layer and selection of cell type of hidden neurons,

• 2. selection of appropriate network parameters i.e. weights and biases,

• 3. selection of an appropriate optimisation algorithm to obtain satisfactory quality indicators that measure the deviation between the training/validation data and the output of a given recursive network.

Referring to the first problem, selecting an appropriate network architecture is a complex task. The research was limited only to increasing the number of neurons/cells in one hidden network layer. It was assumed that networks will consist of 1 to 5 cells/neurons in the hidden layer respectively. During this research, the performance of Elman-type networks (Elman RNN), networks consisting of GRU cells and networks consisting of LSTM cells was compared.

With regard to the second problem, the choice of network parameters was made using optimisation techniques. It should be noted here, that on the basis of the universal approximation theorem, it can be concluded that such a recurrent neural network exists, which will be able to approximate with satisfactory accuracy the dynamic system of a fractional order. Also, it should be important to note that there is no certainty of finding the appropriate set of network parameters that will allow for satisfactory approximation.

The last of the problems mentioned above concerns the optimisation algorithm that is used to select network parameters. In the research, the L-BFGS algorithm [11] was used, which belongs to the family of 2nd order quasi-Newton methods. This method has been chosen because it is characterised by the fact that during one optimisation step, an immediate jump to the local minimum is possible and also there is a built-in mechanism for selecting the optimiser step size. Additionally, the L-BFGS algorithm is less memory demanding in comparison to the standard BFGS algorithm. It was also noted that Hessian information processed by the algorithm significantly accelerates the optimisation process so that multiple optimiser runs were not an issue.

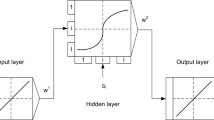
2.1 Recurrent Neural Network Architectures Used in the Research

As mentioned earlier in Sect. 2, in this study three recursive neural network architectures were used. These architectures are described below in a compact form [1]:

Elman RNN

$$\begin{aligned} h_t = \tanh (W_{ih}x_t + b_{ih} + W_{hh}h_{(t-1)} + b_{hh}) \end{aligned}$$

(1)

where $h_t$ is the hidden state at time t, $x_t$ is the input at time t and $h_{(t-1)}$ is the hidden state at time $t-1$ or the initial hidden state at time 0, $W_{ih}$ is the learnable input-hidden weights matrix, $W_{hh}$ is the learnable hidden-hidden weights matrix, $b_{ih}$ is the learnable input-hidden bias and $b_{hh}$ is the learnable hidden-hidden bias. As the authors of the PyTorch library state, that the second bias vector is included for NVIDIA CUDA® Deep Neural Network library compatibility.

GRU

$$\begin{aligned} \begin{aligned} r_t&= \sigma (W_{ir}x_t + b_{ir} + W_{hr}h_{(t-1)} + b_{hr}) \\ z_t&= \sigma (W_{iz}x_t + b_{iz} + W_{hz}h_{(t-1)} + b_{hz}) \\ n_t&= \tanh (W_{in}x_t + b_{in} + r_t * (W_{hh}h_{(h-1)} + b_{hn})) \\ h_t&= (1-z_t) * n_t + z_t * h_{(t-1)} \end{aligned} \end{aligned}$$

(2)

where $r_t$, $z_t$, $n_t$ are the reset, update and new gates, respectively, $\sigma$ is the sigmoid function, $*$ is the Hadamard product, $W_{ir}$, $W_{iz}$, $W_{in}$ are learnable input-reset, input-update and input-new weights matrices, $W_{hr}$, $W_{hz}$ are hidden-reset and hidden-update weights matrices, $b_{ir}$, $b_{iz}$, $b_{in}$ are lernable input-reset, input-update and input-new biases, $b_{hr}$, $b_{hz}$, $b_{hn}$ are learnable hidden-reset, hidden-update, and hidden-new biases.

LSTM

$$\begin{aligned} \begin{aligned} i_t&= \sigma (W_{ii}x_t + b_{ii} + W_{hi}h_{(t-1)} + b_{hi}) \\ f_t&= \sigma (W_{if}x_t + b_{if} + W_{hf}h_{(t-1)} + b_{hf}) \\ g_t&= \tanh (W_{ig}x_t + b_{ig} + W_{hg}h_{(t-1)} + b_{hg}) \\ o_t&= \sigma (W_{io}x_t + b_{io} + W_{ho}h_{(t-1)} + b_{ho}) \\ c_t&= f_t * c_{(t-1)} + i_t * g_t \\ h_t&= o_t * \tanh (c_t) \end{aligned} \end{aligned}$$

(3)

where $c_t$ is the cell state at time t, $i_t$, $f_t$, $g_t$, $o_t$ are input, forget, cell and output gates respectively, $W_{ii}$, $W_{if}$, $W_{ig}$, $W_{io}$, are learnable input-input, input-forget, input-cell and input-output weights matrices, $W_{hi}$, $W_{hf}$, $W_{hg}$, $W_{ho}$ are learnable hidden-input, hidden-forget, hidden-cell and hidden-output weights matrices, $b_{hi}$, $b_{hf}$, $b_{hg}$, $b_{ho}$ are learnable hidden-input, hidden-forget, hidden-cell, hidden-output biases.

Hidden state in each analysed neural network was subjected to linear transformation in order to obtain a single network output. The first network used in the presented study, i.e. Elman RNN is a classic recurrent neural network. In fact, it was used as background for more advanced architectures that use gated units. In general, gated neural networks, such as GRU and LSTM networks are based on the idea of creating paths through time that have derivatives that neither vanish nor explode [6]. This is achieved by allowing connection weights to change at each time step. Such a mechanism, together with the network’s ability to learn when the self-decision about clearing the state should be taken, allows to accumulate information over long periods of time [6]. These properties match closely with the problem of approximation of dynamic systems of fractional order discussed in the article and therefore it was decided to use gated networks such as GRU and LSTM networks for this purpose.

3 Research Method

3.1 Fractional Order Dynamic Systems Models

In order to examine the approximation performance of fractional systems by recurrent neural networks, four mathematical models involving fractional operators were used. The first model is a fractional first order LTI system (FFOS). This model is described by the following fractional order differential equation

$$\begin{aligned} \tau \mathscr {D}^{\alpha _1} x(t) + x(t) = k_1 u(t) \end{aligned}$$

(4)

where $\tau = 1,5$ is exponential decay time constant, $\alpha _1 = 0,8$ is fractional order of differential operator $\mathscr {D}$ $(\mathscr {D}^{\alpha }=\frac{d^{\alpha }}{dt^{\alpha }}$, $\alpha \epsilon R, \alpha > 0 )$, $k_1 = 0,8$ is the forcing function gain, u(t) is the forcing function and x(t) is a function of time.

The second model is a fractional second order LTI system (FSOS) of an oscillatory character described by the following system of fractional commensurate order differential equations

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \mathscr {D}^{\alpha _{2}} x_1(t) &{}= x_2(t) \\ \mathscr {D}^{\alpha _{2}} x_2(t) &{}= -\omega _n^2 x_1(t) - 2\zeta \omega _n x_2(t) + k_2\omega _n^2 u(t) \end{array}\right. } \end{aligned} \end{aligned}$$

(5)

where $\alpha _2 = 1,2$ parameter is used as the base order of the system, $\omega _n = 2$ is natural frequency of the system and $\zeta = 0,707$ is the damping ratio of the system. The initial conditions for LTI models were set to 0. In order to obtain responses to the above mentioned models, the definition of Grunwald-Letnikov fractional order operator was used.

The third system used in the study is a nonlinear nuclear reactor model in which point-neutron kinetics is described by a system of fractional-order differential equations, based on one group of delayed-neutron precursor nuclei (6–7). In the later part of the article this model is referred to as Nuclear Reactor model. The fractional model retains the main dynamic characteristics of the neutron motion in which the relaxation time associated with a rapid variation in the neutron flux contains a fractional order, acting as an exponent of the relaxation time, to obtain the better representation of a nuclear reactor dynamics with anomalous diffusion (the diffusion processes do not follow the Fick’s diffusion law) [14]. The kinetic model is presented as follows

$$\begin{aligned} \begin{aligned} \mathscr {D}^{1+\kappa }n(t)+\frac{1}{\tau ^{\kappa }}\mathscr {D}^{1}n(t)+\left( \frac{1}{l}+\frac{1-\beta }{\varLambda } \right) \mathscr {D}^{\kappa }n(t)\\ +\frac{1}{\tau ^{\kappa }} \left( \frac{\beta -\rho (t)}{\varLambda } \right) n(t) = \lambda \mathscr {D}^{\kappa }c(t)+\frac{\lambda }{\tau ^{\kappa }}c(t), \end{aligned} \end{aligned}$$

(6)

$$\begin{aligned} \begin{aligned} \mathscr {D}^{1}c(t)+\lambda c(t)=\frac{\beta }{\varLambda }n(t), \end{aligned} \end{aligned}$$

(7)

where ${\tau }$ is the relaxation time, ${\kappa }$ is the anomalous diffusion order ${(0 < \kappa \le 1)}$, n is the neutron density, c is the concentration of the neutron delayed precursor, l is the mean prompt-neutron lifetime, ${\varLambda }$ is the neutron generation time, ${\beta }$ is the fraction of delayed neutrons, ${\lambda }$ is the decay constant and ${\rho }$ is the reactivity. The initial conditions for equations (6–7) are specified as follows $n(0)=n_0$, $c(0)=c_0$.

The Nuclear Reactor model also contains equations describing the thermal-hydraulic relations and the reactivity feedback from fuel and coolant temperature, which are described by means of integer-order differential equations and algebraic equations based on the classic Newton law of cooling [15, 16]

$$\begin{aligned} \mathscr {D}^{1}T_{F}(t)=\frac{1}{m_{F}c_{pF}}\left( f_{F}P_{th}(t)-Ah(T_{F}(t)-T_{C}(t))\right) , \end{aligned}$$

(8)

$$\begin{aligned} \mathscr {D}^{1}T_{C}(t)&=\frac{1}{m_{C}c_{pC}} ((1-f_{F})P_{th}(t)+Ah(T_{F}(t)-T_{C}(t))+ \nonumber \\&\quad -2W_{C}c_{pC}(T_{C}(t)-T_{Cin}))), \end{aligned}$$

(9)

where $m_{F}$ is the mass of the fuel, $c_{pF}$ is the specific heat capacity of the fuel, $T_{F}$ is the fuel temperature, $f_{F}$ is the fraction of the total power generated in the fuel, $P_{th}$ is the nominal reactor thermal power, A is the effective heat transfer area, h is the average overall heat transfer coefficient, $T_{C}$ is the average coolant temperature, $m_{C}$ is the mass of the coolant, $c_{pC}$ is the specific heat capacity of the coolant, $W_{C}$ is the coolant mass flow rate within the core, $T_{Cout}$ is the coolant outlet temperature, and $T_{Cin}$ is the coolant inlet temperature.

While the reactivity feedback balance related to the main internal mechanisms (fuel and coolant temperature effects) and external mechanisms (control rod bank movements) is represented by the following algebraic equation [15, 16].

$$\begin{aligned} \rho (t)=\rho _{ext}+\alpha _{F}(T_{F}(t)-T_{F,0})+\alpha _{C}(T_{C}(t)-T_{C,0}), \end{aligned}$$

(10)

where $\rho _{ext}$ is the deviation of the external reactivity from the initial (critical) value, $\alpha _{F}$ is the fuel reactivity coefficient, $T_{F,0}$ is the initial condition for the fuel temperature, $\alpha _{C}$ is the coolant reactivity coefficient, $T_{C,0}$ is the initial condition for the average coolant temperature. Parameters used in this research for the fractional nuclear reactor model are presented in Table 1. The nuclear model equations were discretised using the Diethelms approach and the trapezoidal method.

Table 1. Parameters of the fractional nuclear reactor model

The last but no less important model used in the study was a non-linear system of fractional order described by the following equation

$$\begin{aligned} y(t) = \frac{3}{4} \left[ 5 \sin (10t) - \frac{3 \mathscr {D}^{0.9} y(t) }{3 + 0.2 \mathscr {D}^{0.8} y(t) + 0.9 \mathscr {D}^{0.2} y(t)} - \left| 2\mathscr {D}^{0.7} y(t) \right| ^{1.5} \right] \end{aligned}$$

(11)

This model was taken from [19] as an example of a system that is characterised by dynamics of fractional order and a strongly non-linear structure of the mathematical model. In terms of sophistication, this model is the most complex, and it is expected to be the most difficult to approximate by neural networks used in the research. In the later part of the article, this model is referred to as a Nonlinear model.

3.2 Data

In order to generate the training and validation data, Amplitude Modulated Pseudo Random Binary Sequence (APRBS) was introduced as the input for each examined dynamic system. For all systems except Nonlinear model the APRBS consisted of 600 samples, minimum hold time was 10 samples and maximum hold time was 100 samples. For Nonlinear model the APRBS consisted of 3000 samples, minimum hold time was 50 samples and maximum hold time was 400 samples.

For Fractional LTI systems the amplitude was within a range of $\left[ -1, 1 \right]$, for the Nuclear Reactor system the amplitude was within a range of $\left[ -0.005, 0.005 \right]$, and for Nonlinear system the amplitude was within a range of $\left[ -3, 3 \right]$ (Figs. 1, 2, 3 and 4). In order to check the ability of investigated networks to generalise, a study was carried out based on two test signals, the sinusoidal signal and the saw tooth signal respectively (Figs. 1, 2, 3 and 4).

Fig. 1.

Data generated on the basis of the FFOS model.

Fig. 2.

Data generated on the basis of the FSOS model.

Fig. 3.

Data generated on the basis of the Nuclear Reactor model. For presentation purposes, the input data has been scaled to output data level.

Fig. 4.

Data generated on the basis of the Nonlinear model.

3.3 Software Environment and Optimisation

The research presented in the paper was conducted using Python [2] environment in version 3.8.2 and PyTorch [1] library in version 1.4. The optimisation was performed using the L-BFGS algorithm, which is part of the PyTorch library.

In order to maintain consistency of computations between optimisation of different neural networks, the following common optimisation conditions have been defined: (i) update history size of the L-BFGS algorithm was set to , (ii) maximum number of iterations per optimisation step of the L-BFGS algorithm was set to , (iii) line search conditions of the L-BFGS algorithm were set to , (iv) number of training epochs was set to , (v) number of optimiser runs for a specific neural network was set to , (vi) the initial neural network parameters are randomly selected from uniform distribution $\mathcal {U} \left( - \sqrt{k}, \sqrt{k} \right)$ where $k = \frac{1}{\text {hidden size}}$, (vii) the loss function has been set as . Other properties of the optimisation package included in the PyTorch library were left as .

4 Results

In this section, tables with mean and minimum loss functions values are presented (Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13). The abbreviations in the column names of the tables are as follows: HU - hidden units, Train - training data, Val - validation data, P.no. - number of parameters. The mean values were arranged for the training, validation and test data depending on the number of neurons/units in the hidden layer of each neural network. The last row in each table contains the minimum value of the loss function for each data set. In this row, the hidden column contains information about the number of neurons/units in the hidden layer for which the minimum value of the loss function was obtained. Tables 2–4, 5–7, 8–10 and 11–13 contain results for FFOS, FSOS, Nuclear Reactor and Nonlinear dynamic systems respectively.

This section also contains exemplary plots (Figs. 5, 6, 7 and 8) which contain outputs from the considered dynamic systems (System) and outputs from the considered neural networks (Net). The plots contain only the results from neural networks, which were characterised by the lowest value of the loss function for the second testing data set. For each data set, the best network was the GRU network with 4 units in the hidden layer and 89 learnable parameters. The exception to this was a network approximating a Nonlinear model, which was characterised by 2 units in the hidden layer and 33 learnable parameters. As in previous cases, it was also a GRU network. Tables 2, 3 and 4 also contain information on the number of all learnable parameters according to the number of neurons in the hidden layer, which are similar for other tables. The last figure in this section (Fig. 9) presents exemplary residual error plots for the neural networks under consideration. This figure is based on Figs. 5, 6, 7 and 8 labelled ‘Test data 2’.

Table 2. Mean and minimal Loss of Elman RNN for FFOS data

Table 3. Mean and minimal Loss of GRU nets for FFOS data

Table 4. Mean and minimal Loss of LSTM nets for FFOS data

Table 5. Mean and minimal Loss of Elman RNN for FSOS data

Table 6. Mean and minimal Loss of GRU nets for FSOS data

Table 7. Mean and minimal Loss of LSTM nets for FSOS data

Table 8. Mean and minimal Loss of Elman RNN for Reactor data

Table 9. Mean and minimal Loss of GRU nets for Reactor data

Table 10. Mean and minimal Loss of LSTM nets for Reactor data

Table 11. Mean and minimal Loss of Elman RNN for Nonlinear model data

Table 12. Mean and minimal loss of GRU nets for Nonlinear model data

Table 13. Mean and minimal Loss of LSTM nets for Nonlinear model data

Fig. 5.

The best approximation for the FFOS Testing2 data @ GRU net with 4 hidden units.

Fig. 6.

The best approximation for the FSOS Testing2 data @ GRU net with 4 hidden units.

Fig. 7.

The best approximation for the nuclear reactor Testing2 data @ GRU net with 4 hidden units.

Fig. 8.

The best approximation for the Nonlinear model Testing2 data @ GRU net with 2 hidden units.

Fig. 9.

Residual error plot for the best fitted networks based on Test2 data

5 Conclusions

In this paper, the capabilities of recurrent neural networks (RNN) were examined as the fractional-order dynamic systems approximators. Their effectiveness in that approach was validated based on the linear, first and second fractional-order systems and two nonlinear fractional-order systems. The RNN networks parameters were optimised with the least squares criterion by the L-BFGS algorithm. The presented numerical simulation results, in most cases, showed satisfactory approximation performance and reliability of examined recurrent artificial neural networks structures: Elman, GRU and LSTM. Especially the GRU network showed its potential in its practical applicability in the real digital control platform. The advantages are high accuracy with a relatively small network structure and a relatively low number of parameters to be determined. The presented methodology with additional extensions may be used to cover approximations of fractional-order operators occurring in the control algorithms which are planned for implementation in the digital control platforms such as FPGA, DSP or PLC controllers.

During the study, a typical phenomenon associated with neural network over fitting was observed. The more complicated the neural network is, the lower the average loss for training data is observed. This relationship is visible for each neural net structure involved and for each dynamic system studied. In the case of conducted research, the phenomenon of over fitting is reflected especially in the loss function values for two approximated models, i.e. a nuclear reactor model and a complex non-linear model.

In the case of recurrent neural networks, this problem can be addressed by focusing on the analysis of signals processed by neural network structures and, in particular, on the analysis of the effectiveness of the utilisation and impact of historical samples of processed signals stored within the network on the network output. A second element that can reduce the over fitting problem in this type of networks would be to develop training signals that allow to recognise both the dynamics of the fractional order and the nonlinearities present in the dynamic system under consideration. The problems mentioned here represent a very interesting extension of the research presented in the article, which the authors would like to focus on in the future.

The second open research path related to the presented work focuses on the problem of modification of existing structures and, in general, the development of new recursive structures. These will be able to approximate objects with fractional dynamics to a suitable degree. The authors also plan to address this direction of research in the future.