Keywords

1 Introduction

The slope stability problem has been studied for years, being of considerable concern due to its effects on geotechnical designs [1]. Generally, slopes are categorized as a cut slope, natural slope or fill slope, and physical and geometric factors influence their stability. Also, the parameters which are related to soil strength affect the slope behavior too. The safety factor (Fs) of a cohesive slope is related to a well-recognized parameter named the dimensionless stability number (N2c). One of the first studies that led to the development of useful design charts for the slope stability issue was implemented by Taylor [2]. More recently, various research studies have concentrated on providing design chart solutions (e.g., Qian et al. [3], Abuel-Naga et al. [4], Aksoy et al. [5] and Moayedi and Hayati [6]). Some time and cost constraints are constraints of using the new advances in mathematical and computer modeling tools. Therefore, the importance of providing the design charts is becoming more highlighted. As a novel idea, intelligent predictive tools (i.e., artificial neural networks (ANNs) and particle swarm optimization (PSO)) are being employed for the subject of slope stability evaluation [7, 8]. Jiang et al. [9] applied the UB method to investigate a rock slope’s seismic behavior and safety factor with a tunnel. As a result, they found three factors, namely the horizontal seismic force coefficient, the slope height, and the internal friction angle, to be the most influential parameters influencing the safety factor’s sensitivity. In another study, Pan and Dias [10] assessed the face stability for the case of a non-circular tunnel through an upper bound limit analysis model, synthesized with the technique of strength reduction. According to their results, this approach presents conservative results and can be applied in safety factor evaluation in a particular design.

The number of studies concerned about the feasibility of neural network modeling to solve slope stability is limited. The hybrid GP model that is presented in this study has not been proposed for the problem of slope stability previously. There is almost no study on using hybrid GP-based learning systems to predict the factor of safety and its key parameters. In the following, the GP prediction models’ results were compared with the results of an optimized ANN feedforward learning system. Similarly, to find the best ANN structure, all the proposed models were evaluated with a trial and error process on their influential parameters. Finally, each model’s design chart solution was depicted; and the formula was presented for both the GP and ANN models to be used for slopes with the same conditions. In this paper, optimal forms of genetic programming (GP) and ANN models have been utilized to predict the N2c in a two-layered cohesive slope, based on the upper bound (UB) limit analysis method. The UB model is broadly applied for similar engineering problems. The slope proposed for this work was constructed from two separate clayey layers, lying on a rigid rock bed. The ratio of the first soil layer thickness to the full height of the slope, d/H, the slope angle, β, and the ratio of the undrained shear strength of the first soil layer to that of the slope layer, Cu1/Cu2, were considered as three efficacious parameters that affect the slope situation. These parameters also form the input dataset. Meanwhile, the N2c was taken as the output of the networks. 80% of the dataset was devoted to the training part, and the remaining 20% was selected to test the networks.

2 Artificial Intelligence Systems

Genetic Programming.

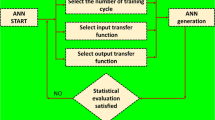
Genetic programming is a powerful computing technology that has been initiated based on genetic algorithms (GA). This model was first introduced in 1985 by Cramer [11]. Another scholar, Ref Koza, later improves it in 1984 [12]. It is widely used in solving engineering problems by numerous scholars such as Johari et al. [13], Makkeasorn et al. [14], Garg et al. [15], and Garg et al. [16]. During the GP process, particular computer programs are applied to predict the problem’s potential outputs by linking the input data layers and main output(s). One of the critical issues in using the GP algorithm is that the user will have a simpler finalized algorithm. The overall procedure of GP prediction performance is illustrated in Fig. 1. The complete detail of the applied GP technique is well described in Ref. [12, 15,16,17].

Fig. 1.
figure 1

Typical GP tree presented for the function [(X1-5)/(X2 + X3)]2

Full size image

Artificial Neural Network.

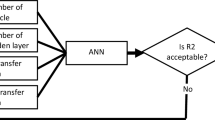
The artificial neural networks (ANNs), which mainly inspired by a biological neural network, are well established as one of the most applicable approaches that have been employed in the last two decades is, which were first introduced by McCulloch and Pitts [18]. These tools are widely employed for prediction purposes [19]. Numerous scholars such as Rao [20], El-Bakry [21], Samui and Kumar [7], and Moayedi and Hayati [22] are experiences successful use of ANN in predicting complex engineering solutions. Overall, the primary objective is to establish a non-linear equation (i.e., trained based on the initial learning process) between the inputs and output(s) dataset [20]. In this sense, a neural network’s typical architecture is prepared according to components of so-called neurons. As illustrated in Fig. 2, the input layer includes layers of the input(s) data. As a predefined model, the number of nodes is considered the same as the input parameters. During the neural network training processes, there can be one or more hidden layer(s) finally, and the calculation process will end to one or more output layer(s). More precisely, for each node, if we assume the term X as the main input and the term W as the interconnected weight (which is also shown as Iw), the bias (which is shown by the term of β) will be added to the summation of WXs. In this regard, an activation function (f(I)) will be applied to the acquired term (\( \sum {\mathbf{WX}} \) + β) to produce the outputs. The activation function for this case was considered as Tan-sigmoid (Tansig) which is defined by Eq. (1):

Fig. 2.
figure 2

Typical structure and operation of ANNs

Full size image
$$ Tansig\left( x \right) = \frac{2}{{1 + e^{ - 2x} }} - 1 $$
(1)

3 Data Collection and Problem Statement

In this research, the results from the upper bound (UB) type of limit analysis method were employed to assess the short-term stability situation of a cohesive slope. This method is well discussed in other studies (e.g., Florkiewicz [23], Donald and Chen [24], Karkanaki et al. [25], and Jiang et al. [9]). The slope is constructed from a maximum of two different soil layers with separate material properties lying on a bedrock layer in the present case. Besides, Fig. 3 shows a graphical description of the input data range versus the data numbers for d/H, the slope angle of β° and the Cu1/Cu2 ratio. The analysis is performed with new computer software called OptumG2. It is based on finite element limit analysis and has been widely used in other studies (e.g., Karkanaki et al. [25]; Caër et al. [26] and Zhou et al. [27]). The analytical method used and the 2D boundary conditions applied in this study, i.e., to illustrate the pure cohesive slope, are similar to the research performed by Qian et al. [3]. A view of the slope model is presented in Fig. 4. As can be obtained from this figure, the proposed slope has been formed from two cohesive soil layers having only consistent undrained strength (cu1) with a zero undrained internal friction angle. Cu1 and Cu2, respectively define the undrained cohesive strength for the top and bottom soil layers. The influential parameters and an example of output from OptumG2 are illustrated in Figs. 4a and 4b, respectively.

Fig. 3.
figure 3

Graphical description of the range of input data versus data numbers for (a) d/H, (b) slope angle, (c) Cu1/Cu2

Full size image
Fig. 4.
figure 4

A view of the model for cohesive slope (a) schematic model, (b) OptumG2 stability output for upper bound limit analysis

Full size image

4 Model Development for Prediction of N2c

A proper estimation process, which is used by hybrid ANN models, should be formed from several steps such as (i) data processing and normalization, (ii) selecting a suitable hybrid model, and finally (iii) finding an appropriate hybrid structure for the proposed model, which can be achieved through a trial and error procedure. For the aim of producing the design chart solutions, N2c (a dimensionless stability number, which was first investigated by Taylor [2]) was obtained from Eq. (2):

$$ N_{2c} = c_{u1} /\gamma HF_{s} $$
(2)

where N2c, \( C_{u1} \), and \( F_{s} \) define the dimensionless stability number, the undrained shear strength of the second soil layer, and the factor of safety obtained from the OptumG2 modeling, respectively. Also, \( \gamma \) describes the soil unit weight, which is taken as 20 kN/m3.

The dataset used is constructed from three inputs: the three influential parameters affecting the slope stability situation. The first factor is related to depth (d/H). It defines the ratio of both soil layer thicknesses, d, to the slope’s top layer height, H. The angle of the present slope (β) was considered the second parameter. The third effective factor defines the undrained shear strength ratio (Cu1/Cu2). An example of the mentioned data is presented in Table 1. Note that these values are derived from the OptumG2 simulation, and, as illustrated, the three useful parameters of d/H, β, and Cu1/Cu2 are employed to estimate the N2c in the three FEM methods of LB, UB, and LEM limit analysis.

Table 1. Example of inputs and output dataset applied for modeling purpose
Full size table

5 Results and Discussion

The present study intends to evaluate the stability of a two-layered cohesive slope by using two intelligent techniques. An MLP neural network and a GP mode were applied to approximate the stability of the slope. The important parameter of the dimensionless stability number (N2c) was considered the networks’ output. It was estimated to be influenced by three effective factors, which were considered as (i) the layer’s height ratio (d/H), (ii) the slope angle (β), and (iii) the undrained cohesive strength ratio (Cu1/Cu2) as the input dataset. Similar to previous research, the stock dataset was randomly divided into two parts to train and test the networks, with a ratio of 80% and 20%, respectively (e.g., Moayedi and Hayati [28], Moayedi and Hayati [22], Koopialipoor et al. [29] and Moayedi and Hayati [6]). Also, for each model, the performance was measured by the index of the statistical error terms RMSE and R2. Equations (3) and (4) explain these indices:

$$ RMSE = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left[ {\left( {Y_{{i_{actual} }} - Y_{{i_{produced} }} } \right)} \right]^{2} } $$
(3)
$$ {\text{R}}^{2} = 1 - \frac{{\mathop \sum \nolimits_{{{\text{j}} = 1}}^{\text{N}} \left[ {\left( {\text{Y}} \right)_{{{\text{actual}},{\text{j}}}} - \left( {\text{Y}} \right)_{{{\text{produced}},{\text{j}}}} } \right]^{2} }}{{\mathop \sum \nolimits_{{{\text{j}} = 1}}^{\text{N}} \left[ {\left( {\text{Y}} \right)_{{{\text{actual}},{\text{j}}}} - \left( {\text{Y}} \right)_{\text{mean }} } \right]^{2} }} $$
(4)

Where Yi actual and Yi produced stand for the actual and predicted values of N2c, respectively. N is the indicator of the number of data, and Ymean is the average of the actual slope stability values. The mentioned indices have been widely used in other earlier studies (e.g., Momeni et al. [30], Armaghani et al. [31], Mohamad et al. [32] and [33]).

Optimal Hybrid GP Model Predicting N2c.

Determining proper network architecture is a necessary step in the utilization of artificial intelligence. For GP optimization, many trial and error processes, including 36 various GP models, were performed to find an appropriate GP structure for estimating the N2c. The feasibility of the GP technique was evaluated for different numbers of generations, values of swarm sizes, and selection tournament sizes. For all three mentioned parameters, 12 values, including 50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 750, and 1000 were considered, and the performance was evaluated by means of the RMSE reduction procedure. Regarding the trial and error processes provided in Figs. 5, 6 and 7, the GP model with the values of 750, 200, and 250 respectively for the population size, some generations and selection tournament size showed the best performance, as indicated by its lower RMSE value. Therefore, this structure was introduced as the optimal architecture of the GP for any further N2c estimation.

Fig. 5.
figure 5

GP network performance results for different population sizes

Full size image
Fig. 6.
figure 6

GP network performance results for different tournament sizes

Full size image
Fig. 7.
figure 7

GP network performance results for a different number of generations

Full size image

Optimal Artificial Neural Network Predicting N2c.

Like the GP model, the best ANN architecture was obtained by assessing several ANN structures’ performance. For the ANN, a multilayer perceptron network was verified with various numbers of neurons in its single hidden layer. After a trial and error process, the network that reported the lowest RMSE and the highest R2 was selected as the optimum model. The results of this are depicted in Fig. 8. Note that every structure was performed for six iterations. As a general deduction, the MLP network with at least eight neurons in its hidden layer could present an accruable performance for modeling the problem.

Fig. 8.
figure 8

Sensitivity analysis for ANN, based on (a) R2 and (b) RMSE values reported for training and testing datasets

Full size image

6 Models Evaluation and Design Solution Charts

After obtaining the optimum structures of both the GP and ANN methods, they were applied to the prepared dataset for the proposed estimation of the dimensionless slope stability number. The training dataset did a training operation, and the performance of each model was evaluated using the testing data. Two usual types of charts were used to describe and analyze the results. Firstly, the accommodation of the predicted and actual values of N2c was depicted in the form of Fig. 9. Also, Table 2 lists the calculated RMSE and R2. As illustrated in Fig. 9 and Table 2, the GP and ANN models had a robust prediction and sufficient reliability in the slope stability assessment. The high values of R2 can prove this claim, and the low values of RMSE obtained from both model performances. The training results show RMSE of 0.010274 and 0.006112 and R2 of 0.9968 and 0.9989 for the GP and ANN methods. The results of the test phase show a good approximation for these models too. The RMSE and R2 values are 0.011146 and 0.005927, and 0.9967 and 0.9990, respectively, for the GP and ANN methods. Based on the reported results, the optimized ANN had a slightly better performance compared to the optimized GP model, as can be concluded from the lower RMSE and higher R2 values in both the training and testing phases.

Fig. 9.
figure 9

Training (a and b) and testing (c and d) results of GP and ANN models for predicting N2c

Full size image
Table 2. Obtained RMSE and R2 values for GP and ANN results
Full size table

In the following, the measured results from the upper bound analysis of slope stability are compared with the predicted values obtained from the optimal GP and ANN algorithms. Consequently, Figs. 10-a to 10-e present the measured N2c as well as the results obtained from the GP and ANN training networks for slope angles between 15 to 75°, respectively. In this regard, according to the different values of the slope angle (β) (i.e., 15°, 30°, 45°, 60° and 75°), separate solution of designing slope stability charts were provided, noting that in each figure the vertical and horizontal axes stand for the N2c and d/H ratio, respectively. To include the Cu1/Cu2 ratio parameter, Cu1/Cu2 ratios of 0.2, 0.8, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, and 5 were considered through the calculation steps. Therefore, ten different curves are plotted for each of the predefined slopes.

Fig. 10.
figure 10figure 10figure 10

Chart solutions for GP and ANN models for (a) β = 15°, (b) β = 30°, (c) β = 45°, (d) β = 60°, (e) β = 75°

Full size image

The curves showing Cu1/Cu2 = 0.2 to 0.8 are drawn in a relatively straight path, and the N2c does not show noticeable changes as the d/H ratio rises. In contrast, for the remaining eight curves (especially for Cu1/Cu2= 3 to Cu1/Cu2 = 5), the N2c values have an ascending direction as the d/H ratio rises. Note that the distance between these two curves decreases as β rises so that in the last graph (β = 75°), they have covered each other. Also, there is another difference in the last graph. It relates to the fluctuations of the curves (especially for the curves determined by Cu1/Cu2 = 3.5, 4, and 5). In graphs, a – d, a steeper tangent can be observed for d/H values less than 2.5, while it differs for graph e, and camber can be seen in the vicinity of d/H = 2 (especially for Cu1/Cu2 = 5).

As can be obtained from Figs. 10a–e, both the GP and ANN models gave a satisfactory prediction for estimating the slope stability number. This can be concluded from the GP and ANN curves’ appropriate proximity to the measured N2c (target data). It is worth noting that each target curve’s general direction is well approximated by both the GP and ANN tools. Therefore, there is good coverage for all of them.

Focusing on the measured datasets, considering the black and red curves in Figs. 10a–e (Cu1/Cu2 = 4.5 and 5), there are fluctuations and sudden changes for the N2c results provided for d/H ratios, which are lower than 2.0. To evaluate the GP and ANN’s flexibility, it is necessary to compare their reactions against these changes. In cases a–d, it is observed that the GP model had maintained its main direction without significant changes, even for critical d/H ratios (see red and black dash-dot curves). On the contrary, the changes are well distinguished by the ANN curves, especially for the black curves in Figs. 10a–d. In each case, the fluctuation is well followed by the ANN, and there is excellent accommodation between them. Also, for the changes occurring in Fig. 10e (β = 75°), the ANN gave a better approximation, and this is because its curve is closer to the target curve. For another example, the ANN’s higher precision can be deduced considering the grey curve (Cu1/Cu2 = 2) in cases a–c, while more distance between the measured and predicted curves are reported for the GP. Regarding these descriptions and also the obtained RMSE and R2 values, it can be concluded that both the GP and ANN models have sufficient applicability. Besides, the higher flexibility of the ANN in design solution charts can be concluded due to its response against the changes.

To provide a reliable solution equation that reflects the presented design charts, an equation was derived from both the GP and ANN trained networks to be presented in respect of the slope stability issue. The GP and ANN formulas are presented in Eqs. (5) and (6), respectively.

(5)

Where, X1 = d/H; X2 = β; and X3 = Cu1/Cu2.

(6)

Where, Y1, Y2 … Y8 are defined by Eqs. 7–14:

$$ {\text{Y1 }} = {\text{ Tansig }}\left( { - 1.0 8 2 1 { } \times {\text{ X1 }} - \, 0. 4 8 8 7 { } \times {\text{ X2 }} + { 2}. 6 2 4 3 { } \times {\text{ X3 }} + { 3}. 1 1 5 7} \right) $$
(7)
$$ {\text{Y2 }} = {\text{ Tansig }}\left( {0. 1 3 8 6 { } \times {\text{ X1 }} - \, 0. 10 7 1 { } \times {\text{ X2 }} + \, 0. 6 5 4 6 { } \times {\text{ X3 }} - \, 0. 4 3 7 6} \right) $$
(8)
$$ {\text{Y3 }} = {\text{ Tansig }}\left( {0.0 80 4 { } \times {\text{ X1 }} - \, 0.0 9 4 7 { } \times {\text{ X2 }} + \, 0. 2 1 6 8 { } \times {\text{ X3 }} - \, 0.0 9 4 2} \right) $$
(9)
$$ {\text{Y4 }} = {\text{ Tansig }}\left( { 2. 3 2 9 3 { } \times {\text{ X1 }} - { 2}.0 8 5 3 { } \times {\text{ X2 }} + { 2}. 2 8 8 3 { } \times {\text{ X3 }} - \, 0.0 3 7 1} \right) $$
(10)
$$ {\text{Y5 }} = {\text{ Tansig }}\left( { - 0.0 2 8 5 { } \times {\text{ X1 }} + \, 0. 3 6 3 8 { } \times {\text{ X2 }} - { 3}.0 9 8 5 { } \times {\text{ X3 }} - { 1}. 5 4 1 6} \right) $$
(11)
$$ {\text{Y6 }} = {\text{ Tansig }}\left( {0. 90 3 9 { } \times {\text{ X1 }} + \, 0. 3 4 1 9 { } \times {\text{ X2 }} - \, 0. 70 2 1 { } \times {\text{ X3 }} + { 1}. 9 3 6 1} \right) $$
(12)
$$ {\text{Y7 }} = {\text{ Tansig }}\left( { - 1. 6 8 6 5 { } \times {\text{ X1 }} + { 3}. 3 3 7 1 { } \times {\text{ X2 }} + \, 0. 3 80 8 { } \times {\text{ X3 }} - { 1}. 6 1 2 6} \right) $$
(13)
$$ {\text{Y8 }} = {\text{ Tansig }}\left( { - 3. 1 80 7 { } \times {\text{ X1 }} + \, 0. 8 7 2 3 { } \times {\text{ X2 }} + \, 0. 8 3 8 8 { } \times {\text{ X3 }} - { 4}. 1 2 7 7} \right) $$
(14)

where in each equation, X1 = d/H; X2 = β; X3 = Cu1/Cu2.

It is important to note that the proposed formula can be used in the slope stability problem to calculate the dimensionless stability number for slopes with a maximum of two layers with similar material conditions. Besides, there are two crucial advantages for the GP model equation compared with that of the ANN. One of them is the GP equation, which is easier to use than the ANN equation (i.e., the intermediate equations of Y1 to Y8 need to be considered before Eq. (6) can be used). The other is the GP equation that can be used directly and requires no normalization process (while in the ANN, the input layers need to be normalized before any further process).

7 Conclusions

Regarding the importance of the slope stability issue in many engineering projects, the main objective of this research was to evaluate the capability of two artificial intelligence techniques in the assessment of cohesive slope stability. Optimized GP and optimized ANN methods were applied to the dataset collected from a finite-element procedure called upper bound (UB) limit analysis. Three effective factors to the cohesive slope’s stability were considered as input data to produce the dimensionless stability number. The first factor was the d/H ratio, where d is the slope thickness, and H is an indicator of the topsoil layer’s height. Slope angle (β) was the second factor, and the third parameter was the ratio of the undrained shear strength of the first soil layer to the slope layer’s (Cu1/Cu2). Besides the use of the statistical indices of RMSE and R2, the results were compared by the form of design charts solution. From the results, both the RMSE and R2 values showed a slightly better approximation for the ANN than for the GP model in training (RMSE of 0.010274 and 0.006112, and R2 of 0.9968 and 0.9989, respectively for the GP and ANN methods) and testing (RMSE of 0.011146 and 0.005927, and R2 of 0.9967 and 0.9990, respectively for the GP and ANN methods) phases. We also found the ANN to be the more reliable model based on the reported results from the design charts.

Regarding these charts, the ANN showed higher flexibility in fluctuations. In the following, two formulas were extracted based on each of the optimized GP and ANN models, for use in the field of slope stability assessment, in place of the traditional formula of the UB limit analysis method. Note that the GP formula was introduced as the more applicable formula due to its greater brevity and simplicity.