Keywords

1 Introduction

Hamiltonians with singular potentials appeared in the physics literature in the 1930s, in the attempt to describe strong nuclear forces with range negligible compared to the wave-length of the particles. By means of heuristic argument and experimental observations, in [6] Bethe and Peierls argued that the two-particle wave function should behave asymptotically

$$\displaystyle \begin{aligned} \psi(x_1,x_2)\sim\Big( \frac{1}{|x_1-x_2|}-\frac{1}{a}\Big)\xi(x_1)+o(1), \quad |x_1-x_2|\rightarrow 0. \end{aligned} $$
(1)

This boundary condition is named “Bethe-Peierls contact condition” after them. Here the a is interpreted as the scattering length of the interaction, making it the only physical parameter governing the interaction.

The study of more complicated systems, where more particles and various symmetries are taken into account, led the scientific community to conjecture the presence of interesting spectral phenomena. It took many decades for the experimentalist to develop techniques, such as the Feschbach resonance, that made it possible to tune the scattering length and the range of interaction of particles in ultra-cold gases, thus enabling them to study the spectrum of zero-range interaction systems in the laboratories. For an historical summary we refer to [28] and the introduction in [16] (and references therein), while here we only point out two such phenomena:

  1. (a)

    The Thomas effect, which consists on a collapse to −∞ of the ground state energy of a three particle system, while the two-body subsystems energy remain bounded from below. Correspondingly, the ground state collapses onto the barycenter of the system.

  2. (b)

    The Efimov effect, which consists on a sequence of bound states whose energy approach geometrically zero, while the corresponding two-body systems are unstable. Correspondingly, the ground state spreads out to the whole space.

From the mathematical point of view, even the well-posedness for the Hamiltonian of zero-range interactions, formally given by

$$\displaystyle \begin{aligned} H=-\sum_{i=1}^n\frac{1}{2m_i}\varDelta_{x_i}+\sum_{i<j}\alpha_{ij}\delta(x_i-x_j) \end{aligned} $$
(2)

is not obvious. Here n is the number of particles, with respective masses m 1, .., m n in \(\mathbb R^3\) and two-body point interaction between particle i and j of strength α ij. Indeed, this Hamiltonian cannot be viewed as a quadratic form perturbation in the sense of Kato, since wave functions in the domain of the free Schrodinger operator \(H^2(\mathbb R^3)\) are not necessarily continuous. Therefore, the delta-like perturbation is ill defined.

Several ways to circumvent this issue have been proposed, the following three being the most relevant:

  1. (a)

    H can be realized as an opportune limit of H 𝜖. Here H 𝜖 = H 0 + V 𝜖, H 0 being the free Schrodinger operator and V 𝜖 a family of potentials that shrinks around the contact manifold Γ ij = {x i = x j} as 𝜖 → 0. The potentials are chosen so that they have a zero-energy resonance, a condition that implies that existence of the limit in the strong resolvent sense. This approach appears, in [1] and, more recently, in [3] and [13].

  2. (b)

    Using a quadratic form approach, one can look for a closed semibounded quadratic form (thus identifying a unique self-adjoint operator) reproducing the formal action given by (2). This approach is due to the school of Dell’Antonio, see [9], [8] and [30], and subsequently by Moser and Seringer in [26] and [27].

  3. (c)

    H can be viewed as a self-adjoint extension of the free Schrodinger operator 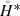acting on wave functions compactly supported away from the coincidence manifolds. This leads to a self-adjoint operator whose action differs from the free Schrodinger operator only on the contact manifolds, thus being a suitable candidate for point interactions. One then selects extensions (i.e., boundary conditions) with local features, possibly reproducing the Bethe-Peierls contact condition. This approach was introduced by Minlos et Faddeev for the model of zero-range interacting particles (see [18, 19, 24, 25]), while Albeverio et al. in [1] consider the case of fixed point interaction.

We will focus on the last approach. In particular, the semi-boundedness of the free Laplacian makes possible the usage of the Krein, Visik, Birman (KVB) theory for self-adjoint extensions of symmetric operators. We refer to [12] for a complete overview on this theory, while here we only sketch the main idea.

Given a positive densely defined symmetric operator , KVB theory labels its self-adjoint extensions H T with self-adjoint operators T acting on closed subsets of . The recipe T → H T is explicit, and it enables us to detect interesting features of H T through the corresponding property of T. This becomes particularly significant for the study of spectral properties, such as finiteness of the spectrum or the existence of a ground state, in that the operator T is usually much more manageable.

From now on, we will focus on a particular system consisting in 2 identical fermions of mass one and a third particle of mass m. In particular, in Sect. 2 we sketch the main ideas from [16] and [17], in which the model is rigorously defined by means of KVB theory. Sections 3, 4, 5, and 6 are dedicated to the spectral analysis of this model, presenting the results from [5]: in particular, in Sect. 3 we reduce the problem to the analysis of a certain pseudo-differential operator, which is then study in full details in the subsequent ones. Finally, in Sect. 7 we present some open questions for the same model and some variants of it.

2 The 2 + 1 Model

We consider a system of three particles, two identical fermions and a third one of a different nature with ratio mass m with respect to the fermions, where the interaction among the particles has zero range. To later use, we introduce the parameters

$$\displaystyle \begin{aligned} \mu:=\frac{2}{m+1},\quad \nu:=\frac{m(m+2)}{(m+1)^2}=1-\frac{\mu^2}{4}. \end{aligned} $$
(3)

We will refer to this system as the 2 + 1 fermionic trimer with contact interaction. Despite its small size, a rich class of spectral properties already emerges in certain regime of the mass m.

We briefly recall the general scheme that gives a rigorous mathematical framework to such a model. Due to translational invariance, we can work in relative coordinates \((x_1,x_2)\in \mathbb R^6\), where x i denotes the position of the i-th fermion with respect to the third particle. The starting point is then the free Schrodinger operator on \(L^2_f(\mathbb R^3\times \mathbb R^3)\) with dense domain

(4)

Here the subscript f denotes the closed subspace of antisymmetric functions, and Γ i := {x i = 0}, i = 1, 2, are called “contact manifolds”, in that they correspond to the situation where a fermion comes on the top of the third particle. Notice that there is no room for a contact interaction between the two fermions, due to the Pauli exclusion principle. In [16] we show that the adjoint of this operator has domain

(5)

and action

(6)

Here, \(\widehat {F}_{\lambda }(p,q):=\widehat {f}(p,q)+\frac {\widehat {u}_\eta (p,q)}{p^2+q^2+\mu \,p\cdot q+\lambda }\) and \(\widehat u^{\lambda }_{\xi }(p,q)=\frac {\widehat \xi (p)-\widehat \xi (q)}{p^2+q^2+\mu p\cdot q+\lambda }\). The latter spans as ξ runs in \(H^{-1/2}(\mathbb R^3)\). The superscript λ will be dropped when the choice of λ is understood.

We are interested in extensions of , i.e., restrictions of , in that they act as the free Schrodinger operator as long as the particles are far apart, and are thus suitable candidates for modeling point interactions. Such extensions should satisfy two properties: (1) self-adjointness, which guarantees a well-posed evolution and real spectrum; (2) locality, in accordance with the local nature of the interactions.

Notice that the self-adjointness, by KVB theory, is tantamount of restricting the domain of the adjoint to g’s in \(\mathscr D(H^*)\) where u η = A λ u ξ for some self-adjoint A λ. As far as the locality is concerned, an easy computation shows that functions in satisfy the pointwise asymptotic

$$\displaystyle \begin{aligned} \quad \int_{q\in \mathbb R^3, |q|<R}\widehat g(p,q)dq=4\pi R\widehat \xi(p)+(-\widehat{T_{\lambda}\xi}(p)+\frac{1}{2}\widehat{W_{\lambda}\eta}(p))+o(1),\quad R\rightarrow +\infty, \end{aligned} $$
(7)

where

$$\displaystyle \begin{aligned} \widehat{(W_\lambda\,\xi)}(p)\;:=\;\frac{2\pi^2}{\sqrt{\nu p^2+\lambda}\,}\,\widehat{\xi}(p)-2\!\int_{\mathbb{R}^3}\frac{\widehat{\xi}(q)}{(p^2+q^2+\mu p\cdot q+\lambda)^2}dq. \end{aligned} $$
(8)

and

$$\displaystyle \begin{aligned} \widehat{T_{\lambda}\xi}(p)=2\pi^2\sqrt{\nu p^2+\lambda}\widehat \xi(p)+\int_{\mathbb R^3}\frac{\widehat \xi(q)}{p^2+q^2+\mu p\cdot q+\lambda}dq \end{aligned} $$
(9)

The asymptotic (7) gives information on the ultra-violet asymptotic of g, which relates to its behavior close to the origin. If one formally prescribe for some \(\alpha \in \mathbb R\)

$$\displaystyle \begin{aligned} \eta=2W_{\lambda}^{-1}(T_{\lambda}+\alpha)\xi, \end{aligned} $$
(10)

one obtains the so called Ter-Martirosyan-Skornyakov condition, introduced in [29],

(11)

which is the momentum analogue of the Bethe-Peierls condition (1) in the two-body channels. The extensions for which is satisfied are called Ter-Martirosyan-Skornyakov (or simply TMS) extensions. However, TMS alone only may not be sufficient to guarantee the self-adjointness. Indeed, one needs to give an appropriate functional meaning to the pointwise identity (10) in order to select a self-adjoint extension.

In [16] we proved that W λ is a positive bounded operator from \(H^{-1/2}(\mathbb R^3)\) to \(H^{1/2}(\mathbb R^3)\), and moreover

$$\displaystyle \begin{aligned} \langle u_{\xi},u_{\xi}\rangle_{L^2_f(\mathbb R^3\times \mathbb R^3)}=\langle \xi,W^{-1}_{\lambda}\xi\rangle_{H^{-1/2},H^{1/2}}=:\langle\xi,\xi\rangle_{H^{-1/2}_{W_{\lambda}}}. \end{aligned} $$

In particular, the map ξ → u ξ is unitary between \(H^{-1/2}(\mathbb R^3)\) equipped with the scalar product induced by W λ (denoted by \(H^{-1/2}_{W_{\lambda }}\)) and \(\ker (H^*+\lambda )\). Therefore, self-adjoint extensions of are labeled by self-adjoint operators acting on \(H^{-1/2}_{W_{\lambda }}\). Collecting everything, the problem of finding self-adjoint TMS extensions boils down to that of finding a domain of self-adjointness for \(A_{\lambda ,\alpha }:=2W^{-1}_{\lambda }(T_{\lambda }+\alpha )\) on \(H^{-1/2}_{W_{\lambda }}\).

In [16] and [17] we give a full classification and understanding of the TMS self-adjoint extensions. In particular, there are three different regimes depending on the mass ratio m:

  1. (a)

    m ∈ (0, m ∗): the TMS condition is not a self-adjoint condition, and for each α there exist infinitely many self-adjoint extensions satisfying the TMS condition for the given α. Moreover, some of them are unbounded from below.

  2. (b)

    m ∈ (m ∗, m ∗∗): The TMS condition is not a self-adjoint condition, but for each α there exists only a one-parameter family H α,β of self-adjoint extensions satisfying the TMS condition for the given α. The real parameter β is related to a boundary condition when the three particle come all on the top of each other simultaneously. We denote by H α := H α,∞ the smallest one.

  3. (c)

    m ∈ (m ∗∗, ∞): the TMS condition is a self-adjoint condition. We denote this unique self-adjoint extension by H α.

The value of m ∗ and m ∗∗ are respectively about 1∕13 and 1∕8, and they are in perfect accordance with the experiments. In the regimes (b) and (c) (i.e., for m > m ∗) one has, for every λ > 0,

(12)

Both (12) and (5) holds for any choice of λ > 0, leading to different but equivalent decomposition (as discussed in Remark 1 of [16]). In the next chapter, we will analyze in details the spectrum of these operator H α. For the regime m < m ∗, some results are known for similar, yet different, models (e.g. appearance of Efimov effect for finite range potentials under mild assumptions proved in [2]), but a complete understanding of the spectrum is yet to be achieved.

3 Properties of T λ and Reduction Lemma

As pointed out in the previous sections, the study of the spectral properties of H α will eventually reduce to those of T λ. Hence, we list the major properties of the latter.

  • First of all, for each λ the operator T λ commutes with the action of the orthogonal group O(3) on \(\mathbb R^3\). As such, if we decompose

    $$\displaystyle \begin{aligned} L^2(\mathbb R^3)=\bigoplus_{\ell\geq 0}L^2(\mathbb R^+,r^2dr)\otimes span\{Y_{\ell,-\ell},..,Y_{\ell,\ell}\}=:\bigoplus_{\ell\geq 0}L^2_{\ell}(\mathbb R^3), \end{aligned}$$

    the Y ℓ,m’s being the spherical harmonics, then each \(L^2_{\ell }\) is invariant under the action T λ, thus leading to the decomposition

    $$\displaystyle \begin{aligned} T_{\lambda}=\;\bigoplus_{\ell\geq 0}T_{\lambda}^{(\ell)}. \end{aligned}$$

    Moreover, the same decomposition apply to every Sobolev space

    $$\displaystyle \begin{aligned}H^s(\mathbb R^3)=\bigoplus_{\ell\geq 0}H^s_{\ell}(\mathbb R^3).\end{aligned}$$

    The expression for \(T_{\lambda }^{(\ell )}\) can be obtained by means of Legendre polynomials

    $$\displaystyle \begin{aligned}P_{\ell}(y)=\frac{1}{2^{\ell}\ell!}\frac{d^{\ell}}{dy^{\ell}}(y^2-1)^{\ell},\end{aligned}$$

    and the formal action on \(f\in L^2(\mathbb R^+,r^2dr)\) is then

    $$\displaystyle \begin{aligned} {T_{\lambda}^{(\ell)}f}(r)=2\pi^2\sqrt{\nu r^2+1}f(r)+2\pi\int_{-1}^1dyP_{\ell}(y)\int_0^{+\infty}\frac{dr'f(r')}{r^2+r^{\prime2}+\mu rr'y+\lambda}. \end{aligned} $$
    (13)

    The decomposition of T λ in angular sector plays a role insofar as the odd and even angular sectors behave very differently. In particular, we will see that all the eigenfunctions sit in the angular sector ℓ = 1.

  • In order to give a rigorous meaning to the formal expression of T λ, it is important to understand its mapping properties. In [16], the following was proven

    Theorem 1

    Let λ > 0 and s ∈ (−1∕2, 3∕2). Then

    $$\displaystyle \begin{aligned} \|T_{\lambda}\xi\|{}_{H^{s-1}}\leq C\|\xi\|{}_{H^s}, \quad \forall\xi\in H^s. \end{aligned} $$
    (14)

    In particular, T λ maps continuously \(H^s(\mathbb R^3)\) into \(H^{s-1}(\mathbb R^3)\) for such s’s. The same holds true for s = {−1∕2, 3∕2} if one restricts its attention to angular sectors ℓ ≥ 1.

    Together with the obvious symmetry with respect to the standard L 2 scalar product, we obtain that T λ is a densely defined symmetric operator on \(L^2(\mathbb R^3)\) with domain H s for every s ≥ 1.

  • The dependence on m of T λ is not immediately clear. However, in [5] it is proven that for any given ξ for which the quadratic form 〈ξ, T λ ξ〉 is well defined, the map m →〈ξ, T λ ξ〉 is increasing.

Owing to (12), we restrict our attention to the ξ’s in H 1∕2 such that T λ ξ ∈ H 1∕2. For such ξ’s, the expression \(A_{\lambda ,\alpha }\xi =2W^{-1}_{\lambda }(T_{\lambda }+\alpha )\xi \) is meaningful in that W λ maps H 1∕2 into H −1∕2, and one has

$$\displaystyle \begin{aligned} \langle u_{\xi}, A_{\lambda} u_{\xi}\rangle_{H^{-1/2}_{W_{\lambda}}} =\langle \xi,(T_{\lambda}+\alpha)\xi\rangle_{H^{-1/2},H^{1/2}}. \end{aligned} $$
(15)

This quadratic form plays a major role in the study of semi-boundedness: in particular, in [9] it is shown that its positivity (depending on α and λ) lead to the bound H α ≥ 0 for α ≥ 0, and \(H_{\alpha }\geq -\frac {\alpha ^2}{4\pi ^4(1-\varLambda (m))^2}\) if α < 0. The function Λ(m) is an explicit monotone decreasing function, and m ∗ := Λ −1(1) is precisely the value for which the positivity of T λ + α cannot be achieved for any λ, α. We are now ready to state the reduction lemma from [5].

Theorem 2

Given α < 0 and \(\lambda \in \Big (\frac {\alpha ^2}{4\pi ^4}, \frac {\alpha ^2}{4\pi ^4(1-\varLambda (m))^2}\Big ]\) , the following are equivalent:

  • − λ is an eigenvalue for H α with corresponding eigenfunction g.

  • \(g=u^{\lambda }_{\xi }\) where ξ ∈ H 1∕2 is an eigenfunction for T λ with eigenvalue − α.

  • \(g=u^{\lambda }_{\xi }\) , where \(\widehat \xi (p)=\widehat {\tilde \xi }(\frac {p}{\sqrt {\lambda }})\) and \(\tilde \xi \in H^{1/2}\) is an eigenfunction for T 1 with eigenvalue \(\frac {|\alpha |}{\sqrt {\lambda }}\).

The restrictions for α and λ are consistent with the results about the essential spectrum we will present later and the lower bound on H α. Indeed, combining the two it is easy to show that the discrete spectrum may appear only in the energy window \(\Big (\frac {\alpha ^2}{4\pi ^4}, \frac {\alpha ^2}{4\pi ^4(1-\varLambda (m))^2}\Big ]\), and only in the repulsive case α < 0.

The reduction lemma is useful because it relates the discrete spectrum of H α and that of T 1. An easy application of min-max shows that the absence of discrete spectrum for H α is equivalent to the positivity of T 1 − 2π 2.

4 Essential Spectrum

We now address the problem of determine the essential spectrum of H α. We recall that is plays a major role in that the long time behavior of the evolution \(e^{itH_{\alpha }}\), and in particular the associate scattering theory, are related to the structure of the essential spectrum of H α. The picture looks different in the case α ≥ 0 and α < 0: the former correspond to a repulsive interaction, the latter to an attractive one.

Once more, we stress that H α is not a small perturbation of the free Laplacian in three dimension, therefore we do not expect to have necessary the same essential spectrum of the free Laplacian. Indeed, here is the result from [5].

Theorem 3

Let m > m ∗ . One has

  • σ ess(H α) = [0, +∞) if α ≥ 0.

  • \(\sigma _{ess}(H_{\alpha })=[-\frac {\alpha ^2}{4\pi ^4},+\infty )\) if α < 0.

For a full proof, we refer to [5], while here we only give a sketch. For the first part, one notices that the quadratic form associated to H α is positive for α positive. This implies, in particular, that σ(H α) ⊂ [0, +∞). Moreover, one can construct a singular sequence at each λ ≥ 0 by choosing a singular sequence for the free Laplacian (whose essential spectrum is [0, +∞)) that also belongs to D(H α). This is easy to do since \(H_0^2(\mathbb R^3\times \mathbb R^3)\subset D(H_{\alpha })\), and singular sequences for the free Laplacian can be chosen to have value 0 at 0.

For the second part, the situation is different. The same proof shows that σ ess(H α) ⊃ [0, +∞), while some works needs to be done in order to find a singular sequence at \(\lambda \in [-\frac {\alpha ^2}{4\pi ^4},0)\). For a given λ, the candidate is a \(g=u_{\xi _n}\) where \(\xi _n\in H^{1/2}_{\ell }(\mathbb R^3)\), and its radial part is an approximated delta at r 0. Here r 0 is defined to be the unique solution to \(2\pi ^2\sqrt {\nu r_0^2+\lambda }=\alpha \). A careful use of the mapping properties of T λ, W λ show that this is indeed a singular sequence at λ.

5 Discrete Spectrum: Finiteness and Existence of Eigenvalues

So far, we have ruled out the possibility of Thomas effect for the 2+1 system in the regime m > m ∗, owing to the semi-boundedness of the operator H α. In this section, we aim to prove the absence of Efimov effect as well in the same regime of mass. We will actually prove a stronger statement, namely the finiteness of the discrete spectrum for m > m ∗. We point out that this result is not expected to hold for masses below the threshold (cfr [28]).

The argument given in the previous section already shows that no discrete spectrum can appear in the regime α ≥ 0. Concerning the case α < 0, here is the main result from [5].

Theorem 4

Let m > m ∗ , α < 0. Then σ disc(H α) consists of finitely many eigenvalues (each of which has finite multiplicity).

While Yoshitomi in [31] proved the result for masses large enough, we pushed this up to the (expected) optimal value m ∗.

Again, we refer to [5] for a complete proof. Here, we only sketch the main idea: first of all, we have already seen how every eigenvalue − λ of H α below the bottom of the essential spectrum corresponds to an eigenvalue − α for T λ. Then, by means of a Birman-Schwinger type of argument, one can reduce the problem to that of the behavior of the off-diagonal part of T λ + α relative to the diagonal part. Concretely, one has the identity

$$\displaystyle \begin{aligned} \langle \xi,T_{\lambda}+\alpha\xi\rangle_{H^{1/2},H^{-1/2}}=\langle \xi, (1-Z_{\lambda,n})\xi\rangle_{\mathscr H^{\lambda,n}}, \end{aligned} $$

where \(\mathscr H_{\lambda ,n}\) is a suitable Hilbert space, and Z λ,n is an Hilbert-Schmidt (hence compact) operator on \(\mathscr H_{\lambda ,n}\). Using the finiteness of the spectrum of a compact operator outside a compact containing the origin, one can obtain the result.

The core of the proof we just outlined relies on the finiteness of the discrete spectrum away from 0 for a compact operator. In particular, it is not clear whether eigenvalues may exist. Equivalently, using Theorem 2, the question becomes whether the operator \(\frac {T_{1}}{2\pi ^2}-1\) may fail to be positive for same value of m.

This question (and more) are also answered in [5]: the first (trivial) observation is that this cannot happen for even angular sectors, exploiting. The second (non-trivial) observation is that the same holds for angular odd sectors with ℓ ≥ 3. Therefore, the question can be formulated for the angular sector ℓ = 1, and here the mass starts playing a role. Rather than presenting the proof, we want to give an heuristic of why the problem is non trivial, and how an eigenfunction should look like.

If ξ(p) = f(|p|)pY 1(Ω), where Ω is a variable on the sphere, Y 1 is the first harmonic function in \(\mathbb R^3\) and \(f\in L^2(\mathbb R^+, \sqrt {r^2+1})\), then the quadratic form \(\langle \xi , (\frac {T_1}{2\pi ^2}-1) \xi \rangle \) becomes (after integrating in the angular variables)

$$\displaystyle \begin{aligned} \langle \xi, (\frac{T_1}{2\pi^2}-1) \xi\rangle=\int_{0}^{+\infty}(\sqrt{\nu r^2+1}-1)|f(r)|{}^2 dr+\frac{1}{2\mu \pi}\int_{0}^{+\infty}\int_{0}^{\infty}drdr'f(r)f(r')G(z), \end{aligned} $$
(16)

where

$$\displaystyle \begin{aligned} z=\frac{r^2+r^{\prime2}+1}{\mu rr'}, \quad G(z)=2-z\ln\Big(\frac{z+1}{z-1}\Big). \end{aligned} $$

Notice that z ∈ (1 + m, +∞). The left extreme correspond to r = r′→ +∞, insofar as \(z\rightarrow \frac {2}{\mu }=1+m\), while the right extreme corresponds to r → 0. The function G(z) is easily seen to be negative, strictly increasing, approaching −∞ when z → 1− and approaching 0 as z → +∞.

In order for the quadratic form (16) to be negative, we need to trade between the mass that f puts close to 0, for which the diagonal part is positive and small but the off-diagonal part is also small, and the mass that f puts at ∞, where the diagonal term becomes huge while the off-diagonal term is significantly larger.

In particular, it is clear that m being smaller and smaller corresponds to z taking values closer and closer to the critical value z = 1, where the off-diagonal term becomes arbitrary big (in absolute value). By carefully checking this trade-off, in [5] we explicit exhibit ξ’s on which the quadratic form (16) have negative expectation (i.e., presence of eigenvalues) for small values of m > m ∗, and we proved the positivity of the quadratic form (i.e., absence of eigenvalues) when the mass is large enough.

Summarizing, in [5] we proved the existence of masses m ∗ < M ∗≤ M ∗, with the following properties:

  1. 1.

    For m ∗ < m < M ∗, there exists a bound states with energy below the bottom of the essential spectrum for the Hamiltonian H α.

  2. 2.

    For m > M ∗, no bound states appear below the bottom of the essential spectrum.

  3. 3.

    One has M ∗ = M ∗, and the analytic estimates (8.587)−1 ≤ M ∗≤ (2.617)−1.

The first two points, as well as the lower and upper bound, originate from the proof of the above results. In the next section, we will deal with the equivalence of M ∗ and M ∗ and the accuracy of our bounds.

6 Monotonicity and Number of Eigenvalues: Rigorous Results and Open Questions

Since, for fixed ξ, the quadratic form m →〈ξ, (T λ + α)ξ〉 is monotone increasing, one may expect, in the spirit of the Hellmann-Feynman-type theorems, the monotonicity of the ground state energy (and other bound states energy) itself in the mass parameter. Moreover, experiments (see, e.g., [10]) naturally lead to the same conjecture, which we eventually proved in [5].

An immediate consequence of this is the equivalence of M ∗ and M ∗, since the monotonicity of eigenvalues implies that their existence below the bottom of the essential spectrum occurs in a whole interval. Another interesting fact emerging from our analysis is that the upper bound (which originates from the variational argument) seems to be almost sharp from the point of view of the experiments (cfr [28]). It would be interesting to increase the lower bound and narrow the window for the threshold mass M ∗, which is a current work in progress.

Here is another natural question for both physicists and mathematicians. Despite its mathematical elegance and simplicity, the Birman-Schwinger-like argument used in the proof of the finiteness of the discrete spectrum is not immediately suited to draw further conclusions about the number of bound states, like for instance estimating their number, which would follow if one was able to extract an analogous estimate out from the auxiliary compact operator Z λ,n.

The monotonicity argument ensures that for m close to M ∗ only the ground state appears, but of much more interest is the region m close to m ∗: is the number of eigenvalues uniformly bounded in m, or does it explode to infinity? In the experiment (e.g., [10]), no more than two bound states are observed, regardless for the value of α. In this sense, m ∗ seems to represent a real phase transition, since the number of bound states goes from infinity to 2 crossing this value.

7 N+1/N+M Fermionic System: Known Results and Open Questions

In this section we briefly survey known results and open questions about general fermionic models of N+M fermions. These are topical models, of great physical relevance, and for which the 2+1 is a prototype, consisting of two different species of identical fermions with an inter-species zero-range two-body interaction. In particular, the N+1 model describes a polaron particle embedded in a fermionic gas of different species.Once more, because of Pauli exclusion principle, interactions can only take place among different particles.

The operator-theoretic construction of the model should follow the same lines as for the 2+1 Hamiltonian: however, to the author knowledge, no such construction within the framework of KVB theory has been done, though in [8, 11] these systems are studied via a quadratic form approach. Consequently, a complete classification of local (TMS in the two-body channels) self-adjoint extensions is lacking, as well as the presence/absence of other boundary conditions to determine a well-posed Hamiltonian.

Even putting aside the classification problem and focusing only on relevant self-adjoint realisations (e.g., the one obtained in [8, 11]), some natural questions arise:

  • Are those system stables? And for which values of the mass ratio m between the mass of the probe particle and the mass of each of the N fermions?

  • In which regimes of m do interesting spectral phenomena such as the Thomas or the Efimov effect occur?

As for the first question, it was first proved in [8] that above a threshold m = m(N) a self-adjoint Hamiltonian can be constructed by quadratic form methods which is also bounded from below, and subsequently in [26] such a threshold was ameliorated from a growing-to-infinity m(N) to a uniform-in-N one, thus ruling out the occurrence of the Thomas effect for sufficiently large mass ratios. However such bounds are still far from the values expected from theoretical-physical heuristic arguments and from experiments. For the few-body problem, sharper results are avaiable via a numerical approach [14, 15].

So far no rigorous derivation of the sharp mass threshold for stability has been established.

Regarding the Efimov effect, the picture is even more challenging. To our knowledge, no rigorous result on the presence of Efimov effect is appeared in the mathematical literature (even in the 2 + 1 system). An extremely inspiring demonstration of such an effect is proposed in the series of works [20,21,22,23], however with a mistake in the identification of the correct space of charges, as was first noticed in [16, 17], which makes the argument not immediately adjustable into the correct setting.

An amount of heuristic arguments are being made within the counterpart physical literature, and we refer to the very recent and comprehensive review [28]. In particular:

  1. 1.

    For the 3 + 1 system, there exists a mass \(m^*_3>m^*\) such that in the region \(m\in (m^*, m^*_3)\), four-body Efimov effect is expected to occur. Notice that the condition m > m ∗ comes from the very definition of four-body Efimov effect (no three-body subsystem should be linked). As in the 3-body case, eigenvalues only seems to occur in the angular sector ℓ = 1.

  2. 2.

    Various partial conjectures and numerical calculations are proposed for generic N, not supported yet by rigorous mathematics.

  3. 3.

    Almost nothing is known about higher N.

We trust to tackle these and further questions in future works!