Abstract
In these lecture notes, we provide an overview of some of the high-level research directions and open questions relating to knowledge graphs. We discuss six high-level concepts relating to knowledge graphs: data models, queries, ontologies, rules, embeddings and graph neural networks. While traditionally these concepts have been explored by different communities in the context of graphs, more recent works have begun to look at how they relate to one another, and how they can be unified. In fact, at a more foundational level, we can find some surprising relations between the different concepts. The research questions we explore mostly involve combinations of these concepts.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Knowledge graphs have been gaining more and more attention in recent years, particularly in settings that involve integrating and making sense of diverse data at large scale. Much of this attention stems from the 2012 announcement of the Google Knowledge Graph [63], which was later followed by further announcements of knowledge graphs by eBay, Facebook, IBM, Microsoft [53], and many more besides [35]. These enterprise knowledge graphs are typically internal to a company, where they aim to serve – per the words of Noy et al. [53] – as a common substrate of knowledge within the organisation, expanding and evolving over time. Other open knowledge graphs – such as BabelNet [49], DBpedia [44], Freebase [14], Wikidata [66], YAGO [33] – are made available to the public.
On a more technical level, there are varying perspectives about how knowledge graphs should be formally defined (if at all) [35]. This stems from the diversity of communities and organisations that have adopted the phrase. However, underlying all such perspectives is the foundational idea of representing knowledge using a graph abstraction, with nodes representing entities of interest in a given domain, and edges representing relations between those entities. Typically a knowledge graph will model different types of relations, which can be captured by labelled edges, with a different label used for each type of relation. Knowledge can consist of simple assertions, such as Charon orbits Pluto, which can be represented as directed labelled edges in a graph. Knowledge may also consist of quantified assertions, such as
 , which require a more expressive formalism to capture, such as an ontology or rule language.
, which require a more expressive formalism to capture, such as an ontology or rule language.
A reader familiar with related concepts may then question: what is the difference between a graph database and a knowledge graph, or an ontology and a knowledge graph? Per the previous definition, both graph databasesFootnote 1 and ontologies can be considered knowledge graphs. It is then natural to ask: what, then, is new about knowledge graphs? What distinguishes research on knowledge graphs from research on graph databases, or ontologies, etc.?
If we so wish, we can choose to see the “vagueness” surrounding knowledge graphs as a feature not a bug: this vagueness offers flexibility for different communities to adapt the concept to their interests. No single research community can “lay claim” to the topic. Knowledge graphs can then become a commons for researchers from different areas to share and exchange techniques relating to the use of graphs to represent data and knowledge. In any case, most of the different choices – what graph model to use, what graph query language to use, whether to use rules or ontologies – end up being quite superficial choices.
Anecdotally, many of the most influential papers on knowledge graphs have emerged from the machine learning community, particularly relating to two main techniques: knowledge graph embeddings [67] and graph neural networks [70] (which we will discuss later). These works are not particularly related to graph databases (they do not consider regular expressions on paths, graph pattern matching, etc.) nor are they particularly related to ontologies (they do not consider interpretations, entailments, etc.), but by exploiting knowledge in the context of large-scale graph-structured data, they are related to knowledge graphs. Subsequently, one can find relations between these ostensibly orthogonal techniques; for example, while graph neural networks are used to inductively classify nodes in the graph based on numerical methods, ontologies can be used to deductively classify nodes in the graph based on symbolic methods, which raises natural questions about how they might compare.
Knowledge graphs, if we so choose, can be seen as an opportunity for researchers to bring together traditionally disparate techniques – relating to the use of graphs to represent and exploit knowledge – from different communities of Computer Science: to share and discuss them, to compare and contrast them, to unify and hybridise them. The goal of these notes will be to introduce examples of some of the principal directions along which such research may follow.
Recently we have published a tutorial paper online that offers a much more extensive (and generally less technical, more example-based) introduction to knowledge graphs than would be possible here, to which we refer readers new to the topic [35].Footnote 2 In the interest of keeping the current notes self-contained, and in order to establish notation, we will re-introduce some of the key concepts underlying knowledge graphs. However, our focus herein is to introduce specific open questions that we think may become of interest for knowledge graphs in the coming years. Specifically, we introduce six main concepts underlying knowledge graphs: data models, queries, ontologies, rules, embeddings and graph neural networks. Most of the questions we introduce intersect these topics.
2 Data Model
Knowledge graphs assume a graph-structured data model. The high-level benefits of modelling data as graphs are as follows:
-
Graphs offer a more intuitive abstraction of certain domains than alternative data models; for example, metro maps, flight routes, social networks, protein pathways, etc., are often visualised as graphs.
-
When compared with (normalised) relational schemas, graphs offer a simpler and more flexible way to represent diverse, incomplete, evolving data, which can be defined independently of a particular schema.
-
Graphs from different sources can be initially combined by taking the union of the constituent elements (nodes, edges, etc.).
-
Unlike other semi-structured data models based on trees, graphs allow for representing and working with cyclic relations and do not assume a hierarchy.
-
Graphs offer a more intuitive representation for querying and working with paths that represent indirect relations between entities.
A number of graph data models have become popular in practice, principally directed edge-labelled graphs, and property graphs [4]. The simpler of the two models is that of directed edge-labelled graphs, or simply del graphs henceforth. To build a del graph we will assume a set of constants \(\mathbf {C} \).
Definition 1 (Directed edge-labelled graph)
A directed edge-labelled graph (or del graph) is a set of triples \(G \subseteq \mathbf {C} \times \mathbf {C} \times \mathbf {C} \).
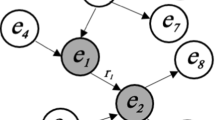
We provide an example of a del graph in Fig. 1, describing various astronomic bodies. The data are incomplete, but more data can be added incrementally by adding new nodes and edges. Each triple \((s,p,o) \in G\) denotes a directed labelled edge of the form \(s \xrightarrow {p} o\). Nodes in the graph denote entities of interest, and edges between them denote (binary) relations. We see both directed and undirected cycles formed from the relationships present between the entities.
The property graph model is more ornate, and allows for adding labels and property–value pairs on both nodes and edges [4].
Definition 2 (Property graph)
A property graph G is a tuple

where \(V \subseteq \mathbf {C} \) is a set of node ids, \(E \subseteq \mathbf {C} \) is a set of edge ids, \(L \subseteq \mathbf {C} \) is a set of labels, \(P \subseteq \mathbf {C} \) is a set of properties, \(U \subseteq \mathbf {C} \) is a set of values, \(e : E \rightarrow V \times V\) maps an edge id to a pair of node ids, \(l : V \cup E \rightarrow 2^L\) maps a node or edge id to a set of labels, and \(p : V \cup E \rightarrow 2^{P \times U}\) maps a node or edge id to a set of property–value pairs.
In Fig. 2 we provide an example of a property graph alongside a del graph representing analogous information. The graph is defined as follows:

While del graphs form the basis of the RDF data model [18], property graphs are used in a variety of popular graphs databases systems, such as Neo4j [48]. Comparing del graphs and property graphs, we can say that del graphs are simpler, but property graphs are more flexible, particularly in terms of the ability to add property–value pairs to edges. However, property graphs can be represented as del graphs (and vice versa) as illustrated in Fig. 2, where edges with property–value pairs in the property graph can be converted to nodes in the del graph, as seen for Pb orbit; edges without property–value pairs in the property graph can be represented directly as edges in the del graph.
We identify two particular topics relating to modelling data as graphs.


Henceforth we will focus on del graphs, as the simpler of the two models.
3 Queries
We may wish to pose questions over the data represented by the graph. While a range of query languages have been proposed for querying graphs – including SPARQL for RDF graphs [29]; Cypher [23], Gremlin [56], and G-CORE [3] for property graphs – the same foundational elements underlie all such languages: graph patterns, relational algebra, and path expressions [4]. Herein we will assume data represented as a del graph, though the concepts we present generalise quite straightforwardly to other graph models, as appropriate [35].
At the core of graph queries is the notion of graph patterns. The most basic form of graph pattern is a graph that additionally allows variables to replace constants in any position. We refer to the set of variables as \(\mathbf {V} \). We refer to the union of constants \(\mathbf {C} \) and variables \(\mathbf {V} \) as terms, denoted \(\mathbf {T} \) (i.e., \(\mathbf {T} = \mathbf {C} \cup \mathbf {V} \)).
Definition 3 (Directed edge-labelled graph pattern)
A directed edge-labelled graph pattern (or del graph pattern) is a set of triples \(Q \subseteq \mathbf {T} \times \mathbf {T} \times \mathbf {T} \).
We provide an example in Fig. 3 of a del graph pattern looking for trinary star systems related (in some way) to Sol. Variables are prefixed with “?”. A graph pattern is then evaluated over a data graph by mapping the variables of the graph pattern to constants such that the image of the graph pattern under the mapping is a sub-graph of the data graph. More formally, let \(\mu : \mathbf {V} \rightarrow \mathbf {C} \) denote a partial mapping from variables to constants, and let \(\mathrm {dom} (\mu )\) denote the set of variables for which \(\mu \) is defined. Further let \(\mathbf {V} (Q)\) denote the set of variables used in Q. We can then define the evaluation of Q over G as:
Definition 4 (Evaluation of a del graph pattern)
Let Q be a del graph pattern and let G be a del graph. We then define the evaluation of graph pattern Q over G, as  .
.
Graph patterns of this form can be seen as transforming graphs into tables. In Table 1 we present the results of evaluating the del graph pattern of Fig. 3 over the del graph of Fig. 1, where each row indicates a solution given by a mapping \(\mu \) per the previous definition. Graph patterns can be evaluated under different semantics by placing further restrictions on \(\mu \). Without further restrictions, a homomorphism-based semantics is considered where two or more variables in an individual solution can be mapped to a single constant in the data. On the other hand, if we restrict \(\mu \) to be one-to-one, a (sub-graph) isomorphism-based semantics is considered, where each variable in an individual solution must map to a different constant. All of the solutions shown in Table 1 are returned under the unrestricted homomorphism-based semantics, while only the first solution is returned under the restricted isomorphism-based semantics.
Given that graph patterns return tables, a natural idea is to introduce the relational algebra to allow the solutions of a graph pattern to be transformed, and the solutions of several graph patterns to be combined: using \(\pi \) to project variables or \(\sigma \) to select rows returned from a single graph pattern, or using \(\cup \), −, or \(\bowtie \) to apply a union, difference, or join (respectively) across the results of two graph patterns. We can also introduce further syntactic operators, such as left-joins ( , aka optionals), anti-joins (
, aka optionals), anti-joins ( ; aka not exists), etc. As a simple example, given the graph pattern Q of Fig. 3, we may define \(\pi _{\textsf {?tstar}}(\sigma _{\textsf {?bstar1} \ne \textsf {?bstar2}}(Q))\) to select only solutions where ?bstar1 and ?bstar2 map to different constants, and subsequently project only the results for the ?tstar variable. Graph patterns extended with the relational algebra are called complex graph patterns [3]. Graph patterns extended with projection alone are called conjunctive queries.
; aka not exists), etc. As a simple example, given the graph pattern Q of Fig. 3, we may define \(\pi _{\textsf {?tstar}}(\sigma _{\textsf {?bstar1} \ne \textsf {?bstar2}}(Q))\) to select only solutions where ?bstar1 and ?bstar2 map to different constants, and subsequently project only the results for the ?tstar variable. Graph patterns extended with the relational algebra are called complex graph patterns [3]. Graph patterns extended with projection alone are called conjunctive queries.
The features we have seen thus far can only match bounded sub-graphs of the data graph (more formally, we can say that they are Gaifman-local [45]). However, we may be interested to find pairs of nodes that are connected by paths of arbitrary lengths. In order to express such queries, we can introduce path expressions and regular path queries.Footnote 3
Definition 5 (Path expression)
A constant \(c \in \mathbf {C} \) is a path expression. Furthermore:
-
If r is a path expression, then \(r^-\) (inverse) and \(r^*\) (Kleene star) are path expressions.
-
If \(r_1\) and \(r_2\) are path expressions, then \(r_1 \cdot r_2\) (concatenation) and \(r_1 \mid r_2\) (disjunction) are path expressions.
In the following we assume that the evaluation of a path expression returns pairs of nodes connected by some path that satisfies the path expression [29]. Other query languages may support returning paths [3, 23]. We will further introduce the notation \(N_G\) to denote the nodes of G; more formally, we define the nodes of G as  .
.
Definition 6 (Path expression evaluation)
Given a del graph G and a path expression r, we define the evaluation of r over G, denoted r[G], as follows:

where by \(r^n\) we denote the nth-concatenation of r (e.g., \(r^3 = r \cdot r \cdot r\)).
Let \(\mathbf {R} \) denote the set of all path expressions. We next define a regular path query and a navigational graph pattern [4].
Definition 7 (Regular path query)
A regular path query is a triple \((x,r,y) \in \mathbf {T} \times (\mathbf {R} \cup \mathbf {V}) \times \mathbf {T} \).
Definition 8 (Navigational graph pattern)
A navigational graph pattern Q is a set of regular path queries.
We provide an example of a navigational graph pattern in Fig. 4, searching for planemos in the Milky Way, along with the star(s) they orbit. The evaluation of a navigational graph pattern is then defined analogously to the evaluation of graph patterns, but where pairs of nodes connected by arbitrary-length paths – rather than simply edges – can now be matched. The navigational graph pattern of Fig. 4 will return four results, with ?star mapped to Sun in each, and ?planemo mapped to Earth, Pluto, Charon and Luna.
Finally, noting that navigational graph patterns again transform graphs into tables, it is natural to define complex navigational graph patterns, which support applying relational algebra over the results of one or more navigational graph patterns. Navigational graph patterns extended with (only) projection are known as conjunctive two-way regular path queries (C2RPQs) [9].
The task of finding solutions for a query over a graph is known as query answering. While query answering have been well-studied in the literature [4, 9], there are a number of interesting problems that arise when considering the evaluation of (complex) navigational graph patterns. We now discuss two topics.


4 Ontologies
Looking more closely at the graph of Fig. 1, we may be able to deduce additional knowledge beyond what is explicitly stated in the graph. For example, we might conclude that Charon and Luna are instances of Moon; that Toliman and Rigil Kentaurus are instances of Binary Stars; that Luna, Earth, Sun, etc., are all part of the Milky Way, etc. In order to be able to draw such conclusions automatically from a graph, we require a formal representation of the semantics of the terms used in the graph. While there are a number of alternatives that we might consider for this task, we initially focus on ontologies, which have long been studied in the context of defining semantics over graphs.
Ontologies centre around three main types of elements: individuals, concepts (aka classes) and roles (aka properties). They allow for making formal, well-defined claims about such elements, which in turn opens up the possibility to perform automated reasoning. In terms of the semantics of ontologies, there are many well-defined syntaxes we can potentially use, but perhaps the most established formalism is taken from Description Logics (DL) [8, 41, 57], which studies logics centring around (unary and) binary relations, and logical primitives for which reasoning tasks remain decidable.
Table 2 defines the typical DL constructs one can find in the literature. The syntax column denotes how the construct is expressed in DL. A DL ontology then consists of an assertional box (A-Box), a T-Box (terminological box), and an R-Box (role box), each of which consists of a set of axioms that describe formal claims about individuals, concepts and properties, respectively.
Definition 9 (DL ontology)
A DL ontology \(\mathsf {O}\) is defined as a tuple \((\mathsf {A},\mathsf {T},\mathsf {R})\), where \(\mathsf {A}\) is the A-Box: a set of assertional axioms; \(\mathsf {T}\) is the T-Box: a set of concept (aka class/terminological) axioms; and \(\mathsf {R}\) is the R-Box: a set of role (aka property/relation) axioms.
Syntactically, DL ontologies can be serialised as (del) graphs. Such a serialisation is defined by the Web Ontology Language (OWL) [31], which draws inspiration from the DL area towards standardising languages for which common reasoning tasks are decidable (or even tractable), and which defines serialisations of OWL ontologies as RDF graphs. In this context, looking at Fig. 1, for example, a triple such as  can be read as a concept axiom \(\texttt {Planet} \sqsubseteq \texttt {Planemo}\), a triple such as
can be read as a concept axiom \(\texttt {Planet} \sqsubseteq \texttt {Planemo}\), a triple such as  can be read as a role axiom \(\texttt {child}(\texttt {Pluto},\texttt {Charon})\), while a triple such as
can be read as a role axiom \(\texttt {child}(\texttt {Pluto},\texttt {Charon})\), while a triple such as
 can be read as a concept assertion \(\texttt {Planemo}(\texttt {Charon})\).
can be read as a concept assertion \(\texttt {Planemo}(\texttt {Charon})\).
Regarding the formal meaning of these axioms, the semantics column of Table 2 defines axioms using interpretations.
Definition 10 (DL interpretation)
A DL interpretation I is defined as a pair \((\varDelta ^I,\cdot ^I)\), where \(\varDelta ^I\) is the interpretation domain, and \(\cdot ^I\) is the interpretation function. The interpretation domain is a set of individuals. The interpretation function accepts a definition of either an individual a, a concept C, or a role R, mapping them, respectively, to an element of the domain (\(a^I \in \varDelta ^I\)), a subset of the domain (\(C^I \subseteq \varDelta ^I\)), or a set of pairs from the domain (\(R^I \subseteq \varDelta ^I\times \varDelta ^I\)).
An interpretation I satisfies an ontology \(\mathsf {O}\) if and only if, for all axioms in \(\mathsf {O}\), the corresponding semantic conditions in Table 2 hold for I. In this case, we call I a model of \(\mathsf {O}\). This notion of a model gives rise to the key notion of entailment.
Definition 11
Given two DL ontologies \(\mathsf {O}_1\) and \(\mathsf {O}_2\), we define that \(\mathsf {O}_1\) entails \(\mathsf {O}_2\), denoted \(\mathsf {O}_1 \models \mathsf {O}_2\), if and only if every model of \(\mathsf {O}_1\) is a model of \(\mathsf {O}_2\).
As an example of a DL ontology, for
 , let:
, let:
-
 ;
; -
 ;
; -
 .
.
For \(I = (\varDelta ^I,\cdot ^I)\), let:
-
 ;
; -
 ,
,  ,
,  ,
,  ;
; -
 ,
,  ;
; -
 ,
,  .
.
The interpretation I is not a model of \(\mathsf {O}\) since it does not have that  is an instance of Moon, nor that
is an instance of Moon, nor that  orbits
orbits  , nor that
, nor that  orbits
orbits  . However, if we extend the interpretation I with the following:
. However, if we extend the interpretation I with the following:
-
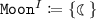 ;
; -
 .
.
then the interpretation of I will satisfy – i.e., will be a model of – the ontology \(\mathsf {O}\). Notably even though the ontology \(\mathsf {O}\) does not entail that \(\texttt {Planemo(Pluto)}\), it is still the case that I satisfies \(\mathsf {O}\); this is often referred to as the Open World Assumption, where ontologies are not assumed to completely describe the world, but rather to be incomplete. Now given the ontology:

we may – with a bit of thought – convince ourselves of the fact that any model I of \(\mathsf {O}\) must also be a model of \(\mathsf {O}'\), and hence that \(\mathsf {O} \models \mathsf {O}'\).
Unfortunately, deciding entailment for DL ontologies using all of the axioms of Table 2 in an unrestricted manner is undecidable. Hence, different DLs then apply different restrictions to the use of these axioms in order to achieve particular guarantees with respect to the complexity of deciding entailment. Most DLs are founded on one of the following base DLs (we use indentation to denote that the child DL extends the parent DL):
-
\(\mathcal {ALC}\) (\(\mathcal {A}\)ttributive \(\mathcal {L}\)anguage with \(\mathcal {C}\)omplement [60]), supports atomic concepts, the top and bottom concepts, concept intersection, concept union, concept negation, universal restrictions and existential restrictions. Role and concept assertions are also supported.
-
\(\mathcal {S}\) extends \(\mathcal {ALC}\) with transitive closure.
-
These base languages can be extended as follows:
-
\(\mathcal {H}\) adds role inclusion.
-
\(\mathcal {R}\) adds (limited) complex role inclusion, as well as role reflexivity, role irreflexivity, role disjointness and the universal role.
-
-
\(\mathcal {O}\) adds nomimals.
-
\(\mathcal {I}\) adds inverse roles.
-
\(\mathcal {F}\) adds (limited) functional properties.
-
\(\mathcal {N}\) adds (limited) number restrictions.
-
\(\mathcal {Q}\) adds (limited) qualified number restrictions (subsuming \(\mathcal {N}\) given \(\top \)).
-
-
We use “(limited)” to indicate that such features are often only allowed under certain restrictions to ensure decidability; for example, complex roles (chains) typically cannot be combined with cardinality restrictions. DLs are then typically named per the following scheme, where [a|b] denotes an alternative between a and b and [c][d] denotes a concatenation cd:
Examples include \(\mathcal {ALCO}\), \(\mathcal {ALCHI}\), \(\mathcal {SHIF}\), \(\mathcal {SROIQ}\), etc. These languages often apply additional restrictions on concept and role axioms to ensure decidability, which we do not discuss here. For further details on Description Logics, we refer to the recent book by Baader et al. [8].
We now discuss a research topic relating to the combination of ontology entailment and graph querying.

5 Rules
Another way to define the semantics of knowledge graphs is to use rules. Rules can be formalised in many ways – as Horn clauses, as Datalog, etc. – but in essence they consist of if-then statements, where if some condition holds, then some entailment holds. Here we define rules based on graph patterns.
Definition 12 (Rule)
A rule is a pair  such that B and H are graph patterns. The graph pattern B is called the body of the rule while H is called the head of the rule.
such that B and H are graph patterns. The graph pattern B is called the body of the rule while H is called the head of the rule.
Given a graph G and a rule \(R = (B,H)\), we can then apply R over G by taking the union of \(\mu (H)\) for all \(\mu \in B(G)\). Typically we will assume that the set of variables used in H will be a subset of those used in B (\(\mathbf {V} (H) \subseteq \mathbf {V} (B)\)), which assures us that \(\mu (H)\) will always result in a graph without variables. Given a set of rules, we can then apply each rule recursively, accumulating the results in the graph until a fixpoint is reached, thus enriching our graph with entailments.
There is a large intersection between the types of semantics we can define with rules and with DL-based ontologies [40]. For example, we can capture the role-inclusion axiom \(\textsf {parent} \sqsubseteq \textsf {orbits}\) as a rule (written \(B \rightarrow H\)):
or we can capture the concept inclusion \(\texttt {Planet} \sqsubseteq \forall \texttt {child}.\texttt {Moon}\) as:
However, we cannot capture axioms such as \(\texttt {BinaryStar} \sqsubseteq \exists \texttt {orbits}.\texttt {BinaryStar}\) with the types of rules we have seen. Such an axiom would need a rule like:
where the head introduces a fresh existential variable y for each binary star, which itself is a binary star. (Note that if left unrestricted, such a rule, applied recursively on a single instance of a binary star, might end up creating an infinite chain of existential binary stars, each orbiting their existential successor!)
Additionally, rules as we have previously defined cannot capture axioms of the form \(\texttt {Planemo} \sqsubseteq \texttt {Moon} \sqcup \texttt {Planet} \sqcup \texttt {DwarfPlanet}\) either. For this we would need a rule along the lines of the following:
Here we introduce the disjunctive connective “\(\vee \)” to state that when the body is matched, then at least one of the heads holds true.
Rules extended with existentials and disjunction have, however, been explored as extensions of Datalog. Datalog\(^\pm \) variants support existential rules (aka tuple generating dependencies (tgds)) that allow for generating existentials in the head of the rule, per the BinaryStar example, but typically in a restricted way to ensure termination. On the other hand, Disjunctive Datalog allows for using disjunction in the head of rules, as seen in the Planemo example. These extensions allow rules to capture semantics similar to more expressive DLs [26, 27, 58].
On the other hand, rules can express entailments not typically supported in DLs, where a simple example of such a rule is:
This type of entailment would require role intersection, which is not typically supported by DLs. More generally, cyclical graph patterns that entail role assertions are typically not supported in DLs, though easily captured by rules.Footnote 4
Efficient reasoning systems have then been developed to support such rules over knowledge graphs, including most recently, Vadalog [11] and VLog [17].

6 Context
All of the data represented in Fig. 1 holds true with respect to a given context: a given scope of truth. As an example of temporal context, the Sun will cease being a G-type Star and will eventually become a White Dwarf in its later years. We may also have spatial context (e.g., to state that something holds true in a particular region of space, such as a solar eclipse affecting parts of Earth), provenance (e.g., to state that something holds true with respect to a given source, such as the mass of a given planet), and so forth.
There are a variety of syntactic ways to embed contextual meta-data in a knowledge graph. Within del graphs, for example, the options include reification [18], n-ary relations [18], and singleton properties [52]. Context can also be represented syntactically using higher-arity models, such as property graphs [4], RDF* [30], or named graphs [18]. For further details on these options for representing context in graphs, we refer to the extended tutorial [35].
Aside from syntactic conventions for representing context in graphs, an important issue is with respect to how the semantics of context should be defined. A general contextual framework for graphs based on annotations has been proposed by Zimmermann et al. [75], based on the notion of an annotation domain.
Definition 13 (Annotation domain)
Let A be a set of annotation values. An annotation domain is defined as an idempotent, commutative semi-ring \(D = \langle A,\oplus ,\otimes ,\mathbf {0},\mathbf {1} \rangle \).
For example, we may define A to be powerset of numbers from \(\{1,\ldots ,365\}\) indicating different days of the year. We may then annotate triples such as  with a set of days in a given year – say \(\{13,245,301\}\) on which the given occultation will occur. Given another similar such triple – say
with a set of days in a given year – say \(\{13,245,301\}\) on which the given occultation will occur. Given another similar such triple – say  annotated with \(\{46,245,323\}\) – we can define \(\oplus \) to be \(\cup \) and use it to find the annotation for days when Luna occults the Sun or Jupiter (\(\{13,46,245,301,323\}\)); we can further define \(\otimes \) to be \(\cap \) and use it to find the annotation for days when Luna occults the Sun and Jupiter (\(\{245\}\)). In this scenario, \(\mathbf {0}\) would then refer to the empty set, while \(\mathbf {1}\) would refer to the set of all days of the year. Custom annotation domains can be defined for custom forms of context, and can be used in the context of querying and rules for computing the annotations corresponding to particular results and entailments.
annotated with \(\{46,245,323\}\) – we can define \(\oplus \) to be \(\cup \) and use it to find the annotation for days when Luna occults the Sun or Jupiter (\(\{13,46,245,301,323\}\)); we can further define \(\otimes \) to be \(\cap \) and use it to find the annotation for days when Luna occults the Sun and Jupiter (\(\{245\}\)). In this scenario, \(\mathbf {0}\) would then refer to the empty set, while \(\mathbf {1}\) would refer to the set of all days of the year. Custom annotation domains can be defined for custom forms of context, and can be used in the context of querying and rules for computing the annotations corresponding to particular results and entailments.
In the context of ontologies, a more declarative framework for handling context – called contextual knowledge repositories – was proposed by Homola and Serafini [37] based on Description Logics, with a related framework more recently proposed by Schuetz et al. [61] based on an OLAP-style abstraction. These frameworks can assign graphs into different hierarchical contexts, which can then be aggregated into higher-level contexts.
Still, there are a number of questions that remain open regarding context.

7 Embeddings
Machine learning has been gaining more and more attention in recent years, particularly due to impressive advances in sub-areas such as Deep Learning, where multi-layer architectures such as Convolutional Neural Networks (CNNs) have led to major strides in tasks involving multi-dimensional inputs (such as image classification), while architectures such as Recurrent Neural Networks (RNNs) have likewise lead to major strides in tasks involving sequential data (such as natural language translation). An obvious question then is: what kinds of learning architectures could be applied to graphs? The answer, unfortunately, is not so obvious. While machine learning architectures typically assume numeric inputs in the form of tensors (multi-dimensional arrays), graphs – unlike, say, images – are not naturally conceptualised in such terms.
A first attempt to encode a graph numerically would be a “one-hot encoding”. Recalling the notation of \(N_G\) for the nodes of a del graph, we introduce a similar notation \(E_G\) to denote the edge-labels (i.e., predicates or properties) of a del graph; formally,  . We could consider creating a 3-mode tensor of size \(|N_G| \cdot |E_G| \cdot |N_G|\), where the element at (i, j, k) is 1 if \((n_i,e_j,n_k) \in G\), or 0 otherwise; here \(n_i\) and \(n_k\) denote the ith and kth nodes in an indexing of \(N_G\), while \(e_j\) indicates the jth edge label in an indexing of \(E_G\). Though we now have a tensor representing the graph, for most graphs in practice, the tensor would be very sparse, with few 1’s relative to 0’s. As a result, using the tensor for the purposes of machine learning would be impractical.
. We could consider creating a 3-mode tensor of size \(|N_G| \cdot |E_G| \cdot |N_G|\), where the element at (i, j, k) is 1 if \((n_i,e_j,n_k) \in G\), or 0 otherwise; here \(n_i\) and \(n_k\) denote the ith and kth nodes in an indexing of \(N_G\), while \(e_j\) indicates the jth edge label in an indexing of \(E_G\). Though we now have a tensor representing the graph, for most graphs in practice, the tensor would be very sparse, with few 1’s relative to 0’s. As a result, using the tensor for the purposes of machine learning would be impractical.
In order to create more practical numeric representations of graphs for machine learning applications, knowledge graph embeddings aim to embed graphs within a low-dimensional, dense, numerical representation. There are many ways in which embeddings may be defined, but typically an embedding will map each node and each edge-label of a graph to an independent vector or matrix. For simplicity, we will assume embeddings that associate nodes and edge-labels to real-valued vectors of fixed dimension d, which we denote by the set \(\mathbb {R}^d\).Footnote 5
Definition 14 (Knowledge graph embedding)
Given a del graph G, a knowledge graph embedding of G is a pair of mappings \((\varepsilon ,\rho )\) such that \(\varepsilon : N_G \rightarrow \mathbb {R}^d\) and \(\rho : E_G \rightarrow \mathbb {R}^d\).
Typically \(\varepsilon \) is known as an entity embedding, while \(\rho \) is known as a relation embedding. The knowledge graph embedding then consists of (typically low-dimensional) numeric representations of the node and edge-labels of the graph G, typically extracted such that the graph G can be (approximately) reconstructed from the embedding. Towards this goal, the graph can be conceptualised as a function \(\gamma : \mathbf {C} \times \mathbf {C} \times \mathbf {C} \rightarrow \mathbb {R}_{[0,1]}\), where \(\gamma (s,p,o) = 1\) if \((s,p,o) \in G\) or \(\gamma (s,p,o) = 0\) if \((s,p,o) \not \in G\). Instead of accepting the constants s, p, o, however, we could rather consider accepting the embeddings of those concepts: \(\varepsilon (s)\), \(\rho (p)\), \(\varepsilon (o)\). This gives rise to the notion of a plausibility scoring function.
Definition 15 (Plausibility)
A plausibility scoring function is a partial function \(\phi : \mathbb {R}^d \times \mathbb {R}^d \times \mathbb {R}^d \rightarrow \mathbb {R}_{[0,1]}\). Given a del graph \(G = (V,E,L)\), a triple \((s,p,o) \in N_G \times E_G \times N_G\), and a knowledge graph embedding \((\varepsilon ,\rho )\) of G, the plausibility of (s, p, o) is given as \(\phi (\varepsilon (s),\rho (p),\varepsilon (o))\).
Triples with scores closer to 1 are considered more plausible, while triples with scores closer to 0 are considered less plausible. We can now learn embeddings that yield a score close to 1 for triples in (s, p, o), and a score close to 0 for a sample of negative triples not in G. Given that G is assumed to be incomplete, we cannot be certain that triples not in G are false. A common heuristic to generate negative examples is to apply the Partial Completeness Assumption (PCA), taking a triple (s, p, o) from G and replacing a term (often o) with another term appearing in G such that the resulting triple does not appear in G. In practice, the dimensions of the embeddings are fixed to a low number such that rather than “remembering” G, the knowledge graph embedding is forced to generalise patterns in how G is connected. Different knowledge graph embeddings instantiate the types of embedding considered and the plausibility scoring function in different ways [67]. We refer to the extended tutorial for details [35].

Once trained over G, knowledge graph embeddings directly allow for estimating the plausibility for triples of the form \((s,p,o) \in N_G \times E_G \times N_G\) (i.e., triples using some combination of terms found in G). This can be used for the purposes of link prediction, whereby considering the graph G of Fig. 1 and given a partial triple such as  , the embedding of G can be used to predict likely completions of the triples, such as Rigil Kentaurus (already in the graph), or perhaps Proxima Centauri, or even Toliman itself. The embeddings themselves can also be useful independently of the plausibility scoring function as numerical representations of the elements of the graph, where, for example, similar numerical values will typically be assigned to similar nodes and edge-labels based on how they are connected in the graph.
, the embedding of G can be used to predict likely completions of the triples, such as Rigil Kentaurus (already in the graph), or perhaps Proxima Centauri, or even Toliman itself. The embeddings themselves can also be useful independently of the plausibility scoring function as numerical representations of the elements of the graph, where, for example, similar numerical values will typically be assigned to similar nodes and edge-labels based on how they are connected in the graph.
In terms of open questions, a natural topic to explore is the combination of knowledge graph embeddings with ontologies and notions of entailment.
8 Graph Neural Networks
Rather than encoding the structure of graphs numerically, an alternative to enable learning over graphs is to design machine learning architectures that operate directly over the structure of a graph. A natural starting point is to consider neural networks, which already form graphs where nodes are (artificial) neurons, and edges are (artificial) axons that pass signals between neurons. Unlike graphs used to represent data, however, traditional neural networks tend to have a much more regular structure, being organised into layers, where all the nodes of one layer are connected pairwise to all the nodes of the next layer.
To enable learning over graphs of data, an alternative approach is to define the structure of the neural network in terms of the structure of the graph. In this case, the nodes of the graph are interpreted as neurons, while edges are interpreted as axons. Thus nodes can pass signals to each other through edges towards solving a given task. In a supervised setting, we may label a subset of nodes in the graph and then learn functions that aggregate information from the neighbourhood of each node, computing a new state for the node; this may continue recursively until a fixpoint, or for a fixed number of steps. Typically nodes and edges in the input graph will be associated with numerical feature vectors that encode pertinent information for the supervised task. Such a learning architecture is known as a graph neural network (GNN) [59].
As an example, assuming a large del graph similar to that shown in Fig. 2, we may label a subset of planets that are known to be in a habitable zone that could support life. We could then associate nodes with vectors that numerically encode their type, their mass, their density, their composition etc.; we may then further associate edges with vectors indicating the type of relation, the astronomic distance between bodies, etc. Based on labelled examples, a graph neural network can then learn aggregation functions that take the information surrounding the neighbourhood of each node – for example, numerical data about the moon(s) of a particular planet, the star(s) of planet, the distances involved, etc. – and generate the expected output; the same functions can then be applied to unlabelled nodes to generate predicted classifications.
We first define a vector-labelled del graph, which serves as input to a GNN:
Definition 16 (Vector-labelled graph)
A vector-labelled del graph \(G_\lambda \) is a pair  where G is a del graph, and \(\lambda : N_G \cup G \rightarrow \mathbb {R}^a\) is a vector labelling function.
where G is a del graph, and \(\lambda : N_G \cup G \rightarrow \mathbb {R}^a\) is a vector labelling function.
For simplicity, we will assume that nodes and triples are labelled with vectors of the same dimension (a). Thereafter, there are two principle architectures for GNNs: recursive and non-recursive graph neural networks. Here we focus on non-recursive graph neural networks, where details of the recursive architecture can rather be found in the extended tutorial [35]. Note that in the following definition, we use \(S \rightarrow \mathbb {N}\) to denote bags (aka multisets) formed from the set S.
Definition 17 (Non-recursive graph neural network)
A non-recursive graph neural network (NRecGNN) \(\mathfrak {N}\) with l layers is an l-tuple of functions  , where \(\textsc {Agg}^{(k)}: \mathbb {R}^{a} \times 2^{(\mathbb {R}^{a} \times \mathbb {R}^a) \rightarrow \mathbb {N}} \rightarrow \mathbb {R}^{a}\) for \(1 \le k \le l\).
, where \(\textsc {Agg}^{(k)}: \mathbb {R}^{a} \times 2^{(\mathbb {R}^{a} \times \mathbb {R}^a) \rightarrow \mathbb {N}} \rightarrow \mathbb {R}^{a}\) for \(1 \le k \le l\).
Each aggregation function \(\textsc {Agg}^{(k)}\) computes a new feature vector for a node, given its previous feature vector and the feature vectors of the nodes and edges forming its neighbourhood. We assume for simplicity that the dimensions of the vectors remain the same throughout, though this is not necessary in practice.Footnote 6 Given an NRecGNN \(\mathfrak {N} = ( \mathrm {\textsc {Agg}}^{(1)},\ldots ,\mathrm {\textsc {Agg}}^{(l)} )\), a vector-labelled graph \(G_\lambda \), and a node \(u \in N_G\), we define the output vector assigned to node u in \(G_\lambda \) by \(\mathfrak {N}\) (written \(\mathfrak {N}(G_\lambda ,u)\)) as follows. First let  . For all \(i \ge 1\), let:
. For all \(i \ge 1\), let:

Then  .
.
In an l-layer NRecGNN, a different aggregation function is applied at each step (i.e., in each layer), up to a fixed number of steps l. These aggregation functions are typically parametrised and learnt based on labelled training data. When the aggregation functions are based on a convolutional operator, the result is a convolutional graph neural network (ConvGNN).
Though initially it may seem as if GNNs and ontologies are orthogonal concepts for graphs, there are some correspondences between both.

9 Conclusions
The growing popularity of knowledge graphs presents an opportunity for research that combines various technical perspectives on how graphs can be used to represent and exploit knowledge at large scale. Within the intersection of these varying perspectives lies interesting research questions in terms of how concepts from graph databases and knowledge representation can be fruitfully combined, how techniques from machine learning relate to logical languages, and so forth.
Here we have mentioned a number of key concepts relating to knowledge graphs – specifically data models, querying, ontologies, rules, embeddings and graph neural networks – as well as a number of research topics that arise from their combination. We have only scratched the surface. Knowledge graphs encompass an even wider range of topics, where we have not touched upon concepts such as shapes and validation, graph algorithm and analytics, privacy and anonymisation, data quality, knowledge graph creation and completion, knowledge graph refinement, etc. Likewise there are many interesting research questions that arise when considering combinations of these concepts. For discussion on these and other topics we refer to the extended tutorial [35].
Notes
- 1.
- 2.
An abridged version of [35] is currently under review for ACM CSUR.
- 3.
We implicitly refer to two-way regular path queries as inverse expressions are quite widely used in practice [15].
- 4.
Cyclical graph patterns that entail concept assertions can be captured, in a slightly roundabout way, in DLs with Self Restrictions and Complex Role Inclusions.
- 5.
In practice, knowledge graph embeddings can take complex-valued vectors, or real-valued matrices, or have entity and relation embeddings of different dimensions [67], and so forth, but such details are not exigent for our purposes.
- 6.
We can still define a to be the largest dimension needed, padding other vectors.
References
Aberger, C.R., Lamb, A., Tu, S., Nötzli, A., Olukotun, K., Ré, C.: Emptyheaded: a relational engine for graph processing. ACM Trans. Database Syst. (TODS) 42(4), 20 (2017)
Angles, R.: The property graph database model. In: Olteanu, D., Poblete, B. (eds.) Proceedings of the 12th Alberto Mendelzon International Workshop on Foundations of Data Management, Cali, Colombia, 21–25 May 2018, CEUR Workshop Proceedings, vol. 2100. Sun SITE Central Europe (CEUR) (2018), http://ceur-ws.org/Vol-2100/paper26.pdf
Angles, R., et al.: G-CORE: a core for future graph query languages. In: [19], pp. 1421–1432
Angles, R., Arenas, M., Barceló, P., Hogan, A., Reutter, J.L., Vrgoc, D.: Foundations of modern query languages for graph databases. ACM Comput. Surv. 50(5), 68:1–68:40 (2017)
Arenas, M., Conca, S., Pérez, J.: Counting beyond a Yottabyte, or how SPARQL 1.1 property paths will prevent adoption of the standard. In: Mille, A., Gandon, F.L., Misselis, J., Rabinovich, M., Staab, S. (eds.) Proceedings of the 21st World Wide Web Conference 2012, WWW 2012, Lyon, France, 16–20 April 2012, pp. 629–638. ACM Press, April 2012
Artale, A., Calvanese, D., Kontchakov, R., Zakharyaschev, M.: The DL-lite family and relations. J. Artif. Intell. Res. 36, 1–69 (2009)
Atserias, A., Grohe, M., Marx, D.: Size bounds and query plans for relational joins. SIAM J. Comput. 42(4), 1737–1767 (2013). https://doi.org/10.1137/110859440
Baader, F., Horrocks, I., Lutz, C., Sattler, U.: An Introduction to Description Logic. Cambridge University Press, Cambridge (2017)
Barceló, P.: Querying graph databases. In: Hull, R., Fan, W. (eds.) Proceedings of the 32nd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, PODS 2013, New York, NY, USA, 22–27 June 2013, pp. 175–188. ACM Press, June 2013. https://doi.org/10.1145/2463664.2465216
Barceló, P., Kostylev, E.V., Monet, M., Peréz, J., Reutter, J., Silva, J.P.: The Logical Expressiveness of Graph Neural Networks. In: 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. OpenReview.net, April 2020. https://openreview.net/forum?id=r1lZ7AEKvB
Bellomarini, L., Sallinger, E., Gottlob, G.: The vadalog system: datalog-based reasoning for knowledge graphs. Proc. VLDB Endowment 11(9), 975–987 (2018)
Bienvenu, M., Ortiz, M., Simkus, M.: Regular path queries in lightweight description logics: complexity and algorithms. J. Artif. Intell. Res. 53, 315–374 (2015)
Bischof, S., Krötzsch, M., Polleres, A., Rudolph, S.: Schema-agnostic query rewriting in SPARQL 1.1. In: Mika, P., et al. (eds.) ISWC 2014. LNCS, vol. 8796, pp. 584–600. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11964-9_37
Bollacker, K., Tufts, P., Pierce, T., Cook, R.: A platform for scalable, collaborative, structured information integration. In: Nambiar, U., Nie, Z. (eds.) International Workshop on Information Integration on the Web (IIWeb 2007) (2007)
Bonifati, A., Martens, W., Timm, T.: An analytical study of large SPARQL query logs. Proc. VLDB Endowment 11(2), 149–161 (2017)
Capadisli, S., Auer, S., Ngomo, A.N.: Linked SDMX data: path to high fidelity statistical linked data. Semantic Web 6(2), 105–112 (2015)
Carral, D., Dragoste, I., González, L., Jacobs, C.J.H., Krötzsch, M., Urbani, J.: VLog: a rule engine for knowledge graphs. In: [25], pp. 19–35
Cyganiak, R., Wood, D., Lanthaler, M.: RDF 1.1 concepts and abstract syntax, W3C Recommendation 25 February 2014. W3c recommendation, World Wide Web Consortium, 25 February 2014. https://www.w3.org/TR/2014/REC-rdf11-concepts-20140225/
Das, G., Jermaine, C.M., Bernstein, P.A. (eds.): Proceedings of the 2018 International Conference on Management of Data, SIGMOD Conference 2018, Houston, TX, USA, 10–15 June 2018. ACM Press, June 2018
Demeester, T., Rocktäschel, T., Riedel, S.: Lifted rule injection for relation embeddings. In: [65], pp. 1389–1399
Dimartino, M.M., Calì, A., Poulovassilis, A., Wood, P.T.: Efficient ontological query answering by rewriting into graph queries. In: Cuzzocrea, A., Greco, S., Larsen, H.L., Saccà, D., Andreasen, T., Christiansen, H. (eds.) FQAS 2019. LNCS (LNAI), vol. 11529, pp. 75–84. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-27629-4_10
Feier, C., Kuusisto, A., Lutz, C.: Rewritability in Monadic Disjunctive Datalog, MMSNP, and Expressive Description Logics. Log. Methods Comput. Sci. 15(2), 15:1–15:46 (2019)
Francis, N., et al.: Cypher: an evolving query language for property graphs. In: [19], pp. 1433–1445
Galárraga, L., Teflioudi, C., Hose, K., Suchanek, F.M.: Fast rule mining in ontological knowledge bases with AMIE+. Very Large Data Base J. 24(6), 707–730 (2015). https://doi.org/10.1007/s00778-015-0394-1
Ghidini, C., et al. (eds.): ISWC 2019. LNCS, vol. 11779. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30796-7
Gottlob, G., Orsi, G., Pieris, A., Šimkus, M.: Datalog and its extensions for semantic web databases. In: Eiter, T., Krennwallner, T. (eds.) Reasoning Web 2012. LNCS, vol. 7487, pp. 54–77. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33158-9_2
Grau, B.C., Motik, B., Stoilos, G., Horrocks, I.: Computing datalog rewritings beyond horn ontologies. In: Rossi, F. (ed.) IJCAI 2013, Proceedings of the 23rd International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013, pp. 832–838. IJCAI/AAAI, August 2013
Guo, S., Wang, Q., Wang, L., Wang, B., Guo, L.: Jointly embedding knowledge graphs and logical rules. In: [65], pp. 192–202
Harris, S., Seaborne, A., Prud’hommeaux, E.: SPARQL 1.1 Query Language, W3C Recommendation 21 March 2013. W3C recommendation, World Wide Web Consortium, 21 March 2013. https://www.w3.org/TR/2013/REC-sparql11-query-20130321/
Hartig, O.: Foundations of RDF* and SPARQL* - an alternative approach to statement-level metadata in RDF. In: Reutter, J.L., Srivastava, D. (eds.) Proceedings of the 11th Alberto Mendelzon International Workshop on Foundations of Data Management and the Web, Montevideo, Uruguay, 7–9 June 2017. CEUR Workshop Proceedings, vol. 1912. Sun SITE Central Europe (CEUR) (2017). http://ceur-ws.org/Vol-1912/paper12.pdf
Hitzler, P., Krötzsch, M., Parsia, B., Patel-Schneider, P.F., Rudolph, S.: OWL 2 web ontology language primer (Second edn), W3C Recommendation 11 December 2012. W3C recommendation, World Wide Web Consortium, 11 December 2012. https://www.w3.org/TR/2012/REC-owl2-primer-20121211/
Ho, V.T., Stepanova, D., Gad-Elrab, M.H., Kharlamov, E., Weikum, G.: Rule learning from knowledge graphs guided by embedding models. In: Vrandečić, D., et al. (eds.) ISWC 2018. LNCS, vol. 11136, pp. 72–90. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00671-6_5
Hoffart, J., Suchanek, F.M., Berberich, K., Lewis-Kelham, E., de Melo, G., Weikum, G.: YAGO2: exploring and querying world knowledge in time, space, context, and many languages. In: Srinivasan, S., Ramamritham, K., Kumar, A., Ravindra, M.P., Bertino, E., Kumar, R. (eds.) Proceedings of the 20th International Conference on World Wide Web, WWW 2011, Hyderabad, India, 28 March – 1 April 2011 (Companion Volume), pp. 229–232. ACM Press, March 2011
Hogan, A., Arenas, M., Mallea, A., Polleres, A.: Everything you always wanted to know about blank nodes. J. Web Semantics 27–28, 42–69 (2014)
Hogan, A., et al.: Knowledge graphs. CoRR abs/2003.02320 (2020). https://arxiv.org/abs/2003.02320
Hogan, A., Riveros, C., Rojas, C., Soto, A.: A worst-case optimal join algorithm for SPARQL. In: Ghidini, C., et al. (eds.) ISWC 2019. LNCS, vol. 11778, pp. 258–275. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30793-6_15
Homola, M., Serafini, L.: Contextualized knowledge repositories for the semantic web. J. Web Semantics 12, 64–87 (2012)
Kalinsky, O., Etsion, Y., Kimelfeld, B.: Flexible caching in Trie joins. In: International Conference on Extending Database Technology (EDBT), pp. 282–293. OpenProceedings.org (2017)
Krötzsch, M., Marx, M., Ozaki, A., Thost, V.: Attributed description logics: reasoning on knowledge graphs. In: IJCAI, pp. 5309–5313 (2018). https://doi.org/10.24963/ijcai.2018/743
Krötzsch, M., Rudolph, S., Schmitt, P.H.: A closer look at the semantic relationship between datalog and description logics. Semantic Web 6(1), 63–79 (2015)
Krötzsch, M., Simancik, F., Horrocks, I.: Description logics. IEEE Intell. Syst. 29(1), 12–19 (2014)
LaPaugh, A.S., Papadimitriou, C.H.: The even-path problem for graphs and digraphs. Networks 14(4), 507–513 (1984). https://doi.org/10.1002/net.3230140403
Lefrançois, M., Zimmermann, A.: The unified code for units of measure in RDF: cdt:ucum and other UCUM datatypes. In: Gangemi, A., et al. (eds.) ESWC 2018. LNCS, vol. 11155, pp. 196–201. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98192-5_37
Lehmann, J., et al.: DBpedia - a large-scale, multilingual knowledge base extracted from Wikipedia. Semantic Web J. 6(2), 167–195 (2015)
Libkin, L.: Locality of queries and transformations. Electron. Notes Theor. Comput. Sci. 143, 115–127 (2006). https://doi.org/10.1016/j.entcs.2005.04.041
Meroño-Peñuela, A., Daga, E.: List.MID: a MIDI-based benchmark for evaluating RDF lists. In: Ghidini, C., Hartig, O., Maleshkova, M., Svátek, V., Cruz, I., Hogan, A., Song, J., Lefrançois, M., Gandon, F. (eds.) ISWC 2019. LNCS, vol. 11779, pp. 246–260. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30796-7_16
Mika, P., et al. (eds.): ISWC 2014. LNCS, vol. 8797. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11915-1
Miller, J.J.: Graph Database Applications and Concepts with Neo4j. In: Proceedings of the Southern Association for Information Systems Conference, Atlanta, GA, USA, 23rd-24th March 2013, pp. 141–147. AIS eLibrary (2013). https://aisel.aisnet.org/sais2013/24
Navigli, R., Ponzetto, S.P.: BabelNet: the automatic construction, evaluation and application of a wide-coverage multilingual semantic network. Artif. Intell. 193, 217–250 (2012)
Ngo, H.Q., Porat, E., Ré, C., Rudra, A.: Worst-case optimal join algorithms. J. ACM 65(3), 16:1–16:40 (2018). https://doi.org/10.1145/3180143
Nguyen, D., et al.: Join processing for graph patterns: an old dog with new tricks. In: GRADES, p. 2. ACM (2015)
Nguyen, V., Bodenreider, O., Sheth, A.: Don’t like RDF reification?: Making statements about statements using singleton property. In: Chung, C.W., Broder, A.Z., Shim, K., Suel, T. (eds.) 23rd International World Wide Web Conference, WWW 2014, Seoul, Republic of Korea, 7–11 April 2014, pp. 759–770. ACM Press, April 2014
Noy, N.F., Gao, Y., Jain, A., Narayanan, A., Patterson, A., Taylor, J.: Industry-scale knowledge graphs: lessons and challenges. ACM Queue 17(2), 20 (2019)
Ortiz, M., Rudolph, S., Simkus, M.: Query answering in the horn fragments of the description logics SHOIQ and SROIQ. In: Walsh, T. (ed.) IJCAI 2011, Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Catalonia, Spain, 16–22 July 2011, pp. 1039–1044. IJCAI/AAAI, August 2011
Reutter, J.L., Soto, A., Vrgoč, D.: Recursion in SPARQL. In: Arenas, M., et al. (eds.) ISWC 2015. LNCS, vol. 9366, pp. 19–35. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25007-6_2
Rodriguez, M.A.: The Gremlin graph traversal machine and language. In: Cheney, J., Neumann, T. (eds.) Proceedings of the 15th Symposium on Database Programming Languages, Pittsburgh, PA, USA, 25–30 October 2015, pp. 1–10. ACM Press, October 2015
Rudolph, S.: Foundations of description logics. In: Polleres, A., et al. (eds.) Reasoning Web 2011. LNCS, vol. 6848, pp. 76–136. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23032-5_2
Rudolph, S., Krötzsch, M., Hitzler, P.: Description logic reasoning with decision diagrams. In: Sheth, A., et al. (eds.) ISWC 2008. LNCS, vol. 5318, pp. 435–450. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-88564-1_28
Scarselli, F., Gori, M., Tsoi, A.C., Hagenbuchner, M., Monfardini, G.: The graph neural network model. IEEE Trans. Neural Netw. 20(1), 61–80 (2009)
Schmidt-Schauß, M., Smolka, G.: Attributive concept descriptions with complements. Artif. Intell. 48(1), 1–26 (1991)
Schuetz, C., Bozzato, L., Neumayr, B., Schrefl, M., Serafini, L.: Knowledge graph OLAP: a multidimensional model and query operations for contextualized knowledge graphs. Semantic Web J. (2020). (Under open review)
Sequeda, J.F., Arenas, M., Miranker, D.P.: OBDA: query rewriting or materialization? In practice, both!. In: Mika, P., et al. (eds.) ISWC 2014. LNCS, vol. 8796, pp. 535–551. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11964-9_34
Singhal, A.: Introducing the Knowledge Graph: things, not strings. Google Blog, May 2012. https://www.blog.google/products/search/introducing-knowledge-graph-things-not/
Stefanoni, G., Motik, B., Krötzsch, M., Rudolph, S.: The complexity of answering conjunctive and navigational queries over OWL 2 EL knowledge bases. J. Artif. Intell. Res. 51, 645–705 (2014)
Su, J., Carreras, X., Duh, K. (eds.): Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, EMNLP 2016, Austin, Texas, USA, 1–4 November 2016. The Association for Computational Linguistics, November 2016
Vrandečić, D., Krötzsch, M.: Wikidata: a free collaborative knowledgebase. Commun. ACM 57(10), 78–85 (2014)
Wang, Q., Mao, Z., Wang, B., Guo, L.: Knowledge graph embedding: a survey of approaches and applications. IEEE Trans. Knowledge Data Eng. 29(12), 2724–2743 (2017)
Wang, Q., Wang, B., Guo, L.: Knowledge base completion using embeddings and rules. In: Yang, Q., Wooldridge, M.J. (eds.) Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, IJCAI 2015, Buenos Aires, Argentina, 25–31 July 2015, pp. 1859–1866. IJCAI/AAAI, July 2015
Wang, S., Schlobach, S., Klein, M.C.A.: Concept drift and how to identify it. J. Web Semantics 9(3), 247–265 (2011)
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., Yu, P.S.: A comprehensive survey on graph neural networks. CoRR abs/1901.00596 (2019). http://arxiv.org/abs/1901.00596
Xiao, G., et al.: Ontology-based data access: a survey. In: Lang, J. (ed.) Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI 2018, 13–19 July 2018, Stockholm, Sweden, pp. 5511–5519. IJCAI/AAAI, July 2018
Xiao, G., Rezk, M., Rodríguez-Muro, M., Calvanese, D.: Rules and ontology based data access. In: Kontchakov, R., Mugnier, M.-L. (eds.) RR 2014. LNCS, vol. 8741, pp. 157–172. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11113-1_11
Xu, K., Hu, W., Leskovec, J., Jegelka, S.: How powerful are graph neural networks? In: 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. OpenReview.net, May 2019. https://openreview.net/forum?id=ryGs6iA5Km
Zablith, F., et al.: Ontology evolution: a process-centric survey. Knowledge Eng. Rev. 30(1), 45–75 (2015)
Zimmermann, A., Lopes, N., Polleres, A., Straccia, U.: A general framework for representing, reasoning and querying with annotated semantic web data. J. Web Semantics 12, 72–95 (2012)
Acknowledgements
This work was supported by Fondecyt Grant No. 1181896 and by the Millennium Institute for Foundational Research on Data (IMFD). I would like to thank my co-authors on the extended tutorial for the various discussions and contributions that helped to inform these lecture notes. I also wish to thank the anonymous reviewers’ for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Hogan, A. (2020). Knowledge Graphs: Research Directions. In: Manna, M., Pieris, A. (eds) Reasoning Web. Declarative Artificial Intelligence. Reasoning Web 2020. Lecture Notes in Computer Science(), vol 12258. Springer, Cham. https://doi.org/10.1007/978-3-030-60067-9_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-60067-9_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-60066-2
Online ISBN: 978-3-030-60067-9
eBook Packages: Computer ScienceComputer Science (R0)








 ;
; ;
; .
. ;
; ,
,  ,
,  ,
,  ;
; ,
,  ;
; ,
,  .
.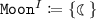 ;
; .
.