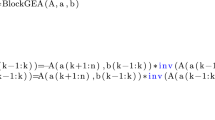Complexity Estimates for Fourier-Motzkin Elimination

Abstract

In this paper, we propose an efficient method for removing all redundant inequalities generated by Fourier-Motzkin Elimination. This method is based on an improved version of Balas’ work and can also be used to remove all redundant inequalities in the input system. Moreover, our method only uses arithmetic operations on matrices and avoids resorting to linear programming techniques. Algebraic complexity estimates and experimental results show that our method outperforms alternative approaches, in particular those based on linear programming and the simplex algorithm.

1 Introduction

Polyhedral sets play an important role in computational sciences. For instance, they are used to model, analyze, transform and schedule for-loops of computer programs; we refer to  [3, 4, 6, 15, 16, 21, 38]. Of prime importance are the following operations on polyhedral sets: (i) conversion between H-representation and V-representation (performed, for instance, by the double description method); and (ii) projection, as performed by Fourier-Motzkin Elimination.

Although the double description (DD) method and Fourier-Motzkin Elimination (FME) have a lot in common, and, they are considered as the same algorithm in the paper  [8] of Winfried Bruns and Bogdan Ichim, they are not totally similar. Quoting Komei Fukuda and Alain Prodon from  [18]: “The FME algorithm is more general than the DD method, but often considered as the same method partly because it can be used to solve the extreme ray enumeration problem”.

Fourier-Motzkin Elimination is an algorithmic tool for projecting a polyhedral set onto a linear subspace. It was proposed independently by Joseph Fourier and Theodore Motzkin, respectively in 1827 and 1936. See the paper  [14] of George Danzing and Section 12.2 of the book  [35] of Alexander Schrijver, for a presentation of Fourier-Motzkin Elimination. The original version of this algorithm produces large amounts of redundant inequalities and has a double exponential algebraic complexity. Removing all these redundancies is equivalent to giving the so-called minimal representation of the projection of a polyhedron. Leonid Khachiyan explained in  [28] how linear programming (LP) could be used to remove all redundant inequalities, thereby reducing the cost of Fourier-Motzkin Elimination to a number of machine word operations singly exponential in the dimension of the ambient space. However, Khachiyan did not state a more precise running time estimate taking into account the characteristics of the polyhedron being projected, such as the number of its facets.

As we shall prove in this paper, rather than using linear programming one may use only matrix arithmetic, increasing the theoretical and practical efficiency of Fourier-Motzkin Elimination while still producing an irredundant representation of the projected polyhedron.

Other algorithms for projecting polyhedral sets remove some (but not all) redundant inequalities with the help of extreme rays: see the work of David A. Kohler  [29]. As observed by Jean-Louis Imbert in  [24], the method he proposed in that paper and that of Sergei N. Chernikov in  [11] are equivalent. On the topic of finding extreme rays of a polyhedral set in H-representation, see Nataĺja V. Chernikova  [12], Hervé Le Verge  [30] and Komei Fukuda  [18]. These methods are very effective in practice, but none of them can remove all redundant inequalities generated by Fourier-Motzkin Elimination.

Fourier-Motzkin Elimination is well suited for projecting a polyhedron, described by its facets (given by linear inequalities), onto different sub-spaces. And our paper is about projecting polyhedral sets to lower dimensions, eliminating one variable after another, thanks to the Fourier-Motzkin Elimination algorithm as described in Schrijver’s book  [35]. In fact, our goal is to find the minimal representations of all of the successive projections of a given polyhedron (in H-representation, thus given by linear inequalities), by eliminating variables one after another, using the Fourier-Motzkin Elimination algorithm. Computing these successive projections has applications in the analysis, scheduling and transformation of for-loop nests of computer programs. For instance, after applying a uni-modular transformation to the loop counters of a for-loop nest, the loop bounds of the new for-loop nest are derived from the successive projections of a well-chosen polyhedron.

In this paper, we show how to remove all the redundant inequalities generated by Fourier-Motzkin Elimination, considering a non-empty, full-dimensional, and pointed polyhedron as the input. Our approach is based on an improved version of a method proposed by Egon Balas in  [2]. To be more specific, we first compute a so-called initial redundancy test cone from which we can derive the so-called redundancy test cone, which is used to detect the redundant inequalities generated after each elimination of a variable.

Consider a non-empty, full-dimensional, and pointed polyhedron ${Q \subseteq {\mathbb {Q}}^n}$ as input, given by a system of m linear inequalities of height h. We show, see Theorem 5, that eliminating the variables from that system, one after another (thus performing Fourier-Motzkin Elimination) can be done within $O(m^{\frac{5n}{2}} n^{\theta + 1 + \epsilon } h^{1+\epsilon })$ bit operations, for any $\epsilon > 0$, where $\theta$ is the exponent of linear algebra, as defined in the landmark book  [19].

Therefore, we obtain a more favourable estimate than the one presented in  [25, 26] for Fourier-Motzkin Elimination with a removal of the redundant inequalities via linear programming. Indeed, in those papers, the estimate is $O(n^2 \, m^{2 n} \, \mathsf{LP}{(n, 2^n h n^2 m^n)})$ bit operations, where LP $(d,H)$ is an upper bound for the number of bit operations required for solving a linear program in n variables and with total bit size H. For instance, in the case of Karmarkar’s algorithm  [27], we have $\mathsf{LP}{(d,H)} \in O(d^{3.5} H^2 \cdot \log H \cdot \log \log H)$. Then, comparing the exponents of m, n and h, we have $\frac{5n}{2}$, ${\theta + 1 + \epsilon }$, ${1+\epsilon }$ respectively with the method proposed in the present paper and $4n +\epsilon$, $6 + \epsilon$, ${2+\epsilon }$ respectively with the estimate of  [25, 26].

Our algorithm is stated in Sect. 4 and follows the revisited version of Balas’ algorithm presented in Sect. 3. Since the maximum number of facets of any standard projection of Q is $O(m^{\lfloor n/2 \rfloor })$, our running time for Fourier-Motzkin Elimination is satisfactory; the other factors in our estimate come from the cost of linear algebra operations for testing redundancy.

We have implemented the algorithms proposed in Sect. 4 using the BPAS library  [10] publicly available at www.bpaslib.org. We have compared our code against other implementations of Fourier-Motzkin Elimination including the CDD library  [17]. Our experimental results, reported in Sect. 6, show that our proposed method can solve more test-cases (actually all) that we used, while the counterpart software failed to solve some of them.

Section 2 provides background materials about polyhedral sets and polyhedral cones together with the original version of Fourier-Motzkin Elimination. As mentioned above, Sect. 3 contains our revisited version of Balas’ method and detailed proofs of its correctness. Based on this, Sect. 4 presents a new algorithm producing a minimal projected representation for a given full-dimensional pointed polyhedron. Complexity results are established in Sect. 5. In Sect. 6 we report on our experimentation and in Sect. 7 we discuss related works.

To summarize, our contributions are: (i) making Balas’ algorithm to be practical, by devising a method for finding the initial redundancy test cone efficiently and using it in the Fourier-Motzkin Elimination, (ii) exhibiting the theoretical efficiency of the proposed algorithm by analyzing its bit complexity, and, (iii) demonstrating its practical effectiveness (implemented as part of the BPAS library) compared to other available related software.

2 Background

In this section, we review the basics of polyhedral geometry. Section 2.1 is dedicated to the notions of polyhedral sets and polyhedral cones. Sections 2.2 and 2.3 review the double description method and Fourier-Motzkin elimination. We conclude this section with the cost model that we shall use for complexity analysis, see Sect. 2.4. As we omit most proofs, for more details please refer to  [18, 35, 37]. For the sake of simplicity in the complexity analysis of the presented algorithms, we constraint our coefficient field to the field of rational numbers ${\mathbb {Q}}$. However, all of the algorithms presented in this paper apply to polyhedral sets with coefficients in the field ${\mathbb {R}}$ of real numbers.

Throughout this paper, we use bold letters, e.g. $\mathbf {v}$, to denote vectors and we use capital letters, e.g. A, to denote matrices. Also, we assume that vectors are column vectors. For row vectors, we use the transposition notation, as in $A^t$ for the transposition of matrix A. The concatenation of two column vectors $\mathbf {v}$ and $\mathbf {w}$ is denoted $(\mathbf {v},\mathbf {w})$, thus using parentheses, while the concatenation of two row vector $\mathbf {v}^t$ and $\mathbf {w}^t$ is denothed $[\mathbf {v}^t,\mathbf {w}^t]$, thus using square brackets. For a matrix A and an integer k, we denote by $A_k$ is the row of index k in A. More generally, if K is a set of integers, we denote by $A_K$ the sub-matrix of A with row indices in K.

2.1 Polyhedral Cones and Polyhedra

Polyhedral Cone. A set of points $C \subseteq {\mathbb {Q}}^n$ is called a cone if for each $\mathbf {x}\in C$ and each real number $\lambda \ge 0$ we have $\lambda \mathbf {x}\in C$. A cone $C \subseteq {\mathbb {Q}}^n$ is called convex if for all $\mathbf {x}, \mathbf {y}\in C$, we have $\mathbf {x}+ \mathbf {y}\in C$. If $C \subseteq {\mathbb {Q}}^n$ is a convex cone, then its elements are called the rays of C. For two rays $\mathbf {r}$ and $\mathbf {r}'$ of C, we write $\mathbf {r}' \simeq \mathbf {r}$ whenever there exists $\lambda \ge 0$ such that we have $\mathbf {r}' = \lambda \mathbf {r}$. A cone $C \subseteq {\mathbb {Q}}^n$ is a polyhedral cone if it is the intersection of finitely many half-spaces, that is, $C = \{x\in {\mathbb {Q}}^n \ | \ Ax \le \mathbf {0}\}$ for some matrix $A \in {\mathbb {Q}}^{m \times n}$. Let $\{\mathbf {x}_1,\ldots ,\mathbf {x}_m\}$ be a set of vectors in ${\mathbb {Q}}^n$. The cone generated by $\{\mathbf {x}_1,\ldots ,\mathbf {x}_m\}$, denoted by $\mathsf{Cone}(\mathbf {x}_1,\cdots ,\mathbf {x}_m)$, is the smallest convex cone containing those vectors. In other words, we have $\mathsf{Cone}(\mathbf {x}_1,\ldots ,\mathbf {x}_m) = \{\lambda _1 \mathbf {x}_1 + \cdots + \lambda _m\mathbf {x}_m \ | \ \lambda _1 \ge 0, \ldots , \lambda _m \ge 0 \}$. A cone obtained in this way is called a finitely generated cone.

Polyhedron. A set of vectors $P \subseteq {\mathbb {Q}}^n$ is called a convex polyhedron if ${P = \{\mathbf {x}\ | \ A\mathbf {x}\le \mathbf {b}\}}$ holds, for a matrix $A \in {\mathbb {Q}}^{m \times n}$ and a vector $\mathbf {b}\in {\mathbb {Q}}^m$, for some positive integer m. Moreover, the polyhedron P is called a polytope if P is bounded. From now on, we always use the notation $P = \{\mathbf {x}\ | \ A\mathbf {x}\le \mathbf {b}\}$ to represent a polyhedron in ${\mathbb {Q}}^n$. The system of linear inequalities $\{ A \mathbf {x}\le \mathbf {b}\}$ is called a representation of P. We say an inequality $\mathbf {c}^t \mathbf {x}\le c_0$ is redundant w.r.t. a polyhedron representation $A \mathbf {x}\le \mathbf {b}$ if this inequality is implied by $A \mathbf {x}\le \mathbf {b}$. A representation of a polyhedron is minimal if no inequality of that representation is implied by the other inequalities of that representation. To obtain a minimal representation for the polyhedron P, we need to remove all the redundant inequalities in its representation. This requires the famous Farkas’ lemma. Since this lemma has different variants, we simply mention here the variant from  [35] which we use in this paper.

Lemma 1 (Farkas’ lemma)

Let $A \in {\mathbb {Q}}^{m \times n}$ be a matrix and $\mathbf {b}\in {\mathbb {Q}}^m$ be a vector. Then, there exists a vector $\mathbf {t}\in {\mathbb {Q}}^n$ with $\mathbf {t}\ge \mathbf {0}$ satisfying $A \mathbf {t}= \mathbf {b}$ if and if $\mathbf {y}^t \mathbf {b}\ge 0$ holds for every vector $\mathbf {y}\in {\mathbb {Q}}^m$ satisfying $\mathbf {y}^t A \ge 0$.

A consequence of Farkas’ lemma is the following criterion for testing whether an inequality $\mathbf {c}^t \mathbf {x}\le c_0$ is redundant w.r.t. a polyhedron representation $A \mathbf {x}\le \mathbf {b}$.

Lemma 2 (Redundancy test criterion)

Let $\mathbf {c}\in {\mathbb {Q}}^n$, $c_0 \in {\mathbb {Q}}$, $A \in {\mathbb {Q}}^{m \times n}$ and $\mathbf {b}\in {\mathbb {Q}}^m$. Assume $A\mathbf {x}\le \mathbf {b}$ is a consistent linear inequality system. Then, the inequality $\mathbf {c}^t \mathbf {x}\le c_0$ is redundant w.r.t. $A \mathbf {x}\le \mathbf {b}$ if and only if there exists a vector $\mathbf {t}\ge \mathbf {0}$ and a number $\lambda \ge 0$ satisfying $\mathbf {c}^t = \mathbf {t}^t A$ and $c_0 = \mathbf {t}^t \mathbf {b}+ \lambda$.

Characteristic Cone and Pointed Polyhedron.The characteristic cone of P is the polyhedral cone denoted by $\mathsf{CharCone}(P)$ and defined by $\mathsf{CharCone}(P) = \{\mathbf {y}\in {\mathbb {Q}}^n \ |\ \mathbf {x}+\mathbf {y}\in P, \ \forall \mathbf {x}\in P\} = \{ \mathbf {y}\ | \ A\mathbf {y}\le \mathbf {0}\}.$ The linearity space of the polyhedron P is the linear space denoted by $\mathsf{LinearSpace}(P)$ and defined as $\mathsf{CharCone}(P) \cap -\mathsf{CharCone}(P) = \{\mathbf {y}\ | \ A\mathbf {y}= \mathbf {0}\}$, where $-\mathsf{CharCone}(P)$ is the set of the $-\mathbf {y}$ for $\mathbf {y}\in \mathsf{CharCone}(P)$. The polyhedron P is pointed if its linearity space is $\{ \mathbf {0}\}$.

Lemma 3 (Pointed polyhedron criterion)

The polyhedron P is pointed if and only if the matrix A is full column rank.

Extreme Point and Extreme Ray. The dimension of the polyhedron P, denoted by $\dim (P)$, is the maximum number of linearly independent vectors in P. We say that P is full-dimensional whenever $\dim (P) = n$ holds. An inequality $\ \mathbf {a}^t \mathbf {x}\le b$ (with ${\mathbf {a}\in {\mathbb {Q}}^n}$ and ${b \in {\mathbb {Q}}}$) is an implicit equation of the inequality system $A\mathbf {x}\le \mathbf {b}$ if $\mathbf {a}^t \mathbf {x}= b$ holds for all $\mathbf {x}\in P$. Then, P is full-dimensional if and only if it does not have any implicit equation. A subset F of the polyhedron P is called a face of P if F equals $\{\mathbf {x}\in P \ | \ A_{\text {sub}} \mathbf {x}= \mathbf {b}_{\text {sub}} \}$ for a sub-matrix $A_{\text {sub}}$ of A and a sub-vector $\mathbf {b}_{\text {sub}}$ of $\mathbf {b}$. A face of P, distinct from P and of maximum dimension is called a facet of P. A non-empty face that does not contain any other face of a polyhedron is called a minimal face of that polyhedron. Specifically, if the polyhedron P is pointed, each minimal face of P is just a point and is called an extreme point or vertex of P. Let C be a cone such that $\dim (\mathsf{LinearSpace}(C)) = t$. Then, a face of C of dimension $t+1$ is called a minimal proper face of C. In the special case of a pointed cone, that is, whenever $t = 0$ holds, the dimension of a minimal proper face is 1 and such a face is called an extreme ray. We call an extreme ray of the polyhedron P any extreme ray of its characteristic cone $\mathsf{CharCone}(P)$. We say that two extreme rays $\mathbf {r}$ and $\mathbf {r}'$ of the polyhedron P are equivalent, and denote it by $\mathbf {r}\simeq \mathbf {r}'$, if one is a positive multiple of the other. When we consider the set of all extreme rays of the polyhedron P (or the polyhedral cone C) we will only consider one ray from each equivalence class. A pointed cone C can be generated by its extreme rays, that is, we have $C \ = \ \{\mathbf {x}\in {\mathbb {Q}}^n \ | \ ({ \exists \mathbf {c}\ge \mathbf {0}}) \ \mathbf {x}= R \mathbf {c}\}$, where the columns of R are the extreme rays of C. We denote by $\mathsf{ExtremeRays}(C)$ the set of extreme rays of the cone C. Recall that all cones considered here are polyhedral. The following, see  [32, 37], is helpful in the analysis of algorithms manipulating extreme rays of cones and polyhedra. Let E(C) be the number of extreme rays of a polyhedral cone $C \in {{\mathbb {Q}}}^n$ with m facets. Then, we have:

$$\begin{aligned} E(C) \le \left( {\begin{array}{c}m-\lfloor {\frac{n+1}{2}}\rfloor \\ m-1\end{array}}\right) + \left( {\begin{array}{c}m- \lfloor {\frac{n+2}{2}}\rfloor \\ m-n\end{array}}\right) \le m^{\lfloor {\frac{n}{2}}\rfloor }. \end{aligned}$$

(1)

Algebraic Test of (Adjacent) Extreme Rays. Given $\mathbf {t}\in C$ and a cone $C = \{\mathbf {x}\in {\mathbb {Q}}^n \mid A \mathbf {x}\le \mathbf {0}\}$, we define the zero set $\zeta _A(\mathbf {t})$ as the set of row indices i such that $A_i \mathbf {t}= 0$, where $A_i$ is the i-th row of A. For simplicity, we use $\zeta (\mathbf {t})$ instead of $\zeta _A(\mathbf {t})$ when there is no ambiguity. The proof of the following, which we call the algebraic test, can be found in [18]: Let $\mathbf {r}\in C$. Then, the ray $\mathbf {r}$ is an extreme ray of C if and only if we have $\mathrm{rank}(A_{\zeta (\mathbf {r})}) = n-1$. Two distinct extreme rays $\mathbf {r}$ and $\mathbf {r}'$ of the polyhedral cone C are called adjacent if they span a 2-dimensional face of C. From  [18], we have: Two distinct extreme rays, $\mathbf {r}$ and $\mathbf {r}'$, of C are adjacent if and only if $\mathrm{rank}(A_{\zeta (\mathbf {r}) \cap \zeta (\mathbf {r}')}) = n-2$ holds.

Polar Cone. Given a polyhedral cone $C \subseteq {\mathbb {Q}}^n$, the polar cone induced by C, denoted by $C^*$, is defined as: $C^* = \{\mathbf {y}\in {\mathbb {Q}}^n \ | \ \mathbf {y}^t \mathbf {x}\le \mathbf {0}, \forall \mathbf {x}\in C \}.$ The proof of the following property can be found in [35]: For a given cone $C \in {\mathbb {Q}}^n$, there is a one-to-one correspondence between the faces of C of dimension k and the faces of $C^*$ of dimension $n-k$. In particular, there is a one-to-one correspondence between the facets of C and the extreme rays of $C^*$.

Homogenized Cone. The homogenized cone of the polyhedron $P = \{\mathbf {x}\in {\mathbb {Q}} ^ n \ | \ A\mathbf {x}\le \mathbf {b}\}$ is denoted by $\mathsf{HomCone}(P)$ and defined by: $\mathsf{HomCone}(P) = \{(\mathbf {x}, x_\mathrm{last}) \in {\mathbb {Q}}^{n + 1} \ | \ A \mathbf {x}- \mathbf {b}x_\mathrm{last}\le \mathbf {0}, x_\mathrm{last}\ge 0\}$.

Lemma 4 (H-representation correspondence)

An inequality $A_i \mathbf {x}\le b_i$ is redundant in P if and only if the corresponding inequality $A_i \mathbf {x}- b_i x_\mathrm{last}\le 0$ is redundant in $\mathsf{HomCone}(P)$.

Theorem 1 (Extreme rays of the homogenized cone)

Every extreme ray of the homogenized cone $\mathsf{HomCone}(P)$ associated with the polyhedron P is either of the form $(\mathbf {x},0)$ where $\mathbf {x}$ is an extreme ray of P, or $(\mathbf {x},1)$ where $\mathbf {x}$ is an extreme point of P.

2.2 The Double Description Method

It follows from Sect. 2.1 that any pointed polyhedral cone C can be represented either as the intersection of finitely many half-spaces (given as a system of linear inequalities $A \mathbf {x}\le \mathbf {0}$ and called H-representation of C) or as $\mathsf{Cone}(R)$, where R is a matrix, the columns of which are the extreme rays of C (called V-representation of C). The pseudo-code of the double description method, as presented in  [18], and implemented in the CDD library [17] is shown in Algorithm 1. This algorithm calls partition and AdjacencyTest functions. Given a set of vectors J and an inequality $A_i$, the partition function places each member j of J into one of the sets $J^+,J^0,J^-$, according to the sign (positive, null or negative) of $A_{ij}$. Moreover, the AdjacencyTest determines adjacency of the input extreme rays. This algorithm produces the V-representation of a pointed polyhedral cone given by its H-representation. Some of the results presented in our paper depend on algebraic complexity estimates for the double description method. In  [18], one can find an estimate in terms of arithmetic operations on the coefficients of the input H-representation. Since we need a bit complexity estimate, we provide one as Lemma 9.

2.3 Fourier-Motzkin Elimination

Let $A \in {\mathbb {Q}}^{m \times p}$ and $B \in {\mathbb {Q}}^{m \times q}$ be matrices. Let $\mathbf {c}\in {\mathbb {Q}}^m$ be a vector. Consider the polyhedron $P = \{(\mathbf {u},\mathbf {x}) \in {\mathbb {Q}}^{p+q} \ | \ A\mathbf {u}+ B\mathbf {x}\le \mathbf {c}\}$. We denote by $\mathsf{proj}{(P;\mathbf {x})}$ the projection of P on $\mathbf {x}$, that is, the subset of ${\mathbb {Q}}^q$ defined by $\mathsf{proj}{(P;\mathbf {x})} = \{\mathbf {x}\in {\mathbb {Q}}^q \ | \ \exists \ \mathbf {u}\in {\mathbb {Q}}^p , \ (\mathbf {u},\mathbf {x}) \in P \}.$

Fourier-Motzkin elimination (FME for short) is an algorithm computing the projection $\mathsf{proj}{(P;\mathbf {x})}$ of the polyhedron of P by successively eliminating the $\mathbf {u}$-variables from the inequality system $A\mathbf {u}+ B\mathbf {x}\le \mathbf {c}$. This process shows that $\mathsf{proj}{(P;\mathbf {x})}$ is also a polyhedron.

Let $\ell _1, \ell _2$ be two inequalities: $a_1x_1 + \cdots + a_nx_n \le c_1$ and $b_1x_1 + \cdots + b_n x_n \le c_2$. Let $1 \le i \le n$ such that the coefficients $a_i$ and $b_i$ of $x_i$ in $\ell _1$ and $\ell _2$ are positive and negative, respectively. The combination of $\ell _1$ and $\ell _2$ w.r.t. $x_i$, denoted by $\mathsf{Combine}(\ell _1,\ell _2,x_i)$, is:

$$\begin{aligned} -b_i(a_1x_1 + \cdots + a_nx_n) + a_i(b_1x_1 + \cdots + b_n x_n) \le -b_i c_1 + a_i c_2. \end{aligned}$$

Theorem 2 shows how to compute $\mathsf{proj}{(P;\mathbf {x})}$ when $\mathbf {u}$ consists of a single variable $x_i$. When $\mathbf {u}$ consists of several variables, FME obtains the projection $\mathsf{proj}{(P;\mathbf {x})}$ by repeated applications of Theorem 2.

Theorem 2

(Fourier-Motzkin theorem [29]). Let $A \in {\mathbb {Q}}^{m \times n}$ be a matrix and let $\mathbf {c}\in {\mathbb {Q}}^m$ be a vector. Consider the polyhedron $P = \{ \mathbf {x}\in {\mathbb {Q}}^n \ | \ A \mathbf {x}\le \mathbf {c}\}$. Let S be the set of inequalities defined by $A\mathbf {x}\le \mathbf {c}$. Also, let $1 \le i \le n$. We partition S according to the sign of the coefficient of $x_i$:

$$\begin{aligned} S^+&= \{\ell \in S \ | \ \mathrm {coeff}(\ell ,x_i) > 0 \}, \\ S^-&= \{\ell \in S \ | \ \mathrm {coeff}(\ell ,x_i) < 0 \}, \\ S^0&= \{\ell \in S \ | \ \mathrm {coeff}(\ell ,x_i) = 0 \}. \end{aligned}$$

We construct the following system of linear inequalities:

$$\begin{aligned} S^\prime = \{ \mathsf{Combine}(s_p,s_n,x_i) \ | \ (s_p, s_n) \in S^+ \times S^- \} \ \cup \ S^0. \end{aligned}$$

Then, $S^\prime$ is a representation of $\mathsf{proj}{(P; \{ \mathbf {x}\setminus \{ x_i \} \})}.$

With the notations of Theorem 2, assume that each of $S^+$ and $S^-$ counts $\frac{m}{2}$ inequalities. Then, the set $S^\prime$ counts $(\frac{m}{2})^2$ inequalities. After eliminating p variables, the projection would be given by $O( {(\frac{m}{2})^{2^{p}}} )$ inequalities. Thus, FME is double exponential in p.

On the other hand, from [33] and [26], we know that the maximum number of facets of the projection on ${{\mathbb {Q}}}^{n-p}$ of a polyhedron in ${{\mathbb {Q}}}^{n}$ with m facets is $O(m^{\lfloor n/2 \rfloor })$. Hence, it can be concluded that most of the generated inequalities by FME are redundant. Eliminating these redundancies is the main subject of the subsequent sections.

2.4 Cost Model

For any rational number $\frac{a}{b}$, thus with $b \ne 0$, we define the height of $\frac{a}{b}$, denoted as $\mathsf{height}(\frac{a}{b})$, as $\log \max (|a|,|b|)$. For a given matrix $A \in {\mathbb {Q}}^{m \times n}$, let $\Vert A \Vert$ denote the infinity norm of A, that is, the maximum absolute value of a coefficient in A. We define the height of A, denoted by $\mathsf{height}(A) := \mathsf{height}(\Vert A \Vert )$, as the maximal height of a coefficient in A. For the rest of this section, our main reference is the PhD thesis of Arne Storjohann  [36]. Let k be a non-negative integer. We denote by ${\mathcal {M}}(k)$ an upper bound for the number of bit operations required for performing any of the basic operations (addition, multiplication, and division with remainder) on input $a, b \in {\mathbb {Z}}$ with $|a|, |b| < 2^k$. Using the multiplication algorithm of Arnold Schönhage and Volker Strassen  [34] one can choose ${\mathcal {M}}(k) \in O(k \log k \log \log k)$.

We also need complexity estimates for some matrix operations. For positive integers a, b, c, let us denote by ${\mathcal {M}}{\mathcal {M}}(a,b,c)$ an upper bound for the number of arithmetic operations (on the coefficients) required for multiplying an $(a \times b)$-matrix by an $(b \times c)$-matrix. In the case of square matrices of order n, we simply write ${\mathcal {M}}{\mathcal {M}}(n)$ instead of ${\mathcal {M}}{\mathcal {M}}(n,n,n)$. We denote by $\theta$ the exponent of linear algebra, that is, the smallest real positive number such that ${\mathcal {M}}{\mathcal {M}}(n) \in O (n^{\theta } )$.

We now give the complexity estimates in terms of ${\mathcal {M}}(k) \in$ $O(k \log k \log \log k)$ and ${\mathcal {B}}(k) = {\mathcal {M}}(k) \log k \in O(k (\log k)^2 \log \log k)$. We replace every term of the form $(\log k)^p (\log \log k)^q (\log \log \log k)^r$, (where p, q, r are positive real numbers) with $O(k^{\epsilon })$ where ${\epsilon }$ is a (positive) infinitesimal. Furthermore, in the complexity estimates of algorithms operating on matrices and vectors over $\mathbb {Z}$, we use a parameter $\beta$, which is a bound on the magnitude of the integers occurring during the algorithm. Our complexity estimates are measured in terms of machine word operations. Let ${A \in {\mathbb {Z}}^{m \times n}}$ and $B \in {\mathbb {Z}}^{n \times p}$. Then, the product of A by B can be computed within $O({\mathcal {M}}{\mathcal {M}}(m,n,p)(\log \beta ) + (mn+np+mp){\mathcal {B}}(\log \beta ))$ word operations, where $\beta = n \, \Vert A\Vert \, \Vert B\Vert$ and $\Vert A\Vert$ (resp. $\Vert B\Vert$) denotes the maximum absolute value of a coefficient in A (resp. B). Neglecting logarithmic factors, this estimate becomes $O(\max (m,n,p)^\theta \max (h_A,h_b))$ where $h_A = \mathsf{height}(A)$ and $h_B = \mathsf{height}(B)$. For a matrix $A \in {\mathbb {Z}}^{m \times n}$, a cost estimate of Gauss-Jordan transform is $O (nmr^{\theta -2}(\log \beta ) + nm(\log r){\mathcal {B}}(\log \beta ))$ word operations, where r is the rank of the input matrix A and $\beta = (\sqrt{r} \Vert A\Vert )^r$. Let h be the height of A, for a matrix $A \in {\mathbb {Z}}^{m \times n}$, with height h, the rank of A is computed within $O(mn^{\theta + \epsilon }h^{1 + \epsilon })$ word operations, and the inverse of A (when this matrix is invertible over ${\mathbb {Q}}$ and $m = n$) is computed within $O(m^{\theta + 1 + \epsilon }h^{1 + \epsilon })$ word operations. Let ${A \in {\mathbb {Z}}^{ n \times n}}$ be an integer matrix, which is invertible over ${\mathbb {Q}}$. Then, the absolute value of any coefficient in $A^{-1}$ (inverse of A) can be bounded up to $(\sqrt{n-1}\Vert A\Vert ^{(n-1)})$.

3 Revisiting Balas’ Method

As recalled in Sect. 2, FME produces a representation of the projection of a polyhedron by eliminating one variable at a time. However, this procedure generates lots of redundant inequalities limiting its use in practice to polyhedral sets with a handful of variables only. In this section, we propose an efficient algorithm which generates the minimal representation of a full-dimensional pointed polyhedron, as well as its projections. Throughout this section, we use Q to denote a full-dimensional pointed polyhedron in ${\mathbb {Q}}^n$, where

$$\begin{aligned} Q = \{(\mathbf {u},\mathbf {x}) \in {\mathbb {Q}}^p \times {\mathbb {Q}}^q \ | \ A\mathbf {u}+ B\mathbf {x}\le \mathbf {c}\}, \end{aligned}$$

(2)

with $A \in {\mathbb {Q}}^{m \times p}$, $B \in {\mathbb {Q}}^{m \times q}$ and $\mathbf {c}\in {\mathbb {Q}}^{m}$. Thus, Q has no implicit equations in its representation and the coefficient matrix [A, B] has full column rank. Our goal in this section is to compute the minimal representation of the projection $\mathsf{proj}{(Q;\mathbf {x})}$ given by $\mathsf{proj}{(Q;\mathbf {x})} := \{ \mathbf {x}\ | \ \exists \mathbf {u}, s.t. (\mathbf {u}, \mathbf {x}) \in Q \}.$ We call the cone the projection cone of Q w.r.t.$\mathbf {u}$. When there is no ambiguity, we simply call C the projection cone of Q. Using the following so-called projection lemma, we can compute a representation for the projection $\mathsf{proj}{(Q; \mathbf {x})}$:

Lemma 5

( [11]). The projection $\mathsf{proj}{(Q;\mathbf {x})}$ of the polyhedron Q can be represented by

$$ S := \{ \mathbf {y}^tB\mathbf {x}\le \mathbf {y}^t \mathbf {c}, \forall \mathbf {y}\in \mathsf {ExtremeRays}(C) \}, $$

where C is the projection cone of Q defined above.

Lemm 5 provides the main idea of the block elimination method. However, the represention produced in this way may have redundant inequalities. In  [2], Balas observed that if the matrix B is invertible, then we can find a cone such that its extreme rays are in one-to-one correspondence with the facets of the projection of the polyhedron (the proof of this fact is similar to the proof of our Theorem 3). Using this fact, Balas developed an algorithm to find all redundant inequalities for all cases, including the cases where B is singular.

In this section, we will explain Balas’ algorithm¹ in detail. To achieve this, we lift the polyhedron Q to a space in higher dimension by constructing the following objects.

Assume that the first q rows of B, denoted as $B_1$, are independent. Denote the last $m-q$ rows of B as $B_2$. Add $m-q$ columns, $\mathbf {e}_{q+1}, \ldots , \mathbf {e}_{m}$, to B, where $\mathbf {e}_i$ is the i-th vector in the canonical basis of ${\mathbb {Q}}^m$, thus with 1 in the i-th position and 0’s anywhere else. The matrix $B_0$ has the following form:

$$B_0 = \left[ \begin{aligned} B_1&\quad \mathbf {0}\\ B_2&\quad I_{m-q} \end{aligned} \right] .$$

To maintain consistency in the notation, let $A_0 = A$ and $\mathbf {c}_0 = \mathbf {c}$.

We define:

$$\begin{aligned} Q^0 := \{(\mathbf {u},{\mathbf {x}^{\prime }}) \in {\mathbb {Q}}^p \times {\mathbb {Q}}^m \ | \ A_0\mathbf {u}+ B_0\mathbf {x}^\prime \le \mathbf {c}_0 \ , \ x_{q+1}=\cdots =x_{m} = 0\}. \end{aligned}$$

From now on, we use $\mathbf {x}^{\prime }$ to represent the vector $\mathbf {x}\in {\mathbb {Q}}^q$, augmented with $m-q$ variables ($x_{q+1},\ldots ,x_m$). Since the extra variables $(x_{q+1},\ldots ,x_m)$ are assigned to zero, we note that $\mathsf{proj}{(Q;\mathbf {x})}$ and $\mathsf{proj}{(Q^0;{\mathbf {x}^{\prime }})}$ are “isomorphic” by means of the bijection $\varPhi$:

$$\begin{aligned} \varPhi : \begin{aligned} \mathsf{proj}{(Q;\mathbf {x})}&\rightarrow \mathsf{proj}{(Q^0;\mathbf {x}')} \\ (x_1, \ldots , x_q)&\mapsto (x_1, \ldots , x_q, 0, \ldots , 0) \end{aligned} \end{aligned}$$

In the following, we will treat $\mathsf{proj}{(Q;\mathbf {x})}$ and $\mathsf{proj}{(Q^0;{\mathbf {x}'})}$ as the same polyhedron when there is no ambiguity.

Define $W^0$ to be the set of all $(\mathbf {v}, \mathbf {w}, v_0)\in {\mathbb {Q}}^q \times {\mathbb {Q}}^{m-q} \times {\mathbb {Q}}$ satisfying

$$\begin{aligned} \begin{array}{cc} W^0 = \{ (\mathbf {v}, \mathbf {w}, v_0)\ | \ [\mathbf {v}^t, \mathbf {w}^t]B_0^{-1}A_0 = 0, [\mathbf {v}^t, \mathbf {w}^t]B_0^{-1} \ge 0, \\ \qquad \qquad -[\mathbf {v}^t, \mathbf {w}^t]B_0^{-1}\mathbf {c}_0+v_0 \ge 0 \}. \end{array} \end{aligned}$$

(3)

Similar to the discussion in the work of Balas, the extreme rays of the cone $\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \})}$ are used to construct the minimal representation of the projection $\mathsf{proj}{(Q; \mathbf {x})}$.

Theorem 3 shows that extreme rays of the cone $\overline{\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \} )}}$, which is defined as

$$\overline{\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \} )}}:=\{ (\mathbf {v}, -v_0) \ | \ (\mathbf {v}, v_0) \in \mathsf{proj}{(W^0; \{\mathbf {v}, v_0\})} \},$$

are in one-to-one correspondence with the facets of the homogenized cone of $\mathsf{proj}{(Q; \mathbf {x})}$. As a result its extreme rays can be used to find the minimal representation of $\mathsf{HomCone}( \mathsf{proj}{(Q; \mathbf {x})})$.

Lemma 6

The operations “computing the characteristic cone” and “computing projections” commute. To be precise, we have:

$$\begin{aligned} \mathsf{CharCone}(\mathsf{proj}{(Q; \mathbf {x})}) = \mathsf{proj}{(\mathsf{CharCone}(Q); \mathbf {x})}. \end{aligned}$$

Proof

By the definition of the characteristic cone, we have $\mathsf{CharCone}(Q) = \{ (\mathbf {u}, \mathbf {x}) \ | \ A \mathbf {u}+ B \mathbf {x}\le \mathbf {0}\}$, whose representation has the same left-hand side as the one of Q. The lemma is valid if we can show that the representation of $\mathsf{proj}{(\mathsf{CharCone}(Q); \mathbf {x})}$ has the same left-hand side as $\mathsf{proj}{(Q; \mathbf {x})}$. This is obvious with the Fourier-Motzkin Elimination procedure.

Theorem 3

The polar cone of $\mathsf{HomCone}( \mathsf{proj}{(Q; \mathbf {x})})$ equals to $\overline{\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \} )}}$.

Proof

By definition, the polar cone $(\mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})^*$ is equal to

$$\{ (\mathbf {y}, y_0) \ | \ [\mathbf {y}^t, y_0] [\mathbf {x}^t, x_\mathrm{last}]^t \le 0 , \forall \ (\mathbf {x}, x_\mathrm{last}) \in \mathsf{HomCone}( \mathsf{proj}{(Q; \mathbf {x})}) \}.$$

This claim follows immediately from $(\mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})^* = \overline{\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \} )}}$. We prove this latter equality in two steps.

$(\supseteq )$ For any $(\overline{\mathbf {v}}, -\overline{v}_0) \in \overline{\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \} )}}$, we need to show that

$$[\overline{\mathbf {v}}^t, -\overline{v}_0][\mathbf {x}^t, x_\mathrm{last}]^t \le 0$$

holds when $(\mathbf {x}, x_\mathrm{last}) \in \mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})$. Remember that Q is pointed. As a result, $\mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})$ is also pointed. Therefore, we only need to verify the desired property for the extreme rays of $\mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})$, which either have the form $(\mathbf {s}, 1)$ or $(\mathbf {s}, 0)$ (Theorem 1). Before continuing, we should notice that since $(\overline{\mathbf {v}}, \overline{v}_0) \in \mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \})}$, there exists $\overline{\mathbf {w}}$ such that $[\overline{\mathbf {v}}^t, \overline{\mathbf {w}}^t,\overline{v}_0 ] \in W^0$. Cases 1 and 2 below conclude that $(\overline{\mathbf {v}}, -\overline{v}_0) \in \mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})^*$ holds.

Case 1: for the form $(\mathbf {s},1)$, we have $\mathbf {s}\in \mathsf{proj}{(Q; \mathbf {x})}$. Indeed, $\mathbf {s}$ is an extreme point of $\mathsf{proj}{(Q; \mathbf {x})}$. Hence, there exists $\overline{\mathbf {u}} \in {\mathbb {Q}}^{p}$, such that we have $A \overline{\mathbf {u}} + B \mathbf {s}\le \mathbf {c}$. By construction of $Q^0$, we have $A_0 \overline{\mathbf {u}} + B_0 \mathbf {s}' \le \mathbf {c}_0$, where $\mathbf {s}' = [\mathbf {s}^t , s_{q+1}, \ldots ,s_m]^t$ with $s_{q+1} = \cdots = s_m = 0$. Therefore, we have:

$$[\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} A_0 \overline{\mathbf {u}} + [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} B_0 \mathbf {s}' \le [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} \mathbf {c}_0.$$

This leads us to $\overline{\mathbf {v}}^t \mathbf {s}= [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]\mathbf {s}' \le [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} \mathbf {c}_0 \le \overline{v}_0$. Therefore, we have $[\overline{\mathbf {v}}^t, -\overline{v}_0][\mathbf {s}^t, x_\mathrm{last}]^t \le 0$, as desired.

Case 2: for the form $(\mathbf {s}, 0)$, we have

$$\mathbf {s}\in \mathsf{CharCone}(\mathsf{proj}{(Q; \mathbf {x})}) = \mathsf{proj}{(\mathsf{CharCone}(Q); \mathbf {x})}.$$

Thus, there exists $\overline{\mathbf {u}} \in {\mathbb {Q}}^{p}$ such that $A \overline{\mathbf {u}} + B \mathbf {s}\le \mathbf {0}$. Similarly to Case 1, we have $[\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} A_0 \overline{\mathbf {u}} + [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} B_0 \mathbf {s}' \le [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} \mathbf {0}$. Therefore, we have $\overline{\mathbf {v}}^t \mathbf {s}= [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]\mathbf {s}' \le [\overline{\mathbf {v}}^t , \overline{\mathbf {w}}^t]B_0^{-1} \mathbf {0}= 0$, and thus, we have $[\overline{\mathbf {v}}^t, -\overline{v}_0][\mathbf {s}^t, x_\mathrm{last}]^t \le 0$, as desired.

$(\subseteq )$ For any $(\overline{\mathbf {y}}, \overline{y}_0) \in \mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})^*$, we have $[\overline{\mathbf {y}}^t,\overline{y}_0][\mathbf {x}^t, x_\mathrm{last}]^t \le 0$ for all $(\mathbf {x},x_\mathrm{last}) \in \mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})$. For any $\overline{\mathbf {x}} \in \mathsf{proj}{(Q; \mathbf {x})}$, we have $\overline{\mathbf {y}}^t \overline{\mathbf {x}} \le -\overline{y}_0$ since $(\overline{\mathbf {x}},1) \in \mathsf{HomCone}(\mathsf{proj}{(Q; \mathbf {x})})$. Therefore, we have $\overline{\mathbf {y}}^t \mathbf {x}\le -\overline{y}_0$, for all $\mathbf {x}\in \mathsf{proj}{(Q; \mathbf {x})}$, which makes the inequality $\overline{\mathbf {y}}^t \mathbf {x}\le -\overline{y}_0$ redundant in the system $\{A\mathbf {u}+ B\mathbf {x}\le \mathbf {c}\}$. By Farkas’ Lemma (see Lemma 2), there exists $\mathbf {p}\ge \mathbf {0}, \mathbf {p}\in {\mathbb {Q}}^m$ and $\lambda \ge 0$ such that $\mathbf {p}^t A = \mathbf {0}$, $\overline{\mathbf {y}} = \mathbf {p}^t B$, $\overline{y}_0 = \mathbf {p}^t \mathbf {c}+ \lambda$. Remember that $A_0 = A$, $B_0 = [B, B']$, $\mathbf {c}_0 = \mathbf {c}$. Here $B'$ is the last $m-q$ columns of $B_0$ consisting of $\mathbf {e}_{q+1}, \ldots , \mathbf {e}_m$. Let $\overline{\mathbf {w}} = \mathbf {p}^t B'$. We then have

$$\{ \mathbf {p}^t A_0 = \mathbf {0}, \ [\overline{\mathbf {y}}^t, \overline{\mathbf {w}}^t] = \mathbf {p}^t B_0, -\overline{y}_0 \ge \mathbf {p}^t \mathbf {c}_0, \mathbf {p}\ge \mathbf {0}\},$$

which is equivalent to

$$\begin{aligned}&\{\mathbf {p}^t = [\overline{\mathbf {y}}^t, \overline{\mathbf {w}}^t] B_0^{-1}, [\overline{\mathbf {y}}^t, \overline{\mathbf {w}}^t] B_0^{-1} A_0 = \mathbf {0}, \\&-\overline{y}_0 \ge [\overline{\mathbf {y}}^t, \overline{\mathbf {w}}^t] B_0^{-1} \mathbf {c}_0, [\overline{\mathbf {y}}^t, \overline{\mathbf {w}}^t] B_0^{-1} \ge \mathbf {0}\}. \end{aligned}$$

Therefore, $(\overline{\mathbf {y}}, \overline{\mathbf {w}}, -\overline{y}_0) \in W^0$, and $(\overline{\mathbf {y}}, -\overline{y}_0) \in \mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \})}$. From this, we deduce that $(\overline{\mathbf {y}}, \overline{y}_0) \in \overline{\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \} )}}$ holds.

Theorem 4

The minimal representation of $\mathsf{proj}{(Q; \mathbf {x})}$ is given exactly by

$$\begin{aligned} \{ \mathbf {v}^t \mathbf {x}\le v_0 \ | \ (\mathbf {v}, v_0) \in \mathsf {ExtremeRays}(\mathsf{proj}{(W^0; (\mathbf {v}, v_0))}) \setminus \{(\mathbf{0}, 1) \}\}. \end{aligned}$$

Proof

By Theorem 3, the minimal representation of the homogenized cone $\mathsf{HomCone}(\mathsf{proj}{(Q;\mathbf {x})})$ is given exactly by

$$\{ \mathbf {v}\mathbf {x}- v_0 x_\mathrm{last}\le 0 \ | \ (\mathbf {v}, v_0) \in \mathsf {ExtremeRays} (\mathsf{proj}{(W^0; (\mathbf {v}, v_0))}) \}.$$

Using Lemma 4, any minimal representation of $\mathsf{HomCone}(\mathsf{proj}{(Q;\mathbf {x})})$ has at most one more inequality than any minimal representation of $\mathsf{proj}{(Q;\mathbf {x})}$. This extra inequality is $x_\mathrm{last}\ge 0$ and, in this case, $\mathsf{proj}{(W^0; (\mathbf {v}, v_0))}$ will have the extreme ray $(\mathbf {0}, 1)$, which can be detected easily. Therefore, the minimal representation of $\mathsf{proj}{(Q; \mathbf {x})}$ is given by

$$ \{ \mathbf {v}^t \mathbf {x}\le v_0 \ | \ (\mathbf {v}, v_0) \in \mathsf {ExtremeRays}(\mathsf{proj}{(W^0; (\mathbf {v}, v_0))})\setminus \{(\mathbf{0}, 1)\} \}.$$

For simplicity, we call the cone $\mathsf{proj}{(W^0; \{ \mathbf {v}, v_0 \})}$ the redundancy test cone of Q w.r.t. $\mathbf {u}$ and denote it by $\mathcal {P}_{\mathbf {u}}(Q)$. When $\mathbf {u}$ is empty, we define $\mathcal {P}(Q) := \mathcal {P}_{\mathbf {u}}(Q)$ and we call it the initial redundancy test cone. It should be noted that $\mathcal {P}(Q)$ can be used to detect redundant inequalities in the input system, as it is shown in Steps 3 to 8 of Algorithm 4.

4 Minimal Representation of the Projected Polyhedron

In this section, we present our algorithm for removing all the redundant inequalities generated during Fourier-Motzkin elimination. Our algorithm detects and eliminates redundant inequalities, right after their generation, using the redundancy test cone introduced in Sect. 3. Intuitively, we need to construct the cone $W^0$ and obtain a representation of the redundancy test cone, $\mathcal {P}_\mathbf {u}(Q)$, where $\mathbf {u}$ is the vector of eliminated variables, each time we eliminate a variable during FME. This method is time consuming because it requires to compute the projection of $W^0$ onto $\{ \mathbf {v}, v_0 \}$ space at each step. However, as we prove in Lemma 7, we only need to compute the initial redundancy test cone, using Algorithm 2, and the redundancy test cones, used in the subsequent variable eliminations, can be found incrementally without any extra cost. After generating the redundancy test cone, the algorithm, using Algorithm 3, keeps the newly generated inequality only if it is an extreme ray of the redundancy test cone.

Note that a byproduct of this process is a minimal projected representation of the input system, according to the specified variable ordering. This representation is useful for finding solutions of linear inequality systems. The notion of projected representation was introduced in  [25, 26] and will be reviewed in Definition 1.

For convenience, we rewrite the input polyhedron Q defined in Eq. (2) as: $Q = \{ \mathbf {y}\in {\mathbb {Q}}^{n} \ | \ \mathbf {A}\mathbf {y}\le \mathbf {c}\}$, where $\mathbf {A}= [A, B]\in {\mathbb {Q}}^{m \times n}$, $n=p+q$ and $\mathbf {y}= [\mathbf {u}^t, \mathbf {x}^t]^t \in {\mathbb {Q}}^n$. We assume the first n rows of $\mathbf {A}$ are linearly independent.

Remark 1

There are two important points about Algorithm 2. First, we only need a representation of the initial redundancy test cone. This representation does not need to be minimal. Therefore, calling Algorithm 2 in Algorithm 4 (which computes a minimal projected representation of a polyhedron) does not lead to a recursive call to Algorithm 4. Second, to compute the projection $\mathsf{proj}{(W; \{ \mathbf {v}, v_0 \})}$, we need to eliminate $m-n$ variables from $m+1$ inequalities. The block elimination method is applied to achieve this. As it is shown in Lemma 5, the block elimination method will require to compute the extreme rays of the projection cone (denoted by C), which contains $m+1$ inequalities and $m+1$ variables. However, considering the structural properties of the coefficient matrix of the representation of C, we found out that computing the extreme rays of C is equivalent to computing the extreme rays of another simpler cone, which still has $m+1$ inequalities but only $n+1$ variables.

Lemma 7

A representation of the redundancy test cone $\mathcal {P}_{\mathbf {u}}(Q)$ can be obtained from $\mathcal {P}(Q)$ by setting coefficients of the corresponding p eliminated variables to 0 in the representation of $\mathcal {P}(Q)$.

Proof

To distinguish from the construction of $\mathcal {P}(Q)$, we rename the variables $\mathbf {v}, \mathbf {w}, v_0$ as $\mathbf {v}_{\mathbf {u}}, \mathbf {w}_{\mathbf {u}}, v_{\mathbf {u}}$, when constructing $W^0$ and computing the test cone $\mathcal {P}_{\mathbf {u}}(Q)$.

That is, we have $\mathcal {P}_{\mathbf {u}}(Q) = \mathsf{proj}{(W^0; \{ \mathbf {v}_{\mathbf {u}}, v_{\mathbf {u}} \})}$, where $W^0$ is the set of all $(\mathbf {v}_{\mathbf {u}} , \mathbf {w}_{\mathbf {u}} , v_{\mathbf {u}}) \in {\mathbb {Q}}^q \times {\mathbb {Q}}^{m-q} \times {\mathbb {Q}}$ satisfying

$$\{ (\mathbf {v}_{\mathbf {u}}, \mathbf {w}_{\mathbf {u}}, v_{\mathbf {u}} ) \ | \ [\mathbf {v}_{\mathbf {u}}^t, \mathbf {w}_{\mathbf {u}}^t] B_0^{-1}A = \mathbf {0}, -[\mathbf {v}_{\mathbf {u}}^t, \mathbf {w}_{\mathbf {u}}^t] B_0^{-1} \mathbf {c}+ v_{\mathbf {u}} \ge 0, [\mathbf {v}_{\mathbf {u}}^t, \mathbf {w}_{\mathbf {u}}^t]B_0^{-1} \ge \mathbf {0}\},$$

while we have $\mathcal {P}(Q) = \mathsf{proj}{(W; \{ \mathbf {v}, v_0\})}$ where W is the set of all $(\mathbf {v}, \mathbf {w}, v_0)\in {\mathbb {Q}}^n \times {\mathbb {Q}}^{m-n} \times {\mathbb {Q}}$ satisfying $\{ (\mathbf {v}, \mathbf {w}, v_0 ) \ | \ - [\mathbf {v}^t, \mathbf {w}^t]\mathbf {A}_0^{-1} \mathbf {c}+ v_0 \ge 0, [\mathbf {v}^t, \mathbf {w}^t]\mathbf {A}_0^{-1} \ge \mathbf {0}\}.$

By Step 1 of Algorithm 2, $[\mathbf {v}^t, \mathbf {w}^t] \mathbf {A}_0^{-1} \mathbf {A}= \mathbf {v}^t$ holds for all $(\mathbf {v}, \mathbf {w}, v_0) \in W$. We can rewrite $\mathbf {v}$ as $\mathbf {v}^t = [\mathbf {v}_1^t, \mathbf {v}_2^t]$, where $\mathbf {v}_1$ and $\mathbf {v}_2$ are the first p and last $n-p$ variables of $\mathbf {v}$. Then, we have $[\mathbf {v}^t, \mathbf {w}^t] \mathbf {A}_0^{-1}A = \mathbf {v}_1^t$ and $[\mathbf {v}^t, \mathbf {w}^t] \mathbf {A}_0^{-1}B = \mathbf {v}_2^t$. Similarly, we have $[\mathbf {v}_{\mathbf {u}}^t, \mathbf {w}_{\mathbf {u}}^t] B_0^{-1} A = \mathbf {0}$ and $[\mathbf {v}_{\mathbf {u}}^t, \mathbf {w}_{\mathbf {u}}^t] B_0^{-1} B = \mathbf {v}_{\mathbf {u}}^t$ for all $(\mathbf {v}_{\mathbf {u}}, \mathbf {w}_{\mathbf {u}}, v_{\mathbf {u}}) \in W^0$. This lemma holds if we can show $\mathcal {P}_{\mathbf {u}} = \mathcal {P}| _{\mathbf {v}_1 = \mathbf {0}}$. We prove this in two steps:

$(\subseteq )$ For any $(\overline{\mathbf {v}}_{\mathbf {u}}, \overline{v}_{\mathbf {u}}) \in \mathcal {P}_{\mathbf {u}}(Q)$, there exists $\overline{\mathbf {w}}_{\mathbf {u}} \in {\mathbb {Q}}^{m-q}$, such that

$$(\overline{\mathbf {v}}_{\mathbf {u}}, \overline{\mathbf {w}}_{\mathbf {u}}, \overline{v}_{\mathbf {u}}) \in W^0.$$

Let $[\overline{\mathbf {v}}^t, \overline{\mathbf {w}}^t] := [\overline{\mathbf {v}}_{\mathbf {u}}^t, \overline{\mathbf {w}}_{\mathbf {u}}^t] B_0^{-1} \mathbf {A}_0$, where $\overline{\mathbf {v}}^t = [\overline{\mathbf {v}}_1^t, \overline{\mathbf {v}}_2^t]$ ($\overline{\mathbf {v}}_1 \in {\mathbb {Q}}^{p}, \overline{\mathbf {v}}_2 \in {\mathbb {Q}}^{n-p}$, and $\overline{\mathbf {w}} \in {\mathbb {Q}}^{m-n}$). Then, because $(\overline{\mathbf {v}}_{\mathbf {u}}, \overline{\mathbf {w}}_{\mathbf {u}}, \overline{v}_{\mathbf {u}}) \in W^0$, we have $\overline{\mathbf {v}}_1^t = [\overline{\mathbf {v}}_{\mathbf {u}}^t, \overline{\mathbf {w}}_{\mathbf {u}}^t] B_0^{-1} A = \mathbf {0}$ and $\overline{\mathbf {v}}_2^t = [\overline{\mathbf {v}}_{\mathbf {u}}^t, \overline{\mathbf {w}}_{\mathbf {u}}^t] B_0^{-1} B = \overline{\mathbf {v}}_{\mathbf {u}}$. Let $\overline{v}_0 = \overline{v}_{\mathbf {u}}$, it is easy to verify that $(\overline{\mathbf {v}}, \overline{\mathbf {w}}, \overline{v}_0) \in W$. Therefore, $(\mathbf {0}, \overline{\mathbf {v}}_{\mathbf {u}},\overline{v}_{\mathbf {u}}) = (\overline{\mathbf {v}}, \overline{v}_0) \in \mathcal {P}(Q)$.

$(\supseteq )$ For any $(\mathbf {0}, \overline{\mathbf {v}}_2, \overline{v}_0) \in \mathcal {P}(Q)$, there exists $\overline{\mathbf {w}} \in {\mathbb {Q}}^{m-n}$, such that

$$(\mathbf {0}, \overline{\mathbf {v}}_2, \overline{\mathbf {w}}, \overline{v}_0) \in W.$$

Let $[\overline{\mathbf {v}}_{\mathbf {u}}^t, \overline{\mathbf {w}}_{\mathbf {u}}^t] := [\mathbf {0}, \overline{\mathbf {v}}_2^t, \overline{\mathbf {w}}^t] \mathbf {A}_0^{-1}B_0$. We have $\overline{\mathbf {v}}_{\mathbf {u}} = [\mathbf {0}, \overline{\mathbf {v}}_2^t, \overline{\mathbf {w}}^t] \mathbf {A}_0^{-1}B = \overline{\mathbf {v}}_2$. Let $\overline{v}_{\mathbf {u}} = \overline{v}_0$, it is easy to verify that $(\overline{\mathbf {v}}_{\mathbf {u}}, \overline{\mathbf {w}}_{\mathbf {u}}, \overline{v}_{\mathbf {u}}) \in W^0$. Therefore, $(\overline{\mathbf {v}}_2, \overline{v}_0) = (\overline{\mathbf {v}}_{\mathbf {u}}, \overline{v}_{\mathbf {u}}) \in \mathcal {P}_{\mathbf {u}}(Q)$.

Consider again the polyhedron $Q = \{ \mathbf {y}\in {\mathbb {Q}}^{n} \ | \ \mathbf {A}\mathbf {y}\le \mathbf {c}\}$, where $\mathbf {A}= [A, B]\in {\mathbb {Q}}^{m \times n}$, $n=p+q$ and $\mathbf {y}= [\mathbf {u}^t, \mathbf {x}^t]^t \in {\mathbb {Q}}^n$. Fix a variable ordering, say $y_1> \cdots > y_{n}$, For $1\le i \le n$, we denote by ${\mathbf {A}}^{(y_i)}$ the inequalities in the representation $\mathbf {A}\mathbf {y}\le \mathbf {c}$ of Q whose largest variable is $y_i$. We denote by $\mathsf{ProjRep}(Q; y_1> \cdots > y_{n})$ the linear system ${\mathbf {A}}^{(y_1)}$ if $n=1$ and the conjunction of ${\mathbf {A}}^{(y_1)}$ and $\mathsf{ProjRep}(\mathsf{proj}{(Q; {\mathbf {y}_2})}; y_2> \cdots > y_n)$ otherwise, where ${\mathbf {y}_2} = (y_2, \ldots , y_n)$. Of course, $\mathsf{ProjRep}(Q; y_1> \cdots > y_{n})$ depends on the representation which is used of Q.

Definition 1 (Projected representation)

For the polyhedron $Q \subseteq {\mathbb {Q}}^{n}$, we call projected representation of Q w.r.t. the variable order $y_1> \cdots > y_{n}$ any linear system of the form $\mathsf{ProjRep}(Q; y_1> \cdots > y_{n})$. We say that such a linear system P is a minimal projected representation of Q if, for all $1 \le k \le n$, every inequality of P, with $y_k$ as largest variable, is not redundant among all the inequalities of P with variables among $y_k, \ldots , y_n$.

We can generate a minimal projected representation of a polyhedron, w.r.t. an specific variable ordering by Algorithm 4.

5 Complexity Estimates

In this section, we analyze the computational complexity of Algorithm 4, which computes a minimal projected representation of a given polyhedron. This computation is equivalent to eliminating all variables, one after another, in Fourier-Motzkin elimination. We prove that using our algorithm, finding a minimal projected representation of a polyhedron is singly exponential in the dimension n of the ambient space. The most consuming procedure in Algorithm 4 is finding the initial redundancy test cone. This operation requires another polyhedron projection in higher dimension. As it is shown in Remark 1, we can use block elimination method to perform this task efficiently. This requires the computation of the extreme rays of the projection cone. The double description method is an efficient way to solve this problem. We begin this section by computing the bit complexity of the double description algorithm.

Lemma 8 (Coefficient bound of extreme rays)

Let

$$S = \{ \mathbf {x}\in {\mathbb {Q}}^n \ | \ A \mathbf {x}\le \mathbf {0}\}$$

be a minimal representation of a cone $C \subseteq {\mathbb {Q}}^n$, where $A \in {\mathbb {Q}}^{m \times n}$. Then, the absolute value of a coefficient in any extreme ray of C is bounded over by $(n-1)^n \Vert A \Vert ^{2(n-1)}$.

Proof

From the properties of extreme rays, see Sect. 2.1, we know that when $\mathbf {r}$ is an extreme ray, there exists a sub-matrix $A' \in {\mathbb {Q}}^{(n-1) \times n}$ of A, such that $A'\mathbf {r}=0$. This means that $\mathbf {r}$ is in the null-space of $A'$. Thus, the claim follows by proposition 6.6 of [36].

Lemma 9

Let $S = \{ \mathbf {x}\in {\mathbb {Q}}^n \ | \ A\mathbf {x}\le \mathbf {0}\}$ be the minimal representation of a cone $C \subseteq {\mathbb {Q}}^n$, where $A \in {\mathbb {Q}}^{m \times n}$. The double description method requires $O(m^{n+2} n^{\theta +\epsilon }{h}^{1+\epsilon })$ bit operations, where h is the height of the matrix A.

Proof

The cost of Algorithm 1 during the processing of the first n inequalities (Line 4) is negligible (in comparison to the subsequent computations) since it is equivalent to find the inverse of an $n \times n$ matrix. Therefore, to analyze the complexity of the DD method, we focus on the while-loop located at Line 6 of the Algorithm 1. After adding t inequalities, with $n \le t \le m$, the first step is to partition the extreme rays at the ${t-1}$-iteration, with respect to the newly added inequality (Line 9 of Algorithm 1). Note that we have at most $(t-1)^{\lfloor {\frac{n}{2}}\rfloor }$ extreme rays (Eq. (1)) whose coefficients can be bounded over by $(n-1)^n \Vert A\Vert ^{2(n-1)}$ (Lemma 8) at the ${t-1}$-iteration. Hence, this step needs at most $C_1 := (t-1)^{\lfloor {\frac{n}{2}}\rfloor } \times n \times {\mathcal {M}}(\log ((n-1)^n \Vert A\Vert ^{2(n-1)})) \le O(t^{ \lfloor \frac{n}{2} \rfloor } n^{2+\epsilon } h^{1+\epsilon })$ bit operations. After partitioning the vectors, the next step is to check adjacency for each pair of vectors (Line 13 of of Algorithm 1). The cost of this step is equivalent to computing the rank of a sub-matrix $A' \in {\mathbb {Q}}^{(t-1) \times n}$ of A. This should be done for $\frac{t^n}{4}$ pairs of vectors. This step needs at most $C_2 := \frac{t^n}{4} \times O((t-1)n^{\theta +\epsilon }h^{1+\epsilon }) \le O(t^{n+1}n^{\theta +\epsilon }h^{1+\epsilon })$ bit operations. We know there are at most $t^{\lfloor {\frac{n}{2}}\rfloor }$ pairs of adjacent extreme rays. The next step is to combine every pair of adjacent vectors in order to obtain a new extreme ray (Line 14 of Algorithm 1). This step consists of n multiplications in ${{\mathbb {Q}}}$ of coefficients with absolute value bounded over by $(n-1)^n \Vert A\Vert ^{2(n-1)}$ (Lemma 8) and this should be done for at most $t^{\lfloor {\frac{n}{2}}\rfloor }$ vectors. Therefore, the bit complexity of this step, is no more than $C_3 := t^{\lfloor {\frac{n}{2}}\rfloor } \times n \times {\mathcal {M}}(\log ((n-1)^n \Vert A\Vert ^{2(n-1)})) \le O(t^{\lfloor \frac{n}{2} \rfloor } n^{2+\epsilon } h^{1+\epsilon })$. Finally, the complexity of iteration t of the while loop is $C := C_1+ C_2+C_3$. The claim follows after simplifying $m \times C$.

Lemma 10 (Complexity of constructing the initial redundancy test cone)

Let h be the maximum height of A and $\mathbf {c}$ in the input system, then generating the initial redundancy test cone (Algorithm 1) requires at most

$$O(m^{n+3+\epsilon }(n+1)^{\theta +\epsilon }h^{1+\epsilon })$$

bit operations. Moreover, $\mathsf{proj}{(W; \{\mathbf {v}, v_0\})}$ can be represented by $O(m^{\lfloor \frac{ n+1 }{2}\rfloor })$ inequalities, each with a height bound of $O(m^{\epsilon }n^{2+\epsilon }h)$.

Proof

We analyze Algorithm 2 step by step.

Step 1: Construction of $A_0$ from A. The cost of this step can be neglected. However, it should be noticed that the matrix $A_0$ has a special structure. Without loss of generality, we can assume that the first n rows of A are linearly independent. The matrix $A_0$ has the following structure:

$$A_0 =\left( \begin{aligned} A_1&\quad \mathbf {0}\\ A_2&\quad I_{m-n} \end{aligned} \right) ,$$

where $A_1$ is a full rank matrix in ${\mathbb {Q}}^{n \times n}$ and $A_2 \in {\mathbb {Q}}^{(m-n) \times n}$.

Step 2: Construction of the Cone W. Using the structure of the matrix $A_0$, its inverse can be expressed as

$$A_0^{-1} = \left( \begin{aligned} A_1^{-1}&\quad \mathbf {0}\\ -A_2A_1^{-1}&\quad I_{m-n} \end{aligned} \right) .$$

Also, from Sect. 2.4 we have $\Vert A_1^{-1} \Vert \le (\sqrt{n-1} \Vert A_1 \Vert )^{n-1}$. Therefore, $\Vert A_0^{-1}\Vert \le n^{\frac{n+1}{2}} \Vert A \Vert ^n$, and $\Vert A_0^{-1} \mathbf {c}\Vert \le n^{\frac{n+3}{2}} \Vert A \Vert ^n \Vert \mathbf {c}\Vert + (m-n)\Vert \mathbf {c}\Vert$. That is, $\mathsf{height}(A_0^{-1}) \in O(n^{1+\epsilon }h)$ and $\mathsf{height}(A_0^{-1} \mathbf {c}) \in O(m^{\epsilon } + n^{1+\epsilon }h)$. As a result, height of coefficients of W can be bounded over by $O(m^{\epsilon } + n^{1+\epsilon }h)$.

To estimate the bit complexity, we need the following consecutive steps:

• Computing $A_0^{-1}$, which requires

  $$\begin{aligned} \begin{aligned}&O(n^{\theta + 1 + \epsilon }h^{1+\epsilon }) +O((m-n) n^2 {\mathcal {M}}(\max (\mathsf{height}(A_2), \mathsf{height}(A_1^{-1}))))\\ \le \,&O(mn^{\theta + 1 + \epsilon }h^{1+\epsilon }) \text { bit operations;} \end{aligned} \end{aligned}$$

• Constructing $W:= \{ (\mathbf {v}, \mathbf {w}, v_0 ) \ | \ - [\mathbf {v}^t, \mathbf {w}^t]\mathbf {A}_0^{-1} \mathbf {c}+ v_0 \ge 0, [\mathbf {v}^t, \mathbf {w}^t]\mathbf {A}_0^{-1} \ge \mathbf {0}\}$ requires at most

  $$\begin{aligned} \begin{aligned} C_1:=\,&O(m^{1+\epsilon }n^{\theta + 1 + \epsilon }h^{1+\epsilon })+{O(m n {\mathcal {M}}(\mathsf{height}(A_0^{-1},\mathbf {c})))}\\ +\,&O((m-n)h) \le O(m^{1+\epsilon }n^{\theta +\epsilon +1}h^{1+\epsilon }) \text { bit operations.} \end{aligned} \end{aligned}$$

Step 3: Projecting W and Finding the Initial Redundancy Test Cone. Following Lemma 5, we obtain a representation of $\mathsf{proj}{(W; \{\mathbf {v}, v_0\})}$ through finding extreme rays of the corresponding projection cone.

Let $E = (-A_2A_1^{-1})^t \in {\mathbb {Q}}^{n \times (m-n)}$ and $\mathbf {g}^t$ be the last $m-n$ elements of $(A_0^{-1}\mathbf {c})^t$. Then, the projection cone can be represented by:

$$\begin{aligned} C =\{ \mathbf {y}\in {\mathbb {Q}}^{m+1} \ | \ \mathbf {y}^t \left( \begin{aligned} E \\ \mathbf {g}^t \\ I_{m-n} \end{aligned} \right) = \mathbf {0}, \mathbf {y}\ge \mathbf {0}\}. \end{aligned}$$

Note that $y_{n+2}, \ldots , y_{m+1}$ can be solved from the system of equations in the representation of C. We substitute them in the inequalities and obtain a representation of the cone $C'$, given by:

$$\begin{aligned} C' = \{ \mathbf {y}' \in {\mathbb {Q}}^{n+1} \ | \ \mathbf {y}'^t \left( \begin{aligned} E \\ \mathbf {g}^t \end{aligned}\right) \le \mathbf {0}, \mathbf {y}' \ge \mathbf {0}\} \end{aligned}$$

In order to find the extreme rays of the cone C, we can find the extreme rays of the cone $C'$ and then back-substitute them into the equations to find the extreme rays of C. Applying the double description algorithm to $C'$, we can obtain all extreme rays of $C'$, and subsequently, the extreme rays of C. The cost estimate of this step is bounded over by the complexity of the double description algorithm with $C'$ as input. This operation requires at most $C_2 := O(m^{n+3} (n+1)^{\theta +\epsilon } \max (\mathsf{height}(E,\mathbf {g}^t))^{1+\epsilon }) \le O(m^{n+3+\epsilon } (n+1)^{\theta +\epsilon }h^{1+\epsilon })$ bit operations. The overall complexity of the algorithm can be bounded over by: $C_1+C_2 \le O(m^{n+3+\epsilon }(n+1)^{\theta +\epsilon }h^{1+\epsilon }).$ Also, by Lemma 8 and Lemma 9, we know that the cone C has at most $O(m^{\lfloor \frac{n+1}{2} \rfloor })$ distinct extreme rays, each with height no more than $O(m^{\epsilon }n^{2+\epsilon }h)$. That is, $\mathsf{proj}{(W^0; \{\mathbf {v}, v_0\})}$ can be represented by at most $O(m^{\lfloor \frac{ n+1 }{2}\rfloor })$ inequalities, each with a height bound of $O(m^{\epsilon }n^{2+\epsilon }h)$.

Lemma 11

Algorithm 3 runs within $O(m^{\frac{n}{2}}n^{\theta +\epsilon }h^{1+\epsilon })$ bit operations.

Proof

The first step is to multiply the matrix M and the vector $(\mathbf {t},t_0)$. Let $d_M$ and $c_M$ be the number of rows and columns of M, respectively. Thus, $M \in {\mathbb {Q}}^{d_M \times c_M}$. We know that M is the coefficient matrix of $\mathsf{proj}{(W^0, \{ \mathbf {v}, v_0 \})}$. Therefore, after eliminating p variables $c_M = q+1$, where $q = n-p$ and $d_M \le m^{\frac{n}{2}}$. Also, we have $\mathsf{height}(M) \in O(m^{\epsilon }n^{2+\epsilon }h)$. With these specifications, the multiplication step and the rank computation step need $O(m^{\frac{n}{2}}n^{2+\epsilon }h^{1+\epsilon })$ and $O(m^{\frac{n}{2}}(q+1)^{\theta +\epsilon }h^{1+\epsilon })$ bit operations, respectively. The claim follows after simplification.

Using Algorithms 2 and 3, we can find the minimal projected representation of a polyhedron in singly exponential time w.r.t. the number of variables n.

Theorem 5

Algorithm 4 is correct. Moreover, a minimal projected representation of Q can be produced within $O(m^{\frac{5n}{2}} n^{\theta + 1 + \epsilon } h^{1+\epsilon })$ bit operations.

Proof

The correctness of the algorithm follows from Theorem 4 and Lemma 7.

By [24, 29], we know that after eliminating p variables, the projection of the polyhedron has at most $m^{p+1}$ facets. For eliminating the next variable, there will be at most $(\frac{m^{p+1}}{2})^2$ pairs of inequalities to be considered and each of the pairs generate a new inequality which should be checked for redundancy. Therefore, the overall complexity of the algorithm is:

$$\begin{aligned} O(m^{n+3+\epsilon }(n+1)^{\theta +\epsilon }h^{1+\epsilon }) + \sum _{p=0}^{n} m^{2p+2} O(m^{\frac{n}{2}}n^{\theta +\epsilon }h^{1+\epsilon }) = O(m^{\frac{5n}{2}} n^{\theta + 1 + \epsilon } h^{1+\epsilon }). \end{aligned}$$

6 Experimentation

In this section we report on our software implementation of the algorithms presented in the previous sections. Our implementation as well as our test cases are part of the BPAS library, available at http://www.bpaslib.org/.

We report on serial and parallel implementation of the Minimal Projected Representation (MPR) algorithm. Comparing with the Project command of the PolyhedralSets package of Maple 2017 and the famous CDD library (version 2018), we have been able to solve our test cases more efficiently. We believe that this is the result of using a more effective algorithm and an efficient implementation in C.

As test cases we use 16 consistent linear inequality systems. The first 9 test cases, (t1 to t9) are linear inequality systems that are randomly generated. The systems S24 and S35 are 24-simplex and 35-simplex polytopes. The systems C56 and C510 are cyclic polytopes in dimension five with six and ten vertices, The system C68 is a cyclic polytope in dimension six with eight vertices, C1011 is cyclic polytope in dimension ten with eleven vertices, and, Cro6 is the cross polytope in 6 dimension  [22]. The test column of Table 1 shows these systems along with the number of variables and the number of inequalities for each of them.

We implemented the MPR algorithm with two different approaches: one iterative following closely Algorithm 4, and the other reorganizing that algorithm by means of a divide and conquer scheme. In both implementations, we use a dense representation for the linear inequalities. In the first approach, we use unrolled linked lists to encode linear inequality systems. Indeed, using this data structure, we are able to store an array of inequalities in each node of a linked list and we can improve data locality. However, we use simple linked lists in the divide and conquer version to save time on dividing and joining lists. Although both these approaches have shown quite similar and promising results in terms of running time, we anticipate to get better results if we combine unrolled linked lists with the divide and conquer scheme while using a varying threshold for recursion as the algorithm goes on.

Columns MPR-itr and MPR-rec of the Table 1 give the running time (in milliseconds) of these implementations on a configuration with an Intel-i7-7700T CPU (4 cores, 8 threads, clocking at 3.8 GHz). Also, columns CDD, Maple, and are corresponding to running times of the Fourier algorithm in the CDD library, which uses LP for redundancy elimination, the function of Maple, and, an implementation of our algorithm in the Maple programming language, on the same system, respectively.

Table 1. Running time (in milliseconds) table for a set of examples, varying in the number of variables and inequalities, collected on a system with Intel-i7-7700T 4-core processor, clocking at 3.8 GHz.

Using the divide and conquer scheme, we have been able to parallelize our program, with Cilk [5]. We call this algorithm Parallel Minimal Projected Representation (PMPR). Table 2 presents the running time (in milliseconds) and speedup of the multi-core version of the algorithm. The columns PMPR-1, PMPR-4, PMPR-8, and, PMPR-12 demonstrate the running time of the multi-core program on a system with Intel-Xeon-X5650 (12 cores, 24 threads, clocking at 2.6 GHz), using 1, 4, 8, and 12 Cilk workers, respectively. The numbers in brackets show the speedup we gain using multi-threading.

Table 2. Running time (in milliseconds) table for our set of examples, with different number of Cilk workers, collected on a system Intel-Xeon-X5650 and 12 CPU cores, clocking at 2.6GHz.

7 Related Works and Concluding Remarks

As we previously discussed, removing redundant inequalities during the execution of Fourier-Motzkin Elimination is the central issue towards efficiency. Different algorithms have been developed to solve this problem. They also have been implemented in the various software libraries, including but not limited to: CDD [17], VPL [7], PPL [1], Normaliz [9], PORTA [13], and Polymake [20] In this section, we briefly review some of these works.

In  [11], Chernikov proposed a redundancy test with little added work, which greatly improves the practical efficiency of Fourier-Motzkin Elimination. Kohler proposed a method in [29] which only uses matrix arithmetic operations to test the redundancy of inequalities. As observed by Imbert in his work  [24], the method he proposed in his paper as well as those of Chernikov and Kohler are essentially equivalent. Even though these works are effective in practice, none of them can remove all redundant inequalities generated by Fourier-Motzkin Elimination.

Besides Fourier-Motzkin Elimination, block elimination is another algorithmic tool to project polyhedra on a lower dimensional subspace. This method relies on the extreme rays of the so-called projection cone. Although there exist efficient methods to enumerate the extreme rays of this projection cone, like the double description method  [18] (also known as Chernikova’s algorithm  [12, 30]), this method can not remove all the redundant inequalities.

In  [2], Balas shows that if certain inconvertibility conditions are satisfied, then the extreme rays of the redundancy test cone exactly defines a minimal representation of the projection of a polyhedron. As Balas mentioned in his paper, this method can be extended to any polyhedron.

A drawback of Balas’ work is the necessity of enumerating the extreme rays of the redundancy test cone (so as to produce a minimal representation of the projection $\mathsf{proj}{(Q;\mathbf {x})}$) which is time consuming. Our algorithm tests the redundancy of the inequality $\mathbf {a}\mathbf {x}\le c$ by checking whether $(\mathbf {a}, c)$ is an extreme ray of the redundancy test cone or not.

Another related topic to our work is the concept of subsumption cone, as defined in  [23]. Consider the polyhedron Q given in Eq. (2), define $T := \{ ( \mathbf{\lambda }, \mathbf{\alpha }, \beta ) \ | \ \mathbf{\lambda }^t \mathbf {A}= \mathbf{\alpha }^t, \mathbf{\lambda }^t \mathbf {c}\le \beta , \mathbf{\lambda }\ge \mathbf {0}\}$, where $\mathbf{\lambda }$ and $\mathbf{\alpha }$ are vectors of dimension m and n respectively, and $\beta$ is a variable. The subsumption cone of Q is obtained by eliminating $\mathbf{\lambda }$ in T, that is, $\mathsf{proj}{(T; \{ \mathbf{\alpha }, \beta \})}$. We proved that considering a full-dimensional, pointed polyhedron, where the first n rows of the coefficient matrix are linearly independent, the initial redundancy test cone and the subsumption cone are equivalent.

Given a V-representation of a polyhedron P, one can obtain the V-representation of any projection of P². The double description method turns the V-representation of the projection to its H-representation. Most existing software libraries dealing with polyhedral sets store a polyhedron with these two representations, like the Parma Polyhedra Library (PPL) [1]. In this case, it is convenient to compute the projection using the block elimination method. When we are only given the H-representation, the first thing is to compute the V-representation, which is equivalent to the procedure of computing the initial test cone in our method. When we need to perform successive projections, it is well-known that Fourier-Motzkin Elimination performs better than repeated applications of the double description method.

Recently, the verified polyhedron library (VPL)  [7] takes advantage of parametric linear programming to project a polyhedron. Like PPL, VPL may not beat Fourier-Motzkin Elimination when we need to perform successive projections. In VPL, the authors rely on raytracing to remove redundant inequalities. This is an efficient way of removing redundancies, but this cannot remove them all, thus Linear Programming (LP) is still needed. As pointed out in  [31], raytracing is effective when there are not many redundancies; unfortunately, Fourier-Motzkin Elimination typically generates lots of redundancies.

Another modern library dealing with polyhedral sets computation is the Normaliz library  [9]. In this library, Fourier-Motzkin Elimination is used for conversion between different descriptions of polyhedral sets. This is a different strategy than the one of our paper. As discussed in the introduction, we are motivated here by performing successive projections as required in the analysis, scheduling and transformation of for loop nests of computer programs.