2D X-Ray Mammogram and 3D Breast MRI Registration

Abstract

X-ray mammography and breast Magnetic Resonance Imaging (MRI) are two principal imaging modalities which are currently used for detection and diagnosis of breast disease in women. Since these imaging modalities exploit different contrast mechanisms, establishing spatial correspondence between mammograms and volumetric breast MRI scans is expected to aid the assessment and quantification of different type of breast malignancies. Finding such correspondence is, unfortunately, far from being a trivial problem – not only that the images have different contrasts and dimensionality, they are also acquired under vastly different physical conditions. As opposed to many complex standard methods relying on patient-specific bio-mechanical modelling, we developed a new simple approach to find the correspondences. This paper introduces a two-stage computational scheme which estimates the global (compression dependent) part of the spatial transformation first, followed by estimating the residual (tissue dependent) part of the transformation of much smaller magnitude. Experimental results on a clinical data-set, containing 10 subjects, validated the efficiency of the proposed approach. The average Target Registration Error (TRE) on the data-set is 5.44 mm with a standard deviation of 3.61 mm.

1 Introduction

Breast cancer is the most common malignancy diagnosed in women worldwide, with about 1.1 million cases of breast cancer diagnosed each year and the annual fatality costing 400,000 lives worldwide  [1]. Since its establishment as a method of population-wise screening, X-ray mammography has helped to slash the mortality rates to a remarkable extent. The relatively low sensitivity of mammography limits its efficacy in patients with relatively dense composition of breast tissue. For this reason, in the cases of newly diagnosed breast cancer as well as in patients considered to be at an elevated risk of developing breast disease, it is nowadays a standard practice to warrant MRI examination  [2]. In such cases, to improve the specificity of MRI findings as well as to facilitate biopsy, it is often necessary to locate the same lesion in the MRI and mammography scans concurrently. Establishing such correspondence requires one to find a spatial transformation that relates the coordinates of breast tissue in its pendulous and compressed states based on the imaging data alone. This problem can be conveniently formulated as problems of image registration, which, in the case at hand, can be further characterized as being both cross-modal and cross dimensional (CMCD). Moreover, the expected ill-posedness of CMCD formulation is further exacerbated by the effect of mechanical compression of the breast during mammography examination along with the fact that, as opposed to MRI scans, mammographic images are, in fact, projective. Hence, it hardly comes as a surprise that the range of approaches to the problem of 3D breast MRI to 2D mammography (MRI/MMG) registration remains comparatively limited, while the drawbacks of existing solutions hamper their widespread adoption into clinical practice.

The problem of MRI/MMG registration have been addressed in several studies using a range of different approaches. At a conceptual level, the solutions proposed hitherto differ in how they: a) deal with the change in the dimensionality of imaging data, b) model and estimate the geometric transformation, and c) assess image similarity. Thus, for example, to address the cross-dimensional aspects of the registration problem at hand,  [3] relied on landmark-based registration of mammographic scans with 2D MRI images derived from their associated 3-D MRI volumes via radiographic projection. It was proposed in  [4] to restrict all admissible transformations to a low-dimensional space of para-metric models, affine transformation, which is commonly used to describe image deformation due to shifts, rotations, scaling and shearing of spatial coordinates. Moreover, assuming the breast volume to be invariant under the change of coordinates allowed the authors to reduce the number of unknown transformation parameters (from 12 to 11), while improving the stability of overall estimation to a substantial degree. However, by its very nature, affine transformation is incapable of describing curvilinear displacements of matter, which are likely to take place in the breast under deformation.

The most promising results have been thus far obtained with the help of biomechanical Finite Element Models (FEMs), which can be used to predict the deformation of breast tissue due to compression  [6, 7]. While different in their finer details, all FEM-based methods share a common algorithmic structure consisting of four principal stages, viz.: MRI image segmentation, material modelling, computation of the displacement, and registration  [5]. Note that, in this case, image segmentation is a key step required to discriminate between different types of breast tissue (e.g., adipose and fibro-glandular tissue, skin, etc.), which is critical for accuracte material modelling. Following the “compression stage”, the pre-warped MRI volumes are reduced to their 2D projections by means of ray-tracing  [4], followed by estimating a transformation between the latter and their associated mammograms. Thus, for example,  [8] relied on a rigid-body transformation model, with Normalized Cross Correlation (NCC) used a similarity measure between the “simulated” and real mammograms. A fully automated method has been proposed in  [9] which performs a complete registration of MRI volumes and X-ray images in both directions, i.e. from MRI to mammogram and from mammogram to MRI. In  [10], in contrary to other FEM-approaches, it was proposed to perform registration on the density maps extracted from both MRI and mammography scans by means of Vollpara software suit  [11]. In  [12], the same group of authors proposed to define the similarity measure using intensity gradients, which was shown to be much less sensitive to the difference in imaging contrasts between MRI and mammography.

One of the main disadvantages of using FEM-based methods are due to their computational complexity, high sensitivity to the results of image segmentation as well as their dependency on third-party numerical solvers. Moreover, the biomechanical models used by FEM are build individually for each subject, thus ignoring the common characteristics of the compression-related displacement of breast tissue which are likely to be shared between different cases. To overcome some of these drawbacks, this paper introduces a new approach to the problem of MRI/MMG registration that does not require the use of FEM-based modelling to account for the large-amplitude component of breast deformation. To this end, given a mammography scan, the breast boundary is used to build a 3D reference surface that predicts the shape of compressed breast. Subsequently, the MRI volume is registered to the reference shape (thus accounting for the major portion of breast motion), followed by estimating the residual deformation in a non-rigid intensity-based registration setting. The proposed approach has been observed to be both numerically straightforward and accurate, as supported by a series of our experiments conducted on clinical datasets.

2 Method

Let f and g denote a 3D breast MRI volume and a 2D mammography scan defined over a rectangular domain $\varOmega$, respectively. Also, let $\mathcal {P}$ denote a projection operator such that $\mathcal {P}(f)$ is defined over $\varOmega$ as well. Then, given an appropriate distance $d(\cdot , \cdot )$ between two (planar) images, the problem of MRI/MMG registration can be formulated as one of finding the optimal spatial transformation $\phi ^*\in \varPhi$ which solves

$$\begin{aligned} \phi ^*=\arg \min _{\phi \in \varPhi } \, d( \mathcal {P}(f \circ \phi ), g), \end{aligned}$$

(1)

with . Note that, in the above formulation, all admissible transformations are limited to the set $\varPhi$ which could be, e.g., the set of topology preserving homeomorphisms.

Fig. 1.

Scheme of the proposed method.

Let $\phi$ be an admissible deformation which brings $\mathcal {P}(f\circ \phi )$ and g into a close correspondence w.r.t. the chosen metric d. In this work, the entire deformation $\phi$ is decomposed into two constituents, namely $\phi =\phi _\mathrm{glb} \circ \phi _\mathrm{res}$, with $\phi _\mathrm{glb}$ and $\phi _\mathrm{res}$ being the global and residual components of $\phi$. Each of the two components is then estimated separately according to the algorithmic steps depicted in flowchart shown in Fig. 1. In the preprocessing step, the breast geometry is extracted from MRI volume, and then MRI voxels are segmented to either to adipose (fat) or fibroglandular  [13]. The particular methods for estimation of $\phi _\mathrm{glb}$ and $\phi _\mathrm{res}$ are described next.

2.1 Estimation of Global Deformation

The global deformation of the breast during mammographic compression has many properties and characteristics which appear to be common to subjects within different breast geometry and composition. Thus, in particular, the boundary of a compressed breast can be closely approximated by a super-quadratic  [18] of the form

$$\begin{aligned} \left| \frac{x}{a}\right| ^{r} + \left| \frac{y}{b}\right| ^{s} + \left| \frac{z}{c}\right| ^{t}= 1, \quad y \ge 0, \end{aligned}$$

(2)

where the x, y and z coordinates are aligned with the left-right, posterior-anterior and inferior-superior directions, respectively. Note that the condition $y \ge 0$ is added to keep the anterior part of the surface only.

The parameter $\theta = \{a, b, c, r, s, t\}$ control the shape of the super-quadratic and, hence, they need to be properly defined. To this end, we first notice that the projection of the super-quadratic onto the (x, y) plane is described by a simplified equation of the form $|x/a|^r + |y/b|^s = 1$. This shape can be reasonably expected to be aligned with the mammographic boundary of the breast. Consequently, the parameters $\{a, b, c, r\}$ can be estimated from mammographic data using, e.g., the heuristic optimization algorithm of  [14].

To estimate the remaining parameters of the super-quadratic (i.e., c and t), we take advantage of the fact that information about the distance between compression paddles is always indicated in the header of mammography (DICOM) files. Consequently, denoting this distance by h, it is straightforward that $c = h/2$. Finally, to estimate t, the compression is assumed to be volume preserving. Thus, given an estimate of the breast volume derived from 3D MRI, one can simply find a value of t yielding a super-quadratic (2) of the equal volume.

Fig. 2.

Deformation of breast MRI under $\phi _\mathrm{glb}$. (a) Digital mammogram, (b) Original breast MRI boundary, (c) Deformed breast MRI boundary, (d) Examples of coronal (XZ) and sagittal (YZ) slices of the deformed MRI.

Given the original boundary of the breast (as observed in MRI scans) and its referenced “compressed” boundary (as represented by the fitted super-quadratic), the final step in estimation of $\phi _\mathrm{glb}$ consists in finding a spatial transformation that aligns these surfaces. Note that, in practical computations, the surfaces are represented by sets of discrete point coordinates. Consequently, in this work, we took advantage of the Coherent Point Drift (CPD) point registration algorithm  [15], which is a set-point registration technique allowing one to determine a spatial transformation that brings the two sets of discrete (surface) points into close correspondence with each other. This method was chosen because of the simplicity of its algorithmic structure that requires neither pre-processing nor special initialization.

It should be noted that the above method of surface registration can only be used to predict the motion of the boundary points, while remaining oblivious to what happens inside the breast mass. To overcome this problem, we extrapolate the boundary motion inside the breast volume by means of Thin Plate Spline (TPS) interpolation  [19]. Note that this type of interpolation is guaranteed to find a spatial transformation of minimum possible bending energy, which agrees well with the general tendency of soft biological tissue to deform in the most “ergonomic” way. Figure 2 provides an illustration of the above-described process.

It should be noted that the proposed method for estimating $\phi _\mathrm{glb}$ does not take into consideration the actual composition of breast tissue, effectively assuming it to be homogeneous. As a result, it would be unreasonable to expect $\phi _\mathrm{glb}$ thus obtained to be sufficient to explain the real displacement. This brings us to the problem of estimation of the residual transformation $\phi _\mathrm{res}$, which is detailed next.

2.2 Estimation of Residual Deformation

Let the estimated global transformation be denoted by $\phi _\mathrm{glb}^*$. Then, the residual deformation is estimated by registering $\mathcal {P}(f \circ \phi _\mathrm{glb}^*)$ to g, with a proper choice of the projection operator $\mathcal {P}$. It goes without saying, such a registration task is far from being trivial on the account of vast differences in the contrast mechanisms of the images being registered. One way to overcome this problem is to subject the images to an intensity transformation which would make them appear as if they have been unimodal. In particular, in this work, we compare two types of such transformations which are described below.

The first type of intensity transformation was based on the method proposed in   [12], which can be used to transform the intensities of $f \circ \phi _\mathrm{glb}^*$ to emulate the contrast of X-ray images (before applying the projection transform $\mathcal {P}$). The second approach, on the other hand, used the thickness of dense (fibroglandular) tissue as a “contrast independent” measure of image content. In particular, the thickness measurements are straightforward to extract from MRI volumes based on the results of image segmentation, while in the case of mammograms, these measurements are straightforward to compute using the method in  [16]. Note that, in this work, $\mathcal {P}$ was assumed to be a parallel-ray radiological projection, as suggested in  [17]. In both cases, we applied a free-form deformation model to describe $\phi _\mathrm{res}$. In particular, the latter has been modelled as a linear combination of separable cubic b-splines, with their knots distributed uniformly across $\varOmega$.

Mutual Information (MI)  [20, 21] and Cross Correlation (CC)  [22] are two common metrics being commonly used in the literature. However, since the intensities of MRI and mammogram have been normalized to be comparable, we used the Sum of Square Distance (SSD) criterion as a similarity measure in order to quantitatively asses the alignment of the images under registration. Formally, the problem of finding an optimal $\phi _\mathrm{res}$ can be formulated as given by

$$\begin{aligned} \phi _\mathrm{res}^*=\arg \min _{\phi _\mathrm{res}} \, \frac{1}{2} \iint \limits _\varOmega \Big | \int _z \Big ( f (\mathbf {r}+\phi _\mathrm{res} (\mathbf {r}\, | \,\mu )) \, dz \Big ) -g (x,y) \Big |^2 dx \, dy, \end{aligned}$$

(3)

where $\mathbf {r}= (x, y, z)$ and $\phi (\mathbf {r}|\mu )=\sum ^M_{i=1} \mu _i \mathbf {\beta }^3 (\mathbf {r}-\mathbf {r}_i)$. Note that the projection operator is incorporated in (3) explicitly, i.e. as an integration over z. Also note that the separability of b-splines implies that $\mathbf {\beta }^3(\mathbf {r})=\beta ^3(x)\beta ^3(y)\beta ^3(z)$.

The image deformation is defined on a sparse, regular grid of control points ($\mathbf {r}_i$) placed over the $\varOmega$. Each control point $\mathbf {r}_i$ has an associated three-element deformation coefficient, describing the x-, y-, and z-components of the deformation. The aim of the registration is to find optimal $\mu =\{\mu _i\}_{i=1}^M$ which minimizes the SSD criterion. Differentiating the latter w.r.t. the spline parameters produces the gradient vector $\nabla S (\mu )=[\frac{\partial S (\mu )}{\partial \mu _1}, \frac{\partial S (\mu )}{\partial \mu _2},\,\,.\,\,.\,\,.\,\,,\frac{\partial S (\mu )}{\partial \mu _M}]^T$, whose components are given by

$$\begin{aligned} \frac{\partial S (\mu )}{\partial \mu _i}=\iint \limits _{\varOmega }\bigg \{ \Big [ \int \limits _{z}f (\mathbf {r}+\phi (\mathbf {r}) \, dz-g (x,y) \Big ] \cdot \int \limits _{z}\nabla f (\mathbf {r}+\phi (\mathbf {r}\,|\, \mu ))^T \frac{\partial \phi (\mathbf {r})}{\partial \mu _i}dz \bigg \} dx dy. \end{aligned}$$

(4)

Subsequently, the minimization of SSD is carried out by means of the Gradient Descent algorithm, the iteration of which are given by

$$\begin{aligned} \mu ^{(t+1)}=\mu ^{(t)}-\tau \nabla S (\mu ^{(t)}), \end{aligned}$$

(5)

where $\tau > 0$ is a predefined step-size. In order to avoid local optima and decrease computation time, we used a multi-grid optimization scheme, where the registration is initiated at a coarse resolution level, followed by its gradual refinement at finer resolutions. By increasing the number of control points in multi-grid scheme, the deformation may not remain locally smooth (i.e. the deformation is not feasible). To further stabilize the numerical behaviour of image registration, the SSD cost function has been augmented by an additional (regularization) term given by

$$\begin{aligned} R(\mu )=\int _{\mathbf {r}\in \varOmega } \Big ( \Vert \nabla \phi _x (\mathbf {r}\,|\, \mu ) \Vert _2^2 + \Vert \nabla \phi _y (\mathbf {r}\, | \, \mu ) \Vert _2^2 + \Vert \nabla \phi _z (\mathbf {r}\, | \, \mu ) \Vert _2^2 \Big ) d\mathbf {r}, \end{aligned}$$

(6)

where $\phi _x (\mathbf {r}| \mu )$, $\phi _y (\mathbf {r}| \mu )$ and $\phi _z (\mathbf {r}| \mu )$ indicate deformation in x, y and z directions, respectively. Again as before, one needs to take gradient of $R(\mu )$ respect to $\mu _i$ to compute the gradient of R and, eventually, the gradient of the augmented cost.

In Eq. (4) we need to compute the gradient of $f(\mathbf {x})$ at any $\mathbf {x}\in \varOmega$. However, values of f are only available at a relatively small number of grid points. Therefore, an interpolation procedure is required in order to compute f at $\mathbf {x}$. To this end, we again used cubic B-splines to define f continuously over $\varOmega$ as $f (\mathbf {x})=\sum _{j} \alpha _{j} \beta ^{ (3)}\left( \mathbf {x}-\mathbf {x}_{j}\right)$, where $\alpha _j$ are the spline coefficients. To compute the gradient of f w.r.t. the latter, one needs to take the derivatives of f respect to x, y and z, i.e. $\nabla f=[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}]^T$. Thus, for instance, the first-order derivative of f w.r.t. x is computed as

$$\begin{aligned} \frac{\partial f (\mathbf {\mathbf {r}})}{\partial x}=\sum _{j} \alpha _{j}\left( \left. \frac{d \beta ^{ (3)} (u)}{d u}\right| _{u=x-x_{j}} \beta ^{ (3)}\left( y-y_{j}\right) \beta ^{ (3)}\left( z-z_{j}\right) \right) , \end{aligned}$$

(7)

where $\frac{d \beta ^{ (3)} (u)}{d u}=\beta ^{ (2)}\left( u+\frac{1}{2}\right) -\beta ^{ (2)}\left( u-\frac{1}{2}\right) .$

3 Experimental Results

To validate our proposed framework, we used a clinical dataset containing 10 clinical cases from 10 different subjects. Each case consisted of one MRI volume and two mammographic images (i.e., two projections in the cranio-caudal (CC) and medio-lateral oblique directions). All the subjects in our database had a unilateral breast lesion. The images were acquired approximately at the same time point to avoid significant change of tissues inside the breast. Breast MRI scans were acquired at the Princess Margaret Cancer Center (Toronto, Canada) with a 3T $Signa^{TM}$ Premier MRI scanner (GE Healthcare, Inc.). MRI volumes had a size of $[448 \times 448 \times 210]$ voxels and $[0.76\,\times \,0.76\,\times \,1.2]$ mm$^3$ per voxel. Mammograms were, acquired at the same center, composed of $[2294\,\times \,1914]$ pixels, with $[0.094\,\times \,0.094]$ mm$^2$ per pixel. Both MRI and mammograms were re-sampled to 1 mm resolution. Furthermore, histogram equalization was applied to increase the contrast of the glandular tissue. In the experiments reported in this paper, we focused only on registering breast MRI to CC view.

Fig. 3.

Registration results for case 1. (a) is the mammogram, (b) is the thickness image computed from mammogram, (c) shows aligned tumors using pseudo-CT image and (d) shows aligned tumors using fibroglandular thickness images (Color figure online)

The TRE criterion has been used to quantitatively assess the accuracy of the proposed framework. To compute TRE, it is necessary to have reference points in both images, which usually landmarks are used in the literature. We used the lesion centres as landmarks to compute registration error. All the lesions have been delineated by a trained radiologist, with the resulting segmentations used as a reference for error computation. The TRE figures have been computed as the Euclidean distance between the centroid of the 2D lesion in the mammogram and the centroid of the same lesion in the projected MRI.

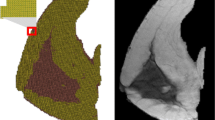
As it was mentioned before, we applied two approaches to transform the intensity of breast MRI images to be comparable with mammograms: a) building “emulated” X-ray images (pseudo-CT) from MRI volumes and projecting then onto the x-y plane, and b) computing the fibroglandular thickness from both MRI images and mammograms. Figure 3 shows the registration results for case 1. Lesions are approximately shown by a red circle in thickness image. deformed and projected lesions are shown with green colour, while purple colour shows the lesion mask annotated from the mammogram. The overlap between the two lesions is white. As it can be seen, in both cases, the projected lesions from MRI appear to be very close to the lesions visible in the mammograms.

Table 1. Target registration error, in millimeters, for the 10 CC-mammograms using pseudo-CT and thickness image

Table 2. TRE of recent FEM-based methods in the literature

Table 1 summarizes the registration results on all 10 cases in dataset. The obtained TRE for registration by thickness images is $5.44\,\pm \,3.61$ mm and it is $7.49\,\pm \,3.72$ mm for registration using pseudo-CT images. These values are comparable with TRE obtained from FEM-based method (shown in Table 2) in the literature. All of these methods use image intensity to optimize the objective function over registration parameters. Note that there is no standard database and one should be cautious comparing the results provided by previous works. However, comparing the TRE figures obtained by our approach as well as by the FEM-based methods, we can see that results are of the same order of accuracy. On the other hand, the computational time of the proposed registration (including segmentation, surface fitting and registration refinement) using MATLAB on CPU (Intel(R) CORE (TM) -i7 6500U) is about 40 min on average. At the same time, FEM-based methods can complete a single registration in an hour or few hours, even using numerical accelerations by means of GPUs. Finally, the proposed approach is fully automatic and can be executed on a standard PC at a reasonable time.

4 Conclusion

In this paper, we introduced a new registration framework to align breast MRIs and X-ray mammograms. We used surface registration and the FDD model to estimate the breast deformation in mammography. The proposed solution is simpler than FEM-based methods and requires less computational resources. The average target registration error of the presented registration approach was less than 6 mm which is an assumable error in the clinical practice with the aim of localizing susceptible areas within the MRI or the mammogram. Our approach is automatic and can run in an acceptable time with regular CPUs in hospitals.