Keywords

1 Endoscope Tracking

Endoscope three-dimensional (3-D) motion tracking is the key of image-guided minimally-invasive procedures that use endoscopes to visually examine and treat diseases in the interior of the organ cavity (tubular structures) through a natural orifice or transcutaneous port. Such a tracking aims to synchronize pre- and intra-operative image spaces in real time to provide surgeons with on-line 3-D visualization of tumor targets precisely located in the body and multimodal images. Numerous tracking methods have been discussed in the literature.

Image-based tracking aligns 2-D endoscopic video images to 3-D pre-operative volumetric data, especially performing 2-D/3-D registration to locate the endoscope  [1]. Shen et al.  [2] proposed to recognize typical structures to navigate the endoscope, while Byrnes et al.  [3] automatically summarized endoscopic video images to indicate the endoscope’s position in the body. More recently, Luo et al.  [4] used multiple instance learning and a discrepancy similarity to estimate the endoscope motion, while Shen et al.  [5] recovered the context-aware depth to predict the endoscopic camera pose. On the other hand, electromagnetic (EM) tracking is widely used to endoscope 3-D tracking  [6,7,8]. Hofstad et al.  [9] proposed a global to local registration method to improve the performance of EM tracking, while Attivissimo et al.  [10] discussed a new EM tracking system for computer assisted surgery. Kugler et al.  [11] established an experimental environment to precisely evaluate the performance of the EM tracking techniques. While image-based and EM-based endoscope tracking methods have their own advantages, they still suffer from limitations  [4, 12], e.g., image uncertainties, magnetic field distortion, tissue deformation, and patient movements (e.g., breathing, coughing, and beating). To deal with these limitations, a joint strategy of EM and image-based tracking provides a promising solution.

This work proposes a new hybrid strategy for smooth and accurate endoscope tracking that incorporates three new principles. First, we propose an anatomical constraint to spatially or physically limit EM sensor outputs inside anatomical tubular structures (e.g., bronchus, colon, and nasal sinus). Based on the segmented information from preoperative CT images, i.e., the centerline of the organ cavity, we constrain the current EM sensor output to be on this centerline. Such a constraint potentially keeps the EM sensor outputs inside the cavity interior under respiratory motion and tissue deformation. Next, we modify differential evolution and present a historically observed differential evolution (HODE) method to stochastically optimize EM sensor outputs and simultaneously fuse endoscopic video images. Additionally, a selective structural measure is introduced to evaluate the HODE optimization, which is robust to image artifacts or uncertainties and can accurately describe individual during iteration.

2 Approaches

The new joint EM-video endoscope tracking method consists of two main steps: (1) anatomical constraint and (2) historically observed differential evolution with parameter and fitness computation, all of which are discussed as follows.

Without loss of generality, we introduce some notations. Let \(\mathbf {I}_i\) and \((\mathbf {P}_i, \mathbf {Q}_i)\) be the endoscopic video image and EM sensor tracked camera 3-D pose (including position and orientation) at time or frame i. The endoscopic camera’s position is \(\mathbf {P}_i\) and its orientation is represented by a unit quaternion \(\mathbf {Q}_i\).

Fig. 1.
figure 1

Anatomical centerlines constrain the EM tracked pose inside the tubular structure to obtain the camera’s projected position and updated orientation.

Full size image

2.1 Anatomical Constraint

The idea of the anatomical constraint is to use the centerline of the hollow or tubular organ to limit or project the EM tracked position and orientation on the centerline. Hence, we first segment preoperative CT images to obtain a set of centerlines (curves) \(\mathcal {C} = \{\mathbf {C}_k=(\mathbf {C}^{s}_k,\mathbf {C}^{e}_k)\}^{K}_{k=1}\) (K is the number of the extracted centerlines, \(\mathbf {C}^{s}_k\) and \(\mathbf {C}^{e}_k\) are the centerline’s start and end points, respectively), and actually \(\mathbf {C}_k\) consists of a set of 3-D points \(\mathbf {C}_k=\{\mathbf {C}^{s}_k,\cdots ,\mathbf {C}^{e}_k\}\).

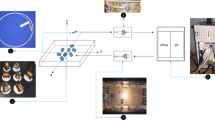
We then assign the closest centerline \(\mathbf {\hat{C}}_k\) to the position \(\mathbf {P}_i\) by minimizing the distance between the 3-D position or point \(\mathbf {P}_i\) and centerline set \(\mathcal {C}\) (Fig. 1)

$$\begin{aligned} \mathbf {\hat{C}}_k = \arg \min _{\mathbf {C}_k \in \mathcal {C} } H(\mathbf {P}_i,\mathbf {C}_k), \end{aligned}$$
(1)

where the distance \(H(\mathbf {P}_i,\mathbf {C}_k)\) from the position \(\mathbf {P}_i\) to \(\mathbf {C}_k\) is calculate by

$$\begin{aligned} H(\mathbf {P}_i,\mathbf {C}_k) = \left\{ \begin{array}{ll} ||\mathbf {P}_i - \mathbf {C}^s_k|| &{}\gamma < 0\\ ||\mathbf {P}_i - \mathbf {C}^e_k|| &{}\gamma > L_k\\ \sqrt{||\mathbf {P}_i - \mathbf {C}^s_k||^2 - {\gamma }^2} &{}\text {otherwise} \end{array} \right. , \end{aligned}$$
(2)

where the centerline length \(L_k=||\mathbf {C}^e_k - \mathbf {C}^s_k||\) and \(\gamma \) denotes the length of the vector \((\mathbf {P}_i - \mathbf {C}^{s}_k)\) that is projected on the centerline \(\mathbf {C}_k\), which is computed by

$$\begin{aligned} \gamma = \left\langle \mathbf {P}_i - \mathbf {C}^{s}_k,\;\mathbf {C}^{e}_k - \mathbf {C}^{s}_k \right\rangle /{||\mathbf {C}^{e}_k - \mathbf {C}^{s}_k||}, \end{aligned}$$
(3)

where \(\gamma < 0\) and \(\gamma > L_k\) indicate that projected point \(\mathbf {\hat{P}}_i\) is located on the parent and child centerlines of the centerline \(\mathbf {C}_k\), respectively; otherwise, it will be located on the centerline \(\mathbf {C}_k\), and \(\left\langle ,\right\rangle \) denotes the dot product.

Note that we possibly obtain several closest centerlines \(\{\mathbf {\hat{C}}_{k}\}_{k=1,2,3,\cdots }\) that have the same distance to the point \(\mathbf {P}_i\) after the minimization procedure (Eq. 1). We compute the angle between the orientation \(\mathbf {Q}_i\) in \(z-\)direction \(\mathbf {Q}_i^z\) and centerline direction \((\mathbf {\hat{C}}^{e}_{k} - \mathbf {\hat{C}}^{s}_{k})||\mathbf {\hat{C}}^{e}_{k} - \mathbf {\hat{C}}^{s}_{k}||^{-1}\) to determine optimal centerline \(\mathbf {\tilde{C}}_k\):

$$\begin{aligned} \mathbf {\tilde{C}}_k = \arg \min _{\{\mathbf {\hat{C}}_k\}_{k=1,2,3,\cdots }} \arccos \left\langle \frac{\mathbf {\hat{C}}^e_k - \mathbf {\hat{C}}^s_k}{||\mathbf {\hat{C}}^e_k - \mathbf {\hat{C}}^s_k||},\; \frac{\mathbf {Q}_i^z}{||\mathbf {Q}_i^z||}\right\rangle . \end{aligned}$$
(4)

After finding the optimal centerline \(\mathbf {\tilde{C}}_k\), we project the EM sensor tracked position \(\mathbf {P}_i\) on the centerline \(\mathbf {\tilde{C}}_k\) and obtain the projected point \(\mathbf {\tilde{P}}_i\) by

$$\begin{aligned} \mathbf {\tilde{P}}_i = \mathbf {\tilde{C}}^s_k + \frac{\left\langle \mathbf {P}_i - \mathbf {\tilde{C}}^s_k,\;\mathbf {\tilde{C}}^e_k - \mathbf {\tilde{C}}^s_k\right\rangle }{||\mathbf {\tilde{C}}^e_k - \mathbf {\tilde{C}}^s_k||} \frac{(\mathbf {\tilde{C}}^e_k - \mathbf {\tilde{C}}^s_k)}{||\mathbf {\tilde{C}}^e_k - \mathbf {\tilde{C}}^s_k||}. \end{aligned}$$
(5)

We also update the camera orientation in \(z-\)direction by the optimal centerline

$$\begin{aligned} \mathbf {\tilde{Q}}^z_i = (\mathbf {\tilde{C}}^e_k - \mathbf {\tilde{C}}^s_k)/||\mathbf {\tilde{C}}^e_k - \mathbf {\tilde{C}}^s_k||. \end{aligned}$$
(6)

Finally, we obtain the constrained camera position \(\mathbf {\tilde{P}}_i\) and orientation \(\mathbf {\tilde{Q}}_i\) that are further updated by the following stochastic optimization procedure.

2.2 Historically Observed Differential Evolution

Differential evolution (DE) is a powerful tool for various stochastic optimization problems and applications  [13]. Basically, DE performs three main operators: (1) mutation, (2) crossover, and (3) selection. The mutation and crossover operators play an essential role in DE, and balance convergence and computational efficiency. Improper mutation and crossover potentially result in premature convergence and local minima. The selection operator should be appropriate to precisely evaluate the quality of the solution during stochastic optimization.

DE has no any strategies to recall historical solutions that are the best solutions in the previous generation, while it also does not incorporate the current observation (the current endoscopic image and camera pose) in mutation and crossover. Moreover, accurate initialization of a population of target vectors implies that all potential solutions are powerful and fast to find the optimal solution. Unfortunately, inaccurate initialization and improper mutation or crossover possibly lead to get trapped in local minima with premature convergence. Our idea is to recall historical best solutions and simultaneously introduce the current observation into DE and presents a new version of DE discussed as follows.

Accurately Observed Initialization. Let \(\mathbf {X}^g_{i,j}\) be an individual or target vector in a population of vector cloud \(\mathcal {X}^g_{i}=\{\mathbf {X}^g_{i,j}\in \mathcal {R}^D\}^J_{j=1}\) (J is the population size) at generation or iteration g (\(g=1,2,3, \cdots , G)\) at frame i, and \(\mathbf {X}^g_{i,j}=(X^g_{i,j,1},X^g_{i,j,2},X^g_{i,j,d},\cdots , X^g_{i,j,D})\) in a D-dimensional space.

Before the target vector propagation (mutation and crossover), \(\mathbf {X}^g_{i,j}\) is usually initialized in accordance with the search space constrained by the prescribed minimal and maximal bounds (\(\mathbf {X}^g_{i,min}\) and \(\mathbf {X}^g_{i,max}\)):

$$\begin{aligned} X^g_{i,j,d} = X^g_{i,min,d}+ Rand[0,1](X^g_{i,max,d}-X^g_{i,min,d}),\, d=1,2,\cdots ,D, \end{aligned}$$
(7)

where Rand[0, 1] is a random number that yields uniform distribution between 0 and 1. This initialization has two potential problems: first is difficult to find or determine the bounds of \(\mathbf {X}^g_{i,j}\) in practice and second is that the population gets trapped in a impoverishment problem which implies that the population lose the diversity with weak exploration after several iteration.

To avoid the impoverishment problem, we introduce the previous global best \(\mathbf {X}^g_{i-1,best}\) at generation g and current observation (pose), which is the constrained camera position \(\mathbf {\tilde{P}}_i\) and orientation \(\mathbf {\tilde{Q}}_i\) obtained above, to initialize \(\mathbf {X}^g_{i,j}\)

$$\begin{aligned} \mathbf {X}^g_{i,j} = \underbrace{\mathbf {X}^g_{i-1,best}}_{History} + Rand[0,1]\varDelta , \varDelta =\underbrace{[\mathbf {\tilde{P}}_i - \mathbf {\tilde{P}}_{i-1},\mathbf {\tilde{Q}}_i-\mathbf {\tilde{Q}}_{i-1}]^T}_{Incremental\; observation}, \end{aligned}$$
(8)

which is a seven-dimensional vector (\(D=7\)) and the transpose T.

Cloud Mutation. The mutation operator aims to generate mutant or perturbed vectors in accordance with \(\mathbf {X}^g_{i,j}\) difference vectors and evolutionary factors, i.e., explore more potential solutions in the search space. Five mutation strategies are most commonly used to generate the mutant vector \(\mathbf {V}^g_{i,j}\)  [13]. Basically, the two-difference-vector based mutation strategies provide better perturbation than others but their performance requires to be further investigated.

To exploratively propagate \(\mathbf {X}^g_{i,best}\), this work proposes a new mutation strategy that integrates the cognitive and social elements defined as follows:

$$\begin{aligned} \mathbf {V}^g_{i,j}= \mathbf {X}^g_{i,j} + F_1(\underbrace{\mathbf {X}^g_{i,local}-\mathbf {X}^g_{i,j}}_{Cognitive \;element})+F_2(\underbrace{\mathbf {X}^g_{i,global}-\mathbf {X}^g_{i,j}}_{Social \;element}), \end{aligned}$$
(9)

where \(\mathbf {X}^g_{i,local}\) and \(\mathbf {X}^g_{i,global}\) are the local and global best individuals at generation g. While the cognitive part aims to make individuals exploring most competitive solutions in the previous iteration, the social part establishes a good solution where the population tends to reach. Two evolutionary factors \(F_1\) and \(F_2\) control the perturbation of two differential variations and are adaptively calculated by

$$\begin{aligned} F_1=\mathcal {W}(\mathbf {I}_i, \mathbf {X}^g_{i,local})/\mathcal {W}( \mathbf {I}_i, \mathbf {X}^g_{i,low} ), \; F_2 = \mathcal {W}(\mathbf {I}_i, \mathbf {X}^g_{i,global})/\mathcal {W}(\mathbf {I}_i, \mathbf {X}^g_{i,low}), \end{aligned}$$
(10)

where \(\mathcal {W}\) is a fitness function related to the current observed endoscopic image \(\mathbf {I}_i\) and \(\mathbf {X}^g_{i,lowest}\) denotes the target vector with the lowest fitness value.

figure a

Cloud Crossover. The crossover operator aims to improve the population diversity and avoid premature convergence and local minima by creating a set of trial vector \(\mathbf {U}^g_{i,j}=\{U^g_{i,j,1},U^g_{i,j,2}, U^g_{i,j,d},\cdots , U^g_{i,j,D}\}\). Traditional crossover operators like binomial distribution provide the target and mutant vectors without any perturbation, resulting in a faster but premature convergence.

Based on our concept of using the current observation, we introduce a new crossover operator with the incremental observation \(\varDelta \) (Eq. 8) to obtain \(\mathbf {U}^g_{i,j}\).

$$\begin{aligned} \mathbf {U}^g_{i,j}= \left\{ \begin{array}{ll} \mathbf {V}^g_{i,j} + Rand[0,1]\varDelta &{} \quad \mathrm {if} \; (Rand[0,1]\le C_r) \;\text {or}\; (d = d_r) \\ \mathbf {X}^g_{i,j} + Rand[0,1]\varDelta &{} \quad \mathrm {if} \; (Rand[0,1]\ge C_r) \;\text {or}\; (d \ne d_r) \end{array} \right. , \end{aligned}$$
(11)

where \(C_r\) is the crossover rate and \(d_r\) is randomly selected from \(\{1,2,d,\cdots ,D\}\).

History Update and Recall. After the mutation and crossover, we need to update \(\mathbf {X}^g_{i,j}\) by computing and comparing the fitness \(\mathcal {W}\) of \(\mathbf {U}^g_{i,j}\) and \(\mathbf {X}^g_{i,j}\).

For each vector in two clouds \(\mathcal {U}^g_i=\{\mathbf {U}^g_{i,j}\}^J_{j=1}\) and \(\mathcal {X}^g_i=\{\mathbf {X}^g_{i,j}\}^J_{j=1}\), we calculate its fitness \(\mathcal {W}(\mathbf {I}_i,\mathbf {X}^g_{i,j})\) that is defined as the similarity between the current endoscopic image \(\mathbf {I}_i\) and 2-D virtual image generated by the camera pose (i.e., \(\mathbf {X}^g_{i,j}\) or \(\mathbf {U}^g_{i,j}\)) using volume rendering techniques:

$$\begin{aligned} \mathcal {W}(\mathbf {I}_i,\mathbf {X}^g_{i,j}) = \frac{1}{M} \sum _{\{\varOmega ^m_i\}^M_{m=1}} {\frac{1}{\left| \varOmega ^m_i\right| }} {\sum _{\varOmega ^m_i}} \frac{\left( 2\mu _i \mu _x + C_1\right) \left( 2\sigma _{i,x} + C_2\right) }{\left( \mu ^2_i + \mu ^2_x+C_1\right) \left( \sigma ^2_i + \sigma ^2_x+C_2\right) }, \end{aligned}$$
(12)

where \(\sigma _{i,x}\) is the correlation between images \(\mathbf {I}_i\) and \(\mathbf {I}_x(\mathbf {X}^g_{i,j})\) at region \(\varOmega ^m_i\) with \(|\varOmega ^m_i|\) pixels (\(m=1,2,\cdots ,M)\); \(\mu _i\) and \(\mu _x\) are the mean intensity, \(\sigma _i\) and \(\sigma _x\) are the intensity variance, and \(C_1\) and \(C_2\) are constants. Our fitness function selects specific structural regions \(\varOmega ^m_i\) on \(\mathbf {I}_i\) to precisely compute the fitness value.

While we ascendingly sort all the vectors in \(\mathcal {U}^g_i\) and \(\mathcal {X}^g_i\) in accordance with their fitness values, we choose the half better-fitness vectors from \(\mathcal {X}^g_i\) (recall the history) and select the half better-fitness vectors from \(\mathcal {U}^g_i\) (update the history) to generate new target vector \(\mathcal {X}^{g+1}_i=\{\mathbf {X}^{g+1}_{i,j}\}^J_{j=1}\) for the next iteration.

After each iteration (generation), we select the best vector \(\mathbf {X}^g_i\) with the best fitness from \(\mathcal {U}^g_i\) and \(\mathcal {X}^g_i\) at iteration g. This implies that we obtain the best vector set \(\mathcal {X}_i=\{\mathbf {X}^1_i,\cdots ,\mathbf {X}^g_i,\cdots ,\mathbf {X}^G_i\}\) after iteration G. Therefore, the endoscope’s position and orientation \([\mathbf {\tilde{P}}^*_i, \mathbf {\tilde{Q}}^*_i]^T\) at frame i are determined by

$$\begin{aligned} \mathbf {X}^*_i = \arg \max _{\mathbf {X}^g_i\in \mathcal {X}_i} \mathcal {W}(\mathbf {I}_i,\mathbf {X}^g_i), \quad \mathbf {X}^*_i\mapsto [\mathbf {\tilde{P}}^*_i, \mathbf {\tilde{Q}}^*_i]^T \end{aligned}$$
(13)

Eventually, we summarized our new tracking method that combines anatomical constraint with historically observed differential evolution in Algorithm 1.

Fig. 2.
figure 2

Tracking error and smoothness of different methods on Case 6

Full size image

3 Results

We validate our method on six patient datasets more than 9,000 frames and compare it to several methods: (1) M1  [6], a hybrid method based on Kalman filtering, (2) M2  [7]: a stochastic optimization based method, and (3) M3  [9]: a global-to-local registration method. We manually generated ground truth and calculate the position and orientation errors, while we define the smoothness as the average Euclidean distance of the estimated positions among continuous frames as well as the orientations to evaluate if a tracking is large jitter or jump. Additionally, we investigate the fitness (similarity) of the compared methods.

Table 1. Comparison of tracking error, smoothness, fitness, and runtime of using the methods (the units of position and orientation are millimeter and degree)
Full size table
Fig. 3.
figure 3

Visual comparison of the results on Case 2. The first row shows real images and other rows illustrate 2-D virtual images generated by the estimated positions and orientations of using M1  [6], M2  [7], M3  [9], and ours, respectively.

Full size image

Figure 2 shows the tracking error and smoothness of using the different methods. Table 1 quantitatively summarizes all the tracking results. The tracking error was reduced from (5.9 mm, 9.9\(^\circ \)) to (3.3 mm, 8.6\(^\circ \)). Figure 3 visually compares the tracked results of using the four methods. Based on volume rendering methods and the estimated position and orientation, we can generate 2-D virtual images and check if they resemble real endoscopic video images: the more closely resembling, the more accurately tracking. All the experimental results demonstrate that our method significantly outperforms others.

4 Discussion and Conclusion

The objective of this work is to deal with the problems of image artifacts, patient movements, and inaccurate EM sensor outputs in endoscope tracking. Our idea to tackle these problems is to constrain the outputs and stochastically optimize the endoscope pose based on a new algorithm of historically observed differential evolution, and the experimental results demonstrate its effectiveness.

Although our proposed method is a promising and effective strategy, it still has potential limitations. First, the anatomical constraint depends on the segmentation accuracy of the bronchial tree. Next, low-quality endoscopic video images with artifacts increase the error of the fitness computation. Moreover, we further investigate the iteration and population size to improve the performance of historically observed differential evolution. Additionally, the computational time of our method was 2.6 s per frame. We will further improve the computational efficiency to meet real-time requirement of clinical applications.

In summary, this work develops a new hybrid endoscope tracking method that combines anatomical constraint and historically observed differential evolution. The experimental results demonstrate that our methods outperforms others, especially it reduced the tracking error from (5.9 mm, 9.9\(^\circ \)) to (3.3 mm, 8.6\(^\circ \)).