A Novel Method to Estimate Students’ Knowledge Assessment

Abstract

Performance of learning can be enriched with proper and timely feedback. This paper proposes a solution based on a Bayesian network in machine learning that can examine and judge students’ written response to identify evidences that students fully comprehend concepts being considered in a certain knowledge domain. In particular, it can estimate probabilities that a student has known concepts in computer science at different cognitive ability levels in a sense. Thus, the method can offer learners personalized feedbacks on their strengths and shortcomings, as well as advising them and instructors of supplementary education actions that may help students to resolve any lacks to improve their knowledge and exam score.

1 Introduction

In a learning process, an assessment is essential to help instructors to evaluate if learners’ activities or performances get along with the academic community’s expectations, understand dimensions of studies to improve learners’ achievement, design course materials and learning activities. Educators have often tried to design an sufficient assessment to cover broader objectives of their courses [22]. Its purpose is to arrange a superlative educational process to inspire students to learn both skills directly related to their specialty and additional knowledge domains in the professional working environment. Knowing what and how students learn is important for judging the appropriateness of learning objectives and deciding how to improve instructions [9]. In an education circumstance, instructors usually want their learners by themselves to discover connections between concepts they study in their major and materials they study across other courses in their curriculum from a basic understanding of concepts to asking more complex questions via assessments. For the time being, Concept Mapping (CM) [1] and Bloom’s Taxonomy (BT) [2] have been becoming common assessment techniques in science education. Concept mapping is one of the most powerful graphical tools for the knowledge acquisition [10, 11], showing what learners see as important concepts and how they relate these concepts. Valery et al. in [9] delineates how the concept mapping technology is utilized in engineering education in the field of electronics to help learners to see what they have acquired from lessons. Nevertheless, cognitive ability levels of students are not well-thought-out. The studies [3,4,5] research the problem in evaluation by using semantic network ontology and do not come up with understandable estimation for students. BT is to organize higher forms of knowledge in education from simple to more complex levels [15]. To reach a higher level, the previous level must be mastered. The authors in [21] using BT levels to validate learners’ concept states by using analysis methods without taking relationships between concepts at multiple cognitive bloom levels, or “lucky guess” and “careless mistake” reliance, as well as fairly considered academic concepts in a dimension into account. “Lucky guess” is a case that a student doesn’t know an answer, but he/she can guess it correctly while “careless mistake” is a case that a student knows an answer, but he/she answers it incorrectly. From this perspective, we utilize the two techniques to simply present a concept based assessment method by using Cognitive Ability Levels, which are in reference to BT [2, 3]. In this paper, we introduce a novel model called Cognitive Ability Level Concept based Graphs which maps entire concepts in computer sciences into one concept domain space used for checking students’ knowledge. A concept domain space is a knowledge space along with relationships between concepts of an assessed domain, and multi Cognitive Ability Levels (CALs) indicate levels of “Remember”, “Understand”, “Apply”, “Analyze”, “Evaluate”, “Create” that students have achieved. In addition, we propose a Bayesian network based technique to deeply estimate students’ knowledge at different ability levels in an assessment with respect to concepts and their multiple CAL relationship in a sense while taking into account “Lucky guess” and “careless mistake” reliance, fair pedagogical concepts consideration. As a result, it can give learners feedbacks on their strengths and shortcomings, along with advising learners and instructors of additional learning exertions that may help learners to resolve any weakness. Besides, it can also assist instructors to verify exactly the covered knowledge of a course objective and answer a question of whether an assessment model can be constructed properly and build a new prototype of learning analytics such as course and learning activity design, knowledge based test design, assessment of learning activity design, building a learning map of curriculum areas from this point forward. Moreover, to validate the cognitive ability levels and concept states which inform if a student has already learned, is ready to learn, or is not ready to learn knowledge at a certain ability level, the approach is experimentally conducted and the experiment results can show the efficiency and usability of our method.

Further sections of the study are organized as follows: Sect. 2 provides information about related work, Sect. 3 discusses the knowledge representation, Sect. 4 details the problem statement and its corresponding solution approach, Sect. 5 describes experiments and results. Section 6 concludes the paper and outlines future work.

2 Related Studies and Background

Various researches have been done to solve related problems to develop the knowledge assessment theory as adaptive assessment [8, 10, 19]. Yusuf Kavurucu et al. in [12] presents an approach where data is symbolized in graph structures and graph mining techniques are used for knowledge detection. Concept detection in multi-relational data mining is to find relational policies that best define a relation, called target relation, with regard to other relations in a database, called background knowledge. The proposed method, namely G-CDS (Graph-based Concept Discovery System), utilizes methods both from substructure-based and path-finding based approaches, hence it can be considered as a hybrid method. G-CDS generates disconnected graph structures for each target relation and its related background knowledge, which are initially stored in a relational database, and utilizes them to guide generation of a summary graph. The summary graph is traversed to find concept descriptors. In [6], Falmagne et al. introduced the knowledge state assessment theory. This theory was derived from the Knowledge Space Theory earlier proposed by Falmagne, Doignon and Thiery [7]. Many research works tried to develop the knowledge assessment theory as adaptive assessment [8, 10, 19]. The work in [6] is in reality accomplished by establishing an Assessment and Learning in Knowledge Spaces (ALEKS). Much research work has been done for ALEKS such as [11, 12]. Systems like ALEKS, which are applications of Flamagne’s theory, so far have only been applied to mathematics and chemistry. It does not recognize finer distinctions of concepts. Although, such coarse definition of competency generates useful results in some disciplines, finer distinctions of skill levels, for example given links of verbs describing the skills required to attain the concepts, are very important for giving accurate results in applied disciplines such as all the branches of engineering education as well as computer science and technology education. During 1990’s, Anderson [2] revised the Bloom category to ponder the levels as verbs rather than nouns. His efforts were to use verbs to create sufficient understanding of learning results and student performance. Using revised Bloom Taxonomy [2] for educational assessment has been an extremely rich and interesting research area. Some scientists try to apply pedagogical taxonomy in a learning space of a learning subject such as [16,17,18]. In the most related work [16], they used the ideas of Competence-based Knowledge Space Theory. They propose a skill characterized as a pair consisting of a concept and an activity. Some other researchers try to use the revised Bloom Taxonomy for assessment and present new assessment approaches such as the work of [19,20,21]. None of them used the verbs of revised Bloom’s Taxonomy to identify the relation between the concepts in the assessed domain and the assessment. However, Rania Aboalela et al. [18] assumed that those cognitive Bloom’s taxonomy levels (understanding, applying, analyzing, evaluating, creating) are given then testing can be done based on Bayesian inference to determine student’s proficiency levels (specific to only a cognitive domain level) from student test results with an assumption that there is no relation between “lucky guess” and “careless mistake” and no fair consideration among concepts. Moreover, a major unsolved problem in the new paradigm of learning analytics is the automatic inference of cognitive domain relationship between domain-concepts in a particular context (sense) and the link between two concepts are only at a specific cognitive ability level. Fatema Nafa et al. [19] proposes a platform that can infer cognitive relationship (Cognitive Skill Dependencies) among domain concepts as they appear in the text in either phrase or single word form by identifying the link between the concepts as the skill required to learn the concepts at a certain skill level, which identifies the prerequisite relations between the concepts. For ease of understanding, we present an overview of common related approaches along with ours in Table 1.

Table 1. Existing methods and ours.

As shown in Table 1, our study considers all of the three factors comprising:

• Concept relationships at multiple cognitive ability levels at a sense.

• Dependency of “Lucky guess” and “careless mistake”.

• In a dimension, fair pedagogical concept consideration.

Moreover, it focuses on more precisely Bayesian estimating ability levels of student knowledge in an assessment in order to offer students feedbacks on strengths and shortcomings, as well as advising students and instructors of additional learning activities that may help students to resolve any shortages.

3 Representation

In this section, some terms, notations used in the paper are defined and some assumptions are delivered.

Content skill knowledge representation here is visualized by graphs in a dimension and used natural language to represent concepts and propositions, i.e. to represent semantic knowledge and its conceptual organization (structure).

Pedagocal Knowledge Dimesional Lattice (PKDL) (e.g., as in Fig. 1) is an arrangement which is a combination of pedagogical knowledge unit concept nodes and their relationships in three dimensions (or perspectives): Collection dimension (CoD), Cognitive Ability Level (CAL) dimension and Ontology dimension (OnD) defined together with related definitions as follows:

Fig. 1.

Composition graph

• Pedagogical knowledge unit concept (C): Basic elements of this lattice are Pedagogical knowledge unit concepts C and their relationships. C is the smallest unit in knowledge representation [17], means mental representations, abstract objects or abilities that make up the fundamental building blocks of thoughts and beliefs. They play an important role in all aspects of cognition in pedagogy. A concept can have one sense or many senses (called sense set). A sense of a concept is like a meaning of a concept based on the context of the concept’s usage in a sentence. In the composition graph at the Fig. 1, concepts are enclosed in ovals such as the concept “State”, which has 4 senses s1, s2, s3, s4.

• Pedagogical Knowledge Concept Graph (PKCG): PKCG is a graph including all elementary concepts covered in a knowledge domain in a collection dimension. A PKCG contains Pedagogical knowledge unit concepts nodes, collection nodes and their links. A textbook provides an organization of concepts in a tree hierarchy. A PKCG tries to capture a book’s presentation or organization. Thus, leaves of PKCG are concepts either in single words or phrase words. The location of a node in PKCG indicates the concept occurs in the textbook. For example: collection area. book title. author. publisher. ISBN. date of publication. chapter. section. subsection. sentence. word location. A concept can appear in sentences of multiple paragraphs. The role of concept graph is to support personal learning, thus, help instructors or students to find errors in knowledge acquisition. For instance, the part G1 of the Fig. 1 represents a fragment of concept graph built for a science domain. The graph developed includes nodes with key concepts enclosed in ovals, connecting to other collection nodes in circles.

In PKDL, each dimension provides additional classifications of knowledge units and their relationships.

Collection Dimension

Collection Dimension classifies the nodes into following types. Collection nodes: a collection includes atomic concepts, and higher level aggregations of atomic concepts used in pedagogy. These can be chapters, sections, subsections, sentences of book, or learning materials such as syllabus, test, questions, etc. Collection nodes are the nodes S1, S2, S3 in circles as shown in the Fig. 1. Besides CoD includes the link type ‘Collection’ which is a directed round dot link representing ‘member of’ relationship between sink node and source nodes at specific senses. For example, the link in the part G1 of the Fig. 1 represents that the concepts “Country” at the sense s2, “Florida” at the sense s2, and “Liberty” at the sense s2 are members of the sentence node S1.

Cognitive Ability Level Dimension (CAL)

Cognitive Ability Level Dimension (CAL): CAL Dimension presents relationships between pedagogical knowledge unit concepts regarding ability supports needed from a source concept $C_{s}^{{L_{s} }}$ $\forall s \in N$ at a certain cognitive ability level L_i at a sense set element s_s, to a target concept $C_{t}^{{L_{t} }}$ at a specific cognitive ability level L_t at a sense set element s_t, $\forall t_{{}} \in N$. When there is a directed link from the source concept $C_{s}^{{L_{s} }}$ to the target concept $C_{t}^{{L_{t} }}$, it means that knowing $C_{t}^{{L_{t} }}$ correctly at a cognitive ability level L_t at the sense s_t is dependent on knowing $C_{s}^{{L_{s} }}$ correctly at a cognitive ability level L_s at the sense s_s. The cognitive ability levels refer to 6 levels such as “Remember”, “Understand”, “Apply”, “Analyze”, “Evaluate”, “Create” [2] which are equal to $\left\{ {b_{1} ,b_{2} ,b_{3} ,b_{4} ,b_{5} ,b_{6} } \right\}$ with the same order. The part G₃ of the Fig. 1 illustrates that a direct dash link from the concept “Executive” to the concept “Operation” means that to know the concept “Operation” at the cognitive ability level b₂ at the sense s₅ $\forall \,b_{ 2} \in BTS = \left\{ {b_{1} ,b_{2} ,b_{3} ,b_{4} ,b_{5} ,b_{6} } \right\}$, the concept “Executive” must be known at the level b₁ at the sense s₃ in advance. A defined concept is described by a particular entry while earlier entries used to explain the defined concept are called parents.

Ontology Dimension

Ontology is the philosophical study of being. More broadly, it studies concepts that directly relate to being, in particular becoming, existence, reality, as well as the basic categories of being and their relations [16]. An ontology link presents the ontological relationship between concepts. We identified the ontological relationship between concepts based on WordNet [19]. There are 10 types of links of ontological relationships between concepts including: Synonym (Syno), Antonym (Anto), Hyponym (Hypo), Subpart (Subp), Subclass (Subc), Instance (Inst), Attribute (Attr), Functional Property (FPro), Environment (Envi), and Measure (Meas). In a graph, ontological relationships are characterized as directed links from a source to a target. E.g. if A is, Subpart, Subclass, Instance of, or Synonym of concept B then the concept A is represented as a source node at a sense and the concept B is represented as a target node at another sense. In the part G2 of the Fig. 1, the ontological relationship shows that the concept “State” at the sense s4 is a hyponym of the concept “Freedom” at the sense s4.

4 Problem Definition and Solution

This section discusses some terms used, and then we are going to describe the problem statement.

• Evidence Set (ES) [18]: in an assessment, a test is introduced to students in a class. A test normally is composed of a set of questions. Answering a question qi with a response Qi requires knowledge about a set of concepts. A set of responses is called an evidence set. When a student successfully answers a question, we can conclude that he has learned the concept set at a certain skill level, which is asked by the question. After the test, an examiner can evaluate and grade for the test.

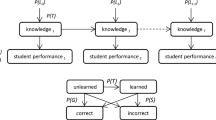
• Confirmed Ability set (CA): CA [6] is defined as where there is a direct evidence that an individual knowing or not knowing a concept C_y at a cognitive ability level L_y at a sense s_y. The concept is considered a part of Confirmed Ability set at a cognitive ability level L_y if C_y is a correct concept at the cognitive ability level L_y at a sense s_y. We denote $C_{y}^{{L_{y} }} \in CA\left( {L_{\text{y}} , \, s_{\text{y}} } \right)\,\forall \,C_{y,} s_{\text{y}}$. The collection answer node denoted by Q_i in squares and the concept node $C_{y}^{{}}$ at a cognitive ability level L_y denoted by $C_{y}^{{L_{y} }} \,\,\forall_{i,y} \in N$ at the sense s_y $\forall y \in N$ in ovals. When there is a directed link from the collection node Q_i to the concept node $C_{y}^{{L_{y} }}$ (indicated by a dash arrow) it means that the ability to have the answer Q_i correctly is dependent on knowing the concept $C_{y}^{{L_{y} }}$ correctly. In other words, to answer the question q_i correctly, a student should know the concept C_y at the level L_y at the sense s_y as an example presented in Fig. 2.

  Fig. 2.

  

  Confirmed Ability illustration

• Derived Ability set (DA): DA indicates there is an indirect evidence that learners know a specific concept at a certain ability level at a specific sense. Thus, DA is an essential set of confirmed concepts at a certain ability level, but they have never been directly tested. In Fig. 3, there is an indirect evidence that the concept node Cw at Cognitive Ability Level Lw can be understood by learners, then the concept Cw belongs to DA set.

  Fig. 3.

  

  Derived Ability

Let a learner answer a question q_r with an answer Q_r, which gives evidence of his/her state of prior knowledge about a set of concepts $S = \, \{ C_{u}^{{L_{u} }} , \ldots ,C_{z}^{{L_{z} }} \}$, $S \in CG$, including children nodes of Q_r and $L_{u} ,L_{z} \in BTS$. A correct answer is denoted by Q_r, and an in correct answer is denoted by $\bar{Q}_{r}$. We are going to define other terms as follows.

• Apriority probability (non-evidence based probability): Without evidences, unconditional probability of knowing the concept $C_{i}^{{L_{i} }}$ is $P(C_{i}^{{L_{i} }} ) = k$ and unconditional probability of giving the correct answer Q_r is $P\left( {Q_{r} } \right) = a$.

• Evidence based probability: Supposing parent of a concept $C_{i}^{{L_{i} }}$ is unknown, a conditional probability of knowing concept $C_{i}^{{L_{i} }}$ based on its unknown parents is $P\left( {C_{i}^{{L_{i} }} \left| {\overline{{C_{i - x}^{{L_{i} }} }} } \right.} \right) = u^{1/h}$ with h being the number of parent’s children nodes, $\forall x < i, x \in N$.

• Lucky guess: In case a response’s dependence concepts are not known, it is still correct. That is a “lucky guess”. Assumed the response is correct, the probability of not knowing the dependence concepts $S = \{ C_{u}^{{L_{u} }} , \ldots ,C_{z}^{{L_{z} }} \}$, is $P\left( {\left. {\overline{{C_{u}^{{L_{u} }} \ldots C_{z}^{{L_{z} }} }} } \right|Q_{r} } \right) = l_{r}$ $\forall l_{r}$ $\in \left[ {0, 1} \right)$ (called “lucky guess” probability), then probability of not knowing the concept $C_{i} \in S$ is $P\left( {\left. {\overline{{C_{i}^{{L_{i} }} }} } \right|Q_{r} } \right) = l_{r}^{1/y}$ with y being the number of concepts of the set S because according to the conditional independence probability [20] $P\left( {\left. {\overline{{C_{u}^{{L_{u} }} \ldots C_{z}^{{L_{z} }} }} } \right|Q_{r} } \right) = P\left( {\left. {\overline{{C_{u}^{{L_{u} }} }} } \right|Q_{r} } \right) \ldots P\left( {\left. {\overline{{C_{z}^{{L_{z} }} }} } \right|Q_{r} } \right)$. The subscript r indicates an index of the question number. This can lead us to consider concepts in a dimension fairly.

• Careless mistake: Oppositely, in the event of known dependence concepts of a response, the response is incorrect. That is a “careless mistake”. If the response $Q_{r}$ to a question q_r is incorrect, the probability of knowing the dependence concept $S = \, \{ C_{u}^{{L_{u} }} \ldots C_{z}^{{L_{z} }} \}$, which has been asked by the question $q_{r}$. is $P\left( {C_{u}^{{L_{u} }} \ldots C_{z}^{{L_{z} }} \left| {\bar{Q}_{r} } \right.} \right) = m_{r}$ (called “careless mistake” probability), then probability of knowing the concept C_i $\in S$ $P\left( {C_{i}^{{L_{i} }} \left| {\bar{Q}_{r} } \right.} \right) = m_{r}^{{1/{\text{y}}}} \forall m_{r} \in \left[ {0, 1} \right)$.

In addition, there is a constraint between m_r and l_r as follows:

$$ l_{r}^{{\frac{1}{y}}} = P\left( {\bar{C}_{i}^{{L_{i} }} |Q_{r} } \right) = \frac{{P\left( {Q_{r} |\bar{C}_{i}^{{L_{i} }} } \right).P\left( {\bar{C}_{i}^{{L_{i} }} } \right)}}{{P\left( {Q_{r} } \right)}} = \frac{{\left[ {1 - P\left( {\bar{Q}_{r} |\bar{C}_{i}^{{L_{i} }} } \right)} \right].P\left( {\bar{C}_{i}^{{L_{i} }} } \right)}}{{P\left( {Q_{r} } \right)}} $$

$$ = \left[ {1 - \frac{{P\left( {\bar{C}_{i}^{{L_{i} }} |\bar{Q}_{r} } \right).P\left( {\bar{Q}_{r} } \right)}}{{P\left( {\bar{C}_{i}^{{L_{i} }} } \right)}}} \right]\frac{{P\left( {\bar{C}_{i}^{{L_{i} }} } \right)}}{{P\left( {Q_{r} } \right)}} = \frac{{P\left( {\bar{C}_{i}^{{L_{i} }} } \right) - P\left( {\bar{C}_{i}^{{L_{i} }} |\bar{Q}_{r} } \right).P\left( {\bar{Q}_{r} } \right)}}{{P\left( {Q_{r} } \right)}} $$

$$ = \frac{{P\left( {\bar{C}_{i}^{{L_{i} }} } \right) - \left[ {1 - P\left( {C_{i}^{{L_{i} }} |\bar{Q}_{r} } \right)} \right].P\left( {\bar{Q}_{r} } \right)}}{{P\left( {Q_{r} } \right)}} = \frac{{k - \left( {1 - m_{r}^{{\frac{1}{y}}} } \right)\left( {1 - a} \right)}}{a} $$

4.1 Problem Statement

Given a set of questions $q = \, \left\{ {q_{1} , \, q_{2} ,_{{}} q_{3} , \, \ldots \, q_{n} } \right\}$ with their corresponding evaluated answers $R_{j} = \, \left\{ {Q_{1} , \, Q_{2} ,_{{}} Q_{3} , \, \ldots \, Q_{n} } \right\}$. Let apriority probability $P\left( {C_{i}^{{L_{i} }} } \right)$ = k and $P\left( {Q_{r} } \right) = a$, evidence based probability $P\left( {C_{i}^{{L_{i} }} \left| {\overline{{C_{i - x}^{{L_{i} }} }} } \right.} \right) = u^{1/h}$. Our purpose is to find any $P(C_{i}^{{L_{i} }} |R_{j} )$ which is the conditional probability of knowing a concept $C_{i}^{{}}$ at a cognitive ability L_i with the observing set of responses R_j at a sense.

Next, we explain how a Bayesian based method calculated for learning assessment to solve the above problem.

4.2 Solution

This section explains how to build a formula to estimate probability of knowing pedagogical concepts of students [6, 21]. Intuitively, it is suggested Bayes’ Theorem [13] and Bayesian networks could be used to compute the probability of knowing a concept even though the concept is evaluated based on reflected evaluations of the concept. It could also be used to calculate the probability of knowing the concept even in the existence of complex connections between concepts in a concept space. Bayesian networks are a sort of probabilistic graphical model that uses Bayesian inference for probability calculations. Bayesian networks aim to model conditional dependence, and therefore causation, by representing conditional dependence by edges in a directed graph. Via these connections, we can competently carry out inference on the random variables in the graph through the use of factors. It is first useful for us to review probability theory before going into precisely what a Bayesian network is.

First, recall that the joint probability distribution of random variables $C_{1}^{{L_{1} }} , \ldots ,C_{n}^{{L_{n} }}$, denoted as $P(C_{1}^{{L_{1} }} , \ldots ,C_{n}^{{L_{n} }} )$, is equal to $P(C_{1}^{{L_{1} }} |C_{2}^{{L_{2} }} , \ldots ,C_{n}^{{L_{n} }} )\,*$ $P(C_{2}^{{L_{2} }} |C_{3}^{{L_{3} }} , \ldots ,C_{n}^{{L_{n} }} ) \, * \ldots \, *P(C_{n}^{{L_{n} }} )$ by the chain rule of probability [15]. We can consider this a factorized representation of the distribution, since it is a product of n factors that are localized probabilities.

$$ P\left( {\bigcap\nolimits_{k = 1}^{n} {C_{k}^{{L_{k} }} } } \right) = \prod\nolimits_{k = 1}^{n} {P(C_{k}^{{L_{k} }} \bigcap\nolimits_{i = 1}^{k - 1} {|C_{i}^{{L_{i} }} )} } $$

(4.1)

Next, remember that conditional independence [20]  between two random variables, A and B, given another random variable, C, is equivalent to satisfying the following property: $P\left( {A,B|C} \right) \, = P\left( {A|C} \right) \, *\,P\left( {B|C} \right)$. That is to say, as long as the value of C is known and fixed, A and B are independent. Another way of stating this is that $P\left( {A|B,C} \right) \, = P\left( {A|C} \right)$. If n random variables $A_{1} , \, A_{2} , \, \ldots , \, A_{n}$ are independent, then

$$ P\left( {\bigcap\nolimits_{k = 1}^{n} {A_{k} |C} } \right) = \prod\nolimits_{k = 1}^{n} {P(A_{k} |C} ) $$

(4.2)

At that point, we describe a Bayesian network as follows:

A Bayesian network is a directed acyclic graph [14]  in which each edge corresponds to a conditional dependency, and each node corresponds to a unique random variable as shown in the Fig. 3. In a Bayesian networks, a node is conditionally independent of its non-descendants given its parents. Its parents are incoming nodes linking to the node. In the above example in the Fig. 4, $P\left( {C_{3} |C_{1} ,C_{4} } \right)$ is equal to $P\left( {C_{3} |C_{1} } \right)$ since C₃ is conditionally independent of its non-descendant, C₄, given its parents C₁. This property allows us to simplify the joint distribution, obtained in the previous section using the chain rule, to a smaller form. After simplification, the joint distribution for a Bayesian network is equal to the product of P(node|Parents (node)) for all nodes, stated below:

$$ P\left( {C_{1}^{{L_{1} }} \ldots C_{n}^{{L_{n} }} } \right) = \prod\nolimits_{i = 1}^{n} {P\left( {C_{i}^{{L_{i} }} |C_{1}^{{L_{1} }} , \ldots ,C_{i - 1}^{{L_{i - 1} }} } \right)} = \prod\nolimits_{i = 1}^{n} P \left( {C_{i}^{{L_{i} }} |Parents\left( {C_{i}^{{L_{i} }} } \right)} \right) $$

(4.3)

where Parents($C_{i}^{{L_{i} }}$) is a set of concepts connecting directly to the node $C_{i}^{{L_{i} }}$ then

$$ P(C_{1}^{{L_{1} }} \ldots C_{n}^{{L_{n} }} |R_{j} ) = \prod\nolimits_{i = 1}^{n} {P\left( {C_{i}^{{L_{i} }} |R_{j} .Parents\left( {C_{i}^{{L_{i} }} } \right)} \right)} $$

(4.4)

In a larger concept graph, this property lets us significantly decrease the amount of required computation, since generally, most nodes will have few parents relative to the overall size of the graph. In order to calculate $P(C_{i}^{{L_{i} }} |R_{j} )$, we must marginalize the joint probability distribution over the variables that do not appear in $C = \{ C_{1}^{{L_{1} }} , \ldots ,C_{n}^{{L_{n} }} )$. Therefore,

$$ P(C_{k}^{{L_{k} }} |R_{j} ) = \sum\nolimits_{{dom\left( {C_{n}^{{L_{n} }} } \right)}} { \ldots \sum\nolimits_{{dom\left( {C_{i}^{{L_{i} }} } \right)}} {P(C_{k}^{{L_{k} }} C_{i}^{{L_{i} }} \ldots C_{n}^{{L_{n} }} |R_{j} )} } $$

(4.5)

where dom is a domain consisting of all possible value of the concepts $C_{i}^{{L_{i} }} , \ldots ,C_{n}^{{L_{n} }} .$.

From (4.4), (4.5), we can calculate the probability of knowing a concept C_k given knowing the response R_j based on the relations of all concepts as follows:

$$ P(C_{k}^{{L_{k} }} |R_{j} ) = \sum\nolimits_{{dom\left( {C_{n}^{{L_{n} }} } \right) \ldots }} {\sum\nolimits_{{dom\left( {C_{i}^{{L_{i} }} } \right)}} {\prod\nolimits_{i = k}^{n} {P\left( {C_{i}^{{L_{i} }} |R_{j} .Parents\left( {C_{i}^{{L_{i} }} } \right)} \right)} } } $$

(4.6)

5 Implementation and Validation

5.1 Experiment Overview

We organize an experiment to validate the pedagogical knowledge unit concept states proposed in the assessment. With the intention of proving the efficient estimation of our proposal in a concept space, we have conducted an experiment while considering relationships between concepts at multiple cognitive ability levels at a sense, dependency of “Lucky guess” and “careless mistake” as well as fairly considered pedagogical concepts in a CAL dimension according to the formula (4.6). In this experiment, an assessment includes a set of questions. The questions are designed to test students’ knowledge related to thinkable concept sets at cognitive ability level. Instructors prepare any questions, which specifies skill levels of concepts. There are two types of questions: Implicit Questions and Direct Questions. The Implicit Question (IQ) is prepared by instructors to implicitly test ability levels of students while the Direct Question (DQ) is used to directly test ability levels of students. When IQ is examined, we can determine which ability level was included in that IQ. Consequently, for each detected concept Ci at a certain cognitive ability level, either CA set or DA set, DQ are planned for directly verifying the matching of related skills between OQ and DQ based on the relation within the sets of concept states CA, DA. If a student answers a question correctly, we can conclude that he/she has known concepts required to answer the question.

Fig. 4.

Input CAL graph

The simulations are developed on Java with jdk-8u161, Eclipse Jee 2019-06. In our experiment at this current step, number of concepts increase from 5 to 30. All parameters are reflected in Table 2. A particular CAL graph input is in the Fig. 4.

Table 2. Parameter table

5.2 Validation Test and Analysis Results

The following figures show the measured results of the experimentation. It is understandable to see that there are some changes between the simulated results. This is chiefly caused by the partial order instability combination of the input questions.

The Fig. 5, 6, 7, 8, 9 provides a summary of the conditional probability values of knowing the concept $C_{i}^{{}}$ at a cognitive ability L_i given the observing set of responses R_j of students. Let $\alpha \left( {R_{j} } \right), \alpha \left( {R_{t} } \right)$ be the number of correct answers in responses $R_{j} = \{ \bar{Q}_{1} , \, Q_{2} ,Q_{3} , \, \ldots \, Q_{n} \} ,$ $R_{t} = \left\{ {\bar{Q}_{1} , \bar{Q}_{1} , Q_{3} , \ldots , Qn} \right\}$, respectively. Intuitively, if $\alpha \left( {R_{j} } \right) \ge \alpha \left( {R_{t} } \right)$ then $P\left( {C_{k}^{{L_{k} }} |R_{j} } \right) \ge P\left( {C_{k}^{{L_{k} }} |R_{t} } \right)$. This is still correct for our particular cases whose results presented in the Fig. 5, 6, 7, 8, 9. The Figures indicates that $P(C_{i}^{{L_{i} }} |R_{1} ) > = P(C_{i}^{{L_{i} }} |R_{2} )$, $P(C_{i}^{{L_{i} }} |R_{1} ) > = P(C_{i}^{{L_{i} }} |R_{3} )$ and $P(C_{i}^{{L_{i} }} |R_{2} ) > = P(C_{i}^{{L_{i} }} |R_{4} )$, $P(C_{i}^{{L_{i} }} |R_{3} ) > = P(C_{i}^{{L_{i} }} |R_{4} )$ with $R_{ 1} = Q_{ 1} Q_{ 2} ,R_{ 2} = \bar{Q}_{1}$, $Q_{ 2} ,R_{ 3} = Q_{ 1,} \,\bar{Q}_{2} ,R_{ 4} = \bar{Q}_{1}$, $\bar{Q}_{2}$. This means the more accuracy response at cognitive ability levels, the higher probability of knowing the concepts students can get. Probabilities $P(C_{2}^{{L_{i} }} |R_{i} ) > = P(C_{1}^{{L_{i} }} |R_{i} )$ and $P(C_{4}^{{L_{i} }} |R_{i} ) > = P(C_{3}^{{L_{i} }} |R_{i} )$ in the Fig. 5, 6, 7, 8, 9 are because $C_{2}^{{L_{i} }} ,C_{4}^{{L_{i} }}$ have more related incoming evidences than $C_{1}^{{L_{i} }} ,C_{3}^{{L_{i} }}$.

Fig. 5.

Concept probabilities with Q₁, Q₂ combination

Fig. 6.

Concept probabilities with $\bar{Q}_{1}$, Q₂ combination

Fig. 7.

Concept probabilities with Q₁, $\bar{Q}_{2}$ combination

Fig. 8.

Concept probabilities with $\bar{Q}_{1}$, $\bar{Q}_{2}$ combination

Fig. 9.

Concept probabilities at different Bloom levels

Fig. 10.

Concept probabilities at different Bloom levels

In addition, the graph in the Fig. 5, which shows probabilities of knowing concepts given a Q1, Q2 combination evidence at six Bloom levels, displays variety of students’ knowledge while the Fig. 10 illustrates how deep students’ knowledge is at different Bloom levels. According to this, an instructor can decide whether he/she needs to teach concepts again or not. The instructor can clearly build questions that assess precise expertise of students. If majority of students find it tough to understand the concept, then the instructor can take on another instruction style and the institution can offer support for the teacher.

6 Conclusion

This paper proposed a Bayesian network based technique to estimate probabilities of knowing concepts at different Bloom levels given responses of students to evaluate students’ knowledge. The composition graph of the method can also make simpler building questions that measure precise skills of students. Besides, the proposed method can maximize the quality of estimations of students’ knowledge by giving students feedbacks on strong points and weaknesses, along with advising instructors to design appropriate assessments that accurately measure the required skills of students to achieve course goals. Moreover, we conducted simulations to evaluate our approach. Through the implementation, it has been seen that our solution is usable and efficient to measure an assessment properly. Hereafter, we will spread out our approach in diverse environments to achieve higher trustworthiness and better performance.